Keywords

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Introduction

The equatorial region is a hot spot of variability and host to many small to decadal scale atmospheric disturbances and myriad oceanic processes, the understanding of which remains nascent. It has been widely accepted that the Indian Summer Monsoon (ISM) is an intense phenomena, which affects the livelihoods of more than a billion people in the Indian Ocean rim nations (Gadgil 2003). Therefore, for a tropical climate like that of India, the understanding of atmosphere and ocean dynamics at mesoscale and submesoscale play an important role in monsoon prediction. The influence of the surface energy fluxes are important for understanding the wind patterns, temperature variations, and turbulence profiles over a region, the understanding of which has crucial implications for ISM (Mahadevan et al. 2016). This is because the surface energy balance is directly related to air–sea interactions, height of the atmospheric boundary layer, and the thermal stratification, which in combination are key parameters controlling the sea surface temperature, turbulence, wind profiles, updrafts and downdrafts, and cloud dynamics. Although circulation models incorporate the influence of surface energy and fluxes, the fundamental understanding of mesoscale and submesoscale processes on the ocean and atmosphere dynamics is lacking. In general, the synoptical scale processes are well parameterized in the global models. However, the synoptic scale processes have a strong correlation with the regional scale processes, which are dynamically difficult to model. For example, in both atmosphere and ocean, wind shear and fluid stratification coexist, widely referred to as shear-stratified flows (examples include forced convective plumes and gravity currents) (Thorpe 1969). In these flows, a range of process scales exists (mesoscale and submesoscale), the modeling of which would provide a good basis for improving the crude parameterization during periods of weak and strong stratifications. Additionally, the presence of orography and the forcing induced due to it creates a multitude of time-dependent submesoscale phenomena that contribute to the variability in the weather and climate. Therefore, the process modeling approach proposed in this study would help in improving the understanding at mesoscale and submesoscale levels and provide useful insights into improving the parameterizations used in weather and climate modeling.

2 Forced Plumes and Gravity Currents: A Brief Overview

Forced plumes and gravity currents are two variants of shear-stratified flows that are common occurrences in many geophysical situations. A few examples include hydrothermal vents and oil spills in ocean, rising ash plume from the volcanic eruptions, katabatic wind flows, ocean overflows, and dense water discharges. These flows occur whenever a constant source of buoyancy creates a motion of fluid away from the source. Typically, a forced plume is an initial momentum-dominated flow that has a nonzero density difference between medium and the surrounding ambient fluid, and at some distance becomes dominated by buoyancy (Mirajkar et al. 2015). In most situations, the ambient is in a linear stably stratified state such that the density gradient \(\frac{d\rho }{dz}<0\). The low density plume (\(\rho _{p}\)) fluid intrudes vertically into the linearly stratified ambient leading to complex flow dynamics. An important parameter governing the evolution, growth, and mixing dynamics of a plume is the stratification strength that is characterized by the buoyancy frequency, \(N^{2}=-\frac{g d\rho }{\rho _{0}dz}\), where g is the gravity and \(\rho _{0}\) is some reference fluid density (generally taken as the ambient density at the source). A forced plume interacting with a stably stratified environment behaves differently compared to a uniform environment, since the mixing near the source diminishes the momentum and buoyancy, thereby rendering the plume to reach a spreading height (\(Z_{s}\)) and spread radially outwards. The intrusion process governs the radial propagation (\(R_{f}\)) of the plume. Past studies on forced plume focussed on scaling arguments and variability of the bulk parameters such as \(Z_{m}\) and \(R_{f}\) and their behaviour with changing buoyancy frequency, \(N^{2}\) (see Turner 1986; Papanicolaou and Stamoulis 2010; Mirajkar and Balasubramanian 2017 and references therein). Using scaling arguments, Hunt and Kaye (2005) suggested that based on the balance of source momentum flux (\(M_0\)), buoyancy flux (\(B_0\)), and volume flux (\(Q_{0}\)) at the plume source, different flow regimes for a single-phase plume could be defined using a parameter \(\varGamma _{0}=\frac{5Q_{0}^{2}B_{0}}{4\alpha M_{0}^{5/2}}\), where \(\alpha \) is the entrainment coefficient that takes a constant value of \(\alpha =0.08\) for plume-like flows (Turner 1986). Balancing the fluxes at the source, the classifications are as follows: lazy plume (\(\varGamma _{0}>1\)), pure plume (\(\varGamma _{0}=1\)), and forced plume (\(\varGamma _{0}<1\)). Pioneer research on this topic was first done by Morton et al. (1956) to measure the spreading height, \(Z_s\), for the forced plume in the stratified flow using the source conditions and the buoyancy frequency (\(N^2\)).

$$\begin{aligned} B_{0} = g \left( \frac{{\rho _p - \rho _{0}}}{\rho _{0}} \right) Q_{0} = g^{'}Q_{0} \end{aligned}$$
(1)
$$\begin{aligned} M_{0}=Q_{0}U \end{aligned}$$
(2)
$$\begin{aligned} Q_{0}=\frac{1}{4} \pi D^{2} U \end{aligned}$$
(3)

Here, U is the mean plume velocity, and D is the diameter of the plume. Based on self-similarity arguments, a theoretical formula for \(Z_{s}\) was proposed by Morton et al. (1956) as follows,

$$\begin{aligned} Z_{m}=2.8\alpha ^{-0.5}B_{0}^{0.25}N^{-0.75} \end{aligned}$$
(4)

The theory by Morton et al. (1956) works well for large-scale flow parameters, but fails to predict the mesoscale and submesoscale plume characteristics (such as turbulent kinetic energy, local momentum and buoyancy fluxes, viscous dissipation, and mixing efficiency). Following the seminal work of Morton et al. (1956), other researchers have also studied the plume dynamics in a stably stratified environment, where the results were extended for fountains, lazy plumes, along with characterisation of bulk quantities and plume entrainment dynamics (see Bloomfield and Kerr 1998; Hunt and Kaye 2005; Devenish et al. 2010; Kaye 2008; Papanicolaou et al. 2008; Papanicolaou and Stamoulis 2010 and references therein). Recently, experiments on forced plume in linear stratification for a varying range of \(N^{2}\) were performed to study the intrusions from buoyancy-dominated as well as momentum-dominated source conditions (Richards et al. 2014), Mirajkar and Balasubramanian (2017). However, the results were limited to the characterization of radial propagation of plume, \(R_{f}\), plume thickness, \(t_{p}\), and plume spreading height, \(Z_{s}\). None of the previous studies on forced plume have focused on turbulence and mixing characterization using the kinetic energy budget, which is needed for a better understanding of the mesoscale and submesoscale flow physics. The governing parameter for a forced plume is the bulk Richardson number, given as \(Ri_{b}=\frac{g^{'}D}{U^{2}}\).

A gravity current is driven by horizontal pressure gradients arising due to density variations between the denser fluid (\(\rho _{1}\)) and the lighter fluid (\(\rho _{2}\)) (Ellison and Turner 1959). The important parameters determining gravity currents propagation are the density difference between the two fluids (\(\Delta \rho =\rho _{1}-\rho _{2}\)), gravity (g), the depth of the gravity current (h), total depth of the fluid layer (H), and the slope of the terrain (\(\alpha \)) (Balasubramanian et al. 2015). For a gravity current, the active regions of gravity currents have been well established (Simpson 1982; Simpson and Britter 1979). The interface between two fluids close to the head of a gravity current is a typical frontal zone, that is, a region in which, notwithstanding intense mixing, a high density gradient is present. The frontal zone is immediately followed by the head, which has some fractional depth of the initial height, H, depending on the nature of the gravity current. The head of the current is the region where the fractional depth is \(\ge \frac{H}{3}\). The scaling for velocity and depth of two counterflowing gravity currents, produced by lock-exchange, has been well understood (Simpson 1982; Shin et al. 2004; Cantero et al. 2007). For the Boussinesq case, Yih (1965) proposed that the depths of two currents are equal in height, \(h=\frac{H}{2}\), along their entire lengths. The speed of both gravity currents are the same and have the value proposed by Benjamin (1968) for energy-conserving gravity currents. Klemp et al. (1994) argued, based on shallow-water theory that idealized energy-conserving gravity currents cannot be realized in a lock-exchange initial-value configuration, as the speed of this current would be faster than the fastest characteristic speed in the channel predicted by the shallow-water theory. Extensive measurements show that, on a horizontal surface, the mean velocity of the current is given by U = 1.05\(\sqrt{g^{'}h}\), where \(g^{'}=\frac{\rho _{1}-\rho _{2}}{\rho _{1}}\) is the reduced gravity, and h is the depth of the steady current (Benjamin 1968). These results were mainly obtained from flows occupying about 1/5 of the total depth H, but recent work with lock-exchange flows has shown that U is sensitive to changes in the value of \(\frac{h}{H}\) in the range 1/3–1/10 H as proposed by Simpson and Britter (1979). They argue that the inviscid gravity current depth can never be greater than 0.35H, wherein according to Benjamin’s theory (Benjamin 1968), the gravity current has its fastest speed. Therefore, Benjamin’s theory for energy-conserving gravity currents is widely accepted, and the velocity and depth of a gravity current are given as,

$$\begin{aligned} U=0.4\sqrt{g^{'}H}, \quad h=\frac{H}{2} \end{aligned}$$
(5)

Most previous studies have focussed on the dynamics of the head, turbulence dissipation and mixing, as well as scaling for the front velocity and fractional depth. The gravity current entrainment as a function of bulk Richardson number, \(Ri_{b}\) was quantified by Ellison and Turner (1959). In their configuration, the bulk Richardson number was variable, since the inertial and buoyancy forces were decoupled. In the present case, however, the governing parameters are \(g^{'}\) and H, and in view of Eq. (5) the bulk Richardson number is a constant (\(\approx \)1). For the configuration of gravity currents considered in our study, the only possible variable is the Reynolds number \(Re=\frac{Uh}{\nu }=\frac{UH}{2\nu }\) (Simpson and Britter 1979), which has been consistently used for lock-exchange flows (Shin et al. 2004; Cantero et al. 2007). Similar to the case of a forced plume, none of the previous studies on gravity current have focused on turbulence and mixing characterization near the head of the current using the kinetic energy budget, which is needed for a better understanding of the mesoscale and submesoscale flow physics. Based on this gap, we formulate the problem statement for this communication.

3 Problem Statement

As established from the literature review, most studies have primarily focussed on the bulk characteristics of a forced plume and gravity currents, but not the turbulence and mixing dynamics. The mixing across density interface is a frequent phenomenon in geophysical and engineering flows and there is extensive interest on understanding the turbulent mixing in flows with stable density stratification. For example, the surface wind and temperature advection between ocean and atmosphere drive the upper mixing layer of ocean into stably stratified oceanic pycnocline and this process is important to the dispersion of pollutants. Different to the commonly stable stratification in oceanic flows, the density (or temperature) stratification along gravity direction in the atmospheric boundary layer changes periodically, leading to fundamental differences in the mixing process, where the governing mechanisms are different. The turbulent kinetic energy, shear production flux, buoyancy flux, and viscous dissipation give the local nature of the flow. One key interest is on quantifying the mixing efficiency, which has been studied by in-situ field measurements. The laboratory-based measurements in mixing efficiency is very limited, which prohibits the quantitative characterization of turbulent mixing in density stratified geophysical flows. Accurate quantification of both momentum and scalar diffusivities is imperative given their importance for many practical applications such as air quality prediction, nutrient transport in water bodies and ocean circulation. It is a common practice to quantify turbulent mixing in such flows using a turbulent (eddy) viscosity \(K_{t}\) for momentum and a turbulent (eddy) diffusivity \(K_{\rho }\) for density, which are based on the gradient-diffusion hypothesis (Pope 2000). For a unidirectional shear flow, the momentum eddy diffusivity, \(K_{t}\), and scalar eddy diffusivity, \(K_{\rho }\), are defined as

$$\begin{aligned} K_{t}=-\frac{\overline{u^{'}v^{'}}}{\frac{\partial \overline{U}}{\partial z}} \end{aligned}$$
(6)
$$\begin{aligned} K_{\rho }=-\frac{\overline{\rho ^{'}v^{'}}}{\frac{\partial \overline{\rho }}{\partial z}} \end{aligned}$$
(7)

In order to characterize turbulence in stratified flows, it is important to understand the evolution of turbulent kinetic energy (TKE). The transport equation of turbulent kinetic energy in stratified flows, \(K=\frac{1}{2}\overline{u_{i}^{'}u_{i}^{'}}\) is (Pope 2000):

$$\begin{aligned} \frac{\partial K}{\partial t}+U_{j}\frac{\partial K}{\partial x_{j}}+Tr=P-B-\varepsilon \end{aligned}$$
(8)

Here, Tr is the transport term given as (\(\frac{1}{\rho _{0}}\frac{\partial \overline{u_{i}^{'}p^{'}}}{\partial x_{i}}+\frac{\partial \overline{u_{j}^{'}u_{j}^{'}u_{i}^{'}}}{\partial x_{i}}-\nu \frac{\partial ^{2}K}{\partial x_{j}^{2}})\), \(P=-\overline{u_{i}^{'}u_{j}^{'}}\frac{\partial U_{i}}{\partial x_{j}}\) is the shear production, \(B=\frac{g}{\rho _{0}}\overline{\rho ^{'}u_{i}^{'}}\) is the buoyancy flux and \(\varepsilon =2\nu e_{ij}e_{ij}\), where \(e_{ij}=\frac{1}{2}(\frac{\partial u^{'}_{i}}{\partial x_{j}}+\frac{\partial u^{'}_{j}}{\partial x_{i}})\), is the dissipation of energy due to viscous effects. The term \(\overline{u_{i}^{'}u_{j}^{'}}\) is the Reynolds stress term, which gives the correlation between the stream-wise and transverse fluctuating velocity components. Major inherent assumptions while using the transport equation for K are that the turbulent flow is statistically stationary and homogeneous. These assumptions are used to simplify the energetics of the turbulent flow field. Under these assumptions, the left-hand side terms of Eq. (8) vanishes, giving a simple balance that yields \(P-B-\varepsilon =0\). Consider, for instance, the model proposed by Osborn (1980) where (under stationary and homogeneous assumptions), the turbulent kinetic energy (TKE) equation can be simplified to obtain the diapycnal diffusivity of density as

$$\begin{aligned} K_{\rho }=\frac{{Ri}_{f}}{1-{Ri}_{f}}\frac{\varepsilon }{N^{2}} = \varGamma \frac{\varepsilon }{N^{2}} \end{aligned}$$
(9)
$$\begin{aligned} K_{t}=\frac{1}{1-{Ri}_{f}}\frac{\varepsilon }{S^{2}} \end{aligned}$$
(10)

where \(\varGamma \) is known as the mixing efficiency of the flow, and \(S=\frac{\partial U}{\partial z}\) is the mean velocity shear present in the flow. Varying definitions of calculating flux Richardson number, \({Ri}_{f}\), has been defined by past researchers (see Osborn 1980; Venayagamoorthy and Koseff 2016) to measure the amount of TKE that is irreversibly converted to potential energy. The most common definition, under the assumption of stationary and homogeneous flow is as follows,

$$\begin{aligned} {Ri}_{f}=\frac{B}{B+\varepsilon } \end{aligned}$$
(11)

A value of \({Ri}_{f} = 0.2\) was proposed by Osborn based on experiments by Britter (1974), but it is unclear if this value holds good for all genres of shear-stratified flows. Given the fact that the inherent assumptions of statistical stationarity and homogeneity are not always applicable in practice, be it in direct numerical simulations (DNS) or observational studies of geophysical flows, Ivey and Imberger (1991) proposed an alternative definition of \({Ri}_{f}\) (denoted by \({Ri}_{f}^{II}\)) as

$$\begin{aligned} {Ri}_{f}^{II}=\frac{B}{B+m} \end{aligned}$$
(12)

where m accounts for contributions from all the terms in Eq. (8). This definition is free from the assumption that turbulence is stationary and homogeneous and hence is a better representation of the flux Richardson number (\({Ri}_{f}\)). Venayagamoorthy and Koseff (2016) recently showed that the above definition of \({Ri}_{f}\) (Eq. 11) suffers from the effects of counter-gradient fluxes that are common in strongly stratified flows. They proposed another definition based on available potential energy and total dissipation rate. However, to understand the flow energetics, in the present study we stick to the first definition of \({Ri}_{f}\) given by Eq. (11).

In order to understand the dynamics of shear-stratified flow (such as a forced plume and gravity currents) at local scales, we need to accurately measure the turbulence quantities such as TKE, Reynolds stresses, production flux (P), buoyancy flux (B), dissipation (\(\varepsilon \)), flux Richardson number (\({Ri}_{f}\)), and mixing efficiency (\(\varGamma \)). Experimentally, this is possible only using simultaneous measurements of velocity and density fields, which is the focus of this present work. Detailed experimental investigations are imminently needed to obtain understanding of the mixing mechanisms for modeling stratified flows, e.g., in the atmospheric boundary layer and the global thermohaline circulation, in particular, to quantify the mixing efficiency and entrainment rate under different stratification and turbulent levels. For measurements of velocity and density fields, we employ particle image velocimetry (PIV) and planar laser-induced fluorescence (PLIF) techniques, respectively. Briefly, Webster et al. (2001) developed simultaneous measurements of the velocity and concentration field using digital particle image velocimetry (DPIV) and planar laser-induced fluorescence (PLIF) for a turbulent jet in the uniform medium to measure the mean velocity, turbulent stresses, mean concentration variance. The results for the stratified case, obtained using DPIV, showed that the mean centreline velocity decreases much more rapidly than the unstratified case, where Reynolds stress profiles never reached a self-similar state, indicating that stratification changes both the overall turbulence characteristics and mixing. Recently, Duo and Chen (2012) observed a horizontal dense jet injected into a lighter stratified solution using combined particle image velocimetry and planar laser-induced fluorescence. They studied flow structure and mixing dynamics of the dense jet in the lighter solution. From the literature, it is clear that simultaneous measurements of velocity and density, using PIV–PLIF technique, for a forced plume and gravity current have not been carried. Below, we will briefly talk about the methodology, followed by results and discussions.

4 Methods

4.1 Experimental Modeling

Due to the complexity involved in measurement of turbulence statistics and related mixing parameter in field observations, it is prudent to study the dynamics of forced plumes and gravity currents using an experimental analogue of the particular geophysical process. By accounting for the unboundedness of the ocean and atmosphere (i.e., shallow-water approximation) through appropriate non-dimensionalization, we gather the rich flow physics embedded in these flows through measurement of various mean and fluctuating quantities. Below, details of the experimental setup along with the important non-dimensional number for each configuration is given.

Fig. 1
figure 1

a Schematic of the experimental setup for a forced plume. (1) Reservoir tank (T1), (2) Centrifugal pump, (3, 5, 12) Control valve, (4) Flow meter, (6) Non-return value, (7) Jet nozzle, (8) Stratification tank (T2), (9) Perforated wooden plate, (10) Salt water bucket, (11) Fresh water bucket, (13) Fluid mixer. (a1) Image of a forced plume with representation of bulk parameters. Note Both (a) and a(1) reproduced with permission from ASCE. b Schematic of experimental setup for a gravity current. (b1). Image of a gravity current at two different instances, (top) at a time instant t, (bottom) at a time instant \(t+\Delta t\). Contours represent density. In both the experimental settings, horizontal is the stream-wise coordinate, x, and normal is the vertical coordinate, z

Full size image

4.2 Experiments on Forced Plume

The experiments were carried out in a tank facility, whose configuration is illustrated in Fig. 1a. The tank T2 is made of plexiglas, measuring 91 cm long by 91 cm wide by 60 cm high. The second tank (T1), a 60 cm cubical tank, was used as the reservoir for storing the jet fluid. The density of the plume fluid \(\rho _p= 998\) kg/m\(^{3}\) was kept constant in all the experiments. The tank (T2) was linearly stratified using the double bucket technique as discussed in Oster and Yamamoto (1963), Mirajkar and Balasubramanian (2017). The strength of the stratification was maintained at \(N= 0.2\) s\(^{-1}\). A portable densitometer (AntonPaarDMA35) was used to check the density in the two buckets. Density profile in the stratified tank was checked by collecting the samples at every intervals in the experimental tank to ensure the density profile is linear. A centrifugal pump was used to discharge the jet fluid into the ambient linearly stratified environment using a round jet nozzle fixed at the bottom of tank (T2). The jet nozzle was 160 mm in length with diameter \(D = 12.7\) mm. It was made of aluminum and comprised of a diffuser, settling chamber, and a contraction section. A honeycomb was placed in the settling chamber to reduce the flow fluctuations and to generate a stable flow at the nozzle exit. The exit vertical velocity at the nozzle was maintained constant at \(U = 17\) cm/s, thereby giving a jet Reynolds number \(Re= 2400\), and the initial bulk Richardson number was, \({Ri}_{b}=0.008\). A linear stable stratification with salt–water–ethanol mixture was obtained in T2, such that heavy fluid settles at the bottom and lighter fluid on the top. Once the fluid is filled into tank T2 using the two-bucket technique, it is allowed to stabilize for approximately 2 h to achieve stable uniform linear stratification with height. Upon achieving a stable stratification, the forced plume was injected and the local flow dynamics were captured to understand the flow physics. An experimental image of a forced plume with bulk parameter is shown in Fig. 1a1.

4.3 Experiments on Gravity Current

The experiments on gravity currents were conducted in a plexiglass tank equipped with a lock-exchange mechanism. The tank dimensions were 175 cm long, 15 cm wide, and 30 cm high. A schematic of the apparatus is shown in Fig. 1b. The tank was separated into two parts by a lock gate located at 30 cm from right end. The dense fluid \(\rho _{2}\) in the right slot occupies a predetermined depth H before the gate is released. The dense solution is prepared by adding requisite amount of NaCl to water and mixing it to get a uniform density fluid. The rest of the tank is filled with lighter ambient fluid, \(\rho _{1}\), to the same depth H, which is separated by the gate. Upon removing the gate instantly, a gravity current is initiated due the difference in the hydrostatic pressure between the two fluids. The quick motion of the gate ensures that perturbations due to gate opening are extremely small, and no relative fluid motion is generated in the direction of the pull. Thus, there are is no secondary flows or disturbances due to the gate release. The denser gravity current undercuts the lighter fluid, which flows in the opposite direction. The measurement section is located at the middle of the tank.

Two different Reynolds numbers were used for the present study, namely \(Re=3090\) and \(Re=9950\), which covers flow transitioning from weak to strong mixing. The dense and light fluid were created using salt solution and an aqueous solution of ethanol, respectively. This salt–ethanol technique was introduced to match the refractive indices accurately, enabling the use of optical measurement techniques. This method ensured that the images quality is high, which allows accurate measurements. A densitometer (make: Mettle Toledo Densito 30PX) and a refractometer (make: Leica handheld analog refractometer) were used to match the refractive indices and measure the density of the two fluid. Details of the method of matching the refractive indices using salt and alcohol are given in Duo and Chen (2012), Daviero et al. (2001). Two different intensities of gravity currents (represented by Re values) were generated to understand the flow physics of such a dense current propagating in ambient lighter medium. Contour image of a propagating gravity current is shown in Fig. 1b1.

4.4 Imaging Technique

A combination of Particle Image Velocimetry (PIV) and Planar Laser-Induced Fluorescence (PLIF) is used for simultaneous velocity and density measurements as illustrated above in Fig. 1. Before the experiments, the refractive indices of the different fluids in use were matched as explained in the Daviero et al. (2001) and Mirajkar and Balasubramanian (2016). In the present work, the density and the refractive indices were measured using a densitometer and a refractometer (make: AntonPaar). A dual-head Nd:YAG pulse laser (532 nm, maximum intensity 145 mJ/pulse) was used for both PIV illumination and PLIF excitation. Through PIV optics, the laser beam is expanded into a 1-mm thick laser sheet illuminating the sample area in the x-z plane along the centre line of the tank. The fluid was uniformly seeded with polyamide tracer particles (median diameter 50 \(\upmu \)m, and specific gravity \(\rho _{sg}=1.1\)) for PIV measurement. For the PLIF measurement, Rhodamine 6G dye was uniformly mixed to the plume and the gravity current fluid in order for measurement of density. The dye fluoresces at 532 nm and gives an excitation signal at 560 nm. In order to implement the simultaneous PIV/PLIF measurement, the camera lens, PIV filter, PLIF filter, and two cameras are mounted in an optical housing as shown in Fig. 1. The PIV filter (bandpass, 530 nm) blocks most of the fluorescence and passes scattered light from PIV seeding particles. The PLIF filter (high pass in wavelength with cut-off 550 nm) blocks the scattered light and only passes the fluorescence signal. The time delay between the two pulses was set in millisecond. An image acquisition and laser control system synchronized the measurements with a sampling rate of 10 Hz. A two-step processing is applied: \(64\,\times \,64\) pixels interrogation window and 50% overlap for the first step, and \(32\,\times \,32\) pixels interrogation window and 50% overlap for the second step. The raw images obtained from PLIF camera were de-warped and then processed using an in-house algorithm to get the density field.

For experiments of forced plume, we observed that intensity of the background image and density was found behave approximately as a linear function. Based on the linear function, the following equation was used to convert intensity to density. The laser light variation was considered while doing this transformation. The final form of the density formula is

$$\begin{aligned} \rho =\rho _{p}-\frac{I}{I_{1}(z,t))}\left[ \rho _{p}- \rho _{0}(z,t)\right] \end{aligned}$$
(13)

where \(\rho _{p}\) is the density of the plume fluid. I is the intensity of the evolving plume and \(I_{1}(z,t)\) is the intensity of the background medium, which also takes care of the laser intensity absorption factor in the medium. \(\rho _{0}{(z,t)}\) is the density of the background image.

For experiments on gravity current, the local R6G concentration can be found from the local gray value, and the local R6G concentration has a linear relationship with the local density (Balasubramanian and Zhong 2018). When the dense fluid (Volume V and density \(\rho _{2}\)) and a lighter fluid (Volume eV and density \(\rho _{1}\), R6G concentration \(C_{1}\)) are mixed uniformly, the density and the R6G concentration of the mixture are:

$$\begin{aligned} \rho =\frac{\rho _{1}eV+\rho _{2}V}{eV+V}=\frac{\rho _{1}e+\rho _{2}}{e+1}\\ C=\frac{C_{1}eV}{eV+V}=\frac{eC_{1}}{e+1} \end{aligned}$$

Thus, if the local R6G concentration C is known, the local density can be found using:

$$\begin{aligned} \rho =\rho _{2}-\frac{C}{C_{1}}(\rho _{2}-\rho _{1}) \end{aligned}$$
(14)

As seen from this equation, if the local concentration, C equals the known concentration of the lighter fluid, \(C_{1}\), then the local density is same as that of the lighter fluid. This is the initial state, when both the fluids are separated by the gate. Upon the release of the gate, entrainment occurs causing change in the local density.

5 Results and Discussion

The simultaneous velocity and density measurements help in characterization of the turbulence and mixing in shear-stratified flows. Below, we independently discuss the results for the two different cases, namely a forced plume and a gravity current.

5.1 Dynamics of a Forced Plume

The energetics of an evolving forced plume were captured from the source of the plume (\(\frac{z}{D}=0\)) to a finite vertical distance such that \(\frac{z}{D}=15\). This finite height corresponds to the fluid layer below the spreading height, \(Z_{s}\) of the plume. The results presented here correspond to the dynamics of moderate stratification strength (\(N=0.2\) s\(^{-1}\)). Turbulent kinetic energy, K, is one of the most important statistics in stratified flows, which shows the turbulence distribution in the flow. For 2-D flows, this parameter is given as \(K=\frac{1}{2}[\overline{u^{'2}} + \overline{v^{'2}}]\). The turbulent kinetic energy profile evolution for the plume was recorded at three different downstream locations \(\frac{z}{D} = 4, 8\), and 12. The normalized turbulent kinetic energy was plotted with the normalized radial coordinate and is shown in Fig. 2a. It is seen that for lower \(\frac{z}{D}\) values, i.e., close to the source region, the turbulence kinetic energy is very high and it gradually decreases with increasing \(\frac{z}{D}\) values. Such a behavior is expected since the forced plume is losing momentum due to the entrainment between the plume and ambient fluids. The profile of K shows broadening which is attributed to the plume expansion as it moves upwards. Lastly, a double peak structure is seen, which slowly disappears with increasing \(\frac{z}{D}\). This trend is attributed to the high shear present near the edges of the plume in comparison to the plume centre. As the \(\frac{z}{D}\) increases, the shear reduces and the associated turbulent energy also decreases, thereby reducing the imprint of the double peak in the TKE profiles. The radial Reynolds stress can be plotted to confirm the results from the turbulent kinetic energy profiles. The normalized radial stress plot is shown in Fig. 2b. An off-center peak is seen due to the production of turbulence energy by Reynolds stress working against the mean shear. This further confirms the fact that the flow energetics are predominant in the edges of the plume than at the central region. It is also documented that the Reynolds stress components decrease with increase in the downstream direction, a trend attributed to the reduction in the magnitude of fluctuating components of velocity due to entrainment. The profiles for turbulent kinetic energy and Reynolds stress are in agreement with some of the existing literature for turbulent buoyant jets (Shiri 2010).

Fig. 2
figure 2

Profiles of a normalized turbulent kinetic energy and b normalized radial Reynolds stress, at different normalized vertical locations

Full size image
Fig. 3
figure 3

Turbulent kinetic energy budget terms under stationary and homogeneous assumption. a Production flux P, b Buoyancy flux, B, and c viscous dissipation \(\varepsilon \). The mixing efficiency (\(\varGamma \)) as a function of z is shown in (d)

Full size image

The turbulent kinetic energy budget equation given by Eq. (8), under the assumption of stationary and homogeneous turbulence, has three important terms, namely production flux, P, buoyancy flux, B, and viscous dissipation, \(\varepsilon \), that govern its evolution. Using the simultaneous velocity and density fields, we can extract all these three terms and study their dynamics. This is done for a forced plume with a stratification strength \(N=0.2\) s\(^{-1}\), and the results are shown in Fig. 3. Evident from Fig. 3a is that the production flux term is always positive indicating mechanical gain of turbulent energy due to the eddies present in the flow. The magnitude of P decreases as z increases due to the plume transitioning from a momentum-dominated to buoyancy-dominated flow. In Fig. 3b, the buoyancy flux is plotted, which has a negative value indicative of unstable stratification. This is a good representation of our flow, since the flow is unstable owing to the upward movement of the lighter fluid. Due to strong density gradients at low z levels, the buoyancy flux is higher. As the plume evolves downstream, the entrainment of the plume fluid with the ambient reduces the density gradient, thereby causing reduction in the buoyancy flux. Nevertheless, the value of B always stays negative, indicating unstable convection in the flow. It should be noted that the magnitude of buoyancy flux is low, which is representative of the low value of bulk Richardson number, \({Ri}_{b}=0.008\), used in this study. Finally, the nature of viscous dissipation is revealed in Fig. 3c. The positive value of \(\varepsilon \) indicates that turbulent energy is being lost to friction and dissipation of energy from large scales to small scales in the flow. From the kinetic energy budget, we can write \(P-B-\varepsilon =0\), which means that the under stationary and homogeneous assumption, the production flux and buoyancy flux must balance dissipation (i.e., \(P+B=\varepsilon \)). However, this is not evident from Fig. 3 that confirms that the transport term (Tr) also plays an important role in the kinetic energy budget. Despite this, the results from the present work are extremely useful in understanding the dynamics of turbulence and mixing in forced plumes, since it is first of its kind. In Fig. 3d, we present the mixing efficiency, \(\varGamma \) as a function of z. It is observed that \(\varGamma \) increases with z, showing the nature of scalar mixing in the flow. This is expected since dissipation, \(\varepsilon \), reduces at a faster rate than the buoyancy flux, B, causing an increase in the value of \(\varGamma \).

An estimate for \(K_{\rho }\) was also deduced from the experimental results and was found to be of the order of \(K_{\rho } \approx 3\,\times \,10^{-4}\) m\(^{2}\) s\(^{-1}\). This value is seldom seen in field observation depending on the flow conditions (Lozovatsky and Fernando 2012). Therefore, we conclude that the estimate of scalar eddy diffusivity measured in our present study is legit, which gives further confidence in the turbulence characterization of the flow.

Fig. 4
figure 4

Turbulent kinetic energy profile at two different values of Reynolds number, a \(Re=3090\) and b \(Re=9950\)

Full size image

5.2 Dynamics of Gravity Currents

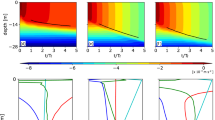
The energetics of a gravity current were studied near the head region to understand the turbulence and mixing dynamics of the flow. This was done for two different values of Reynolds numbers, namely \(Re=3090\) and \(Re=9950\). These two values were chosen based on the qualitative differences in the nature of the evolving flow. The turbulent kinetic energy, K, being an important statistics in stratified flows, which shows the turbulence distribution in the flow, it was plotted for these two Re values as shown in Fig. 4. It is clearly seen that the TKE peaks near the central region (\(z=30\) cm to \(z=50\) cm for \(Re=3090\) and \(z=40\) cm to \(z=60\) cm for \(Re=9950\)), where the dense and the lighter fluids mix due to strong shear. This is the zone where the energetics of the flow and mixing are dominant. We also notice that the value of TKE is an order of magnitude higher for the case of \(Re=9950\). This is expected since the initial momentum in the flow is large resulting in strong TKE generation.

Fig. 5
figure 5

Turbulent kinetic energy budget terms for two different values of Reynolds number, (left) \(Re=3090\) and (right) \(Re=9950\)

Full size image

As given by Eq. (8), the turbulent kinetic energy budget equation, under the assumption of stationary and homogeneous turbulence, is governed by the contributions from production flux, P, buoyancy flux, B, and viscous dissipation, \(\varepsilon \). These three terms were plotted as a function of z and for the two Re cases and the results are shown in Fig. 5. An immediate observation from this figure is that P, B, and \(\varepsilon \) for both values of Re show a peak value in the central z region. This is expected since most of the turbulence and mixing is generated in the central portion allowing the two fluids to mix vigorously. For dissipation, \(\varepsilon \), a higher value is also seen near \(z=0\) due to the frictional effect of the wall. For the case of \(Re=3090\), the production flux term is always positive indicating mechanical gain of turbulent energy due to the eddies present in the flow. The buoyancy flux, B, is also positive indicative of stable stratification. This is a good representation of our flow, since the flow is stable owing to the downward movement of the denser fluid, such that it leads to dense fluid settling below lighter fluid, thereby giving a stably stratified profile. The positive value of \(\varepsilon \) indicates that turbulent energy is being lost due to friction and cascade of energy from large scales to small scales in the flow. From the kinetic energy budget, we can write \(P-B-\varepsilon =0\), which means that the under stationary and homogeneous assumption, the production flux must balance buoyancy flux and dissipation (i.e., \(P=B+\varepsilon \)). However, this is not evident from Fig. 5 (left plot for \(Re=3090\)) that again confirms that the transport terms (Tr) may play an important role in the kinetic energy budget. Despite this, the results from the present work are extremely useful in understanding the turbulence and nature of mixing in gravity currents. A very similar picture emerges for \(Re=9950\) (right plot in Fig. 5), the only difference being the magnitude of P, B, and \(\varepsilon \) are higher than for \(Re=3090\) case due to the higher inertia in the flow.

In Fig. 6, the mixing efficiency \(\varGamma \) as a function of stream-wise location x for the two Reynolds numbers is shown. It is observed that \(\varGamma \) shows a spatial variation showing the random nature of scalar mixing along the stream-wise direction of the gravity current. This is expected due to the chaotic nature of fluid mixing owing to interfacial instabilities. In order to get an estimate of the turbulent diffusivity, a mean value of \(\varGamma \) could be used (shown by the dashed line in Fig. 6). The mean value of \(\varGamma \) is lower for \(Re=3090\) compared to \(Re=9950\), indicated that mixing is vigorous in the high Reynolds number case. Following this, an estimate for \(K_{\rho }\) could deduced from the experimental results using the values of \(\varGamma \), \(\varepsilon \), and \(N^{2}\). The value of \(N^{2}\) for the case of gravity current is measured from the vertical density profile that is inherently developed for the particular Re due to the flow dynamics (Balasubramanian and Zhong 2018). The value of \(K_{\rho }\) was found to be of the order of \(K_{\rho } \approx 4 \,\times \,10^{-6}\) m\(^{2}\) s\(^{-1}\) for both \(Re=3090\) and \(Re=9950\). The similar values indicate that the increase in \(\varGamma \) is offset by the corresponding increase in the stability of the density profile yielding higher values of \(N^{2}\), which appears in the denominator of Eq. (9). Similar values of \(K_{\rho }\) were also recorded in field observation depending on the initial flow conditions. Therefore, we conclude that the estimate of scalar eddy diffusivity measured in our present study is legit, which gives further confidence in the turbulence characterization of the flow. Finally, it is interesting to note that the scalar eddy diffusivity value, \(K_{\rho }\), is lower for gravity currents than for the forced plume case. This could be attributed to the fact that the turbulence is inhibited by stably stratified fluid layers in gravity current. On the other hand, turbulence is augmented for a forced plume due to an unstable configuration.

Fig. 6
figure 6

Mixing efficiency (\(\varGamma \)) as a function of stream-wise distance (x) at two different values of Reynolds number, a \(Re=3090\) and b \(Re=9950\)

Full size image

6 Summary

The dynamics of a shear-stratified flow were studied using experiments by measuring the small-scale flow features and the turbulence statistics. Two variants of such a flow were considered: (a) forced plume evolving in a linearly stratified environment with a low stratification strength of \(N=0.2\) s\(^{-1}\) and (b) dense gravity current intruding in a lighter environment for two different Reynolds number namely \(Re=3090\) and \(Re=9950\). The flow evolution was studied using the simultaneous PIV/PLIF measurement technique, which enables capturing velocity and density fields. For a forced plume, the turbulent kinetic energy (K) showed a double peak structure due to vigorous entrainment near the plume edges. It was seen that K was higher near the plume source and the value decreases as the plume moves downstream, indicating decaying nature of the turbulence as the plume evolves. An off-center peak was seen in the radial Reynolds stress plot owing to the production of turbulence energy by the stress working against mean shear. The buoyancy flux, B, confirmed the unstable nature of the plume and its value reduces with increasing \(\frac{z}{D}\), as the plume evolves, due to entrainment and reduction in the density gradient between the plume and the ambient fluid. The magnitude of B was small owing to a low value of \({Ri}_{b}\). The production flux, P, and dissipation, \(\varepsilon \), also showed decreasing trend with increasing \(\frac{z}{D}\). Out of the three budget terms, P was seen to be dominant indicating production of turbulent kinetic energy is mainly due to the stress terms. Due to unstable nature of the flow, the buoyancy flux aids in the TKE production. However, the dissipation acts as a sink for the TKE. A balance between P, B, and \(\varepsilon \) was not seen indicating that the transport term may also play an important role in governing the flow dynamics. Based on the mixing efficiency, \(\varGamma \), an estimate for the scalar eddy diffusivity (\(K_{\rho }\)) was found, which had an order of magnitude as that observed in field conditions.

For a gravity current, the turbulent kinetic energy (K) peaks at the central region (between \(z=30\) cm and \(z=50\) cm for \(Re=3090\) and \(z=40\) cm and \(z=60\) cm for \(Re=9950\)), where the two fluids mix due to strong shear present in the flow. This region is also known as the mixing layer. The results revealed that K was more for higher Re due to the increased inertia in the flow. The production flux, P, buoyancy flux, B, and viscous dissipation, \(\varepsilon \), for both values of Re also show a peak value in the central z region. The buoyancy flux profile revealed the stably stratified nature of gravity current. Unlike for the plume case, the stability of the system acts as a sink for the TKE along with the viscous dissipation. Therefore, for gravity currents, the TKE production is only due to the P term. The terms B and \(\varepsilon \) act to dissipate this energy through the mechanism of energy cascade and eddy viscosity effects. For \(Re=3090\), all the three terms had similar magnitude, but for \(Re=9950\), the P term was dominant due to increased inertial force. Similar to the plume case, a balance between P, B, and \(\varepsilon \) was not observed indicating the importance of transport term on the flow dynamics. The value of \(\varGamma \) was more for \(Re=9950\), which translates to more efficient mixing at higher Reynolds number. Using the value of \(\varGamma \), an estimate for the scalar eddy diffusivity (\(K_{\rho }\)) was found, which had an order of magnitude as that observed in field conditions. The results significantly improve our understanding of the mixing dynamics of shear-stratified flows.