Keywords

1 Introduction

Graph coloring problem has three different areas of problem. Fist is vertex coloring; second edge coloring and third one is phase coloring. This paper is focused on vertex coloring problem. In the vertex coloring for any given graph G = (V, E), where V is set of vertices E is set of edges, and C = {1, 2, 3, …, K} is set of colors, each vertex must assign a color from set of color in such a way that colors of two connected vertices must be different, i.e., f: V_C such that for each [u, v], f(v) is not equal to find f(u).

1.1 Applications of Graph Coloring Problem

Graph coloring problem has a wide area of applications like nearest neighbor search [1], register allocation in compiler [2], social networking, puzzles like Sudoku solving, frequency allocation in cellular network, cognitive radio dynamic frequency distribution and many more.

1.2 Algorithms of Graph Coloring Problem

Vertex coloring or more formally it can be called as graph coloring algorithms are designed and implemented to solve the graph coloring problems. There are certain objectives to design graph coloring algorithm. The primary objective of most graph coloring algorithm is to find minimum number of colors for coloring vertices of graphs. Many algorithms also try to achieve some other objectives like optimization of time and space complexity, improvement in execution success rate [3], finding efficient algorithm for large graphs where number of vertices in graph is high and many more.

On the basis of execution pattern, graph coloring algorithm can be sequential and parallel. Graph coloring algorithm is broadly divided into two categories one is exact approach and another next one is approximate [4]. Exact method’s execution success rate is high but they are not efficient for the large graphs. Approximate algorithm give results on optimum time for large graphs but their execution success rate is low.

There are many algorithms already proposed by researchers like ant colony optimization algorithm [5, 6], Cuckoo optimization, Parallel genetic algorithm [7], Modified cuckoo optimization GCA [3], constructive hyper heuristic algorithm [8], and many more.

2 Proposed Algorithm

This paper proposed an algorithm to solve the vertex coloring problem for higher degree graph. Proposed algorithm is based on finding maximum independent set using tree data structure.

2.1 Maximum Independent Sets

The subsets of the graph containing those vertices that are not connected, i.e. no element in the set is connected to any other element of the same set, are known as independent sets. And, as the name suggests “Maximal Independent Sets” are those independent sets that contain maximum number of vertices.

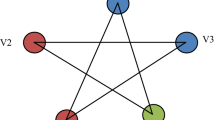
2.2 Proposed Algorithm on Petersen Graph

For the graph in Fig. 1 the independent sets are shown in Table 1.

Fig. 1
figure 1

Petersen graph

Full size image
Table 1 Independent sets starting from vertex 1
Full size table

In Table 1, there are two maximal independent sets starting from vertex 1, i.e., Set1 and Set5. Based on the rules of proposed algorithm, Set1 is selected for further exploration.

Now, as Vertex 2 is not included in Set1, Vertex 2 is to explore independent sets for with those vertices that are not included in Set1. Table 2 shows the independent set starts from vertex 2.

Table 2 Independent sets starting from vertex 2
Full size table

Again, based on the rules, according to algorithm Set11 is selected and so Vertex 5 is explored as shown in Table 3, being the first un-included vertex till now.

Table 3 Independent sets starting from vertex 3
Full size table

As, all the vertices of graph are now included, three maximal independent sets can be selected, Set1, Set11, and Set17. Now, as it is known that each element in a maximal independent set is disconnected with others. A single color can be assigned to all the elements of each maximal independent set. Thus, assigning every maximal independent set a different color, proper minimum coloring can be assigned as shown in Fig. 2. C1 color is assigned to Set1, C2 color to Set11, and C3 color to Set17.

Fig. 2
figure 2

Colored Petersen graph using the proposed algorithm

Full size image

2.3 Algorithm

Here, this paper proposed a vertex coloring algorithm that calculates minimum colors for graphs. Entire algorithm is divided into three steps. The first step is the development of complement edge table. Second, is finding maximum independent sets. And the third step is coloring of the maximal independent sets.

Step 1: Complement Edge Table

Complement edge table is the opposite of edge table. In order to find maximal independent sets, it is required to put together those vertices that are not connected by each other. And, so if complement edge table defines which vertices are not connected, it would reduce the time complexity significantly.

By scanning the edge table, make a new edge table that comprises of only those edges which were not in the original edge table. Also, include only those edges which originate from a vertex of smaller numbering than its destination.

In this step, when making the complement edge table, the algorithm also calculates the number of occurrences of every vertex, i.e., the degree of each vertex.

Step 2: Finding Maximal Independent Sets

This is the core of proposed algorithm. In this step, algorithm proceeds by exploring a tree for each maximal independent set. This step itself is a multistep process, which are as follows:

  1. i.

    Initiation Step: To find the sets, algorithm needs to commence from somewhere, and so, the initiation step is defined to select the first vertex that is not yet included in any maximal independent set. If, there is no maximal independent set yet, algorithm can be start from vertex 1. Make a new empty maximal independent set.

  2. ii.

    Tree exploration: This section has two main activities.

    1. a.

      Every vertex that is greater in numbering than the selected vertex and is a connection in the complement edge table is made a child of the selected vertex given it is not included in any maximal set till now.

    2. b.

      For all children, explore one by one by making the vertices that are in connection with complement edge table, are not included in any maximal set, and are siblings of the vertex being explored. This step is repeated till there are no more vertices which can be explored.

  3. iii.

    Path selection: Then select the path with maximum length. If more than one path has maximum length, then the sum of degree for each such path is calculated and selects the path with minimum sum of degrees. The sum of degree is calculated as

$$ {\text{Sum}}\, = \,{\text{sum}}\,{\text{of}}\,{\text{degrees}}\,{\text{of}}\,{\text{all}}\,{\text{vertices}}\,{\text{in}}\,{\text{the}}\,{\text{path}}\,{-}\,{\text{L}}\,*\,\left( {{\text{L}} - 1} \right)/2 $$
(1)

where L is the length of the path.

If, more than one longest path has minimum sum of degrees, first traversing left to right is selected.

  1. iv.

    Path to the maximal independent set is added for each vertex in the paths, degree of all its connections is decremented.

  2. v.

    Step i through iv is repeated until all the vertices are included in some maximal independent set.

Step 3: Coloring the Maximal Independent Sets

This is the final step of the proposed minimum coloring algorithm. This step assigns a different color to each maximal independent set, i.e. all the vertices that belong to the same maximal independent set are assigned the same color and all the vertices that belong to different independent sets, now have different colors.

In Fig. 3 entire flow of the proposed algorithm has been shown.

Fig. 3
figure 3

Flowchart of the proposed algorithm

Full size image

3 Complexity Analysis

Worst-Case Complexity: The complexity of the proposed algorithm depends on the tree exploration. And, the maximum number of nodes would be explored when all the vertices are isolated, i.e., the edge table is empty, making nC2/2 edges in the complement edge table, where n is the number of vertices. So, complexity can be calculated for exploring the tree when all the vertices are isolated.

If n is the number of vertices, then V1 would have n − 1 connections. Similarly, V2 would have n − 2, V3 would have n − 3 connections, and so on, since the algorithm is accounting only the edges to vertices greater in numbering. Equation 2 is the recursion equation for the exploration.

$$ {\text{T}}\left( {\text{n}} \right) = {\text{T}}\left( {{\text{n}} - 1} \right) + {\text{T}}\left( {{\text{n}} - 2} \right) + {\text{T}}\left( {{\text{n}} - 3} \right) + \, \cdots \, + {\text{T}}\left( 2 \right) + {\text{T}}\left( 1 \right) $$
(2)

And the initial conditions would be

T(1) = 0 and T(2) = 1

From Eq. (2)

$$ {\text{T}}\left( {{\text{n}} - 1} \right) = {\text{T}}\left( {{\text{n}} - 2} \right) + {\text{T}}\left( {{\text{n}} - 3} \right) + \, \cdots \, + {\text{T}}\left( 2 \right) + {\text{T}}\left( 1 \right) $$
(3)

Subtracting (3) from (2)

$$ \begin{array}{*{20}c} {{\text{T}}\left( {\text{n}} \right) - {\text{T}}\left( {{\text{n}} - 1} \right) = {\text{T}}\left( {{\text{n}} - 1} \right),} \\ {{\text{T}}\left( {\text{n}} \right) = 2\,*\,{\text{T}}\left( {{\text{n}} - 1} \right)} \\ \end{array} $$
(4)

By Eq. 4, the worst-case complexity of the algorithm is O(2n − 1).

4 Result Analysis

4.1 Test Data Sets

DIMACS graph instances are taken as data set for experiment results analysis of the proposed algorithm. DIMACS (Center for Discrete Mathematics and Theoretical Computer Science) defined a format to represent undirected graphs [9], which has been used by most of the researchers for analysis of their graph coloring algorithms. In this format graph data are stored in an input file, which contains all information about graph. In this input file, nodes are numbered from 1 to n. Edges are stored in the form of edge list like “e 1 2”.

4.2 Algorithm Implementation Platform

The proposed algorithm is implemented using Java programming language. Window 7 Ultimate 64-bit operating system platform with Intel(R) Core(TM) 2 Duo 2.10 GHz with 2 GB Installed memory (RAM) is used for algorithm execution.

4.3 Experimental Results

The proposed algorithm is tested on 26 DIMACS graph instances, includes queen graphs, DSJC series graphs, miles graphs, random series graphs, insertion and full insertion graphs. In Table 4 all experimental results are shown. Table contains the instance name, number of vertices in graph (V), number of edges in graph (E), average degree of vertices in graph (AvgDegree) and number of colors required to color the graph, which are generated by the proposed algorithm (K).

Table 4 Experimental results of the proposed algorithm
Full size table

From the experimental results, it has been found that proposed algorithm gives optimum results for high degree of graphs.

The proposed algorithm implementation is also tested on 12 geometric series graphs, these are weighted with bandwidth. But proposed algorithm implementation is not for weighted graphs so in algorithm weight is ignored from the data records. Also there is no use of bandwidth in the proposed algorithm, so that bandwidth is also ignored. In Table 5 experimental results of geometric series graphs (GEOM) can be seen.

Table 5 Experimental results of the proposed algorithm on geometric series graphs
Full size table

In Table 6 few experimental results are also compared with a well-known hybrid genetic algorithm for graph coloring problem (HPGAGCP) [9]. Some interesting results are found in Table 6.

Table 6 Comparison of the proposed algorithm with HPGAGCP
Full size table

5 Conclusion

Generally complexity of any graph coloring algorithm is high for high degree graphs. But the proposed algorithm is based on complementary edge table. If the degree of graph is higher then size of complement edge table is small. Exploring tree through this complement edge table does not extend up to high level, i.e., algorithm is executed in optimum time and space complexity.

Tree-based graph coloring algorithm using independent set (proposed algorithm) is an efficient algorithm to calculate the number of colors required and assign to vertices. Time complexity of this algorithm is optimum for high degree graphs. The algorithm gives number of colors precisely equal to the chromatic number of graphs.