Keywords

1 Introduction

Deep saturated soft soil in the east coastal area of China poses many challenges to geotechnical engineers, such as low bearing capacity, excessive settlement, and slope instability. Recently, a new technology called Stiffened Deep Mixed (SDM) column was proposed (Ling et al. 2001). SDM column is formed by inserting a precast concrete core pile into the center of DM column immediately after construction of DM column. Core pile is installed to increase strength of column and reduce ground settlement. Meanwhile, DM column is used to increase skin friction along the core pile shaft. Moreover, bearing capacity provided by the SDM column was similar to the cast-in-place pile with the same diameter and length while the SDM column can save cost nearly by 30% (Qian et al. 2013).

Various studies have been conducted to investigate the behavior of SDM column-reinforced soft soil (Tanchaisawat et al. 2009; Zhao et al. 2010; Ye et al. 2016). However, there was still no feasible design method to calculate the settlement of ground reinforced by SDM columns. This paper developed an analytical method to calculate the settlement of SDM column-supported embankment over soft clay. Punching effect of concrete core pile was considered in the analysis. Finally, the proposed method was applied to predict the settlement of a case history.

2 Calculation Model

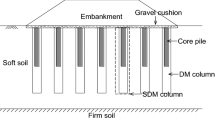
Figure 1 shows the typical cross section of SDM column-reinforced soil. Based on the geometry characteristic in cross section, the profile could be divided into three regions: Region I (the soil within the length of concrete core pile), Region II (the soil between the core pile base and the DM column base), and Region III (the soil below the DM column base). Thus, the total settlement of SDM column-reinforced subsoil is a sum of the compressions of the three regions,

Fig. 1.
figure 1

Cross section of subsoil with SDM column

Full size image
$$ S_{\text{total}} = S_{\text{I}} + S_{\text{II}} + S_{\text{III}} $$
(1)

in which, \( S_{\text{total}} \) is the total settlement, \( S_{\text{I}} \) is the compression of Region I, \( S_{\text{II}} \) is the compression of Region II, and \( S_{\text{III}} \) is the compression of Region III.

The main assumptions made in the analysis are summarized as: (a) concrete core pile, DM column and subsoil behave as isotropic linear-elastic materials, and radial deformation is ignored; (b) DM column and soil below the core pile base deform under an equal strain condition; (c) skin friction is distributed linearly along the core pile shaft.

3 Derivation of the Theoretical Method

3.1 Compression of Soil in Region I

Considering the punching effect of the core pile (see Fig. 1), \( S_{\text{I}} \) can be expressed as,

$$ S_{\text{I}}\,{=}\,\delta_{\text{up}} + \delta_{\text{down}} + \delta_{\text{core}} $$
(2)

in which, \( \delta_{\text{up}} \) is the upward punching deformation of the core pile, \( \delta_{\text{down}} \) is the downward punching deformation of the core pile, and \( \delta_{\text{core}} \) is the compression of the core pile. Since the surrounding soil settles more than the core pile, negative frictional force occurs on the core pile shaft. Taking the equal settlement plane as a datum plane, Eq. (2) can be rewritten as,

$$ S_{\text{I}} = S_{\text{su}} + S_{\text{sd}} = \left( {\delta_{\text{up}} + \delta_{1} } \right) + \left( {\delta_{\text{down}} + \delta_{2} } \right) $$
(3)

in which \( S_{\text{su}} \) and \( \delta_{1} \) are the compressions of the surrounding soil and the core pile above the equal settlement plane, and \( S_{\text{sd}} \) and \( \delta_{2} \) are those below the equal settlement plane. Ye et al. (2016) illustrated that the distribution of the skin friction along the core pile was curved as shown in Fig. 2(a). For simplicity, the skin friction along the core pile is assumed to have a linear distribution as illustrated in Fig. 2(b).

Fig. 2.
figure 2

Simplification of concrete core pile skin friction

Full size image

The Bjerrum method (1969) is used to calculate the maximum negative friction,

$$ \tau_{0} = k\sigma_{\text{s}} \;{ \tan }\;\varphi_{\text{i}} $$
(4)

in which \( k = { \tan }^{2} \left( {45^\circ + {\varphi \mathord{\left/ {\vphantom {\varphi 2}} \right. \kern-0pt} 2}} \right) \), \( \varphi \) is the frictional angle of DM column, \( \varphi_{\text{i}} \) is the frictional angle of the interface between core pile and DM column, and \( \sigma_{\text{s}} \) is the vertical stress on the top of surrounding soil. Thus, the concrete core skin friction can be expressed as, \( \tau (z) = \tau_{0} (1 - {z \mathord{\left/ {\vphantom {z {l_{0} }}} \right. \kern-0pt} {l_{0} }}) \), in which \( l_{0} \) is the depth of the equal settlement plane, positive value of \( \tau (z) \) means negative friction, vice versa.

Based on the equilibrium of the forces in a vertical direction, an equation can be established as \( P = m\alpha \sigma_{\text{p}} + (1 - m\alpha )\sigma_{\text{s}} \), in which \( P \) is the average loading on the ground, \( m \) is the replacement ratio of SDM column, \( \alpha \) is the area ratio of core pile, and \( \sigma_{\text{p}} \) and \( \sigma_{\text{s}} \) are the vertical stresses on the top of core pile and surrounding soil. Setting the stress concentration ratio \( n = {{\sigma_{\text{p}} } \mathord{\left/ {\vphantom {{\sigma_{\text{p}} } {\sigma_{\text{s}} }}} \right. \kern-0pt} {\sigma_{\text{s}} }} \), one can obtain \( \sigma_{\text{s}} = {P \mathord{\left/ {\vphantom {P {((n - 1)\alpha m + 1)}}} \right. \kern-0pt} {((n - 1)\alpha m + 1)}} \), and \( \sigma_{\text{p}} = {{nP} \mathord{\left/ {\vphantom {{nP} {((n - 1)\alpha m + 1)}}} \right. \kern-0pt} {((n - 1)\alpha m + 1)}} \). The equivalent compression modulus of the soil and the DM column in Region I (\( E_{\text{I}}^{\text{eq}} \)) is considered as an area-weighted average value of DM column and subsoil, i.e., \( E_{\text{I}}^{\text{eq}} = m(1 - \alpha )E_{\text{DM}} + (1 - m)E_{\text{sI}} \), in which \( E_{\text{DM}} \) is the compression modulus of DM column, and \( E_{{{\text{s}}{\rm I}}} \) is the compression modulus of the soil in Region I. Figure 3 shows a slice of the unit cell with a thickness of \( {\text{d}}z \). The differential equation can be obtained based on the equilibrium of the forces in a vertical direction,

Fig. 3.
figure 3

Slice of unit cell in Region I

Full size image
$$ {{{\text{d}}\sigma_{\text{sz}} } \mathord{\left/ {\vphantom {{{\text{d}}\sigma_{\text{sz}} } {{\text{d}}z}}} \right. \kern-0pt} {{\text{d}}z}} + \lambda \tau (z) = 0 $$
(5)

in which, \( \sigma_{\text{sz}} \) is the vertical stress of surrounding soil at depth \( {\text{z}} \); \( A_{\text{s}} \) is the area of surrounding soil; \( c_{\text{p}} \) is the perimeter of core pile; and \( \lambda = {{c_{\text{p}} } \mathord{\left/ {\vphantom {{c_{\text{p}} } {A_{\text{s}} }}} \right. \kern-0pt} {A_{\text{s}} }} \). Using the boundary condition \( \sigma_{\text{sz}} = \sigma_{\text{s}} \) at \( {\text{z}} = 0 \), \( \sigma_{\text{sz}} \) can be solved as,

$$ \sigma_{\text{sz}} = {{(\lambda \tau_{0} z^{2} )} \mathord{\left/ {\vphantom {{(\lambda \tau_{0} z^{2} )} {(2l_{0} )}}} \right. \kern-0pt} {(2l_{0} )}} - \lambda \tau_{0} z + \sigma_{\text{s}} $$
(6)

At depth \( {\text{z}} \), the vertical stress in the core pile is,

$$ \sigma_{\text{pz}} = \sigma_{\text{p}} + A_{\text{p}}^{ - 1} \int_{0}^{z} {\tau (z)c_{\text{p}} {\text{d}}z} = \sigma_{\text{p}} + \gamma (\tau_{0} z - {{\tau_{0} z^{2} } \mathord{\left/ {\vphantom {{\tau_{0} z^{2} } {(2l_{0} )}}} \right. \kern-0pt} {(2l_{0} )}}) $$
(7)

in which, \( A_{\text{p}} \) is the area of core pile, \( \gamma = {{c_{\text{p}} } \mathord{\left/ {\vphantom {{c_{\text{p}} } {A_{\text{p}} }}} \right. \kern-0pt} {A_{\text{p}} }} \). Thus, some terms on the right side of Eq. (3) can be solved as, \( S_{\text{su}} = \int_{0}^{{l_{0} }} {\left( {{{\sigma_{\text{sz}} } \mathord{\left/ {\vphantom {{\sigma_{\text{sz}} } {E_{\text{I}}^{\text{eq}} }}} \right. \kern-0pt} {E_{\text{I}}^{\text{eq}} }}} \right){\text{d}}z} \), \( S_{\text{sd}} = \int_{{l_{0} }}^{{l_{1} }} {\left( {{{\sigma_{\text{sz}} } \mathord{\left/ {\vphantom {{\sigma_{\text{sz}} } {E_{\text{I}}^{\text{eq}} }}} \right. \kern-0pt} {E_{\text{I}}^{\text{eq}} }}} \right){\text{d}}z} \), \( \delta_{1} = \int_{0}^{{l_{0} }} {\left( {{{\sigma_{\text{pz}} } \mathord{\left/ {\vphantom {{\sigma_{\text{pz}} } {E_{\text{p}} }}} \right. \kern-0pt} {E_{\text{p}} }}} \right){\text{d}}z} \), and \( \delta_{2} = \int_{{l_{0} }}^{{l_{1} }} {\left( {{{\sigma_{\text{pz}} } \mathord{\left/ {\vphantom {{\sigma_{\text{pz}} } {E_{\text{p}} }}} \right. \kern-0pt} {E_{\text{p}} }}} \right){\text{d}}z} \).

The upward punching deformation of the core pile can be considered as,

$$ \delta_{\text{up}} = p_{\text{c}} (\sigma_{\text{p}} - \sigma_{\text{s}} ) $$
(8)

where \( p_{\text{c}} \) is the upward punching under an uniform force. It can be considered as \( p_{\text{c}} = {{L_{\text{c}} } \mathord{\left/ {\vphantom {{L_{\text{c}} } {E_{\text{c}} }}} \right. \kern-0pt} {E_{\text{c}} }} \), where \( L_{\text{c}} \) is the thickness of cushion, \( E_{\text{c}} \) is the compression modulus of cushion, and \( E_{\text{p}} \) is the compression modulus of core pile.

The downward punching deformation of the core pile can be considered as,

$$ \delta_{\text{down}} = p_{\text{s}} (\sigma_{{{\text{p}}l_{1} }} - \sigma_{{{\text{s}}l_{1} }} ) $$
(9)

in which, \( \sigma_{{{\text{p}}l_{1} }} \) is the vertical stress at the bottom of core pile; \( \sigma_{{{\text{s}}l_{1} }} \) is the vertical stress at the same depth of subsoil; and \( p_{\text{s}} \) is the downward punching under an uniform force. Chen (2005) proposed a method to calculate \( p_{\text{s}} \),

$$ p_{\text{s}} = {{(1 - \mu_{0}^{2} )\omega \sqrt {A_{\text{p}} } } \mathord{\left/ {\vphantom {{(1 - \mu_{0}^{2} )\omega \sqrt {A_{\text{p}} } } {E_{0} }}} \right. \kern-0pt} {E_{0} }} $$
(10)
$$ E_{0} = (1 - {{2\mu_{0}^{2} } \mathord{\left/ {\vphantom {{2\mu_{0}^{2} } {(1 - \mu_{0} )}}} \right. \kern-0pt} {(1 - \mu_{0} )}})E_{\text{II}}^{\text{eq}} $$
(11)

in which \( \mu_{0} \) is the Poisson’s ratio of DM column, \( \omega \) is a parameter decided by the shape of loading plane. \( E_{{\text{II}}}^{\text{eq}} \) is the compression modulus of the soil in Region II.

Thus, combining Eq. (8), \( S_{\text{su}} \), \( \delta_{1} \) and Eq. (3), it can be written as,

$$ (\sigma_{\text{s}} l_{0} - {{\lambda \tau_{0} l_{0}^{2} } \mathord{\left/ {\vphantom {{\lambda \tau_{0} l_{0}^{2} } 3}} \right. \kern-0pt} 3})/E_{\text{I}}^{\text{eq}} = p_{\text{c}} (\sigma_{\text{p}} - \sigma_{\text{s}} ) + {{(\sigma_{\text{p}} l_{0} + {{\gamma \tau_{0} l_{0}^{2} } \mathord{\left/ {\vphantom {{\gamma \tau_{0} l_{0}^{2} } 3}} \right. \kern-0pt} 3})} \mathord{\left/ {\vphantom {{(\sigma_{\text{p}} l_{0} + {{\gamma \tau_{0} l_{0}^{2} } \mathord{\left/ {\vphantom {{\gamma \tau_{0} l_{0}^{2} } 3}} \right. \kern-0pt} 3})} {E_{\text{p}} }}} \right. \kern-0pt} {E_{\text{p}} }} $$
(12)

Similarly, combining Eq. (9), \( S_{\text{sd}} \), \( \delta_{2} \) and Eq. (3), it can be written as,

$$ \begin{aligned} & \frac{1}{{E_{\text{I}}^{\text{eq}} }}(\frac{{\lambda \tau_{0} }}{{6l_{0} }}l_{1}^{3} - \frac{{\lambda \tau_{0} }}{2}l_{1}^{2} + \sigma_{\text{s}} l_{1} - \sigma_{\text{s}} l_{0} + \frac{{\lambda \tau_{0} }}{3}l_{0}^{2} ) \\ & = \frac{1}{{E_{\text{p}} }}( - \frac{{\gamma \tau_{0} }}{{6l_{0} }}l_{1}^{3} + \frac{{\gamma \tau_{0} }}{2}l_{1}^{2} + \sigma_{\text{p}} l_{1} - \sigma_{\text{p}} l_{0} - \frac{{\gamma \tau_{0} }}{3}l_{0}^{2} ) + p_{\text{s}} \left[ {\sigma_{\text{p}} - \sigma_{\text{s}} + (\gamma + \lambda )\tau_{0} l_{1} - \frac{{(\gamma + \lambda )\tau_{0} l_{1}^{2} }}{{2l_{0} }}} \right] \\ \end{aligned} $$
(13)

By substituting Eq. (4) into Eqs. (12) and (13), it can be written as,

$$ n = \frac{{\sigma_{\text{p}} }}{{\sigma_{\text{s}} }} = \frac{{\theta_{1} }}{{\theta_{2} }} = \frac{{\theta_{3} }}{{\theta_{4} }} $$
(14)

in which, \( n \) is the stress concentration ratio on the top of core pile, \( \theta_{1} = \frac{{l_{0} }}{{E_{\text{I}}^{\text{eq}} }} + p_{\text{c}} - \frac{{\lambda k\tan \varphi_{\text{i}} }}{{3E_{\text{I}}^{\text{eq}} }}l_{0}^{2} - \frac{{\gamma k\tan \varphi_{\text{i}} }}{{3E_{\text{p}} }}l_{0}^{2} \), \( \theta_{2} = p_{\text{c}} + \frac{{l_{0} }}{{E_{\text{p}} }} \), \( \theta_{4} = p_{\text{s}} + \frac{{(l_{1} - l_{0} )}}{{E_{\text{p}} }} \)

$$ \begin{aligned} & \theta_{3} = \frac{1}{{E_{\text{I}}^{\text{eq}} }}(\frac{{\lambda kl_{1}^{3} \tan \varphi_{\text{i}} }}{{6l_{0} }} - \frac{{\lambda kl_{1}^{2} \tan \varphi_{\text{i}} }}{2} + l_{1} - l_{0} + \frac{{\lambda kl_{0}^{2} \tan \varphi_{\text{i}} }}{3}) \\ & - \frac{1}{{E_{\text{p}} }}( - \frac{{\gamma kl_{1}^{3} \tan \varphi_{\text{i}} }}{{6l_{0} }} + \frac{{\gamma kl_{1}^{2} \tan \varphi_{\text{i}} }}{2} - \frac{{\gamma kl_{0}^{2} \tan \varphi_{\text{i}} }}{3}) - p_{\text{s}} ( - 1 + (\gamma + \lambda )kl_{1} \tan \varphi_{\text{i}} - \frac{{(\gamma + \lambda )kl_{1}^{2} \tan \varphi_{\text{i}} }}{{2l_{0} }}) \\ \end{aligned} $$

In Eq. (14), \( l_{0} \) is the only unknown variation. By solving Eq. (14), \( l_{0} \) and n can be obtained, then \( \sigma_{\text{p}} \) and \( \sigma_{\text{s}} \) can be solved. Thus, the compression of Region I can be calculated as,

$$ S_{\rm I} = S_{\text{su}} + S_{\text{sd}} = {{({{\lambda \tau_{0} l_{1}^{3} } \mathord{\left/ {\vphantom {{\lambda \tau_{0} l_{1}^{3} } {(6l_{0} ) - {{\lambda \tau_{0} l_{1}^{2} } \mathord{\left/ {\vphantom {{\lambda \tau_{0} l_{1}^{2} } 2}} \right. \kern-0pt} 2} + \sigma_{s} l_{1} }}} \right. \kern-0pt} {(6l_{0} ) - {{\lambda \tau_{0} l_{1}^{2} } \mathord{\left/ {\vphantom {{\lambda \tau_{0} l_{1}^{2} } 2}} \right. \kern-0pt} 2} + \sigma_{s} l_{1} }})} \mathord{\left/ {\vphantom {{({{\lambda \tau_{0} l_{1}^{3} } \mathord{\left/ {\vphantom {{\lambda \tau_{0} l_{1}^{3} } {(6l_{0} ) - {{\lambda \tau_{0} l_{1}^{2} } \mathord{\left/ {\vphantom {{\lambda \tau_{0} l_{1}^{2} } 2}} \right. \kern-0pt} 2} + \sigma_{s} l_{1} }}} \right. \kern-0pt} {(6l_{0} ) - {{\lambda \tau_{0} l_{1}^{2} } \mathord{\left/ {\vphantom {{\lambda \tau_{0} l_{1}^{2} } 2}} \right. \kern-0pt} 2} + \sigma_{s} l_{1} }})} {E_{\rm I}^{\text{eq}} }}} \right. \kern-0pt} {E_{\rm I}^{\text{eq}} }} $$
(15)

3.2 Compression of Soil in Region II

Since the difference in the moduli of DM column and surrounding soil is not so great, the compression of the soil in Region II is considered to settle under an equal strain condition. The equivalent modulus of Region II is computed using an area-weighted average value of the compression moduli of the DM column and the surrounding soft soil. The additional stress in Region II is computed using Jones’s solution (1962), which is a plane stress solution for the vertical stress caused by embankment load in two-layer or three-layer systems. The compression of the soil in Region II (\( S_{\text{II}} \)) can be expressed as,

$$ S_{{\text{II}}} = {{\left[ {\left( {\sigma_{1} + \sigma_{2} } \right)l_{2} } \right]} \mathord{\left/ {\vphantom {{\left[ {\left( {\sigma_{1} + \sigma_{2} } \right)l_{2} } \right]} {\left( {2E_{{\text{II}}}^{\text{eq}} } \right)}}} \right. \kern-0pt} {\left( {2E_{{\text{II}}}^{\text{eq}} } \right)}} $$
(16)

in which, \( \sigma_{1} \) is the vertical stress on the bottom of Region I, \( \sigma_{2} \) is the vertical stress on the bottom of Region II, \( l_{2} \) is the thickness of Region II, and \( E_{{\text{II}}}^{\text{eq}} \) is the compression modulus of soil in Region II, i.e., \( E_{{\text{II}}}^{\text{eq}} = mE_{\text{DM}} + (1 - m)E_{\text{s}} \).

3.3 Compression of Soil in Region III

The compression of the soil in Region III is computed using Boussinesq’s solution:

$$ S_{{\text{III}}} = {{\eta \sigma_{2} l_{3} } \mathord{\left/ {\vphantom {{\eta \sigma_{2} l_{3} } {E_{{\text{III}}}^{\text{eq}} }}} \right. \kern-0pt} {E_{{\text{III}}}^{\text{eq}} }} $$
(17)

in which \( \eta \) is the coefficient of average superimposed stress, \( E_{{\text{III}}}^{\text{eq}} \) is the compression modulus of soil in Region III, \( l_{3} \) is the thickness of Region III.

Based on the above derivations, the solution to calculate the compressions of the three regions were developed and the total settlement of the soil with SDM column can be obtained.

4 Application of the Proposed Method

A test embankment was constructed at the northern part of the Asian Institute of Technology (AIT) Campus, Thailand (Vootttipruex et al. 2011). Figure 4 shows the configuration of the test embankment. The height of the embankment was 6 m consisting of a 1 m thick sand cushion on the pile head. SDM columns were installed in a square pattern at a spacing of 2.0 m with a diameter of 0.6 m and a length of 7 m. The concrete core pile had a square cross section of 0.22 m × 0.22 m and a length of 6 m. Table 1 tabulates the main properties of the soil layers and the SDM columns used in the field test.

Fig. 4.
figure 4

Test embankment (unit: m): (a) Plan view; (b) Cross section

Full size image
Table 1. Table captions should be placed above the tables.
Full size table

According to the Asaoka method (1978), the final settlement can be predicted based on the field data. Table 2 presents the comparison of the settlement calculated using the proposed method with that using the Asaoka method and a good agreement was obtained with each other. The settlements calculated by the technical specification for strength composite piles in China (JGJ/T 327-2014 2014) are also listed in Table 2. It can be seen that this code significantly underestimates the settlement of SDM column-reinforced soil, especially in Region I. It might be due to the reason that this code did not consider the punching effect of core pile. The above analysis is demonstrated that the proposed method is feasible for the calculation of SDM column-supported embankment over soft soil.

Table 2. Comparison of predictions (mm)
Full size table

5 Conclusions

An analytical method was proposed to calculate the settlement of SDM column-supported embankment over soft clay. The total settlement of the SDM column-reinforced subsoil is a sum of the compression of three regions: Region I (the soil within the length of concrete core pile), Region II (the soil between core pile base and DM column base), and Region III (the soil below DM column base). The punching effect of core pile upward to the sand cushion and downward to the DM column is considered. The solutions for calculating the compressions of the soils in the three regions were developed. Finally the proposed method was used to predict the settlement of a case history. The feasibility of the proposed method was verified by a comparison between the analytical results and the field measurements.