Keywords

1 Introduction

The impacts of stress field, seepage field, and temperature field of the rock as well as their coupling effects on projects are important issues which should be urgently studied for oil and gas exploitation. Research on these problems goes from focusing on uncoupling to coupling. To be specific, studies in uncoupled conditions have no regard for interactions between fluid seepage and rock deformation; however, such mutual interactions were taken into consideration during the studies on fluid–solid coupling [1]. Comparing with the uncoupled model, the fluid–solid-coupled model could be employed to reveal the rules of rock deformation caused by fluid seepage in a more accurate method. Nevertheless, fluid–solid coupling theories fail to cover the coupling effects between temperature field changes and rock deformation/fluid flow. In terms of such problems, especially calculations performed in a condition of large temperature difference, seepage and deformation laws simulated by a fluid–solid-coupled model can become inaccurate apparently. Reasons are that thermal effects and porosity pressure jointly affect rock deformation that, together with fluid seepage, further causes temperature field changes on one hand; on the other hand, rock deformation and thermal effects lead to variations in pore pressure so as to affect fluid seepage. When the above three effects take place simultaneously, it is referred to as thermo-hydro-mechanical coupling [2].

There are many scholars to study THM coupling. The majority of research emphasize on deep burial treatment of nuclear wastes, heat injection exploitation of shale oil and frozen region engineering, etc. Based on principles of consolidation and thermoelasticity, Noorishad [3] proposes a basic THM coupling equation for saturated porous media for the first time, which neglects both heat exchange between fluid and solid as well as the impacts of heat on mechanical properties of rock. Tortike [4, 5] studies reservoirs of saturated porous media in coupling and uncoupling conditions by numerical simulation according to a geomechanical reservoir method. By connecting TOUGH2 to Flac3D, Rutqvist [6] simulated heat transfer and deformation in condition of multiphase flows in fractured porous media and set up a thermo-hydro-mechanical-coupled equation. In China, Lai [7] derives governing equations for 2D TH-coupled and THM-coupled model of tunnel surrounding rocks in cold zones by means of classical theories of seepage mechanics and heat transfer. Finite element simulation is performed in combination with Daban Mountain Tunnel of the Qinghai-Tibet Highway. Zhang [8, 9] sets up a 3D THM coupling governing equation for tunnels in the cold zone and also conducted finite element calculations for 3D frozen-thaw processes of Fenghuoshan Tunnel. Based on thermodynamics of irreversible processes and continuum mechanics, Xu [10] builds a nonlinear THM coupling governing equation for rocks in freezing temperature and analyzes frost-heave force of the rock by defining the expansion coupling coefficient of frozen rock and ice.

The existing domestic and overseas research findings about low-temperature multi-field coupling of the rock signify that studies on problems associated with low-temperature rock masses, especially the low-temperature coal, are far from being mature. Major difficulty is that, the rock is deemed as isotropic porous media and theory of frozen soil mechanics is adopted directly without regard to effects of cleat and joint, which fails to resolve low-temperature multi-field coupling problems during cryogenic volume fracturing in coal seam. In this paper, cleat and joint of the coal were taken into consideration to study interaction between frozen-thaw action and THM to provide temperature field, stress field, and seepage field data for fracture propagation simulation under the alternative injection of cryogenic volume fracturing.

2 Laboratory Investigation

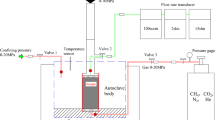
All coal samples used in experiments were taken from the 3# coal seam of the Sihe Coal Mine in Jincheng, Shanxi Province. By a series of cryogenic experiments, interactive relationship among temperature, mechanics, and seepage was investigated.

2.1 Cryogenic Permeability Experiment

For dried and saturated coal samples, permeability tests were conducted at different temperatures for by a nitrogen permeability tester. Regarding permeability tests of both samples, they all experienced drying processes; especially for the latter, coal samples were saturated with clean water before low-temperature treatment, and finally utterly dried in formation temperature after frozen, which is followed by such tests.

As Figs. 162.1 and 162.2 shown, permeability of the dried coal sample goes up after low-temperature treatment, demonstrating that shrinkage stress can generate in matrix at low temperature. If shrinkage stress exceeds tensile strength of coal matrix, low temperature causes micro-fractures. As soon as the ambient temperature has been recovered, such irreversible damages lead to permeability increase. In addition of matrix shrinkage stress, frost-heave forces induced by water freezing further cause damages of matrix in saturated sample. Permeability percentage of the saturated samples is also higher than the sample of dried coal. Fitting the experimental data, relational expressions are acquired for permeability variations of the coal recovering from freezing and thawing.

Fig. 162.1.
figure 1

Permeability variations of dried coal

Full size image
Fig. 162.2.
figure 2

Permeability variations of saturated coal

Full size image
$$ {\text{For}}\;{\text{dried}}\;{\text{coal}}\quad P_{\text{Kd}} = 0.0745\text{e}^{ - 0.067T} $$
(162.1)
$$ {\text{For}}\;{\text{saturated}}\;{\text{coal}}\quad P_{\text{Ks}} = 0.1238\text{e}^{ - 0.06T} $$
(162.2)

where \( P_{\text{Kd}} \) is permeability percentage improvement of dried coal after freezing, and \( P_{\text{Ks}} \) is permeability percentage improvement of saturated coal after freezing.

2.2 Cryogenic Rock Mechanics Experiment

Specific to saturated coal samples, the rock mechanics parameters were respectively tested at different cryogenic temperatures. According to experimental results, Figs. 162.3 and 162.4, Young’s modulus of the coal rises and its Poisson’s ratio declines, when temperature goes down. Because water freezes into ice, low temperature makes the coal more compact and leads to the rise of strength and stiffness and fragility. Fitting the experimental data, relational expressions are acquired for rock mechanics parameters in low-temperature conditions.

Fig. 162.3.
figure 3

Poisson’s ratio at different temperatures

Full size image
Fig. 162.4.
figure 4

Young’s modulus at different temperatures

Full size image
$$ \upupsilon_{c} = 0.0019T + 0.3764 $$
(162.3)
$$ E_{c} = 0.0012T^{2} - 0.0535T + 7.0028 $$
(162.4)

where \( \upupsilon_{\text{c}} \) is Poisson’ ratio of cryogenic coal, and \( E_{\text{c}} \) is Young’s modulus of cryogenic coal.

As Figs. 162.5 and 162.6 shown after freezing and thawing of the rock, ice frost heaving and coal matrix shrinkage cause irrevocable structural damages that can further lead to strength reduction, Poisson ratio increase, and Young’s modulus decline. According to frozen-thaw experiments at diverse temperatures, the following curves are obtained.

Fig. 162.5.
figure 5

Poisson’s ratio at different temperatures

Full size image
Fig. 162.6.
figure 6

Young’s modulus at different temperatures

Full size image
$$ \upupsilon_{\text{af}} = 0.00005T^{2} - 0.0012T + 0.3877 $$
(162.5)
$$ E_{\text{af}} = - 0.0009T^{2} + 0.0272T + 6.2258 $$
(162.6)

where \( \upupsilon_{\text{f}} \) is Poisson’ ratio after freezing, and \( E_{\text{f}} \) is Young’s modulus after freezing.

2.3 Stress–Permeability Experiment

GCTS-RTR-1000 electric-fluid servo compression machine and HPPD-20 fast pulse-decay permeability apparatus were used to test permeability of the coal in triaxial compression to acquire its permeability under diverse stresses. Based on the stress–strain–permeability experiment, coefficient of coal compressibility in the complete stress–strain course was figured out, as shown in Fig. 162.7. Such a coefficient satisfied an equation below.

Fig. 162.7.
figure 7

Permeability variation in complete stress–strain process

Full size image
$$ C_{\text{f}} = - \frac{1}{V}\,\frac{\partial V}{\partial \delta } = - \frac{{3\ln\left( {1 - \varepsilon_{v} } \right)}}{{\delta_{t} - \delta_{0} }} $$
(162.7)

where V is volume of coal, \( \delta \) is stress variation, \( C_{\text{f}} \) is coefficient of its pore/fracture compressibility, \( \varepsilon_{v} \) is volumetric strain, \( \delta_{t} \) is axial stress at t, and \( \delta_{0} \) to the initial axial stress.

In the process of compression, permeability tends to decline exponentially and the reduction result of it is just coincident with S-D model. Moreover, the corresponding relational expression is given below.

$$ K_{\text{t}} = K_{0} \text{e}^{{ - 3C_{\text{f}} \left( {\delta_{t} - \delta_{0} } \right)}} $$
(162.8)

where \( K_{\text{t}} \) is the permeability under an axial stress of \( \delta_{\text{t}} \), and \( K_{0} \) is that when axial stress related is equal to \( \delta_{0} \).

3 THM Coupling Model

Cryogenic fracture propagation simulation in coal seam was involved with the complex coupling issues among temperature field, seepage field, and stress field at low temperature. Comparing with normal-temperature THM coupling, the phase of water in fractures and pores in the condition changes along with the low temperature, which further gives rise to frost heaving, water migration, ice temporary plugging, and frozen-thaw damages. In detail, frost heaving caused by water freezing leads to volume expansion; in this case, an additional stress field can be formed. During ice crystal generating, ice/water pressure causes the water to migrate. Due to ice temporary plugging, permeability of the coal falls. After the ambient temperature is recovered, mechanical properties of rock weaken owing to frozen-thaw damages of the coal. When the temperature goes beyond freezing point, low-temperature THM coupling mode is the same as that in a condition of normal temperature. As Fig. 162.8 shown depending on interactions among three fields at low temperature, a THM coupling mode that considers phase changes was constructed for such fields and their modes of interactions are as follows.

Fig. 162.8.
figure 8

Sketch of THM coupling mode during cryogenic volume fracturing of the coal

Full size image

Here, it was attempted to study cryogenic THM coupling issues of the frozen coal seam based on a double-porosity theory. Additionally, cryogenic THM coupling equation was also derived for coal reservoirs with cracks according to the mass conservation, the energy conservation, the principle of statical equilibrium, and the corresponding thermodynamic property equations.

3.1 Theoretical Heat Transfer Governing Equation

As for the fractured coal reservoirs, main ways of heat transfer include heat conduction, latent heat of phase change, and fissure water seepage migration. Energy conservation equation for ice-water phase change in the rock is expressed as follows.

$$ C_{\text{v}} \frac{\partial T}{\partial t} + \nabla ( - \lambda \nabla T) + L\rho_{i} \frac{\partial u}{\partial t} + C_{\text{w}} \rho_{\text{w}} \frac{\partial T}{\partial t}\left( {\nabla \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {q}_{\text{v}} } \right) = 0 $$
(162.9)

where \( C_{\text{v}} \) is equivalent volumetric heat capacity of system, \( C_{\text{w}} \) heat capacity of water, \( \lambda \) is equivalent coefficient of thermal conductivity of the coal reservoirs (values taken before/after frost are different), L is coefficient of latent heat, \( \rho_{\text{i}} \) and \( \rho_{\text{w}} \) are, respectively, densities of ice and water, and \( \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {q}_{\text{v}} \) is heat change caused by water seepage.

From the left side of this equation to its right, items successively are the heat energy change of system, heat transfer, latent heat of phase change and heat energy caused by water seepage separately.

Heat transfer governing equation for porous media in the fractured coal is presented below.

$$ \left( {\rho C_{p} } \right)_{\text{eff}} \frac{\partial T}{\partial t} + \rho C_{\text{p}} \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {u} \nabla T = \nabla \left( {k_{\text{eff}} \nabla T} \right) + Q $$
(162.10)

where \( \rho \) is fluid density; \( C_{\text{p}} \) is heat capacity under normal pressure; \( \left( {\rho C_{\text{p}} } \right)_{\text{eff}} \) is equivalent volumetric heat capacity under constant pressure; \( k_{\text{eff}} \) is equivalent thermal conductivity; \( \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {u} \) is fluid velocity; Q is thermal sources.

Flow velocity in fractures of porous media can be expressed in fracture permeability \( K_{\text{f}} \). An equation used to express the continuity in cracks can be written as follows.

$$ \frac{\partial }{{\partial {\text{t}}}}d_{\text{fr}} \varphi \rho + \nabla_{t} \left( {d_{\text{fr}} \rho \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {u} } \right) = d_{\text{fr}} Q_{\text{f}} $$
(162.11)

where \( d_{\text{fr}} \) is fracture width, \( \varphi \) is void ratio, \( Q_{\text{f}} \) is the mass source within fractures.

Control equation for heat transfer inside fractures is,

$$ d_{\text{fr}} \left( {\rho C_{\text{p}} } \right)_{\text{eff}} \frac{\partial T}{\partial t} + d_{\text{fr}} (\rho C)_{\text{eff}} \left( {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {u} \nabla_{t} T} \right) = \nabla_{t} \left( {d_{\text{fr}} k_{\text{eff}} } \right) + d_{\text{fr}} \left( {Q_{\text{h}} + q_{\text{s}} T} \right) $$
(162.12)

where \( Q_{\text{h}} \) is heat source, \( q_{\text{s}} \) is dissipation factor, \( \left( {\rho C} \right)_{\text{eff}} \) is effective heat capacity of fluids inside fractures under constant pressure, \( k_{\text{eff}} \) is equivalent coefficient of thermal conductivity of the fracture, and \( \rho \) is fluid density.

3.2 Seepage Governing Equation

Major driving forces of water migration are gradient of water potential and initial stress both of which are caused by frost-heave force, as well as segregation potential energy and temperature gradient. As shown in Fig. 162.9, freezing pressure potential energy brings about water migration against frozen fringe; by contrast, segregation potential energy and temperature gradient make unfrozen water migrate toward the fringe.

Fig. 162.9.
figure 9

Sketch of moisture field movement

Full size image

Equation of continuity for frozen water can be expressed as follows.

$$ \frac{\partial }{\partial t}\left[ {\rho_{\text{w}} nS_{\text{r}} (1 - u)} \right] - \frac{\partial }{\partial t}\left( {\rho_{i} nS_{\text{r}} u} \right) + \nabla \left( {\rho_{\text{w}} nq_{\text{w}}^{\text{v}} } \right) = 0 $$
(162.13)

where n, u, \( S_{\text{r}} \), and \( q_{\text{w}}^{\text{v}} \) represent porosity, freezing ratio, saturability, and current vector one by one.

In terms of pore media, \( q_{\text{w}}^{\text{v}} \) can be expressed in a formula below.

$$ q_{\text{w}}^{\text{v}} = - \frac{{k_{\text{w}} \kappa }}{{\mu_{\text{w}} }}\left( {\nabla P_{\text{w}} - \rho_{\text{w}} g^{\text{r}} } \right) - \kappa_{\text{lt}} \nabla T $$
(162.14)

where \( k_{\text{w}} \) is relative permeability of aqueous phase; \( \kappa \) is inherent permeability tensor of rock media; \( \mu_{\text{w}} \) is viscosity, \( \nabla P_{\text{w}} \) is pressure gradient of aqueous phase; \( \kappa_{\text{lt}} \) is thermal-fluid-coupled coefficient tensor that expresses impacts of thermal gradient on flow velocity of water; and, \( \nabla T \) is temperature gradient.

As for a dual porous medium model, permeability of coal fracture is far greater than pore media of matrix. It is assumed that seepage of a single crack abides by the following relational expression [11].

$$ q = k_{\text{f}} bJ_{\text{f}} = \frac{{\varsigma \psi \gamma_{\text{w}} }}{\upsilon }b^{3} J_{\text{f}} $$
(162.15)

where \( \varsigma \) is a coefficient associated with fracture surface roughness; \( \psi \) is a freezing ratio-seepage-coupled coefficient (fracture permeability decline incurred by phase change frozen); b is opening with; \( J_{\text{f}} \) is pressure gradient along cracks; \( \gamma_{\text{w}} \) is weight of water in unit volume; and, \( \upsilon \) is dynamic viscosity of water.

Due to influence of multiple fractures, the equation above can be rewritten as,

$$ q_{\text{w}}^{\text{v}} = k_{\text{f}} J_{\text{f}} = \frac{{\gamma_{w} \varsigma }}{\nu }\sum\limits_{i = 1}^{m} b_{i}^{3} S_{i} \left( {I - \alpha_{i} \alpha_{i} } \right)J_{\text{f}} $$
(162.16)

where m is the number of crack sets in coal; \( S_{i} \) is the average density of crack set i; \( b_{i} \) is the average opening of crack set i; I is unit vector; \( \alpha_{i} \) is the average vector of direction cosine.

Considering impacts of external stress and freezing process, permeability tensor is modified.

$$ k_{\text{f}} = k_{{\text{f}0}} \sigma^{{ - D_\text{f} }} \psi (u) $$
(162.17)

where \( k_{{\text{f}0}} \) is initial permeability tensor, \( D_{\text{f}} \) is fractal dimension of crack distribution(\( 0 < D_{\text{f}} \le 2 \) and \( D_{\text{f}} = 0 \) signifies that no cracks exist in the coal), \( \psi (u) \) is freezing ratio-seepage-coupled coefficient (it can be also deemed as a function of freezing ratio if \( 0 < \psi (u) \le 1 \); moreover, when \( u = 0 \), \( \psi (u) = 1 \); but, if \( u = 1 \), \( \psi (u) = 0 \)), is stress.

3.3 Stress Balance Governing Equation

A double-porosity model was utilized to study freezing fractured coal. By using fractured media descriptions given by Zhang [12] for reference and taking plane stress into consideration, it was assumed that m sets of cracks were distributed inside the coal reservoir. The strain–stress increment can be expressed in the following equation.

$$ \text{d}\varepsilon_{ij} = C\text{d}\sigma_{ij} + \alpha_{s} \text{d}T\delta_{\text{ij}} $$
(162.18)

where

$$ \begin{aligned} & C = C_{0} + \sum\limits_{i = 0}^{m} {} C_{fi} \\ & C_{0} = \frac{1 + \mu }{E}\left[ {\begin{array}{*{20}c} {1 - \mu } & { - \mu } & 0 \\ { - \mu } & {1 - \mu } & 0 \\ 0 & 0 & 2 \\ \end{array} } \right] \\ & C_{fi} = L_{i} C_{fi}^{{\prime }} L_{i}^{T} = L_{i} \left[ {\begin{array}{*{20}c} 0 & 0 & 0 \\ 0 & {l_{i} /\left( {K_{ni} A_{i} } \right)} & 0 \\ 0 & 0 & {l_{i} /\left( {K_{si} A_{i} } \right)} \\ \end{array} } \right]L_{i}^{T} \\ \end{aligned} $$

where \( \varepsilon_{ij} \) and \( \sigma_{ij} \) are strain and stress tensor, \( \delta_{ij} \) is Kronecker symbol, \( \alpha_{s} \) is linear coefficient of thermal expansion of rock matrix, C is total flexibility matrix, \( C_{0} \) is flexibility matrix of porous media, \( C_{\text{fi}} \) is flexibility matrix of crack set i in a global coordinate system, \( C_{fi}^{\prime} \) is flexibility matrix of crack set i in a local coordinate system, \( K_{\text{ni}} \), \( K_{\text{si}} \), \( l_{\text{i}} \;{\text{and}}\;A_{\text{i}} \) are, respectively, normal stiffness, shear stiffness, connectivity rate, and spacing of cracks, \( L_{i} \) is a coordinate transformation matrix, E is Young’s modulus, and \( \mu \) is Poisson’s ratio.

The strain-stress increment equation with ice-water.

$$ d\sigma_{ij} = d\sigma_{ij}^{s} - \kappa_{c} dp\delta_{ij} $$
(162.19)

where \( \sigma_{ij}^{s} \) is stress tensor without frost-heaving action, \( \kappa_{\text{c}} \) is frost-heaving pressure transmitting coefficient.

The stress balance equation is simplified by equivalent method.

$$ - \nabla\upsigma = \rho_{\text{av}} \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {g} = \left( {\rho_{\text{f}} \varepsilon_{\text{p}} + \rho_{\text{d}} } \right)\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {g} $$
(162.20)

where \( \upsigma \) is total tress tensor, \( \rho_{\text{av}} \) is average density, \( \rho_{\text{f}} \) is fluid density, \( \rho_{\text{d}} \) is matrix density, \( \varepsilon_{\text{p}} \) is porosity.

4 Numerical Simulation and Analysis

Two models were set up targeted at uniform formation and that with artificial cleats, as shown in Fig. 162.10. Then, COMSOL Multiphysics was adopted to solve the THM coupling models. Impacts of 10 parameters on three physical fields were also investigated separately, including cryogenic fluid temperature and pressure, heat conductivity coefficient, specific heat capacity of the coal, the initial formation temperature, porosity, permeability, thermal expansion coefficient, density, and elasticity modulus of the coal.

Fig. 162.10.
figure 10

Coal reservoir model

Full size image

4.1 Factors Influencing Temperature Field

As shown in Table 162.1, the temperature around a well drops along with the decline of injection temperature and the increase of injection pressure. The higher the permeability is, the larger the scope of influence of the low-temperature field will, due to the rise of seepage velocity. In the case that porosity, heat capacity and density and heat conductivity coefficient of the coal are larger, heat absorption capacity of formation fluid and coal also becomes higher, and they absorb heat more rapidly. However, the scope of influence of low-temperature field narrows down.

Table 162.1 Impacts of all parameters on temperature around the well. (↑ for positive correlation, ↓ for negative correlation, - for little impact)
Full size table

4.2 Factors Influencing Seepage Field

As shown in Table 162.2, the lower the injection temperature is, the lower the frozen seepage velocity of formation water will be. When injection pressure and permeability go up, the seepage velocity also rises. If the porosity declines, the total mass of formation water within the range of seepage falls, low-temperature freezing speed accelerates, and the seepage velocity becomes lower. In the case that the initial formation temperature elevates, freezing of formation water requires a higher cool energy; as a consequence, it is less likely for such water to freeze so that the corresponding seepage velocity increases.

Table 162.2. Impacts of all parameters on seepage velocity around the well. (↑ for positive correlation, ↓ for negative correlation, - for little impact)
Full size table

4.3 Factors Influencing Stress Field

As shown in Table 162.3, increases in injection temperature and pressure are accompanied with a rise of seepage velocity, a broader reach of seepage pressure field, more significant influences on in situ stress and the improvement of such in situ stress. When porosity and permeability of formation changes, maximum and minimum stress fluctuate or reverse in areas near the well due to impacts of low-temperature injection.

Table 162.3. Impacts of all parameters on in situ stress around the well. (↑ for positive correlation, ↓ for negative correlation, - for little impact)
Full size table

4.4 Impacts of Cleat and Fractures on THM

Both cleat and fractures have rather significant influences on seepage, temperature, and stress fields of coal seam. Figure 162.11 is temperature fields at diverse injection time. As flow velocity of cryogenic fluid in cleat and fractures is dramatically higher than that inside the coal, low-temperature field is formed inside fractures in the first place; after the internal temperature of these fractures reduces, the formation temperature should be lowered along the surface of fracture. Cleat and fractures can promote not only the spread range of temperature field, but its spread velocity.

Fig. 162.11.
figure 11

Temperature fields at different injection time

Full size image

Simulation of seepage field under the THM coupling is presented in Fig. 162.12. Within the range of fractures, an obvious low permeability zone is formed due to freezing of formation water. It indicates that low temperature inside the coal seam can make ice temporary plugging come true, which is beneficial to increase net pressure for fractures diverting.

Fig. 162.12.
figure 12

Seepage velocity at different formation permeability structures

Full size image

As Figure 162.13 shown due to impacts of high net pressure incurred by ice temporary plugging within the fracture, initial stress near fractures and cleats can be rather high. In this period, it is clear that stress concentration occurs significantly within the cross section of cleat, which contributes to further initiate secondary fractures. As time goes on, net pressure inside the fracture increases so that the scope of influence of the stress field gradually spreads toward an area between two fractures.

Fig. 162.13.
figure 13

In situ stress field at different injection time

Full size image

Generally, cleat and fracture systems can effectively increase the scope of influence and diffusion velocity of low-temperature injection. Ice temporary plugging and stress concentration can form rapidly, which is beneficial to shear moving and rupture. In addition, cleat system of coal is able to improve the complexity of h fractures and increase SRV.

5 Conclusions

  1. 1.

    Based on low-temperature experiments, it is found that permeability of the coal in low temperature increases because of clean water frost heaving and matrix shrinkage. Low temperature makes water freezing and mechanical properties of the coal change. For cryogenic coal, Young’s modulus goes up and Poisson’s ratio reduces. After the ambient temperature was recovered, Young’s module declines while the Poisson’s ratio increases due to interior structural damage of the coal. The change rule of permeability under various stresses is obtained by complete stress–strain experiments.

  2. 2.

    A THM coupling model is established for the coal in conditions of low-temperature injection.

  3. 3.

    Change rules of temperature, seepage, and stress fields under the influence of diverse factors were analyzed. The temperature field is under the influence of injection parameters, porosity, and permeability as well as thermal parameters of the coal; as for the seepage field, major influencing factors on it include injection and mechanical parameters; at last, the stress field suffers impacts of treatment parameters, permeability, and elasticity modulus. Additionally, the cleat has the capability to dramatically increase the scope and diffusion rate of the influence of low-temperature fluids on temperature, seepage, and stress fields, which is in favor of secondary fracture initiation.