Fast Architecture of Modular Inversion Using Itoh-Tsujii Algorithm

Abstract

Modular inversion is a very common primitive used for the cryptographic computations. It is the most computation intensive unit which demands more resources as compared to other primitives. Inside the modular inversion arithmetic circuits, considerable speed up with optimized architecture is required. This paper proposes an optimized parallel architecture for Itoh-Tsujii modular inversion algorithm for the field GF(2²⁵⁶) by introducing 2³ blocks. The comparative results with conventional architecture show the 30% reduction in LUT requirement with 37% in combinational delay.

1 Introduction

Galois Field arithmetic grabs a substantial growth in recent years due to its applications in numerous cryptographic systems. The mathematics in the Galois Field basically includes three types of function: (i) modular addition (ii) modular multiplication and (iii) modular inversion. Among them, the modular inversion has gathered significant attention as its properties are proven to be useful in the field of cryptography. The Extended Euclidean algorithm and Fermat’s little theorem are two most popular methods for large finite field inversion [1]. For extension fields GF(2 ^m ), the Itoh-Tsujii inversion algorithm [2] is the best alternative. It reduces extension field inversion to inversion in binary field for which inversion operation becomes easier. The inversion in binary field is done either using look-up tables or with a series of binary squaring and multiplication operations. The Itoh-Tsujii algorithm is applicable to finite fields GF(2 ^m ) in normal basis representation. However, the original reference deals with composite fields GF((2 ⁿ ) ^m ). This paper applies the idea of Itoh-Tsujii algorithm to composite fields GF((2 ⁿ ) ^m ) in polynomial basis representation. Although the use of exponentiation operations required in the algorithm make it much complex for general fields in a polynomial basis representation. The exponentiations can be computed with a very low complexity for certain classes of finite fields.

This paper is organized as follows; Sect. 2 discusses brief overview of mathematical background and related work of Itoh-Tsujii Algorithm, equations for Fermat’s little algorithm and develops a method for realizing Itoh-Tsujii algorithm. Section 3 gives an idea about previous works done in this field. Section 4 proposes the modifications in hardware implementation of Itoh-Tsujii algorithm. Experimental results are discussed in Sect. 5 and Sect. 6 concludes the paper.

2 Mathematical Background

The extended Euclidean algorithm is a modification of the Euclidean algorithm used to calculate GCD of two numbers. It contains recursive division operations that are not suitable for hardware implementation. Hence, this procedure is mainly used in software that is based on modular inversion. The Fermat’s little theorem [1], on the other hand, is mainly based on exponentiation of numbers which are relatively more hardware oriented. This approach is used as a reference to implement modular inversion in hardware architectures. The following subsection describes the mathematics of Fermat’s little theorem.

2.1 Fermat’s Little Theorem Based Inversion in GF(2 ^m )

Let $\alpha$ is an element in a Galois Field GF(2 ^m ). The term $\alpha^{ - 1} \in GF(2^{m} )$ can be determined using following expression:

$$ \alpha^{ - 1} = \alpha^{{2^{m} - 2}} = \alpha^{{2(2^{m - 1} - 1)}} = \alpha^{{2(1 + 2 + \ldots + 2^{m - 2} )}} $$

(1)

Now the term 1 + 2+… + 2 ^m−2 can be factorized in two ways:

$$ \begin{aligned} & {\text{a}}.1 + 2\left( {1 + 2} \right).\left( {1 + 2^{2} + 2^{4} + \ldots + 2^{{{\text{m}} - 4}} } \right) \;{\text{if}}\,{\text{m}} - 1\,{\text{is}}\,{\text{odd}} \\ & {\text{b}}. \left( {1 + 2} \right).\left( {1 + 2^{2} + 2^{4} + \ldots + 2^{{{\text{m}} - 3}} } \right) \;{\text{if}}\,{\text{m}} - 1\,{\text{is}}\,{\text{even}} \\ \end{aligned} $$

(2)

2.2 Itoh-Tsujii Multiplicative Inversion in GF(2 ^m )

The Itoh-Tsujii algorithm is the modified form of Fermat’s little theorem. It evaluates the inversion using a series of recursive multiplications and squarings. Factorization of the expression $1 + 2 + 2^{2} + \ldots + 2^{{{\text{m}} - 2}}$ is carried out in such a way that minimum number of additions are required for implementation. For example, if m = 9, then the above expression can be decomposed as $1 + 2 + 2^{2} + \ldots + 2^{7} = \left( {1 + 2} \right).\left( {1 + 2^{2} } \right).\left( {1 + 2^{4} } \right)$. Since, it includes only three additions, it is most useful for hardware implementation. The number of plus signs in the decomposition of the statement $1 + 2+ \ldots + 2 ^{\text{m - 2}}$ denotes the number of multiplications required to implement the inversion. The job of this algorithm is to reduce the number of multiplication blocks as much as possible. The Itoh-Tsujii algorithm is based on the simple idea shown in (2) [3]. From these two expressions one can easily derive that the number of multiplications sufficient to determine the inverse of an element $\alpha \in GF(2^{m} )$.

Addition chain can also be used to reduce the number of multiplications [4]. It is a series of successive numbers formulated such that each number can be obtained by addition of two of its precedent numbers. An addition chain with minimum number of elements is generated and inverse can be computed using the expression

$$ \alpha^{ - 1} = [\beta_{m - 1} (\alpha )]^{2} $$

Where $\beta_{k} = \alpha^{{2^{k} - 1}}$

For simplicity, we shall denote $\beta_{k} (\alpha )$ by $\beta_{k}$. For the analytical approach, we use the identity

$$ \beta_{k + j} = (\beta_{k} )^{{2^{j} }} \beta_{j} = (\beta_{j} )^{{2^{k} }} \beta_{k} $$

(3)

For an element $\alpha \in GF(2^{m} )$ the inverse can be calculated as $\alpha^{ - 1} = [\beta_{255} (\alpha )]^{2}$ [5]. The term $\beta_{255} (\alpha )$ is obtained using (3) and an addition chain for 255 given by

$$ {\text{U}}_{255} = \left\{ {1,2,3,6,12,15,30,60,120,240,255} \right\} $$

3 Related Work

Hardware architectures for modular inversion are proposed in [1] for extended Euclidean algorithm and Itoh-Tsujii algorithm, using polynomial as well as Gaussian normal basis. The Itoh-Tsujii algorithm is used to determine the modular inversion for the field GF(2 ^m ). It was first proposed in [2] for the normal basis representation. A lot of work has been done to improve the original algorithm and make it feasible to analyse for different basis representation. In [4], a theoretical model to implement Itoh-Tsujii algorithm on a k-input LUT based FPGA is presented. This idea was further reviewed in [5], where a modified Itoh-Tsujii algorithm was proposed for efficient implementations on FPGA platforms. A fast implementation of the algorithm was proposed in [6] which can evaluate the inverse in 10 clock cycles for GF(2 ²³³ ) and GF(2 ⁴⁰⁹ ) fields. In [7], the Itoh-Tsujii algorithm is generalized for the fields GF(q ^m ) using polynomial basis representation. In this paper, we propose an optimized parallel architecture of Itoh-Tsujii algorithm for GF(2 ²⁵⁶ ) on FPGA platform.

4 Proposed Work

In this paper, the architecture of Itoh-Tsujii algorithm is modified in order to achieve efficient implementation on FPGA. We assess the analytical complexity of the addition chain shown in Table 1 as follows. The algorithm performs 10 iterations (since $\beta_{1} (\alpha )$ is $\alpha$ itself) and one field multiplication per iteration. Thus, we conclude that a total of 10 field multiplication calculations are required. This is much better than the Fermat’s little theorem implementation which requires 255 multiplications. However, the number of square blocks required is still very high. The Itoh-Tsujii algorithm requires 254 square computation blocks. A hybrid Karatsuba multiplier is used for multiplication operation in binary field. The efficiency of architecture is estimated in terms of maximum combinational delay and power. In case of conventional (parallel) architecture of Itoh-Tsujii algorithm, a large number of cascaded square blocks are used, which degrades the performance of the device. The use of Quad [5] and Octet block improves the speed of modified architecture.

Table 1. Inverse of $\alpha \in GF(2^{256} )$ using conventional squarer blocks [5]

4.1 Significance of Quad Circuits

Since the number of squaring operations is as high as 255 for conventional Itoh-Tsujii algorithm over the GF(2 ²⁵⁶ ), we need to improve the circuit in order to reduce the number of blocks for square operation. The quad circuit can be used to overcome this problem [6]. A quad circuit is a block which performs the operation of raising the input by a power of four instead of squaring operation. In Itoh-Tsujii algorithm, we can use any exponentiation circuit of the form 2ⁿ. In this paper, the advantages of using 2² circuits on FPGAs for exponentiation in fields with irreducible trinomials are observed. Quad circuits offer the best LUT utilization for an FPGA with four or six input LUTs. The irreducible trinomial for the field is x ⁹ + x + 1. We observe from Table 2 that the quad circuit’s LUT requirement significantly reduced by around 25% [5]. This is because the quad circuit utilizes FPGA resources better than the squarer. Moreover, since quad is a single stage combinational circuit, both circuits have the same delay of one LUT. These observations are scalable to larger fields like GF(2 ²³³ ) and GF(2 ¹⁹³ ) [4].

Table 2. LUTs required for a squarer and quad circuit for GF(2 ⁹ ) [5]

The limitation of using quad circuits instead of squarers depends on the fields generated by irreducible polynomial. When irreducible pentanomials are used for generating the field instead of irreducible trinomials, the saving of area is almost negligible due to the fact that a quad circuit and two cascaded squarers will have about the same area. Unfortunately there is no irreducible trinomial for GF(2 ²⁵⁶ ) field. However, the combination of squarer and quad computation blocks, significant improvement in overall area delay product is possible. Based on these observations we propose a hybrid-Itoh-Tsujii algorithm for fields generated by irreducible pentanomials which use quad exponentiation circuits as well as squarer circuits. Table 3 shows the evaluation of $\beta_{255} (\alpha )$ using an improved Itoh-Tsujii algorithm implemented using hybrid approach.

Table 3. Inverse of $\alpha \in GF(2^{256} )$ using quad blocks [5]

4.2 Significance of 2 ³ Circuits

The idea of combining multiple squarer blocks into a single unit is further explored using a 2³ circuit. The proposed logic block is a combinational unit, mathematically equivalent to three cascaded squarer blocks. However, combining multiple blocks into a single unit results in efficient LUT utilization and less computation time. Also, 3 completly divides 255, the architecture consists of 2³ blocks only, except at the initial stage for precomputation of the term $\alpha^{7}$ and the final stage of inversion [5]. Table 4 shows the evaluation of $\beta_{255} (\alpha )$ using an optimized Itoh-Tsujii algorithm architecture implemented using 2³ blocks. It is observed that the cascade blocks of Quads and Squarer block shown in Table 3 is completely eliminated.

Table 4. Inverse of $\alpha \in GF(2^{256} )$ using Octet blocks

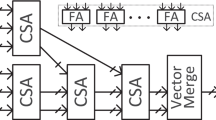
The architecture for Itoh-Tsujii algorithm considering a special class of irreducible polynomial, $m\left( x \right) = x^{256} + x^{10} + x^{5} + x^{2} + 1$ for GF(2 ²⁵⁶ ) is presented in Fig. 1. It uses field multiplication, field squaring and field Octet operators as its primary building blocks. We also show how this version of the algorithm can be parallelized to improve the efficiency when implemented in hardware platforms.

Fig. 1.

Architecture of ITA for GF(2 ²⁵⁶ ) using Octet Blocks

5 Result and Discussions

The comparison of performance of various exponentiation blocks on the binary fields with irreducible polynomials is shown in Table 5. The use of 2ⁿ circuit improves the performance of exponentiation. For Virtex-6 and 7, both area and speed of Octet architecture is improved. This is due to higher utilization factor of respective FPGAs. The purpose of optimization of FPGA design is to ensure that the resources of the device are utilized completely. The smallest programmable unit in the FPGA is the lookup table, which generally has four (or six) inputs. The LUTs are used to implement any Boolean logic function of four (or six) variables. When a logic function with less than four (or six) variables is implemented using LUT, the LUT is underutilized. An optimized implementation is obtained when each LUT is utilized up to the maximum extent. The proposed 2³ blocks are best-utilized using Virtex-6 and Virtex-7 FPGA platforms.

Table 5. Comparison of squarer and quad circuits on xilinx virtex FPGAs

Table 6 compares various parameters of our architectures with generic architectures. These results show that in case of finite fields with irreducible pentanomial, the parameters of the circuit can be improved enough to be compared with finite fields with irreducible trinomials. The results show almost 40% improvement in cumulative delay when octet architecture is used.

Table 6. Comparison with NIST binary fields having irreducible trinomials

6 Conclusion

This paper optimizes the parallel Itoh-Tsujii inverse algorithm to implement on FPGA platforms using Squarer, Quad and Octet blocks. Hybrid Itoh-Tsujii algorithm is put forward for the fields generated by irreducible pentanomials. Area-delay product is considerably reduced by using Octet block. The octet block of proposed architecture requires 30% less area and increases the speed of operation by 37%. An FPGA architecture of the Octet Itoh-Tsujii algorithm architecture results in 40% and 20% improved delay as compared with squarer and quad architectures respectively.