Keywords

1 Introduction

The availability of a huge amount of data from infrastructure networks, e.g., water distribution networks (WDNs), continuously encourages researchers expanding the technical tasks that water companies could consider in order to increase service reliability and quality [1]. These complex networks present many problems related with their nonhomogeneous behavior and, simplifying these systems into smaller monitored modules/districts, could reduce many of management difficulties (e.g., managing pressures, demands, leakages, rehabilitation works, etc.). Several approaches to segmentation have been proposed [2,3,4,5,6,7,8,9,10,11] for identifying the optimal division of the network into districts with respect to WDN characteristics (e.g., diameter, leakages, elevations, etc.) and topology.

A way to segment networks, using a paradigm from complex network theory [12, 13], is to refer to community detection strategies. The most popular community detection strategy is based on modularity index [14], i.e., a descriptive measure of topology that relies strictly on the network structure. Newman [14] firstly proposed the modularity index as metric to measure the propensity of the network division into modules. High values of the modularity index indicate a better identification of communities and to the maximum value of the modularity corresponds the maximum degree of segmentation [13, 15]. The original formulation of the modularity index for segmentation of immaterial networks has been proposed by Barthélemy [16], which stressed the need for paying attention to the uncritical application of complex network tools to infrastructure networks, i.e., networks strongly affected by a number of physical constraints (two-dimensionality, urban structure and planning, etc.). Afterwards, Giustolisi, and Ridolfi [17] tailored the original modularity index in order to obtain a WDN segmentation-oriented modularity index by means of the topological incidence matrix of WDNs (commonly used to describe the network topology of the hydraulic systems). They developed a cut position-sensitive index in order to account for the actual position along pipes (i.e., close to ending nodes instead of the middle of pipes) of devices generating districts, introducing the pipe weights (i.e., asset and/or hydraulic information at pipe level) in the formulation of the segmentation-oriented modularity index. The tailored modularity index allows dividing the network into districts similar to each other with respect to the assumed weight (e.g., pipe lengths, leakages, etc.). Giustolisi and Ridolfi [17] also proposed the extension of the tailored modularity to the division into districts having internal similar attribute (e.g., material, diameter, age, average elevation, average pressure, etc.). Since the proposed segmentation-oriented modularity index was affected by a resolution limit [18], i.e., a limit to the ability in identifying small districts whose size is related to the network dimension, Giustolisi, and Ridolfi [19] proposed the infrastructure modularity index. They demonstrated that the infrastructure index increases the resolution in identifying small districts also in large size networks and is unbiased with respect to the optimal planning considering already existing devices in the network.

Simone et al. [15] extended the concepts of network segmentation to pressure sampling design, introducing the sampling-oriented modularity index and the concept of “pressure” measurement districts extending the concept of “flow” measurement districts related to the “classic” district metering areas. This way the need of dividing a WDN considering pressure meters was introduced. Furthermore, the strategy has several analogies with the optimal segmentation design for “classic” district monitoring areas (DMAs) in order to allow the integration of the WDN division in districts to account for the mass and energy standpoints, which drives the hydraulic behavior of the system. Planning is a continuous and sequential process supporting management of WDNs, which is driven by budget and available information about the hydraulic system. Therefore, the budget and information uncertainties ask for flexibility of plans, i.e., a multi-objective optimal planning of sensor placement should account for the fact that a water company will start installing a lower number of devices which will be increased in the future also based on the information coming from the installed monitoring system itself. Therefore, the multi-objective strategy needs to provide solutions, which, increasing the number of devices, are one the starting point of the other. In other words, both optimal segmentation and optimal sampling design need to provide solutions which are nested, i.e., each scenario of districts corresponding to a greater resolution solution (i.e., greater number of districts) has to correspond to a nested scenario with respect to lower resolution solutions. Another issue is the integration of the optimal segmentation with the optimal sampling design.

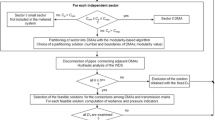
The present paper proposes a novel two-phase strategy for optimal flow and pressure sensors placement. The first step involves the optimal segmentation design in order to achieve scenarios of optimal positions of “conceptual cuts” dividing the network in “flow” measurement districts. Actually, the segmentation is the first phase to identify “classic” DMAs, which are formed deciding to install in the “conceptual cuts” flow meters or closed gate valves for example in order to reduce leakages [1].

The second phase involves the optimal sampling design [15] starting from the placement of pressure meters indicated by the optimal segmentation [17]. This way the “classic” DMAs (or “flow” measurement districts) are bounded by pressure meters, and the optimal sampling involves planning further pressure meters internal to “classic” DMAs. In other words, the optimal sampling starts assuming existing pressure meters on the boundary of the “flow” measurement districts of the optimal segmentation and the optimal planning of further pressure meters identifies internal “pressure” measurement districts. Therefore, the integrated optimal sensor placement allows planning “classic” DMAs coinciding with “pressure” DMAs once the pressure meters are assumed at their boundary. Then, other “pressure” DMAs [15] are designed internal to “classic” ones. The integrated strategy for optimal placement of flow and pressure meters is demonstrated and discussed using a real network of the Apulia region in Italy.

2 Modularity Index for WDN

The modularity index, Q, is a measure of the strength of a network division in modules. Newman and Girvan [10] proposed the first formulation of the modularity index:

$$Q = \frac{1}{{2n_{\text{l}} }}\sum\limits_{ij} {\left( {A_{ij} - P_{ij} } \right)\delta } \left( {{\rm M}_{i} ,\,{\rm M}_{j} } \right) = \frac{1}{{2n_{\text{l}} }}\sum\limits_{ij} {\left( {A_{ij} - \frac{{k_{i} k_{j} }}{{2n_{\text{l}} }}} \right)\delta } \left( {{\rm M}_{i} ,\,{\rm M}_{j} } \right)$$
(1)

where n l is the number of links/edges (pipes for WDN) in the network, A ij are the elements of the adjacency matrix, P ij is the expected fraction of links between nodes i and j in the random network, M i is the identifier of network modules, δ is the function to apply the summation to the elements of the same module (i.e., δ = 1 if M j  = M i and δ = 0 otherwise), k i (k j ) is the degree of the i-th (j-th) node and summation runs on all the possible node couples (i, j), with i ≠ j.

The term Σ ij A ij δ(M i , M j )/2n i represents the fraction of links connecting nodes that are in the same module and the term Σ ij k i k j δ(M i , M j )/2n i represents the expected fraction of links connecting nodes in the same module in a random graph having the same degree distribution of the original graph [20].

The classic formulation of the modularity index, tailored for WDNs using the general topological incidence matrix (A pn ), is

$$Q = 1 - \frac{{n_{\text{c}} }}{{n_{\text{p}} }} - \sum\limits_{m = 1}^{{n_{\text{m}} }} {\left[ {\sum\limits_{i = 1}^{{n_{\text{n}} }} {\frac{{\left( {\left| {{\mathbf{A}}_{pn}^{T} } \right|{\mathbf{u}}_{\text{p}} } \right)_{i} \delta \left( {{\rm M}_{m} ,\,{\rm M}_{i} } \right)}}{{2n_{\text{p}} }}} } \right]^{2} }$$
(2)

where u p is the unit vector, n p is the number of pipes, n n is the number of nodes, n m is the number of modules and n c is the number of pipes linking modules, i.e., the number of cuts in the middle of the pipes. The modularity index formulation can be divided into two components:

$$\begin{aligned} Q & = Q_{1} + Q_{2} \\ Q_{1} & = 1 - \frac{{n_{\text{c}} }}{{n_{\text{p}} }}\quad \quad Q_{2} = - \sum\limits_{m = 1}^{{n_{\text{m}} }} {a_{\text{m}}^{2} } = - \sum\limits_{m = 1}^{{n_{\text{m}} }} {\left[ {\sum\limits_{i = 1}^{{n_{\text{n}} }} {\frac{{\left( {\left| {{\mathbf{A}}_{pn}^{T} } \right|{\mathbf{u}}_{\text{p}} } \right)_{i} \delta \left( {{\rm M}_{m} ,\,{\rm M}_{i} } \right)}}{{2n_{\text{p}} }}} } \right]^{2} } \\ \end{aligned}$$
(3)

where Q 1 represents the fraction of the pipes with both the end nodes belonging to the m-th module and a m is the fraction of pipes having at least one end node in the module m. The pipes dividing modules are counted ½ when computing a. Therefore, a m is half the summation, divided by n p, of the number of pipes connected to nodes (degree) falling in the module m.

Q 1 strictly decreases with the number of cuts and penalizes the excess of cuts for a given number of modules and Q 2 generally is an increasing function of the number of modules (and generally of n c), driving the search to the set of most similar modules for a given number of cuts. Those cuts are virtual and relate to the division into modules (“flow” measurement districts), i.e., the metric Q can be explained as a measure of the module decomposition of the adjacency matrix of the network. The maximization of modularity index in Eq. (3) implies the minimization of the number of cuts in order to obtain the highest number of modules, which are similar to each other. The formulation of the modularity index was then tailored in order to develop a cut position-sensitive metric [17]. In fact, the segmentation for WDNs aims at designing DMAs through the installation of real devices (closing gates or flow meters), that are installed close to nodes where vaults or manholes are located [1]. Therefore, the “conceptual cuts” of the modularity index need to be close to the end nodes of pipes, whereas the original modularity assumes that they are in the middle. Then, the segmentation-oriented formulation of the modularity index [17] is:

$$Q\left( {{\mathbf{w}}_{\text{p}} } \right) = \left\{ {1 - \frac{{n_{\text{c}} }}{{n_{\text{p}} }}} \right\} + \left\{ { - \sum\limits_{m = 1}^{{n_{\text{m}} }} {\left[ {\sum\limits_{k = 1}^{{n_{\text{p}} }} {\frac{{\left( {{\mathbf{w}}_{\text{p}} } \right)_{k} \delta \left( {{\rm M}_{m} ,\,{\rm M}_{k} } \right)}}{W}} } \right]}^{{{\kern 1pt} 2}} } \right\} = Q_{1} + Q_{2}$$
(4)

where n c is the number of pipes linking modules of the network, namely the number of “conceptual cuts” in the network (i.e., the decision variables of the WDN segmentation problem) and n m is the number of network modules. The summation inside the square brackets is related to pipe weights stored in the vector w p, whose sum is W, and Kronecker’s δ function makes that the sum refers only to the weights of pipes belonging to the m-th module (i.e., δ = 1 if M m  = M k and δ = 0 otherwise).

It is worth noting that the term Q 1 of Eq. (4) decreases with the number of cuts, while Q 2 generally increases with the number of modules and, for a given number of modules, it increases with the similarity between modules. The resolution limit problem [18] for both original and segmentation-oriented modularity indexes was analyzed by Giustolisi and Ridolfi [19], whose proposed a new infrastructure segmentation-oriented modularity index to overcome such limit:

$$IQ\left( {{\mathbf{w}}_{\text{p}} } \right) = 1 - \frac{{n_{\text{c}} - \left( {n_{\text{act}} - 1} \right)}}{{n_{\text{p}} }} - \sum\limits_{m = 1}^{{n_{\text{m}} }} {\left[ {\sum\limits_{k = 1}^{{n_{\text{p}} }} {\frac{{\left( {{\mathbf{w}}_{\text{p}} } \right)_{k} \delta \left( {{\rm M}_{m} ,\,{\rm M}_{k} } \right)}}{W}} } \right]}^{{{\kern 1pt} 2}}$$
(5)

where nact is the actual number of modules satisfying given constraints (e.g., the minimum length of the modules, the minimum number of pipes, etc.). Accordingly, the same authors demonstrated that the infrastructure modularity resolves the resolution limit, but might require the definition of technical constraints to avoid a resolution of the segmentation beyond the required by specific technical tasks [19]. The maximum value of the infrastructure modularity index IQ results:

$$IQ_{\hbox{max} } = 1 - \frac{1}{{n_{\text{m}} }}$$
(6)

It is worth noting that the maximum value of IQ is asymptotically upper bounded to unit (for an infinite number of modules) as well as in the case of Q, while IQ = 0 for an unsegmented network, i.e., it strictly depends on the number of modules. A variety of purposes for designing “flow” monitoring districts exists, e.g., managing leakage management [1]. Consequently, various pipe weights can be defined considering the specific management task. For example, it is possible to define w k  = L k  = pipe length; w k  = \({\alpha L_{k} P_{k}}^{\alpha }\) = background leakages along a pipe; etc. Giustolisi and Ridolfi [17] also proposed a segmentation-oriented metric, named attribute based, measuring the similarity into each module with respect to a specified attribute, which is not length based:

$$Q_{a} = 1 - \frac{{n_{c} }}{{n_{p} }} - \sum\limits_{m = 1}^{{n_{m} }} {\left[ {\frac{{\sum\nolimits_{k = 1}^{{n_{p} }} {\left| {{\mathbf{a}}_{p} - \bar{a}\left( {{\rm M}_{m} } \right)} \right|_{k} \delta \left( {{\rm M}_{m} ,{\rm M}_{k} } \right)} }}{{\sum\nolimits_{k = 1}^{{n_{p} }} {\left| {{\mathbf{a}}_{p} - \bar{a}\left( {\rm N} \right)} \right|_{k} } }}} \right]^{2} }$$
(7)

where a p is the vector of pipe attributes, ā(N) is the mean value of the pipe attributes of the network N, i.e., of a p, and ā(M m ) is the mean value of the pipe attributes in M m . Function δ limits the summation of the pipe attributes to the elements belonging to the same module.

Giustolisi et al. [20] extended the infrastructure modularity index to attribute-based infrastructure segmentation index:

$$IQ_{a} = 1 - \frac{{n_{\text{c}} - \left( {n_{\text{act}} - 1} \right)}}{{n_{\text{p}} }} - \sum\limits_{m = 1}^{{n_{\text{m}} }} {\left[ {\frac{{\sum\nolimits_{k = 1}^{{n_{\text{p}} }} {\left| {{\mathbf{a}}_{\text{p}} - \bar{a}\left( {{\rm M}_{m} } \right)} \right|_{k} \delta \left( {{\rm M}_{m} ,\,{\rm M}_{k} } \right)} }}{{\sum\nolimits_{k = 1}^{{n_{\text{p}} }} {\left| {{\mathbf{a}}_{\text{p}} - \bar{a}\left( {\rm N} \right)} \right|_{k} } }}} \right]^{2} }$$
(8)

Afterwards, Simone et al. [15] proposed a novel modularity index named sampling-oriented modularity for an optimal sampling design approach. The segmentation-oriented and sampling-oriented modularity metrics differ for the approach of identifying monitoring districts in WDNs. The first approach segments the network considering pipes, i.e., by means of “conceptual cuts”, the second considers “pressure nodes”. This way the extension of the segmentation-oriented modularity to sampling can be performed by substituting the concept of “pressure nodes” to “conceptual cuts” as follows:

$$\begin{aligned} Q_{\text{s}} \left( {{\mathbf{w}}_{\text{p}} } \right) & = 1 - \frac{{n_{\text{obs}} }}{{n_{\text{n}} }} - \sum\limits_{m = 1}^{{n_{\text{m}} }} {\left[ {\sum\limits_{k = 1}^{{n_{\text{p}} }} {\frac{{\left( {{\mathbf{w}}_{\text{p}} } \right)_{k} \delta \left( {{\rm M}_{m} ,\,{\rm M}_{k} } \right)}}{W}} } \right]}^{2} \\ IQ_{\text{s}} \left( {{\mathbf{w}}_{\text{p}} } \right) & = 1 - \frac{{n_{\text{obs}} - \left( {n_{\text{act}} - 1} \right)}}{{n_{\text{n}} }} - \sum\limits_{m = 1}^{{n_{\text{m}} }} {\left[ {\sum\limits_{k = 1}^{{n_{\text{p}} }} {\frac{{\left( {{\mathbf{w}}_{\text{p}} } \right)_{k} \delta \left( {{\rm M}_{m} ,{\rm M}_{k} } \right)}}{W}} } \right]}^{2} \\ Q_{{{\text{a}} - {\text{s}}}} \left( {{\mathbf{a}}_{\text{p}} } \right) & = 1 - \frac{{n_{\text{obs}} }}{{n_{\text{n}} }} - \sum\limits_{m = 1}^{{n_{\text{m}} }} {\left[ {\frac{{\sum\nolimits_{k = 1}^{{n_{\text{p}} }} {\left| {{\mathbf{a}}_{\text{p}} - \bar{a}\left( {{\rm M}_{m} } \right)} \right|_{k} \delta \left( {{\rm M}_{m} ,\,{\rm M}_{k} } \right)} }}{{\sum\nolimits_{k = 1}^{{n_{p} }} {\left| {{\mathbf{a}}_{p} - \bar{a}\left( {\rm N} \right)} \right|_{k} } }}} \right]^{2} } \\ IQ_{{{\text{a}} - {\text{s}}}} \left( {{\mathbf{a}}_{\text{p}} } \right) & = 1 - \frac{{n_{\text{obs}} - \left( {n_{\text{act}} - 1} \right)}}{{n_{\text{n}} }} - \sum\limits_{m = 1}^{{n_{\text{m}} }} {\left[ {\frac{{\sum\nolimits_{k = 1}^{{n_{\text{p}} }} {\left| {{\mathbf{a}}_{\text{p}} - \bar{a}\left( {{\rm M}_{m} } \right)} \right|_{k} \delta \left( {{\rm M}_{m} ,{\rm M}_{k} } \right)} }}{{\sum\nolimits_{k = 1}^{{n_{p} }} {\left| {{\mathbf{a}}_{p} - \bar{a}\left( {\rm N} \right)} \right|_{k} } }}} \right]^{2} } \\ \end{aligned}$$
(9)

where n obs are the number of “pressure nodes”. The number of modules n m has the same meaning of the segmentation case, as well as the actual number of modules matching the technical constraints to avoid excessive resolution of the segmentation, n act, of the infrastructure version. Note that the term Q 2 is unchanged because it refers to the characteristics of modules, which are now created by removed nodes. Therefore, the Eq. (9) define, respectively, the sampling-oriented modularity Q s, sampling-oriented infrastructure modularity IQ s, sampling-oriented attribute-based modularity Q a–s and sampling-oriented infrastructure attribute-based modularity IQ a–s. The first two divide the network in “pressure” monitoring districts similar to each other with respect to the assumed pipe weights, while the last two divide the network in “pressure” monitoring districts having similar internal characteristics with respect to the assumed pipe weights.

3 Monitoring Strategy

The division of WDNs into districts by means of “flow” and “pressure” monitoring is a useful practice for system management. In fact, a rationale system of flow and pressure observations allows monitoring and analyzing the hydraulic system behavior. For example, it is useful for assessing leakage level and designing optimal actions for leakage management activities [1].

To this purpose, it is here proposed an optimal monitoring strategy, i.e., an optimal sensor placement strategy. Two main phases drive the strategy:

  1. (i)

    The optimal segmentation design [17] minimizes the number of “conceptual cuts” versus the maximization of the segmentation-oriented modularity index reported in Eqs. (5) or (8). It returns a Pareto set of solutions, which are optimal with respect to the number of “conceptual cuts” (i.e., the candidate positions for flow meters, but also for pressure reduction valves and closed gates once the DMA are built). The multi-objective optimization is constrained to search for nested solutions providing flexibility to the entire procedure. This means that each segmentation solution can be generated starting from the one having the lowest number of districts increasing number of districts, which are nested in the previous segmentation. Such feature allows dynamical planning of the segmentation increasing over time its resolution (i.e., the number of districts) considering budget uncertainty and growing of the system knowledge.

  2. (ii)

    The optimal sampling design starts from the selected optimal segmentation solution assuming pressure meters at the boundary nodes of each district forming the “classic DMAs”. This way, the optimal sampling design returns the placement of pressure meters inside the “classic” DMAs forming internal “pressure” DMAs. The optimal sampling design [15] minimizes the number of “pressure nodes” versus the maximization of one of the sampling-oriented modularity index reported in Eq. (9). Clearly, the procedure is biased by the assumed pressure meters at the boundary of the already designed “flow” districts.

For the sake of clarity, the strategy is here applied to a very small network, named Apulian [15].

The first phase of the strategy, i.e., the optimal segmentation design, returns a Pareto set of optimal segmentation solutions by solving the following problem:

$$\left\{ {\begin{array}{*{20}l} {[M,\,n_{\text{c}} ,\,n_{\text{act}} ] = {\text{Connectivity}}\left( {I_{\text{c}} ,\,\left| {{\mathbf{A}}_{\text{np}} } \right|} \right)} \hfill \\ {f_{1} = \hbox{max} \left\{ {IQ\left( {{\mathbf{w}}_{\text{p}} } \right)} \right\} = \hbox{max} \left\{ {IQ\left( {{\mathbf{w}}_{\text{p}} } \right) = 1 - \frac{{n_{\text{c}} - \left( {n_{\text{act}} - 1} \right)}}{{n_{\text{p}} }} - \sum\limits_{m = 1}^{{n_{m} }} {\left[ {\sum\limits_{k = 1}^{{n_{p} }} {\frac{{\left( {{\mathbf{w}}_{\text{p}} } \right)_{k} \delta \left( {{\rm M}_{m} ,{\rm M}_{k} } \right)}}{W}} } \right]}^{{{\kern 1pt} 2}} } \right\}} \hfill \\ {f_{2} = \hbox{min} \left\{ {n_{\text{c}} } \right\}} \hfill \\ \end{array} } \right.$$
(10)

where A np is the incidence matrix, I c is the set of n c cuts in the network, the Connectivity(I c, |A np|) stands for component analysis of the undirected graph for the given cuts, n act indicate the cuts that are used to separate modules and W is the sum of pipe weights stored in the vector w p [17].

It is important to note that the existing flow meters (e.g., of pumps, tanks, reservoirs, etc.) are considered as constraints corresponding to existing “conceptual cuts”. It represents an initial configuration biasing the optimization; therefore, the proposed procedure is flexible with respect to the applications in real hydraulic systems [17, 19]. Figure 1 reports a “flow” districts scenario corresponding to the optimal solution having the maximum value of the segmentation-oriented modularity. The “conceptual cuts”, equal to nine, divide the network into five “flow” measurement districts, i.e., “classic” DMAs once the closed gates are installed [1].

Fig. 1
figure 1

Apulian network: a scenario of “flow” measurement districts. Each district corresponds to a color

Full size image

As introduced above, the “conceptual cut” close to the unique reservoir of the network is assumed because the correct practice asks for a flow measurement. Therefore, this existing device is not counted during the optimization procedure, which starts from an initial configuration that already contains the “conceptual cut” related to the flow observation at the reservoir.

The second phase involves the optimal sampling design starting from the placement of pressure meters indicated by the optimal segmentation. In fact, “conceptual cuts” identified in the first phase suggests the placement of pressure meters at the boundary of the “flow” districts as reported in Fig. 2.

Fig. 2
figure 2

Apulian network: pressure meters on the boundary of districts of Fig. 1

Full size image

This way, the “flow” districts of Fig. 1 becomes “pressure” districts [15], i.e., the “classic” DMAs coincide with the “pressure” DMAs. The sampling design phase have to be completed, for large size networks, by planning further internal pressure meters identifying “pressure” districts internal to “flow” ones. The problem to solve is similar to that of Eq. (10):

$$\left\{ {\begin{array}{*{20}l} {[M,\,n_{\text{obs}} ,\,n_{\text{act}} ] = {\text{connectivity}}\left( {I_{\text{c}} ,\,{\mathbf{L}}} \right)} \hfill \\ {f_{1} = \hbox{max} \left\{ {IQ_{\text{s}} \left( {{\mathbf{w}}_{\text{p}} } \right)} \right\} = \hbox{max} \left\{ {1 - \frac{{n_{\text{obs}} - \left( {n_{\text{act}} - 1} \right)}}{{n_{\text{n}} }} - \sum\limits_{m = 1}^{{n_{\text{m}} }} {\left[ {\sum\limits_{k = 1}^{{n_{\text{p}} }} {\frac{{\left( {{\mathbf{w}}_{\text{p}} } \right)_{k} \delta \left( {{\rm M}_{m} ,\,{\rm M}_{k} } \right)}}{W}} } \right]}^{{{\kern 1pt} 2}} } \right\}} \hfill \\ {f_{2} = \underbrace {\hbox{min} }_{{I_{\text{c}} }}\left\{ {n_{\text{obs}} } \right\}} \hfill \\ \end{array} } \right.$$
(11)

where L is the edge adjacency matrix, I c is the set of n obs (i.e., pressure nodes) and connectivity(I c, A) stands for component analysis of the graph with respect to edge matrix. Note that being the decision variables related to new pressure meters to be installed, in this case, the pressure measurements from segmentation and, e.g., of control valves, pumps, tanks, reservoirs, etc., are considered as constraints. The case study will show this last part of the strategy.

4 Case Study

The optimal monitoring strategy is here presented using a real WDN serving a town in Southern Italy with about 24,000 inhabitants. The network is composed of 2099 pipes and 1762 nodes and its layout is reported in Fig. 3. The node elevation ranges between 302 and 218 m a.s.l. and the highest point of the hill where the town is located is about 261 m a.s.l. The network is served by gravity from the unique reservoir, which is about 4 km far from the distribution network, by two feeding lines having, respectively, nominal diameters of 500 and 300 mm.

Fig. 3
figure 3

Network layout

Full size image

The optimal segmentation returned a Pareto set of optimal segmentation solutions (Fig. 4), where the black circles represent the optimal tradeoffs between the number of “conceptual cuts” (x-axis) on the border of each “flow” measurement district versus the maximization of the segmentation-oriented modularity (y-axis). It is worth noting that the number of “conceptual cuts” (x-axis) starts from a value equal to one, to indicate that the strategy starts from a basic configuration that already contains a cut, a flow meter, close to the reservoir.

Fig. 4
figure 4

Pareto set of optimal segmentation solutions

Full size image

The solution with the maximum number of “conceptual cuts” corresponds to the maximum value of the segmentation-oriented modularity index. A number of “conceptual cuts” equal to 76 and a number of “flow” districts equal to 19 characterize the last solution (Fig. 5). It is here selected as the basis for the second phase also considering flexibility of the segmentation solutions.

Fig. 5
figure 5

Colored scenario of flow measurement districts corresponding to the maximum value of the segmentation-oriented modularity

Full size image

The optimal sampling is biased by the decision to place pressure meters on the boundary of the “flow” districts, i.e., in nodes adjacent to “conceptual cuts”, see Fig. 6.

Fig. 6
figure 6

Pressure meters at the boundary of the “flow” districts of Fig. 5

Full size image

The task of the optimal sampling is then to plan internal “pressure” measurement districts. The two-objective optimization returns a Pareto set of optimal sampling solutions (Fig. 7), where the black circles represent the optimal tradeoffs between the number of pressure nodes (x-axis) on the border of each “pressure” district versus the maximization of the sampling-oriented modularity (y-axis). It is worth noting that the number of “pressure nodes” (x-axis) starts from a value equal to 75, to indicate that the strategy starts from the pressure meters conceived at the boundary of “flow” measurement districts.

Fig. 7
figure 7

Pareto set of optimal sampling solutions

Full size image

The solution with the maximum number of “pressure nodes”, equal to 104, and a number of “pressure” districts equal to 78 characterizes the scenario having the maximum value of the sampling-oriented index.

The optimal monitoring solution for this network, with flow and pressure observations, is reported in Fig. 8, where the red squares represent the location of existing pressure measurements close to flow ones and the blue squares represent the location of pressure measurements from the optimal sampling.

Fig. 8
figure 8

Optimal monitoring solution

Full size image

Figure 9 expands a small portion of the network and shows the configurations from the first phase to the second one. The left panel of Fig. 9 shows the “pressure” districts based on the segmentation procedure and the right panel shows the additional “pressure” districts based on the optimal sampling procedure, which divides internally the existing ones.

Fig. 9
figure 9

“Pressure” districts based on segmentation (left panel) and internal “pressure” districts based on optimal sampling (right panel)

Full size image

5 Conclusions

The integrated planning of the monitoring system strategy is conceived to support water utilities for different management targets, choosing the optimal solution considering, for example, the available budget for flow/pressure observations.

The present work proposes a novel methodology, with a two-phase strategy for optimal placement of flow and pressure meters. The first phase deals with the optimal segmentation using the segmentation-oriented modularity index in order to plan flow and pressure meters at the boundary of “classic” DMAs.

The second phase, starting from the scenario of pressure meters of the first phase, deals with the optimal sampling design using the sampling-oriented modularity. The second phase allows designing “pressure” DMAs, which are internal to “classic” DMAs. They are also “pressure” DMAs because of the assumption to install pressure meters at their boundary nodes.