1 Introduction

Recently a comprehensive measurement of agent behavior can be conducted based on high-resolution data on socioeconomic systems due to the development of information and communication technology. In particular, we want to consider a problem that we need to deal with the collective behavior of millions of nodes contribute to the observable dynamical features of such a complex system (de Menezes and Barabási 2004).

To do so, it is necessary to develop an adequate model both which considers states of agent behavior from the comprehensive point of view and which is as simple as one can estimate its parameters from actual data under assumptions. Specifically in socioeconomic activities, if we regard the situation where people exchange things, money, and information with each other as a network, then it further seems to be fruitful to study such social or economic systems from a network point of view.

To make advances in this direction, we need to treat structure on the basis of information transmission among heterogeneous agents in a given socioeconomic system from a limited amount of available data without precise knowledge on communication networks.

Several networks relating to human activity can be described as bipartite graphs with two kinds of nodes as shown in Fig. 1. For example, it is known that financial markets (financial commodities and participants), blog systems (blogs and bloggers), and economic systems (firms and goods/consumers) can be described as a directed bipartite graph (Lambiotte et al. 2007; Chmiel et al. 2007; Sato 2007; Sato and Hołyst 2008).

Fig. 1
figure 1

A conceptual illustration of social systems where M agents (B node) communicate with one another in K groups (A node)

Full size image

Such a bipartite network is recognized by observers when constituents are transmitted between two kinds of nodes. Links are recognized by observers when a constituent moves from one node to another node. Therefore bipartite network representation also seems to be one of our cognitive categories such as causality, time and space, intensity, quantity, and so on.

This chapter considers a model-based comparative measurement of collective behavior of groups based on their activities (Sato 2017). Specifically, a descriptive multivariate model of a financial market is proposed from a comprehensive point of view. Using comprehensive high-resolution data on the behavior of market participants, correlations of log returns and quotations (transactions) are analyzed on the basis of theoretical insights from the proposed model.

As a subject, we focus on financial markets which are attracting numerous researchers in various fields since they are of complex systems consisting of various types of heterogeneous agents. In the context of finance, the normal mixture hypothesis (or more generally “mixture of distribution hypothesis”) has been proposed as an alternative explanation for the description of return distribution of financial assets by several studies (Mandelbrot and Taylor 1967; Clark 1973; Tauchen and Pitts 1983; Richardson and Smith 1994). They have considered trading volume or the number of transactions (or quotations) as a proxy of the latent number of information arrivals. The proposed model may lead to better understanding of dynamics for return-volume relationship including volatility persistence (Lamoureux and Lastrapes 1990; Andersen 1996; Liesenfeld 1998; Watanabe 2000).

Cloud-based services can be used to provide various kinds of real-world applications. In fact, rich data on both mobility and activity of users have been accumulated by the cloud service providers. If secondary usage of the data collected in the cloud-based servers is permitted both legally and adequately and data analytics procedures for anonymized data can be developed, then we will be able to quantify risk and chance of our society based on rich data on human mobility and activity with high resolution.

The chapter aims to propose a method to detect change points of temporally evolutionary bipartite network regarding anonymity of personal information. Moreover, in order to confirm an ability of the proposed method empirically, the proposed method is applied to data of trading activity collected in a cloud-based service of the foreign exchange market and quantified trading activity of the foreign exchange market from a comprehensive point of view.

The network structure of various kinds of physical and social systems has attracted considerable research attention. A many-body system can be described as a network, and the nature of growing networks has been examined well (Albert and Barabási 2002; Miura et al. 2012). Power-law properties can be found in the growing networks, which are called complex networks. These properties are related to the growth of elements and preferential attachment (Albert and Barabási 2002).

A network consists of several nodes and links that connect nodes. In the literature on the physics of socioeconomic systems (Carbone et al. 2007), nodes are assumed to represent agents, goods, and computers, while links express the relationships between nodes (Milaković et al. 2010; Lämmer et al. 2006). The network structure is perceived in many cases through the conveyance of information, knowledge, and energy, among others.

In statistical physics, the number of combinations of possible configurations under given energy constraints is related to “entropy.” Entropy is a measure that quantifies the states of thermodynamic systems. In physical systems, entropy naturally increases because of the thermal fluctuations on elements. Boltzmann proposed that entropy S is computed from the possible number of ensembles g by \(S = \log g\). For a system that consists of two sub-systems whose respective entropies are S 1 and S 2, the total entropy S is calculated as the sum of one of two subsystems S 1 + S 2. This case is attributed to the possible number of ensembles g 1 g 2. Entropy in statistical physics is also related to the degree of complexity of a physical system. If the entropy is low (high), then the physical configuration is rarely (often) realized. Energy injection or work in an observed system may be assumed to represent rare situations. Shannon entropy is also used to measure the uncertainty of time series (Carbone and Stanley 2007).

The concept of statistical–physical entropy was applied by Bianconi (2009) to measure network structure. She considered that the complexity of a network is related to the number of possible configurations of nodes and links under some constraints determined by observations. She calculated the network entropy of an arbitrary network in several cases of constraints.

Researchers have used a methodology to characterize network structure with information-theoretic entropy (Dehmer and Mowshowitz 2011; Wilhelm and Hollunder 2007; Rashevsky 1955; Trucco 1956; Mowshowitz 1968; Sato 2009). Several graph invariants such as the number of vertices, vertex degree sequence, and extended degree sequences have been used in the construction of entropy-based measures (Wilhelm and Hollunder 2007; Sato 2009).

2 An Entropy Measure on a Bipartite Network

The number of elements in socioeconomic systems is usually very large, and several restrictions or finiteness of observations can be found. Therefore, we need to develop a method to infer or quantify the affairs of the entire network structure from partial observations. Specifically, many affiliation relationships of socioeconomic systems can be expressed as a bipartite network. Describing the network structure of complex systems that consist of two types of nodes by using the bipartite network is important. A bipartite graph model also can be used as a general model for complex networks (Guillaume and Latapy 2006; Chmiel et al. 2007; Tumminello et al. 2011). Tumminello et al. proposed a statistical method to validate the heterogeneity of bipartite networks (Tumminello et al. 2011).

Suppose a symmetric binary two-mode network can be constructed by linking K groups (A node) and M participants (B node) if the participants belong to groups (Fig. 1). Assume that we can count the number of participants in each group within the time window [tδ, (t + 1)δ] (t = 1, 2, 3, …), which is defined as m i(t) (i = 1, 2, …, K).

Let us assume a bipartite graph consisting of A nodes and B nodes, of which the structure at time t is described as an adjacency matrix C ij(t). We also assume that A nodes are observable and B nodes are unobservable. That is, we only know the number of participants (B node) belonging to A nodes m i(t). We do not know the correct number of B nodes, but we assume that it is M. In this setting, how do we measure the complexity of the bipartite graph from m i(t) at each observation time t?

The network entropy is defined as a logarithmic form of the number of possible configurations of a network under a constraint (Bianconi 2009). We can introduce the network entropy at time t as a measure to quantify the complexity of a bipartite network structure. The number of possible configurations under the constraint \(m_i(t)=\sum _{j=1}^MC_{ij}(t)\) may be counted as

$$\displaystyle \begin{aligned} N(t) = \prod_{i=1}^K \left( \begin{array}{c} M \\ m_i(t) \end{array} \right) = \prod_{i=1}^K\frac{M!}{m_i(t)!(M-m_i(t))!}. {} \end{aligned} $$
(1)

Then, the network entropy is defined as \(\varSigma (t)=\ln N(t)\). Inserting Eq. (1) into this definition, we have

$$\displaystyle \begin{aligned} \varSigma(t) = K \sum_{n=1}^M\ln n - \sum_{i=1}^K \sum_{n=1}^{M-m_i(t)} \ln n - \sum_{i=1}^K \sum_{n=1}^{m_i(t)} \ln n. {} \end{aligned} $$
(2)

Note that because 0! = 1, \(\sum _{n=1}^{0} \ln n =0\). Obviously, if m i(t) = M for any i, then Σ(t) = 0. If m i(t) = 0 for any i, then Σ(t) = 0. The lower number of combinations gives a lower value of Σ(t). To eliminate a difference in the number of links, we consider the network entropy per link defined as

$$\displaystyle \begin{aligned} \sigma(t) = \frac{\varSigma(t)}{\sum_{i=1}^K m_i(t)}. {} \end{aligned} $$
(3)

This quantity shows the degree of complexity of the bipartite network structure. We may capture the temporal development of the network structure from the value of σ(t). The network entropy per link σ(t) is also an approximation of the ratio of the entropy rate for m i(t) to its mean so that

$$\displaystyle \begin{aligned} \sigma[m_1(t),\ldots,m_K(t)] = \frac{\frac{1}{K}\varSigma[m_1(t),\ldots,m_K(t)]}{\frac{1}{K}\sum_{i=1}^K m_i(t)} \approx \frac{\varSigma[\mathbf{m}(t)]}{\langle m(t) \rangle}, \end{aligned} $$
(4)

where the entropy rate and the mean are, respectively, defined as

$$\displaystyle \begin{aligned} \begin{array}{rcl} \varSigma[\mathbf{m}(t)] &\displaystyle =&\displaystyle \lim_{K\rightarrow \infty}\frac{1}{K}\varSigma[m_1(t),\ldots,m_K(t)], \end{array} \end{aligned} $$
(5)
$$\displaystyle \begin{aligned} \begin{array}{rcl} \langle m(t) \rangle &\displaystyle =&\displaystyle \lim_{K\rightarrow\infty}\frac{1}{K}\sum_{i=1}^K m_i(t). \end{array} \end{aligned} $$
(6)

The ratio of the entropy rate to the mean tells us the uncertainty of the mean from a different point of view from the coefficient of variation (C.V. = standard deviation∕mean).

To understand the fundamental properties of Eq. (3), we compute σ(t) in simple cases. Consider values of entropy for several cases at K = 100 with different M. We assume that the total number of links is fixed at 100, which is the same as the number of A nodes, and we confirm the dependence of σ(t) on the degree of monopolization. We assign the same number of links at each A node. That is, we set

$$\displaystyle \begin{aligned} m_i(t) = \left\{ \begin{array}{ll} 100/k & (i=1,\ldots,k) \\ 0 & (i=k+1,\ldots,K) \end{array} \right., \end{aligned} $$
(7)

where k can be set as 1, 2, 4, 5, 10, 20, 50, or 100. In this case, we can calculate σ(t) as follows:

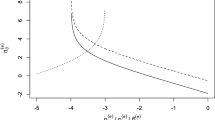
$$\displaystyle \begin{aligned} \begin{array}{rcl} \sigma(t) &=& \frac{\sum_{i=1}^k \ln\left(\begin{array}{c}M \\ 100/k \end{array}\right)}{\sum_{i=1}^k 100/k} \\ &=& \frac{k}{100}\Bigl(\ln M! - \ln (100/k)! - \ln(M-100/k)! \Bigr). \end{array} \end{aligned} $$
(8)

Figure 2a shows the relationship between σ(t) and the degree of monopolization at M = 1000, 2000, 3000, and 4000. The network entropy per link σ(t) is small if a small population of nodes occupies a large number of links. The multiplication regime gives a large value of σ(t). The value of σ(t) is a monotonically increasing function in terms of k. As M increases, the value of σ(t) increases. From this instance, we confirmed that σ(t) decreases with the degree of monopolization at A nodes.

Fig. 2
figure 2

(a) Plots between σ(t) and degree of monopolization k. Each curve represents the relation between σ(t) and k. Filled squares numerical values for M = 1000, unfilled circles for M = 2000, filled circles for M = 3000, and unfilled triangle for M = 4000. (b) Plots between σ(t) and density of links p. Each curve represents the relation between σ(t) and k. Filled squares numerical values for M = 1000, unfilled circles for M = 2000, filled circles for M = 3000, and unfilled triangle for M = 4000

Full size image

Next, we confirm the dependency of σ(t) on the density of links. We assume that each element of an adjacency matrix C ij(t) is given by an i.i.d. Bernoulli random variable with a successful probability of p. Then, \(m_i(t)=\sum _{j=1}^MC_{ij}(t)\) is sampled from an i.i.d. binomial distribution Bin(p, M). In this case, one can approximate σ(t) as

$$\displaystyle \begin{aligned} \begin{array}{rcl} \sigma(t) &=& \frac{\frac{1}{K}\sum_{i=1}^K \varSigma[m_i(t)] }{\frac{1}{K}\sum_{i=1}^K m_i(t)} \\ & \approx & \frac{\langle \varSigma[m_1(t)] \rangle}{\langle m_1(t) \rangle} \\ &=& \frac{1}{M}\sum_{k=1}^M \left(\begin{array}{c}M \\ k\end{array}\right)p^{k-1}(1-p)^{M-k}\ln\left(\begin{array}{c}M \\ k\end{array}\right). {} \end{array} \end{aligned} $$
(9)

Figure 2b shows the plots of σ(t) versus p obtained from both Monte Carlo simulation with random links drawn from Bernoulli trials and Eq. (9). The number of links at each A node monotonically increases as p increases. σ(t) decreases as the density of links decreases. The dependence of the entropy per link on p is independent of M.

3 Empirical Analysis

The application of network analysis to financial time series has been advancing. Several researchers have investigated the network structure of financial markets (Bonanno et al. 2003; Gworek et al. 2010; Podobnik et al. 2009; Iori et al. 2008). Bonanno et al. examined the topological characterization of the correlation-based minimum spanning tree (MST) of real data (Bonanno et al. 2003). Gworek et al. analyzed the exchange rate returns of 38 currencies (including gold) and computed the characteristic path length and average weighted clustering coefficient of the MST topology of the graph extracted from the cross-correlations for several base currencies (Gworek et al. 2010). Podobnik et al. (2009) examined the cross-correlations between volume changes and price changes for the New York Stock Exchange, Standard and Poor’s 500 index, and 28 worldwide financial indices. Iori et al. (2008) analyzed the network topology of the Italian segment of the European overnight money market and investigated the evolution of these banks’ connectivity structure over the maintenance period. These studies collectively aimed to detect the susceptibility of network structures to macroeconomic situations.

Data collected from the ICAP EBS platform were used. The data period spanned May 28, 2007 to November 30, 2012 (ICAP 2013). The data included records for orders (BID/OFFER) and transactions for currencies and precious metals with a 1-s resolution. The total number of orders included in the data set is 520,973,843, and the total number of transactions is 58,679,809. The data set involved 94 currency pairs consisting of 39 currencies, 11 precious metals, and 2 basket currencies (AUD, NZD, USD, CHF, JPY, EUR, CZK, DKK, GBP, HUF, ISK, NOK, PLN, SEK, SKK, ZAR, CAD, HKD, MXC, MXN, MXT, RUB, SGD, XAG, XAU, XPD, XPT, TRY, THB, RON, BKT, ILS, SAU, DLR, KES, KET, AED, BHD, KWD, SAR, EUQ, USQ, CNH, AUQ, GBQ, KZA, KZT, BAG, BAU, BKQ, LPD, and LPT).Footnote 1 Figure 3 shows a network representation of 94 currency pairs.

Fig. 3
figure 3

A network representation of 94 currency pairs included in the data sets. Nodes show currencies and links currency pairs. If there is a link between two currencies, it is shown that the currency pair consisting of them is included in the data set

Full size image

3.1 The Total Number

The number of quotations and transactions in each currency pair was extracted from the raw data. Let m X,i(t) (t = 0, …;i = 1, …, K) be the number of quotations (X = P) or transactions (X = D) within every minute (δ = 1 [min]) for a currency pair i (K = 94) at time t. Let c X(t) be denoted as the total number of quotations (X = P) and transactions (X = D), which is defined as

$$\displaystyle \begin{aligned} c_{X}(t) = \sum_{i=1}^K m_{X,i}(t). \end{aligned} $$
(10)

Let us consider the maximum value of c X(t) in each week:

$$\displaystyle \begin{aligned} w_X(s) = \max_{t \in W(s)}\{ c_X(t) \}, \end{aligned} $$
(11)

where W(s) (s = 1, …, T) represents a set of times included in the s-th week. A total of 288 weeks are included in the data set (T = 288). Figure 4 shows the maximum values c X(t) for the period from May 28, 2007 to November 30, 2012.

Fig. 4
figure 4

(a) The maximum values of the number of quotations within 1 min in every week. (b) The maximum values of the number of transactions within 1 min in every week

Full size image

According to the extreme value theorem, the probability density for maximum values can be assumed to be a Gumbel density:

$$\displaystyle \begin{aligned} P(w_X; \mu_X, \rho_X) = \frac{1}{\rho_X}\exp\Bigl(-\frac{w_X-\mu_X}{\rho_X}-e^{-\frac{w_X-\mu_X}{\rho_X}}\Bigr), {} \end{aligned} $$
(12)

where μ X and ρ X are the location and scale parameters, respectively. Under the assumption of the Gumbel density, these parameters are estimated with the maximum likelihood procedure. The log-likelihood function for T observations w X(s′) (s′ = 1, …, T) under Eq. (12) is defined as

$$\displaystyle \begin{aligned} l(\mu_X,\rho_X) = \sum_{s'=1}^T \ln\Bigl[ \frac{1}{\rho_X}\exp\Bigl(-\frac{w_X(s')-\mu_X}{\rho_X}-e^{-\frac{w_X(s')-\mu_X}{\rho_X}}\Bigr) \Bigr]. \end{aligned} $$
(13)

The maximum likelihood estimators are obtained by maximizing the log-likelihood function. Partially differentiating l(μ X, ρ X) in terms of μ X and ρ X and setting them to zero, one has its maximum likelihood estimators as

$$\displaystyle \begin{aligned} \begin{array}{rcl} e^{-\frac{\hat{\mu}_X}{\hat{\rho}_X}} &\displaystyle =&\displaystyle \frac{1}{T} \sum_{s'=1}^T e^{-\frac{w_X(s')}{\hat{\rho}_X}}, {} \end{array} \end{aligned} $$
(14)
$$\displaystyle \begin{aligned} \begin{array}{rcl} \hat{\rho}_X &\displaystyle =&\displaystyle \frac{1}{T}\sum_{s'=1}^T w_X(s') - \frac{\sum_{s'=1}^T e^{-\frac{w_X(s')}{\hat{\rho}_X}}w_X(s')}{\sum_{s'=1}^T e^{-\frac{w_X(s')}{\hat{\rho}_X}}} {} \end{array} \end{aligned} $$
(15)

The parameters are estimated as \(\hat {\mu }_P = 772.179499\), \(\hat {\rho }_P = 281.741815\), \(\hat {\mu }_D = 206.454884\), and \(\hat {\rho }_D = 35.984804\).

The Kolmogorov–Smirnov (KS) test is conducted to determine the statistical significance of the estimated distributions. The KS test is a popular statistical method of assessing the difference between observations and its assumed distribution by p-value, which is a measure of probability where a difference between the two distributions happens by chance. Large p-values imply that the observations are sampled from the assumed distribution in the null hypothesis with high significance. Let w X(s) (s = 1, …, T) be T observations, and let K T be a test statistic

$$\displaystyle \begin{aligned} K_{T} = \sup_{1 \le s' \le T}\sqrt{T}\Big|F_{T}(w_{X}(s'))-F(w_{X}(s'))\Big|, {} \end{aligned} $$
(16)

where 0 ≤ F(v) ≤ 1 is an assumed cumulative distribution in a null hypothesis and F T(v) an empirical one based on T observations such that F T(v) = k∕T, in which k represents the number of observations satisfying v X(s) ≤ v(s = 1, …, T). The p-value is computed from the Kolmogorov–Smirnov distribution.

The KS test is conducted under the assumption of the Gumbel distribution for the maximum value corresponding to Eq. (19):

$$\displaystyle \begin{aligned} F(w_X; \mu_X, \rho_X) = \exp\Bigl[-\exp\bigl(-\frac{w_X - \mu_X}{\rho_X}\bigr)\Bigr]. \end{aligned} $$
(17)

The p-values of the KS test are shown in Table 1. The stationary Gumbel assumption cannot explain the maximum values for quotes with a 5% significance level in the KS test. The stationary Gumbel assumption may not be accepted in the case of the block maximum number of quotes. The dominant reason is the strong nonstationarity of the maximum number of quotes. During the last 5 years, the currencies and pairs quoted in the electronic brokerage market increased. The mean value of the total number constantly increased. In fact, the maximum number of quotations w P(t) reached the maximum value on 30 July, 2012. The nonstationarity breaks the assumption of the extreme value theorem.

Table 1 The p-values of statistical tests under a stationary assumption of the Gumbel distribution for the maximum values
Full size table

It is confirmed that the stationary Gumbel assumption can be accepted for the block maxima of transactions in each week using the KS test with a 5% significance level. The maximum number of transactions w D(t) was reached on on January 30, 2012. This period seems to be related to the extreme synchrony.

3.2 Network Entropy Per Link

The proposed method based on statistical–physical entropy is applied to measure the states of the foreign exchange market. The relationship between a bipartite network structure and macroeconomic shocks or crises was investigated, and the occurrence probabilities of extreme synchrony were inferred. We compute a statistical–physical entropy per link from m X,i(t)(X ∈{P, D}) with Eqs. (2) and (3), which are denoted as σ X(t). σ P(t) and σ D(t).

Since small values of σ X(t) correspond to a concentration of links at a few nodes or a dense network structure, let us consider the minimum value of σ X(t) every week:

$$\displaystyle \begin{aligned} v_X(s) = \min_{t \in W(s)}\{\sigma_X(t)\}, \end{aligned} $$
(18)

where W(s) (s = 1, …, T) represents a set of times included in the s-th week. A total of 288 weeks are included in the data set (T = 288). According to the extreme value theorem, the probability density for minimum values can be assumed to be the Gumbel density:

$$\displaystyle \begin{aligned} P(v_X; \mu_X, \rho_X) = \frac{1}{\rho_X}\exp\Bigl(\frac{v_X+\mu_X}{\rho_X}-e^{\frac{v_X+\mu_X}{\rho_X}}\Bigr), {} \end{aligned} $$
(19)

where μ X and ρ X are the location and scale parameters, respectively. Under the assumption of the Gumbel density, these parameters are estimated with the maximum likelihood procedure. The log-likelihood function for T observations v X(s′) (s′ = 1, …, T) under Eq. (19) is defined as

$$\displaystyle \begin{aligned} l(\mu_X,\rho_X) = \sum_{s'=1}^T \ln\Bigl[ \frac{1}{\rho_X}\exp\Bigl(\frac{v_X(s')+\mu_X}{\rho_X}-e^{\frac{v_X(s')+\mu_X}{\rho_X}}\Bigr) \Bigr]. \end{aligned} $$
(20)

Partially differentiating l(μ X, ρ X) in terms of μ X and ρ X and setting them to zero yields its maximum likelihood estimators as

$$\displaystyle \begin{aligned} \begin{array}{rcl} e^{-\frac{\hat{\mu}_X}{\hat{\rho}_X}} &\displaystyle =&\displaystyle \frac{1}{T} \sum_{s'=1}^T e^{\frac{v_X(s')}{\hat{\rho}_X}}, {} \end{array} \end{aligned} $$
(21)
$$\displaystyle \begin{aligned} \begin{array}{rcl} \hat{\rho}_X &\displaystyle =&\displaystyle \frac{\sum_{s'=1}^T e^{\frac{v_X(s')}{\hat{\rho}_X}}v_X(s')}{\sum_{s'=1}^T e^{\frac{v_X(s')}{\hat{\rho}_X}}} - \frac{1}{T}\sum_{s'=1}^T v_X(s'). {} \end{array} \end{aligned} $$
(22)

The parameter estimates are computed as \(\hat {\mu }_P=-4.865382\), \(\hat {\rho }_P=0.110136\), \(\hat {\mu }_D=-5.010175\), and \(\hat {\rho }_D=0.120809\) with Eqs. (21) and (22).

The KS test is conducted for the Gumbel distribution for the minimum values corresponding to Eq. (19):

$$\displaystyle \begin{aligned} F(v_X; \mu_X, \rho_X) = 1 - \exp\Bigl[-\exp\bigl(\frac{v_X+\mu_X}{\rho_X}\bigr)\Bigr]. \end{aligned} $$
(23)

The p-value of the distribution is shown in Table 2. The stationary Gumbel assumption cannot explain the synchronizations observed in both quotes and transactions completely with a 5% significance level. The stationary Gumbel assumption is rejected because there is a stationary assumption to derive the extreme value distribution. If we can weaken this assumption, then the goodness of fit may be improved.

Table 2 The p-values of statistical tests under a stationary Gumbel ssumption
Full size table

4 Probability of Extreme Synchrony

The literature detecting structural breaks or change points in an economic time series (Goldfeld and Quandt 1973; Preis et al. 2011; Scalas 2007; Cheong et al. 2012) points out that nonstationary time series are constructed from locally stationary segments sampled from different distributions. Goldfeld and Quandt conducted a pioneering work on the separation of stationary segments (Goldfeld and Quandt 1973). Recently, a hierarchical segmentation procedure was also proposed by Choeng et al. under the Gaussian assumption (Cheong et al. 2012). We applied this concept to define the segments for v X(s′) (s′ = 1, …, T).

Let us consider the null model L 1, which assumes that all the observations v X(s′) (s′ = 1, …, T) are sampled from a stationary Gumbel density parameterized as μ and ρ. An alternative model L 2(s) assumes that the left observations v X(s′) (s′ = 1, …, s) are sampled from a stationary Gumbel density parameterized as μ L and ρ L and that the right observations v X(s′) (s′ = s + 1, …, T) are sampled from a stationary Gumbel density parameterized as μ R and ρ R.

Denoting likelihood functions as

$$\displaystyle \begin{aligned} \begin{array}{rcl} L_1(\mu,\rho) &\displaystyle =&\displaystyle \prod_{s'=1}^T P(v_X(s');\mu,\rho), \end{array} \end{aligned} $$
(24)
$$\displaystyle \begin{aligned} \begin{array}{rcl} L_2(s;\mu_L,\rho_L,\mu_R,\rho_R) &\displaystyle =&\displaystyle \prod_{s'=1}^s P(v_X(s');\mu_{L},\rho_{L}) \\ &\displaystyle \times&\displaystyle \prod_{s'=s+1}^{T} P(v_X(s');\mu_{R},\rho_{R}), \end{array} \end{aligned} $$
(25)

the difference between the log-likelihood functions can be defined as

$$\displaystyle \begin{aligned} \varDelta(s) = \log L_2(s) - \log L_1. \end{aligned} $$
(26)

Δ(s) can be approximated as the Shannon entropy \(H[p]=-\int _{-\infty }^{\infty }\mbox{d}v \log p(v)p(v)\):

$$\displaystyle \begin{aligned} \begin{array}{rcl} \varDelta(s) &\displaystyle \approx&\displaystyle T H[P(v_X;\mu,\rho)] \\ &\displaystyle -&\displaystyle s H[P(v_X;\mu_L,\rho_L)] - (T-s) H[P(v_X;\mu_R,\rho_R)]. \end{array} \end{aligned} $$
(27)

Since the Shannon entropy of the Gumbel density expressed in Eq. (12) is calculated as

$$\displaystyle \begin{aligned} H[P(v_X;\mu_X,\rho_X)] = \ln \rho_X - \gamma_E + 1, \end{aligned} $$
(28)

where γ E represents Euler’s constant, defined as

$$\displaystyle \begin{aligned} \gamma_E = \int_{0}^{\infty} \ln t e^{-t}\mbox{d}t, \end{aligned} $$
(29)

we obtain

$$\displaystyle \begin{aligned} \varDelta(s) \approx T\ln \rho - s\ln \rho_L - (T-s)\ln \rho_R. \end{aligned} $$
(30)

In the context of model selection, several information criteria are proposed. The information criterion provides both goodness of fit of the model to the data and model complexity. For the sake of simplicity, we use the Akaike information criterion (AIC) to determine the adequate model. The AIC for a model with the number of parameters K and the maximum likelihood of L is defined as

$$\displaystyle \begin{aligned} AIC = -2 \ln L + 2K. \end{aligned} $$
(31)

We can compute the difference in AIC between model L 2 and model L 1(s) as

$$\displaystyle \begin{aligned} \begin{array}{rcl} \varDelta_{AIC}(s) &\displaystyle =&\displaystyle \mbox{AIC of}\ L_2(s) - \mbox{AIC of}\ L_1 \\ &\displaystyle \approx&\displaystyle -2\bigl(T\ln \hat{\rho} - s\ln \hat{\rho}_L - (T-s)\ln \hat{\rho}_R\bigr) + 4, \\ &\displaystyle =&\displaystyle -2\varDelta(s) + 4 \end{array} \end{aligned} $$
(32)

since the number of parameters of L 1 is 2, that of L 2(s) is 4, and the maximum likelihood is obtained by using their maximum likelihood estimators calculated from

$$\displaystyle \begin{aligned} \begin{array}{rcl} \hat{\rho} &\displaystyle =&\displaystyle \frac{\sum_{s'=1}^T e^{\frac{v_X(s')}{\hat{\rho}_X}}v_X(s')}{\sum_{s'=1}^T e^{\frac{v_X(s')}{\hat{\rho}_X}}} - \frac{1}{T}\sum_{s'=1}^Tv_X(s') \end{array} \end{aligned} $$
(33)
$$\displaystyle \begin{aligned} \begin{array}{rcl} \hat{\rho}_L &\displaystyle =&\displaystyle \frac{\sum_{s'=1}^s e^{\frac{v_X(s')}{\hat{\rho}_L}}v_X(s')}{\sum_{s'=1}^s e^{\frac{v_X(s')}{\hat{\rho}_L}}} - \frac{1}{s}\sum_{s'=1}^{s}v_X(s') \end{array} \end{aligned} $$
(34)
$$\displaystyle \begin{aligned} \begin{array}{rcl} \hat{\rho}_R &\displaystyle =&\displaystyle \frac{\sum_{s'=s+1}^T e^{\frac{v_X(s')}{\hat{\rho}_R}}v_X(s')}{\sum_{s'=s+1}^T e^{\frac{v_X(s')}{\hat{\rho}_R}}} - \frac{1}{T-s}\sum_{s'=s+1}^Tv_X(s') \end{array} \end{aligned} $$
(35)

Therefore, P(v X;μ L, ρ L) is maximally different from P(v X;μ R, ρ R) when Δ(s) assumes a maximal value. This spectrum has a maximum at some time s ∗, which is denoted as

$$\displaystyle \begin{aligned} \varDelta^*_{AIC} = \varDelta_{AIC}(s^*) = \max_{s} \varDelta_{AIC}(s). \end{aligned} $$
(36)

The segmentation can be used recursively to separate the time series into further smaller segments. We do this iteratively until all segment boundaries have converged onto their optimal segment, defined by a stopping (termination) condition.

Several termination conditions were discussed in previous studies (Cheong et al. 2012). Assuming that Δ 0 > 0, we terminate the iteration if \(\varDelta _{AIC}^{*}\) is less than a typical conservative threshold of Δ 0 = 10, while the procedure is recursively conducted if \(\varDelta _{AIC}^*\) is larger than Δ 0. We checked the robustness of this segmentation procedure for Δ 0. Δ 0 gives a statistical significance level of termination. The value of Δ 0 is related to statistical significance. According to Wilks theorem, − 2Δ(s) follows a chi-squared distribution with a degree of freedom r, where r is given by the difference between the number of parameters assumed in the null hypothesis and one in the alternative hypothesis. In this case, r = 2. Hence, the cumulative distribution function of \(\varDelta ^*_{AIC}\) may follow

$$\displaystyle \begin{aligned} \mbox{Pr}[\varDelta^*_{AIC} > x] = 1- \gamma\Bigl(1,\frac{x-4}{2}\Bigr), \end{aligned} $$
(37)

where γ(x, a) is the regularized incomplete gamma function defined as

$$\displaystyle \begin{aligned} \gamma(a,x)=\frac{\int_0^x t^{a-1}e^{-t} \mbox{d}t}{\int_0^{\infty} t^{a-1}e^{-t} \mbox{d}t}. \end{aligned} $$
(38)

Therefore, setting the threshold Δ 0 = 10 implies that the segmentation procedure is tuned as a 4.928% statistical significance level.

Let the number of segments be L X, the parameter estimates be {μ X,j, ρ X,j} at the j-th segment, and the length of the j-th segment be τ X,j, where \(\sum _{j=1}^{R_X}\tau _{X,j}=T\). The cumulative probability distribution for v X(s) (s = 1, …, T) may be assumed to be a finite mixture of Gumbel distributions:

$$\displaystyle \begin{aligned} \begin{array}{rcl} \mbox{Pr}(V_X\leq v_X) &\displaystyle =&\displaystyle \int_{-\infty}^{v_X}\sum_{j=1}^{R_X}\frac{\tau_{X,j}}{T}P(v_X^{\prime};\mu_{X,j},\rho_{X,j})\mbox{d}v_X^{\prime} \\ &\displaystyle =&\displaystyle \sum_{j=1}^{R_X} \frac{\tau_{X,j}}{T} \Bigl\{1-\exp\bigl[-e^{\frac{v_X+\mu_{X,j}}{\rho_{X,j}}}\bigr]\Bigr\}, {} \end{array} \end{aligned} $$
(39)

Tables 3 and 4 show parameter estimates of v P(s) and v D(s) using the recursive segmentation procedure. Figure 5 shows the temporal development of v P(s) and v D(s) from May 28, 2007 to November 30, 2012. R P = 6 and R D = 6 are obtained from v X(s) using the proposed segmentation procedure. During the observation period, the global financial system suffered from the following significant macroeconomic shocks and crises: (I) the BNP Paribas shock (August 2007), (II) the Bear Stearns shock (February 2008), (III) the Lehman shock (September 2008 to March 2009), (IV) the European sovereign debt crisis (April to May 2010), (V) the East Japan tsunami (March 2011), (VI) the United States debt-ceiling crisis (May 2011), and (VII) the Bank of Japan’s 10 trillion JPY gift on Valentine’s Day (February 2012).

Fig. 5
figure 5

Temporal development of (a) v P(s) and (b) v D(s) from May 28, 2007 to November 30, 2012. Each color corresponds to a segment which is shown in Tables 3 and 4

Full size image
Table 3 Parameter estimates obtained from the weekly minimum values of network entropy for quotations with the recursive segmentation procedure
Full size table
Table 4 Parameter estimates obtained from the weekly minimum values of network entropy for transactions with the recursive segmentation procedure
Full size table

Before entering these global affairs, both v P(s) and v D(s) took large values. Note that, during the (I) Paribas shock, the (II) Bear Stearns and the (III) Lehman shock v P(s) and v D(s) took smaller values than they did during the previous term. This implies that a global shock may drive many participants and that these participants may trade the same currencies at the same time. The smallest values v P(s) and v D(t) correspond to the days of the (II) Bear Stearns shock, the (III) Lehman shock, and the (VI) Euro crisis. These days are generally related to the start or the end of macroeconomic shocks or crises. The period from December 2011 to March 2012 shows that the values of v D(s) are smaller than they were during other periods. This result implies that, during period, singular patterns appeared in the transactions.

Figure 6 shows both the empirical and estimated cumulative distribution functions of v P(s) and v D(s). The estimated cumulative distributions are drawn from Eq. (39) with parameter estimates. The KS test verifies this mixing assumption. The distribution estimated by the finite mixture of Gumbel distributions for quotes is well fitted, as shown in Table 5. From the p-values, the mixture of Gumbel distributions for quotations accepts the null hypothesis that v P(s) is sampled from the mixing distribution with a 5% significance level. The mixture of Gumbel distributions for transactions also accepts the null hypothesis that v D(s) is sampled from the mixing distribution with a 5% significance level. Extrapolation of cumulative distribution function also provides a guideline of the future probability of extreme events. The finite mixture Gumbel distributions with parameter estimates may be used as an inference of probable extreme synchrony.

Fig. 6
figure 6

Cumulative distribution functions for the minimum values of the entropy per link in each week (a) v P(s) and (b) v D(s). Filled squares represent the empirical distribution of v P(s), and unfilled circles represent the empirical distribution of v D(s). A solid curve represents the estimated distribution of v P(s), and a dashed curve represents the estimated distribution of v D(s)

Full size image
Table 5 The p-values of statistical tests under the assumption of a finite mixture of Gumbel distributions
Full size table

5 Conclusion

A method based on the concept of “entropy” in statistical physics was proposed to quantify states of a bipartite network under constraints. The statistical–physical network entropy of a bipartite network was derived under the constraints for the number of links at each group node. Both numerical and theoretical calculations for a binary bipartite graph with random links showed that the network entropy per link can capture both the density and the concentration of links in the bipartite network. The proposed method was applied to measure the structure of bipartite networks consisting of currency pairs and participants in the foreign exchange market.

An empirical investigation of the total number of quotes and transactions was conducted. The nonstationarity of the number of quotes and transactions strongly affected the extreme value distributions. The empirical investigation confirmed that the entropy per link decreased before and after the latest global shocks that have influenced the world economy. A method was proposed to determine segments with recursive segmentation based on the Akaike information criterion between Gumbel distributions with different parameters. Under the assumption of a finite mixture of Gumbel distributions, the estimated distributions were verified by the Kolmogorov–Smirnov test. The finite mixture of Gumbel distributions can estimate the occurrence probabilities of extreme synchrony of a nonstationary system extracted as a bipartite network. The extrapolation of the extreme synchrony can be done based on the estimated mixture of Gumbel distributions.