Keywords

1 Introduction

Space information networks (SIN) have attracted considerable research interest in last few years [1]. With the development of Ka/Q/V millimeter-wave (mmWave) band high throughput satellites (HTS), people believe that HTSs deployed in different level of orbits can be connected to form a high throughput SIN, and together with 5G terrestrial networks will enable broadband wireless access and offer the access availability of anywhere and anytime [2].

Delay/disruption tolerant networking (DTN) Licklider transmission protocol (LTP) has recently been developed to support space communications which are largely different from terrestrial networks in terms of link delay, channel error rates, and data-rate asymmetry [3]. On other hand, multiple-input multiple-output (MIMO) technology has received a great deal of interest in last few years for enhancing mmWave HTS power and/or spectral efficiency [4]. Further, to achieve robust reception in the time-varying SIN channels, the physical-layer design requires the adoption of a low-rate FEC scheme combined with long time interleaving and robust modulation formats, e.g., MIMO with orthogonal space-time block coding (OSTBC) [5]. Therefore, in this paper, we propose an LTP-HARQ scheme over an OSTBC-MIMO block fading AWGN channel for SIN.

To analyze HARQ in LTP for SIN, an information-theoretic performance metric is needed. As the reliable data delivery in LTP-ARQ and -HARQ schemes is the most important data service mode, and consider the long propagation delay in SIN communications, we mainly choose the mean number of transmission rounds M for reliable data delivery in ARQ and HARQ schemes [6]. Note that other potentially metrics [7, 8], such as throughput and file delivery time can also be computed/computable by M in this work.

In general, the expected value of M in AWGN channel is expressed on an infinite-sum form [9]: \( {M = \sum \nolimits _{k=1}^{\infty }Q_k} \), where \({{Q_\mathrm{{k}}}}\) represents the decoding failure probabilities after k-th transmission. [10] presented a Laplace-transform-based approach that avoided the infinite-sum of decoding error probabilities, thereby giving a more compact representation for the mean number of transmissions. Further, we address lossless- and truncated-HARQ in this paper, where lossless means unlimited number of retransmissions and truncated means the number of retransmission is upper limited. More specifically, we investigate with repetition redundancy (H)ARQ (ARQ- and HARQ-RR).

The reminder of this paper is organized as follows. In Sect. 2, we present the system model. The mean number of transmission rounds for reliable data delivery in (H)ARQ schemes over Rayleigh and Rician fading channels are derived in Sect. 3, and the throughput and file delivery time in LTP is also analyzed. Numerical and simulation results are presented in Sect. 4. Finally, we conclude the paper.

2 System Model

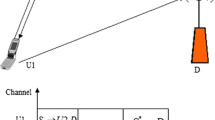
In this section, we build analytical models to characterize the operation and performance of LTP-HARQ scheme in SIN. A communication scenario is show in Fig. 1, where data blocks communicating over an OSTBC-MIMO block fading AWGN channel where each of the transmitter and the receiver has one or more antennas.

Fig. 1.
figure 1

HARQ-RR transmission mechanism in LTP

Full size image

In this scenario of LTP-HARQ, the sender transmits the data blocks or segments in sequence continuously. When the sender receives the retransmission request of sent Block1, the sender starts to resend the lost segments via the retransmission request after the current Block2 (or other transmitting Block) transmitting finished. Each block is fragmented into LTP data segments, which concludes red data and green data. Green data just need one transmission effort, and the red data requires correct reception without error. The segments data are divided into Report Segment (RS), Report-acknowledge Segment (RA), Cancel Segment (CS), Cancel-acknowledge Segment (CAS), Check point (CP)and data segment.

Each segment is considered as the original data of the OSTBC-MIMO system, and data is transmitted by \({N_t}\) antennas and received by \({N_r}\) antennas. r means OSTBC code rate. The diversity order with maximum ratio combing (MRC) for OSTBC-MIMO system are calculated by \({N = {N_t} \times {N_r}}\). We consider the HARQ mechanism of OSTBC-MIMO communication system over a block fading AWGN channel and give the receiver loss-pass signal model as

$$\begin{aligned} \mathbf{{Y}} = \sqrt{S} \mathbf{{HX + W}} \end{aligned}$$
(1)

where \({\mathbf{{Y}},\mathbf{{H}},\mathbf{{X}},\mathbf{{W}}}\) are complex matrices with dimension of \({{C^{{N_r} \times {N_x}}},{C^{{N_r} \times {N_t}}}}\), \({{C^{{N_t} \times {N_x}}},{C^{{N_r} \times {N_x}}}}\), and \({{\mathbf{{H}}_{ij}}}\) means the power gain from i-th transmitter antenna to j-th receiver antenna. Assume that \({{\mathbf{{H}}_{ij}}}\) is independent identically distributed (iid), and \({{\mathbf{{H}}_{ij}} \sim CN(0,1)}\). Also, \({\mathbf{{W}} \sim CN(0,1)}\). S is the average SNR over Single-Input Single-Output AWGN channel, and the average noise power is 1. In block fading channel, we assume that channel transmission characteristics remain constant over a fixed character period, but the retention time is much smaller than the total transmission time, which means \({{\mathbf{{H}}_{ij}}}\) is quasi-static and the value remain constant in the slot. Multiple complex Gauss signals are superimposed on the receiver due to diversity, and the channel gain is following the \({\chi ^2}\) distribution of freedom degrees 2N. Data packets are assumed encoded with a capacity achieving Shannon AWGN capacity limit and we mainly consider the performance analysis of ARQ lossless-HARQ and truncated HARQ mechanisms.

3 Performance Analysis

We mainly investigate the mean number of transmission rounds M in LTP-HARQ schemes, which affect the file delivery time performance, throughput and energy consumption. The file delivery time [9] of one daya block in LTP transmission is given as (2):

The file delivery time of single block \({D_{block}}\) includes segments transmission time \({D_{trans}}\), propagation time of entire block \({D_{prop\_total}}\), CP retransmission time \({D_{CP\_total}}\), and RS retransmission time \({D_{RS\_total}}\). \(M_{seg}\) denotes the mean number of transmissions of one segment, and \({D_{seg}}\) means single segment’s transmitting time. Define the bandwidth-normalized information rate per transmission \(R = L_{seg}/B{D_{seg}}\), which means, under the bandwidth of B, \(L_{seg}\) nats information are transmitted in slot \(D_{seg}\). The number of segment in one block is \(Num = {L_{block}}/{L_{seg}}\), where \(L_{block}\) is the size of the block and \(L_{seg}\) is the segment size. Total propagation time \({D_{prop\_total}}\) is the main delay in long distance communication link. We set the timeout of CP segment timer \({D_{CP\_\mathrm{{timer}}}} = 2{D_{prop}}\, +\, {D_{RS}}\) and the timeout of RS segment timer \({D_{RS\_\mathrm{{timer}}}} = 2{D_{prop}} + {D_{CP}}\) for the best transmission efficiency. When CP, RS and data Segment are almost the same size, we have the transmitting time \({D_{CP}} = {D_{RS}} = {D_{seg}}\).

$$\begin{aligned} \begin{array}{l} {D_{block}} = {D_{trans}} + {D_{prop\_total}} + {D_{CP\_total}} + {D_{RS\_total}}\\ = Num \times {D_{seg}} \times {M_{seg}} + \left( {2{M_{LTP}} - 1} \right) {D_{prop}} \\ +\, ({M_{seg}} - 1)({M_{LTP}} - 1)({D_{CP}} + {D_{CP\_timer}} + {D_{RS}} + {D_{RS\_timer}}) \end{array} \end{aligned}$$
(2)

The mean number of LTP block transmissions \({M_{LTP}}\) is defined by the maximum transmission times for all segments in one block, which greatly affects the LTP file delivery time along with \({M_{seg}}\). In the traditional LTP-ARQ mechanism, \({M_{seg}}\) is given by \({M_{seg}} = 1/(1 - Q)\), where Q is the decoding failure probability of the segment calculated by bit error rate, and \({M_{LTP}}\) is given as

$$\begin{aligned} \begin{array}{l} {M_{LTP}} = 1{{ \,+\, }}\sum \limits _{m = 2}^\infty {[1 - {{(1 - {Q^{m - 1}})}^{Num}}]} \end{array} \end{aligned}$$
(3)

where Q has the different expressions in different fading channel or transmission scheme. Define R as the bandwidth-normalized information rate, M is the mean number of transmission rounds per segment, and we have the throughput expressions without considering the influence of propagation delay as follows

$$\begin{aligned} T = R/M \end{aligned}$$
(4)

The mean number of transmission rounds (including the first transmission effort and retransmissions) per segment is denoted by

$$\begin{aligned} M = \sum \limits _{k = 1}^\infty {k{P_k}} = \sum \limits _{k = 1}^\infty {k({Q_{k - 1}} - {Q_k}) = } \sum \limits _{k = 0}^\infty {{Q_k}} \end{aligned}$$
(5)

where \({P_k}\) represents the successful decoding probability of the kth transmission, and \({Q_k}\) means the failure probability, where \({Q_0} = 1\) means the failure probability is 1 without transmission. In the kth transmission of HARQ, the data transmitted by the previous \(k-1\) times will be jointly decoded with kth transmission. Set the decoding failure probability \({Q_{k-1}}\) after \(k-1\) times transmission, the success probability of k-th transmission \({P_k}\) and failure probability of kth transmission \({Q_k}\), satisfying \({Q_{k - 1}} = {P_k} + {Q_k}\). The decoding failure probability and outage probability from the perspective of information theory is

$$\begin{aligned} {Q_k} = P({i_k} \le R) \end{aligned}$$
(6)

where \({i_k}\) less than or equal to R, which means the k-th transmission accumulated mutual information realization for a segment does not satisfy the decoding threshold. When the data decoding fails in ARQ-RR scheme, the error data is discarded, and the success of k-th transmission is independent of the previous \(k-1\) transmission, which there is no accumulated mutual information, \({i_k} = {i_{k - 1}}\). However, in HARQ-RR scheme, the mutual information is obtained by accumulating the previous data packet and current received data packet. Thus, the mutual information is denoted by \({i_k}^{RR} = \ln (1 + S\sum \limits _{u = 1}^k {{z_u}} )\), where the random variable \({z_k}\) presents the channel power gain for the k-th transmission and the pdf \({f_Z}(z)\) is following different distributions over different fading channels. We can further derive (6) in SISO system as

$$\begin{aligned} {Q_k} = P\left\{ {{i_k} \le R} \right\} = P(\sum \limits _{u = 1}^k {{z_u}} \le \varTheta ) = \int \limits _0^\varTheta {{f_Z}^{ \otimes (k)}(z)\mathrm{{d}}z} \end{aligned}$$
(7)

where we define the decoding threshold \({\varTheta ^{RR}} = \left( {{\mathrm{{e}}^R} - 1} \right) /S\). \({z_u}\) is independent and identically distributed, \(z \sim {f_Z}(z)\), and \({f_Z}^{ \otimes (k)}\) is the k-fold convolution. According to the different distribution of \({f_Z}(z)\), we obtain the \({Q_k}\) corresponding to the different fading channels.

3.1 Lossless-HARQ

We consider the lossless HARQ-RR over OSTBC-MIMO channel with N order diversity. In the case of OSTBC, the signals transmitted by different antennas are uncorrelated and the MIMO channel is degenerated into an effective SISO channel. The segment decoding failure of k-th transmission can be written as

$$\begin{aligned} \begin{array}{l} {Q_k} = P\left\{ {r\ln (1 + \frac{S}{{r{N_t}}}\sum \limits _{u = 1}^k {{z_u}} ) \le R} \right\} = {\mathrm{{e}}^{ - \left( {kKN} \right) }}\sum \limits _{i = 0}^\infty {\frac{{{{\left( {kKN} \right) }^i}}}{{\varGamma \left( {i + 1} \right) }}} {\gamma _r}(kN + i,\varTheta ) \end{array} \end{aligned}$$
(8)

where \(\varTheta = ({\mathrm{{e}}^{R/r}} - 1)/\mathop {S}\limits ^ \sim \) means the decoding threshold and \(\mathop {S}\limits ^ \sim = S/r{N_t}\) is called the effective SNR. r is the code rate of OSTBC. \({z_u}\) presents the channel power gain. The derivation of (8) is omitted due to the limitation of space, and the detail proof please refer to our future extension work. Moreover, We can get the mean number of transmission rounds of HARQ-RR over Rician fading channel by the definition (5) as

$$\begin{aligned} \begin{array}{l} M_{Ric}^{RR} = \sum \limits _{k = 0}^\infty {{\mathrm{{e}}^{ - \left( {kKN} \right) }}\sum \limits _{i = 0}^\infty {\frac{{{{\left( {kKN} \right) }^i}}}{{\varGamma \left( {i + 1} \right) }}} {\gamma _r}(kN + i,\varTheta )} \end{array} \end{aligned}$$
(9)

The throughput of HARQ-RR over Rician fading channel is given as

$$\begin{aligned} T_{Ric}^{RR} = \frac{R}{{\sum \limits _{k = 0}^\infty {{\mathrm{{e}}^{ - \left( {kKN} \right) }}\sum \limits _{i = 0}^\infty {\frac{{{{\left( {kKN} \right) }^i}}}{{\varGamma \left( {i + 1} \right) }}} {\gamma _r}(kN + i,\varTheta )} }} \end{aligned}$$
(10)

where K is defined to be the Shape Parameter, \(K = {{{D^2}}/ {2{\sigma ^2}}} = {D^2}\), which means the ratio of the power contributions by line-of-sight path to the remaining multipaths. The mmWave HTS could degenerate to Rayleigh fading channel under special weather conditions. The expected transmission rounds and throughput over Rayleigh fading channels are given by setting \(K=0\). We also can obtain the HARQ-RR mean number of transmission rounds over Rician fading channel by simultaneous formulas (3) and (8)

$$\begin{aligned} M_{_{LTP}}^{RR\_Ric} = 1\mathrm{{ + }}\sum \limits _{m = 2}^\infty {[1 - {{(1 - \prod \limits _{j = 1}^{m - 1} {P_{seg}^{RR\_Ric}\mathrm{{(}}m,N\mathrm{{,}}\varTheta \mathrm{{)}}} )}^{Num}}]} \end{aligned}$$
(11)

where \(P_{seg}^{RR\_Ric}\mathrm{{(}}k,N\mathrm{{,}}\varTheta ) = {Q_k}\) can be obtained by (8).

3.2 Truncated-HARQ and ARQ

Unlike the lossless-HARQ, the expected transmissions of truncated-HARQ has upper limited C. When the retransmission rounds reaches the upper limited C with unsuccessful recovery data block, then the transmitter will drop the data block and begin the next transmission. Therefore, the truncated-HARQ can not guarantee the full reliability of file delivery, but also avoid the energy waste caused by unlimited retransmissions. By combing (5) and (8), we derive the expected transmissions of truncated-HARQ over Rician fading channel as

$$\begin{aligned} M_{Ric}^C = \sum \limits _{k = 0}^{C - 1} {{Q_k}} = \sum \limits _{k = 0}^{C - 1} {{\mathrm{{e}}^{ - \left( {kKN} \right) }}\sum \limits _{i = 0}^\infty {\frac{{{{\left( {kKN} \right) }^i}}}{{\varGamma \left( {i + 1} \right) }}} {\gamma _r}(kN + i,\varTheta )} \end{aligned}$$
(12)

So the throughput expression of the truncated-HARQ is given as follows

$$\begin{aligned} T_{Ric}^C = \frac{{R\left\{ {\mathrm{{1}} - {\mathrm{{e}}^{ - \left( {CKN} \right) }}\sum \limits _{i = 0}^\infty {\frac{{{{\left( {CKN} \right) }^i}}}{{\varGamma \left( {i + 1} \right) }}} {\gamma _r}(CN + i,\varTheta )} \right\} }}{{\left\{ {\sum \limits _{k = 0}^{C - 1} {{\mathrm{{e}}^{ - \left( {kKN} \right) }}\sum \limits _{i = 0}^\infty {\frac{{{{\left( {kKN} \right) }^i}}}{{\varGamma \left( {i + 1} \right) }}} {\gamma _r}(kN + i,\varTheta )} } \right\} }} \end{aligned}$$
(13)

Because the truncated-HARQ mechanism can not completely meet the reliability requirements of LTP for red data transmission, we only consider the lossless-ARQ and -ARQ transmission mechanism in LTP.

In the ARQ scheme, decoding failure probability has nothing to help with transmission times. The mean number of transmissions is \({M^{ARQ}} = 1/(1 - {Q_1})\) and throughput \({T^{ARQ}} = R(1 - {Q_1}) = R(1 - \int _0^\varTheta {{f_Z}(z)\mathrm{{d}}z} )\). Further, we get the expected transmissions and throughput expressions of ARQ over Rician fading channels as follows

$$\begin{aligned} M_{Ric}^{ARQ} = \frac{1}{{1 - \sum \limits _{i = 0}^\infty {\frac{{\exp \left( { - KN} \right) {{\left( {KN} \right) }^i}}}{{\varGamma \left( {i + 1} \right) }}} {\gamma _r}(N + i,\varTheta )}} \end{aligned}$$
(14)
$$\begin{aligned} T_{Ric}^{ARQ} = R\left\{ {1 - \sum \limits _{i = 0}^\infty {\frac{{\exp \left( { - KN} \right) {{\left( {KN} \right) }^i}}}{{\varGamma \left( {i + 1} \right) }}} {\gamma _r}(N + i,\varTheta )} \right\} \end{aligned}$$
(15)

where (14) and (15) represent the performance of expected transmissions and throughput over Rician fading channels. We should notice the result that for truncated-HARQ \(C=1\) and ARQ, both throughput expressions are same as \(T_{Ric}^C=T_{Ric}^{ARQ}\) and \(T_{Ray}^C=T_{Ray}^{ARQ}\) despite of their different retransmission schemes [5].

4 Numerical Results and Discussion

In this section, monte carlo simulations carries on the mean number of transmission rounds in Fig. 2(a), and we investigate the delay performance of LTP-HARQ protocol in Fig. 2(b). The parameters are set as follows: The diversity order of OSTBC-MIMO \(N=1\) and the channel is degraded into SISO channel; The upper limited of truncated-HARQ transmission rounds is \(C=2\); The Shape Parameter of Rician fading is \(K=0.1\); Data rate \(R=2\,\mathrm{nat/Hz/s}\). Segment size is 1400 byte, block size is 244000 byte and one-way propagation delay is 1.2 s.

Fig. 2.
figure 2

Performance of ARQ, truncated-HARQ with \(C=2\) and lossless-HARQ over Rician and Rayleigh fading channels

Full size image

From Fig. 2, both sub-figures show that the performance in Rician fading is better than in Rayleigh fading because of the line-of-sight path, and the lossless-HARQ transmission delay and transmission has better performance than the original ARQ mechanism in LTP.

5 Conclusion

In this paper, we propose a novel performance analysis framework for LTP-HARQ scheme over OSTBC-MIMO channels for the upcoming SIN, the closed-form expressions of the mean number of transmission rounds for reliable data delivery in proposed schemes is derived by using Laplace transform. Furthermore, we derive throughput expressions for lossless- and truncated-HARQ schemes, and investigate the file delivery time in LTP over Rayleigh and Rician fading channels. Numerical and simulation results are validated the accuracy of our derived closed-form expressions.