A Particle Swarm Optimization Based Predictive Controller for Delay Compensation in Networked Control Systems

Abstract

This paper addresses transmission delays problem in network control systems. Network-induced delay is an inherent constraint in NCS implementation that could lead to system degradation and destabilization. A particle swarm optimization (PSO) tuning algorithm was adopted to optimally tune the parameters of Generalized Predictive Controller (GPC) to solve networked-induced delay problem. Furthermore, a modified PSO-GPC was designed by replacing the standard GPC objective function with an Integral Time Squared Error (ITSE) performance index in the GPC controller design. A particle swarm optimization based PI controller in the Smith predictor structure is designed to compare the performances of the original PSO-GPC and the modified PSO-GPC. The results show that the modified PSO-GPC performed better than the PSO-GPC in terms of transient response and enhanced NCS performance in the occurrence of network delays.

1 Introduction

NCS are started to be utilized in various industrial applications such as automotive [1], human surveillance [2], and process control [3] due to several clear advantages. When control system is designed using communication network, it is known as a networked control system (NCS). In NCS, the control signals are shared among the system’s elements in form of information packets through wireless or hard wired connections. Utilization of networks communication allow for efficient centralized control systems with minimal wiring across the system, hence reducing initial cost of a system [4]. Furthermore, NCS is a flexible structure that allows the addition or reduction of system components without any significant change to the hardware of the system [5].

In general, there are two common problems with NCS application. NCS prone to problem of network delay and data dropout. These problems may lead to system performance degradation or even system destabilization. Current progress in data dropout management can be review in [5,6,7]. Network-induced delay occurred due to number of factor, such as limited bandwidth, network congestion, and network transmission protocols. Short time delays delay effect on the NCS is studied using Markov model shows that network-induced delays can lead to uncontrollable or unobservable system [8, 9]. In case of network-induced delay, system stability depends on the upper and lower bounds of the time delay [10]. Several control methodologies have been formulated to compensate the negative effects of network delays in NCS based on different network configurations, constraints, and behaviors.

The event-based control methodology is introduced to control robotic manipulators over the Internet. For example, in [11, 12] the optimal stochastic control methodology is used, which treat the network delays as a Linear–Quadratic–Gaussian (LQG) problem. There is time-based methodology such as Model Predictive Control (MPC) which predict future plant output to compensate network delay problem. The main difference between event-based and time-based control methodology is that the event-based control treats a system motion as a system reference [8]. Other than that, robust control theory which doesn’t need any prior knowledge about the network delays have been studied in [13]. Combination of these methodology has also been explored by other researchers [14,15,16].

There is a growing interest in MPC-based approach due to its ability to predict future plant outputs, hence effectively compensate the network induced constraints such has network delay and packets dropouts [17, 18] even within system with state and input constraints [19, 20]. In model predictive control, there is no unique method to determine the control algorithm, but rather a wide variety of methods to predict future plant outputs from current plant outputs along a specific prediction horizon at each sampling interval [21]. In a study conducted in [17], a novel generalized predictive control (GPC) algorithm is proposed to design the control signals which include the employment of buffer in order to compensate both the control-to-actuator (C-A) and sensor-to-controller (S-C) delays. In [18], to solve for random time delays and packet dropouts, the delays are modeled using Markov chains, a modified GPC algorithm is proposed and the stability analysis is established.

The study of MPC for nonlinear NCSs is more practical than linear NCSs. However nonlinear NCS is more technically challenging due to increased computational complexities. In literature, several promising results of networked nonlinear MPC have been proposed such as Lyapunov based MPC (LMPC) strategy which able to control a nonlinear system subjected to constraints [22] and LMPC strategy for nonlinear NCSs with time-varying network-induced delays [23].

Many studies have been conducted in MPC tuning, both heuristic and deterministic [24,25,26]. However, most previous research focused on improving performance for systems without consideration of communication networks-induced problems. A summary of tuning methods for GPC and Dynamical matrix control (DMC) based on the Integral Square Error (ISE) as a performance criterion is illustrated in [27]. Some methods suggest heuristics while others are based on stability criteria, closed loop analysis, analysis of variance [28], optimization-based algorithms [29]. Most studies agree on the influence of these parameters in improving the system performance but which parameter has the highest influence is still debatable. While some suggest that the weighting factor is the most significant parameter, others suggest the prediction horizon having the most effect on system performance [30]. In this paper, a particle swarm optimization (PSO) is adopted to optimally tune the parameters of the generalized predictive control (GPC) algorithm. PSO effects on NCS performance is investigated with focus on constant network-induced delay. The main aim of the algorithm is to compensate the network-induced delays through the generated output and control input prediction sequences.

This paper is structured as follows: Sect. 2 introduces the generalized predictive control algorithm and its parameters; Sect. 3 introduces the particle swarm optimization algorithm and its formulation to solve the GPC cost function; Sect. 4 presents results from MATLAB simulation; the conclusion is presented in Sect. 5.

2 Generalized Predictive Control in Delay Compensation

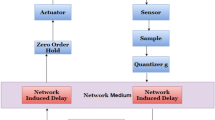
Characteristic of network delay depends on the network and transmission protocol which can be constant or time variant [31]. In this paper, Fig. 1 represents the basic structure of the considered NCS consisting of a sensor that sends information through a network to a controller, which then produced control signals to an actuator.

Fig. 1.

A NCS with time delays

2.1 NCS with Network-Induced Delays

Network-induced delay exist in the controller to actuator channel (feed forward delay) and the sensor to controller channel (feedback delay), denoted by $\tau^{ca}$ and $\tau^{sc}$ respectively.

From Fig. 1, $\tau^{sc}$ is the first delay which represents the time taken to generate a control signal from the sensor. The controller to actuator delay $\tau^{ca}$ indicates the time taken for a control signal to reach the actuator. Another delay called the computation delay $\tau^{c}$ also exists in the system and is defined as the time taken to generate a control signal from the sensor feedback signal. However, for simplification the computation delay $\tau^{c}$ is considered to be embedded within the overall network-induced delays $\tau$ [7].

Assumption 1.

The clock-driven sensor samples the plant outputs periodically at specific sampling instant $T_{S}$.

Assumption 2.

The event-driven controller and actuator act as soon as the sensor data and control data become available.

Assumption 3.

The network-induced delays in the system are time varying but bounded. Moreover, let $\overline{{a_{k}^{max} }}$, $\overline{{{\text{b}}_{\text{k}}^{\hbox{max} } }}$, $\overline{{a_{k}^{min} }}$ and $\overline{{b_{k}^{min} }}$ symbolize the maximum and minimum delays in the feedforward channel and in the feedback channel. Number of sampling periods is a positive integer.

Remark 1.

The delay considered in the feed forward and feedback channels have maximum and minimum value, therefore we can treat the network delays as dead time denoted by d.

Since the delays present in the system are time varying but bounded by maximum and minimum values,

$$ d_{m} \le d \le d_{M} . $$

(1)

Where $d_{m}$ is the minimum delay and $d_{M}$ is the maximum delay which determined by the following equations,

$$ d_{m} = \overline{{a_{k}^{min} }} + \overline{{b_{k}^{min} }} . $$

(2)

$$ d_{M} = \overline{{a_{k}^{max} }} + \overline{{b_{k}^{max} }} . $$

(3)

Based on (2) and (3), the delay d is calculated using the mean value of the delays present in the communication network which is described by the following relation [23],

$$ d = \frac{{d_{m} + d_{M} }}{2}. $$

(4)

2.2 Generalized Predictive Control Algorithm

Generalized predictive control uses the following CARIMA model to describe the controlled object

$$ A(z^{ - 1} )y(t) = z^{ - d} B(z^{ - 1} )u\,(t - 1) + \frac{{e\,(t)C(z^{ - 1} )}}{{D\,(z^{ - 1} )}}. $$

(5)

Where $(t)$, $u\,(t - 1)$ and $e\,(t)$ are the plant output, control signal, and white noise with zero mean value. It is assumed that there is no disturbance acting on the system, therefore $e(t)$ will be zero. $A(z^{ - 1} )$ and $B(z^{ - 1} )$ are the plant polynomials while $C(z^{ - 1} )$ and $D(z^{ - 1} )$ are the disturbance polynomials having the following expressions,

$$ A(z^{ - 1} ) = 1 + a_{1} z^{ - 1} + \cdots + a_{{n_{A} }} z^{{ - n_{A} }} . $$

(6)

$$ {\text{B}}({\text{z}}^{ - 1} ) = {\text{b}}_{0} + {\text{b}}_{1} {\text{z}}^{ - 1} + \cdots + {\text{b}}_{{{\text{n}}_{\text{A}} }} {\text{z}}^{{ - {\text{n}}_{\text{B}} }} . $$

(7)

$$ C\,(z^{ - 1} ) = 1. $$

(8)

$$ {\text{D}}\,({\text{z}}^{ - 1} ) = 1 - {\text{z}}^{ - 1} . $$

(9)

Where $n_{A}$ and $n_{A}$ represent the polynomial degrees.

The control algorithm for a generalized predictive controller (GPC) consists of two steps, first is the prediction model which predicts the future plant outputs, based on past and current input values. The prediction model has the form below

$$ \begin{aligned} \hat{y}\left( {t + N|T_{S} } \right) & = G(z^{ - 1} )D(z^{ - 1} )z^{ - d - 1} u\left( {t + N|T_{S} } \right) + \\ & \quad \frac{{H(z^{ - 1} )D(z^{ - 1} )}}{{C(z^{ - 1} )}}u\left( {t - 1|T_{S} } \right) + \frac{{F(z^{ - 1} )}}{{C(z^{ - 1} )}}y(t|T_{S} ). \\ \end{aligned} $$

(10)

Where N is the prediction horizon, $\hat{y}\left( {t + N|T_{S} } \right)$ are the predicted plant outputs a computed at time k and $u\left( {t + N|T_{S} } \right)$ are the future control signals computed at every sampling time $T_{S}$. To determine the polynomial $G(z^{ - 1} )$, $H(z^{ - 1} )$ and $F(z^{ - 1} )$ two Diophantine equations are used,

$$ \frac{{C(z^{ - 1} )}}{{A(z^{ - 1} )D(z^{ - 1} )}} = E(z^{ - 1} ) + z^{ - (N - d)} \frac{{F(z^{ - 1} )}}{{A(z^{ - 1} )D(z^{ - 1} )}}. $$

(11)

$$ E(z^{ - 1} )B(z^{ - 1} ) = C(z^{ - 1} )G(z^{ - 1} ) + z^{ - (N - d)} H(z^{ - 1} ). $$

(12)

Where

$$ E(z^{ - 1} ) = 1 + e_{1} z^{ - 1} + \cdots + a_{{n_{E} }} z^{{ - n_{E} }} . $$

(13)

$$ F(z^{ - 1} ) = f_{0} + f_{1} z^{ - 1} + \cdots + f_{{n_{F} }} z^{{ - n_{F} }} . $$

(14)

$$ G(z^{ - 1} ) = g_{0} + g_{1} z^{ - 1} + \cdots + g_{{n_{G} }} z^{{ - n_{G} }} . $$

(15)

$$ H(z^{ - 1} ) = h_{0} + h_{1} z^{ - 1} + \cdots + h_{{n_{H} }} z^{{ - n_{H} }} . $$

(16)

With

$$ n_{E} = N - d - 1. $$

(17)

$$ n_{F} = \hbox{max} \left( {n_{A} + n_{D} - 1,n_{c} - (N - d)} \right). $$

(18)

$$ n_{G} = N - d - 1. $$

(19)

$$ n_{H} = \hbox{max} \left( {n_{C} ,n_{B} + d} \right) - 1. $$

(20)

After determining the values of the previous polynomials and collecting the N step predictions, the prediction model can be written in a matrix notation as,

$$ \hat{y} = Gu_{d} + \hat{y}_{0} . $$

(21)

Where $\hat{y}$ is predicted plant output vector, $u_{d}$ is the vector of future control sequences, G is the system dynamic matrix and $\hat{y}_{0}$ represents the predicted free response vector.

$$ \hat{y} = [\hat{y}\left( {t + d + 1|T_{S} } \right)\quad \hat{y}\left( {t + d + 2|T_{S} } \right)\, \ldots \,\hat{y}\left( {t + d + N|T_{S} } \right)]^{T} . $$

(22)

$$ u_{d} = [\Delta u\left( {t|T_{S} } \right)\quad \Delta u\left( {t + 1|T_{S} } \right)\, \ldots \,\Delta u\left( {k + N - 1|T_{S} } \right)]^{T} . $$

(23)

$$ \hat{y}_{0} = [\hat{y}_{0} \left( {t + d + 1|T_{S} } \right)\quad \hat{y}_{0} \left( {t + d + 1|T_{S} } \right)\, \ldots \,\hat{y}_{0} \left( {t + d + 1|T_{S} } \right)]^{T} . $$

(24)

$$ G = \left[ {\begin{array}{*{20}c} {g_{0} } & 0 & \ldots & 0 \\ {g_{1} } & {g_{0} } & \ldots & 0 \\ \vdots & \vdots & \ddots & \vdots \\ {g_{N - 1} } & {g_{N - 2} } & \ldots & {g_{0} } \\ \end{array} } \right]. $$

(25)

The second step in the GPC controller design consists on determining the optimal control sequence. The optimizer calculates these signals by taking into consideration the objective function J. The objective function is based on the minimization of both the controller output and tracking error, the control weighting factor λ is introduced to make a trade-off between these objectives.

$$ J = \left( {Gu_{d} + \hat{y}_{0} - w} \right)^{T} \left( {Gu_{d} + \hat{y}_{0} - w} \right) + \lambda u_{d}^{T} u_{d} . $$

(26)

Where w is the reference trajectory vector, by minimizing the above objective function $\left( {\frac{\partial J}{{\partial u_{d} }} = 0} \right)$ the optimal control signal is expressed as,

$$ u_{d}^{*} = \left( {G^{T} G + \lambda I} \right)^{ - 1} G^{T} \left[ {w - \hat{y}_{0} } \right]. $$

(27)

The control algorithm is calculated in a recursive (off-line) manner, which has the advantage of very fast computation.

2.3 GPC Parameter Tuning

The objective function from (26) can be rewritten as

$$ j = \sum\nolimits_{k = 1}^{N} {\left( {\hat{y}(t + k) - w(t + k)} \right)} + \lambda \sum\nolimits_{k = 1}^{{N_{u} }} {\Delta {\text{u}}({\text{t}} + {\text{k}} - 1)} . $$

(28)

Equation (28) shows there are three parameters that affect the control signal generated in (27); N, N_U, and λ. Prediction horizon N and control horizon N_U are related to each other. Prediction horizon is selected early in the controller design and then holds it constant while tuning other controller settings. The control horizon is used to reduce computational processes by minimizing computational variables at each control interval. The value of the control horizon is in between 1 and the value of the prediction horizon. To deal with network-induced delays, its recommended that the difference between the prediction horizon and the control horizon must be larger than delay introduced by the communication network at each sampling instant, which is denoted by d [32]. The control weighting factor λ is present in (26) to restrict the control signal. The aggressiveness of the control signal is inversely proportional to λ. If λ has a small value, the controller will minimize the error between the reference and the output, forgetting about the control effort. Thus, the response of the system will tend to be faster but this might also result in an increase in overshoot and response oscillation.

3 Particle Swarm Optimization Based Approach for GPC Tuning

In this section, an overview on particle swarm optimization will be presented. The particle swarm optimization algorithm will then be implemented to tune the parameters of the GPC controller based on two objective functions. Finally, the PSO-GPC controller performance will be compared with the performance of a Smith predictor-PI controller in which the PSO will be applied to tune $K_{p}$ and $K_{i}$.

3.1 Particle Swarm Optimization

The term optimization refers to the process of selecting the best element from a group of alternative elements based on a defined goal called the objective function. Mathematically, this is achieved by finding the values of the parameters that will maximize or minimize the objective function. Solving optimization problems analytically is quite tedious because the objective function might be non-linear, multidimensional, constrained or have many local optimums. Heuristic optimization method is an efficient alternative to solve the problem [29,30,31].

Particle swarm optimization is meta-heuristic optimization method developed by Kennedy and Eberhart to imitate the seeking behavior in bird flocks or fish schools [33]. In PSO, the solution for the optimization problem is represented by a vector called a particle which contains a set of parameters and every particle has the same number of parameters. Initially, a population containing a number of particles is initialized with random parameters and then enters an iterative process to search for the optimum solution. After each iteration, particles are compared and evaluated by substituting the values of their parameters in the objective function. In one iteration it might occur that one of the particles comes out with the best solution, called the globally best solution. In the succeeding iteration, another particle might be the globally best solution. Hence, at the end of each iteration, a velocity estimate for each particle is calculated based on its best solution called the personal best and the globally best. Furthermore, the velocity is used to update the particle following these equations,

$$ v_{i}^{K + 1} = Wv_{i}^{k} + C_{1} R_{1} \left( {P_{i} - x_{i}^{k} } \right) + C_{2} R_{2} \left( {P_{g} - x_{i}^{k} } \right). $$

(29)

$$ x_{i}^{k + 1} = x_{i}^{k} + v_{i}^{K + 1} . $$

(30)

Where $v_{i}^{k}$ represents the current velocity for particle i at iteration k while $v_{i}^{K + 1}$ is the velocity at iteration $K + 1$. $x_{i}^{k}$ represents the current position for particle i at iteration k while $x_{i}^{k + 1}$ is the updated position at iteration $K + 1$. $C_{1}$ and $C_{2}$ are the cognitive coefficient and social coefficient which help modulate the steps taken by a particle in the direction of its personal best and global best. $R_{1}$ and $R_{2}$ are random values between 0 and 1. $P_{i}$ represents the personal best of the particle i, $P_{g}$ is the global best and W is the inertia weighting coefficient. As iterations continue, the particles are updated and they all move from different directions towards the global best which results in the best solution.

3.2 PSO Based Generalized Predictive Control Design

As mentioned in the previous section, the main parts of the GPC are (10) and (26). Other equations are used to get the optimal control input in (27) to minimize the objective function found in (26). However, the objective function relies on three GPC parameters which are the prediction horizon N, control horizon N_U and the weighting factor λ. Hence, a particle swarm optimization method can be implemented to tune these parameters and minimize the objective function as shown in Fig. 2. The particles are represented by $P = \left[ {N,N_{u} ,\lambda } \right]^{T}$ and formulated as follows:

Fig. 2.

PSO-GPC block diagram

• (1) Identify the number of particles, the upper and the lower boundary of each tunable parameter, number of iterations and search parameters: cognitive coefficient $(C_{1} )$, social coefficient $(C_{2} )$ and inertia weighting coefficient (W).

• (2) The particle position and velocity are initialized randomly.

• (3) Simulate the GPC with the tuning parameters (N, N_U and λ) for each particle.

• (4) Evaluate the objective function for each particle.

• (5) Update, if any, the personal best Pi and global best Pg.

• (6) Update the particle positions and velocities with values of step 5.

• (7) Repeat step 3 to 6 until the last iteration count or the desired precision is achieved. The particle that produces the latest global best is the optimal value.

Equation 26 reveals the objective function as a summation of two terms. The first term is $\sum\nolimits_{k = 1}^{N} {\left( {\hat{y}(t + k) - w(t + k)} \right)}$ which ensures fast transient response, settling time, and minimizes overshoot. The other term is $\lambda \sum\nolimits_{k = 1}^{{N_{u} }} {\Delta {\text{u}}({\text{t}} + {\text{k}} - 1)}$ that prevents the control signal from increasing indefinitely as it can lead to actuator saturation. Furthermore, to achieve better performance and tracking accuracy, the objective function in (28) will be replaced by one of the time domain integral performance indices called the Integral Time Square Error (ITSE) which will be solved by the particle swarm optimization.

$$ e(t) = w(t) - y(t). $$

(31)

$$ ISE = \int_{0}^{{t_{ss} }} {e(t)^{2} dt} . $$

(32)

$$ IAE = \int_{0}^{{t_{ss} }} {\left| {e(t)} \right|dt} . $$

(33)

$$ ITSE = \int_{0}^{{t_{ss} }} {te(t)^{2} dt} . $$

(34)

Where $e(t)$ is the error signal and $t_{ss}$ is the time it takes to reach steady state. The goal behind this replacement is to formulate the tuning selection to account for the time domain performance goals such as settling time, rise time, and overshoot. The control systems based on these indices has fast response speed, large oscillation, relatively weak stability. In addition, control system based on ITSE force the error to be small at future instants with minimal oscillation compared to other performance indices such as Integral Absolute Error (IAE) and Integral Squared Error (ISE) [34].

3.3 PSO Implemented on a Smith Predictor Controller

The Smith predictor is one of the most used control strategies for time delay compensation. Smith predictor introduces an internal feedback into a controller to counterbalance the effects of delays on the main controller. Figure 3 illustrates the basic structure of a smith predictor controller in NCS [35].

Fig. 3.

Smith predictor structure in NCS

In Fig. 2, u, y, y _m , y _p and e _p are the control signal, actual output, predicted output, estimated output and output error, respectively. The controller shown above is selected to be a PI controller, which is described by the discrete form,

$$ G_{PI} (z) = \frac{{K_{p} T_{s} z}}{{K_{i} z - K_{i} }}. $$

(35)

$K_{p}$ and $K_{i}$ represent the proportional gain and the integral gain respectively and are the controller parameters that will be tuned offline with the particle swarm optimization algorithm. The Integral Square Error (ISE) is used as the objective function to ensure the error signal approach zero while achieving faster transient response and minimum overshoot.

4 Results and Discussion

Simulation is carried out using MATLAB/Simulink 2016a, and it is assumed that both feedback and feedforward channel exhibit constant network-induced delays of 2 s $(\tau^{ca} = \tau^{sc} = 2)$. The controlled plant is a liquid level tank with the following discrete transfer function,

$$ G(z^{ - 1} ) = \frac{{0.001703z^{ - 1} + 0.005419z^{ - 2} }}{{1 - 0.9718z^{ - 1} - 0.025z^{ - 2} }} = \frac{{A(z^{ - 1} )}}{{B(z^{ - 1} )}} $$

The particle swarm optimization method is then used to tune the parameters of the GPC over a predefined search region such that the objective functions in (28) is minimized. The upper and lower value of the search regions are specified as listed in Table 1. The lower values of the prediction horizon and control horizon are selected based on the works in [24] to address the network-induced delays. The upper bound of the prediction horizon and control horizon are set at 40 and 10 respectively to minimize computational time. The lower search region for the Smith Predictor parameters are chosen to be 0.0001 for both, while the upper values have a value of 200 to prevent destabilizing the plant by introducing high value gains. In PSO, the number of particles crucial in ensuring accurate results. The number of particles is set to 20 based on the work in [33] which illustrate that a suitable number of particles is in between 20 to 50. The number of iterations and the PSO search parameters used in the simulation is presented in Table 2.

Table 1. Search region of the tunable parameters

Table 2. Parameters of the PSO algorithm

To compare with GPC, the PSO procedure is repeated on a Smith predictor to obtain the optimal parameter values as tabulated in Table 3. In Table 4, the control performance in terms of transient response of each controller is presented. It is clear that the PSO-Smith predictor outperformed the PSO-GPC in terms of transient response.

Table 3. Tuning parameters obtained through PSO

Table 4. Transient response analysis for step input signal

In Fig. 4, it is obvious that the PSO-Smith predictor produces larger undershoot compared to the PSO-GPC when the water level is reduced. This indicates that the PSO-GPC is more efficient in dealing with non-minimum phase systems compared to PSO-Smith Predictor. However, the PSO-GPC resulted with a small overshoot and slower transient response toward the set point. Thus, a modified PSO-GPC is proposed through the replacement of the cost function in (28) by the ITSE objective function shown in (34). With a modified PSO-GPC, faster settling time and rise time can be achieved. Plus, GPC algorithm also allows for incorporation of output constraint in the optimization to tackle the overshoot problem. This is a clear advantage of GPC compared to the other control algorithm.

Fig. 4.

Comparison of closed-loop step response

From Fig. 5, it can be seen that the modified PSO-GPC produced a better transient response than the original PSO-GPC. When compared with PSO-Smith predictor, the modified controller was slightly outperformed in terms of settling time and rise time as illustrated in Table 4, but produced a smaller undershoot. Thus, it can be concluded that GPC is a preferable controller in NCS applications because it is capable to deal with non-minimum systems, ability to handle constraints and its clear potential for other types of network-induced delays such as random time delay.

Fig. 5.

Modified PSO-GPC closed-loop step response

5 Conclusion

In this paper, a standard GPC objective function and an ITSE performance index were applied in the generalized predictive controller design by using a particle swarm optimization to compensate the network-induced delays occurring between the components of a networked control system. The aim of the particle swarm optimization is to optimally tune the GPC parameters based on the above objective functions. The simulations result in MATLAB/SIMULINK show significant improvement of the controllers using the proposed techniques compared to PSO-Smith predictor. Although both predictive controllers can compensate the effects of network delays, the modified PSO-GPC, which is based on the ITSE performance index, achieved better transient response when compared with the original PSO-GPC.