Event-Triggered Adaptive Dynamic Programming for Uncertain Nonlinear Systems

Abstract

In this paper, the robust control for a class of continuous-time nonlinear system with unmatched uncertainties is investigated using an event-triggered adaptive dynamic programming method. First, the robust control problem is solved using the optimal control method. Under the event-triggered mechanism, the solution of the optimal control problem can asymptotically stabilize the uncertain system with an designed triggering condition. That is, the designed event-triggered controller is robust to the original uncertain system. Then, a single critic network structure with experience replay technique is constructed to approach the optimal control policies. Finally, a simulation example is provided to demonstrate the effectiveness of the proposed control scheme.

1 Introduction

As many practical control systems become more and more complex, the uncertainties arise in the system models frequently. These uncertainties may severely degrade the system performance, and even lead to system instability, so it is necessary to design the robust controller for uncertain nonlinear systems. Lin et al. [1] established a connection between the robust control problem and optimal control problem. They proposed an indirect approach for the robust stabilization by designing a corresponding optimal controller. In [2], the uncertainties was divided into matched and unmatched ones and proved that the optimal controller can stabilize the linear and nonlinear robust control systems in the same way. However, the detailed approach to solve the Hamilton-Jacobi-Bellman (HJB) equation to obtain the optimal control policy was not discussed.

As is known, it is intractable to give an analytic solution to the HJB equation for the nonlinear systems [3]. Recently, adaptive dynamic programming (ADP) which was proposed by Werbos [4] has been widely applied to approximate the solution of the HJB equation. For example, the $H_\infty$ control approach based on ADP was investigated for the uncertain nonlinear systems in [5]. Jiang et al. proposed a robust adaptive dynamic programming (RADP) methodology in [6]. Liu et al. [7] investigated the optimal robust guaranteed cost control problem using corresponding optimal control method. In [8], the robust control problem of nonlinear systems with matched uncertainties was converted into an optimal control problem of an nominal system. For the nonlinear deterministic systems, Zhao et al. developed several ADP methods to solve the corresponding optimal control problems [9, 10]. However, the aforementioned approaches are conducted predicated on the traditional time-triggered strategy.

In general, the amount of transmitted data is huge using the traditional time-triggered approach. To mitigate the unnecessary waste of communication resources, event-triggered control (ETC) method has received great interests among the control researchers. Recently, the ETC method has been integrated with the ADP approach to solve the optimal control problems [11]. In [12], Sahoo et al. proposed a neural network (NN)-based ETC scheme for nonlinear discrete-time systems using ADP approach. Vamvoudakis proposed an optimal adaptive ETC algorithm based on the actor-critic structure for CT nonlinear systems with guaranteed performance in [13]. In [14], the event-triggered reinforcement learning approach was developed for the nonlinear systems without requiring exact knowledge of system dynamics. However, the system uncertainties are not concerned in the existing work of event-triggered optimal control.

In this paper, we investigate the robust control problem of nonlinear systems with unmatched uncertainties using an optimal control approach.

Section 2 introduces the robust control problem of the nonlinear system with unmatched uncertainties and the traditional optimal control problem. In Sect. 3, the connection between the robust stabilization and the optimal control problem is discussed. In Sect. 4, the event-triggered ADP algorithm is proposed to approximate the optimal control policy. Simulation results and the conclusion are presented in the end.

2 Problem Statement

Consider the following CT uncertain nonlinear system

$$\begin{aligned} \dot{x}(t)=f(x(t))+g(x(t)){u}(x)+{k}(x(t))W(x(t)) \end{aligned}$$

(1)

where $x =x(t) \subseteq {\mathbb {R}^n}$ is the state vector, ${u}=u(x)\in {\mathbb {R}^{m}}$ is the control input, $f(\cdot )\in {\mathbb {R}^n}$, $g(\cdot )\in {\mathbb {R}^{n\times m}}$ and $k(\cdot )\in \mathbb {R}^{n\times q}$ are differentiable nonlinear dynamics with $f(0)=0$, and $W(\cdot )\in {\mathbb {R}^q}$ is the unknown nonlinear perturbation. Assume that ${W}(0)=0$, so that $x=0$ is an equilibrium of system (1).

The uncertainty W(x) is known as an unmatched uncertainty for system (1), if $k(x)\ne g(x)$. In this paper, we aim to find a control policy so that the system (1) is globally asymptotically stable for all unmatched uncertainties W(x) satisfying the following assumption.

Assumption 1

[2]

• 1. The uncertainty W(x) is bounded by a known non-negative function $W_M(x)$, i.e., $\Vert W(x)\Vert \le W_M(x)$ with $W_M(0)=0$.

• 2. There exists a non-negative function $g_M(x)$ such that

  $$\begin{aligned} \Vert g^{+}(x)k(x)W(x)\Vert ^2 \le \frac{g_M^{2}(x)}{2} \end{aligned}$$

  (2)

  where $g^{+}(x)$ denotes the (Moore-Penrose) pseudoinverse of function g(x).

Motivated by [2], the robust control problem of the uncertain nonlinear system will be converted into an optimal control problem of a corresponding auxiliary system with an appropriate cost function. First, the uncertainty term k(x)W(x) is decomposed into a matched component and an unmatched one in the range space of g(x).

$$\begin{aligned} k(x)W(x)=g(x)g^{+}(x)k(x)W(x)+(I-g(x)g^{+}(x))k(x)W(x) \end{aligned}$$

(3)

Then, we can transform the robust control problem into an optimal control problem as follows.

Optimal Control Problem: For the corresponding auxiliary system

$$\begin{aligned} \dot{x}=f(x)+g(x)u(x)+\left( I-g(x)g^{+}(x)\right) k(x)w(x) \end{aligned}$$

(4)

where $w=w(x)\in \mathbb {R}^q$ is an augmented control to deal with the unmatched uncertainty component, and $[u^\text {T}(x),w^\text {T}(x)]^\text {T}$ is a control policy pair of system (4).

Assume that the auxiliary system (4) is controllable. It is desired to find the optimal control policy pair $[u^{*\text {T}}(x),w^{*\text {T}}(x)]^\text {T}$ that minimizes the cost function given by

$$\begin{aligned} V\big (x(0)\big )=\int _0^\infty \Vert r^\text {T}\Vert ^2g_M^2(x)+\eta ^2\Vert m^\text {T}\Vert ^2 W_M^2(x)+U(x,u,w)\text {d}t \end{aligned}$$

(5)

where the utility $U(x,u,w)=x^\text {T}Qx+u^\text {T}(x)Ru(x)+\eta ^2 w^\text {T}(x)Mw(x)$, and $\eta >0$ is a designed parameter. Here, Q, R and M are positive definite symmetric matrices. According to the principle of Cholesky decomposition, we have $R=rr^\text {T}$ and $M=mm^\text {T}$, where r and m are two appropriate lower triangular matrices.

Remark 1

For the optimal control problem of the auxiliary system (4), the designed feedback control inputs should be admissible (see [5] for definition). In this paper, we use $\varPhi (\varOmega )$ to denote the set of admissible policies on a compact set $\varOmega$.

For any admissible policies $u,w\in \varPhi (\varOmega )$, if the cost function (5) is continuously differentiable, the infinitesimal version of (5) is the so-called nonlinear Lyapunov equation

$$\begin{aligned} \begin{aligned}&\nabla V^\text {T} \left( f(x)+g(x)u(t)+(I-g(x)g^{+}(x))k(x)w(t)\right) \\&+\Vert r^\text {T} \Vert ^2g_M^2(x)+\eta ^2\Vert m^\text {T} \Vert ^2 W_M^2(x)+U(x,u,w)=0, \end{aligned} \end{aligned}$$

(6)

where $\nabla V={\partial V(x)}/{\partial x}$ is the partial derivative of the cost function V(x) with respect to the state x, and $V(0)=0$.

Define the Hamiltonian function of system (4) as

$$\begin{aligned} \begin{aligned} H(x,\nabla V, u,w) =&\Vert r^\text {T}\Vert ^2g_M^2(x)+\eta ^2\Vert m^\text {T} \Vert ^2 W_M^2(x)+U(x,u,w)\\&+(\nabla V)^\text {T} \left( f(x)+g(x)u(t)+(I-g(x)g^{+}(x))k(x)w(t)\right) \end{aligned} \end{aligned}$$

(7)

Then the optimal cost function of system (4)

$$\begin{aligned} \begin{aligned} V^*\big (x(0)\big )=&\mathop {\min }\limits _{{u,w}\in \varPhi (\varOmega )} \int _0^\infty \left\{ \Vert r^\text {T}\Vert ^2g_M^2(x(\tau ))+\eta ^2 \Vert m^\text {T}\Vert ^2 \right. \\&\times W_M^2(x(\tau ))\left. +U(x(\tau ),u(\tau ),w(\tau ))\right\} \text {d}\tau \end{aligned} \end{aligned}$$

(8)

satisfies the associated HJB equation

$$\begin{aligned} \mathop {\min }\limits _{{u,w}\in \varPhi (\varOmega )}H(x,\nabla V^*,u,w)=0 \end{aligned}$$

(9)

where $V^*(x)$ is a solution of the HJB equation.

Assume that the minimum policy pair on the left-hand side of (9) exists and is unique. According to the stationary conditions, the optimal control policies are given by

$$\begin{aligned} u^*(x)=-\frac{1}{2}R^{-1}g^\text {T}(x)\nabla V^* \end{aligned}$$

(10)

$$\begin{aligned} w^*(x)=-\frac{1}{2\eta ^2}M^{-1}k^\text {T}(x)(I-g(x)g^{+}(x))^\text {T}\nabla V^* \end{aligned}$$

(11)

Denote $d(x)=(I-g(x)g^{+}(x))k(x)$. Based on (10) and (11), the HJB Eq. (9) can be rewritten as

$$\begin{aligned} \begin{aligned}&H(x,\nabla V^*, u^*,w^*)\\ =~&(\nabla V^*)^\text {T}f(x)+x^\text {T}Qx+\Vert r^\text {T}\Vert ^2g_M^2(x) +\eta ^2\Vert m^\text {T}\Vert ^2 W_M^2(x)\\&-\frac{1}{4}(\nabla V^*)^\text {T}g(x)R^{-1}g^\text {T}(x)\nabla V^*-\frac{1}{4\eta ^2}(\nabla V^*)^\text {T}d(x)M^{-1}d^\text {T}(x)\nabla V^*=0 \end{aligned} \end{aligned}$$

(12)

So far, the robust control problem is transformed into a corresponding time-triggered optimal control problem. Then the traditional ADP technique can be employed to approximate the solution $V^*(x)$ of the HJB equation. In order to reduce the computational burden and save communication resources, the ETC mechanism is introduced in this paper. And an adaptive triggering condition will be designed to guarantee the stability of the uncertain system with an event-triggered optimal controller.

3 Event-Triggered Robust Optimal Controller

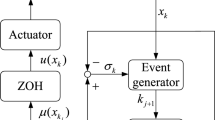
To propose the ETC mechanism, we first define a monotonically increasing sequence of triggering instants ${\{\tau _j\}_{j=0}^\infty }$, where $\tau _j$ is the $j^\text {th}$ consecutive sampling instant with $\tau _j<\tau _{j+1}, j \in \mathbb {N}$ with $\mathbb {N}=\{0,1,2,\cdot \cdot \cdot \}$. Then an sampled-data system characterized by the triggering instants is introduced, where the controller is updated based on the sampled state ${\hat{x}}_j=x(\tau _j)$ for all $t\in [\tau _j,\tau _{j+1})$. Define the event-triggered error as

$$\begin{aligned} e_j(t)={\hat{x}}_j-x(t), \forall t\in [\tau _j,\tau _{j+1}),j \in \mathbb {N} \end{aligned}$$

(13)

where x(t) and ${\hat{x}}_j$ denote the current state and the sampled state, respectively.

In the ETC method, the triggering condition is determined by the event-triggered error and a designed state-dependent threshold. When the event-triggered error exceeds the state-dependent threshold, an event is triggered. Then, the system states are sampled that resets the event-triggered error $e_j(t)$ to zero, and be held until the next triggering instant. Accordingly, the designed event-triggered controller $u ({\hat{x}}_j)\buildrel \varDelta \over =\mu ({\hat{x}}_j)$ is updated. Clearly, the control signal $\mu ({\hat{x}}_j)$ is a function of the event-based state vector, which is executed based on the latest sampled state ${\hat{x}}_j$ instead of the current value x(t). That is, the event-triggered controller is only updated at the triggering instant sequence $\{\tau _j\}_{j=0}^{\infty }$ and remains unchanged in each time interval $t\in [\tau _j,\tau _{j+1})$. Hence, this control signal $\mu ({\hat{x}}_j)$ with $j \in \mathbb {N}$ is a piecewise constant function on each segment $[\tau _j,\tau _{j+1})$.

Under the event-triggering mechanism, the transformed optimal control problem in the previous section can be restated as follows.

With the event-triggered control input $\mu ({\hat{x}}_j)$, the sampled-data version of the auxiliary system (4) can be written as

$$\begin{aligned} \dot{x}(t)=f(x)+g(x)\mu \left( x(t)+e_j(t)\right) +d(x)w\left( x(t)\right) \end{aligned}$$

(14)

Considering the event-triggered sampling rule, the optimal control policy (10) becomes

$$\begin{aligned} \mu ^*({\hat{x}}_j)=-\frac{1}{2}R^{-1}g^\text {T}({\hat{x}}_j)\nabla V^*({\hat{x}}_j) \end{aligned}$$

(15)

for all $t \in [\tau _j,\tau _{j+1})$, where $\nabla V^*({\hat{x}}_j)= {\partial V^*(x)}/{\partial x}|_{x={\hat{x}}_j}$.

By using the optimal cost function $V^*(x)$, the event-triggered controller (15) and the augmented controller (11), the Hamiltonian function (7) becomes

$$\begin{aligned} \begin{aligned}&H(x,\nabla V^*,\mu ^*({\hat{x}}_j),w^*(x))\\ =&\ (\nabla V^*)^\text {T}f(x)+x^\text {T}Qx+\Vert r^\text {T}\Vert ^2g_M^2(x)+\eta ^2\Vert m^\text {T}\Vert ^2 W_M^2(x)\\&-\frac{1}{2}(\nabla V^*)^\text {T}g(x)R^{-1}g^\text {T}({\hat{x}}_j)\nabla V^*({\hat{x}}_j)\\&+\frac{1}{4}(\nabla V^*({\hat{x}}_j))^\text {T}g({\hat{x}}_j)R^{-1}g^\text {T}({\hat{x}}_j)\nabla V^*({\hat{x}}_j)\\&-\frac{1}{4\eta ^2}(\nabla V^*)^\text {T}d(x)M^{-1}d^\text {T}(x)\nabla V^* \end{aligned} \end{aligned}$$

(16)

For convenience of analysis, results of this paper are based on the following assumptions.

Assumption 2

[8]: $f+gu+dw$ is Lipschitz continuous on $\varOmega \in \mathbb {R}^{n}$ containing the origin.

Assumption 3

[13]: The controller u(x) is Lipschitz continuous with respect to the event-triggered error,

$$\begin{aligned} \begin{aligned} \Vert u(x(t))-u({\hat{x}}_j)\Vert =\Vert u(x(t))-u(x(t)+e_j(t))\Vert \le L\Vert e_j(t)\Vert \\ \end{aligned} \end{aligned}$$

(17)

where L is a positive real constant.

Remark 2

This assumption is satisfied in many applications where the controller are affine with respect to $e_j$. Note that w(t) is not the direct control policy of the robust control system (1), but it plays an important role in finding the event-triggered optimal control policy $\mu ^*({\hat{x}}_j)$ for the system (14).

Remark 3

Combined (12) and (16), we have

$$\begin{aligned} \begin{aligned}&H(x,\nabla V^*,\mu ^*({\hat{x}}_j),w^*(x))\\ =&(\nabla V^*)^\textit{T} \left( f(x)+g(x)\mu ^*({\hat{x}}_j)+d(x)w^*(x)\right) +\Vert r^\textit{T} \Vert ^2g_M^2(x)\\&+ \eta ^2\Vert m^\textit{T} \Vert ^2 W_M^2(x)+U\big (x,\mu ^*({\hat{x}}_j),w^*(x)\big )\\ =&\left( r^\textit{T}(u^*(x)-\mu ^*({\hat{x}}_j))\right) ^\textit{T}\left( r^\textit{T}(u^*(x)-\mu ^*({\hat{x}}_j))\right) \end{aligned} \end{aligned}$$

(18)

It is called the event-triggered HJB equation. Different from the traditional HJB Eq. (12), the event-triggered HJB equation is only equal to zero at every triggering instant. In other words, a transformation error is introduced due to the event-triggered transformation from (10) to (15), which makes the function $H(x,\nabla V^*,\mu ^*({\hat{x}}_j),w^*(x))$ not equal to zero during each time interval $t\in (\tau _j,\tau _{j+1})$.

Theorem 1

Suppose that $V^*(x)$ is the solution of the HJB Eq. (12). For all $t\in [\tau _j,\tau _{j+1}), j\in \mathbb {N}$, the control policies are given by (11) and (15), respectively. If the triggering condition is defined as follows

$$\begin{aligned} \begin{aligned} \Vert e_j(t)\Vert ^2&> \frac{(1-\beta ^2)}{2\Vert r^T\Vert ^2\Vert L\Vert ^2}\lambda _{\min }(Q)\Vert x\Vert ^2 - \frac{\eta ^2\Vert m^\textit{T}w^*(x)\Vert ^2}{\Vert r^\textit{T}\Vert ^2\Vert L\Vert ^2} \buildrel \varDelta \over = \Vert e_T\Vert ^2 \end{aligned} \end{aligned}$$

(19)

where $e_T$ denotes the threshold, $\lambda _{\min }(Q)$ is the minimal eigenvalue of Q, and $\beta \in (0,1)$ is a designed sample frequency parameter. Then the solution $\mu ^*({\hat{x}}_j)$ to the optimal control problem is also a solution to the robust control problem. That is, the system (1) can be globally asymptotically stable for all admissible uncertainties W(x) under $\mu ^*({\hat{x}}_j)$.

Remark 4

The corresponding proof will be given in a future work. Note that the control input $\mu ^*({\hat{x}}_j)$ is based on event-triggered mechanism while the augmented control input $w^*(x)$ is based on time-triggered mechanism in this paper.

4 Approximate Optimal Controller Design

In this section, an online event-triggered ADP algorithm with a single NN structure is proposed to approximate the solution of the event-triggered HJB equation.

4.1 Event-Triggered ADP Algorithm via Critic Network

In the event-triggered ADP algorithm, only a single critic network with a three-layer network structure is required to approximate the optimal value function. The optimal value function based on NN can be formulated as

$$\begin{aligned} V^*(x)=W_c^\text {T} \phi (x)+\varepsilon \end{aligned}$$

(20)

where $W_c\in \mathbb {R}^N$ is the critic NN ideal weights, $\phi (x)\in \mathbb {R}^N$ is the activation function vector, N is the number of hidden neurons, and $\varepsilon \in \mathbb {R}$ is the critic NN approximation error. Then, we can obtain

$$\begin{aligned} \nabla V^*(x)=\nabla \phi ^\text {T}(x)W_c+\nabla \varepsilon \end{aligned}$$

(21)

Since the ideal weight matrix is unknown, the actual output of critic NN can be presented as

$$\begin{aligned} {\hat{V}}(x)={\hat{W}}_c^\text {T} \phi (x) \end{aligned}$$

(22)

where ${\hat{W}}_c$ represents the estimation of the unknown weight matrix $W_c$.

Accordingly, the augmented control policy (11) and the event-triggered control policy (15) can be approximated by

$$\begin{aligned} {\hat{w}} (x)=-\frac{1}{2\eta ^2}M^{-1}d^\text {T}(x)\nabla \phi ^\text {T}(x) {\hat{W}}_c \end{aligned}$$

(23)

$$\begin{aligned} \hat{ \mu }({\hat{x}}_j)=-\frac{1}{2}R^{-1}g^\text {T}({\hat{x}}_j)\nabla \phi ^\text {T}({\hat{x}}_j) {\hat{W}}_c \end{aligned}$$

(24)

Using the neural network expression (20), the event-triggered HJB Eq. (18) becomes

$$\begin{aligned} \begin{aligned}&H(x,W_c,\mu ({\hat{x}}_j),w)\\ =~&\Vert r^\text {T}\Vert ^2g_M^2(x)+\eta ^2\Vert m^\text {T}\Vert ^2 W_M^2(x)+U\big (x,\mu ({\hat{x}}_j),w\big )\\&+W_c^\text {T}\nabla \phi (x) \big (f(x)+g(x)\mu ({\hat{x}}_j)+d(x)w\big )\\ =~&\varepsilon _{cH}+\left( r^\text {T}(u(x)-\mu ({\hat{x}}_j))\right) ^\text {T}\left( r^\text {T}(u(x)-\mu ({\hat{x}}_j))\right) \end{aligned} \end{aligned}$$

(25)

where

$$\begin{aligned}\varepsilon _{cH}=-(\nabla \varepsilon )^\text {T} \big (f(x)+g(x)\mu ({\hat{x}}_j)+d(x)w\big ) \end{aligned}$$

denotes the residual error. For fixed N, the NN approximation errors $\varepsilon$ and $\nabla \varepsilon$ are bounded locally [5]. That is, $\forall \nabla \varepsilon _{\max }>0, \exists N (\nabla \varepsilon _{\max }): \sup \Vert \nabla \varepsilon \Vert <\nabla \varepsilon _{\max }$. Then, the residual error is bounded locally under the Lipschitz assumption on the system dynamics. That is, there exists $\varepsilon _{cH\max }>0$ such that $|\varepsilon _{cH}|\le \varepsilon _{cH\max }$.

Using (22) with the estimated weight vector, the approximate event-triggered HJB equation is

$$\begin{aligned} \begin{aligned}&H(x,{\hat{W}}_c,\mu ({\hat{x}}_j),w)\\ =~&\Vert r^\text {T}\Vert ^2g_M^2(x)+\eta ^2\Vert m^\text {T}\Vert ^2 W_M^2(x)+U\big (x,\mu ({\hat{x}}_j),w\big )\\&+{\hat{W}}_c^\text {T}\nabla \phi (x) \left( f(x)+g(x)\mu ({\hat{x}}_j)+d(x)w\right) \\ \buildrel \varDelta \over =&e_c \end{aligned} \end{aligned}$$

(26)

where $e_c$ is a residual equation error.

Define $\varepsilon _u=\left( r^\text {T}(u(x)-\mu ({\hat{x}}_j))\right) ^\text {T}\left( r^\text {T}(u(x)-\mu ({\hat{x}}_j))\right)$ as the event-triggered transformation error. Letting the weight estimation error of the critic NN be $\tilde{W}_c=W_c-{\hat{W}}_c$ and by combining (25) with (26), we have

$$\begin{aligned} e_c=-\tilde{W}_c^\text {T}\nabla \phi (x) \left( f(x)+g(x)\mu ({\hat{x}}_j)+d(x)w\right) +\varepsilon _{cH}+\varepsilon _u \end{aligned}$$

(27)

Based on experience replay technique [15], it is desired to choose ${\hat{W}}_c$ to minimize the corresponding squared residual error

$$\begin{aligned} E=\frac{1}{2}\left( e_c^\text {T}e_c+\sum _{k=1}^p e^{\text {T}}(t_k)e(t_k)\right) \end{aligned}$$

where $e(t_k)=U\left( x(t_k),\hat{\mu }({\hat{x}}_i),{\hat{w}}(t_k) \right) +{\hat{W}}_c^{\text {T}}(t) \sigma _{k}$, $\sigma _{k}=\nabla \phi (x(t_k))(f(x(t_k)) + g(x(t_k))\hat{\mu }({\hat{x}}_i)+k(x(t_k)){\hat{w}}(t_k))$ are stored data at time $t_k\in [\tau _i,\tau _{i+1})$, $i\in \mathbb {N}$, and p is the number of stored samples.

PE-Like Condition: The recorded data matrix $M=[\sigma _1,...,\sigma _p]$ contains as many as linearly independent elements as the number of the critic NN’s hidden neurons, such that $\text {rank}(M)=N$.

The weights of the critic NN are tuned using the standard steepest descent algorithm, which is given by

$$\begin{aligned} \begin{aligned} \dot{{\hat{W}}}_c =&-\alpha _c \frac{\partial E}{\partial {\hat{W}}_c}\\ =&-\alpha _c \sigma \left( \Vert r^\text {T}\Vert ^2g_M^2(x)+\eta ^2\Vert m^\text {T}\Vert ^2 W_M^2(x)\right. \\ {}&\left. +~\sigma ^\text {T} {\hat{W}}_c+U\big (x,\hat{\mu }({\hat{x}}_j),{\hat{w}}(t)\big )\right) \\&- \alpha _c \sum _{k=1}^p \sigma _k \left( \Vert r^\text {T}\Vert ^2g_M^2(x(t_k))+\eta ^2\Vert m^\text {T}\Vert ^2 W_M^2(x(t_k))\right. \\ {}&\left. +~\sigma _k^{\text {T}} {\hat{W}}_c+U\big (x(t_k),\hat{\mu }({\hat{x}}_i),{\hat{w}}(t_k) \big )\right) \end{aligned} \end{aligned}$$

(28)

where $\sigma =\nabla \phi (x) \left( f(x)+g(x)\hat{\mu }({\hat{x}}_j)+d(x){\hat{w}}(t)\right)$, and $\alpha _c$ denotes the learning rate.

Combining (25), (27) and (28), we have

$$\begin{aligned} \begin{aligned} \dot{\tilde{W}}_c=&-\alpha _c\sigma (\sigma ^\text {T} \tilde{W}_c-\varepsilon _{cH}-\varepsilon _{u})\\&-\alpha _c\sum _{k=1}^p \sigma _k\left( \sigma _k^\text {T}\tilde{W}_c-\varepsilon _{cH}(t_k)-\varepsilon _{u}(t_k)\right) \end{aligned} \end{aligned}$$

(29)

where $\varepsilon _{cH}(t_k)$ and $\varepsilon _{u}(t_k)$ denote the residual error and the event-triggered transformation error at $t=t_k$, respectively.

Note that the closed-loop sampled-data system behaves as an impulsive dynamical system with the flow dynamics and jump dynamics. Define the augmented state $\varPsi =[x^\text {T},{\hat{x}}_j^\text {T},{\tilde{W}}_c^\text {T}]^\text {T}$. From (13), (14) and (29), the dynamics of the impulsive system during the flow $t\in [\tau _j,\tau _{j+1}), j\in \mathbb {N}$ can be described by

$$\begin{aligned} {\dot{\varPsi }} = \left[ \ {F(\varPsi )^{\text {T}}}\ \ 0\ \ G(\varPsi )^{\text {T} }\ \right] ^{\text {T}} \end{aligned}$$

(30)

where the nonlinear functions

$$\begin{aligned} \begin{aligned} F(\varPsi )&= f(x)+g(x)\mu ^{*}({\hat{x}}_j)+k(x)w^*(x) \\&+ \frac{1}{2}g(x)R^{-1}g^\text {T}({\hat{x}}_j)\left( \nabla \phi ^\text {T}({\hat{x}}_j){\tilde{W}}_c+\nabla \varepsilon \right) \\ {}&+ \frac{1}{2\eta ^2}d(x)M^{-1}d^\text {T}(x)\left( \nabla \phi ^\text {T}(x){\tilde{W}}_c+\nabla \varepsilon \right) , \end{aligned} \end{aligned}$$

$$\begin{aligned} \begin{aligned} G(\varPsi ) =&-\alpha _c\sigma (\sigma ^\text {T} \tilde{W}_c-\varepsilon _{cH}-\varepsilon _{u})\\ {}&-\alpha _c\sum \limits _{k = 1}^p \sigma _k\left( \sigma _k^\text {T}\tilde{W}_c-\varepsilon _{cH}(t_k)-\varepsilon _{u}(t_k)\right) . \end{aligned} \end{aligned}$$

The jump dynamics at the triggering instant $t=\tau _{j+1}$ can be given by

$$\begin{aligned} \varPsi \left( t \right) = \varPsi \left( {{t^ - }} \right) + \left[ \ 0\ \ (x-{\hat{x}}_j)^{\text {T}}\ \ 0\ \right] ^{\text {T}} \end{aligned}$$

(31)

where $\varPsi \left( {{t^ - }} \right) =\mathop {\lim }\limits _{\varrho \rightarrow 0} \varPsi \left( {{t-\varrho }} \right)$, and 0 s are null vectors with appropriate dimensions.

4.2 Stability Analysis

In this subsection, the main theorem will be presented to guarantee the weight estimation error of the critic NN to be UUB. Meanwhile, the stability of the impulsive dynamical system based on the event-triggered optimal control and the augmented control will be guaranteed with a novel adaptive triggering condition. First, we give the following assumption.

Assumption 4

• 1. g(x) and d(x) are upper bounded by positive constants such that $\Vert g(x)\Vert \le g_{\max }$ and $\Vert d(x)\Vert \le d_{\max }$.

• 2. The critic NN activation function and its gradient are bounded, i.e., $\parallel \phi (x)\parallel \le {\phi _{\max } }$ and $\parallel \nabla \phi (x)\parallel \le {\nabla \phi _{\max }}$, with $\phi _{\max }$, $\nabla \phi _{\max }$ being positive constants.

• 3. The critic NN ideal weight matrix is bounded by a positive constant, that is $\Vert W_c\Vert \le W_{\max }$.

Theorem 2

Suppose that Assumptions 1–4 hold. The tuning law for the CT critic neural network is given by (28). Then the closed-loop sampled-data system (14) is asymptotically stable and the critic weight estimation error is guaranteed to be UUB if the adaptive triggering condition

$$\begin{aligned} \begin{aligned} \Vert e_j(t)\Vert ^2~>~&\frac{1}{L^2 \Vert r^\textit{T}\Vert ^2}\left( (1-\beta ^2)\lambda _{\min }(Q)\Vert x\Vert ^2\right. \\ {}&\left. +~\Vert r^\textit{T}\hat{\mu }({\hat{x}}_j)\Vert ^2-\eta ^2\Vert m^\textit{T} {\hat{w}}(x)\Vert ^2\right) \\ \buildrel \varDelta \over =&\left\| {\hat{e}}_T\left( x,{\hat{x}}_j,{\hat{W}}_c\right) \right\| ^2 \end{aligned} \end{aligned}$$

(32)

holds and the following inequality

$$\begin{aligned} \begin{aligned} \Vert \tilde{W}_c\Vert&> \sqrt{\frac{\alpha _c^2\eta ^2\lambda _{\min }(M)\sum \limits _{k=1}^{p+1}(\varepsilon _{cH\max }+\varepsilon _{u\max })^2+\varGamma }{4\eta ^2(\alpha _c-1)\lambda _{\min }(H)\underline{\theta }(M)} }\\&\buildrel \varDelta \over = \Pi _{\max } \end{aligned} \end{aligned}$$

(33)

is satisfied with $\alpha _c>1$, where $\varGamma =2\left( d_{\max }\nabla \phi _{\max } \left( W_{\max }+\nabla \varepsilon _{\max }\right) \right) ^2$.

Remark 5

The proof of Theorem 2 will be presented in a future paper. Note that the triggering condition (32) is utilized to approximate the optimal control policy pair $[\hat{\mu }^{*\textit{T}}({\hat{x}}_j),{\hat{w}}^{*\textit{T}}(x)]^\textit{T}$ for the auxiliary sampled-date system while the triggering condition (19) in Theorem 1 is utilized to guarantee the robust stabilization of the original uncertain system with the obtained optimal control policy $\hat{\mu }^{*}({\hat{x}}_j)$.

5 Simulation

The example is considered as follows [2]:

$$\begin{aligned} \left[ \begin{array}{l} {{\dot{x}}_1}\\ {{\dot{x}}_2} \end{array} \right] = \left[ {\begin{array}{*{20}{c}} 0&{}1\\ 0&{}0 \end{array}} \right] \left[ \begin{array}{l} {x_1}\\ {x_2} \end{array} \right] + \left[ \begin{array}{l} 0\\ 1 \end{array} \right] u + \left[ \begin{array}{l} 0.2\\ 0 \end{array} \right] W\left( x \right) \end{aligned}$$

(34)

where $W(x)={\lambda _1}{x_1}\cos \left( {\frac{1}{{{x_2} + {\lambda _2}}}} \right) + {\lambda _3}{x_2}\sin \left( {{\lambda _4}{x_1}{x_2}} \right)$, and $\lambda _1, \lambda _2, \lambda _3, \lambda _4$ are the unknown parameters. The last term reflects the unmatched uncertainty in the system. Assume that $\lambda _1 \in [-1,1]$, $\lambda _2 \in [-100,100]$, $\lambda _3 \in [-0.2,1]$, and $\lambda _4 \in [-100,0]$.

Clearly,

Set Q, R, r and m are the identity matrices with appropriate dimensions. We experimentally choose $\eta =1$, $p=10$, $\beta =0.1$ and $L=3$.

During the implementation process of the event-triggered ADP method, we choose a three-layer feedforward NN with structure 2-8-1 as the critic network. The critic NN activation function is chosen as $\phi (x)=[x_1^2\ x_1x_2\ x_2^2\ x_1^4 \ x_1^3x_2\ x_1^2x_2^2\ x_1x_2^3\ x_2^4]^\text {T}$. The initial state is selected as $x_0=[1,-1]^\text {T}$, the learning rate is $\alpha _c=0.1$, and the sampling time is chosen as 0.05 s. The trajectories of the critic parameters are shown in Fig. 1. At the end of learning process, the parameters converge to ${\hat{W}}_c=[1.8594 \ 0.8845 \ 1.1560 \ 1.9860 \ 0.9272 \ 0.5403 \ 0.4344 \ 0.3737]^\text {T}$. From Fig. 2, one can get the event-triggered error $e_j(t)$ and the threshold $e_T$ converge to zero as the states converge to zero. In addition, the event-triggered error is forced to zero when the triggering condition is satisfied, that is the system states are sampled at the triggering instants. The sampling period during the event-triggered learning process for the control policy is provided in Fig. 3. Furthermore, the lower bound on the inter-sample times is found to be 0.15 s. In particular, the event-triggered controller uses 47 samples of the state while the time-triggered controller uses 1000 samples, which means fewer transmissions are needed between the plant and the controller due to event-triggered sampling. That will reduce the number of controller updates during the learning process.

Fig. 1.

Convergence of the critic parameters

Fig. 2.

Response of $\Vert e_j(t)\Vert ^2$ and $\Vert {\hat{e}}_T\Vert ^2$

Fig. 3.

Triggering instants during the learning process of the control input

Based on the converged weights ${\hat{W}}_c$, we can obtain the near-optimal control laws as

$$\begin{aligned} \left[ \begin{array}{l} \hat{\mu }^*({\hat{x}}_j)\\ {\hat{w}}^*(x) \end{array} \right] =\left[ \begin{array}{l} -\frac{1}{2}[0 \ 1]\nabla \phi ^\text {T}({\hat{x}}_j) {\hat{W}}_c\\ -\frac{1}{2}[1 \ 0]\nabla \phi ^\text {T}(x){\hat{W}}_c \end{array} \right] \end{aligned}$$

(35)

From [2], the optimal control laws are given as

$$\begin{aligned} \left[ \begin{array}{l} u^*(x)\\ w^*(x) \end{array} \right] =\left[ \begin{array}{l} -1.2906x_1-2.1247x_2\\ -0.5783x_1-0.2581x_2 \end{array} \right] \end{aligned}$$

(36)

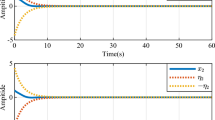
Now, we apply the near-optimal control laws (35) with the triggering condition (19) and the optimal control laws (36) for the uncertain nonlinear system with $\lambda _1=-1,\lambda _2=-100,\lambda _3=0,\lambda _4=-100$. Set the initial state be $x_0=[1,-1]^\text {T}$, and the sampling time be 0.05 s. The simulation results are given in Fig. 4.

Fig. 4.

Case 1: (a) State trajectory. (b) Near-optimal and optimal control inputs. (c) Response of $\Vert e_T\Vert ^2$ and $\Vert e(t)\Vert ^2$. (d) Sampling period.

We can observe the near-optimal controller is robust for the uncertain nonlinear system and adjusted with events.

6 Conclusion

In this paper, we propose an event-triggered ADP algorithm to solve the robust control problem of uncertain nonlinear systems. The robust control problem is described as an optimal control problem with an modified cost function. For implementation purpose, a critic NN is constructed to approximate the optimal value function. Finally, simulation results are given to demonstrate the effective of the event-triggered ADP scheme.