Keywords

1 Introduction

The k-nearest neighbor classifier (kNN) can be considered as one of pioneers among the supervised methods – proposed originally by Fix and Hodges [7]. The idea behind the method is rather simple. Considering an annotated data collection, for an unknown data sample the class label is assigned based on the majority of its k-nearest neighbors. The so-called nearest neighbor classifier is a special case of the previously mentioned one for \(k=1\). Even though it is a rather simple method, it has some indisputable advantages such as: simplicity, effectiveness, intuitivity, non-parametric nature, and high performance for different classification tasks [20]. The proper selection of parameter k responsible for the neighborhood size, and the distance function responsible for the quality of the topological representation can have a significant impact on the underlying results [11].

Formally, the problem can be stated as follows. Let \(T =\{t_1,t_2,\cdots ,t_m\}\) be a template or reference set, containing m number of points taking values in \(R^d\), d denotes the dimension of the data. Let \(Q = \{q_1,q_2,\cdots ,q_n\}\) a query set containing n different points with the same dimension. The k-nearest neighbor problem consist in searching for each point \(q_i \in Q\) in the template set T given a specific distance metric. The Euclidean distance, Manhattan distance, cosine similarity measures are commonly used, but other distances measures such as Hamming, cityblock (sum of absolute differences) can also be considered. The computational complexity of the method in case of linear search is \(\mathcal {O}(md)\), which for large data collections (m), and high dimensional data (d) can be an expensive operation. Its parameters (neighborhood size, distance function) – though they are simple, are also the major challenges.

In this paper, we propose a fast k-nearest neighbor classifier by reducing the number of reference points that need to be considered in the distance computation. The reduction is achieved by clustering the data points first, - using unsupervised clustering to find a stable cluster setup, followed by selecting the closest points and the furthest points, respectively. The rest of the paper is organized as follows. Section 2 briefly reviews different attempts to reduce the linear search in the k-nearest neighbor method, Sect. 3 describes the proposed reference points reduction strategy, while Sect. 4 describes the different data collections involved in the experiments, as well the results, and some comparisons. Finally, Sect. 5 draws the conclusions.

2 Related Work

In order to lower the linear search complexity, different solutions have been proposed. Some methods use graph based methods to approximate the nearest neighbor [12], while some others sub-sample the reference set to diminish the number of distance calculation between the reference points and the query point [2, 8, 13], and others invoke parallel calculation supported by GPU [9].

Peredes et al. [18] proposed a method to minimize the number of distance calculations considering a graph, built from the data set. Knowing that the distance between two elements is the shortest path, they filter out points which are far away from the query point, hence reducing the search space, and apply linear search for the remaining points. In the work [17], the authors build a visibility graph followed by a greedy type search. An extension of their work is proposed by Hajebi et al. [12], where instead of the a visibility graph, the search is made on a k-NN graph, which is a directed graph structure. The complexity of building such a graph is \(\mathcal {O}(md)\), but more efficient methods were proposed by several other authors [4, 6].

Another type of solution proposed by Indyk and Motwani [13] involves hash functions, in order to create a hash value for each point. Each hash function reduces the dimensionality by projecting the original point into a lower dimensional random space. The projected points are partitioned into bins considering a uniform grid. To reduce even further the search space, a second hashing is applied. The query point is matched only with those ones falling in the same bin, where a classical linear search is applied to distinguish the closest match.

The KD-tree proposed by Friedman et al. [8] and Bentley [2] is based on partitioning the search space by hyperplanes that are perpendicular to the coordinate axes. The root of the tree is a hyperplane orthogonal to one of the dimensions, splits the data into two separate half planes. Each half is recursively partitioned into another two half planes, and so forth. The partitioning stops at log(m), so at each leaf there will be only one data point. The query point is compared to the root element, and all the subsequent ones, while traversing the tree to find the best match. As the leaf points are not always the nearest points, a simple backtracking is applied to analyze the closest ones. Instead of using backtracking Hajebi applied best bin first, proposed first by Beis and Lowe [1].

Zhang and Srihari [22] propose for handwritten digits classification a hierarchical search using a non-metric measure applied to a binary feature space. In the training phase, the set is organized in a multi-level tree, while for the test phase, a hierarchical search is applied based on a subset of templates selected on the upper levels.

A rather modern and new GPU based solution is proposed by Garcia and Debreuve [10], where instead of reducing the size of the reference points, or organizing the points in a tree structure, the authors concentrate more on the distance calculation part, which can be formulated as a highly parallel process. Each distance calculation can be done separately as each point is independent.

The proposed method is aligning with the methods proposed in [2, 8, 13]. Instead of using hash functions, or tree representations, a data sampling has been proposed, by discarding those samples which based on some distance metric do not contribute to build reliable cluster representations. For the best cluster representation a so-called “jump method” has been invoked. For the selected data points we also apply linear search to find the nearest neighbors.

3 Method

In this section we introduce the proposed method. First, we will briefly describe the “jump method” [19], followed by the data selection criterion to reduce the number of reference points.

The original method proposed by Sugar and James [19] provides a systematic analysis to automatically discover the number of clusters for an unknown data collection. They propose an efficient, non-parametric solution involving distortion, a quantity that measures the average distance, per dimension, between each sample of a cluster and its cluster center. The algorithm can be summarized as follows:

  1. (1)

    Apply k-means algorithm [14] to the unknown data, and after each iteration calculate \(d_k = \frac{1}{d}\min _{c_1,c_2,\cdots ,c_K}\{\frac{1}{n}\sum _{i=1}^{K}\sum _{i \in k}(x_i-c_k)^T(x_i-c_k)\}\), where \(x_i\) is the \(i^{th}\) sample belonging to the \(k^{th}\) cluster, \(c_k\) is the \(k^{th}\) cluster center, n is the number of samples, while d is the dimension of the data.

  2. (2)

    Pick a suitable transformation power \(Y>0\). If the clusters are assumed to be generated by a Gaussian process, the theory suggests \(Y=\frac{d}{2}\).

  3. (3)

    Apply the first order forward difference operator to the transformed curve \(d_{k}^{-Y}\) in order to get the “jump” statistic \(J_K=d_{K}^{-Y} - d_{K-1}^{-Y}\). For practical reasons \(d_{0}^{-Y}=0\) should be defined.

  4. (4)

    For the K for which the \(J_K\) is the largest will provide the optimal number for the clusters. The number of clusters \(C =argmax_{K}\{J_k\)}.

Once the optimal number of clusters is estimated for the data points, the data is clustered in exactly C clusters, as per suggested by the algorithm. Due to the nature of the method, the C number of clusters assures a low intra-class variability reported to each dimension. In other words, those clusters represent the most the underlying data. This information is used to select from each cluster a certain number of points. Two selection criteria were considered. For each cluster, the distance between each sample \(x_i\) and \(c_k, k \in \{1,\cdots ,C\}\) were calculated considering Euclidean distance. The different distances were sorted first, and different percentages considering the closest (min rule) and furthest samples (max rule) from the centroids were retained as reference points for the upcoming k-nearest neighbor clustering. Instead of calculating the distances in a brute force manner, we propose a selection, a subsampling. The min rule selects those samples closer to the cluster center, therefore the cluster is represented by strong representatives, while the max rule selects those candidates which are lying on the shell of the d dimensional hyper sphere defining the cluster. Those samples are far from the center, and one might think they can not attract many samples from the test set, as they themselves could be considered as possible outliers, but according to Bishop [3], “for points which are uniformly distributed inside a sphere of d dimension, where d is large, almost all of the points are concentrated in a thin shell close to the surface”.

The amount of data added by the min/max rule is increased incrementally, and accuracy performances are calculated. One could argue, that the selection method should not consider similar percentage of points from each cluster. Large clusters should get more importance over smaller clusters, but this one is assured by the percentile based selection. This type of selection is also supported by the fact that k-means clustering -by its nature-, tries to build uniform and equally distributed (balanced) clusters, and therefore a heuristic based selection could underestimate or overestimate the importance of one cluster or another. The optimal reference set is selected based on the accuracy performance. Speed factor which is linear in relation to the points selected in the reference set will decrease.

4 Experiments

This section is meant to first present the datasets used, followed by the achieved results, and a comparison at accuracy level as well as speed with the classical k-nearest neighbor utilizing brute force - by comparing each query example with all the reference samples [9].

4.1 Data Description

MNIST Digits. MNIST [16] is a well-known benchmark datasetFootnote 1 containing separated Latin digits assigned to 10 different classes. The images coming mainly from census forms, are size normalized and centered to 28\(\,\times \,\)28 gray level images. The data set contains 60, 000 and 10, 000 images for training and test, respectively.

Lampung Characters. The Lampung charactersFootnote 2 used in our experiments were extracted from a multi-writer handwritten collection produced by 82 high school students from Bandar Lampung, Indonesia. The Lampung texts are created as transcriptions of some fairy tales. One exemplary document snippet can be seen in Fig. 1.

Some 23, 447 characters were used as training set, while 7, 853 characters were considered for test. Altogether 18 different character classes were identified. Each character is represented by a centered and normalized \(32\times 32\) gray scale image. More details about this publicly available data is to be found in [15, 21].

Fig. 1.
figure 1

A Lampung document snippet.

Full size image

4.2 Results

First, the results achieved by the previously described “jump” method are shown in Fig. 2. For features we considered the intensity values of the gray scale images. This choice is motivated by the fact, that the best scores achieved on both data sets were using intensity values [5, 15, 16, 21]. Our goal is not to find the best feature describing these digits and characters, but to show that using a common feature such as the intensity value we can considerably speed-up the recognition process by avoiding unnecessary distance calculations.

One might observe that the curve proposed by Sugar and James is not as smooth as discussed in their previous paper [19]. This can be explained by the fact that the authors analyzed their method only for low dimensional data, while here the dimensionality is rather high, comprising 784 and 1024 dimensions, respectively. However, in both cases a diminishing tendency is observed, hence the possibility to select the optimal number of clusters for both collections. In case of MNIST 76 clusters were found to be optimal, while for the Lampung collection 186 is the cluster number which indicates an optimal setup. The optimal cluster number assures that those centers are representative enough, and the surrounding data points should not be split further in smaller clusters.

Fig. 2.
figure 2

The results of the “jump” method.

Full size image

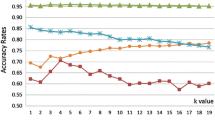
Once the optimal cluster number is detected using the “jump” method, the selected cluster arrangement is considered, and for each cluster 5%, 10%, ...., 100% of the data is considered using the min and max rule for the k-nearest neighbor scenario (\(k=1\)). While the min rule is responsible to select those samples close to the centroids, the max rule selects the samples lying furthest from the cluster centers. The data points collected using these two methods are than used to build two different reference data collections, used in a kNN classification - performing linear search as in case of the classical k-nearest neighbor. The results can be observed in Fig. 3.

A similar trend can be observed for both collections. The more data is considered, the more precise the results reported. However, it is really important to note that, for a small amount of data (up to 40%), the results provided by the min selection are much better, while for larger data selections comprising more than 40% for each cluster, the trend changes completely, and those samples selected by the max rule take over by producing far better scores than the other collection selected by the min rule. The min selection rule provides those samples closer to the cluster centers, while the max rule goes for those sample close to the cluster boundaries. One explanation for this rather interesting finding could be the fact supported also by Bishop [3], stating that for large collections with high dimensionality the samples are arranged on a thin shell close to the surface bounding the cluster in question.

To compare the performance versus the time necessary to perform the linear search applicable for k-nearest neighbor, we analyzed the performance charts depicted in Fig. 3. Selecting for both collections those settings when only 65% of the data is used in the search - using the max rule, we can state that our selection can reduce the time performance by 71% for MNIST, and 56% for Lampung, while still performing in the same range. The exact results are reported in Table 1. The results go up as high as 96.91% when 100% of the data is considered (classical case), while for the selection proposed by us, the scores are in the same range, obtaining 96.12% accuracy, but reducing the search time by 71%. Similarly, for the Lampung collection, considering the classical k-nearest neighbor classifier, the results for the complete set can go up to 83.94%, while selecting only 65% of the data (using the max rule), there is only a 0.86% drop in performance, but there is a gain in speed of 56%.

Fig. 3.
figure 3

The performance improvements using different data selection criteria and different amount of data.

Full size image

In order to compare the efficiency of our selection method, we conducted a Monte Carlo simulation by randomly selecting 65% of the data, and observed for those randomly selected data how the performance measures look like. The average scores achieved by repeating the experiments 100 times can be seen also in Table 1. The lower scores indicates that our selection method is better, and therefore our method is empirically validated.

Table 1. Comparing performance and speed using the complete data collections and using the selection strategy.
Full size table

5 Conclusion

In this paper, we proposed a straightforward way to reduce the linear search applied to k-nearest neighbor by reducing the number of reference points considering using different benchmark handwritten character collections as test bed. The method can be considered a data reduction strategy based on optimization. The data points are first clustered in an optimal number of clusters using the so-called “jump” method, which is based on the optimization of inter-class variability. Once the samples are clustered using the optimal number of clusters, we select the closest and the furthest samples alike, and using a certain percentage of the data, we build several subsets of the original data, and run the k-nearest neighbor classifier. Analyzing the performances for the different amounts of data, we can clearly detect an optimum point in the size of the data for which the scores are similar as the whole data would be considered, but due to the reduction the search time is also reduced up to 71%.

Along the speed gain achieved by the data reduction, an interesting fact was observed when altering the min and max rules. For a smaller amount of data the min rule selects better candidates. However, when the selected data becomes larger the samples residing on the boundaries outperform those close to the center. This supports the idea that for larger data sets with high dimensional representatives, it is very likely that the data is organized in the outer shell of the sphere incorporating the data.