Keywords

1 Introduction

Often, pattern recognition systems are dedicated to judge the (dis)similarity between two patterns. It can either be a set of measurements performed on the patterns, forming a vector of features, or a symbolic description of how the pattern can be divided into basic shapes. A decision rule is often built from the representation of the pattern. Such rule predicts to which class an observed pattern most likely belongs to. It can either be built by introducing some expert knowledge about the patterns, or learned on a representative subset of labelled patterns. Rather, a collection of techniques has been developed to address domain specific issues. Pattern recognition has rich state-of-the-art. Many classifier combination systems have been proposed and compared [17, 18, 32, 37], and a full presentation of most of these could be found in a reference book by Duda et al. [6]. Handling several classifiers means finding their complements (helping each other) so that recognition/classification can be improved as expected [19, 25]. At the same time, we note that methods are generally independently built. Their combination may lead to positive correlations, because both aim at achieving the same goal, and both are based on the same learning data [13, 22]. Nonetheless, even when approaches like Adaboost, arcing [3], and boosting [33] try to limit this dependence by reinforcing diversity, it is difficult to measure and to efficiently incorporate into the classification process [12, 25]. Currently deep learning based approaches [27, 28] provided interesting results (using large databases), but parameters setting is not so trivial. Such methods often require a consistent as well as large amount of data to optimize their efficiency. In our study, we focus on databases having few samples per classes, which is often the case in industrial applications – real-world cases.

Surveys on pattern representation and classification techniques over the last decade fail to conclude whether a set of generic methods perform best for all applications [2, 5, 14, 21]. This means that methods are application dependent. For a given application, the choice of a pattern representation or a decision scheme relies at best on the extensive testing of several combinations of techniques. It is not surprising that a designer chooses by making an educated guess between the techniques he has at hand, or between those he is the most acquainted with. A tempting approach is to combine several decision rules, based on various representations and classification schemes, instead of electing only one. The expected outcome is a more robust final decision, taking advantage of all the decision rules qualities. This approach appears to be well suited to cope cases, where the available data is too scarce to determine the best method by thorough testing, or to build robust decision rules by learning. Well-known operators applying this scheme include the quasi-arithmetic means, the weighted minimum and maximum, and the ordered weighted averaging [40]. None of these operators families, however, take the possible interactions between the constituents of the aggregation into account. The Choquet integral can be considered, since it allows to take such interactions into account while generalizing many aggregation operators and by choosing specific fuzzy measure such as weighted arithmetic means, ordered weighted averages, order statistics, and median [8, 23]. Fuzzy integrals, and the Choquet integral in particular, have been successfully used as fusion operators in various applications. Previous works were dedicated to define an efficient global scheme from the study of learning confusion matrices [31]. This scheme was also combined with a fuzzy inference system and applied to an industrial fabric textile context using non-relevant learning data [34]. The method were adapted to process with speech recognition problem based on overlapping features [9] and also to provide breast cancer diagnosis to be further assessed by an expert [10] Such an approach allows to provide a set of suitable decision rules considering a whole application. The method is extended here to consider independently all possible classes and so to automatically extract a set of decision rules per class. With such an extension, in this paper, a new hierarchical description of decision rules based on two aggregation levels of Choquet integrals is also provided. Proposed methods can be considered as wrapper [20], since they focus on selection of decision rules rather than on filter from the handling of rough data.

The remainder of the paper is outlined as follows. In Sect. 2, we recall background on Choquet integral properties and associated fuzzy measure indexes. In Sect. 3 two complementary schemes allowing to discard weaker decision rules are defined. Section 4 presents the application of these methods on well-known databases: shapes (from Sharvit) and handwritten graphical symbols (from CVC – Barcelona), and a discussion about the interest of each scheme. Section 5 concludes the paper.

2 Background on Choquet Integral Fusion

2.1 Decision Rule Fusion

Let us consider m classes, \(\mathcal {C}=\{C_1,\dots ,C_m\}\), and n Decision Rules (DRs) \(X=\{D_1,\dots , D_n\}\). When a new pattern \(x^o\) is observed, we wish to find the class it most likely belongs to. Labelling this unknown pattern is a three-steps process.

  • Firstly, for each decision rule j and each class i, we compute \(\phi ^i_j\) the degree of confidence in the statement “According to \(D_j\), \(x^o\) belongs to the class \(C_i\)”.

  • Secondly, we combine all these partial confidence degrees into a global confidence degree by choosing a suitable aggregation operator \(\mathcal {H}\). Thus, the global confidence degree in the statement “\(x^o\) belongs to \(C_i\)”, noted \(\varPhi (C_i|x^o)\), is given by:

    $$ \varPhi (C_i|x^o) = \mathcal {H}(\phi ^i_1,\dots ,\phi ^i_n). $$

  • Finally, \(x^o\) is assigned to the class for which the confidence degree is the highest:

    $$ label(x^o) = \mathop {\arg }\limits _{i=1}^{m}\ max\ \varPhi (C_i|x^o). $$

Many aggregation operators were introduced in the literature. If the classification issue implies more than two classes, two learning approaches can be followed. Either each class \(C_i\) is paired with his own aggregation operator \(\mathcal {H}^i\), or a single global aggregation operator. In the former case, the final decision is slightly modified as the global confidence degree depends on the operator associated with the class:

$$ \varPhi (C_i|x^o) = \mathcal {H}^i(\phi ^i_1,\dots ,\phi ^i_n) . $$

2.2 Fuzzy Measures and the Choquet Integral

The Choquet integral was first introduced in the capacity theory [4, 30]. Let us denote by \(X=\{D_1, \dots ,D_n\}\) the set of n decision rules, and \(\mathcal {P}\) the power set of X, i.e. the set of all subsets of X.

Definition 1

A fuzzy measure or capacity, \(\mu \), defined on X is a set function \(\mu : \mathcal {P}(X) \longrightarrow [0,1]\), verifying the following axioms:

\(\mu (\emptyset ) = 0\), \(\mu (X) = 1\), and

\(A \subseteq B \Longrightarrow \mu (A) \leqslant \mu (B).\)

Fuzzy measures generalize additive measures, by replacing the additivity axiom by a weaker one (monotonicity). Fuzzy measures embed particular cases including probability measure, possibility and necessity measures, or belief and plausibility functions.

In our context of decision rule fusion, \(\mu (A)\) represents the importance, or the degree of trust in the decision provided by the subset A of DRs. The next step in building a final decision, is to combine the partial confidence degree according to each DR into a global confidence degree, taking those weights into account.

Definition 2

Let \(\mu \) be a fuzzy measure on X. The discrete Choquet integral of \(\mathbf {\phi }=[\phi _1,\dots ,\phi _n]^t\) with respect to \(\mu \), noted \({\mathcal {C}}_\mu (\mathbf {\phi })\), is defined by:

$$ {\mathcal {C}}_\mu (\mathbf {\phi })=\sum _{j=1}^n \phi _{(j)}[\mu (A_{(j)})-\mu (A_{(j+1)})], $$

where (.) is a permutation and \(A_{(j)}=\{(j), \ldots , (n)\}\) represents the [j..n] associated criteria in increasing order and \(A_{(n+1)}=\emptyset \).

2.3 Determining the Fuzzy Measure

There are several methods to determine the most adequate fuzzy measure to be used for a given application and the most straightforward learning approach is based on optimization techniques. The aim is to find the fuzzy measure that minimizes best a criterion on the training set, such has the square error. Considering \((x^k, y^k), k=1,\dots ,l\), l learning samples where \(x^k=[x_{1}^{k},\dots ,x_{n}^{k}]^t\) is a n-dimensional vector, and \(y^k\) the expected global evaluation of object k, the fuzzy measure can be determined by minimizing [11]:

$$E^2 = \sum \limits _{k=1}^{l}(\mathcal {C}_\mu (x_{1}^k,\dots ,x_{n}^k)-y^k)^2.$$

This criterion can be put under a quadratic program form and solved by the Lemke method. Nevertheless the method requires at least \(n!/[(n/2)!]^2\) learning samples. When little data is available, matrices may be ill-conditioned, causing a negative impact on the algorithm. To cope with the above problems, “heuristic” algorithms have been developed.

To the best of our knowledge, the algorithm providing the best approximation was proposed by Grabisch in [7]. It assumes that in the absence of any information, the most reasonable way to aggregate the partial matching degrees is to compute the arithmetic mean on all the inputs.

2.4 Behavioral Analysis of the Aggregation

The importance index is based on the definition proposed by Shapley in game theory [35]. It is defined for a fuzzy measure \(\mu \) and a rule i as:

$$ \sigma (\mu , i)=\frac{1}{n} \sum \limits _{t=0}^{n-1} \frac{1}{ {n-1 \atopwithdelims ()t}} \sum _{{T \subseteq X \backslash i} \atop {|T| = t}} [\mu (T \cup i) - \mu (T)]. $$

It can be interpreted as a average value of the marginal contribution \(\mu (T \cup i) - \mu (T)\) of the decision rule i alone in all combinations. The interaction index [29] represents the degree of interaction between two decision rules. If the fuzzy measure is non-additive then some sources interact. The marginal interaction between I and j, conditioned to the presence of elements of the combination \(T \subseteq X \backslash ij\) is:

$$ (\varDelta _{ij}\mu )(T) = \mu (T \cup ij) + \mu (T) - \mu (T \cup i) - \mu (T \cup j). $$

Averaging this criterion over all the subsets of \(T \subseteq X \backslash ij\) gives the interaction index of sources i and j:

$$ I(\mu , ij)=\sum _{T \subseteq X\backslash ij} \frac{(n-t-2)!t!}{(n-1)!}(\varDelta _{ij}\mu )(T). $$

A positive interaction index for two DRs i and j means that the importance of one DR is reinforced by the second. A negative interaction index indicates that the sources are antagonist, and their combined use impairs the final decision.

3 Selection of Decision Rules

3.1 Local Scheme

Handling with Learning Error. All the lattices associated to fuzzy measures are initialized at the arithmetic mean, and are approximated using a training set via a gradient descent. From training pattern, m training samples are created \(\varPhi ^1, \dots , \varPhi ^m\), with \(\varPhi ^i=(\phi ^i_1,\dots ,\phi ^i_m)\) where \(\phi ^i_j\) represents the confidence in the fact that the sample belongs to class i, according to DR j. Each of these samples is paired with a target value, i.e. the value an ideal operator would output using this sample as input. For techniques that use a single fuzzy measure no real formula exists and often the following one is used:

$$ \mathcal {C}_\mu (\varPhi ^i) = \left\{ \begin{array}{l} 1,\, \text{ if } \text{ sample } \text{ belongs } \text{ to } \text{ class } i, \\ 0,\, \text{ otherwise }. \end{array} \right. $$

For techniques that use a different fuzzy measure per class, the optimal target value minimizing the quadratic error is known for two classes [7]. Best criterion is defined as follows:

$$ E^2=\sum _i\sum _j | \varPsi (\varDelta \varPhi _{12}(X^j_k))-1 | ^2 $$

with \(X^j_k\) is the kth training data of class j, \(\varPsi \) a sigmoid-type function and \(\varDelta \varPhi _{12}\) is given by:

$$ \varDelta \varPhi _{12}=\varPhi _{\mu _1}(C_1|X^j_k)-\varPhi _{\mu _2}(C_2|X^j_k). $$

Two class errors used in the gradient descent algorithm is given by:

$$ e=\varPsi (\varDelta \varPhi _{12}(X^j_k))-1). $$

The criterion is modified as follows to process with m classes,

$$ \varDelta \varPhi _{qr_{r \in X - \{q\}}} =\varPhi _{\mu _q}(C_q|X^j_k)-\bigotimes _{ \{r \in X- \{q\} \} } \varPhi _{\mu _r} (C_r|X^j_k) $$

with q and r two classes. Operator \(\bigotimes \) can be a median, min... Here the \(\max \) was kept to move away ambiguous classes and so to favor a discriminate behavior. Median is interesting to preserve acceptable results even some sources can be contradictory. The sign of \( \varDelta \varPhi _{qr_{r \in X - \{q\}}}\) is studied to set the error to be propagated in the lattice as follows:

$$ sign ( \varDelta \varPhi _{qr_{r \in X - \{q\}}}) = \left\{ \begin{array}{l} + e=1./f( \varDelta \varPhi _{qr_{r \in X - \{q\}}} )\\ - 0,\, e=0 \text{ for } \text{ q, } \text{1 } \text{ for } \text{ others }, \end{array} \right. $$

with f an increasing function. Obviously the relevant and the irrelevant learning data are alternated while training the fuzzy measures.

Weaker Decision Rules. Once the lattice is learned, the individual performance of each DR is analyzed in the produced fuzzy measure. This analysis is performed using the importance and interaction indexes defined in Sect. 2.4. The aim is to track the DRs having the weak importance in the final decision, and that positively interact the least with the other rules. Such DRs are assuming to blur the final decision. First low significant rules \(S_L\) having an importance index lower than 1 are selected:

$$ S_L =\{k|n \cdot \sigma (\mu ,k)<1 \}. $$

The set of rules to be removed \(MS_L\) is composed of the rules having an interaction index lower than the mean of the interaction indexes of \(S_L\):

$$ MS_L=argmin_k \{\sum _{j=1,n} I(\mu ,kj) < h \}_{k \in S_L} $$

with the global mean interaction index:

$$ h=\frac{1}{|S_L|}\sum _{k \in S_L}\sum _{j=1,n} I(\mu ,kj). $$

Main Selection Algorithm. We use the classic fuzzy pattern matching setup. All the classes \(C_1,\dots ,C_m\) are associated with a fuzzy measure \(\mu _1,\dots ,\mu _m\). The evaluation measures are generally classifier dependent [26]. For their computation the classification of training data must be performed to identify the fuzzy measure for each class. Furthermore, we need to fix thresholds for the interaction indexes. This must be done by an expert and for each class. In this case, selection is performed dependently. The application of our learning algorithm followed by the extraction of the most relevant DRs forms a training epoch. As it is not easy to evaluate each combination of classes without an expert, we consider them independently. The overall algorithm is described below.

% Initialization %

For Each \(C_i\) in \(\mathcal {C}=\{C_1, \ldots , C_m\}\)

  • Learned associated capacity \(\mu _i\)

  • Extract weakest descriptor

End For Each

% Main %

While Minimization is on the way

  • Replace old capacity with new capacity

  • Evaluate gain (how the new capacity minimizes a cost function)

  • Keep the new capacity that provides best minimization

  • Extract feature for that new capacity

End while

A Greedy feature selection algorithm is used to ensure a continuous extraction of unexpected features per class. At each epoch, the weakest descriptor calculated from indices is removed and so on, while improving a gain (recognition rates).

3.2 Hierarchical Scheme

Usually decision rules are embedded in an aggregation way to combine them. The problem is rewritten here in a 2-class description scheme by aggregating local decisions between two classes \(C_i\) and \(C_j\). We aim here to reconsider the problem by specifying fuzzy measure \(\mu _i^j\) to distinguish pairs of classes. That remains to specialize a set of fuzzy measures to assess each one the comparison between two classes with respect to Choquet integral. Roughly speaking, each capacity becomes an “expert” able to compare one class to another one.

The learning of \(\mu _i^j\) is performed from the decisions rules computed from the set of training samples \(\phi ^i_j\), that is the samples belonging to \(C_i\) and \(C_j\), using the sigmoid-type function \(\varPsi \) as two classes are studied (see Sect. 3.1). The symmetry is not warranted due to gradient algorithm (that is \(\mu _i^j\) can differ from \(1-\mu _j^i\)) and the computation of \(\mu _j^i\) is done separately.

For each class \(C_i\), a vector of fuzzy measures \(V^i\) is built by considering all the other classes:

$$ V^i= [\mu _i^1, \mu _i^2, \ldots , \mu _i^m]. $$

All the vectors can be stored in a matrix M containing all the possible cases:

$$ M= \begin{pmatrix} T &{} \mu _1^2 &{} \ldots &{} \mu _1^m \\ \mu _2^1 &{} T &{} \ldots &{} \mu _2^m \\ \vdots &{} \vdots &{} \ddots &{} \vdots \\ \mu _m^1 &{} \mu _m^2 &{} \ldots &{} T \\ \end{pmatrix}. $$

Obviously we assume that recognizing the class i from class i is always true (tautology) and brings no interest for the approach. It is denoted by T in the above matrix.

Considering a pattern \(x_0\), the achieved vectors should be handled to give a decision about its target class by aggregating 2-class models assumed to be new decision rules. For each class a new learning is done at this step from the values taken by each vector. So each vector were assumed to be input of an high level Choquet integral to confront them and to express a decision per class. Then a new learning step is performed for each class.

To summarize, let us consider one pattern to be classified during the recognition step. Basic decision rules defined from shape descriptors are calculated and given as input to the capacities compounding M. Let us consider one class. The values obtained by calculating Choquet integral for all the elements of the vector are then aggregated by a high level capacity and associated Choquet integral. Same process is carried out for all the classes. At last a classical argmax is applied to assign this pattern to its nearest class.

The previous algorithm (see Fig. 1) is adapted to remove none relevant capacities that brings no interest to the learning and so to the recognition. The stopping criterion relies on the number of samples correctly classified. Then weakest capacities are taken off until no improvement is achieved. Obviously each removing requires a new learning step.

Fig. 1.
figure 1

The first Sharvit’ database (B1).

Full size image

4 Experimental Results

4.1 Set of Decision Rules

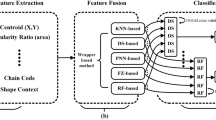
The proposed approaches being aimed at situations where little information is available for training, databases having a fair number of categories and a small number of samples have been used. For the experiments, several decision rules are set from different photometric descriptors associated to a basic similarity measure to belong in the same range. A set of nine pattern recognition methods \(R=\{R_i\}_{i=1,9}\) is used here, most of them having a low processing time, easy to implement, and invariant to affine transforms such as translation, rotation, or scaling. The descriptors computed on the samples are: \(DC=\{\)ART [16], angular signature [1], Generic Fourier Descriptors [42], degree of ellipticity [39], \(f_0\) and \(f_2\)-histograms [24], moments of Zernike [15], Yang histograms [41], Radon signature [38]\(\}\).

Fig. 2.
figure 2

Samples of the CVC database (B3).

Full size image

4.2 Experimental Data Sets

Experimental results gathered during shape recognition process are presented to show the efficiency of the proposed algorithm. The method was tested on several databases. First, two databases of Sharvit et al. kindly made available to us on his website [36], URL: http://www.lems.brown.edu/vision/researchAreas/SIID/ have been used: B1(9 classes \(\times \) 11samples) and B2(18 classes \(\times \) 12 samples). As shown in Fig. 1 (i.e., from B1), a few of the shapes are occluded (classes airplanes and hands) and some shapes are partially represented (classes rabbits, men, and hands). There are also distorted objects (class 6) and very heterogeneous shapes in the same class (animals).

B3(10\(\,\times \,\)300) is a database kindly provided by the CVC Barcelona. Symbols have been drawn by ten people using “anoto” concept. Few samples are provided in Fig. 2.

4.3 Applications

An experimental study is carried out from each decision rules \(R_i\), basic aggregation operators as Min, Max, Median and the proposed methods based on Choquet integral.

Table 1. Recognition rates reached for each method.
Full size table

For each test, a cross validation was applied (1/3 and 2/3). Table 1 shows the good behavior of the method on these databases. The results reached independently by each decision rule \(R_i\) are coherent with the amount of information processed by associated features. Simple aggregation operators: minimum, maximum and median exhibit various behavior depending on the database. In terms of recognition rates, only the maximum achieves better results than the best simple DR on two databases. In comparison to the simple DRs and the simple aggregation operators, our fusion operators based on the Choquet integral consistently achieve better results on each database, in terms of recognition rates. On each dataset, our recognition method at worse improves a little the recognition rates; it never worsens them.

4.4 Discussion

The first scheme allows to define a kind of identity map per class consisting in the most suitable decision rules and their importance weight following the application under consideration. When the number of classes grows this method allows to reach better results than considering a global scheme removing the same decision rules for all the classes.

The hierarchical scheme has the highest computing time considering the training step due to its own representation. Nonetheless it gives rise to good results while allowing to reach a powerful description which is more efficient to process with inconsistent data. Furthermore, oracles may be easily introduced in this structure to improve the recognition. Such scheme is very promising and might be the base of a wrapper-filter hybrid method by combining the selection of decisions rules and the extraction of irrelevant data from a study of the matrix.

Both models are easy to implement and the decision part is very fast as only a sort of decision rule values and the search of associated path in the lattice are useful to calculate the Choquet integral. At last, the best choice so far of cost function (experimentation based) is simple zero-one loss function. Other functions were tested as MSE for all items, or MSE for just badly classified items but not really gave improvements certainly due to the weak amount of learning data.

5 Conclusion

In this paper, we have discussed a hierarchical approach to automatically extract subsets of soft output classifiers, assumed to decision rules. Output of classifiers are aggregated into a decision scheme using the Choquet integral. The algorithm appears to be well suited for different situations: (a) when no a priori knowledge is provided about the relevance of a set of decision rules for a given dataset; (b) when the training set available is to small to build reliable decision rules; and (c) in case we are required to determine the best performer. It finds the best consensus between the rules, taking their interaction into account, and discards the undependable or redundant ones. A new way to merge both numerical and expert decision rules in order to improve the recognition process is under consideration.