Keywords

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Introduction

When a box, a partitioned container, a U-shaped tube with particles, and a tube floating or inserting in a granular bed is vibrated vertically , the granular system may display a diversity of complex phenomena such as heap formation [1, 2], accumulation of particles at one side of the container or the U-tube [3, 4] and particle climbing along the tube [5–8], which still pose challenging open questions. In particular, the problem of particle climbing in the vibrating pipe is of special interest because it offers a potential method for particle transportation in industrial applications.

Results of particle climbing from two different vibrating systems were reported by Liu et al. [7–9]. For one system they placed a container upside down on the surface of the granular bed and vibrated the bed. They owed the particle climbing in such a system to the reciprocating air flow between the bed and the container [7]. For another system they inserted an open pipe in granular layer and vibrated the pipe. In this case they found the interstitial air is not necessary for particle climbing, although the air may influence the climbing velocity [8]. To explain the mechanism of particle climbing in the vibrating pipe, Liu et al. [8, 9] presented a force model for particles in the pipe during vibration, in which the gravity, the normal force between the particles in the pipe and the granular layer in the silo as well as the friction force between the particles and the pipe wall are included. Their model can be used to qualitatively explain the particle climbing, but it fails to give more information on the dynamical behavior of individual particles because it focus on all the particles in the pipe instead of tracking each particle in the system. Such information, which is essential for understanding the physical mechanisms underlying the phenomenon of particle climbing along the vibrating pipe, is also difficult to obtain by experimental methods. Zhang et al. [10] examined the forces acting on the individual particles during a vibration cycle using the discrete element method (DEM). However, more details on the particle climbing process are still lack to understand the behavior of the granular system. Most recently, Liu et al. [11] analyzed the mechanism of the particle climbing and derived a theoretical expression of the final steady climbing height, however, the assumptions introduced in their work need to be carefully verified.

The DEM originally developed by Cundall and Strack [12] has been widely used to describe the flow of granular materials [13–16]. The method offers a helpful tool for investigating the behavior of granular systems at particle scale in which the motion of each particle in the system is traced. In this paper we present numerical simulations of the particle climbing using the DEM. The Open-Source DEM particulate simulation software of [17] (LIGGGHTS) is applied. The simulations allow us to obtain a detailed insight into the behavior of the granular system.

2 Computational Model

According to the DEM, the translational and rotational motion of each individual particle is governed by Newton’s second law of motion. For particle i with mass m i and moment of inertia I i , these equations read

$$m_{i} \frac{{d\vec{v}_{i} }}{dt} =\sum_{j = 1}^{n} {\left( {\vec{F}_{ij}^{n} + \vec{F}_{ij}^{t} } \right)} + m_{i} \vec{g}$$
(1)
$$I_{i} \frac{{d\vec{\omega }_{i} }}{dt} = \sum_{j = 1}^n {\left( {\vec{M}_{ij,t} + \vec{M}_{ij,r} } \right)}$$
(2)

where \(\vec{v}_{i}\) and \(\vec{\omega }_{i}\) are the translational and angular velocities of the particle i, t is the time, n is the number of particles in contact with particle i, \(\vec{F}_{ij}^{n}\) and \(\vec{F}_{ij}^{t}\) are the interaction forces in the normal and tangential directions, and \(\vec{g}\) is the acceleration due to gravity. Moreover, the torques acting on particle i are \(\vec{M}_{ij,t}\), which is due to the tangential force \(\vec{F}_{ij}^{t}\), and \(\vec{M}_{ij,r}\), which is the rolling resistance, described below.

Here we assume viscoelastic interaction for the normal force \(\vec{F}_{ij}^{n}\) [18] and applying a modified Cundall-Stract model [12] for the tangential force \(\vec{F}_{ij}^{t}\). Hence the forces read

$$\vec{F}_{ij}^{n} = min\left( {0, - \rho \delta_{nij}^{3/2} - \frac{3}{2}A_{n} \rho \sqrt {\delta_{nij} } \dot{\delta }_{nij} } \right)\vec{e}_{n}$$
(3)
$$\vec{F}_{ij}^{t} = min\left( {\mu_{s} \left| {\vec{F}_{ij}^{n} } \right|,\int\limits_{path} {\frac{4G}{2 - \nu }\sqrt {R_{eff} \delta_{nij} } ds + A_{t} \sqrt {R_{eff} \delta_{nij} } v_{tij} } } \right)\vec{e}_{t}$$
(4)

where \(\delta_{nij} = R_{i} + R_{j} - \left| {\vec{r}_{i} - \vec{r}_{j} } \right|\) is the overlap distance between the particles of radii R i and R j at positions \(\vec{r}_{i}\) and \(\vec{r}_{j}, \vec{e}_{n} = \left( {\vec{r}_{j} - \vec{r}_{i} } \right)/\left( {\left| {\vec{r}_{j} - \vec{r}_{i} } \right|} \right)\) is the normal unit vector, ρ is the elastic parameter, which is a function of the Young’s modulus, Y, the Poisson’s ratio, ν, and the effective radius, R eff  = R i R j /(R i  + R j),

$$\rho = \frac{2Y}{{3\left( {1 - \nu^{2} } \right)}}\sqrt {R_{eff} }$$
(5)

and A n is the dissipative parameter, which depends not only on the Young’s modulus and the Poisson’s ratio, which are easily available for a variety of materials, but also on the material viscosities, which are not directly available. In order to determine A n , we use an expression of the coefficient of restitution, ε, for the collision of the particles i and j. More details of A n refer to [18, 19]. Moreover, μ s is the sliding friction coefficient, G = Y/[2(1 + ν)] is the shear modus, v tij is the relative tangential velocity at the point of contact, A t  = A n Y/(1−ν 2) is the tangential dissipative parameter [20, 21] and \(\vec{e}_{t}\) is the tangential unit vector. The integral in (4) is performed over the displacement of the particles at the point of contact for the duration of the contact.

According to the directional constant torque model [13], the torque associated with the rolling resistance, \(\vec{M}_{ij,r}\), can be expressed as

$$\vec{M}_{ij,r} = - \mu_{r} k_{n} \delta_{nij} \frac{{\vec{\omega }_{ij} }}{{\left| {\vec{\omega }_{ij} } \right|}}R_{eff}$$
(6)

where μ r is the coefficient of rolling resistance, \(\vec{\omega }_{ij}\) is the relative angular velocity between particles i and j, and k n is the elastic coefficient for the normal contact, which can be expressed as

$$k_{n} = \rho \sqrt {\delta_{nij} }$$
(7)

In the DEM simulation, the time step Δt must be small enough to make sure that the Newton’s equations are accurately solved. In this work we take Δt = t col /30, where t col is the collision time. t col can be estimated by the expression of the contact time for the center-to-center collision of frictionless elastic particles [21],

$$t_{col} \approx 3.21\left( {\frac{{m_{eff}^{2/5} }}{\rho }} \right)v_{imp}^{ - 1/5}$$
(8)

where m eff  = m i m j /(m i  + m j ) is effective mass and v imp is the impact velocity. Here a reference impact velocity v imp  = 1.0 m/s is adopted to compute t col .

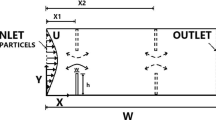
We perform DEM simulations in a rectangular box of lateral dimensions L x  × L y , where L x  = L y  = 24 mm. The bottom of the box is at z = −18 mm, while the height of the box is large enough such as to avoid particle collision with the top of the box in the simulation. We place a pipe with diameter D along the vertical (z) axis up to its lower end at z = 0 mm in the center of box, and insert N mono-sized particles of diameter d and density ρ p at random positions within the inner volume of the box leading to a solid fraction of about 25 %, whereupon the particles settle due to the action of gravity.

The fixed frictional wall boundary conditions are applied for the walls of both the simulation box and the pipe. The equations used for computing the forces between particles and the frictional walls are the same used for modelling particle-particle collisions where one of the contact partners is of infinite mass and radius. We wait for the particles to relax, and then vibrate the pipe by applying a vertically displacement z which is a sinusoidal function of time,

$$z = a\,\sin \left( {2\pi ft} \right)$$
(9)

where a is the amplitude of vibration and f is the frequency.

The results shown in the following sections are obtained using the parameters listed in Table 1.

Table 1 Parameters used in simulation
Full size table

3 Results and Discussion

3.1 Evolution of Particle Climbing Height

As we mentioned in Sect. 1, when the pipe is vertically vibrated, the particles climb along the pipe . Figure 1 shows the general behavior of particle climbing obtained from our simulation, where T is the period of pipe vibration, T = 1/f. As shown in Fig. 1, the climbing height grows rapidly with time and finally becomes saturated. This behavior has been demonstrated experimentally [8, 10]. Here we report the use of DEM to reproduce the process of particle climbing.

Fig. 1
figure 1

Particle climbing along the pipe

Full size image

We plot the granular free surface height in and outside the pipe as a function of time in Fig. 2. During the first 2T, the climbing height (z in ) increases largely, reaches a peak value and then decreases to a value slightly greater than the value of the original height. This can be explained by the initial effect. When the pipe starts to vibrate the particles are densely packed, hence a strong upward force is acted upon the particles in the pipe, causing the particles in the pipe to rise rapidly. Meanwhile, the particle packing becomes loose, and thus the interaction between the particles and the pipe wall becomes weak. Therefore, the motion of the pipe has little effect on that of the particles until the particles fall down and are then elevated due to the upward motion of the pipe again. After the initial stage, the climbing height fluctuates as it increases gradually and the fluctuation period is the same as the period of pipe vibration (T), which can characterized as steady climbing stage. During 20T ~ 24T, transition of the fluctuation period of the climbing height from T to 2T occurs. After 24T, the particle climbing height shows strong fluctuation with a period of 2T, while it decreases gradually, finally gets to a saturation stage and stabilizes at a saturation climbing height. Moreover, the fluctuation of the granular free surface height outside the pipe (z out ) is negligibly small compared to that of z in as observed in Fig. 2.

Fig. 2
figure 2

Evolution of the granular free surface height in and outside the pipe

Full size image

3.2 Motion of Tracers During Steady Climbing

To understand the process of particle climbing at particle scale, we plot the z-displacements of tracer particles initially in the center of the pipe but with different heights in Fig. 3. The particles in the pipe exhibit an oscillatory motion due to the periodic vibration of the pipe, however, the vertically positions of the particles is higher at the end of a pipe vibration cycle compared with at the beginning of the cycle, resulting a height increase of the particles in the pipe, that is the particle climbing observed in both previous experiments and our DEM simulation. As can be seen from Fig. 3, there is a phase lag between the particles at different vertical positions. The phase lag increases with the height. Thus, as the particle climbing continues, the phase lag increases, which may accounts for the transition of the period of particle climbing. Furthermore, the void left by particles rising within the pipe is filled with particles that are initially at the pipe’s outer volume, leading eventually to the particle climbing in the pipe.

Fig. 3
figure 3

Motion of tracers during steady climbing

Full size image

3.3 Effect of Void Filling

Since the particle climbing may be explained by a void filling mechanism, to clarify the effect of the void filling, we show the relative particle number change in the pipe as a function of time in Fig. 4. Here the particles in the pipe correspond to the ones with radial positions r i  < D/2 and vertical positions z i  > −a. As we can see from Fig. 4, the number of particles in the pipe increases during the pipe’s upward motion as a result of void filling. In addition, the particle number decreases at the end of the pipe’s downward movement, resulting from the particle diffusion caused by the collision between the particles falling within the pipe and the granular bed. However, the particle gain due to the void filling effect is more significant than the particle loss due to the diffusion effect, leading to the particle number increase within the pipe and thus observable particle climbing .

Fig. 4
figure 4

Relative particle number change as a function of time

Full size image

4 Conclusion

The DEM simulation reproduces the process of particle climbing along a vibrating pipe and gives a detailed insight into the process of particle climbing. The evolution of the climbing height has been shown, elucidating two stages in particle climbing, the steady climbing stage and the saturation stage. The motion of individual particles as well as the void filling during the steady climbing stage has been clarified. The particles are filled into the void left by the pipe during the upward movement of the pipe, while the particle loss due to the collision between the falling particles and the particle bed is observed during the downward movement of the pipe. The net increase in particle number in each cycle contributes to the particle climbing .