Keywords

1 Introduction

With the development of BeiDou Navigation Satellite System (BDS) and the Global Navigation Satellite System (GLONASS), together with mature Global Positioning System (GPS), there will be enough satellites under operation. Compared with a single system, combination of the three systems will improve the geometric structure of satellites, avoid generating ill-conditioned normal equation coefficients, and ensure the stability and reliability of the satellite navigation system [1]. In recent years, the static positioning of GNSS is almost mature, however, kinematic positioning, especially the high-accuracy real-time positioning is still under development [2]. As is well known that the positioning accuracy using observation of carrier phase is 2–3 orders of magnitude higher than using observation of pseudorange [3], so it is necessary for us to use the observation of carrier phase. However, it is difficult to calculate the ambiguity in kinematic positioning because of the satellite unlock and cycle slip caused by the complex environment and the movement of receivers. To solve this problem, many scholars have already made an intensive study [4–7]. In this paper, our study focuses on the kinematic differential positioning technology of GNSS based on single epoch in the least squares method with broadcast ephemeris and dual-frequency data, and then analyzes the accuracy and stability. The process can be shown in Fig. 1.

Fig. 1
figure 1

Kinematic differential process

Full size image

2 Mathematical Model

The measurement data composed of GPS, BDS, and GLONASS was used in this paper, and the across-satellite difference was just used in respective system. If the satellites number is n, there will be n − 3 double difference observation equations available including 3 position parameters and n − 3 double difference ambiguities. As a result, the number of unknown parameters is more than the number of equations. When using the least squares method for kinematic positioning, we need to search the ambiguity in rapid first, according to the wide-lane ambiguity to fix basic ambiguity that was used in this paper. Therefore, using the linear combination between dual-frequency P-code and carrier phase can obtain the floating value of double difference wide-lane ambiguity. The equation is shown as follows [8]:

$$ \nabla\Delta N_{WL} = \frac{{f_{1} - f_{2} }}{{f_{1} +\, f_{2} }}\left( {\frac{{\nabla\Delta P_{1} }}{{\lambda_{1} }} + \frac{{\nabla\Delta P_{2} }}{{\lambda_{2} }}} \right) - \left( {\nabla {\Delta }\varphi_{1} - \nabla {\Delta }\varphi_{2} } \right) $$
(1)

where \( \nabla\Delta \) represents double difference operator, \( N_{WL} \) represents the floating value of wide-lane ambiguity, \( f \) represents frequency, \( P \) represents the observation of code pseudorange, \( \lambda \) represents wavelength of frequency, and \( \varphi \) represents the observation of carrier phase. When using this method to solve wide-lane ambiguity instantaneously, the key is that the code pseudorange needs enough accuracy. So, some satellites with poor quality of code pseudorange can be eliminated in the process of preprocessing. After the floating value of wide-lane ambiguity is obtained, the integer solution of wide-lane ambiguity will also be obtained by searching it. In this paper, the ratio value and unit weight of standard error were used to determine whether the wide-lane ambiguity was successfully fixed. After the wide-lane ambiguity is fixed, the floating value of basic ambiguity can be obtained by wide-lane observation equation and L1 observation equation. The double difference observation equation of carrier phase for GPS and BDS is as follows [9]:

$$ \begin{aligned} \lambda_{i} \nabla\Delta \varphi_{i} & = \nabla\Delta \rho - \lambda_{i} \nabla\Delta N_{i} - \nabla\Delta I + \nabla\Delta T + \nabla\Delta \left( {H + h_{i} } \right)\sin E \\ & \quad + \nabla\Delta O + \nabla\Delta m_{i,\varphi } + \nabla\Delta d_{\text{other}} + \nabla\Delta \varepsilon_{i,\varphi } \\ \end{aligned} $$
(2)

where \( i = 1,2 \) represents the band of signal, \( \rho \) represents the distance of satellite receiver, \( N \) represents ambiguity, and \( I \) and \( T \) represent ionosphere delay and troposphere delay on propagation path, respectively, \( H \) represents receiver’s instrument height, \( h_{i} \) represents the correction of receiver’s antenna phase center, \( E \) represents elevation angle of satellite, \( O \) represents the errors of satellite orbit, \( m_{i,\varphi } \) represents multipath effects in carrier phase surveying, \( d_{\text{others}} \) represents other errors, including the earth rotation, relativistic effects, etc., \( \varepsilon_{i,\varphi } \) and represents noise of carrier phase. Other symbols represent the same as Eq. (1).

Because GLONASS uses a signal system of frequency division multiple access (FDMA), the ambiguity needs to be decomposed into a double difference ambiguity and an across-receiver difference ambiguity of reference satellite.

Here, assuming that the satellite \( b \) and reference satellite \( r \) carry out across-satellite difference after across-receiver difference, the process of decomposition is as follows [9]:

$$ \begin{aligned} \lambda_{i}^{b}\Delta N_{i}^{b} - \lambda_{i}^{r}\Delta N_{i}^{r} & = \lambda_{i}^{b}\Delta N_{i}^{b} - \lambda_{i}^{b}\Delta N_{i}^{r} + \lambda_{i}^{b}\Delta N_{i}^{r} - \lambda_{i}^{r}\Delta N_{i}^{r} \\ & \quad = \lambda_{i}^{b} \left( {\Delta N_{i}^{b} -\Delta N_{i}^{r} } \right) + \left( {\lambda_{i}^{b} - \lambda_{i}^{r} } \right)\Delta N_{i}^{r} \\ & \quad = \lambda_{i}^{b} \nabla\Delta N_{i} + \left( {\lambda_{i}^{b} - \lambda_{i}^{r} } \right)\Delta N_{i}^{r} \\ \end{aligned} $$
(3)

The double difference observation equation of carrier phase for GLONASS is as follows [9]:

$$ \begin{aligned} \nabla\Delta \lambda_{i} \varphi_{i} & = \nabla\Delta \rho - \lambda_{i}^{b} \nabla\Delta N - \left( {\lambda_{i}^{b} - \lambda_{i}^{r} } \right)\Delta N^{r} - \nabla\Delta I + \nabla\Delta T + \nabla\Delta \left( {H + h_{i} } \right)\sin E \\ & \quad + \nabla\Delta O + \nabla\Delta d_{i,\varphi } + \nabla\Delta m_{i,\varphi } + \nabla\Delta d_{\text{other}} + \nabla\Delta \varepsilon_{i,\varphi } \\ \end{aligned} $$
(4)

where \( d_{i,\varphi } \) represents receiver’s hardware delay of carrier phase, \( \Delta N \) represents the ambiguity of across-receiver difference. Other symbols represent the same as Eq. (2). Because medium-short baseline was resolved in this paper, only the troposphere delay was considered.

Similarly, the two kinds of wide-lane observation equation of carrier phase are as follows:

$$ \nabla\Delta \lambda_{W} \varphi_{W} = \nabla\Delta \rho - \lambda_{W}^{b} \nabla\Delta N_{WL} + \nabla\Delta T $$
(5)
$$ \nabla\Delta \lambda_{W} \varphi_{W} = \nabla\Delta \rho - \lambda_{W}^{b} \nabla\Delta N_{WL} - \left( {\lambda_{W}^{b} - \lambda_{W}^{r} } \right)\Delta N_{WL}^{r} + \nabla\Delta T $$
(6)

where the other errors are not listed compared with Eqs. (2) and (4), \( \lambda_{W} \) represents wavelength of wide lane, \( \varphi_{W} \) represents carrier phase of wide lane. Other symbols represent the same as Eq. (2). The single difference ambiguity of Eqs. (4) and (6) can be resolved by the observation equations of pseudorange and carrier phase.

Here, we just use Eqs. (2) and (5) to show the solution of basic ambiguity. The floating value of basic ambiguity can be obtained via the following equation that uses simplified Eq. (2) to subtract simplified Eq. (5).

$$ \nabla\Delta N_{i} = \frac{1}{{\lambda_{i} }}\left( {\lambda_{W} \nabla\Delta N_{W} - \lambda_{W} \nabla\Delta \varphi_{W} + \lambda_{i} \nabla\Delta \varphi_{i} } \right) $$
(7)

The integer basic ambiguity can be obtained by rounding Eq. (7) directly. The integer basic ambiguity is substituted into the observation equation, and then error equation can be obtained by the linearization of observation equation. Thus Eq. (8) is formed.

$$ V = Bx - L $$
(8)

where \( V \) represents error correction of observation, \( B \) represents coefficient matrix, \( x \) represents coordinate increments, and \( L \) represents the difference between observation value and approximate theoretical value.

According to the principle of least squares, the normal equation can be written as the following equation:

$$ B^{T} PBx = B^{T} PL $$
(9)

where \( P \) represents weight matrix, and the ratio of weight among systems are 1:1:1.

$$ P = \left( {\begin{array}{*{20}c} {P_{\text{GPS}} } & {} & {} \\ {} & {P_{\text{GLONASS}} } & {} \\ {} & {} & {P_{\text{BDS}} } \\ \end{array} } \right) $$
(10)

where \( P_{\text{GPS}} \) represents weight matrix of GPS, \( P_{\text{GLONASS}} \) represents weight matrix of GLONASS, and \( P_{\text{BDS}} \) represents weight matrix of BDS.

The following equations can be obtained by resolving Eq. (9):

$$ x = \left( {B^{T} PB} \right)^{ - 1} B^{T} PL $$
(11)
$$ \sigma_{0} = \sqrt {\left( {V^{T} PV} \right)/(n - t)} $$
(12)

where \( \sigma_{0} \) represents unit weight of standard error, \( n \) represents the number of observations, and \( t \) represents the number of essential observations.

The above ambiguity could have incorrect ambiguity, which will make the observation equation to contain gross error. Furthermore, the quadratic form of residual error, \( V^{T} PV \), is particularly sensitive to gross errors, and the presence of single gross error can lead to collapse of the estimated values [10]. In order to resist gross error, robust estimation was used. The IGG-III scheme of iteration and variable weights was used in this paper, and the equation is as follows [11]:

$$ \overline{{P_{i} }} = \left\{ {\begin{array}{*{20}l} {P_{i} ,\left| {\bar{v}_{i} } \right| \le k_{0} } \hfill \\ {P_{i} \frac{{k_{0} }}{{\left| {\bar{v}_{i} } \right|}}\left( {\frac{{k_{1} - \left| {\bar{v}_{i} } \right|}}{{k_{1} - k_{0} }}} \right)^{2} ,} \hfill \\ {0,\left| {\bar{v}_{i} } \right| > k_{1} } \hfill \\ \end{array} } \right.k_{0} < \left| {\bar{v}_{i} } \right| \le k_{1} $$
(13)

where \( \overline{{P_{i} }} \) represents equivalent weight, \( \bar{v}_{i} \) represents standardized residual error, \( k_{0} \) represents quantile parameter, and \( k_{1} \) represents elimination point. The robust estimation is through constant iteration and weight making to decrease the effect of gross error on parameter estimation. Considering the efficiency and preventing filter divergence, the number of iterations is generally 3–5 times [11]. In addition, the use of robust estimation requires sufficient original data.

3 Case Analysis

In order to verify this method, this paper applied the GNSS 20 Hz data which had been collected from the V-Surs I vehicle-borne three-dimensional mobile surveying system for about 3 h. This system has been researched and developed by Shandong University of Science and Technology and the company of Supersurs mobile surveying service (shown in Fig. 2). It is equipped with a three-system receiver of NovAtel Propak6 and inertial measurement unit (IMU) of span LCI type. The type of antenna and the sampling rate of the receiver are NOV703GGG and 0.05 s, respectively. The base station of this experiment was set up on the roof of S2 laboratory in Shandong University of Science and Technology.

Fig. 2
figure 2

V-Surs I vehicle-borne three-dimensional mobile surveying system

Full size image

The ratio >2 and \( \sigma_{0} < 0.01 \) were used as the conditions that the wide-lane ambiguity was fixed successfully in this paper. When the robust estimation was used to process gross error, \( k_{0} \) equaled 1.2 and \( k_{1} \) equaled 2.8. In addition, when the degree of freedom was less than 3, the robust estimation was not used.

The trajectory of this experiment is shown in Fig. 3. The real-time baseline length between base station and user station is shown in Fig. 4. As shown in Fig. 4, the baseline length is more than 10 km most of the time.

Fig. 3
figure 3

The trajectory of this experiment

Full size image
Fig. 4
figure 4

Baseline length between base station and user station

Full size image

We used GNSS/INS tightly coupled resolution of Inertial Explorer 8.60 software (IE 8.60) to resolve this data, and the results were used as true values. The differences in N, E, and U directions between this method and IE 8.60 are shown in Fig. 5, as well as the standard errors in N, E, and U directions are shown in Fig. 6. As shown in Fig. 5, the differences are mostly within 5 cm in N direction, and E direction is slightly worse than N direction, however, the differences largely change in U direction. From Fig. 6, it can be noticed that standard errors are basically within 1 cm in N direction, within 2 cm in E direction, mostly within 3 cm in U direction. As thus, it can be concluded that this method has higher precision. Comparing Figs. 5 and 6, it is noticed that if this time has a larger difference in Fig. 5, at the same time there has been a larger standard error in Fig. 6. Based on these results, it can be concluded that this method has higher reliability.

Fig. 5
figure 5

Position error between this method and benchmark in different directions

Full size image
Fig. 6
figure 6

Standard error of this method in different directions

Full size image

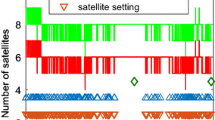
Figures 7 and 8 represent PDOP values and the number of satellites, respectively. As we know, PDOP values can reflect the geometric structure of the visible satellites. The larger the PDOP value is, the worse the geometric structure of the satellites are, which may make the positioning result worse. As shown in Fig. 7, there are many PDOP values larger than 3, partly larger than the acceptable 6. Comparing Figs. 5, 7 and 8, it can be shown if PDOP value is larger at some time, the numbers of satellite is smaller, and the positioning results are also poor. Because of the limited space, this paper only analyzes the condition of the marked area in Figs. 7 and 8. Fig. 9 shows surrounding environment of the marked area. As shown in Figs. 7, 8 and 9, in the marked area, the receiver is under the corridor with less satellites and poor geometric structure of satellites, at the same time poor positioning results are shown in Fig. 5.

Fig. 7
figure 7

PDOP values of observation epoch

Full size image
Fig. 8
figure 8

The number of satellites

Full size image
Fig. 9
figure 9

The surrounding environment of the marked area

Full size image

Table 1 shows errors and RMS between this method and IE 8.60. As shown in Table 1, there have been systematic differences in E and U directions from this column of mean, and this is because the error model of troposphere is different between IE 8.60 software and this method. The column of RMS demonstrates a RMS within 2 cm in N direction, a RMS within 3 cm in E direction, and these illustrate that this method has high outside accuracy. Due to the medium-short baseline used in this paper, \( \sqrt {N^{2} + E^{2} + U^{2}} \) < 10 cm is the condition that ambiguity was fixed successfully. Experimental results show that the successful rate of ambiguity fixed is 94.87 % in this data, and single epoch is convergence at the beginning of this experiment.

Table 1 The accuracy statistics of single-epoch positioning results
Full size table

4 Conclusion

In this paper, a method of single-epoch carrier-phase kinematic differential positioning is presented. In this method, robust estimation and residual correction are used to further ensure the correctness of the method as well as the accuracy. To verify this method, the real collected GPS/GLONASS/BDS kinematic data are applied to analyze the internal and external accuracy of the method. Results demonstrate that this method has higher accuracy and reliability. For the medium-short baseline, this method can achieve centimeter-level precision and fully meet the requirements of vehicle-borne mobile measurement. Thus, this method can be used for high-accuracy positioning, and it has great practical significance. However, this paper shows that under some severe environment (i.e., PDOP values become larger), the accuracy decreases. Moreover, there are certain epochs when the number of satellites is not sufficient to use the least squares estimation before the receiver lock enough satellites again, this often needs several epochs to fully fix the ambiguities, which needs further study.