Analytic Method for Solving Heat and Heat-Like Equations with Classical and Non Local Boundary Conditions

Abstract

In this paper, heat and heat-like equations with classical and non local boundary conditions are presented and a homotopy perturbation method (HPM) is utilized for solving the problems. The obtained results as compared with previous works are highly accurate. Also HPM provides continuous solutions in contrast to traditional methods, like finite difference method, which only provides discrete approximations. It is found that this method is a powerful mathematical tool and can be applied to a large class of linear and non linear problems in different fields of science and technology.

1 Introduction

Recently, new analytical methods have gained the interest of researchers for finding approximate solutions to partial differential equations. This interest was driven by the needs from applications both in industry and sciences. Theory and numerical methods for solving initial boundary value problems were investigated by many researchers see for instance [1–9] and the reference therein. In the last decade, there has been a growing interest in the new analytical techniques for linear and non linear initial boundary value problems. The widely applied techniques are perturbation methods. He [10] has proposed a new perturbation technique coupled with the homotopy technique, which is called the homotopy perturbation method (HPM) for solving non linear problems. In contrast to the traditional perturbation methods, a homotopy is constructed with an embedding parameter $p \in [0,1]$, which is considered as a small parameter. Homotopy perturbation method has gained reputation as being a powerful tool for solving linear or non linear partial differential equations. He [11], applied HPM to solve initial boundary value problems which is governed by the non linear ordinary (partial) differential equations, the method has been shown to effectively, easily and accurately solve a large class of linear and non linear problems with components converging rapidly to exact solutions. Thus the main goal of this work is to apply the homotopy perturbation method (HPM) for solving heat and heat-like equations subject to different type of boundary conditions. The obtained results are more accurate than those obtained recently by Damrongsak et al. [12]. In this paper we consider a one-dimensional heat equation, one-dimensional and three-dimensional heat-like equations. The implementation of the method has shown reliable results in that few terms are needed to obtain either exact solution or to find an approximate solution of a reasonable degree of accuracy in real physical models. Numerical examples are presented to illustrate the efficiency of the homotopy perturbation method, the obtained results are all in good agreement with exact ones.

2 The Linear Heat Equation with Dirichlet and Neumann Conditions

2.1 Problem Definition

We consider the diffusion equation given by

$$ \frac{\partial u}{\partial t} = \alpha \frac{{\partial^{2} u}}{{\partial x^{2} }},\;0 < x < l,\quad t > 0 $$

(1)

subject to the Initial condition:

$$ u\left( {x,0} \right) = u_{0} \left( x \right), \quad 0 < x < a $$

(2)

and the boundary conditions:

$$ u\left( {0,t} \right) = g_{0} \left( t \right),\quad t > 0 $$

(3)

$$ u\left( {1,t} \right) = g_{1} \left( t \right),\quad t > 0 $$

(4)

$$ u_{x} \left( {0,t} \right) = g_{2} \left( t \right), \quad t > 0 $$

(5)

$$ u_{x} \left( {1,t} \right) = g_{3} \left( t \right),\quad t > 0 $$

(6)

where the diffusion coefficient α is positive, $u(x,t)$ represents the the temperature at point $(x,t)$ and $f\left( {x,t} \right),\;g_{0} \left( t \right),\;g_{1} \left( t \right),\;g_{2} \left( t \right),\;g_{3} (t)$ are sufficiently smooth known functions.

2.2 Analysis of Homotopy Perturbation Method

To illustrate the basic ideas, let $X,\;and\;Y$ be two topological spaces. If $f\;and\;g$ are continuous maps of the spaces $X\;into\;Y,$ it is said that $f$ is homotopic to $g$, if there is continuous map $F:X \times [0,1] \to Y$ such that $F\left( {x,0} \right) = f\left( x \right)\;and\;F\left( {x,1} \right) = g\left( x \right)\;for\;each\;x\epsilon X$, then the map is called homotopy between $f\;and\;g$. We consider the following nonlinear partial differential equation:

$$ A\left( u \right) - f\left( r \right) = 0,\;r \in \varOmega $$

(7)

subject to the boundary conditions

$$ B(u,\partial u/\partial \eta ) = 0,\;r \in\Gamma $$

(8)

where $A$ is a general differential operator, $f$ is a known analytic function, Γ is the boundary of Ω and $\partial /\partial \eta$ denotes directional derivative in outward normal direction to Ω. The operator $A$, generally divided into two parts, $L$ and $N,$ where $L$ is linear while $N$ is nonlinear. Using $A = L + N,$ Eq. (7) can be rewritten as follows:

$$ L\left( v \right) + N\left( v \right) - f\left( r \right) = 0 $$

(9)

by the homotopy technique, we construct a homotopy defined as

$$ H\left( {v,p} \right):\varOmega \times [0,1] \to R $$

(10)

which satisfies:

$$ \begin{aligned} & H\left( {v,p} \right) = \left( {1 - p} \right)\left( {L\left( v \right) - L\left( {u_{0} } \right)} \right) + p\left( {A\left( v \right) - f\left( r \right)} \right),\\ & p \in \left[ {0,1} \right], r \in \varOmega . \\ \end{aligned} $$

(11)

Or

$$ \begin{aligned} & H\left( {v,p} \right) = L\left( v \right) - L\left( {u_{0} } \right) + pL\left( {u_{0} } \right) + p\left( {N\left( v \right) - f\left( r \right)} \right) = 0, \\ & p \in \left[ {0,1} \right],\;r \in \varOmega . \\ \end{aligned} $$

(12)

Where $p$ is an embedding parameter, $u_{0}$ is an initial approximation of Eq. (7), which satisfies the boundary conditions. It follows from Eq. (12) that:

$$ H\left( {v,0} \right) = L\left( v \right) - L\left( {u_{0} } \right) = 0 $$

(13)

$$ H\left( {v,1} \right) = A\left( v \right) - f\left( r \right) = 0 $$

(14)

The changing process of $p$ from 0 to 1 monotonically is a trivial problem. $H\left( {v,0} \right) = L\left( v \right) - L\left( {u_{0} } \right) = 0$ is continuously transformed to the original problem

$$ H\left( {v,1} \right) = A\left( v \right) - f\left( r \right) = 0 $$

(15)

In topology, this process is known as continuous deformation.

$L\left( v \right) - L(u_{0} )$ and $A\left( v \right) - f(r)$ are called homotopic. We use the embedding parameter $p$ as a small parameter, and assume that the solution of Eq. (12) can be written as power series of p:

$$ v = p^{0} v_{0} + p^{1} v_{1} + p^{2} v_{2} + p^{3} v_{3} + \cdots + p^{n} v_{n} + \cdots $$

(16)

Setting $p = 1$ we obtain the approximate solution of Eq. (7) as:

$$ u = \mathop {\lim }\limits_{p \to 1} v = v_{0} + v_{1} + v_{2} + v_{3} + \cdots + v_{n} + \cdots $$

(17)

The series of Eq. (17) is convergent for most of the cases. But the rate of the convergence depends on the linear operator $N(v)$. He [13] has suggested that:

• 1. The second derivative of $N(v)$ with respect to $v$ should be small because the parameter may be relatively large i.e. $p = 1.$

• 2. The norm of $L^{ - 1} (\partial N/\partial v)$ must be smaller than one so that the series converges.

2.3 Solution Procedure

The solution is considered in the form below:

$$ v = p^{0} v_{0} + p^{1} v_{0} + p^{2} v_{2} + \cdots $$

(18)

Setting $p = 1$, we obtain the approximate solution of Eq. (1) as follows:

$$ u = \mathop {\lim }\limits_{p \to 1} v = v_{0} + v_{1} + v_{2} + \cdots $$

(19)

Substituting Eq. (18) into Eq. (12) and comparing the coefficient of like powers of $p$, we have

$$ \begin{aligned} & p^{0} :(v_{0} )_{t} - (u_{0} )_{t} = 0,\quad v_{0} = u_{0} = u\left( {x,0} \right) \\ & p^{1} :(v_{1} )_{t} - \left( {v_{0} } \right)_{xx} - s\left( {x,t} \right) = 0 \\ & v_{1} = \mathop \smallint \limits_{0}^{t} ((v_{0} )_{xx} - s(x,t))dt,\quad v_{1} (x,0) = 0 \\ & p^{2} :(v_{2} )_{t} - (v_{1} )_{xx} = 0 \Rightarrow v_{2} = \mathop \smallint \limits_{0}^{t} (v_{1} )_{xx} dt,\;v_{2} \left( {x,0} \right) = 0 \\ & p^{3} :(v_{3} )_{t} - (v_{2} )_{xx} = 0 \Rightarrow v_{3} = \mathop \smallint \limits_{0}^{t} (v_{2} )_{xx} dt,\; v_{3} \left( {x,0} \right) = 0 \\ & \vdots \\ & \\ \end{aligned} $$

(20)

Hence the approximate or exact solution of problem (1) is obtained as:

$$ u\left( {x,t} \right) = v_{0} + v_{1} + v_{2} + v_{3} + \cdots $$

(21)

3 The One Dimensional Heat-Like Equation

3.1 Problem Definition

We consider the problem in two cases one-dimensional heat-like equation given by:

$$ u_{t} = a\left( x \right) + b\left( x \right)u_{xx} , \quad 0 < x < 1, $$

(22)

subject to the initial condition

$$ u\left( {x,0} \right) = x^{2} $$

(23)

and the boundary conditions

$$ u\left( {0,t} \right) = \mathop \smallint \limits_{0}^{1} u\left( {x,t} \right)dx + c_{1} = c(t) $$

(24)

$$ u\left( {1,t} \right) = \mathop \smallint \limits_{0}^{1} u\left( {x,t} \right)dt + c_{2} = d(t) $$

(25)

3.2 Solution Procedure

Writing the approximate solution in the series form as the following:

$$ v = p^{0} v_{0} + p^{1} v_{1} + p^{2} v_{2} + \cdots + p^{n} v_{n} + \cdots $$

(26)

Substituting Eq. (26) into Eq. (22) and equating the coefficients of the same powers of $p$ we get the system of equations as follows:

$$ \begin{aligned} & v_{0t} - u_{0t} = 0 \Rightarrow v_{0} = u_{0} \\ & v_{1t} - a\left( x \right) - b\left( x \right)v_{0xx} = 0,\quad v_{1} \left( {x,0} \right) = 0 \\ & v_{1} = \mathop \smallint \limits_{0}^{t} \left( {a\left( x \right) - b\left( x \right)v_{0xx} } \right)dt \\ & v_{2t} - v_{1xx} = 0,\quad v_{2} \left( {x,0} \right) = 0 \\ & v_{2} = \mathop \smallint \limits_{0}^{t} v_{1xx} dt \\ & \vdots \\ & \\ \end{aligned} $$

(27)

and so on, we obtain the approximate solution in a series form as below:

$$ u\left( {x,t} \right) = \mathop \sum \limits_{i = 0}^{\infty } v_{i}. $$

4 Three-Dimensional Heat-Like Equation

4.1 Problem Definition

Consider the three-dimensional heat-like equation as

$$ u_{t} = p\left( x \right)q\left( y \right)r\left( z \right) + \alpha \left( x \right)u_{xx} + \beta \left( y \right)u_{yy} + \gamma \left( z \right)u_{zz} ,\quad 0 < x,y,z < 1,\;0 < t \le T $$

(28)

subject to the initial and boundary conditions

$$ u\left( {x,y,z,0} \right) = f(x,y,z) $$

(29)

$$ \begin{aligned} u\left( {0,y,z,t} \right) & = \mathop \smallint \limits_{0}^{1} \mathop \smallint \limits_{0}^{1} \mathop \smallint \limits_{0}^{1} u\left( {x,y,z,t} \right)dxdydz + g_{1} = k_{1} (t) \\ u\left( {1,y,z,t} \right) & = \mathop \smallint \limits_{0}^{1} \mathop \smallint \limits_{0}^{1} \mathop \smallint \limits_{0}^{1} u\left( {x,y,z,t} \right)dxdydz + g_{2} = k_{2} (t) \\ u\left( {x,0,z,t} \right) & = \mathop \smallint \limits_{0}^{1} \mathop \smallint \limits_{0}^{1} \mathop \smallint \limits_{0}^{1} u\left( {x,y,z,t} \right)dxdydz + g_{3} = k_{3} (t) \\ u\left( {x,1,z,t} \right) & = \mathop \smallint \limits_{0}^{1} \mathop \smallint \limits_{0}^{1} \mathop \smallint \limits_{0}^{1} u\left( {x,y,z,t} \right)dxdydz + g_{4} = k_{4} (t) \\ u\left( {x,y,0,t} \right) & = \mathop \smallint \limits_{0}^{1} \mathop \smallint \limits_{0}^{1} \mathop \smallint \limits_{0}^{1} u\left( {x,y,z,t} \right)dxdydz + g_{5} = k_{5} (t) \\ u\left( {x,y,1,t} \right) & = \mathop \smallint \limits_{0}^{1} \mathop \smallint \limits_{0}^{1} \mathop \smallint \limits_{0}^{1} u\left( {x,y,z,t} \right)dxdydz + g_{6} = k_{6} \\ \end{aligned} $$

(30)

4.2 Solution Procedure

We just consider three-dimensional equation which includes two other cases. Substituting Eq. (18) into Eq. (28) and equating the terms with identical powers of $p$, we have

$$ p^{0} {:} (v_{0} )_{t} - (u_{0} )_{t} = 0 \Rightarrow v_{0} = u(x,0) $$

(31)

$$ p^{1} {:}(v_{1} )_{t} - p\left( x \right)q\left( y \right)r\left( z \right) - ((\alpha \left( x \right)v_{0} )_{xx} + (\beta \left( y \right)v_{0} )_{vv} + (\gamma \left( z \right)v_{0} )_{zz} ) = 0 $$

$$ v_{1} = \mathop \smallint \limits_{0}^{t} (p\left( x \right)q\left( y \right)r\left( z \right) + ((\alpha \left( x \right)v_{0} )_{xx} + (\beta (y)v_{0} )_{yy} + (\gamma \left( z \right)v_{0} )_{zz} ))dt $$

(32)

$$ \begin{aligned} & p^{2} {:}(v_{2} )_{t} - (p\left( x \right)q\left( y \right)r\left( z \right) - (\alpha \left( x \right)v_{1} )_{xx} - (\beta \left( y \right)v_{1} )_{yy} - (\gamma \left( z \right)v_{1} )_{zz} ) = 0 \\ & v_{2} = \mathop \smallint \limits_{0}^{t} (p\left( x \right)q\left( y \right)r\left( z \right) + ((\alpha (x)v_{1} )_{xx} + (\beta \left( y \right)v_{1} )_{yy} + \left( {\gamma \left( z \right)v_{1} )_{zz} } \right))dt \\ & p^{3} {:} (v_{3} )_{t} - p\left( x \right)q\left( y \right)r\left( z \right) - (\alpha \left( x \right)v_{2} )_{xx} - (\beta \left( y \right)v_{2} )_{yy} - (\gamma \left( z \right)v_{2} )_{zz} = 0 \\ & v_{3} = \mathop \smallint \limits_{0}^{t} (p\left( x \right)q\left( y \right)r\left( z \right) + ((\alpha (x)v_{2} )_{xx} + (\beta \left( y \right)v_{2} )_{yy} + \left( {\gamma \left( z \right)v_{2} )_{zz} } \right))dt \\ & . \\ & . \\ \end{aligned} $$

So we can calculate the terms of $\mathop \sum \nolimits_{k = 0}^{\infty } v_{k}$, term by term and the series solution thus entirely determined. However, in many cases the exact solution in a closed form may be obtained. For numerical purposes, we can use the approximation

$$ u\left( {x,y,z,t} \right) = \mathop {\lim }\limits_{m \to \infty } \emptyset_{m} $$

where

$$ \emptyset_{m} = \mathop \sum \limits_{k = 0}^{m - 1} v_{k} $$

(33)

It is worth to mention that the errors are getting smaller with the growing number of terms in the sum (33).

5 Numerical Examples

5.1 Example 1: One Dimensional Homogeneous Heat Equation

We consider the one-dimensional diffusion equation:

$$ \frac{\partial u}{\partial t} = \frac{{\partial^{2} u}}{{\partial x^{2} }},\quad 0 \le x \le 1,\;t > 0 $$

(34)

with the Initial condition:

$$ u(x,0) = { \sin }(\pi x) . $$

(35)

and the boundary conditions

$$ u\left( {0,t} \right) = 0,\quad u\left( {1,t} \right) = 0 $$

(36)

To solve (34) with initial condition (35), according to the homotopy perturbation technique, we construct the following homotopy:

$$ H\left( {v,p} \right) = \left( {1 - p} \right)(\left( {v_{0} } \right)_{t} - \left( {u_{0} )_{t} } \right) + p\left( {v_{t} - v_{xx} } \right) = 0 $$

(37)

Substituting of Eq. (16) into Eq. (37) and then equating the terms with like powers of $p$, we get the following

$$ \begin{aligned} & (v_{0} )_{t} - (u_{0} )_{t} = 0,\quad v_{0} = u\left( {x,0} \right) = { \sin }(\pi x) \\ & (v_{1} )_{t} - (v_{0} )_{xx} = 0,\quad v_{1} \left( {x,0} \right) = 0 \\ & (v_{1} )_{t} = - \pi^{2} { \sin }(\pi x) \\ & v_{1} = \mathop \smallint \limits_{0}^{t} ( - \pi^{2} \sin \left( {\pi x} \right)dt = - \pi^{2} \sin \left( {\pi x} \right) \times t \\ & (v_{2} )_{t} - (v_{1} )_{xx} = 0,\quad v_{2} \left( {x,0} \right) = 0 \\ & v_{2} = \mathop \smallint \limits_{0}^{t} \pi^{4} \sin \left( {\pi x} \right) \times tdt = \pi^{4} { \sin }(\pi x) \times \frac{{t^{2} }}{2!} \\ & (v_{3} )_{t} - (v_{2} )_{xx} = 0,\quad v_{3} \left( {x,0} \right) = 0 \\ & v_{3} = \mathop \smallint \limits_{0}^{t} - \pi^{6} \sin \left( {\pi x} \right) \times \frac{{t^{2} }}{2!}dt = - \pi^{6} { \sin }(\pi x) \times \frac{{t^{3} }}{3!} \\ & \vdots \\ & \\ \end{aligned} $$

(38)

and so on, we can calculate $v_{n}$ as follows:

$$ (v_{n} )_{t} - (v_{n - 1} )_{t} = 0,\quad v_{n} \left( {x,0} \right) = 0 $$

$$ v_{n} = \mathop \smallint \limits_{0}^{t} ( - 1)^{n} \pi^{2n} \sin \left( {\pi x} \right) \times \frac{{t^{n - 1} }}{{\left( {n - 1} \right)!}}dt = \left( { - 1} \right)^{n} \pi^{2n} sin(\pi x) \times \frac{{t^{n} }}{n!} $$

Finally, we obtain the approximate solution as follows:

$$ u = \mathop {\lim }\limits_{p \to 1} v = v_{0} + v_{1} + v_{2} + v_{3} + \cdots + v_{n} + \cdots $$

And this leads to the following solution

$$ u\left( {x,t} \right) = { \sin }(\pi x)e^{{ - \pi^{2} t}} $$

(39)

Substituting Eq. (39) into Eq. (34), we conclude that the approximate solution coincides with the exact one.

5.2 Example 2

Consider the diffusion problem:

$$ u_{t} = u_{xx} ,\;0 \le x \le 1,\quad t > 0 $$

(40)

subject to the Initial condition

$$ u\left( {x,0} \right) = { \cos }(\pi x) $$

(41)

and the boundary conditions:

$$ u_{x} \left( {0,t} \right) = 0,\quad u_{x} \left( {1,t} \right) = 0 $$

(42)

solving the Eq. (40) with the initial condition (41), yields:

$$ (v_{0} )_{t} - (u_{0} )_{t} = 0,\quad v_{0} = u_{0} = { \cos }(\pi x) $$

(43)

$$ \begin{aligned} & (v_{1} )_{t} - (v_{0} )_{xx} = 0,\quad v_{1} \left( {x,0} \right) = 0 \\ & v_{1} = - \pi^{2} \cos \left( {\pi x} \right) \times t \\ & (v_{2} )_{t} - (v_{1} )_{xx} = 0,\quad v_{2} \left( {x,0} \right) = 0 \\ & v_{2} = - \pi^{4} { \cos }(\pi x) \times t^{2} /2! \\ \end{aligned} $$

The next components $v_{k} ,\;k \ge 3$ are calculated as the following:

$$ \begin{aligned} & (v_{k} )_{t} - (v_{k} )_{xx} = 0,\quad v_{k} \left( {x,0} \right) = 0 \\ & v_{k} = ( - 1)^{k} \pi^{2k} { \cos }(\pi x) \times t^{k} /k! \\ \end{aligned} $$

(44)

Combining all the terms in the above gives

$$ u\left( {x,t} \right) = \cos \left( {\pi x} \right)(1 - \pi^{2} t/1! + \left( {\pi^{2} t} \right)^{2} /2! - (\pi^{2} t)^{3} /3! + \cdots) $$

The series solution is:

$$ u\left( {x,t} \right) = \text{e}^{{ - \pi^{2} t}} { \cos }(\pi x) $$

(45)

5.3 Example 3: One Dimensional Non Homogeneous Heat Equation

Consider the non homogeneous diffusion equation:

$$ u_{t} = u_{xx} + \left( {\pi^{2} - 1} \right)\text{e}^{ - t} \times \cos \left( {\pi x} \right) + 4x - 2 $$

(46)

with the initial condition

$$ u\left( {x,0} \right) = \cos \left( {\pi x} \right) + x^{2} $$

(47)

and the boundary conditions

$$ u\left( {0,t} \right) = \text{e}^{ - t} ,\quad u\left( {1,t} \right) = - \text{e}^{t} + 4t + 1 $$

(48)

according to HPM algorithm, we have

$$ H\left( {p,v} \right) = \left( {1 - p} \right)((v_{0} )_{t} - (u_{0} )_{t} ) + p\left( {v_{t} - v_{xx} - f} \right) = 0 $$

(49)

where $f = \left( {\pi^{2} - 1} \right) \text{e}^{ - t} + 4x - 2$

by equating the terms with the identical powers of $p$, yields

$$ \begin{aligned} & (v_{0} )_{t} - (u_{0} )_{t} = 0,\quad v_{0} = u_{0} = { \cos }(\pi x) + x^{2} \\ & (v_{1} )_{t} - (v_{0} )_{xx} - 4x + 2 - \left( {\pi^{2} - 1} \right) \text{e}^{ - t} = 0,\quad v_{1} \left( {x,0} \right) = 0 \\ & v_{1} = 4xt + \cos \left( {\pi x} \right)( - \pi^{2} t + \left( {\pi^{2} - 1} \right)\left( {1 - \text{e}^{ - t} } \right)) \\ & v_{2t} - v_{1xx} = 0,\quad v_{2t} = \cos \left( {\pi x} \right)(\pi^{4} t - \pi^{2} \left( {\pi^{2} - 1} \right)\left( {1 - \text{e}^{ - t} } \right)) \\ & v_{2} = \cos \left( {\pi x} \right)(\left( {\pi^{4} - \pi^{2} } \right)\left( {1 - t/1! - \text{e}^{ - t} } \right) + (\pi^{2} t)^{2} /2!)) \\ \end{aligned} $$

continuing like-wise we get:

$$ \begin{aligned} v_{3} & = \cos \left( {\pi x} \right)(( {\pi^{6} - \pi^{4} } )\left( {1 - t/1! + t^{2} /2! - \text{e}^{ - t} } \right) - ( {\pi^{2} t)^{3} /3!} )) \\ v_{4} & = \cos \left( {\pi x} \right)(( {\pi^{8} - \pi^{6} } )\left( {1 - t/1! + t^{2} /2! - t^{3} /3! - \text{e}^{ - t} } \right) + \left( {\pi^{2} t} \right)^{4} /4!) \\ \end{aligned} $$

and so on we then have

$$ u_{5hpm} = x^{2} + 4xt + \cos \left( {\pi x} \right)\left( {\pi^{8} \left( {1 - t/1! + t^{2} /2! - t^{3} /3! - \text{e}^{ - t} } \right) + \text{e}^{ - t} } \right) $$

(50)

From this result we deduce that the series solution converges to the exact one:

$$ u\left( {x,t} \right) = x^{2} + 4xt + { \cos }(\pi x) \text{e}^{ - t} $$

5.4 Example 4

Once again, consider the non-homogeneous heat equation with non-homogeneous Neumann boundary conditions:

$$ u_{t} = u_{xx} + (\pi^{2} /2) \text{e}^{{( - \pi^{2} /2)t}} \cos \left( {\pi x} \right) + x - 2,\quad 0 \le x, \le 1,t > 0 $$

(51)

$$ u_{x} \left( {0,t} \right) = t,\quad u_{x} \left( {1,t} \right) = 2 + t $$

and the initial condition

$$ u\left( {x,0} \right) = x^{2} + { \cos }(\pi x) $$

(52)

The theoretical solution is:

$$ u\left( {x,t} \right) = x^{2} + xt + e^{{( - \pi^{2} /2)t}} { \cos }(\pi x) $$

now, applying the homotopy perturbation method we get:

$$ \begin{aligned} & p^{0} {:}v_{0t} - u_{0t} = 0,\quad v_{0} = u_{0} = { \cos }(\pi x) + x^{2} \\ & p^{1} {:} v_{1t} - v_{0xx} - (\pi^{2} /2) \text{e}^{{( - \pi^{2} /2)t}} \cos \left( {\pi x} \right) - x + 2 = 0,\;v_{1} \left( {x,0} \right) = 0 \\ & v_{1} = xt + \cos \left( {\pi x} \right)(1 - \pi^{2} t - \text{e}^{{( - \pi^{2} /2)t}} ) \\ & p^{2} {:} v_{2t} - v_{1xx} = 0,\quad v_{2} \left( {x,0} \right) = 0 \\ & v_{2} = \cos \left( {\pi x} \right)(2 - \pi^{2} t + (\pi^{2} t)^{2} /2! - 2 \text{e}^{{( - \pi^{2} /2)t}} ) \\ & p^{3} {:} v_{3t} - v_{2xx} = 0,\quad v_{3} \left( {x,0} \right) = 0 \\ & v_{3} = \cos \left( {\pi x} \right)(4 - 2\pi^{2} t + (\pi^{2} t)^{2} /2! - (\pi^{2} t)^{3} /3! - 4 \text{e}^{{( - \pi^{2} /2)t}} ) \\ \end{aligned} $$

(53)

$$ \begin{aligned} & p^{4} :v_{4t} - v_{3t} = 0,\;v_{4} \left( {x,0} \right) = 0 \\ & v_{4} = \cos \left( {\pi x} \right)(8 - 4\left( {\pi^{2} t} \right) + (\pi^{2} t)^{2} - (\pi^{2} t)^{3} /3! + (\pi^{2} t)^{4} /4! - 8 \text{e}^{{( - \pi^{2} /2)t}} ) \\ \end{aligned} $$

Continuing in this way, we obtain

$$ u\left( {x,t} \right) = \mathop {\lim }\limits_{p \to 1} v = v_{0} + v_{1} + v_{2} + v_{3} + v_{4} + \cdots $$

or

$$ \begin{aligned} u\left( {x,t} \right) & = x^{2} + xt + \cos \left( {\pi x} \right){\text{e}}^{{( - \pi ^{2} /2)t}} \\ & \quad + 15\left[ {\left\{ {1 - (\pi ^{2} /2)t/1! + ((\pi ^{2} /2)\;t)^{2} /2! - ((\pi ^{2} /2)t)^{3} /3!} \right.} \right. \\ & \qquad \qquad +\left. {\left. { ((\pi ^{2} /2)t)^{4} /4! - . + \cdots )} \right\} - e^{{( - \pi ^{2} /2)t}} } \right] \\ \end{aligned}$$

and this leads to the following solution

$$ u\left( {x,t} \right) = x^{2} + xt + { \cos }(\pi x)e^{{( - \pi^{2} /2)t}} $$

(54)

this solution coincides with the exact one.

5.5 Example 5: One Dimensional Non Homogeneous Heat-Like Equation

Consider the problem

$$ u_{t} = x^{5} + 1/20(x^{2} u_{xx} ),\quad 0 < x < 1,\;0 < t \le $$

(55)

subject to the initial condition

$$ u\left( {x,0} \right) = 0 $$

(56)

and the boundary conditions

$$ \begin{aligned} u\left( {0,t} \right) & = \mathop \smallint \limits_{0}^{1} u\left( {x,t} \right)dx + g_{1} = 1/6(\text{e}^{t} - 1),\quad g_{1} = 0 \\ u\left( {1,t} \right) & = \mathop \smallint \limits_{0}^{1} u\left( {x,t} \right)dx + g_{2} = (1/6) \text{e}^{t} ,\quad g_{2} = 1/6 \\ \end{aligned} $$

(57)

After substitution of Eq. (18) into Eq. (55) and identifying the terms of the same powers of $p$, we obtain the system of equations:

$$ \begin{aligned} & p^{0} {:}v_{0t} - u_{0t} = 0,\quad v_{0} = u_{0} = 0 \\ & p^{1} {:}v_{1t} - (1/20)x^{2} v_{0xx} = 0,\quad v_{1} \left( {x,0} \right) = 0 \\ & v_{1} = x^{5} t \\ & p^{2} {:}v_{2t} - (1/20)x^{2} v_{1t} = 0,\quad v_{2} \left( {x,0} \right) = 0 \\ & v_{2} = x^{5} t^{2} /2! \\ & p^{3} {:}v_{3t} - (1/20)x^{2} v_{2t} = 0,\quad v_{3} \left( {x,0} \right) = 0 \\ & v_{3} = x^{5} t^{3} /3! \\ & \vdots \\ & \\ & p^{n} {:}v_{nt} - (1/20)x^{2} v_{{\left( {n - 1} \right)t}} = 0,\quad v_{n} \left( {x,0} \right) = 0 \\ & v_{n} = x^{5} t^{n} /n! \\ \end{aligned} $$

Hence the series solution is given by:

$$ u\left( {x,t} \right) = v_{0} + v_{1} + v_{2} + v_{3} + \cdots + v_{n} + \cdots $$

or

$$ u\left( {x,t} \right) = x^{5} \left( {1 + t/1! + t^{2} /2! + t^{3} /3! + \cdots + t^{n} /n! + \cdots } \right) - x^{5} $$

and in a closed form:

$$ u\left( {x,t} \right) = x^{5} (\text{e}^{t} - 1) $$

(58)

5.6 Example 6: Three Dimensional Non Homogeneous Heat-Like Equation

Let us consider the problem

$$ u_{t} = x^{5} y^{5} z^{5} + (1/60)(x^{2} u_{xx} + y^{2} u_{yy} + z^{2} u_{zz} ),\quad 0 < x,y,z < 1,0 < t \le T $$

(59)

with the following initial condition:

$$ u\left( {x,y,z,0} \right) = 0 $$

(60)

and the boundary conditions

$$ \begin{aligned} u\left( {0,y,z,t} \right) & = \mathop \smallint \limits_{0}^{1} \mathop \smallint \limits_{0}^{1} \mathop \smallint \limits_{0}^{1} u\left( {x,y,z,t} \right)dxdydz + g_{1} = 1/216\left( {\text{e}^{t} - 1} \right),\quad g_{1} = 0 \\ u\left( {1,y,z,t} \right) & = \mathop \smallint \limits_{0}^{1} \mathop \smallint \limits_{0}^{1} \mathop \smallint \limits_{0}^{1} u\left( {x,y,z,t} \right)dxdydz + g_{2} = 1/216(\text{e}^{t} - 1) + (1/2)t,\quad g_{2} = (1/2)t \\ u\left( {x,0,z,t} \right) & = \mathop \smallint \limits_{0}^{1} \mathop \smallint \limits_{0}^{1} \mathop \smallint \limits_{0}^{1} u\left( {x,y,z,t} \right)dxdydz + g_{3} = 1/216\left( {\text{e}^{t} } \right),\quad g_{3} = 1/216 \\ u\left( {x,1,z,t} \right) & = \mathop \smallint \limits_{0}^{1} \mathop \smallint \limits_{0}^{1} \mathop \smallint \limits_{0}^{1} u\left( {x,y,z,t} \right)dxdydz + g_{4} = (1/216)(\text{e}^{t} + 3),\quad g_{4} = (4/216) \\ \end{aligned} $$

(61)

$$ \begin{aligned} u\left( {x,y,0,t} \right) & = \mathop \smallint \limits_{0}^{1} \mathop \smallint \limits_{0}^{1} \mathop \smallint \limits_{0}^{1} u\left( {x,y,z,t} \right)dxdydz + g_{5} = (1/216)(\text{e}^{t} + 4),\quad g_{5} = 5/216 \\ u\left( {x,y,1,t} \right) & = \mathop \smallint \limits_{0}^{1} \mathop \smallint \limits_{0}^{1} \mathop \smallint \limits_{0}^{1} u\left( {x,y,z,t} \right)dxdydz + g_{6} = 1/216(\text{e}^{t} + 1),\quad g_{6} = 1/108 \\ \end{aligned} $$

According to Eqs. (18) and (59) the following terms are calculated successively:

$$ \begin{aligned} & p^{0} {:} v_{0t} - u_{0t} = 0,\quad v_{0} = u_{0} = 0 \\ & p^{1} {:} v_{1t} - x^{5} y^{5} z^{5} - (1/60)(x^{2} v_{0xx} + y^{2} v_{0yy} + z^{2} v_{0zz} ) = 0,\quad v_{1} \left( {x,y,z,0} \right) = 0 \\ & v_{1} = x^{5} y^{5} z^{5} (t/1!) \\ & p^{2} {:} v_{2t} - (1/60)(x^{2} v_{1xx} + y^{2} v_{1yy} + z^{2} v_{1zz} ) = 0,\quad v_{2} \left( {x,y,z,0} \right) = 0 \\ & v_{2} = x^{5} y^{5} z^{5} (t^{2} /2!) \\ & \vdots \\ & p^{n} {:} v_{nt} - (1/60)(x^{2} v_{{\left( {n - 1} \right)xx}} + y^{2} v_{{\left( {n - 1} \right)yy}} + z^{2} v_{{\left( {n - 1} \right)zz}} ) = 0 \\ & v_{n} = x^{5} y^{5} z^{5} (t^{n} /n!) \\ \end{aligned} $$

(62)

Hence, the approximate solution is given by:

$$ u\left( {x,y,z,t} \right) = v_{0} + v_{1} + v_{2} + \cdots +v_{n} + \cdots $$

Or

$$ u\left( {x,y,z,t} \right) = x^{5} y^{5} z^{5} (1 + t/1! + (t^{2} /2!) + \cdots (t^{n} /n!) + \cdots ) - x^{5} y^{5} z^{5} $$

The solution in the closed form is given as

$$ u\left( {x,y,z,t} \right) = x^{5} y^{5} z^{5} (\text{e}^{t} - 1) $$

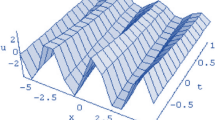
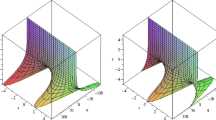
This result is in good agreement with the exact one (Tables 1, 2 and 3).

Table 1 Example 1 $h_{x} = 0.1,\;h_{t} = 0.004$, 3-iterates

Table 2 Example 2 $h_{x} = 0.1,\;h_{t} = 0.004$, 3-Iterates

Table 3 Example 3 $h_{x} = 0.1,\;h_{t} = 0.004$, 2-Iterates

6 Conclusion

The main concern of this work has been to construct an approximate solution to heat and heat-like equations with different types of boundary conditions using homotopy perturbation method (HPM). Our approach differs from existing traditional methods like, finite differences, finite elements, spectral method, … etc., in that we find the solution in a closed form without, linearization, discretization, transformation or restrictive assumptions. The problems solved using (HPM) gave satisfactory results in comparison to those recently obtained other researchers (Figs. 1, 2 and 3).

Fig. 1

Example 1 Variation of the approximate solution for different values of $x$ and $t$

Fig. 2

Example 2 Variation of the approximate solution for different values of $x$ and $t$

Fig. 3

Example 3 Variation of the approximate solution for different values of $x$, $y$ and $z$ when $t=0.004$