Bondonic Chemistry: Non-classical Implications on Classical Carbon Systems

Abstract

The present chapter illustrates our pursuits to correlate the structure and the reactivity of some aliphatic and aromatic compounds making use of quantum-mechanic calculations, while emphasizing the peculiar properties of bondonic influence in driving the chemical bonding in various realizations and respecting various chemical variables. The studied compounds, aromatic amines and their derivates and also hydroxiarens, have been chosen to reveal their usage in diazotization and coupling reactions in order to obtain azoic colorants. For didactic purposes, the results obtained by both Hückel (MO-molecular orbitals) and DFT(density functional theory) models have been correlated considering some aspects of bondonic chemistry. From the bondonic side, the quantum computational information, always relating regarding the bonding energy is projected on the length radii or action, bondonic mass and gravitational effects, all without eigen-equations in “classical” quantum mechanics, although being of observable nature, here discussed and compared for their realization and predictions.

11.1 Introduction

This chapter is addressed in many parts to college and undergraduate studies teachers as well as to freshman chemistry (i.e. students from the first university cycle). It aims at enhancing the perception and comprehension of aliphatic and aromatic concepts (Truhlar 2007; Rzepa 2007) and in relation with advanced/exotic characterization of chemical bonding by the associated quantum quasi-particle called bondon.

The chapter unfolds the correlation of some accessible quantum mechanics results with the physicochemical properties of different compounds. Some of the compounds are used to obtain azoic colorants. Other studied compounds are molecules contributing to the formation of the skeleton of some natural products of vital importance (Avram 1994, Chap. 19, 1995, Chaps. 223132).

From the structural point of view, the ${}\pi{}-{}\pi{}$, ${}\sigma{}-{}\pi{}$, and $\text{n}-{}\pi{}$ electronic interactions are the basis when interpreting the chemical reactivity of hydrocarbons, nitrogen heterocycles and organic functions. The behavior of aromatic hydrocarbons is compared with that of nitrogen heterocycles. Mono- and polyhydroxy arens are analyzed within the class of hydroxo compounds. The character of some aromatic amines as substrates is put into evidence in diazotization and coupling reactions. The thermal and photochemical stability of aromatic diazonium salts , both as diazotization products and electrophilic reactants, certainly dictate their stability.

The aromaticity characterization of the investigated organic structures is undertaken in order to compare their chemical reactivity . In order to do so, common and recent aromaticity indicators are employed against compounds chemical hardness, computed by the modern density functional theory and the classical Hückel one. On the one hand, the values of the energetic indices calculated by the two methods are in good agreement with other data presented in the literature and with the experimental behavior of the studied compounds. On the other hand, the chemical hardness scale determined by Hückel method is in accordance either with the potential contour maps for the sites susceptible for electrophilic attack or with the computed global values or chemical hardness calculated by DFT method. However, all these “classical cases” of carbon systems will be systematically enriched by the bondonic effects at the level of action length in molecule, i.e. predicting on the localization/delocalization degree the chemical bond is spreading over the molecule and surrounding it encountering the reactivity, along the associated mass and gravitational effects that makes the structure stable or prepared to be engaged in further chemical reactions.

11.2 Chemical Bonding by Nonrelativistic Bondons (Putz 2010a)

The general physical origins of bondons and of quantum information implication were extensively exposed in the previous chapter (Putz and Ori 2015) as based on quantum chemical field built within the Dirac-Bohm theory of electronic existence in chemical bonding . In what follows we actually redo the bondonic analytical discovering by following the classical quantum mechanical way, i.e. as based on Schrodinger formalism combined with the Bohmian characterization of non-locality (for accounting for entangled effects of bondons in chemical bonding).

The starting point resides in considering the de Broglie-Bohm electronic wavefunction (de Broglie and Vigier 1953; Bohm and Vigier 1954),

$$ {{\Psi }_{BB}}(x,t)=R(x,t)\,\exp \left(i\frac{S(x,t)}{\hbar } \right) $$

(11.1)

with the R-amplitude and S-phase factors given respectively as:

$$ R(x,t)=\sqrt{\Psi {{(x,t)}^{2}}}={{\rho }^{1/2}}(x) $$

(11.2a)

$$ S(x,t)=px-Et={{S}_{0}}-Et $$

(11.2b)

in terms of electronic density $\rho$, momentum p, total energy E, and space-time (x,t) coordinates, without spin.

In these conditions, since one perfumes the wavefunction partial derivatives respecting space and time,

$$ \frac{{{\partial }^{2}}{{\Psi }_{BB}}}{\partial {{x}^{2}}}=\left[\frac{{{\partial }^{2}}R}{\partial {{x}^{2}}}+2\frac{i}{\hbar }\frac{\partial R}{\partial x}\frac{\partial S}{\partial x}+\frac{i}{\hbar }R\frac{{{\partial }^{2}}S}{\partial {{x}^{2}}}-\frac{R}{{{\hbar }^{2}}}{{\left(\frac{\partial S}{\partial x} \right)}^{2}}\right]\exp \left(\frac{i}{\hbar }S \right) $$

(11.3a)

$$ \frac{\partial {{\Psi }_{BB}}}{\partial t}=\left[\frac{\partial R}{\partial t}+\frac{i}{\hbar }R\frac{\partial S}{\partial t} \right]\exp \left(\frac{i}{\hbar }S \right) $$

(11.3b)

the conventional Schrödinger equation (Schrodinger 1926)

$$ i\hbar \frac{\partial {{\Psi }_{BB}}}{\partial t}=-\frac{{{\hbar }^{2}}}{2m}\frac{{{\partial }^{2}}{{\Psi }_{BB}}}{\partial {{x}^{2}}}+V{{\Psi }_{BB}}$$

(11.4)

takes the real and imaginary forms:

$$ \frac{\partial R}{\partial t}=-\frac{1}{2m}\left[2\frac{\partial R}{\partial x}\frac{\partial S}{\partial x}+R\frac{{{\partial }^{2}}S}{\partial {{x}^{2}}}\right] $$

(11.5a)

$$ -R\frac{\partial S}{\partial t}=-\frac{{{\hbar }^{2}}}{2m}\frac{{{\partial }^{2}}R}{\partial {{x}^{2}}}+\frac{R}{2m}{{\left(\frac{\partial S}{\partial x} \right)}^{2}}+VR $$

(11.5b)

that can be further arranged as:

$$ \frac{\partial {{R}^{2}}}{\partial t}+\frac{\partial }{\partial x}\left[\frac{{{R}^{2}}}{m}\frac{\partial S}{\partial x} \right]=0 $$

(11.6a)

$$ \frac{\partial S}{\partial t}-\frac{{{\hbar }^{2}}}{2m}\frac{1}{R}\frac{{{\partial }^{2}}R}{\partial {{x}^{2}}}+\frac{1}{2m}{{\left(\frac{\partial S}{\partial x} \right)}^{2}}+V=0 $$

(11.6b)

Worth noting that the first Eq. (11.6a) recovers in 3D coordinates the charge current (j) conservation law,

$$ \frac{\partial \rho }{\partial t}+\nabla \text{j}=0,~\text{j}=({{R}^{2}}/m)\overrightarrow{\nabla S} $$

(11.7a)

while the second Eq. (11.6b) in 3D,

$$ \frac{\partial S}{\partial t}-\frac{{{\hbar }^{2}}}{2m}\frac{{{\nabla }^{2}}R}{R}+\frac{1}{2m}{{(\nabla S )}^{2}}+V=0 $$

(11.7b)

extends the basic Schrödinger Eq. (11.4) to include further quantum complexity. It may be clearly seen since recognizing that:

$$ {{(\nabla S )}^{2}}={{p}^{2}}\Rightarrow \frac{1}{2m}{{(\nabla S )}^{2}}=\frac{{{p}^{2}}}{2m}=T;~\frac{\partial S}{\partial t}=-E $$

(11.8)

one gets from (11.7b) the total energy expression:

$$ E=T+V+{{V}_{qua}}$$

(11.9a)

in terms of newly appeared so called quantum (or Bohm) potential

$$ {{V}_{qua}}=-\frac{{{\hbar }^{2}}}{2m}\frac{{{\nabla }^{2}}R}{R} $$

(11.9b)

Exploring the consequences of the existence of the Bohm potential (11.9b) reveals most interesting features of the fundamental nature of electronic quantum behavior. We will survey some of them in what follows.

Since the chemical bonding is carried by electrons only, one can see the basic de Broglie-Bohmwavefunction (11.1) as belonging to gauge U(1) group transformation:

$$ \begin{aligned}& {{\Psi }_{U(1)}}(x,t)={{\Psi }_{BB}}(x,t)\exp \left(\frac{i}{\hbar }\frac{e}{c}\aleph (x,t) \right) \\& =R(x,t)\,\exp \left[\frac{i}{\hbar }\left(S(x,t)+\frac{e}{c}\aleph (x,t) \right) \right],\ e=\frac{e_{0}^{2}}{4\pi {{\varepsilon }_{0}}}\end{aligned} $$

(11.10)

where the chemical field ℵ should account through of variational principle (Schrödinger equation here) by the electronic bond, eventually being quantified by associate corpuscle.

As such, one employs the gauge wavefunction (11.10) to compute the actual Schrödinger partial derivative terms as:

$$ \frac{\partial {{\Psi }_{U(1)}}}{\partial x}=\left[\frac{\partial R}{\partial x}+\frac{i}{\hbar }R\left(\frac{\partial S}{\partial x}+\frac{e}{c}\frac{\partial \aleph }{\partial x} \right) \right]\exp \left[\frac{i}{\hbar }\left(S+\frac{e}{c}\aleph\right) \right] $$

(11.11a)

$$ \begin{aligned}& \frac{{{\partial }^{2}}{{\Psi }_{U(1)}}}{\partial {{x}^{2}}}\\& =\left\{\begin{aligned}& \frac{{{\partial }^{2}}R}{\partial {{x}^{2}}}+2\frac{i}{\hbar }\frac{\partial R}{\partial x}\left(\frac{\partial S}{\partial x}+\frac{e}{c}\frac{\partial \aleph }{\partial x} \right)+\frac{i}{\hbar }R\left(\frac{{{\partial }^{2}}S}{\partial {{x}^{2}}}+\frac{e}{c}\frac{{{\partial }^{2}}\aleph }{\partial {{x}^{2}}}\right) \\& -\frac{R}{{{\hbar }^{2}}}\left[{{\left(\frac{\partial S}{\partial x} \right)}^{2}}+{{\left(\frac{e}{c}\frac{\partial \aleph }{\partial x} \right)}^{2}}\right]-2\frac{e}{{{\hbar }^{2}}c}R\frac{\partial S}{\partial x}\frac{\partial \aleph }{\partial x} \end{aligned} \right\} \\& \times \exp \left[\frac{i}{\hbar }\left(S+\frac{e}{c}\aleph\right) \right] \end{aligned} $$

(11.11b)

$$ \frac{\partial {{\Psi }_{U(1)}}}{\partial t}=\left[\frac{\partial R}{\partial t}+\frac{i}{\hbar }R\left(\frac{\partial S}{\partial t}+\frac{e}{c}\frac{\partial \aleph }{\partial t} \right) \right]\exp \left[\frac{i}{\hbar }\left(S+\frac{e}{c}\aleph\right) \right] $$

(11.11c)

leading with the decomposition of the corresponding Schrödinger U(1) equation on the imaginary and real parts respectively:

$$ -\frac{\partial R}{\partial t}=\frac{1}{m}\left(\frac{\partial R}{\partial x}\frac{\partial S}{\partial x}+\frac{R}{2}\frac{{{\partial }^{2}}S}{\partial {{x}^{2}}}\right)+\frac{e}{mc}\left(\frac{\partial R}{\partial x}\frac{\partial \aleph }{\partial x}+\frac{R}{2}\frac{{{\partial }^{2}}\aleph }{\partial {{x}^{2}}}\right) $$

(11.12a)

$$ \begin{aligned}& -R\frac{\partial S}{\partial t}-R\frac{e}{c}\frac{\partial \aleph }{\partial t} \\& =-\frac{{{\hbar }^{2}}}{2m}\frac{{{\partial }^{2}}R}{\partial {{x}^{2}}}+\frac{R}{2m}\left[{{\left(\frac{\partial S}{\partial x} \right)}^{2}}+{{\left(\frac{e}{c}\frac{\partial \aleph }{\partial x} \right)}^{2}}\right]+\frac{e}{mc}R\frac{\partial S}{\partial x}\frac{\partial \aleph }{\partial x}+VR \end{aligned} $$

(11.12b)

that can be further rearranged as:

$$ -\frac{\partial {{R}^{2}}}{\partial t}=\frac{1}{m}\frac{\partial }{\partial x}\left({{R}^{2}}\frac{\partial S}{\partial x} \right)+\frac{e}{mc}\frac{\partial }{\partial x}\left({{R}^{2}}\frac{\partial \aleph }{\partial x} \right) $$

(11.13a)

$$ \begin{aligned}& -\left(\frac{\partial S}{\partial t}+\frac{e}{c}\frac{\partial \aleph }{\partial t} \right) \\& =-\frac{{{\hbar }^{2}}}{2m}\frac{1}{R}\frac{{{\partial }^{2}}R}{\partial {{x}^{2}}}+\frac{1}{2m}\left[{{\left(\frac{\partial S}{\partial x} \right)}^{2}}+{{\left(\frac{e}{c}\frac{\partial \aleph }{\partial x} \right)}^{2}}\right]+\frac{e}{mc}\frac{\partial S}{\partial x}\frac{\partial \aleph }{\partial x}+V \end{aligned} $$

(11.13b)

Equations (11.13) reveal some interesting features of the chemical bonding to be in next discussed.

The Eq. (11.13a) provides the conserving charge current with the form:

$$ {{\text{j}}_{\text{U(1)}}}=\frac{{{R}^{2}}}{m}\left(\overrightarrow{\nabla S}+\frac{e}{c}\overrightarrow{\nabla \aleph } \right)={{\text{j}}_{\text{S}}}+{{\text{j}}_{\aleph }}$$

(11.14)

leaving with idea that additional current is responsible for the chemical field to be activated, namely:

$$ {{\text{j}}_{\aleph }}=\frac{e}{mc}{{R}^{2}}\overrightarrow{\nabla \aleph } $$

(11.15)

which vanishes when the global gauge condition is considered, i.e. when

$$ \frac{\partial \aleph }{\partial x}=0 $$

(11.16)

Therefore, in order the chemical bonding be created the local gauge transformation should be used that is

$$ \frac{\partial \aleph }{\partial x}\ne 0 $$

(11.17)

In these conditions, the chemical field current (11.15) carries specific bonding particles that can be appropriately called as bondons, closely related with electrons, in fact with the those electrons involved in bonding, either as single, lone pair or delocalized, and having an oriented direction of moving, with an action depending on chemical field itself ℵ.

Nevertheless, another important idea abstracted from above discussion is that going to search the chemical field ℵ no global gauge condition as (11.16) should be used. Worth noting as well that the presence of the chemical field do not change the Bohm quantum potential (11.9b) which is recovered untouched in (11.13b) thus preserving the entanglement of interaction. With his there follows that in order the de Broglie-Bohm-Schrödinger formalism and Eq. (11.6) to be invariant under gauge U(1) transformation (11.10) a couple of gauge conditions the chemical field has to fulfilled out of Eq. (11.13); they are respectively:

$$ \frac{e}{mc}\frac{\partial }{\partial x}\left({{R}^{2}}\frac{\partial \aleph }{\partial x} \right)=0 $$

(11.18a)

$$ \frac{e}{c}\frac{\partial \aleph }{\partial t}+\frac{1}{2m}{{\left(\frac{e}{c}\frac{\partial \aleph }{\partial x} \right)}^{2}}+\frac{e}{mc}\frac{\partial S}{\partial x}\frac{\partial \aleph }{\partial x}=0 $$

(11.18b)

Now, the chemical field ℵ is found through combining its spatial-temporal information contained in Eq. (11.18). From condition (11.18a) is getting that:

$$ \overrightarrow{\nabla \aleph }=-R\frac{{{\nabla }^{2}}\aleph }{\overrightarrow{\nabla R}\cdot \overrightarrow{j}}\overrightarrow{j} $$

(11.19)

where the vectorial feature of the chemical field gradient was emphasized on the direction of its associated charge current (11.15) fixed by the versor $\overrightarrow{\text{j}}=({{\text{j}}^{\text{2}}}\text{=1)}$. We will maintain such procedure whenever necessary for avoiding scalar to vector ratios and preserving the physical sense of the whole construction as well.

Next, the gradient (11.19) is replaced in (11.18b) to obtain a single equation for the chemical field:

$$ \frac{e}{2mc}\frac{{{R}^{2}}}{{{(\nabla R )}^{2}}}{{({{\nabla }^{2}}\aleph)}^{2}}-\frac{R}{m}\frac{\overrightarrow{\nabla S}\cdot \overrightarrow{\nabla S}}{\overrightarrow{\nabla R}\cdot \overrightarrow{\nabla S}}({{\nabla }^{2}}\aleph)+\frac{\partial \aleph }{\partial t}=0 $$

(11.20)

that can be further rewritten as

$$ 2\frac{e}{mc}\frac{{{\rho }^{2}}}{{{(\nabla \rho)}^{2}}}{{({{\nabla }^{2}}\aleph)}^{2}}-2\frac{\rho \overrightarrow{v}\cdot \overrightarrow{j}}{\overrightarrow{\nabla \rho }\cdot \overrightarrow{j}}({{\nabla }^{2}}\aleph)+\frac{\partial \aleph }{\partial t}=0 $$

(11.21)

since calling the relations:

$$ R={{\rho }^{1/2}};\,\overrightarrow{\nabla S}=\overrightarrow{p}\Rightarrow \left\{\begin{aligned}& \nabla R=\frac{1}{2}\frac{\nabla \rho }{{{\rho }^{1/2}}};~~{{(\nabla R )}^{2}}=\frac{1}{4}\frac{{{(\nabla \rho)}^{2}}}{\rho }\, \\& \frac{\overrightarrow{\nabla S}\cdot \overrightarrow{\nabla S}}{\overrightarrow{\nabla R}\cdot \overrightarrow{\nabla S}}=\frac{2{{\rho }^{1/2}}\overrightarrow{p}\cdot \overrightarrow{j}}{\overrightarrow{\nabla \rho }\cdot \overrightarrow{j}}\end{aligned} \right. $$

(11.22)

Equation (11.21) can be solved for the Laplacian of the chemical field with general solutions:

$$ {{({{\nabla }^{2}}\aleph)}_{1,2}}=\frac{2\frac{\rho \overrightarrow{v}\cdot \overrightarrow{j}}{\overrightarrow{\nabla \rho }\cdot \overrightarrow{j}}\pm \sqrt{\frac{4{{\rho }^{2}}{{v}^{2}}}{{{(\nabla \rho)}^{2}}}-4\frac{2e}{mc}\frac{{{\rho }^{2}}}{{{(\nabla \rho)}^{2}}}\frac{\partial \aleph }{\partial t}}}{\frac{4e}{mc}\frac{{{\rho }^{2}}}{{{(\nabla \rho)}^{2}}}}$$

(11.23)

Equation (11.23), is a special propagation equation for the chemical field since it links the spatial Laplacian ${{\nabla }^{2}}\aleph =\Delta \aleph$ with temporal evolution of the chemical field ${{(\partial \aleph /\partial t )}^{1/2}}$; however, it may be considerable be simplified if assuming the stationary chemical field, i.e. chemical field as not explicitly depend on time,

$$ \frac{\partial \aleph }{\partial t}=0 $$

(11.24)

in agreement with the fact that once established the chemical bonding should be manifested stationary in order to preserve the stability of the structure it applies.

With condition (11.24) we may still have two solutions for the chemical field.

One corresponds with the homogeneous chemical bonding field

$$ \Delta \aleph =0\Rightarrow {{\aleph }_{h}}=\frac{mc}{e}{{v}_{\overrightarrow{j}}}\,{{X}_{bond}}$$

(11.25)

with the constant determined such that the field (11.25) to be of the same nature as the Bohm phase action S in (11.10).

The second solution of (11.23) looks like

$$ \Delta \aleph =\frac{mc}{e}\frac{v\cdot \nabla \rho }{\rho } $$

(11.26)

Finally, Eq. (11.26) may be integrated to primarily give:

$$ \overrightarrow{\nabla \aleph }=\frac{mc}{e}\overrightarrow{v}~\int{}_{\infty }^{r}{\frac{\overrightarrow{\nabla \rho }\cdot \overrightarrow{j}}{\rho }dx}=\frac{mc}{e}\overrightarrow{v}~\left[\int{}_{\infty }^{0}{\frac{\overrightarrow{\nabla \rho }\cdot \overrightarrow{j}}{\rho }dx}+\int{}_{0}^{r}{\frac{\overrightarrow{\nabla \rho }\cdot \overrightarrow{j}}{\rho }dx} \right] $$

(11.27)

that can be projected on bondonic current direction $\overrightarrow{j}$ and then further integrated as:

$$ \aleph -{{\aleph }_{0}}=\frac{mc}{e}{{v}_{\overrightarrow{j}}}{{X}_{bond}}\left(\int{}_{\infty }^{0}{\frac{\overrightarrow{\nabla \rho }\cdot \overrightarrow{j}}{\rho }dl} \right)+\frac{mc}{e}{{v}_{\overrightarrow{j}}}\int{}_{0}^{x(t)}{\left(\int{}_{0}^{r}{\frac{\overrightarrow{\nabla \rho }\cdot \overrightarrow{j}}{\rho }dl} \right)dr}\, $$

(11.28)

from where there is identified both the so called manifested chemical bond field:

$$ {{\aleph }_{0}}=\frac{mc}{e}{{v}_{\overrightarrow{j}}}{{X}_{bond}}\left(\int{}_{0}^{\infty }{\frac{\overrightarrow{\nabla \rho }\cdot \overrightarrow{j}}{\rho }dl} \right) $$

(11.29a)

for a given inter-nuclear distance X _bond , as well as the delocalized chemical bond field:

$$ \aleph (x(t))=\frac{mc}{e}{{v}_{\overrightarrow{j}}}\int{}_{0}^{x(t)}{\int{}_{0}^{r}{\frac{\overrightarrow{\nabla \rho }\cdot \overrightarrow{j}}{\rho }drdl}}\, $$

(11.29b)

which is the most general stationary chemical bonding field without spin.

Worth commenting on the integrand of above chemical bonding fields, since it accounts for the entangled distance concerned; as such, the expression (11.29b) converges to (11.29a) when $x(t)\to \infty$ and $r\to {{X}_{bond}}$ meaning that the X _bond is (locally) manifested in the infinite bath of nonlocal (entangled) interactions. Relation (11.25) may be as well recovered from (11.29b) when the density gradient becomes $\nabla \rho \to \rho /{{X}_{bond}}$ and $x(t)\to r\to {{X}_{bond}}$ revealing that the electronic system is completely isolated and with a uniform charge distribution along bonding (no no-local interactions admitted).

Another interesting point regards the general density gradient dependency of the chemical field (11.29b), a feature that finely resembles two important results of quantum chemistry:

• The gradient expansion when chemical structure and bonding is described in the context of density functional theory (Bader 1990, 1994, 1998a, b, Bader and Austin 1997);

• The Bader zero flux condition for defining the basins of bonding (Parr andYang 1989; Putz 2003) that in the present case is represented by the zero chemical boning fields, viz.:

$$ \aleph =0\Leftrightarrow \overrightarrow{\nabla \rho }\cdot \overrightarrow{j}=0 $$

(11.30)

It is this last feature the decisive reason that the aleph function in gauge transformation (11.10) is correctly associated with chemical bonding!

Last issue addresses the range values of the chemical bonding field as well as its physical meaning. For the typical values enough observing that from the gauge U(1) transformation (11.10) that the chemical bonding field has to be in relation with the inverse order of the fine-structure constant:

$$ {{\aleph }_{bondon}}\tilde{\ }\frac{\hbar c}{e}\tilde{\ }137.03599976\frac{Joule\times meter}{Coulomb} $$

(11.31)

an enough small quantity, in quantum range, to be apparently neglected, however with crucial role for chemical bonding where the energies involved are about orders of 10⁻¹⁹ J (electron-volts)! Nevertheless, for establishing the physical significance of the chemical bonding quanta field (11.31) one can proceed with the chain equivalences:

$$ \left\langle \aleph\right\rangle \tilde{\ }\begin{matrix} (\begin{aligned}& \text{potential} \\& \text{difference} \end{aligned} ) & \begin{matrix} \times& \text{distance}\end{matrix}\end{matrix} $$

(11.32)

The combined phenomenology of the results (11.31) and (11.32) states that: the chemical bonding field caries bondons with unit quanta (11.31) along the distance of bonding within the potential gap of stability or by tunneling the potential barrier of encountered bonding attractors.

Alternatively, from the generic form (11.25) for the chemical field, if one replaces the velocity by the kinetic energy and making then use by Heisenberg relationship, viz.

$$ v=\sqrt{\frac{2T}{m}}\tilde{\ }\sqrt{\frac{2}{m}\frac{\hbar }{t}}$$

(11.33a)

the space-chemical bonding field dependence is simply achieved as:

$$ \aleph \tilde{\ }\left(\frac{c\hbar }{e}\sqrt{\frac{2m}{\hbar t}}\, \right){{X}_{bond}}\tilde{\ }4.28715\cdot {{10}^{13}}{{X}_{bond}}$$

(11.33b)

where we can assume various instantaneous times according with the studied phenomena. At one extreme, when the ration of the first Bohr radius (${{a}_{0}}=0.52917\cdot {{10}^{-10}}\,m$) to the speed velocity is assumed, ${\text{t}} \to {{\text{t}}_{\text{0}}}{\text{ = }}{{\text{a}}_{\text{0}}}{\text{/c = 1}}{\text{.76512}} \cdot {\text{1}}{{\text{0}}^{ - {\text{19}}}}{\text{ < seconds> }}$, the two numerical relations for the chemical bonding field, namely (11.31) and (11.33b), are equated to give the typical lengths of the entanglement bond ${{\text{X}}_{{\text{bond}}}} \in \left( {{\text{0,}}\,\,{\text{3}}{\text{.19643}} \cdot {\text{1}}{{\text{0}}^{ - {\text{12}}}}} \right){\text{ < meters> }}$ with an observable character in the fine-structure phenomena ranges. On the other side, on a chemically femto-second scale, i.e. ${{\text{t}}_{\text{bonding}}}{}\tilde{\ }\text{1}{{\text{0}}^{-\text{12}}}\,\text{s}$, one finds ${{\text{X}}_{\text{bond}}}{}\tilde{\ }\text{1}{{\text{0}}^{-\text{8}}}\,\text{m}$ thus widely recovering the custom length of the chemical bonding phenomena at large distance. Further studies may be envisaged from this point concerning the chemical reactivity, times of reactions, i.e. of tunneling the potential barrier between reactants, at whatever chemical scale.

Lastly but not at last, the relations (11.31) and (11.33) may be further used in determining the mass of bondons carried by the chemical field on a given distance:

$$ {{m}_{bondons}}=\frac{\hbar t}{2}\frac{1}{X_{bond}^{2}}$$

(11.34)

For instance, considering the above typical chemical bond length, ${{\text{t}}_{\text{bonding}}}{}\tilde{\ }\text{1}{{\text{0}}^{-\text{12}}}\,\text{s}$ and ${{\text{X}}_{\text{bond}}}{}\tilde{\ }\text{1}{{\text{0}}^{-\text{8}}}\,\text{m}$, one gets the bondon mass about ${{\text{m}}_{\text{bondons}}}{}\tilde{\ }\text{5}\text{.27286}\cdot \text{1}{{\text{0}}^{-\text{31}}}\,\text{kg}$, of electronic mass order, of course, but not necessary the same since in the course of reaction, due to the inner undulatory nature of electron and of the wave-function based phenomena of bonding, the electronic specific mass may decrease. Note that the bondon mass decreases faster by broader the bond distance than the time providing a typical quantum effect without a macroscopic rationalization. In fact as increases the entangled distance to be covered by the chemical interaction not only the time is larger but also the quantum mass carried by the field decreases in order the phenomena be unitary, non-separated, and observable! Most remarkably, the higher limit of bondonic mass correctly stands the electronic mass ${{\text{m}}_{\text{0}}}{}\tilde{\ }\text{9}\text{.1094}\cdot \text{1}{{\text{0}}^{-\text{31}}}\,\text{kg}$ as easily verified when the first Bohr radius and associated time are replaced in (11.34) formula.

In this context, the bondons ${\text{(\rlap{--} B)}}$ represents (Putz 2010a, b, 2012) the bosonic counterpart of the bonding electrons’ wave function carrying the quantized mass related with the bonding length and the energy, with Eq. (11.34) rewritten in the ground state as:

$${m_{\rlap{--} B}} = \frac{{{\hbar ^2}}}{{2{E_{bond}}X_{bond}^2}}$$

(11.35)

At this point one may further inquire on the elementary time-space-gravitation consequences of having the energy-mass form of Eq. (11.35). To unfold this route in a “Fermi calculation” way one may, mutatis-mutandis, considering the macro-micro unification of particle nature, in the same way the early Planck universe is characterized (Putz 2014). Actually, one employs the inertial gravity Newtonian equation with the de Broglie relationship:

$$ \left\{\begin{aligned}& a=G\frac{m}{{{r}^{2}}}\\& p\lambda =h \end{aligned} \right. $$

(11.36a)

into the working parameter bondonic space:

$$\left\{ \begin{aligned} {G_{\rlap{--} B}} = \frac{{{X_{\rlap{--} B}}{c^2}}}{{{m_{\rlap{--} B}}}} \\ \left( {{m_{\rlap{--} B}}c} \right){X_{\rlap{--} B}} = h \\ \end{aligned} \right.$$

(11.36b)

Note that unlike the Planck constant (h) and light speed in vacuum (c) that intervened already in derivation of the bondonic mass (11.35) the gravitation constant (G) behaves here asbeing this the reason it was considered as bondonicdependent in (11.36b); it opens also the insight into evaluating the gravitational effects for the chemical bonding phenomenology. This is not surprising due to the fact such gravitational effects should be present and act towards chemical bonding formation against the inter-electronic electrostatic repulsion; accordingly, like in the “early birth of universe in the Planck era” the chemical bonding should compensate the electronic repelling by gravitational nano-effects sustaining chemical binding; the system (11.36b) nevertheless assures the macroscopic gravitational equation is scaled at the quantum level by corresponding de Broglie equation applied to the same bondon; the price is that we have to assume the bondon as moving with light velocity in bonding (i.e. linking the pairing electrons)—a picture which we can assume at the orbital bonding and which will be avoided for cases the bondon is delocalized over the entire molecule, see the Chaps. 12 and 13 of the same book (Putz et al. 2015a, b). Worth remembering that the bonding-fermionic and condensing-bosonic properties are unified by Bohmian/entangled quantum field quantized by the bondon quasi-particle (Putz 2012) carrying the electronic elementary charge (like a fermion) with almost velocity of light (like a light boson) in the femtoseconds range of observation (Martin et al. 1993) either along bonds (pairing electrons) or networks (connecting many-atoms in nanosystems), respectively (Putz and Ori 2012).

However, the orbitalic treatment of the bondon being of photonic-like nature, is partly justified by the fact the bondon is a boson, like photons, while rooting in the inter-electronic interaction so inheriting some of the fermionic features too.

This way, assuming the bonding energy is given, for a given orbitalic (bonding) state, ${{E}_{bond}},$ one can combine the Eq. (11.35) with the second one in (11.36) to result in the actual bondonic “action radii”

$${X_{\rlap{--} B}} = \frac{{\hbar c}}{{4\pi {E_{bond}}}}.$$

(11.36c)

With this, the corresponding bondonic mass takes the form:

$${m_{\rlap{--} B}} = \frac{{8{\pi ^2}{E_{bond}}}}{{{c^2}}}$$

(11.36d)

which displays the bondonic realization of the Einstein’s mass-energy relationship within the special relativity theory. However, the most exciting consequence here is to evaluate/estimate the Gravitational constant modification or variation in the bondonic universe due to the chemical bonding “attractive” space; with (11.36c) and (11.36d) back in the first equation of (11.36b) one finds the parametric dependency of the gravitational parameter in the bondonic universe:

$${G_{\rlap{--} B}} = \frac{{\hbar {c^5}}}{{32{\pi ^3}E_{bond}^2}}.$$

(11.36e)

One notes that all bondonic measures (radii, mass, gravitation) directly depend on the bonding-energy so making suitable link with quantum chemistry computations in whatever framework of approximation. However, for numerical analysis they will correspond with actual [kcal/mol] implementation for custom chemical energies:

• The absolute photonic-like bondonic radii of action:

$${X_{\rlap{--} B}}\left( {\text{{\AA}}} \right) = \frac{{3621.14}}{{{E_{bond}}\left( {kcal/mol} \right)}}.$$

(11.37a)

Qualitatively, for the chemical range of bonding energies about few tens of kcal/mol the resulted hundred of Angstroms for bondonic radii or action conceptually accords with molecular systems, say carbon systems about and over ten carbon atoms in a chemical bonding compound; this confirm the present approach for the “classical” carbon systems characterization in non-classical (quantum, bondonic) manner.

• The relative photonic-like bondonic motion mass relative to electronic rest mass:

$${\varsigma _m} = \frac{{{m_{\rlap{--} B}}}}{{{m_0}}} = \frac{{8{\pi ^2}{E_{bond}}}}{{{m_0}{c^2}}} = 6.7004 \times {10^{ - 6}} \times {E_{bond}}\left( {kcal/mol} \right).$$

(11.37b)

Qualitatively, the generic bondonic mass is naturally below the electronic value, thus confirming its photonic-like nature here assumed; the other way around, one needs to deal with chemical compound with bonding energies of mega-kcal/mol for that bondons (of photonic-like nature) with an electronic mass be observed in the range of gamma-ray spectroscopy (thousands of electron-volts), however consistent with the present Bohmian (matter-antimatter) treatment of bondons, see also the Chap. 10 of the present book (Putz and Ori 2015a, b); in this line of analysis, for tens of kcal/mol for bonding energy (say 10 kcal/mol) may be found in infra-red (IR) spectra of chemical compounds, see Chap. 13 of the present book (Putz et al. 2015b).

• The relative photonic-like bondonic gravitational influence relative to universal gravitation constant:

$${\varsigma _G} = \frac{{{G_{\rlap{--} B}}}}{G} = \frac{{\hbar {c^5}}}{{32{\pi ^3}GE_{bond}^2}} = \frac{{79895.4 \times {{10}^{53}}}}{{{{\left[ {{E_{bond}}\left( {kcal/mol} \right)} \right]}^2}}}.$$

(11.37c)

Qualitatively, this is the most exciting result: it proves that indeed the gravitation manifestation is huge “inside the chemical bond” so that the chemical bond being created despite the electrostatic repulsion; the gravitation arrives to be of such order of magnitude it certainly curve the space-time in chemical bonding : this may also justifying the orbitals existence in chemical bonding as rooting in the gravitational effect that curved the electronic pairing existence in a closed space of bonding; this phenomenology is at the nano-scale of the level of “black hole” for macro-gravity, of course with the specific adjustments of electronic delocalization nature, etc. Nevertheless, the attractors in chemical bonding behave like “nano-cosmic-systems” such that electrons are the “universe-galactic” particles traveling in between them depending on the gravitation balance manifested at short and long distance in a chemical compound. Such ideas should be further investigated in a more profound manner, eventually involving the space-time metrics itself relating the gravitational-cause-effects of chemical bonding by bondons. Such studies are in the purview of the main author and will be reported in further communications.

However, Eqs. (11.37a–11.37c) are the main bondonic quantities to be evaluated for various instances of chemical bonding as resulted from various carbon systems and quantum computation environments, as following.

11.3 Aliphatic Nature of Symmetric and Asymmetric Hydrocarbons

The quantum mechanical calculations made by the Hückel molecular method have led to the energetic indices and molecular orbital diagrams for ethene, butadiene, propene, allyl, their structural indices being correlated with the chemical reactivity of the atoms of these molecules. Thus, the higher the bond order (p_rs), the higher the reactive capacity of the bonds (multiple bond); the homolytic attack prefers the sublayer atoms with high free valence index (F_r), and the electrophile, unlike the nucleophile, prefers the atoms with high electronic charge density (q_r) (Simon 1973, pp. 29–53).

By applying the Woodward-Hoffmann rule of the conservation of orbital symmetry, we have built the correlation diagrams of the molecular orbitals for ethene hydrogenation and Diels-Alder cycloaddition (4 + 2). Thus, it was possible to anticipate when the reaction occurs thermally and when it would take place under light action (Woodward and Hoffmann 1970, pp. 8–28, 52–75).

In the Hückel approximation for ethene and butadiene the parametric schemes are built (Streitwieser 1961):

$$ \overset{\alpha }{\mathop{\text{C}}}\,\overset{\beta }{\mathop{\text{=}}}\,\overset{\alpha }{\mathop{\text{C}}}\, $$

(11.38a)

$$ \overset{\alpha }{\mathop{\text{C}}}\,\overset{\beta }{\mathop{\text{=}}}\,\overset{\alpha }{\mathop{\text{C}}}\,\overset{\beta }{\mathop{-}}\,\overset{\alpha }{\mathop{\text{C}}}\,\overset{\beta }{\mathop{\text{=}}}\,\overset{\alpha }{\mathop{\text{C}}}\,. $$

(11.38b)

The homogenous equation systems and the normalization conditions for the two molecules are the following:

$$ \text{c}_{\text{1}}^{\text{2}}\text{+c}_{\text{2}}^{\text{2}}\text{=1} $$

(11.38c)

$$ \text{c}_{\text{1}}^{\text{2}}\text{+c}_{\text{2}}^{\text{2}}\text{+c}_{\text{3}}^{\text{2}}\text{+c}_{\text{4}}^{\text{2}}\text{=1}. $$

(11.38d)

Considering the abbreviation

$$ \frac{\alpha -\varepsilon }{\beta }=K $$

(11.39)

the Hückel secular determinants result as:

$$ \left| \begin{aligned}& \text{K}\quad{} \text{1} \\& \text{1}\quad \ \text{K} \end{aligned} \right|\text{=0} $$

(11.40a)

$$ \left| \begin{aligned}& \text{K}\quad{} \text{1}\quad \text{0}\quad \text{0} \\& \text{1}\quad \ \text{K}\quad \text{1}\quad \text{0} \\& \text{0}\quad \text{1}\quad \text{K}\quad \text{1} \\& \text{0}\quad \text{0}\quad \text{1}\quad \text{K} \end{aligned} \right|\text{=0}. $$

(11.40b)

Subsequent to their solving, the following equations are obtained. For ethene ${{\text{K}}^{\text{2}}}-\text{1=0}$, and for butadiene ${{\text{K}}^{\text{4}}}-\text{3}{{\text{K}}^{\text{2}}}\text{+1=0}$, which, by grouping the terms, becomes $({{\text{K}}^{\text{2}}}-\text{K}-\text{1} )({{\text{K}}^{\text{2}}}\text{+K}-\text{1} )\text{=0}$. The K values lead to the energies (ε) and the coefficient sets of molecular orbitals for the two aliphatic hydrocarbons (Table 11.1).

Table 11.1 Energies and coefficients of the atomic orbitals contributions to the molecular orbitals of ethene and butadiene

The values calculated for the energy of the highest occupied molecular orbital (ε_HOMO ) and the energy of the lowest free molecular orbital (ε_LUMO ) are correlated with the butadiene oxidizing character and reducing one, which is stronger that that of ethene. The graphical and mathematical models of the molecular orbitals corresponding to the calculated energies are shown in Fig. 11.1.

Fig. 11.1

Energetic diagrams for ethene (a) and butadiene (b)

Table 11.2 Absolute bonding energies in kcal/mol (α = 0, β = − 18 kcal/mol) for the Hückel orbital HOMO -like levels for molecules of Table 11.1, along the related bondonic radii of action, mass ratio respecting the electronic unit, and the bondonic gravitational ratio respecting the universal gravitational unit, according with Eqs. (11.37a, b, c), respectively.

The bondonic information for molecules of Table 11.1 is reported in Table 11.2 and graphically represented in Fig. 11.2. It provides the specific behavior:

Fig. 11.2

The graphical plot for the bondonic features of ethene and butadiene as computed in Table 11.2 for their lowest orbitals of Fig. 11.1

• The bondonic radii and gravitational actions are parallel increasing, while somehow anti-parallel with the bondonic mass variation as the bonding energy decreases from more to less bonding nature, i.e. from inner molecular orbital to the frontier HOMO ;

• For larger system the HOMO level is less bound so having less bondonic mass and higher radius of action that determine also a higher gravitational influence (in order to keep the bond to a longer range of action).

However, worth noticing that the parallel variation of bondonic radius of action and gravitational influence is a specific quantum manifestation, apparently in contradiction with classical inverse relationship, here interpreted as a Bohmian entangled effect by which to a larger distance the quantum information remains bound under an increasing gravitational action too. The present behavior offers also a subtle way in unifying the quantum with gravitational effects at the chemical bonding level, since at shorter distance gravitation effects should prevail the electrostatic electronic inter-repulsion in order to achieve bonding itself. Further considerations are given in Conclusions section of the present chapter, while more sophisticated geometrical Riemannian quantum-space-time quaternion approach is let for further approach and communication.

Returning to the data inTable 11.1, we can find the energetic and structural indices (Table 11.3).

Table 11.3 Structural indices calculated for ethene and butadiene by the Hückel molecular orbital method

We consider the presentation of the calculation methods for the total energy (E_π) and conjugation or resonance energy (E_R) of the two molecules to be of particular interest.

• For ethene:

$${{E}_{\pi }}=2(\alpha +\beta )=2\alpha +2\beta ;{{E}_{R}}=0$$

(11.41a)

• For butadiene:

$${{\text{E}}_{\pi}}=2(\alpha+{1}\text{.6180}\beta)+2(\alpha+{0.6180}\beta)=4\alpha+{4.4720\beta}$$

(11.41b)

$$ \begin{aligned}&{{\text{E}}_{\pi}}={4\alpha}+{4}{.4720\beta}-{2(2\alpha}+{2\beta)}={0}{.4720\beta} \\& ={8}{.4960kcal}\cdot{\text{mol}^{-{1}}}(-{\beta}=\text{18 kcal}\cdot{\text{mol}^{-{1}}}) \end{aligned}$$

(11.41c)

Using experimental data, we can calculate the butadiene conjugation energy as being the difference between the value of its hydrogenation heat (ΔH = − 57.1 kcal mol⁻¹) and the value calculated from the double hydrogenation heat of ethene (ΔH = − 32.8 kcal mol⁻¹):

$$ {{\text{E}}_{\text{conjugation}}}=-\text{57}\text{.1}-\text{2}(-\text{32}\text{.8} )=\text{8}\text{.5 kcal}\cdot{\text{mol}^{-\text{1}}}$$

(11.41d)

When we compare the butadiene hydrogenation heat with that of 1-butene (− 30.3 kcal mol⁻¹) or with the mean value of an alkene hydrogenation with a marginal double bond, we see a significant difference of 5 kcal mol⁻¹ with respect to our calculations. Anyway, the butadiene conjugation energy is much lower than the one in benzene (22 kcal mol⁻¹) (Avram 1994, pp. 239–241; Nenitzescu 1966, pp. 288–293).

The distribution of the density charge, bond orders and free valences of the two hydrocarbons is a component of the molecular diagrams (Fig. 11.3).

Fig. 11.3

Molecular diagrams for ethene (a) and butadiene (b)

One can see that the carbon atoms in ethene have relatively high free valences , so that the homolytic addition to the C=C bond has free atoms and radicals as intermediates. During this type of reactions, the alkene is transformed into a free radical that is then stabilized through one of the characteristic ways of free radicals.

Hydrogenation with metals and proton donors is not possible, considering the very weak reducing and oxidizing character of ethene. The addition of molecular hydrogen is made in the presence of transition metals such as Ni, Pd, Pt, Rh (heterogeneous catalysis) at normal or increased temperature and pressure (Avram 1994, pp. 162–166; Nenitzescu 1966, pp. 130–132).

The Woodward-Hoffmann correlation diagram of the molecular orbitals of ethene hydrogenation is shown in Fig. 11.4. The preserved symmetry element is a symmetry plane perpendicular on the middle of the two reacting molecules (Woodward and Hoffmann 1970, pp. 52–75; Simon 1973, pp. 29–53).

Fig. 11.4

The Woodward-Hoffmann correlation diagram for the reaction of C₂H₄ with H₂

According to this Woodward-Hoffmann correlation diagram, ethene hydrogenation does not take place through a molecular mechanism (see Fig. 11.4). This is due to the fact that the symmetry correlations between the involved molecular orbitals of the reactants and product attest the existence of a potential barrier to the reaction. Instead, the hydrogenation of ethene with atomic hydrogen takes easily place with ${{\text{E}}_{\text{activation}}}\cong 0$ (Simon 1973, pp. 29–53).

The chemical reactivity of butadiene, in correlation with the calculated structural indices and the reaction mechanisms, is found in its chemical properties (Avram 1994, pp. 349–353; Nenitzescu 1966, pp. 288–293):

• the bond orders (p₁₂ = p₃₄) > p₂₃ indicate the attaching degree of the double bonds but also the possibility of electrophilic additions of halogens, hydracids in 1,2 and 1,4 positions of diene;

• the radicalic additions of CCl₄ or Cl₃CBr in the presence of benzoyl peroxide and the catalytic hydrogenation prefer the 1 and 4 positions in butadiene, with higher free valence index (F₁ = F₄) > (F₂ = F₃);

• the conjugated double bonds of butadiene are easily polarizable, thus offering it the capacity of being reduced with sodium or sodium amalgam as electron donors, and alcohol, water or acids as proton donors;

• the enhanced reactivity of the 1 and 4 positions with higher free valence is also attested by the diene synthesis. Applying the Woodward-Hoffmann rule of conservation of the orbital symmetry with respect to the symmetry plane, which passes through the centre of the butadiene molecule between C₂–C₃, the correlation diagram is obtained; see Fig. 11.5 (Woodward and Hoffmann 1970, pp. 52–75).

  Fig. 11.5

  

  Correlation diagram of molecular orbitals for the cycloaddition of ethene at butadiene

In this cycloaddition (4 + 2), the binding levels of the reactants are correlated with the binding levels of the product. There are no correlations intersecting high-energy intervals between the bonding and antibonding levels. The ground state levels are directly correlated with one another. The diagram shows that, from the symmetry point of view, the thermal process should take place without activation energy. Consequently, there is no barrier conditioned by symmetry, even though experimentally there is found E = 20 kcal mol⁻¹. The activation energy is not directly related to the conservation of the orbital symmetry, but it is determined by rehybridization, increase or decrease of the bond length, or deformation of the valence angles. Therefore, the reaction of butadiene with ethene is slightly thermic, because there are no great electron transitions from the low-energy levels to the higher-energy ones. This diene synthesis can also take place photochemically, but the process is energetically disadvantaged (Simon 1973, pp. 29–53; Avram 1994, pp. 349–353).

In the case of propene with $\sigma -\pi$ conjugation (hyperconjugation) the following parametric scheme is chosen (Nenitzescu 1966, p. 70; Streitwieser 1961):

$$ \overset{{}\alpha{}}{\mathop{\textbf{C}}}\,\underset{{}\beta{}}{\mathop{\text{=}}}\,\overset{\alpha -0.\text{1}\beta{}}{\mathop{\textbf{C}}}\,\underset{0.7\beta }{\mathop{-}}\,\overset{\alpha -0.2{}\beta{}}{\mathop{\textbf{C}}}\,\equiv \overset{\alpha -0.5{}\beta{}}{\mathop{{{\text{H}}_{3}}}}\, $$

(11.42)

The algorithm related to quantum-mechanics calculations leads to the system of homogeneous equations beside the normalization condition of the molecular orbitals:

$$ \left\{\begin{aligned}& {{c}_{1}}(\alpha -\varepsilon)+{{c}_{2}}\beta =0 \\& {{c}_{1}}\beta +{{c}_{2}}(\alpha -0.1\beta -\varepsilon)+{{c}_{3}}0.7\beta =0 \\& {{c}_{2}}0.7\beta +{{c}_{3}}(\alpha -0.2\beta -\varepsilon)+{{c}_{4}}2\beta =0 \\& {{c}_{3}}2\beta +{{c}_{4}}(\alpha -0.5\beta -\varepsilon)=0 \\& c_{1}^{2}+c_{2}^{2}+c_{3}^{2}+c_{4}^{2}=1 \end{aligned} \right.. $$

(11.43)

Considering abbreviation as in (11.43) we obtain the Hückel secular determinant:

$$ \left| \begin{aligned}& \text{K}\quad{} \quad \text{1}\quad \quad \ \ \ \text{0}\quad \quad \quad \ \ \text{0} \\& \text{1}\quad \ \text{(K}-\text{0}\text{.1)}\ \ \ \ \text{0}\text{.7}\quad \quad{}{}{} \text{0} \\& \text{0}\quad \quad \text{0}\text{.7}\quad \,\text{(K}-\text{0}\text{.2)}\quad \quad \text{2} \\& \text{0}\quad \quad \ \,\text{0}\quad \quad \ \ \text{2}\quad \ \ \ \ \text{(K}-\text{0}\text{.5)} \end{aligned} \right|=0 $$

(11.44)

which is successively rewritten till obtaining the simple equation:

$$ \begin{aligned}& ({{\text{K}}^{\text{2}}}-\text{0}\text{.1K)}[\text{(K}-\text{0}\text{.2)(K}-\text{0}\text{.5)}-\text{4} ]-\text{0}\text{.7K}[\text{0}\text{.7(K}-\text{0}\text{.5)} ]-[\text{(K}-\text{0}\text{.2)(K}-\text{0}\text{.5)}-\text{4} ]=\text{0} \\& {{\text{K}}^{\text{4}}}-\text{0}\text{.8}{{\text{K}}^{\text{3}}}-\text{5}\text{.32}{{\text{K}}^{\text{2}}}+\text{1}\text{.335K}+\text{3}\text{.9}=\text{0}. \end{aligned} $$

(11.45)

Using the standard algebraic computational analysis, we obtain the solution values of the secular equation and of the coefficient sets of the molecular orbitals (Table 11.4).

Table 11.4 Molecular orbitals energies of propene and the coefficients of the atomic orbitals contributions to them

Based on Table 11.4 data, the structural indices are calculated as follows:

• charge densities

$$ \begin{aligned}& {{\rho }_{1}}=2[{{0.1878}^{2}}+{{0.7073}^{2}}]=1.0709 \\& {{\rho }_{2}}=2[{{0.3475}^{2}}+{{0.5938}^{2}}]=0.9465 \\& {{\rho }_{3}}=2[{{0.6996}^{2}}+{{(-0.2135 )}^{2}}]=1.0699 \\& {{\rho }_{4}}=2[{{0.5954}^{2}}+{{(-0.3188 )}^{2}}]=0.9122 \end{aligned} $$

(11.46)

• bond orders

$$ \begin{aligned}& {{\text{p}}_{12}}=2(0.1878\times 0.3475+0.7073\times 0.5938 )=0.9704 \\& {{\text{p}}_{23}}=2[0.3475\times 0.6996+0.5938\times (-0.2135 ) ]=0.2326 \\& {{\text{p}}_{34}}=2[0.6996\times 0.5954+(-0.2135 )\times (-0.3188 ) ]=0.9690 \end{aligned} $$

(11.47)

• free valences

$$ \begin{aligned}& {{\text{F}}_{1}}=1.732-{{\text{p}}_{12}}=0.7616 \\& {{\text{F}}_{2}}=1.732-({{\text{p}}_{12}}+{{\text{p}}_{23}})=0.5290 \\& {{\text{F}}_{3}}=1.732-({{\text{p}}_{23}}+{{\text{p}}_{34}})=0.5304 \\& {{\text{F}}_{4}}=1.732-{{\text{p}}_{34}}=0.7630 \end{aligned} $$

(11.48)

Table 11.5 Bonding energies in kcal/mol (α = 0, β = −18 kcal/mol) for the Hückel eigen-orbital levels for propene of Table 11.4, along the related bondonic features of absolute action radii, mass and gravitation effect, as in Table 11.2 reported, according with Eqs. (11.37a, 11.37b, 11.37c), respectively

The bondonic information for molecules of Table 11.4 is reported in Table 11.5 and graphically represented in Fig. 11.6. It provides the specific behavior:

Fig. 11.6

The graphical plot for the bondonic features vs. orbital energies of propene as computed in Table 11.5

• The bondonic radii and gravitational actions are confirmed as parallel in variation, yet increasing for HOMO frontier and decreasing for LUMO excited frontier, with inverse bondonic mass variation as the bonding energy varies from HOMO to LUMO levels;

• The variation shape of bondonic information seems to display an optimum value, under a parabolic form, with maximum/minimum placed on HOMO frontier rather than on LUMO one, for bondonic radius/gravitational action and mass, respectively; this behavior is nevertheless quite relevant for consecrating the parabolic orbitalic bondonic shape and overall on molecular reactivity respecting the orbital occupancy, a matter still being n the middle of debates, without a definite proof (Putz 2011).

Back to “classical” chemical structure-reactivity analysis, for the chemical reactivity of propene we have chosen its reactions with HBr through electrophilic addition and radicalic addition mechanisms, as well as thermal- or photochemical chlorination with radicalic substitution and radicalic addition mechanisms.

The analysis of propene reactivity as substrate also implies a presentation of the HBr reactant with its structural properties in the isolated state, see Table 11.6 (Bâtcă 1981, pp. 115).

Table 11.6 Coefficients of atomic orbitals contribution to the molecular orbitals in HBr

In the case of electrophilic addition mechanism of hydrobromic acid addition, the electrophilic reactant attacks the propene secondary carbon atom with higher charge density (q₁= 1.0709), being thus in accordance with Markovnikov’s rule.

$$ \text{C}{{\text{H}}_{\text{3}}}-\text{CH=C}{{\text{H}}_{\text{2}}}\underset{\text{slow}}{\mathop{\xrightarrow{\text{+}{{\text{H}}^{\text{+}}}}}}\,\ \text{C}{{\text{H}}_{\text{3}}}-\overset{\text{+}}{\mathop{\text{C}}}\,\text{H}-\text{C}{{\text{H}}_{\text{3}}}\underset{\text{fast}}{\mathop{\xrightarrow{\text{+B}{{\text{r}}^{-}}}}}\,\text{C}{{\text{H}}_{\text{3}}}-\text{CHBr}-\text{C}{{\text{H}}_{\text{3}}}$$

(11.49)

In the presence of organic peroxides at high temperature or peroxides and light at low temperature, the Kharash addition takes place (Avram 1994, pp. 170–171). In other words, the hydrobromic acid addition occurs contrary to Markovnikov’s rule. This is explained by the fact that the Br· radical prefers the propene secondary carbon atom with high free valence (F₁ = 0.7616). The propagation stage of the (RA) mechanism is:

$$\begin{aligned} {\text{C}}{{\text{H}}_{\text{3}}} - {\text{CH}} = {\text{C}}{{\text{H}}_{\text{2}}} + {\text{Br}} \cdot \to {\text{C}}{{\text{H}}_3} - \mathop {\text{C}}\limits^{ \bullet } {\text{H}} - {\text{C}}{{\text{H}}_{\text{2}}} - {\text{Br}}\quad \quad \quad \quad \quad \Delta {\text{H}} = - 9\;{\text{kcal}} \cdot {\text{mo}}{{\text{l}}^{ - 1}} \\ {\text{C}}{{\text{H}}_{\text{3}}} - \mathop {\text{C}}\limits^{ \bullet } {\text{H}} - {\text{C}}{{\text{H}}_2} - {\text{Br}} + {\text{HBr}} \to {\text{C}}{{\text{H}}_{\text{3}}} - {\text{C}}{{\text{H}}_2} - {\text{C}}{{\text{H}}_{\text{2}}} - {\text{Br}} + {\text{Br}} \cdot \quad \Delta {\text{H}} = - 7\;{\text{kcal}} \cdot {\text{mo}}{{\text{l}}^{ - 1}} \end{aligned} $$

(11.50)

The hydrobromic acid addition is possible only as described above, because the two stages of the propagation reaction are exothermic and have low activation energy. The fact that the HCl and HI addition does not take place homolitically is due to the unfavourable energetics of the two stages of propagation. In the case of HI, the first elementary reaction is endothermic (ΔH = + 6 kcal mol⁻¹) and the second exothermic (ΔH = − 24 kcal mol⁻¹). In the case of HCl, the first reaction is exothermic (ΔH = − 22 kcal mol⁻¹) and the second, endothermic (ΔH = + 8 kcal mol⁻¹). When propene reacts with chlorine at 500–600 °C, the substitution of the allylic hydrogen takes place. The reaction is industrially used for the synthesis of the allyl chloride through a chained homolytic mechanism (radicalic substitution). The 1,2-dichlorpropane (RA mechanism) is obtained as a by-product. In both cases, during the propagation stages, the radicalic attack occurs at atoms with high free valence .

$$\begin{aligned}& {\text{C}}{{\text{H}}_{\text{2}}} = {\text{CH}} - {\text{C}}{{\text{H}}_3} + {\text{Cl}} \cdot \to {\text{HCl}} + {\text{C}}{{\text{H}}_2} = {\text{CH}} - {\text{C}}{{\text{H}}_2} \cdot \\&{\text{C}}{{\text{H}}_{\text{2}}} = {\text{CH}} - {\text{C}}{{\text{H}}_{\text{2}}} \cdot + {\text{C}}{{\text{l}}_{\text{2}}} \to {\text{C}}{{\text{H}}_{\text{2}}} = {\text{CH}} - {\text{C}}{{\text{H}}_2} - {\text{Cl}} + {\text{Cl}} \cdot \\&{\text{C}}{{\text{H}}_2} = {\text{CH}} - {\text{C}}{{\text{H}}_3} + {\text{Cl}} \cdot \Leftrightarrow {\text{Cl}} - {\text{C}}{{\text{H}}_2} - \mathop {\text{C}}\limits^{ \bullet } {\text{H}} - {\text{C}}{{\text{H}}_3} + {\text{C}}{{\text{l}}_2} \to {\text{Cl}} - {\text{C}}{{\text{H}}_2} - {\text{CHCl}} - {\text{C}}{{\text{H}}_3} + {\text{Cl}} \cdot \end{aligned} $$

(11.51)

The allyl molecule (C₃H₅), as intermediate in the reaction mechanism presented here, may be an example of the application of the algorithm related to the structure-properties correlation for polyatomic molecules (Chiriac et al. 2003, pp. 92–93).

• Hydrogen (H) has 1 atomic orbital; 1 e⁻

• Carbon (C) has 4 atomic orbitals; 4 e⁻

• N = 5 · 1 + 3 · 4 = 17 atomic orbitals ⇒ 17 molecular orbitals

• $\sum{{{e}^{-}}}=5\cdot 1+3\cdot 4=17{{\text{e}}^{-}}\Rightarrow 8.5\,\text{pairs}.$

Even when populated by a single electron, an energy level becomes occupied. As a result, the analysed system present 9 occupied energy levels (8.5 → 9 pairs).

• N₁ = N − p = 17 − 9 = 8 antibonding molecular orbitals ⇒ 8 bonding molecular orbitals.

• N₂ = N − 2N₁ = 17 − 2 · 8 = 1 nonbonding molecular orbital.

As the molecule has 8 atoms, the system should have:

• N₃ = 8 − 1 = 7 σ-bonding molecular orbitals (7 σ*-antibonding molecular orbitals).

The system has a π-symmetry molecular orbital because

• N₄ = N₁ − N₃= 8 − 7 = 1

This one is certainly tricentrically delocalized. It is formed by the linear combination of three p pure atomic orbitals, one from each atom. The independent linear combinations of the three atomic orbitals result in three molecular orbitals with different energies.

• π = p₁ + p₂ + p₃; the combination corresponds to a bonding molecular orbital, because it has no nodal plane.

• π* = p₁ − p₂ + p₃; the combination corresponds to an antibonding molecular orbital, because it has two nodal planes.

Nonbonding molecular orbital π = (p₁ + p₂) − (p₂ + p₃) = p₁ − p₃; the combination has one nodal plane that passes through the central atom. Its energy is intermediate between π and π* molecular orbitals.

The bond order between the carbon atoms is: $1\ \sigma +1\frac{\pi }{2}=1.5.$

As the π-nonbonding tricentric molecular orbital is semi-occupied (the 17th electron), the allyl molecule is paramagnetic.

11.4 On Aromaticity Character of Organic Compounds (Putz et al. 2010)

The aromaticity concept has been recently extended not only to the inorganic systems (Chattaraj et al. 2007; Mandado et al. 2007), but also to zones and molecular fragments, using models, like HOMA (Harmonic Oscillator Model of Aromaticity) (Kruszewski and Krygowski 1972; Krygowski 1993), CRCM (Conjugated Ring Circuits Model) (Mracec and Mracec 2003) and TOPAZ (Topological Path and Aromatic Zones) (Tarko 2008). Even to the transition state of the pericyclic reactions which are constructed within Hückel or Möbius cyclic systems (Rzepa 2007; Putz et al. 2013) one can apply the aromaticity.

The aromaticity of different systems has been assessed using new developed software capable of performing high accuracy calculations, but despite that, as teachers, we could see that our students encounter difficulties in interpreting the obtained results. In order to overcome this inconvenient, the reactivity of some aromatic hydrocarbons and heteroaromatic compounds were explained using a comparison between Hückel molecular orbital theory (HMO), as a highly didactical impact approach, and the new developed density functional theory (DFT ).

Due to the fact that Hückel method is a simple one, it is often used as the basis reference in understanding other methods. Worth notice the fact that, when the static parameters of reactivity are computed with the HMO method, the Coulomb energy $({{\alpha }_{r}}=\alpha +{{\delta }_{r}}\beta)$ is assumed for the atomic orbital “r” and the exchange energy $({{\beta }_{rs}}={{\eta }_{rs}}\beta)$ for the bond between the atomic orbital “r” and “s”, as determined from experimental results.

The standard values of both α and β are benchmarked to the atomic orbital 2p _z of the sp² C and to a π bond for the benzene molecule. The accuracy of this method is high enough; and despite its simplifications it correctly gives the variation of the electronic densities and the energetic levels applied to a series of molecules that slightly differ.

However, DFT is still the most popular and versatile methods available in computational chemistry (Kohn et al. 1996), and the calculations they provide are reflecting the electronic density influence of a chemical structure towards its reactivity (Kohn and Sham 1965), while the electronic energy is approximated by various density functional forms (Putz 2008a)

$$ \text{E}[\rho]=\underbrace{\text{T}[\rho]}_{\text{KINETIC}}+\underbrace{\text{J}[\rho]}_{\text{COULOMB}}+\underbrace{{{\text{E}}_{\text{XC}}}[\rho]}_{\text{EXCHANGE-CORRELATION}}+\underbrace{\int{\text{V}(\text{r})\rho (\text{r})d\text{r}}}_{\text{CHEMICAL}~\text{ACTION}}$$

(11.52)

This expression is the most general to be used in defining electronegativity and chemical hardness indices as its first and second functional derivatives, respectively (Putz 2008b)

$$ \chi \equiv -{{\left(\frac{\delta \text{E}}{\delta \rho } \right)}_{\text{V(r)}}}$$

(11.53)

$$ \eta ={{\left(\frac{{{\delta }^{2}}\text{E}}{\delta {{\rho }^{2}}}\right)}_{\text{V(r)}}}$$

(11.54)

having an important role in assessing the chemical stability and reactivity propensity through the associate principles, especially those referring to the electronegativity equalization and the maximum chemical hardness (Putz 2008c).

The actual working systems presented were selected according to their industrial significance: hydrocarbons (aromatic annulenes), amines, molecules, ions, hydroxyarenes, and heterocycles with nitrogen (e.g. the obtained azo dyes from the aromatic amines and phenols through diazotization and coupling reactions). The heterocyclic compounds are nevertheless vital in some natural product as being part in building up their skeleton (Avram 1994, Chap. 19; Avram 1995, Chaps. 223132).

Remember that the planar molecules of interest, with (4n + 2)π electrons are displaying high stability, low magnetic susceptibility (diamagnetism), and affinity for substitution reactions rather than for addition (Chattaraj et al. 2007; Hendrickson et al. 1976, Chaps. 5, 8). There are several molecules which are fitting to the aromatic (Ar) model Ar-Y $(Y=OH,\ N{{H}_{2}},\ N{{R}_{2}},\ \overset{+}{\mathop{N}}\,{{H}_{3}})$, and they are highly correlated with the substituent constants and the related inductive (σ and π) effects (Katritzky and Topson 1971).

The considered aromatic compounds are: Benzene, Aniline, Phenol, Naphthalene, α-Naphthol, β-Naphthol, α-Naphthylamine, β-Naphthylamine, Pyridine, Pyrimidine, 4-N, N’- dimethylaminoaniline, and monochlorohydrate of 4-N, N’-dimethylaminoaniline. Some of those molecules present symmetry, an important item in lowering the degree of the secular determinant which is obtained following the Hückel molecular orbital (HMO) method (Hückel 1930, 1931; Mandado et al. 2007) in joint using the data from Table 11.7.

Table 11.7 The parameters values considered for the conjugated systems by Hückel molecular orbital (HMO method); the number of points indicates the π electrons/atom. (Putz et al. 2010)

In this computational framework several parameter were calculated: the Hückel matrices, the eigenvectors, the π levels of energy, the total ground state energy (E _π ), the delocalization energy/π electrons $(\overline{\pi })$, the charge densities ( r _r ), the bond orders (p _rs ) and the free valence $\left({{\text{F}}_{\text{r}}}=1.732-\sum{{{\text{p}}_{\text{rs}}}}\right)$ .

On the other side, the present-based molecular computations employ for the DFT computational framework, the exchange sum and the correlation contributions in the mixed functional of Eq. (11.52)

$$ {{\text{E}}_{\text{XC}}}[\rho]=\underbrace{\text{K}[\rho]}_{\text{EXCHANGE}}+\underbrace{{{\text{E}}_{\text{c}}}[\rho]}_{\text{CORRELATION}}$$

(11.55)

under the for of hybrid B3-LYP functional proposed by Becke through empirical comparisons made against very accurate experimental results, containing the exchange contribution (20 % Hartree Fock + 8 % Slater + 81 % Becke88) which was added to the correlation energy (81 % Lee-Yang-Parr + 19 % Vosko-Wilk-Nusair). Nevertheless, the Becke’s functional via the so-called semiempirical (SE) modified $(\beta,\gamma)$-parameterized gradient-corrected functional (Becke 1986) was use for the considered 81 % contribution in the exchange term:

$$ \begin{aligned}& {{\text{K}}^{\text{SE}}}={{\text{K}}_{0}}-\beta \sum{}_{\sigma }{\int{\rho_{\sigma }^{4/3}\frac{\text{x}_{\sigma }^{2}(\text{r})}{1+\gamma \text{x}_{\sigma }^{2}(\text{r})}\text{d}r}}, \\& {{\text{K}}_{0}}=-\frac{3}{2}{{\left(\frac{3}{4\pi } \right)}^{1/3}}\int{{{\rho }^{4/3}}(r )\text{d}r}, \\& {{\text{x}}_{{}\sigma{}}}(r)=\frac{\left| \nabla {{\rho }_{\sigma }}(r) \right|}{\rho_{\sigma }^{4/3}(r)},\end{aligned} $$

(11.56)

so producing the working single-parameter density functional (Becke 1988):

$$ {{\text{K}}^{\text{B}88}}={{\text{K}}_{0}}-\beta \sum{}_{\sigma }{\int{\rho_{\sigma }^{4/3}(r)\frac{\text{x}_{\sigma }^{2}(r)}{1+6\beta {{\text{x}}_{\sigma }}(r){{\sinh }^{-1}}{{\text{x}}_{\sigma }}(r)}dr}}$$

(11.57)

where the value $\beta =0.0042\,[\text{a}\text{.u}.]$ has assessed as the best fit among the noble gases (He to Rn atoms) exchange energies. However, for the counter-side 81 % of the correlation part of energy the Lee, Yang, and Parr (LYP) functional considered the Colle-Salvetti approximation (Lee et al. 1988):

$$ \text{E}_{\text{c}}^{\text{LYP}}=-{{\text{a}}_{\text{c}}}{{\text{b}}_{c}}\int{\text{dr}}\gamma (r)\xi (r)\left(\begin{aligned}& \sum{}_{\sigma }{{{\rho }_{\sigma }}(r)\sum{}_{i}{{{\left| \nabla {{\phi }_{i\sigma }}(r) \right|}^{2}}}}\\& -\frac{1}{4}\sum{}_{\sigma }{{{\rho }_{\sigma }}(r)\Delta {{\rho }_{\sigma }}(r)} \\& -\frac{1}{4}{{\left| \nabla \rho (r) \right|}^{2}}\\& +\frac{1}{4}\rho (r)\Delta \rho (r) \end{aligned} \right)-{{\text{a}}_{\text{c}}}\int{\text{d}r\frac{\gamma (r)}{\eta (r)}\rho (r)} $$

(11.58)

with

$$ \begin{aligned}& \gamma (r)=4\frac{{{\rho }_{\uparrow }}(r){{\rho }_{\downarrow }}(r)}{\rho {{(r)}^{2}}}, \\& \eta (r)=1+{{\text{d}}_{\text{c}}}\rho {{(r)}^{-1/3}}, \\& \xi (r)=\frac{\rho {{(r)}^{-5/3}}}{\eta (r)}\exp [-{{\text{c}}_{\text{c}}}\rho {{(r)}^{-1/3}}] \end{aligned} $$

(11.59)

and where the involved constants are given as: a _c  = 0.04918, b _c  = 0.132, c _c  = 0.2533, d _c  = 0.349.

The simple Hückel method and the advanced DFT one are both adapted for the chemical hardness “frozen core” approximation of Eq. (11.54) (Koopmans 1934) and used in this study to ordering the reactivity of the 12 compounds (among both mononuclear and polynuclear forms)

$$ \eta ={{\left(\frac{{{\partial }^{2}}{{\text{E}}_{\text{N}}}}{\partial {{\text{N}}^{\text{2}}}}\right)}_{\text{V(r)}}}\cong {{\text{E}}_{\text{N+1}}}-2{{\text{E}}_{\text{N}}}+{{\text{E}}_{\text{N-1}}}=\text{IP}-\text{EA}\cong \text{LUMO}-\text{HOMO} $$

(11.60)

in terms of ionization potential IP and electron affinity EA so related (the effective Koopmans’ approximation, see Putz 2013) with the lowest unoccupied molecular orbital (LUMO ) and highest occupied molecular orbital (HOMO ) energies.

The aromaticity of benzene (6 annulene) and its derivates are here to be employed with quantum chemistry DFT and Hückel (1930, 1931) and approximations of quantum mechanics, with the results interpreted with the bondonic chemistry (Putz 2010a, b, 2012; Putz and Ori 2015) as well as by the many valence theories (Saltzman 1974).

Table 11.8 Energetic indices for the organic molecules under study as computed within the density functional theory (DFT ) with B3-LYP exchange-correlation, according with Hypercube, Inc. (2002); all values in electron-volts (eV). (Putz et al. 2010)

Table 11.9 Bonding energies in kcal/mol (1 eV = 23.06035 kcal/mol) for the highest occupied orbital levels (DFT -HOMOs) for molecules of Table 11.8, along the related bondonic features of absolute action radii, mass and gravitation effect, as in Table 11.2 reported, according with Eqs. (11.37a, b, c), respectively

The DFT HOMO /LUMO and Hückel numerical results are presented in Tables 11.8 and 11.10, while the bondonic analysis are presented din the Tables 11.9 and 11.11, respectively. The bondonic information for molecules of Table 11.9 and 11.11 are reported in graphically represented in Figs. 11.7 and 11.8 with the actual specific behavior:

Fig. 11.7

The graphical plot for the bondonic features of aromatic molecules in Table 11.8 for their HOMO energy orbitals of Table 11.9

Fig. 11.8

The graphical plot for the bondonic features of molecules in Table 11.10 for their HOMO energy orbitals of Table 11.11

Table 11.10 Energetic indices for compounds of Table 11.8, supplemented with the delocalization energy per π electrons $(\overline{\pi } )$ as computed within the Hückel theory (HT) or calibrated with the density functional counterparts from Table 11.8 (Putz et al. 2010)

Table 11.11 Bonding energies in kcal/mol (α = 0, β = − 18 kcal/mol) for the Hückel eigen-orbital HOMO levels for molecules of Table 11.10, along the related bondonic features of absolute action radii, mass and gravitation effect, as in Table 11.9 reported, according with Eqs. (11.37a, b, c), respectively

• For DFT shape (Fig. 11.7) the bondonic distribution follow the Gaussian for radii and gravitational actions and with anti-parallel variation for bondonic mass; the extreme behavior is recorded for A06 (4-N, N’-dimethylaminoaniline) aromatics of Table 11.8 which is nevertheless not the most aromatic compound in the series (according with the chemical hardness ordering); this may open further subtle approaches and new definitions for aromaticity itself;

• The Hückel shape (Fig. 11.8) the Gaussian bondonic form of DFT framework is dissolved and another peak appears for the A02 (α-Naphthylamine) aromatics of Table 11.8 which is now the less aromatic according with HT-chemical hardness of Table 11.10, see also the ordering of Eq. (11.62); this leads with the idea that although not as refined in computation as DFT the Hückel theory appears to be consistent with bondonic description, a finding which favors both theories towards their degree of observability, despite the inherent approximations to the first and the entanglement information for the last.

• In both approaches (DFT and Hückel) the higher aromaticity the higher the bondonic mass (however with lighter Hückel bondon so stronger gravitational action), which confirms the inertia in chemical reactivity associated with aromaticity, here physically represented by the bondonic mass.

Continuing with aromatic-chemical hardness connections, from Tables 11.8 and 11.10 the following aromaticity hierarchies are obtained.

DFT hierarchy of aromaticity of Table 11.8:

$$ \begin{aligned}& {{\eta }^{DFT}}(A12 )>{{\eta }^{DFT}}(A11 ) \\&>{{\eta }^{DFT}}(A10 )>{{\eta }^{DFT}}(A09 ) \\&>{{\eta }^{DFT}}(A08 )>{{\eta }^{DFT}}(A07 ) \\&>{{\eta }^{DFT}}(A06 ) \\&>{{\eta }^{DFT}}(A05 )>{{\eta }^{DFT}}(A04 ) \\&>{{\eta }^{DFT}}(\text{A03} )>{{\eta }^{DFT}}(\text{A02} ) \\&>{{\eta }^{DFT}}(A01 ) \end{aligned} $$

(11.61)

HT hierarchy of aromaticity according to the chemical hardness values of Table 11.10 (fourth column), for universal Hückel [- β] integral:

$$ \begin{aligned}& {{\eta }^{HT}}(\text{A12} )>{{\eta }^{HT}}(\text{A11} ) \\&>{{\eta }^{HT}}(\text{A10} )>{{\eta }^{HT}}(\text{A09} )>{{\eta }^{HT}}(\text{A08} ) \\&>{{\eta }^{HT}}(A01 ) \\&>{{\eta }^{HT}}(A06 )>{{\eta }^{HT}}(\text{A07} )>{{\eta }^{HT}}(A05 ) \\&>{{\eta }^{HT}}(A04 )>{{\eta }^{HT}}(\text{A03} )>{{\eta }^{HT}}(\text{A02} ) \end{aligned} $$

(11.62)

HT hierarchy of aromaticity according to the chemical hardness values of Table 11.10 (eighth column), for calibrated Hückel-DFT [- β] integral:

$$ \begin{aligned}& \eta_{DFT}^{HT}(\text{A12} )>\eta_{DFT}^{HT}(A04 ) \\&>\eta_{DFT}^{HT}(\text{A09} )>\eta_{DFT}^{HT}(\text{A10} )>\eta_{DFT}^{HT}(\text{A08} ) \\&>\eta_{DFT}^{HT}(\text{A11} )>\eta_{DFT}^{HT}(\text{A07} ) \\&>\eta_{DFT}^{HT}(A06 )>\eta_{DFT}^{HT}(\text{A05} ) \\&>\eta_{DFT}^{HT}(\text{A03} )>\eta_{DFT}^{HT}(\text{A02} ) \\&>\eta_{DFT}^{HT}(A01 ) \end{aligned} $$

(11.63)

HT hierarchy of aromaticity according to the $\bar{\pi }$ values of Table 11.10 (fifth column), for universal Hückel [- β] integral:

$$ \begin{aligned}& {{{\bar{\pi }}}^{HT}}(\text{A09} )>{{{\bar{\pi }}}^{HT}}(\text{A11} ) \\&>{{{\bar{\pi }}}^{HT}}(A04 )>{{{\bar{\pi }}}^{HT}}(A05 )>{{{\bar{\pi }}}^{HT}}(\text{A08} ) \\&>{{{\bar{\pi }}}^{HT}}(\text{A02} )>{{{\bar{\pi }}}^{HT}}(\text{A03} ) \\&>{{{\bar{\pi }}}^{HT}}(A01 )>{{{\bar{\pi }}}^{HT}}(\text{A10} ) \\&>{{{\bar{\pi }}}^{HT}}(\text{A07} )>{{{\bar{\pi }}}^{HT}}(\text{A12} )>{{{\bar{\pi }}}^{HT}}(A06 ) \end{aligned} $$

(11.64)

HT hierarchy of aromaticity according to the $\bar{\pi }$ values of Table 11.10 (ninth column), for calibrated Hückel-DFT [- β] integral:

$$ \begin{aligned}& \bar{\pi }_{DFT}^{HT}(A04 )>\bar{\pi }_{DFT}^{HT}(\text{A05} ) \\&>\bar{\pi }_{DFT}^{HT}(\text{A09} )>\bar{\pi }_{DFT}^{HT}(\text{A02} ) \\&>\bar{\pi }_{DFT}^{HT}(\text{A03} )>\bar{\pi }_{DFT}^{HT}(\text{A07} ) \\&>\bar{\pi }_{DFT}^{HT}(\text{A08} )>\bar{\pi }_{DFT}^{HT}(\text{A11} ) \\&>\bar{\pi }_{DFT}^{HT}(\text{A10} )>\bar{\pi }_{DFT}^{HT}(\text{A12} ) \\&>\bar{\pi }_{DFT}^{HT}(A01 ) \\&>\bar{\pi }_{DFT}^{HT}(A06 ) \end{aligned} $$

(11.65)

The principal points which arise from the aromaticity scale are:

• There is an agreement between the DFT and Hückel chemical hardness scales, (except for the case of the displacement and the inversion of the 4-N, N’-dimethylaminoaniline/A06 and monochlorohydrate of 4-N, N’-dimethylaminoaniline/A01 in the HT scheme), and also with the aromaticity/stability/reactivity scale for the molecules of interest, using experimental or other presented theoretical methods;

• Unlike the DFT counterpart scale of aromaticity, the mixed DFT-Hückel chemical hardness scale of aromaticity further inverts and departs the two forms of Naphtol (A04 & A05) and the Pyridine & Pyrimidine (A10 & A11) pairs considered;

• The inversion of the Phenol/A09 and Naphtalene/A07 with Benzene/A12 structural inertia in reactivity (aka aromaticity), as an effect of the delocalization energy per pi electrons is present in both realizations as HT and HT-DFT scales;

• Only the A_Phenol > A_Aniline ordering is appearing to be the only invariant across above aromaticity.

Overall, the chemical hardness although custom to be considered a versatile tool in assessing reactivity and aromaticity, conceptually superior to the classical delocalization energy per pi electrons index, it is currently challenged by the bondonic chemistry insight, especially regarding the bondonic mass and gravity production that can reshape the aromaticity concept itself.; however, the DFT approach parallels remarkably well with the simple Hückel quantum picture of organic molecules, which nevertheless appears to be more “spectroscopically reach” in bondonic peaks of information.

11.5 On Reducing Character of Mono- and Polyhydroxy Arens

Selected for their usage to obtain artificial resins, medicines and azo dyes, hydroxyarenes has properties of both hydroxyl groups and the aromatic rings (Avram 1995, Chap. 32). Hückel and DFT specific calculations were performed for these systems in which the conjugation between non participating electrons of oxygen of the hydroxyl groups and π electrons of the aromatic rings takes place (Avram 1994, Chap. 19). Using the Streitwieser parameters (Table 11.7) standardized based on experimental results using computational technique (of the secular determinant and its diagonalization on the irreducible representations of the symmetry group associated to the corresponding molecules) results allowing the correlation with their chemical reactivity have been obtained.

The presence of the (−SO₃H) group does not disturb the electronic state of the carbon atom to which it is linked and it does not participate in conjugation with the aromatic ring (Streitwieser 1961).

The delocalization energy (DE) , ε_HOMO and ε_LUMO enable the estimation of aromaticity, reducing or oxidizing character of these compounds (Table 11.12).

Table 11.12 Energetic indices calculated by HMO method for aromatic hydroxo compounds

Regarding the absorption bands in visible and ultraviolet domains, the first band $({{\lambda }_{\max }})$ corresponds to either the transition between ε_LUMO and ε_HOMO of the large conjugated system or the transition from a non participating atomic orbital to ε_LUMO (Simon 1973, Chap. 2, 1964).

The internal consistency of the data in Table 11.12 is checked with the following relationship by determining the resonance integral parameter for each analyzed system obtaining the results reported in the last column of Table 11.12. Their striking similarity proves the reliability of the used data and the undertaken calculations.

$$ \beta [eV]=\frac{2\pi c\hbar }{\lambda [{{\varepsilon }_{LUMO}}(\beta)-{{\varepsilon }_{HOMO}}(\beta) ]} $$

(11.66)

Moreover, the common value $\beta =-2.3877\ \text{eV}=-55.0819\ \text{kcal/mol}$ predicts the localization of this constant for cyclic aromatic systems under the range of linear polyenes, of approximately − 60 kcal/mol, − 70 kcal/mol.

The obtained results lead us to the following hierarchy on the chemical reactivity of the eight hydroxyl arenes:

• According with ε _HOMO and ε _LUMO values, the C₁₀H₇OH compounds showsuperior tendency to oxidation or reduction processes than the corresponding C₆H₅OH π—systems. Unlike the more stable phenol, the less aromatic naphthols participate in some chemical reactions under tautomeric form (Avram 1994, Chap. 19).

• Phenol (I), more reactive than benzene (DE = 8β) (Simon 1973, Chap. 2), is more sensitive against oxidazing agents (FeCl₃). It easily participates at reactions with SE mechanisms. In contrast to the (II-VIII) compounds, it does not present prototropic tautomerism (Nenitzescu 1966, Part II, Chap. 2).

• Our calculations are consistent with the physico-chemical behavior of diphenols. Thus, 1,2-dihydroxy phenol (II) with 1,2-benzoquinone form an electrochemically reversible redox system. The value of the quinone redox potential is small, therefore this compound is a strong oxidant and consequently the corresponding diphenol is a weaker reductant (Avram 1995, Chap. 25). However, the diphenol is oxidated by the ammoniacal solution of silver at low temperature and by the Fehling reagent at high temperature, while 1,3-dihydroxy phenol (III) only reacts with the Tollens reagent at high temperature (Nenitzescu 1966, Part II, Chap. 2).

Table 11.13 Bonding delocalization energies in kcal/mol (β = − 55.0819 eV) for the aromatic hydroxo compounds of Table 11.12, along the related bondonic radii of action, mass ratio respecting the electronic unit, and the bondonic gravitational ratio respecting the universal gravitational unit, according with Eqs. (11.37a, b, c), respectively

The bondonic information for molecules of Table 11.12 is reported in Table 11.13 and graphically represented in Fig. 11.9. It provides the specific behavior:

Fig. 11.9

The graphical plot for the bondonic features of molecules in Table 11.13 for their delocalization energies of Table 11.12

• The bondonic information goes now with delocalization energy, which is in fact an energy difference driving reactivity; accordingly, the bondonic actions as radii, mass and gravitational effects display a monotonic variation, rather than a parabolic one, while maintaining, nevertheless their already established parallel and anti-parallel relationships, respectively;

• The decreasing in delocalization energy (in energy difference) actually free the bondon to a higher radii and gravitational action, whereas less bondonic mass is accumulated or distributed in between the bonding centers defining the bonding area.

Back to the “classical” quantum structure-reactivity interpretations, among phenols, pyrocatechol (II) and pyrogallol (IV) are the most reducing ones. Consequently, they are used as photographic developer. The alkaline solution of the 1,2,3-trihydroxy phenol (IV) quickly and quantitatively absorbs oxygen, serving for gas analysis (Nenitzescu 1966, Part II, Chap. 2). Phloroglucinol (V), resorcinol (III) and naphtols (VI-VIII) have the practical and theoretical support in their tendency to ketolyse (Avram 1994, Chap. 19). Along with the extension of the conjugated bonds system, the maximum absorption bands moves toward visible (batochromic effect) (Hendrickson et al. 1976, Chap. 7). In this respect, naphtols are more suitable as coupling agents (Avram 1995, Chap. 22; Nenitzescu 1966, Part II, Chap. 5). The structural indices calculated for different atoms in hydroxy arenes (Table 11.14) allow us to establish some structure-property correlations in organic chemical reactions.

Table 11.14 Electron repartition indices calculated by HMO method for different phenols and naphtols atoms

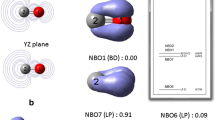
The values ρ _O  >  ρ _C ; F_O > F_C correlate with the higher oxygen electronegativity than that of the carbon atom (Putz 2006, 2007) and also with the potential contours presented in Fig. 11.10.

Fig. 11.10

The potential contour maps for phenol (a), 1-naphthol (b), 2-naphthol-3,6-sodium disulfonate (c) under discussion on their HOMO state. A higher density of contours indicates that the site is susceptible for electrophilic attack either for positive (green) or negative (in cyan) molecular electrostatic potential

The reactions occurring at nucleus with electrophilic substitution mechanism: halogenation, nitrosation, sulfonation, nitration, alkylation, and coupling take place preferentially at carbon atoms possessing the highest electron density. Therefore, the electrophilic reagents turn to C(2) and C(4) of phenol, C(1) of 2-naphthol- 3,6-sodium disulfonate, C(4) of 1-naphthol. The 1,3,5-trihydroxylbenzene carbon atoms are favored by high electron densities, but certainly in substitution reactions they experience steric hindrance (Avram 1994, Chap. 19). The high free valences of some atoms in these molecules indicate their increased reactivity in reactions with both ionic and radicalic mechanisms. The low free valences of the carbon atoms to which hydroxyl groups are bounded confirm that, opposed to alcohols, hydroxyarenes do not participate to reaction during which carbon-oxygen bond is broken (Nenitzescu 1966, Part II, Chap. 2).

Increased reactivity of the hydroxyl group of these compounds show the heterolytic cleavage of the bond during neutralization, etherification, esterification, and also colligation of some intermediary formed radicals (Avram 1994, Chap. 19; Nenitzescu 1966, Part II, Chap. 2).

11.6 Structure and Reactivity of Aromatic Compounds Involved in Azo Dyes Synthesis

Our interest for such compounds resides in their participation to diazotisation and coupling reactions, both as substrates and electrophilic reactants. The aromatic amines and mononuclear/polynuclear hydroxyarenes undergo electrophilic substitution reactions with a higher rate than their reference compounds, benzene and naphthalene, respectively: ${{\text{k}}_{\text{Ar}-\text{Y}}}/{{k}_{\text{ArH}}}>1$ (Y = OH, NH₂) (Nenitzescu 1968, Part IV). This behavior is due to the ring activation by conjugation of the non-participating electrons of nitrogen and oxygen atoms with the π electrons of the aromatic ring (Avram 1994, Chap. 19). In this respect, the aromaticity of these molecules can be discussed using the energetic and π electron density distribution indices calculated by HMO and DFT methods.

The structure and reactivity in diazotization reaction electronic spectra (200–800 nm) are recorded for sulphanilic acid and sulphanilamide, the corresponding hydrochlorides, diazonium salts and hydrolysis products. Molecular orbital calculations by the HMO method are performed for the above molecules (Isac et al. 1981a).

The diazonium salts were obtained through diazotization in acidic solution with sodium nitrite, the nitrous acid excess was destroyed with ammonium sulphamate. The concentrations and the preparation technique were those described in literature (Ciuhandu and Mracec 1968).

Solid sulphanilic acid can also be treated with gaseous NOCl, to give solid diazonium chloride in 100 % yield. The water produced by the reaction is removed in situ reaction with excess of NOCl (Kaupp et al. 2002).

Diazonium salts both as diazotization products and electrophilic reactants in azocoupling processes are also involved in thermal decompositions (Simon and Bădilescu 1967).

The kinetics of thermal decompositions in solution of diazonium salts of sulphanilic acid and sulphanilamide were followed spectrophotometrically. The following activation energies (E) and preexponent (A) were obtained for thermal decompositions of benzenediazonium salts: for the sulphanilic acid derivative E = 127.19 kJ mol⁻¹, A = 6.0 · 10¹⁵ s⁻¹, for the sulphanilamide derivates E = 124.20 kJ mol⁻¹, A = 4.0 · 10¹⁵ s⁻¹(Isac et al. 1981b).

For these quick reactions of breaking the C–N bonds, A > 10¹⁴ s⁻¹ indicates that within the activated complex the interaction of π electrons between the nitrogen atoms and those of the molecule residue is weaken or even cancelled (Simon 1966a).

The correlation diagram of molecular orbitals and the correlation diagram of electronic states for the decomposition reaction of the benzenediazonium cation were established, using Hückel molecular orbital calculations (Isac et al. 1985). The activation energy of the thermal decomposition must be of purely thermodynamic nature, without a certain barrier, as the diazonium cation is more stable than the decomposition products (Simon and Bădilescu 1967).

The following activation enthalpies (ΔH^≠) and activation entropies (ΔS^≠) were obtained for thermal decompositions of benzenediazonium salts: for the sulphanilic acid derivative ΔH^≠ = 124.683 kJ mol⁻¹, ΔS^≠ = 48.116 J K⁻¹ mol⁻¹ for the sulphanilamide derivates ΔH^≠ = 121.336 kJ mol⁻¹, ΔS^≠ = 44.350 J K⁻¹ mol⁻¹ (Isac et al. 1981b). The activation enthalpies were quite high, and in contrast, the corresponding activation entropies have high positive values.

The experimental data indicate that the stability of substituted diazonium ions, precipited as diazoniumfluoroborates, can be increased by complexation with crown ethers (Bräse et al. 2004). Diazonium cations are not strong electrophilic reactants because of their positive charge delocalization. Increased reactivity is found in those diazonium cations containing electron attractive substituents in para position (Neniţescu 1966, Part II, Chap. 5, pp. 590–593).

The azocoupling of these compounds may occur only with strong nucleophiles such as phenolates, naphtholates, and free aromatic amines. In this case the reaction selectivity is high (Nenitzescu 1968, Part IV, Chap. 5, pp. 430–436). This behavior makes the azocoupling processes to occur almost unitary into positions of highest electron density (ρ_r) of the coupling agents (Simon 1973, Chap. 2, pp. 35–50). The reactivity of coupling components variously substituted in the same position falls within the series –O⁻ > – NH₂ > –OH.

Table 11.15 The parameters values considered for the conjugated systems (HMO method)

Table 11.16 Energetic indices calculated by HMO method for the organic compound used in diazotization and coupling reactions

Table 11.17 Bonding delocalization energies in kcal/mol (β = − 55.0819 eV) for the compounds of Table 11.16, along the related bondonic radii of action, mass ratio respecting the electronic unit, and the bondonic gravitational ratio respecting the universal gravitational unit, according with Eqs. (11.37a, b, c), respectively.

The bondonic information for molecules of Table 11.16 is reported in Table 11.17 and graphically represented in Fig. 11.11 with the actual peculiarity:

Fig. 11.11

The graphical plot for the bondonic features of molecules in Table 11.17 for their delocalization energies of Table 11.16

• The monotonic bondonic behavior vs. delocalization energy is maintained, as in the Fig. 11.9 recorded, however, here with a smooth non-linear effect, which somehow extends and generalizes the earlier linear shapes of Fig. 11.9, probably due to the actual ionic/radicalic character of the considered compounds; accordingly, there appears that the bondonic treatment is indeed sensitive, even when about of gravitational effects, by the ionicity character which superimposes the highly covalent (hydrocarbon) compounds.

Bach on the “classical” chemical interpretation of structure-reactivity relationship, the orientation of substitution at polyfunctional components is governed by pH through protolytic equilibrium involving hydroxyl and amino groups (Panchartek and Sterba 1969). Selecting the Streitwieser parameters (Table 11.7) and data of Table 11.15 (Streitwieser 1961) the chemical reactivity indices of conjugated systems containing a number of electrons (n_π) are calculated.

The values obtained by HMO calculations sustain the chemical reactivity of those 15 investigated organic molecules (Table 11.16).

• The hydrochlorides of sulfanilic acid and sulfanilamide (IX), (X), and also their diazonium salts (XI), (XII) present low values of delocalization energy (DE), as these compounds are double substituted in para positions with electron attractive groups. The hydrolysis products of sulfanilic acid and sulfanilamide diazonium salts (XIII), (XIV), and also the salicylic acid (XV) are more aromatic than N, N-dimethyl aniline (XVI) and m-phenylene diamine (XVII), in accordance with TOPAZ aromaticity. Moreover, it can be seen that 1-naphthol (VI) and 2-naphthol (XVIII) are more stable than 1-naphthyl ethylenediamine (XIX) and 2-naphthyl amine (XX), and the (XIII), (XIV) compounds are more aromatic than (XVI) molecule. The favorable effect that first order substituents bring on aromaticity is in accordance with TOPAZ modeling for these compounds, such as A(XVI) ≅ 90 %A[(XIII), (XIV)] relationship (Tarko 2008).

• Based on HOMO -LUMO gap criteria for aromaticity (Table 11.10), the (XIX) and (XX) molecules are less aromatic than (XVI) compound showing properties intermediary to those of pure aromatic amines and aliphatic ones (Nenitzescu 1966/Part I). The monochlorhydrate of 4-N, N-dimethylamino aniline (XXII), one of the amine form in HCl solution, is more aromatic than 4-N, N-dimethylamino aniline (XXI) as predicted by the values of TOPAZ aromaticity (Tarko 2008).

• The ${{\varepsilon }_{LUMO}}$ and ${{\varepsilon }_{HOMO}}$ values indicate that (IX), (X), (XI), (XII) compounds are the most resistant to oxidation, and the (XVI), (XVII), (XXI) molecules are the most resistant to reduction. The (XI), (XII) compounds should be stronger oxidizing agents, and the (XIX), (XXI) compounds should be stronger reducing agent.

• For the (IX), (XI), (XIII) compounds that are present in the acidic solution when sulfanilic acid diazotization occurs, and also the (X), (XII), (XIV) compounds present in the medium when sulfanilamide is diazotized, the correlations between ${{\lambda }_{\text{calculated}}}$ and spectral measurements ${{\lambda }_{\exp }}$ are satisfactory (Isac et al. 1981a).

Regarding the electronic densities (ρ_r) calculated by HMO method (Table 11.18) correlated with the results obtained by DFT method (Fig. 11.12), it should be mentioned that their relative values are more important than their absolute ones within this series of similar compounds, or for different atoms of the same substance.

Fig. 11.12

The potential contour maps for N, N-dimethylaniline (a), 1-naphthylethylendiamine (b), 2-naphthylamine (c), 4-N, N-dimethylamino aniline (d), monochlorohydrate of 4-N, N-dimethylamino aniline (e) under discussion on their HOMO state. A higher density of contours indicates that the site is susceptible for electrophilic attack either for positive (green) or negative (in cyan) molecular electrostatic potential

Table 11.18 Electronic densities (ρ_r) calculated by HMO method for atoms of some coupling components of sulfanilic acid and sulfanilamide diazonium salts

The atoms electronic densities follow the ${{\rho }_{0}}>{{\rho }_{N}}>{{\rho }_{C}}$ relationship being in good agreement with the known electronegativity tendency (Putz 2006, 2007). The usage of phenolates and naphtolates, strong nucleophiles, in azo coupling reactions is based on the fact that the oxygen atom in the $-{{O}^{-}}$anion is less electronegative than in the $-OH$ group due to its negative charge (Simon 1973, Chap. 2, pp. 35–50).

The calculated values in Table 11.18 place the coupling components upon reactivity as follow:

$$\left( {{\text{XVII}}} \right)\,{\text{> }}\,\left( {{\text{XVI}}} \right)\,{\text{> }}\,\left( {{\text{XIII}}} \right)$$

(11.67a)

$$\left( {{\text{XIV}}} \right)\,{\text{> }}\,\left( {{\text{XV}}} \right)$$

(11.67b)

$$\left( {{\text{XIX}}} \right)\,{\text{> }}\,\left( {{\text{VI}}} \right)$$

(11.67c)

$$\left( {{\text{XVIII}}} \right)\,{\text{> }}\,\left( {{\text{VI}}} \right)$$

(11.67d)

$$\left( {{\text{XX}}} \right)\,{\text{> }}\,\left( {{\text{XIX}}} \right)$$

(11.67e)

$$\left( {{\text{XX}}} \right)\,{\text{> }}\,\left( {{\text{XVIII}}} \right)$$

(11.67f)

according to their experimental behavior.

The diazonium cations (XI), (XII) perform electrophilic attacks to the following atoms: C(4) of (XIII), (XIV), (XVI), (XVII), (VI), (XIX), C(5) of (XV) and C(1) of (XVIII), (XX) coupling components. It should be mentioned that the (− SO₃H) group of (XIII) molecule and the (− SO₂NH₂) group of (XIV) molecule are removed through these reactions (Nenitzescu 1966, Part II, Chap. 5, pp. 590–593). Even though the C(2) atoms of (XIII), (XIV), (XVI), (XVII), (VI), (XIX) compounds and C(7) atom of (XV) molecule are positions with the highest electronic density, the electrophilic attacks do not occur at these atoms due to steric impediments. The structural indices (p_rs) and (F_r) calculated by HMO method for the atoms of these molecules, in turn, are correlated with aromaticity, and their basic or acidic character.

Considering the monosubstitued aromatic compounds: (XIII), (XIV), (XVI); (VI), (XIX); (XVIII), (XX), it can be observed the correlation between the decrease of the aromaticity and the increase of the p_C–O, p_C–N, values (Streitwieser 1961), which is in good agreement with the results of TOPAZ model (Tarko 2008).

The elevated values of the free valences calculated for nitrogen $({{\text{F}}_{\text{N}}}=1.42-1.44 )$ of the aromatic amines and oxygen $({{\text{F}}_{\text{O}}}=1.47-1.48 )$ of the hydroxyarenes are reflected in the chemical properties of the corresponding functional groups. Thus, the phenols and naphthols are week acids $({{\text{p}}_{{{\text{K}}_{\text{a}}}}}=9-10 )$ and the aromatic amines are week bases with stronger conjugated acids $({{\text{p}}_{{{\text{K}}_{\text{a}}}}}=4-5 )$ (Avram 1994, Chap. 19, 1995, Chap. 22). The rationale of choosing the molecules investigated within this study is mainly linked to the azo dyes that can be synthesized from these compounds (Table 11.19).

Table 11.19 Aromatic amines, hydroxy arenes and corresponding azo dyes. (Neniţescu 1968, Part IV, Chap. 5, pp. 430–436)

Among other applications, diazotization and coupling reactions are especially suited for measuring nitrites concentration in water samples. In comparison to potentiometric methods (Vlascici et al. 2007), the Aquaquant Kit 1.14408, by Merck KGaA Germany, is based on a colorimetric method which correlates the color intensity of SNED compound obtained from (IX) and (XIX) molecules (see Table 11.19) with the dosed anion concentration (Negreanu-Pirjol et al. 2012).

11.7 The Kinetics of Thermal and Photochemical Decomposition of Some Aromatic Diazonium Salts

Our investigations have been focused on the kinetics and mechanisms of thermal and photochemical decompositions of some diazonium salts, as well as on spectral studies and molecular orbitals in fundamental or excited state.

The HMO calculations of the molecular orbitals have allowed the correlation of thermal and photochemical characteristics with structural parameters. The sulphanilic acid and sulphanilamide diazonium salts , which are used in azo dyes industry, are photochemically stable but thermo-unstable conducting to a rapid decomposition with a high preexponential coefficient.

The ability to form dyes with coupling compounds and the loss of this capacity by exposure to light, encourage the use of diazonium salt of 4-N, N’-dimethylaminoaniline in diazotization processes.

The thermal and photochemical decompositions of the aromatic diazonium salts formally take place according to the same radical or ionic mechanism, depending on the medium and the reacting substances (Boudreaux and Boulet 1958; Simon and Bădilescu 1967; Simon 1966b).

A homolotic process has been reported for basic medium, in buffer alcoholic solutions, or in organic solvents as mixtures (benzene-tetramethylsulphone, or nitrobenzene-tetramethylsulphone) when the decomposition of the diazonium salts leads to the formation of an arylether.

In acidic medium water solutions, the thermal or photochemical decompositions follow a heterolytic mechamism with the formation of the phenol. The first determining rate step is the monomolecular dissociation of the C-N bond with the formation of N₂ and of the phenylcarbonium ion. In the rapid second step, the carbonium ion is saturated owing to the attack of a nucleophilic agent (Avram 1995, pp. 65).

The decomposition reaction rate is practically independent of the concentration and nature of the acids present in solution (De Tar and Kwong 1956). The temperature favors the decomposition of the diazonium salts (Table 11.20) (Isac et al. 1981b).

Table 11.20 Rate constant s for thermal decomposition of some diazonium cations in diluted solution at four different temperature values. (De Tar and Kwong 1956; Isac et al. 1981b)

Table 11.21 Arrhenius parameters for thermal decomposition of some diazonium salts (DS) in diluted solutions. (Crossley et al. 1940; Simon 1966a; Isac et al. 1985)

Table 11.22 Bonding activation energies in kcal/mol (Energy Units Converter 2014) for diazonium salts (DS) of Table 11.21, along the related bondonic radii of action, mass ratio respecting the electronic unit, and the bondonic gravitational ratio respecting the universal gravitational unit, according with Eqs. (11.37a, b, c), respectively

The bondonic information for molecules of Table 11.21 is reported in Table 11.22 and graphically represented in Fig. 11.13. It provides the specific behavior as:

Fig. 11.13

The graphical plot for the bondonic features of Table 11.22 in respecting the rate of reaction (LogK) at 25 °C for molecules of Table 11.21

• The bondonic information shape is presenting the extreme points for all bondonic radii paralleling gravitational and anti-paralleling mass actions: the minimum/maximum point for para and high logK molecular realization in Table 11.21 (DS2), and the maximum/minimum points for meta/ortho and lower rate reaction LogK for the diazonium salts of Table 11.21 (DS9 and DS10), respectively;

• The chemical reactivity may be indeed modeled by chemical bondonic information vs. rate reaction, since this going like a molecular potential itself—see the bondonic mass curve.

Back to the general-chemical structural analysis, the effect of electronegative substituents on the photochemical stability of the diazo compounds is inversed as compared to their effect upon thermal stability. The thermal stability of the 4-amino and N substituted 4-aminophenyldiazonium salts at room temperature is relatively high and the photochemical effects can be easily distinguished (Isac et al. 1981b). The sulphanilic acid, the sulphanilamide and 4-N, N’-dimethylaminoaniline were diazotized according to an analytical method (Ciuhandu and Mracec 1968).

The thermal and photochemical stability of the obtained diazonium salts was verified by a spectrometric method. The diazonium salts of sulphanilic acid and sulphanilamide are photochemically stable up to 353 K, but thermally instable; that is why the kinetics of their decomposition could be followed in the UV domain.

The diazonium salt of 4-N, N’-dimethylaminoaniline is thermally stable, but very sensitive photochemically, which allows the qualitative study of its photodecomposition in the UV and visible domain. There is a surprising effect of substituents upon kinetics of thermal and photochemical decomposition of aromatic diazonium salts (Table 11.21) (Isac et al. 1981b; Simon 1966a).

The substituents with − M and − I effect in meta or para positions decrease the reaction rates. Electron donor substituents in meta position increase the reaction rates, but the same substituents in para position strongly decrease the reaction rates. It is supposed that this stabilization is due to a resonance effect that increases the C–N bond order (Barraclough et al. 1972).

Table 11.23 shows a satisfactory correlation between the positions of experimental absorbtion maxima and the transition energies calculated by the HMO method (Isac et al. 1981a).

Table 11.23 Electronic transitions (nm) and molar extinction coefficients for the diazonium salts of sulphanilic acid, sulphanilamide and 4-N, N’-dimethylaminoaniline

Although the first calculated transition energies for the diazonium salts are too low, the relative order of the calculated transitions corresponds to the experimental one. Based on experimental data and reactivity indices calculated by HMO method we proposed structure-reactivity correlations for some diazonium cations (Table 11.24) (Isac et al. 1981a, 1985).

Table 11.24 Experimental data, energetic and structural indices for the diazonium cations of sulphanilic acid, sulphanilamide, 4-N, N’-dimethylaminoaniline, 1-naphtylamine and 2-naphthylamine

The results indicate a good correlation between the wave numbers (ν’_exp) and the calculated ε transition.

• The bond orders values obtained from calculations are correlated with the compounds structure, considering the single, double and triple character of the bond between the considered atoms. The molecular diagrams of diazonium salts suggest a triple bond character for the N-N bond and explain the fact that the diazo group is the well-known electron withdrawing substituent. The diazo group is a strong perturbator of the aromatic system and in this respect it may be compared with the nitro group (Evleth and Cox 1967).

• The π charge densities of the atoms from the diazonium groups are favored by the electron repulsive substituent (−N(CH₃)₂), but disadvantaged by the electron attractive groups (−SO₃H, −SO₂NH₂, −HN⁺(CH₃)₂).

• The high photochemical reactivity of 4-N, N’-dimethylaminobenzenediazonium cation can be explained as follows: even though present in small fraction, the monocation will have the absorption maximum significantly shifted to red (visible domain of diffuse light) due to the extended conjugated system. Moreover, the monocation has the highest value ε_LUMO  = α + 0.1111β among the diazonium salts. In this case, the pre dissociation mechanism (the transition from the potential curve of the excited state (ππ*) to the triple repulsive curve (πσ*)) would become preponderant (Simon and Bădilescu 1967).

Table 11.25 Transition energies in kcal/mol for the experimental wave-numbers (Energy Units Converter 2014) for the diazonium cations of Table 11.24 (taken as averages for DC1 and DC2 and lower value for lower LUMO and higher value for higher LUMO energies for DC3 and DC4), along the related bondonic radii of action, mass ratio respecting the electronic unit, and the bondonic gravitational ratio respecting the universal gravitational unit, according with Eqs. (11.37a, 11.37b, 11.37c), respectively

Finally, the bondonic information for molecules of Table 11.24 is reported in Table 11.25 and graphically represented in Fig. 11.14 with the following characteristic:

Fig. 11.14

The graphical plot for the bondonic features of diazonium cations of Table 11.24 respecting the related transition wave numbers of Table 11.25

• The bondonic quasi-linear monotonic shape of radii/gravitational and mass actions of associated bondons is again displayed since (i) the variation is respecting the experimental wave-number that is a frequency that is quantum mechanically related with an energy difference accounting for the quantum transition modeled—so again being driven by an energy difference in the same manner as was the case with bondonic vs. delocalization energy (where also an energy difference was assumed as independent variable), see Figs. 11.10 and 11.11; also the smooth non-linear effect is present since dealing with cations of Table 11.24 as were the ionic information present by the same effect in Fig. 11.11 too.

• The difference with Fig. 11.11 comes from the non-convergence of the radii and gravitational curves, here remaining indeed parallel, while both being in inverse variation with respect with bondonic mass, nevertheless still consistent with the phenomenology they represent: e.g. for higher wave-number/frequency a higher energy difference is measured so a heavier bondonic mass is associated; instead, restrained bondonic radii is manifested (due to higher accumulated inertia in bonding) that corresponds with even lower gravitational values since resuming to the chemical localization it encompasses.

11.8 Conclusions

In this chapter we have applied both the Hückel and DFT theory, but mostly the first one in order to describe the physico-chemical properties of some aromatic hydrocarbons and their derivatives with the aim of describing by the structure (valence) properties their reactivity as substrates and reactants involved in addition and substitution reactions with homolitic and ionic mechanisms, including aromaticity effects (Nenitzescu 1968, Part V). These two approaches have provided good correlations among the energetic indices calculated with regard to the substitution reactions in which these compounds are involved and the acidity and basicity of their functional groups, although the Huckel method seems to provide, in spite of their inherent approximation, more insight regarding the frontier electronic behavior and about the delocalization electronic features. This feature was tested also by the vanguardist approach of bondonic chemistry, by which the chemical bond is described with the help of the associated quantum quasi-particle called as bondon, see also the previous chapter (Putz and Ori 2015). By combining the Schrödinger with Bohmian description of electronic motion the main feature of bondonic particle were derived, having in the first site its predicted mass in terms of radii of action and of the binding energy (in kcal/mol); most interestingly, since of bosonic nature, when assuming the bondon as behaving like the photon in communicating the bonding information between the electrons of bonding, interesting features are emerging so that the gravitational effects are involved and predicted such that to overcome the “classical” electrostatic inter-repulsion among electrons in bonding; this approach follows the Fermi-Planck description of the early universe (the so called Planck Universe), however here adapted at the level of quantum nanochemsitry; in this context also the related bondonic action radii emerges as paralleling the gravitational effect: higher the bondonic action radii higher the gravitational influence need in order to keep bound such extended system; also the bondonic mass is reshaped, with gravitational effects, yet spherically correcting the Einstein basic mass-energy relationship, see Eq. (11.37b), due to the gravitational influence at the distance. However, apart of the new insight provided by bondon in the nature of the chemical bond, i.e. by considering its combined features of bosonating fermionic particle with the photonic properties and variable gravity parameter in chemical bonding , the actual bondonic triplet (radii, mass, and gravity) = $\left( {{X_{\rlap{--} B}},{m_{\rlap{--} B}},{G_{\rlap{--} B}}} \right)$ actions were specialized for all “classical” carbon systems considered, in order to explore various shape of information they contain as depending of various energetic representations. Accordingly, one represented the actual bondonic triplet: (i) respecting orbital energies and found the parabolic shape behavior confirming the chemical reactivity ansatz so disputed in conceptual DFT chemistry; (ii) respecting aromaticity (at its turn driven by chemical hardness) and found the bondonic behavior with peaks (of Gaussian type in DFT approach and by double-well potential for Hückel approximation) however different than those provided by chemical hardness driving aromaticity, so opening new perspective of aromaticity aka inertia in chemical reactivity by bondonic insight; (iii) respecting delocalization energies and by energy differences in general when the bondonic information display monotonic variation in chemical bonding, including also non-linear effects for the case of ionicity (salts, cations) present in chemical bonds/compounds; (iv) respecting the chemical reactivity feature as the reaction rate (LogK) when the bondonic information unfolds similar variation with the molecular interaction potential as a whole, so making it most reliable in capturing the very mechanism of chemical bonding at the nano-yet-entangled (long range with memory effects) level, all due to the present gravitational effects. At this point, one readily feels the need to finally re-discuss some consequences of having included gravitational arguments in chemical bonding by bondons, since being of striking interest for the present and future conceptual and predictive quantum chemistry. In this regard, say one likes to calculate the “classical” mechanical work ${{L}_{G}}=Gm_{0}^{2}/r$ produced by two attractive electrons in a chemical bond separated at the long range nano-distance $r=100\,[\text{{}\textrm{\AA}{}}]{}$: that gives about ${{L}_{G}}\cong G\times {{10}^{-52}}[Joule]\cong G\times {{10}^{-33}}[eV]$; next, when further considering the custom kcal/mol conversion and the bondonic representation of the gravitation by the specific transformation (11.37c) one arrives to the actual work function in terms of bonding energy ${{L}_{G}}\cong {{10}^{16}}/E_{bond}^{2}[kcal/mol]$, while not forgetting this expression has inside the electronic origin $(!{{m}_{0}})$ as the base of gravitational work; accordingly, when equating the last gravitational work with the bondonic Einstein energy $\left( {{L_{\rlap{--} B}} = {m_{\rlap{--} B}}{c^2}} \right)$ one gets the bondonic/electronic mass ratio ${m_{\rlap{--} B}}/{m_0} ~{\left[ {10E_{bond}^2(kcal/mol)} \right]^{ - 1}}$ so that generally achieving, e.g. for ${{E}_{bond}}\tilde{\ }100[kcal/mol]$ the correct fraction of ${\varsigma _m} = {m_{\rlap{--} B}}/{m_0} ~{10^{ - 5}}$ as recorded for in Table 11.9 for the specific aromatic compounds of Table 11.8 so confirming the correct and meaningful of the actual numerics as starting from the gravitational work between electrons in keeping/forming/stabilizing the chemical bonding by the bosonic bondon. Finally, worth addressing also the range of prediction for such bondonic information as based on gravitational effects in bonding: when going to thousands of [kcal/mol] in bonding energy , i.e. when dealing with larger molecules, say polymers or fragments of them thereof, one actually deals with bonding-gravitational work in the range of ${L_{G/\rlap{--} B}} ~{10^9}[kcal/mol] ~10'[MeV]$ that is specific to Gama (Y) rays spectroscopy, so experimentally achievable! Moreover, while having present that 1Mev accounts for double the rest energy of an electron $1[MeV]=1.602\times {{10}^{-13}}[Joule]\tilde{\ }2\times ({{m}_{0}}{{c}^{2}})$, there is immediate that the present prediction should correlate also with the number of bonds created or supported/involved in the observed bonding energy, thus giving the information also about the so called “active core” of the chemical compound—that that is activated by the bondonic action range associated with the bond energy detected. We are confident that all these issues will be on the frontline in the XXI structural physical-chemistry in general and in the description of the chemical bonding in special, while being further extended in analytical, conceptual, computational and experimental parts, within the bondonic chemistry.