Keywords

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Introduction

Fluctuations in key state variables (e.g., concentrations, velocities) caused by multi-scale heterogeneities contribute significantly to the space-time distribution of solutes in natural and reconstructed porous media. In reactive transport the fluctuations extend to the nature of chemical reactions between these solute (or reactant) distributions. Differences in theoretical approaches to modelling reactive transport in heterogeneous media lie largely in the treatment of the quantitative aspects of these fluctuations. We will concentrate on an approach that deals with modelling laboratory-scale experimental observations; it is particle tracking (PT), or more specifically, a PT implementation of the continuous time random walk (CTRW) framework (CTRW-PT). The CTRW-PT is a relatively recent treatment of reactive transport and is the basis of the successful modelling of the experimental observations of bimolecular (A + B → C) and multi-step chemical reactions. Treatments of these smaller scales, where the chemical reactions occur, play an important role in understanding upscaled processes such as geochemical effects on aquifer water quality induced by changes in precipitation and patterns of water flow, and the feasibility of CO2 sequestration in geological formations.

Particle tracking (PT) methodologies, first described by Smoluchowski [1] about a century ago, have been implemented widely in various fields of study [e.g., 2–8]. These studies suggest different ways to follow a particle while specifying, probabilistically, reaction rules among particles. Particle tracking techniques are considered to be effective in providing appropriate depictions of some of the salient features of reactive transport scenarios. This is due chiefly to the fact that they are prone to include simple formulations to account for pore-scale fluctuations of relevant quantities [2, 3, 5, 6, 9–12].

A detailed review of particle tracking methods, in the context of random walks, is given in [13]. In [14], a PT modelling approach is applied, within the continuous time random walk (CTRW) framework, to demonstrate the occurrence of non-Fickian transport in a random fracture network. Subsequently, Dentz et al. [15] showed that analytical and numerical solutions of the CTRW equations can be matched well using CTRW-PT simulations. An advantage of the CTRW-PT approach is that it allows considerable flexibility in the choice of probability density functions (pdf’s) that govern particle motion in space and time [16]. The solutions of the advection-dispersion equation (ADE) are reproduced using an exponential (in time) pdf together with a spatial pdf having finite moments (e.g., an exponential pdf). Employing instead a truncated power law (TPL) for the temporal pdf results in a full range of non-Fickian behaviors [16, 17].

The PT approach can be shown to converge to a continuum description, so that PT represents in some sense both a “discrete random walk” and a means to solve a continuum equation, without the need to define a mesh in a numerical solution. Indeed, it has been noted [18] that, at least in principle, Eulerian and Lagrangian descriptions of (reactive) transport should yield identical results. However, to capture (at least partially) fluctuations in the local-scale reactant and product concentration distributions, descriptions based on deterministic models of reactive transport, such as the advective-dispersion reaction equation (ADRE), may require high spatial resolution. A critique of this approach is given by [2], who demonstrate agreement between a high resolution numerical solution of the continuum-scale equation and simulations using the stochastic model of [10, 19, 20].

In Sect. 21.2 we briefly review the salient points of CTRW and its major application to non-Fickian transport, which is ubiquitous in heterogeneous media. We introduce PT techniques and show the connection to CTRW. In Sect. 21.3 we focus on the two different problems, which have been the subject of several theoretical and experimental works: (21.1) a bimolecular reactive transport (A + B → C) scenario in a passive (non-reactive) porous medium, and (21.2) a multi-species reactive system, as exemplified in the context of dedolomitization, where both precipitation and dissolution occur. Section 21.4 contains a discussion of our interpretive results.

2 CTRW and Particle Tracking

Random walk models are among the most significant in science and yet are based on a simple structure: a recursion relation wherein the space-time increment of each step is drawn from a common distribution ψ(s, t) and follows from the previous step,

$$R\left(\boldsymbol{s},t\right)={\displaystyle {\sum}_{s\mathit{{^{\prime}}}}{\displaystyle {\int}_0^t\psi \left(s-s\mathit{{^{\prime}}},t-t\mathit{{^{\prime}}}\right)R\left(s\mathit{{^{\prime}}},t\mathit{{^{\prime}}}\right) dt\mathit{{^{\prime}}}+{\delta}_{\mathbf{s},0}\delta \left(t-{0}^{+}\right)}}$$
(21.1)

where R(s, t) is the probability per time for a walker to just arrive at site s at time t. The CTRW includes a random time for each step, and the main character of the pathways depends on the functional form of ψ(s, t). P(s, t) is the probability to be found at s at time t and is determined by R(s, t) [17]; it is the normalized concentration and is developed into a nonlocal-in-time pde. This equation reduces to an ADE for an exponential Σ s ψ(s, t) ≡ ψ(t). The exponential behavior describes a single rate (or transition time) between sites and is appropriate for a homogeneous material. Heterogeneity induces a spectrum of rates, which can be captured by a power-law time dependence, ψ(t) ∼ t −1−β, β <2, cf. discussion below. A compact illustration of the capacity of CTRW with a truncated power law ψ(t) to account for highly dispersive breakthrough curves (BTC), with essentially one parameter β, is shown in Fig. 21.1; see [17] for full details.

Fig. 21.1
figure 1

Measured BTC with CTRW/ADE fits for a Berea sandstone core, using a truncated power law function with β = 1.59. Here the quantity j represents the normalized, flux-averaged concentration. (top) Complete BTC. (bottom) Region identified by the bold-framed rectangle in top plot. Note the difference in scale units between the plots. Column length equals 0.762 m. Porosity n = 0.204. Flux q = 1.73 cm3/min. Dashed line is the best ADE model fit. Solid line is the best CTRW fit (Data from Scheidegger and Berkowitz [21])

Full size image

As outlined in Sect. 21.1, simulation via PT is highly flexible. The character of the transport and reaction can be changed significantly, with the choice of the pdf’s affecting the space-time transitions. We use PT to implement the CTRW, i.e., equivalent to solving (21.1), with power law pdf’s. This is a relatively new application; it has been demonstrated that the CTRW-PT yields the same results as the solution of the non-local (in time) pde formulation of CTRW [15, 16]. However, in the simulation of reactive transport (see below), the CTRW-PT cannot be compared to a corresponding pde because a reaction term for this non-local pde has not yet been constructed. Hence, the PT implementation of non-Fickian transport in combination with multistep and multi-species reactions is unique.

In this CTRW-PT [15, 16], the movement of each particle is governed by the equation of motion:

$$ {\mathbf{s}}^{\left(N+1\right)}={\mathbf{s}}^{(N)}+{\varsigma}^{(N)};{t}^{\left(N+1\right)}={t}^{(N)}+{\tau}^{(N)} $$
(21.2)

where a random spatial increment ς(N) and a random temporal increment τ (N) are assigned to each particle transition from ψ(s, t) or the decoupled form p(s)ψ (t). For each N step, a velocity v can be derived by ς(N)/τ (N). During a simulation, particles are followed over a set of sample times. At each one, the locations of all particles are recorded (even in “mid-flight”). As described below, this information is of particular value for proper quantification of reactive transport.

The p(s) is chosen to be an exponential λ s 2exp(−λ s s) throughout (for the angular part see [16]). For the ADE (Fickian) the ψ(t) = λ t exp(−λ t t) and for the heterogeneous cases ψ(t) = Ωexp(−t/t 2)/(1 + t/t 1)1+β a truncated power law (TPL), where Ω is a normalization coefficient. The TPL is governed by three parameters: a power law exponent β, a characteristic transition time t 1, and a cut-off time to Fickian transport t 2 (see, e.g., [17] for details).

We now include chemical reactions among particles into the CTRW-PT to simulate reactive transport. In one example, for bimolecular reactions discussed in Sect. 21.3, the CTRW-PT methodology is straightforward. Two types of particles are defined, A (“inflowing” particles) and B (“resident” particles), and their movement is governed by the equations of motion (21.2). At each time interval, Δt, all particles in the system are frozen in mid-flight. The minimum distance between A and B particles is determined iteratively until all possible pairs have been checked; the particular details of the A and B particles are updated and recorded. A reaction A + B → C (where C replaces the A and B particles, which are removed from the simulation) takes place if this minimum distance is smaller than a prescribed radius of interaction, R (see below). Each C particle is located at the average position between the A and B particles it replaces; the motion of the C particles follows the same transport rules as those specified for A and B. In each time interval, the entire process is repeated until all possible reactions between A and B particles, lying within the interaction radius R at a given time interval, are allowed to occur. The reaction behavior is controlled largely by this radius, which is chosen to be at the pore scale. The time interval, Δt, affects the estimated amount of mixing – and thus the degree of reaction – in the sense that increasing the value of Δt allows more time, before carrying out the calculation step for the reactions, for the plumes of A and B particles to spread and overlap. As a consequence, the choice of Δt affects the number of C particles produced at any given time; obtaining a more continuous temporal assessment of the reactions requires that Δt be sufficiently small.

In another example, one can define different ways to account for reactions in a concentration-based algorithm. Each simulated particle is a representation of a fractional mole amount for one reactant in an experiment. The algorithm will divide the simulated domain into a grid, where for each Δt the concentration of reactants is calculated for each cell. From the concentrations, one can establish the local reaction for each cell without using R as the reaction radius. Using such a scheme, we have incorporated, e.g., precipitation and dissolution with multispecies reactive transport; a detailed account can be found in [22] (discussed in detail below, in Sect. 21.3.2).

3 Experimental and PT Modelling of Reactive Transport

3.1 Bimolecular Reactive Transport

We consider the experiment on bimolecular reactive transport presented in detail in [23]. Colorimetric reactions between CuSO4 and EDTA4− were measured in a one-dimensional (on average) flow field; the flow cell has dimensions 36 cm (length) × 5.5 cm (width) × 1.8 cm (depth), and was packed with cryolite beads. The flow cell was saturated with EDTA4− (denoted as B particles) and CuSO4 (denoted as A particles) was subsequently injected as a step input. The mixing and reaction zone of the product CuEDTA2− were measured via fluorescence. These experiments are characterized by large values of Pe (≈O(103)) and Da (≈O(1012)), indicating that advective and reactive processes are significantly faster than diffusion.

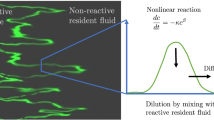
Pore-scale fluctuations in concentrations are visible in the experiments in [23]. Clearly, the dispersion is not uniform and the reaction fronts (forward and backward tailing regions) are not uniform or sharp. Rather, as emphasized in [24], colorized “islands” of pixels are distributed broadly and heterogeneously in these regions, demonstrating “isolated” reactions occurring far from the CuEDTA2− plume center of mass; also sharp localized concentration gradients can be observed. This behavior suggests significant non-uniformity in reactant mixing and product spreading. Close inspection of Fig. 21.4 in [23] reveals pronounced tailing effects in the cross-sectional averaged concentration profile which are not captured by an ADE.

There have been several efforts to model these data [9, 23–26]. Gramling et al. [23] use an analytical solution of the ADRE which was derived on the assumption that the concentration of the limiting reactant is instantaneously and completely consumed in the reaction. They observe that this analytical solution significantly over-estimates the space-time evolution and the total production of C in the system. Indeed, the ADRE solution overestimates the peak concentration value by as much as 40 % as compared to the measured one; similarly, the estimated cumulative mass production is up to 20 % larger than the measured production.

In [9, 24] CTRW-PT simulations consider particle transport in a rectangular, two-dimensional domain, with impermeable horizontal boundaries and fixed flux vertical boundaries. The domain is filled initially with a low concentration (c B ) of uniformly distributed B particles. At t = 0, A particles are introduced at the inlet boundary with the same concentration c A as c B . Technical details regarding insertion of A particles into the domain, treatment of boundary conditions and sensitivity to the selected time interval Δt are reported in [9, 24].

Figure 21.2 contains the experimental data from Figure 5b of [23], showing the temporal evolution of the spatial concentration profile of C particles at three different observation times. The figure reports the results obtained by [24] using a TPL-PT, which is marginally Fickian with the power law exponent β = 1.96 (β ≥2 is Fickian), together with the Fickian ADE-PT. Note that in the CTRW-PT approach, for β >1, the mean location of the tracer plume scales as t, and the standard deviation σ ∼ t (3−β)/2, whereas for the ADE-PT, σ ∼ t 1/2. For discussion of the red line we refer the reader to [26]. The dotted line is the analytical solution adopted in [23] which assumes instantaneous reaction with complete pore-scale mixing. It is significant that [24] calibrated their model parameters against a subset of the measurements, and provided predictions that match the remaining measurements. In these plots, the parameters are tuned manually until a satisfactory visual fit is obtained in [24]. Note that the ADE-PT model is unable to capture the forward and backward tails of the C profiles.

Fig. 21.2
figure 2

(a) Particle tracking simulations with the non-Fickian CTRW [24] (jagged blue line), and ADRE solution of [26] (smooth red line), compared to the experimental measurements of [23] (dots) and the ADRE solution of [23] (dotted line), showing the relative concentration of C particles at different times. (b) Particle tracking simulations with a Fickian ADE [24] (jagged line), compared to the experimental measurements of [23] (dots) and the ADRE solution of [23] (dotted line), showing the relative concentration of C particles at different times. In both (a) and (b), the PT simulations of [24] and ADRE solution of [26] were fit to the measured profile at t = 619 s, and the same parameters were used as predictions for the two later times t = 916 s and t = 1,510 s

Full size image

The time evolution of the measured cumulative mass of CuEDTA2− produced is presented in Fig. 21.3 for the same experiment shown in Fig. 21.2. Data are contrasted against the modelling results of [23, 24, 26]. The agreement between experiments and the models is remarkable, considering the limitations associated with the concept of effective dispersion and reaction rate. One can note that at early times the reaction is relatively fast. The mass production rate, which is the temporal derivative of the curve in Fig. 21.3, then displays a power law decay (see Figure 3a in [24]) with time, being controlled mostly by the slow diffusion of the reacting species into and out of the low velocity pores, causing incomplete mixing. The PT simulations in Figure 3a of Edery et al. [24] indicate ongoing reactions, even after long time periods, which suggest the occurrence of rare fluctuation-dominated dynamics. The fluctuation-dominated dynamics in the velocity are apparent in a phase diagram that shows, for each reactant, the median velocity of the reacted particles vs. median of the total particle velocity (see Figure 7 of [24]). This diagram shows different distribution functions (ADE-PT, TPL-PT), and illustrates that the (inflowing) A reacting particles have an overall higher velocity relative to the mean, or median, velocities of the total set of particles, while the (resident) B reacting particles have an overall lower velocity. These systematic deviations from the average velocity are caused by fluctuation-dominated mechanisms. It is also demonstrated that the TPL-PT, which has a heavier weighting on the tails, affects the magnitude of the fluctuations more strongly than the ADE-PT. The mixing dynamics produce a void area between the A and B profiles. As the void develops only a portion of the A, B transitions can cross the void. An analytic treatment and further theoretical developments are presented in [24].

Fig. 21.3
figure 3

Total mass production given from the particle tracking simulations of [24] (smooth line) and ADRE simulations of [26] (dashed line), compared to the experimental measurements (large dots) and the ADRE standard pore-scale mixed model of [23] (dotted line)

Full size image

3.2 Multispecies Heterogeneous Reaction

In this section, we model a different reactive transport scenario – an experiment of dedolomitization [27]. The major change is the necessity of accounting for multi-step, multi-species reactions, which are both reversible and irreversible in a reactive medium. The framework of the reactions is:

$$ \mathrm{CaMg}{\left({\mathrm{CO}}_3\right)}_2+{4\mathrm{H}}^{+}\to {\mathrm{Ca}}^{2+}{+\mathrm{Mg}}^{2+}{+2\mathrm{H}}_2{\mathrm{CO}}_3 $$
(21.3)
$$ {\mathrm{H}}_2{\mathrm{CO}}_3\leftrightarrow {\mathrm{H}}^{+}+{\mathrm{H}\mathrm{CO}}_3{}^{-} $$
(21.4)
$$ {\mathrm{HCO}}^{-3}\leftrightarrow \mathrm{H}^{+} +{\mathrm{CO}}_3{}^{2-} $$
(21.5)
$$ {\mathrm{Ca}}^{2+}+{\mathrm{CO}}_3{}^{2-}\leftrightarrow {\mathrm{Ca}\mathrm{CO}}_3 $$
(21.6)

In principle one could set up nonlinear coupled pde’s for each reactant and solve the equations with incorporation of the effect of medium heterogeneities or use a PT, Sect. 21.2, for each reactant and specify for each one a local reaction scheme. Both of these alternatives for (21.3), (21.4), (21.5), and (21.6) would be rather daunting. Fortunately, a few simplifications of (21.3), (21.4), (21.5), and (21.6) make the problem tractable.

As detailed in [27], we consider a column packed with crushed sucrosic dolomite, CaMg(CO3)2 (containing 1.5 % calcium carbonate CaCO3), in the form of particles having a diameter range of 350–500 μm; hence it is one of the abundant species. A mixture of CaCl2/HCl in water is injected across the entire inlet boundary of the column, which results in the dissolution of dolomite and precipitation of CaCO3; Ca2+ is also one of the abundant species.

The reaction cascade (21.3), (21.4), (21.5), and (21.6) is irreversibly initiated by the local pH. The two middle reactions, (21.4) and (21.5), are reversible and sensitive to the local pH. We assume these reactions constitute a local carbonate equilibrium and an input of H2CO3 produces an output of CO3 2−, which immediately reacts with the abundant Ca2+ to produce CaCO3. The framework (21.3), (21.4), (21.5), and (21.6) simplifies to

$$ D+2h\to 2A $$
(21.7)
$$ A\leftrightarrow h+C $$
(21.8)

where D = dolomite, A = H2CO3, C = CaCO3 and h = 2H+. In a low pH region, there is dissolution of D, (21.7), and C (in the sucrosic dolomite) h + C → A, (21.8). In a high pH region there is precipitation of C, A → h + C, (21.8).To subordinate (21.4), (21.5), (21.6), and (21.8), we require a figure of merit of the carbonate equilibria to produce A as a function of the local pH. We use as the cumulant of this probability pdf that A is produced as the fraction (as a function of pH) of A in the carbonate equilibria

$$ {a}_1\left(\mathrm{pH}\right)=\frac{10^{-2\mathrm{pH}}}{10^{-2\mathrm{pH}}+{10}^{-2\mathrm{pH}-\mathrm{pKa}1}+{10}^{-\mathrm{pKa}1-\mathrm{pKa}2}\ } $$
(21.9)

with the standard values pKa1 = 6.35, pKa2 = 10.33 [e.g., 28] and a range 0 ≤ α1 ≤ 1. The reactive transport with (21.3), (21.4), (21.5), and (21.6) is represented by the PT of the species h and A with the initiating dissolution reaction governed by the local pH, with accounting for either (21.7) or (21.8) (arrow to the left). The fluctuations of the transport and the chemical reactions are modeled with the TPL-PT resulting in a profile of h, which produces A with the probabilistic weighting of α1(pH). In essence, the system of reactions (21.7) and (21.8) is an interchange of A and h with interaction with the abundant D, C and Ca2+ as sources and sinks.

There is an additional level of fluctuations due to the modification of the medium by the reaction, i.e., changes in local porosity by precipitation of C and dissolution of D and C. The feedback from the porosity change is the effect on the local flow, which can subsequently change the precipitation pattern. This pattern, which we refer to as “banding”, is affected by a number of parameters and is the key to our comparison to the experimental observations. To develop this picture fully, we describe the PT simulation of the h and A dynamics.

The details of the simulation algorithm are contained in [22]; basically we consider a two-dimensional rectangular column medium, with the C and D particles being distributed either uniformly or heterogeneously, divided into cells 1 mm × 1 mm. The numbers of A and h particles, which are advanced by TPL-PT, in each cell, are updated iteratively during each time step. With a uniform injection of Ca2+ and H+ across the entire inlet boundary, we track the local pH fluctuations along the advancing front – the pH in each cell. The updated pH in each cell, denoted pHloc, determines the value α1(pHloc). If a chosen random number U (0 ≤ U ≤ 1) is less than this value, dissolution occurs; otherwise, precipitation occurs. To facilitate the computation, the number of injected H+ particles is restricted to 104, so that each particle carries a parcel of moles of H+ to account for the total injected pH, e.g., pH = 3.5. The time interval Δt sets (using the average velocity) the average distance each particle can traverse before being allowed to react.

At each Δt, all particles are “frozen” in space and the possible chemical reactions are determined. All cells are examined according to the dissolution/precipitation process described above, with reaction (21.8) proceeding in one of two directions. After the dissolution of C do we allow D particles (dolomite) to take part in the dissolution process. In this case, dissolution of D, following (21.7) requires two h particles and produces two A particles in each reaction. The A particles are subsequently transported similar to the h particles. Similarly do we determine calcium carbonate precipitation.

In a porous medium, a particle will in general move more slowly in a denser cell (densities of dolomite or calcium carbonate particles) or, often bypass it, preferring to advance more easily in a less dense cell. These spatial variations will in turn alter the precipitation/dissolution patterns, causing a feedback between the flow pattern and the density in the cells. To mimic these feedback mechanism effects in our PT simulations, we modify the velocity distribution as a function of the local (cell) density of C and D particles.

The key comparisons to the experimental data of [29] (especially Figure 6 within that paper), to our simulation results are given in the patterns of the spatial distributions of CaCO3 as a function of the pH of the injected fluid and the flow rate Q as well as other variables within this broad range we have produced patterns similar to the observations of [29] with the same sensitivity of these patterns to the various parameters.

We restrict our results here to a limited set of parameter values. We fix pH = 4.5, 3.5, Q = 1.5, 5 cm3/min, Δt = 6 s, β = 1.8 and R = 0.03. In Fig. 21.4, observe the strong decrease in the presence of D and C particles near the inlet, at all times. This is due to the rapid drop in pH (from the initial fluid value of 8) with the injection of h particles dissolving C and D particles and producing A particles. Subsequently, downstream each A can precipitate as a C. The overall growth in C is highly irregular in space and time, as in Fig. 21.4 at t = 1,500 min; three maximum concentration values appear at x = 7, 15, and (on average) 22 cm. This corresponds to a banding effect, with a relatively clear temporal evolution. The main difference between this set of bands and the one given in Figure 6 in [29] is the level of “noise”. The statistics of C precipitation are less averaged due to the computational demands involved with tracking each H+ particle discussed above.

Fig. 21.4
figure 4

The time evolution of the amount of calcium carbonate relative to the total amount of initial dolomite and calcium carbonate (C 0), for an initially heterogeneous distribution of dolomite and calcium carbonate, with pH = 4.5, Q = 1.5 cm3/min (After [22])

Full size image

We define a precipitation band as the increase in cross-sectional concentration of C particles, along the x-axis, followed by a subsequent decrease farther along the x-axis. The phenomenon of banding, its detailed shape definition, and its position are due to a number of factors. These factors affect the dynamics of the h particles, which play the main role in the production of A, via (21.7). In a low pH environment, C and D are dissolved where the production of A replaces the h, creating a higher pH environment. The A particles that escape from the low pH cells, due to faster-than-average local velocity, cause precipitation and the peaks of C. When precipitation of C occurs, h particles are released and advance downstream, subsequently dissolving regions beyond the peaks. This process, which leads to distinct regions of precipitation and dissolution, occurs because the advancing h and A particles do not move uniformly in space.

We have demonstrated how simplified chemical rules can be combined with detailed simulation of transport to mimic the dynamic patterning of precipitation and dissolution, and evolution of calcium carbonate banding, which result from dedolomitization. The core of the simulations is the novel treatment of the injected H+ particles as the key reactant. The H+ particles initiate the dissolution reaction and determine the chemical environment for precipitation of CaCO3. In both reactions, there is also modification of the medium leading to local changes in the permeability field and the flow patterns in the cell. The flow patterns effectively change the local pH levels, and the entire cycle is subsequently updated.

4 Discussion and Perspectives

There is a large array of configurations to consider for reactive transport in heterogeneous media, each with distinct subtleties. We specialize to the one common to the laboratory experiments discussed in this paper, namely, the step injection of chemicals into a prepared reservoir of reactants. Distinct features associated with such experiments include the transport or spreading of the reactants, the nature of the chemical reactions, the evolution of the mixing zone, and the feedback of a medium affected by the reactions. We assess the role of fluctuations of pore-scale state variables, induced by the structure of the porous medium, on these features. The accurate characterization of fluctuations necessitates departure from an average quantity. The nature of the average in turn becomes an important issue, e.g., is the particular procedure adopted for averaging concentrations and reactions suppressing the effect of fluctuations? We discussed above these aspects for two prototype scenarios, for which detailed measurements at the laboratory scale are available. We focused on modelling techniques based on a PT approach that involves an implementation of CTRW that is not a particle tracking method per se, in the sense that particles are not advanced by advection along streamlines and by diffusion/dispersion by a random component. Rather, the CTRW-PT involves the use of appropriate pdfs describing the space-time transitions, which have been shown in extensive testing to account for anomalous (non-Fickian) transport in a variety of laboratory and field observations. The method provides a good model to account for the effect of small-scale fluctuations on the advancing profile(s). Hence, the intimate connection between fluctuations in the transport and fluctuations in the reactions is clear.