Instrumental Variables: Conceptual Issues and an Application Considering High School Course Taking

Abstract

Policymakers are becoming increasingly adamant that the research they use to evaluate educational interventions, practices, and programs can support statements about cause and effect. An instrumental variables (IV) estimation approach, which has historically been employed by economists, can be utilized to make causal statements regarding a predictor and an outcome when randomized trials are not feasible. In this chapter, we provide an overview of the IV approach as we explore the causal relationship between taking Algebra II in high school and degree attainment in college. We discuss concepts and terminology related to conducting experimental and quasi-experimental work, present the assumptions that should be met by an IV before a researcher can use it to make causal inferences, and demonstrate several IV estimation strategies. Additionally, we provide the reader with annotated Stata code to facilitate the application of this underutilized methodological approach in higher education research.

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

Introduction

In response to falling high school graduation rates and concerns about college readiness and workforce development over the past decade, 20 states have increased high school graduation requirements. While these requirements vary across states, most mandate that students complete 4 years of math and English coursework in order to graduate (Achieve, 2011).

Michigan is one example of a state implementing curricular changes in favor of more demanding coursework for high school students. In 2006, legislators implemented a statewide college preparatory high school curriculum—the Michigan Merit Curriculum (MMC), one of the most comprehensive sets of high school graduation requirements in the nation. The new courses required in order to graduate are intensive and specific: Algebra II, Geometry, Biology, and Chemistry or Physics and at least 2 years of a foreign language (Michigan Department of Education, 2006).

The curriculum’s focus on math and science is based on historically low enrollments in the state in advanced courses in these areas. Prior to the implementation of the MMC, only one-third of Michigan’s school districts required students to take 4 years of math. As such, only 1 out of 8 students took Algebra II, instead favoring less intensive math courses, or no math courses at all (Michigan Department of Education, 2006).

There is an ample body of research that supports states’ decisions to make these curricular changes and to support an emphasis on math coursework to meet goals related to college and workforce readiness. Research demonstrates that students who take and succeed in intensive math courses have an increased likelihood of attending college and have improved long-term labor market outcomes (Adelman, 1999; Goodman, 2008; Levine & Zimmerman, 1995; Rose & Betts, 2004; Sadler & Tai, 2007; Sells, 1973; Simpkins, Davis-Kean, & Eccles, 2006).

One of the most powerful levers driving these changes to high school curricula in Michigan and throughout the nation is Answers in the Toolbox and The Toolbox Revisited, publications of the United States Department of Education that assert that students who take more intensive math courses, particularly those who take Algebra II or higher, are more likely than their peers who take less intensive math courses to attend a college or university and to attain a degree. The discussion surrounding these publications served as an inspiration for a number of states to begin adopting more intensive graduation requirements, particularly related to math preparation (Adelman, 2006).

It is important to note that the majority of the literature on which the curricular reforms in Michigan and around the nation were based is correlational in nature. The relationship between intensive math courses (e.g., Algebra II) and postsecondary access and completion maybe influenced by many other factors that are not accounted for in the studies touting the merits of students completing challenging math courses. We will provide an example of the influence of other factors in the case of Grace and Adam below.

Consider Grace and Adam, two high school students in Michigan. Prior to the implementation of the MMC, Grace chose to take Algebra II, whereas Adam did not. Grace, a straight A student, was recommended for the course by her guidance counselor, whereas Adam’s teachers suggested that he may be better suited for a lower-level math course. Grace and Adam have different abilities and motivations, and, as such, the highest level math course they choose to take differs.

The methodological issue in the case of Grace and Adam, as well as with some of the studies mentioned above, is one of self-selection. Students like Grace, who chose to take a more intensive math course, are quite likely different than students like Adam, who chose to take a less demanding course. Students like Grace may possess greater academic abilities or may be more motivated to take challenging courses than their peers like Adam. As such, studies that do not account for these differences in student characteristics are making comparisons between groups of students that are not comparable. It is problematic, therefore, when the findings of studies that do not consider these differences in student characteristics are used to drive education policymaking.

The highest level of math that students like Grace and Adam choose to take (Algebra II for the former, something less intensive, like Consumer Math, for the latter) may be related to whether or not they complete college following their graduation from high school. Or, stated differently, the factors that drive them to take a challenging or less challenging math course may also influence college outcomes. However, it is difficult to state, given the differences in Grace’s and Adam’s academic characteristics and motivation, that the highest math course they took caused them to complete college or not. To better determine if a causal relationship exists between a student’s highest math course in high school and college completion, education researchers can employ a number of statistical methods to investigate the variation in an outcome (college completion) that is caused by a particular program or policy—in this case, taking an intensive math course in high school. To be clear, we are interested in determining a causal effect (rather than a simple association) so that policies related to the outcome of interest are made appropriately and efficiently, such that resources are not wasted on a program or intervention that may not have the intended results.

To investigate the causal impacts of educational interventions and policies on student outcomes, many educational researchers have recently begun to employ experimental and quasi-experimental methodologies (Abdulkadiroglu, Angrist, Dynarski, Kane, & Pathak, 2011; Attewell & Domina, 2008; Bettinger & Baker, 2011; Dynarski, Hyman, & Schanzenbach, 2011). In the study presented in this chapter, we follow this lead by employing methods that can help us establish whether a causal relationship exists between taking Algebra II or higher in high school and college completion.

Experimental research is considered the “gold standard” of causal analysis (United States Department of Education, 2008). Performing a random experiment would, in theory, be the most effective way to determine the causal effect of taking Algebra II on academic outcomes (e.g., high school completion, postsecondary attendance and completion, life-course events). For example, students could be randomly assigned to take Algebra II or a less intense math course, and their postsecondary enrollment and completion patterns following graduation could be examined to determine the causal impact of Algebra II. Assuming that the randomization was done properly, the two groups would be, on average, identical on all observable and unobservable outcomes. If so, one could simply compare the rates of degree attainment between the treatment (Algebra II) and control (lower-level math) groups in order to determine the causal effect of high school course taking (McCall & Bielby, 2012).

Experimental research is, however, often difficult or impossible to do in educational settings because of logistical, cost, and ethical constraints. For example, often times educators cannot in good conscience randomly assign students to courses that will disadvantage some students. If an administrator suspects, for example, that enrolling a student in a small class with an outstanding teacher will dramatically improve his learning, how can this administrator support an experiment that will withhold this “treatment” from some students? Randomized trials can also be very costly to conduct or difficult to implement in educational settings. Given these difficulties, researchers have begun to rely on quasi-experimental methods, to be explored in greater depth below, to determine the impact of various education interventions, including those related to intensive math course taking in high school.

The objective of this chapter is to provide the reader with an introduction to the application of one such technique, instrumental variable (IV) estimation, designed to remedy the inferential problem discussed above. We provide the reader with a description of relevant literature and conceptual issues, the terminology used when discussing IV analyses, and how this method can be applied to educational issues. To inform the latter, throughout the chapter, we provide an example of the application of IV methods to study whether taking Algebra II in high school has a causal effect on college completion.

Conceptual Background

Education stakeholders have been concerned about student course taking at the secondary level and its potential impact on educational and labor market outcomes for decades. In A Nation at Risk (National Commission on Excellence in Education, 1983), the American high school was famously characterized as providing a “smorgasbord” of curricular options that were detrimental to the majority of students, as many oversampled the “desserts” (e.g., physical education courses) and left the “main course” (e.g., college prep courses) untouched. Since the 1980s, a widespread increase in the state- and district-mandated minimum number of core academic courses students must complete to graduate has increased the number of units they complete in math, science, English, and other nonvocational subjects (Planty, Provasnik, & Daniel, 2007). However, the intensity of the coursework that students complete within these domains varies considerably.¹

Researchers have documented disparities in the highest level of math coursework taken between racial/ethnic groups and social classes. Analysis of course taking trends in national data indicates that although Black and White students earn the same number of math credits in high school, White students are significantly more likely than Black students to have earned these credits in advanced courses such as Precalculus or Calculus (Dalton, Ingels, Downing, & Bozick, R, 2007). There are also disparities between students from low- and high-socioeconomic (SES) backgrounds in both the number and type of math credits earned. These statistics suggest that access to coursework is distributed through mechanisms that differentially impact students from various backgrounds.

Two mechanisms may determine student access to high school coursework: structural forces and individual choices (Lee, Chow-Hoy, Burkam, Geverdt, & Smerdon, 1998). Structural forces are factors outside the student’s control that serve to constrain his or her options. These include placement into curricular tracks by school personnel or the availability of coursework within their particular school. When schools have fewer structural constraints on course options, students are able to exercise greater individual choice by choosing their coursework from a menu of options that provide credits toward the high school diploma. The following sections discuss how structural and individual factors influence the coursework that high school students take.

Structural Forces

Student course taking patterns are strongly influenced by the options available to them. Schools may vary in their willingness and ability to offer a range of courses that are viewed as solid preparation for college. For instance, analysis of national transcript data indicates that Midwestern, small, rural, and predominately White high schools are the least likely to offer advanced placement (AP) coursework (Planty et al., 2007). The practice of “tracking” in K-12 education, or the grouping of students into curricular pathways based on their perceived academic ability, can also serve to constrain student course taking options (Gamoran, 1987). Research on how tracking decisions are made by high school staff indicates that placement decisions are largely a function of a student’s position in the distribution of standardized test scores, their perceived level of motivation, recommendations from middle school teachers, and the availability of school resources (Hallinan, 1994; Oakes & Guiton, 1995). Also, parent wishes may be accommodated when making track placements, although middle- and upper-class parents are likely to have an advantage in advocating for their preferences, as they more often possess the social capital needed to navigate bureaucratic educational environments (Useem, 1992).

Although formal tracking policies have been abolished in many schools, students may continue to experience barriers to unrestricted enrollment in coursework. This is often due to disparities in information about course options and uneven enforcement of course prerequisites across racial/ethnic, social class, and ability groups (Yonezawa, Wells, & Serna, 2002). Course prerequisites play a significant role in restricting access to math coursework because the courses are typically hierarchically arranged in a specific sequence (e.g., Algebra I is followed by Algebra II) beginning in middle school or even earlier (Schneider, Swanson, & Riegle-Crumb, 1998; Useem, 1992). Therefore, it should come as no surprise that middle school math achievement is one of the most significant predictors of taking advanced math courses in high school (Attewell & Domina, 2008).

Disparities in course placement practices and the availability of information about course options within schools may partially explain the finding that disadvantaged students who attend integrated schools take less intensive coursework than their peers who attend segregated schools (Crosnoe, 2009; Kelly, 2009). For instance, Crosnoe finds that low-income students who attend predominantly middle- or high-income schools take lower levels of coursework than low-income students who attend predominantly low-income schools. Similarly, Kelly finds that the greater the proportion of White students in a school, the lower the representation of Black students in the two highest math courses. These results demonstrate that in addition to the allocation of access to intensive courses across schools, the distribution of access within a school plays a key role in structuring student course taking patterns.

Individual Choices

Despite formal or de facto tracking, most students have the ability to choose some of their high school coursework. Schools are more likely to condone downward “track mobility” than upward, allowing students to choose lower-level coursework than originally assigned (Oakes & Guiton, 1995). Additionally, once minimum graduation requirements are met in each subject, students have the option to continue taking advanced coursework if they have demonstrated competency in previous courses. Researchers often examine the progress of students through the sequence of math courses (the mathematics “pipeline”) to determine the highest level of mathematics coursework students are able to take (Burkam & Lee, 2003; Lee et al., 1998). National data indicate that a large proportion of students—44%—choose to drop out of the pipeline at either Algebra I or Algebra II (Dalton et al., 2007).

Educational aspirations also play a key role in determining the coursework that students pursue. High school freshman and sophomores who report having college aspirations are more likely to take advanced math coursework during subsequent years than their peers with lower educational aspirations (Bozick & Ingels, 2008; Frank et al., 2008). Parent aspirations for their children are important as well. After controlling for confounding factors, parent educational expectations significantly predict whether students take advanced mathematics in the senior year of high school—a year when many students choose to stop taking advanced mathematics (Ma, 2001). Additionally, peers can influence course selection. Frank et al. find that females progress farther in the math pipeline when other females in their “local position” (a cluster of students who tend to take the same sets of courses) also advance in their math coursework. (Note: Peer effects on course taking may have implications for our empirical strategy. We will return to this point later in the chapter)

Factors that are beyond the control of students, parents, and educators may also influence the intensity of coursework that students choose to take. For instance, variations in labor market conditions may modify student postsecondary enrollment plans. Students could infer from a strong labor market that ample employment for the noncollege educated exists, which may tend to decrease their interest in courses that lead to college enrollment. The availability of plentiful and well-paying local jobs for young people may also encourage students to take less intensive courses that allow more time for working while in high school, thus ensuring higher immediate earnings. Economic research on the impact of increasing the minimum wage on high school enrollments indicates that a student’s education decision-making is indeed responsive to labor market conditions. For example, the commitment of lower-ability and lower-income students to completing a high school diploma declines in response to increases in the minimum wage (Ehrenberg & Marcus, 1982; Neumark & Wascher, 1995). Therefore, it is possible that college preparatory course taking and the strength of the local labor market are negatively related.

As the prior literature demonstrates, students’ course taking is conditional on many factors, including their educational aspirations, parental expectations, school resources, and local labor market conditions. In the next section, we present frameworks that offer competing explanations for how student course taking is related to their subsequent educational outcomes. We also examine research on the relationship between high school course taking and educational attainment and consider how research has attempted to isolate the effect of courses from related factors (e.g., student characteristics, school context) that may also influence postsecondary outcomes. The theoretical frameworks and course taking effects in the literature provide justification for our quasi-experimental approach when examining the impact of high school course taking on postsecondary success.

Potential Explanations for High School Course Taking Effects

Research demonstrates that students who take a more intensive secondary curriculum are more likely to persist through college and earn a degree than students who take a less intensive curriculum (Adelman, 1999, 2006; Choy, 2001; Horn & Kojaku, 2001). There are at least two potential explanations for this relationship. The first explanation is that high school courses develop a student’s human capital, providing him or her with skills and knowledge to be parlayed into future success (Rose & Betts, 2004). For instance, Algebra II may provide students with content knowledge that improves their performance in college-level quantitative coursework (Long, Iatarola, & Conger, 2009)—particularly general education math coursework that is required to earn a degree (Rech & Harrington, 2000). In turn, improved academic performance could lead students to integrate into college and commit to degree attainment (Bean, 1980; Tinto, 1975). Human capital development is related to the differential coursework hypothesis put forth by Karl Alexander and colleagues, which served as the basis for Adelman’s Toolbox studies (1999, 2006). Alexander and colleagues propose that a student’s academic preparation in high school is the most salient factor in his or her future educational attainment—much more salient than background characteristics such as race, class, and gender (Alexander, Riordan, Fennessey, & Pallas, 1982; Pallas & Alexander, 1983). When policymakers propose increased course taking requirements, they implicitly assume that higher-level courses lead to improved educational and labor market outcomes for students of all backgrounds by developing their human capital.

Another potential explanation for the relationship between curricular intensity and degree attainment is student self-selection. As we demonstrated in our discussion above, random assignment is not the typical mechanism determining student course placements or course choice. Students elect to take particular courses or are placed into courses according to a number of factors, including their prior achievement, scores on placement examinations, work ethic, parental involvement in the educational process, and the racial and social class composition of their schools. If these factors are also correlated with degree attainment, self-selection into courses during high school may positively bias our estimates of the causal effect of course taking on attainment (i.e., the results are upwardly biased).

It is important for researchers to determine if student self-selection or human capital development is largely responsible for any (hypothesized) positive relationship between curricular intensity and degree attainment because effective policymaking often requires a sound understanding of which practices improve educational outcomes. In studies that use observational data and analytical methods that do not strongly support causal inference, the greater the role of selection, the more the estimates of curricular intensity’s effects on degree attainment may be biased. If positive selection bias is present, the individuals who are the most likely to experience the outcome of interest (e.g., graduate from college) are the individuals who are also the most likely to receive the treatment (e.g., select into taking Algebra II). Practices such as K-12 tracking increase the likelihood that only the most able and motivated students take intensive courses. If, prior to enrolling in Algebra II, these students are more dedicated to earning a bachelor’s degree than their peers who take less intensive coursework, the observed positive association between course taking and educational attainment is attributable to the qualities of students who take intensive courses and not the courses per se. If positive selection bias is largely responsible for any observed relationship between curricular intensity and educational attainment, then state policies such as the Michigan Merit Curriculum that mandate a college preparatory curriculum for all students are unlikely to have the expected impact on college access and success.

However, positive selection is not the only potential reason for bias in studies of course taking effects. Negative selection occurs when the individuals who are the most likely to experience the outcome of interest (e.g., graduate from college) are the individuals who are the least likely to receive the treatment (e.g., select into taking Algebra II). For example, in states that offer merit-based financial aid programs that are distributed according to secondary (and postsecondary) GPAs, high school students who aspire to attend college and earn a degree may avoid challenging courses in high school to gain eligibility for financial aid. While we are unaware of a rigorous study that examines merit aid programs’ impact on high school students’ course taking behavior, Cornwell, Lee, and Mustard find evidence that the Georgia HOPE Scholarship causes some college students to take fewer general education courses in math and science (2006) and to reduce their course load and increase their rate of course withdrawals (2005). If negative selection biases the estimates in studies of course taking effects, policies like the Michigan Merit Curriculum may actually have a larger impact on college access and success than research that does not adjust for such selection would indicate.

High School Coursework and Postsecondary Educational Attainment

Many researchers have attempted to account for confounding factors in order to determine the causal impact of intensive coursework on the likelihood of completing a bachelor’s degree. Arguably the most well-known and influential studies that address this topic are Adelman’s Answers in the Toolbox (1999) and The Toolbox Revisited (2006). In these studies, Adelman uses High School and Beyond (HSB) and National Education Longitudinal Study (NELS:88) data to examine the effect of student effort and high school course taking on their likelihood of college completion. As part of his analyses, he examines the impact of the highest level of math coursework taken by a student on his or her odds of degree attainment, controlling only for socioeconomic status. The results from the 1999 study using HSB data suggest that taking Algebra II or higher has a positive impact on degree completion. However, when analyzing NELS:88 data in 2006, Adelman suggests that taking Trigonometry or above has a positive effect on degree attainment, while taking Algebra II or lower has a negative effect. In summarizing his two studies, Adelman concludes that “the academic intensity of a student’s high school curriculum still counts more than anything else in pre-collegiate history in providing momentum toward completing a bachelor’s degree” (Adelman, 2006, p. xviii). This is a strong claim, given that the studies’ regressions of highest level of math coursework do not account for precollegiate factors beyond socioeconomic status that are hypothesized to impact degree attainment, such as student educational aspirations or their high school contexts.

Like Adelman (1999, 2006), other researchers find that students who take higher-level courses in high school have more successful postsecondary outcomes than their counterparts who take lower-level courses (Bishop & Mane, 2005; Choy, 2001; Fletcher & Zirkle, 2009; Horn & Kojaku, 2001; Rose & Betts, 2001). The majority of these studies employ standard logistic/probit or multinomial regression techniques and control for several (possibly) confounding factors.² Like Adelman (1999), Rose and Betts (2001) employ High School and Beyond (HSB) survey data and find that math course taking influences students’ bachelor’s degree attainment, even after they control for observable factors such as student background, high school characteristics (including student-teacher ratio, high school size, and average per-pupil spending), and prior math course and standardized test performance. Their results suggest that an average student whose highest level of math is Algebra II is 12% more likely to earn a bachelor’s degree than a similar student who only completes Algebra and Geometry.

However, other studies find that accounting for an array of background, academic, and/or state characteristics negates the relationship between taking intensive courses in high school and postsecondary persistence (Bishop & Mane, 2004; Geiser & Santelices, 2004). Using University of California (UC) and College Board data, Geiser and Santelices examine if taking advanced placement (AP) and honors courses in high school affects second-year persistence in college. They find that when high school GPA, socioeconomic indicators, and standardized test scores are included in their models, honors and AP courses are not significantly related to whether UC students remain enrolled into their sophomore year. Similarly, after accounting for high school- and college-level factors—including the non-AP coursework taken by students—Klopfenstein and Thomas (2009) find a null effect of advanced placement coursework, including AP Calculus, on postsecondary persistence using Texas student unit record data.

Bishop and Mane (2004) examine the impact of high school curriculum policies on postsecondary outcomes using the same NELS:88 dataset that Adelman used in his 2006 study. They control for factors unaccounted for in other non-quasi-experimental studies, including Adelman’s, such as student locus of control and state unemployment rates. They find that, controlling for student- and state-level variables, increases in the number of academic courses required to graduate from high school is not associated with college degree attainment. This result suggests that requiring all secondary students to take additional years of academic coursework will not increase college graduation rates, a result congruent with the explanation that selection is largely responsible for the positive association between course intensity and educational attainment.

As the aforementioned studies indicate, research provides conflicting evidence about whether high school courses have a causal impact on postsecondary completion. This conflicting evidence may arise for several reasons. First, the researchers use different datasets to investigate course taking effects. The datasets range from nationally representative to state specific and the points in time in which the surveys were administered span decades. Additionally, among researchers that use the same dataset, their effective samples often differ. For example, Adelman (2006) restricts his analysis of NELS:88 to students who attended high school through the 12th grade. This restriction excludes many dropouts, early graduates, and GED completers who may experience different effects of math coursework than traditional high school graduates. Conversely, Bishop and Mane (2004) include all students who were in the 8th grade in 1988 in their analysis of NELS data. Therefore, Adelman’s and Bishop and Mane’s estimates are based on very different samples.

Second, there is no clearly defined and universally agreed-upon theoretical model of high school course taking and educational attainment. As a result, each researcher proposes a different analytical model with a different set of controls for confounding variables, which means that each study likely contains a different degree of omitted variable bias.³ It is almost certain that these nonexperimental studies suffer from omitted variable bias because it is improbable that researchers are able to control for every covariate that is correlated with both high school course taking and degree attainment. However, some researchers may have been more effective than others in accounting for confounding factors in their models and therefore may provide less biased estimates of the causal effect of course taking on degree attainment. For instance, our review of the literature demonstrates that students who attend rural schools have less access to college preparatory courses than students who attend nonrural schools (Planty et al., 2007). Data indicate that rural residents also have lower levels of degree completion than nonrural residents (United States Department of Agriculture, 2004). Therefore, the urbanicity of students’ communities could be a confounding factor in studies of the effect of course taking on degree attainment. Yet only two of the studies reviewed above control for the impact of hailing from a rural community.⁴

Although it is important to attend to the potential of omitted variable bias by inserting controls, such as urbanicity, we would like to caution readers against including controls that would not be theoretically expected to confound the effects of the treatment variable. The inclusion of such variables would have the potential to negatively impact the model in two ways. First, adding control variables to a regression that are correlated with other omitted predictors could introduce additional bias. If so, the coefficients of the newly added variables will not be accurate because they suffer from omitted variable bias also, due to their relation to other still excluded variables. Additionally, the inclusion of additional variables that are not significant predictors is likely to result in a loss of statistical efficiency and inflate standard errors. This will reduce the accuracy of all estimates in the model. Therefore, it is important to select control variables that are founded in the theoretical underpinnings of the model at hand. Absent knowledge of the true structural model of course taking and degree attainment in the population, it is impossible to know which of the course taking effects studies we reviewed provides the most accurate representation of the factors that predict college completion.

An additional issue with the aforementioned studies is that none employ strategies to eliminate the influence of unobservable factors on course taking and attainment. Some student characteristics may be difficult or impossible to obtain information about in observational datasets, but this does not change the fact that they are confounding factors (Cellini, 2008). Examples of potential unobservable factors in course taking effects research include a student’s enjoyment of the learning process and a student’s desire to undertake and persevere through challenges. It is likely that these unobservable factors contribute to student selection into high school courses and a student’s subsequent choice to attain a bachelor’s degree. However, none of the studies we examined that employ a standard regression approach accounted for a student’s intrinsic love of learning or ability to endure through difficulties; the failure to account for these unobserved factors may bias the estimates that result from these studies.

To minimize omitted variable and selection bias to make stronger causal claims, researchers have recently employed quasi-experimental methods to examine the link between high school course taking and educational attainment. Attewell and Domina (2008) use propensity score matching (PSM) to study the impact of high school curriculum on student outcomes (for an example of the use of PSM in education research, see Reynolds and DesJardins (2009)). PSM may be an improvement over standard regression techniques because it allows researchers to compare outcomes only among students who had similar characteristics before receiving a “treatment”—for example, a high school course or a series of courses—thereby potentially reducing the confounding effects of other observable factors. Attewell and Domina find that PSM estimates of course taking effects are generally smaller than those produced by previous studies, including Adelman’s, that are produced with standard regression. This suggests that a portion of the positive relationship observed between college preparatory courses and educational attainment in correlational studies may be due to the qualities of students who elect to take an intensive curriculum. However, as with all PSM studies, Attewell and Domina are unlikely to completely eliminate selection bias, as their propensity scores were based on a set of observable student background characteristics that may not adequately control for unobservable differences across students.

Altonji (1995) applied an instrumental variables approach in his study of high school curriculum effects on years of postsecondary education. Using data from the National Longitudinal Survey (NLS:72), he first estimates a standard OLS regression model, controlling for confounding student- and school-level factors. His results indicate that each additional year of high school math increases enrollment in postsecondary education by approximately one-quarter of a year. However, when he employs IV techniques using the average number of courses taken in a student’s high school as an instrument, his point estimates change: The effects of additional years of math coursework on degree attainment become minimal to nonexistent. Altonji’s results suggest that studies that fail to control for selection are upwardly biased. However, as Altonji notes, his IV is not optimal. The course taking behavior of students in specific high schools is likely related to unobserved characteristics of their communities, such as neighborhood or school district resources that in turn may influence the future educational outcomes of these students. Therefore, his IV estimates of course taking on years of postsecondary schooling may still be contaminated by selection bias. Including controls for community-level factors could help to mitigate this problem.

Many other researchers (mostly economists) have also employed instrumental variables to answer questions about postsecondary enrollment and attainment (Angrist and Krueger 1991; Card, 1995; Kane & Rouse, 1993; Lemieux & Card, 1998; Staiger and Stock 1997). To investigate the relationship between postsecondary attainment and earnings, for example, Card (1995) considers the distance from a student’s home to the nearest 2- or 4-year institution as an instrument for his or her likelihood of attending college. While his OLS estimates assert that those who attend college earn 7% more over a lifetime than those who do not, his IV model yields estimates closer to 13%—a difference of almost 50%.

Overview of the Empirical Example

Given the inconclusive results of prior studies, an important policy question remains unanswered: What is the causal effect of high school courses on college completion? To address this question, we focus our analysis on the effect of taking Algebra II on a student’s likelihood of earning a bachelor’s degree. We selected the Algebra II course taking margin because, in the hopes of better preparing students for college and career success, almost half of the states in the United States currently mandate that students complete Algebra II in order to earn a high school diploma (Achieve, 2011). Consequently, a large portion of the nation’s high school students stop taking math courses after taking Algebra II (Bozick and Ingels 2008; Dalton et al., 2007; Planty et al. 2007). Given the prominent role that Algebra II plays in educational policy, it is important to determine if this commonly mandated course improves student educational attainment. Previous research on the effects of specific math courses on degree attainment has been inconclusive, with earlier studies finding that taking Algebra II as the highest math course taken improves a student’s odds of degree attainment (Adelman, 1999; Rose & Betts, 2001) and a later study finding that it does not (Adelman, 2006). These inconclusive results may reflect changing standards for math preparation over time if courses higher than Algebra II have become necessary for college-level success (Adelman). Additionally, the inconclusive results could be caused by differences in the samples used and the degree of omitted variable and selection bias present in their estimates.

To determine the causal effect of taking Algebra II on degree attainment over time, we employ data from two nationally representative surveys conducted a decade apart by the National Center for Education Statistics (NCES): the National Education Longitudinal Study of 1988 (NELS:88) and the Education Longitudinal Study of 2002 (ELS:02). Both surveys contain detailed high school transcript information for survey respondents. NELS follows a cohort of students who were in the eighth grade in 1988 through their sophomore year in 1990, their senior year in high school in 1992, and into college and the labor market in 2000. This allows us to observe which students complete a bachelor’s degree in a reasonable time frame. ELS follows a cohort of students who were in the tenth grade in 2002. This cohort was issued follow-up surveys in their senior year of high school in 2004 and 2 years following high school graduation in 2006. Although ELS provides the most recent national data on high school student course taking, it does not contain information on bachelor’s degree attainment because NCES has not yet released the third follow-up survey data.⁵ Therefore, we use persistence to the second year of college as a proxy for degree completion in the ELS data.

To address omitted variable and selection bias, we will conduct our analysis using an instrumental variables approach, to be discussed at length below. We will exploit the influence of local labor market conditions and youth labor laws early in a student’s high school career to account (instrument) for his or her willingness to attempt math courses at the Algebra II level. These local labor market conditions are unlikely to remain fixed as students persist through high school and college and are thus unlikely to impact a student’s ultimate educational attainment. In subsequent sections, we demonstrate how causal inferences can be made about course taking effects using an instrumental variables approach and local labor market conditions and youth labor laws as IVs. As a first step, we present a general introduction to concepts and terminology related to instrumental variable estimation approaches.

Instrumental Variables: Concepts and Terminology

Our goal is to determine whether taking Algebra II (or higher) has a causal effect on student postsecondary completion. However, a more utilitarian goal is to provide some guidance on the proper use of methods that will allow education researchers to make strong inferential statements about the effects of such “treatments” on student outcomes. If successful, we will provide higher education researchers with additional tools for their analytic “toolbox” so that their empirical work will be of the highest quality and able to inform policymakers about the likely effects of practices, interventions, and policies (e.g., high school curriculum standards) on student academic and labor market outcomes. The “wrench” we will add to the toolbox is known as instrumental variable estimation.

As noted earlier in the chapter, students take different levels of math courses while in high school and do so for a variety of reasons including differences in ability, motivation, and encouragement from others. The nonrandom assignment of students into courses presents the researcher with a challenge when attempting to determine the causal effect of a treatment (e.g., whether the student took Algebra II or higher or not) on an outcome (e.g., college completion) because observable (e.g., grades) and unobservable (e.g., motivation) factors may confound the typical multivariate analysis of the relationship between the outcome and the treatment. By employing an instrumental variable estimation strategy, we hope to mitigate this inferential problem.

Before diving into our investigation of the causal effect of taking Algebra II or higher on college completion, we will first discuss some important concepts and terminology related to making causal assertions using an instrumental variables approach. We will attempt to explain each of the concepts and terms using narrative, equations, and figures.

The Concept of a Counterfactual

Perhaps one of the most challenging issues in conducting causal research is determining the correct counterfactual—the group against which the outcomes of the treatment group (e.g., those who take Algebra II) are compared. Using a counterfactual allows researchers to think about the outcomes of those receiving treatment, had the treatment never occurred. In our case, the counterfactual helps researchers to explore the question, “what would the postsecondary outcomes of students who took Algebra II be had they not taken Algebra II?”

The concept of the counterfactual relies on the idea of potential outcomes. A potential outcome is defined as each of the possible outcomes of the dependent variable (e.g., whether or not a student completes college) in different states of the world—provided, of course, that observing different states of the world were possible. In our context, the “different states of the world” are whether or not the student takes Algebra II or higher or not.⁶

Consider again the example of Grace and Adam. Grace, as you recall, takes Algebra II in high school, whereas Adam does not. The best counterfactual for these two students would be themselves: Grace takes Algebra II in high school, and her eventual college completion is measured. Assuming the invention of a time machine, the researcher turns back the clock to high school and Grace takes a lower-level math course instead of Algebra II, and the researcher measures whether she completes college or not. The same strategy could be used for Adam: He takes Consumer Math, the clock is turned back to high school, he takes Algebra II instead, and we measure whether he completes college or not. We would then be able to compare Grace’s and Adam’s outcomes (college completion) under both conditions: taking Algebra II and not taking Algebra II. Absent time travel, this scenario is impossible.

We can also discuss the concept of the counterfactual formally. Let the outcome for Grace be ${Y}_{i}^{1}$if the she is exposed to the treatment (e.g., Algebra II) and be ${Y}_{i}^{0}$if she is not (e.g., does not take Algebra II). Let T _i be a dichotomous variable that equals 1 if Grace takes Algebra II:

$$ {Y}_{i}=\{\begin{array}{c}{Y}_{i}^{1}\text if\text{T}_{i}=1\\ {Y}_{i}^{0}\text if\text{T}_{i}=0\end{array}$$

(6.1)

or

$$ {Y}_{i}={Y}_{i}^{0}+{T}_{i}\left({Y}_{i}^{1}-{Y}_{i}^{0}\right)$$

(6.2)

The value $({Y}_{i}^{1}-{Y}_{i}^{0})$is the causal effect of taking Algebra II. However, the fundamental problem of causal inference, as mentioned above, is that we cannot observe both of these values of Y (takes Algebra II and does not take Algebra II) for Grace or Adam (Angrist & Pischke, 2009; Holland, 1986; McCall & Bielby, 2012; Rubin, 1974). A student either takes Algebra II, allowing us to observe ${Y}_{i}^{1}$(which we would call the “factual”) but not ${Y}_{i}^{0}$(which we would call the “counterfactual”), or, if they do not take Algebra II, we are able to observe ${Y}_{i}^{0}$but not ${Y}_{i}^{1}$.

Absent an experiment, a “naïve” solution to this problem is to compare the average value of Y for all of the students who take Algebra II to the average value of Y for those who do not:

$$ E\left({Y}_{i}|{T}_{i}=1\right)-E({Y}_{i}|{T}_{i}=0)$$

(6.3)

However, it is demonstrable that

$$\begin{array}{l}E\left({Y}_{i}|{T}_{i}=1\right)-E\left({Y}_{i}|{T}_{i}=0\right)=\left\{E\left({Y}_{i}^{1}|{T}_{i}=1\right)-E\left({Y}_{i}^{0}|{T}_{i}=1\right)\right\}\\ -\left\{E\left({Y}_{i}^{0}|{T}_{i}=1\right)-E\left({Y}_{i}^{0}|{T}_{i}=0\right)\right\}\end{array}$$

(6.4)

Each of the elements is defined as above. The first term in brackets on the right-hand side of Eq. 6.4 is the average causal effect of Algebra II on those who took Algebra II. The second bracketed term is the difference in what the average value of Y would have been had the treated remained untreated (e.g., those who took Algebra II had not taken it) and the average value of Y for the untreated. In other words, the second bracketed term shows the difference in outcomes between the treated and the untreated that is due to students’ background characteristics and other variables and not the treatment (Algebra II) itself. This second bracketed term represents selection bias, which will be discussed at greater length below (see McCall & Bielby, 2012, for additional details).

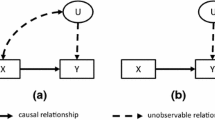
We can also think about the counterfactual as a missing data problem. That is, we have information about the effect of Algebra II on those who took it but are missing this information for those who did not. Conversely, we have information about the control condition for those who did not take Algebra II but are missing this information for those who did. This is depicted in Fig. 6.1.

Fig. 6.1

The concept of the counterfactual as a missing data problem (Owing to Murnane & Willett, 2011)

Endogeneity (“The Selection Problem”) and Exogeneity

As noted above, high school students self-select into specific courses for a variety of reasons. Because the characteristics that lead to specific course selection are internal to the student, their selection into treatment (Algebra II) is endogenous. By this, we mean that a student’s choosing to take Algebra II is the result of his or her own action (or possibly the action of his or her teachers or parents) who exist within the system (in this case, the education system) being investigated (Murnane & Willett, 2011). Endogeneity (which, for our purposes, is a synonym for selection) hinders our ability to make causal assertions about the impact of a program or policy on a given outcome because it is unclear whether it is a student characteristic (observable or otherwise) that influences his or her outcome (college completion) or the treatment itself (Algebra II).

Consider our example in equation form:

$$ y={\beta }_{0}+{\beta }_{1}{x}_{1}+{\beta }_{2}{t}_{i}+e$$

(6.5)

where:

• y  = postsecondary completion (the outcome of interest)

• x ₁ = an exogenous control variable (e.g., parents’ education)

• t _i   = whether a student takes Algebra II or not (the treatment)

• e  = error term

The betas $({\beta }_{0}$, ${\beta }_{1}$, and ${\beta }_{2})$ are parameters to be estimated—${\beta }_{0}$represents the Y intercept, ${\beta }_{1}$is a coefficient for the relationship between our exogenous predictor and postsecondary completion, and ${\beta }_{2}$is a coefficient on whether a student takes Algebra II. In the absence of random assignment to math classes, it is likely that many student characteristics that are excluded from this regression (ability, motivation, encouragement from parents—which can be assumed to be included in the error term) are related to a student’s decision to take Algebra II. Therefore, t_i is an endogenous variable, and its coefficient $\left({\beta }_{2}\right)$ cannot be used to make causal claims about the relationship between Algebra II and college completion. Herein, we dub this the “naïve” statistical model because it does not account for the endogenous relationship between t _i and y.

Endogeneity in the regressor of interest (whether a student takes Algebra II) can potentially bias the magnitude of its estimate (${\beta }_{2}$). In Eq. 6.5 above, it is likely that ${\beta }_{2}$is too high—that the relationship between taking Algebra II and college completion is upwardly biased. Upward bias means that the relationship between Algebra II and college completion appears to be too strong. There are likely many factors other than taking Algebra II (ability, motivation, and encouragement) that may influence whether or not a student completes college. On the other hand, the estimate (${\beta }_{2}$) will be biased downward if it underestimates the relationship that exists between taking Algebra II and college completion.

Exogeneity exists when assignment to treatment (taking Algebra II) happens through a mechanism that is outside the system being investigated: when a lottery, for example, or an otherwise random draw assigns students to a particular math class. Under this condition, assignment is unrelated to student characteristics, the opinions and/or encouragement of teachers and parents, and the characteristics of the math classes themselves. Exogenous variation, to continue with our example, would mean that students are assigned to take Algebra II or a lower-level math class in a way that has nothing to do with their ability, motivation, or how much encouragement they receive from their parents.

Consider Eq. (6.5) above, now assuming that students are assigned to treatment exogenously. Because students are randomly assigned to Algebra II or a lower-level math course, all of their observed and unobserved characteristics should, on average, be statistically identical. This means that we should have treatment and control groups that are identical on average. If so, any bias in the estimates of the effect of Algebra II on college completion will be eliminated—a stark difference from when assignment to treatment is endogenous—and should yield estimates of the relationship between the treatment (Algebra II) and the outcome (college completion) that are much more accurate.

Instrument

To address issues of endogeneity (selection) when attempting to make causal assertions about the relationship between taking Algebra II in high school and completing college, it may be useful to employ an instrumental variable (an “instrument” or an “IV”). An instrument is defined as a variable that is unrelated to the error term and related to the outcome only through the treatment variable. Again, consider Equation 6.5 above. An appropriate instrument must be unrelated to e (the error term) and related to y (postsecondary completion) only through t_i (whether a student takes Algebra II). An instrument allows a researcher to minimize bias due to endogeneity by identifying a source of exogenous variation and uses this exogenous variation to determine the impact of a treatment, policy, or program (e.g., Algebra II) on an outcome (e.g., postsecondary completion).

Using our example, we consider both labor market conditions and youth labor laws during the student’s 10th grade year as instruments for their probability of taking Algebra II. While students are enrolled in high school, local labor market conditions may affect their college preparation decisions, and these decisions may subsequently alter their chances for college access/completion. For example, a strong local labor market when a student is in 10th grade may entice students to avoid a college preparatory curriculum, reasoning that many job opportunities will exist without a college education. On the other hand, an identical student facing a weaker labor market in 10th grade may be more likely to enroll in a college preparatory curriculum, as employment prospects will likely dim without a college education. Additionally, youth labor laws when a student is in high school may influence the amount of time he or she is able to work outside of school. These opportunities for work (or lack thereof) may also influence student decisions about taking (or not) college preparatory coursework, as they may choose to spend time working as opposed to focusing on more challenging coursework.

It is important to note that although the IV approach is an econometric method used by many researchers, there is considerable debate about the application of this methodology. We will discuss this debate below, as well as alternative approaches for making causal claims about the relationship between treatments and outcomes.

Historically, methodologists and researchers considered an instrument to be valid if it met the following two conditions:

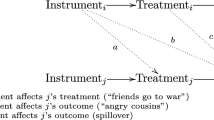
• 1. The exogeneity condition: The instrument must be correlated with Y_i only through t_i and must be uncorrelated with any omitted variables. The key assumption when using an IV is that the only way the instrument affects the outcome is through the treatment (Newhouse & McClellan, 1998).

• 2. The relevance condition: The instrument must be correlated with t_i, the treatment (Algebra II).

These relationships are depicted in the figure below (Fig. 6.2).

Fig. 6.2

Two conditions for a valid instrument

The relevance condition can be verified empirically by determining whether and, if so, how strongly the instrument is correlated with the policy variable of interest (in our case, whether students take Algebra II.) If a strong correlation exists, the relevance condition is met. The exogeneity condition, however, cannot be tested empirically because it is stated in terms of the relationship between the instrument and the population parameters. Population parameters cannot be observed, as researchers have access only to sample data. As such, it is impossible to investigate correlational relationships between the instrument and unobservable parameters. Therefore, this condition requires that researchers think about the potential relationships between the IV, the omitted variables, the treatment, and the outcome. In our running example, some questions to be asked might be the following: How do local labor markets impact college going among high school graduates? How do they impact the quality of the neighborhoods in which students live, a variable that may be omitted from the model? If a logical case can be made and defended, the exogeneity condition is considered to have been met as well. Absent random assignment, this assumption is more challenging to justify than the relevance assumption, and IV exogeneity is often contested among communities of scholars.

Methods to Employ the IV Framework

One can employ an instrumental variables approach using a variety of regression-based techniques, some of which will be discussed at length below. One very common method that researchers use is two-stage least squares (2SLS) regression. 2SLS is performed in two steps that happen sequentially: In the first stage, the main variable of interest (Algebra II) is regressed on the instrumental variable and any other variables that we think might help explain why students take Algebra II. The results of this regression yield a probability of taking Algebra II for all students in the sample. These predicted values are then used in place of the (in our case) dichotomous treatment variable (Algebra II) in a second stage. This and other methods for using IV will be discussed in much greater detail below, in light of the methods employed to explore our causal question of interest: What is the causal relationship between high school course taking and college going?⁷

Data

Before entering into a discussion of the procedures for estimating IV models, we will briefly describe the data and computational methods we employed to apply and test different modeling approaches to IV analysis. The running example will employ data from two National Center for Education Statistics (NCES) datasets: the National Educational Longitudinal Survey of 1988 (NELS:88) and the Educational Longitudinal Survey of 2002 (ELS:02). These datasets provide nationally representative samples of students who are longitudinally tracked beginning in their eighth grade year. NELS:88 tracks students through high school and postsecondary education and into the workplace. ELS:02, the most currently available of the NCES longitudinal datasets, has collected and distributed its most recent survey 1.5 years after students were expected to complete high school. The data provides detailed information on students’ high school-level course taking in addition to a number of other academic preparation variables, demographic variables, and a range of postsecondary outcomes of interest. We leverage this detailed longitudinal data to construct a number of models testing the influence of high school-level course taking, specifically Algebra II, on student probabilities of obtaining a bachelor’s degree.

In our analyses, we focus on two particular outcomes. Our primary outcome of interest is bachelor’s degree attainment; however, this outcome is only available in the NELS:88 data because the most recently available wave of the ELS:02 data only interviewed students 1.5 years after their expected high school graduation date. Therefore, using the ELS:02 data, we use as a proxy for degree completion a variable indicating whether a student persisted from the first to second year of postsecondary education. We will reestimate this model when college completion data is available.

Our variable for bachelor’s degree attainment was constructed from the NELS Postsecondary Education Transcript Study (PETS) data file. The variable was coded as a dummy variable, “1” if a student attained a bachelor’s degree within 8 years of their expected high school graduation and “0” otherwise.

The first- to second-year persistence variable for ELS:02 was developed in two stages. First, a variable was created to indicate the first month, in 2004 or 2005, that a student was enrolled in a postsecondary institution. Then, a dummy variable was created to indicate if that student was enrolled in a postsecondary institution 12 months after their initial month of enrollment, coded “1” if the student was still enrolled 12 months later and “0” otherwise.

One concern with each of these dependent variables, as is a concern with any regression-based modeling technique, is that they are both dichotomous and therefore might not be appropriately estimated using techniques based on ordinary least squares (OLS; or “linear”) regression. While strong arguments have been made in favor of using OLS with dichotomous dependent variables (see Angrist & Pischke, 2009, p. 103) and we do so in this study, we also estimate some IV models using methods that deal with the nonlinearity when estimating dichotomous dependent variables.

The Endogenous Independent Variable

The independent variable of interest in our analysis is high school-level mathematics course taking, specifically whether or not a student took an Algebra II course (or higher) or not in high school. It is operationalized as a dummy variable, coded “1” if a student took more than 0.5 Carnegie units, equivalent to high school credits, in Algebra II while in high school and “0” otherwise.

As was discussed above, this variable is expected to be endogenously related to postsecondary persistence and degree attainment because students self-select into high school courses. In an attempt to account for this endogeneity, we employ instrumental variables in order to more accurately estimate the causal relationship between course taking and degree attainment. The selection of the instrumental variables employed is discussed in detail below.

Exogenous Independent Variables

A set of exogenous controls were incorporated in each model estimated. The inclusion of controls that are expected to significantly predict the outcome variable is an important aspect of reinforcing the exogeneity of the other variables in the model. If factors that are truly related to the dependent variable were excluded, the risk of omitted variable bias in the model estimates would be increased. Therefore, controls included in our models were selected based on their expected relationship with both the dependent variable of interest and the treatment variable. These controls include mathematical ability, measured as a student’s quartile ranking on the NCES-standardized high school mathematics exam (8th grade for NELS and 10th grade for ELS), race/ethnicity, mother’s level of education, and socioeconomic status quartile. State and birth year fixed effects were also included to account for impacts of policies that may differentially influence students’ decisions and/or outcomes based on age and/or state of residence. Each of these controls is included as a predictor in both the first and second stage equations, as will be discussed below. See Table 6.1 for descriptive statistics for variables included in our models.

Table 6.1 Descriptive statistics

Software and Syntax

To conduct this analysis, we chose to use the statistical program Stata. Stata is one of many statistical programs capable of performing the analyses conducted herein (e.g., SPSS, SAS, or R). However, Stata provides a number of preprogrammed instrumental variable modules that are readily accessible and accompanied by clearly written help files and interactive examples that provide a better gateway to IV modeling than might be available in other programs. Additionally, advanced programming options and Stata’s use of open source user-created routines allow for a great deal of flexibility in the number of approaches that can be applied.

Along with each of our analyses, we provide a set of annotated Stata syntax (see Appendix A) that provides step-by-step examples of the code that is necessary to estimate the IV models discussed below.

Assumptions of IV models

As is discussed above, the general objective of applying IV methods is to account for potential bias in traditional regression estimates that are due to the presence of endogeneity. Below, we provide a detailed discussion of a number of assumptions that IV models and instruments are required to meet in order to account for endogeneity and provide more accurate estimates. We begin by discussing tests for the presence of endogeneity in the model. We then move on to discuss the traditional two-assumption approach to IV modeling that dominated IV literature in econometrics for much of the twentieth century. Next, we introduce a relatively new five-assumption approach that acknowledges potential issues with relying only on the two-assumption approach and expands our thinking about the role of assumptions when estimating treatment effects. We then evaluate our empirical example using the five-assumption approach, thereby providing conceptual and empirical support (or not) about our ability to estimate the causal effect of Algebra II course taking on first- to second-year persistence and bachelor’s degree attainment.

Testing for Endogeneity

The application of IV modeling techniques is driven by the assumption that at least one of the independent variables in a model, here Algebra 2 course taking, is endogenous. When there is endogeneity present, naïve regression-based techniques (see Eq. (6.5)) produce inconsistent estimates of all coefficients (Wooldridge, 2002). However, employing IV techniques also results in a loss of statistical efficiency (i.e., inflation of standard errors) when compared to linear regression, so it is important to be certain that the variables that are thought to be endogenous are in fact so. If we knew the true population parameters were not endogenous, then the application of IV approaches would reduce efficiency without accounting for bias; thus, one would be better off to apply a simple (naïve) OLS regression.

There are a number of tests that can be applied to assess the endogeneity of explanatory variables. Many are made available through Stata’s estat endogenous postestimation command (see StataCorp, 2009, p. 757). Additionally, the estimation strategy of some IV approaches, namely, control function approaches (discussed in detail below), directly tests the endogeneity of the independent variable of interest (e.g., Algebra II). Conducting these tests is an essential step when applying the IV approach. If we find that Algebra II is in fact exogenous (in the population), then the use of an IV estimator would be inefficient, inflating our standard errors, without accounting for any potential bias from the more efficient OLS estimator. However, these endogeneity tests are sensitive to the strength of our instruments. If the instrumental variables are only weakly related to the treatment, there is a high potential to falsely reject the endogeneity assumption and assume that the treatment variable is exogenous. Therefore, it is always of primary importance to consider not only statistical tests but conceptual evidence when evaluating the endogeneity of a variable. While the statistical tests might not fully support the presence of endogeneity, this may be largely due to a lack of statistical power in the test, not a truly exogenous treatment variable.

The Two-Assumption Approach

Traditional conceptions of IV models (e.g., Cameron & Trivedi, 2005; Greene, 2011; Wooldridge, 2002) required that instrumental variables meet two assumptions in order to be considered valid. Assume the following simple linear regression:

$$ y={\beta }_{0}+{\beta }_{1}{x}_{1}+{\beta }_{2}t+e$$

(6.6)

If the researcher believes that t is endogenous, then the estimates of ${\beta }_{0}$, ${\beta }_{1}$, and ${\beta }_{2}$will be biased if standard OLS regression methods are employed. One way to remove this bias is to apply an IV method. To do so, we must find an instrument, z, that meets the following assumptions:

A1. Exclusion Restriction

This assumption requires that the instrumental variable is appropriately excluded from the estimation of the dependent variable of interest. When this assumption is satisfied, it guarantees that the instrument, z, only affects the dependent variable, y, through its effect on t.

More formally, there must be no correlation between z and e in Eq. (6.7):

$$ Cov(z,e)=0$$

(6.7)

This assumption is the basic requirement that all exogenous variables in Eq. (6.7) are required to meet. Additionally, the exclusion of z from Eq. (6.7) provides that z has zero effect on the dependent variable, y, when controlling for the effect of all other independent variables. Combining the lack of correlation between z and e and the exclusion of z from (6.7), assumption A1 guarantees that the only effect of z on y is through its effect on t.

A2. Nonzero Partial Correlation with Endogenous Variable

The second assumption requires that the instrument (z) has a measurable effect on the endogenous variable (t). To examine this relationship, the endogenous variable (t) is regressed on the instrument (z) and the other predictor variables (x ₁) from Eq. (6.7) in what is referred to as the reduced form equation, below:

$$ t={\delta }_{0}+{\delta }_{1}{x}_{1}+{\theta }_{1}{z}_{1}+\rho $$

(6.8)

This assumption requires that θ ₁  0. At the most basic level, this means that the instrument must be correlated with the endogenous variable, that is, that the coefficient on the IV (θ ₁) in Equation (6.8) must be nonzero after controlling for all other exogenous variables (x ₁) in the model. Meeting assumptions A1 and A2 is argued to ensure that the IV model is appropriately identified (see Wooldridge, 2002, p. 85) and the instrument is valid.

Although assumptions A1 and A2 have been used to judge whether an instrument is valid, advances in econometrics have driven an interest in applying IV models to estimate causal effects of endogenous variables (t) on dependent variables of interest (y). In order to accomplish this, the traditional IV model must be situated within a broader causal framework based on counterfactuals discussed above. This requires that IV models meet a set of five assumptions in order to estimate causal relationships.

The Five-Assumption Approach

An underlying assumption of the two-assumption model is that the effect of a treatment is the same for all individuals in the sample. No matter who the individual is that receives the treatment, the average influence of the treatment on their outcome of interest is expected to be the same. If this assumption holds, then we are able to estimate the average treatment effect (ATE) for all individuals in the sample. However, Angrist, Imbens and Rubin (1996) argue that treatment effects are likely to be heterogeneous, such that treatments will have differential effects on four different groups of individuals: always-takers, never-takers, defiers, and compliers. Always-takers and never-takers are unaffected by the instrument, such that they will always behave in the same way given a particular treatment. In our example, and using only the county-level employment (not the labor market laws IV) as an example of our instrument, always-taker students will always take Algebra II, whereas never-takers will never take Algebra II, regardless of local labor market conditions. Defiers behave in a manner that is opposite to expectations. Defiers would not take Algebra II when county-level unemployment rates were high but would take Algebra II when unemployment rates were low. Compliers behave according to expectations. When unemployment rates are high, they are more likely to take Algebra II, and when unemployment rates are low, they are less likely to take Algebra II, because they will be entering the labor market after high school instead of attending college.

Among these treatment groups, a causal IV model is only able to estimate the effect of the treatment on compliers, and this estimate is referred to as the local average treatment effect (LATE) (Angrist et al., 1996; Angrist & Pischke, 2009). To estimate the LATE, Angrist et al. argue that the traditional IV model must be embedded within a broader causal structural model referred to as the Rubin causal model (Holland, 1986). Our discussion earlier of causal effects and counterfactuals is a simplified version of the Rubin causal model. This model expands on the traditional two-assumption approach and employs a set of five assumptions that, when met, allow for the estimation of a causal LATE using an IV method. The five assumptions are:

A1b. Stable Unit Treatment Value Assumption (SUTVA)

This assumption requires that the influence of the treatment be the same for all individuals and that the treatment of one individual is not influenced by other individuals being treated. There are two primary concerns when evaluating SUTVA. First, Angrist et al. (1996) and Porter (2012) cite circumstances where groups of individuals are treated as a unit, as opposed to treatment to each individual independently, as possible violations of this assumption. For example, if we randomized students into treatment and control groups by classroom within a school, then we would expect that there might be interactions among teachers instructing the control and treatment group classes. These effects, which are often referred to as “spillovers,” alter the impact of the treatment and controls if the treatment or control teachers alter their administration of the treatment based on their contact with the other teachers.

The second concern deals with how the treatment itself is administered. The SUTVA requires that the implementation of the treatment must be consistent across all treatment groups. Using a clinical example, if the treatment is a drug administered in pill form, then each of the pills given to the treatment group must be exactly the same. If some pills had differing levels of chemicals than other pills, SUTVA would be violated. Therefore, we must consider how the administration of treatments may differ in order to evaluate our model with respect to A1b.

A2b. Random Assignment

This assumption requires that the distribution of the instrumental variable across individuals be comparable to what would be the case given random assignment. In the case of a dichotomous treatment, this can be described as each individual having an equal probability of being treated or untreated. More formally,

$$ \mathrm{Pr}(t=1)=\mathrm{Pr}(t=0)$$

(6.9)

where Pr(t  =  1) is the probability of being treated and Pr(t  =  0) is the probability of not being treated. Any situation in which an individual would have an influence on their level of the instrument would violate this assumption. For example, a student’s college major (Pike, Hansen, & Lin, 2011) would not satisfy this assumption because the student plays a role in selecting the instrument.

A3b. Exclusion Restriction

This assumption parallels assumption A1 in the two-assumption approach from the previous section in that the instrument (z) needs to be uncorrelated with the error term (e) in the second stage equation (6.7). More plainly, assumption A3b requires that the instrument (z) is appropriately excluded from the second stage equation (6.7). As discussed above, this assumption ensures that the only effect that the instrument, z, has on the dependent variable, y, is through its effect on the endogenous independent variable, t, in the reduced form Eq. (6.8).

A4b. Nonzero Average Causal Effect of the Instrument on the Treatment

Also drawing from the two-assumption approach (the “relevance” condition), this assumption requires that there be a nonzero relationship, and preferably a strong relationship, between the instrumental variable and the endogenous independent (or treatment) variable, such that θ ₁  =  0 in Eq. (6.8).

A5b. Monotonicity

Monotonicity assumes that the instrument, z, has a unidirectional effect on the endogenous variable, t. This requires that the relationship between the instrument, z, and the endogenous variable, t, meet one of the following criteria:

$$ {q}_{2}\ge 0$$

(6.10)

or

$$ {q}_{2}\le 0$$

(6.11)

What is required for this to be the case is that the relationship between t and z, as represented by θ ₂, must have only one sign, either positive or negative, for all individuals in the sample.

This assumption stems from our discussion of heterogeneous treatment effects from above. Angrist et al. (1996) describe four groups: always-takers, never-takers, compliers, and defiers. Always-takers and never-takers have predetermined patterns of behavior that are uninfluenced by the instrument. In our running example, always-takers will always take Algebra 2 and never-takers will never take it, and the instrument (local labor market conditions and/or labor laws) will have no influence on these students’ decision. Compliers’ and defiers’ behavior is, however, influenced by the instrument. Compliers will alter their behavior in the direction we would expect from the underlying theory. Using our running example, we would expect compliers’ probability of taking Algebra 2 to rise (fall) as the local unemployment rate increases (decreases). Defiers behave, however, in ways that do not conform to a priori expectations. Using our example, if defiers existed (and we do not believe they do in our case, to be explained in more detail below), we would expect that as the local unemployment rate increased (decreased), their probability of taking Algebra 2 would fall (rise). In order for the assumption of monotonicity to hold, defiers cannot exist because the influence of the instrument on the treatment would not be unidirectional.

In many cases, the assumption of no defiers is a reasonable one, because their behavior would be in contradiction to their own interests. Considering our empirical example, the behavior of a defier would decrease their expected wages and employment prospects. Students with more promising job prospects while in high school would not take advantage of them but instead invest more time in school, whereas students with worse employment prospects in high school would reduce their investment in schooling to increase work time at low-wage jobs or time looking for nonexistent jobs. In both cases, defiers reduce the potential utility they could obtain from the way they allocate their time.

While assumption A5b is required in order to clearly discern the causal relationship between the endogenous independent variable and the dependent variable of interest, the presence of defiers does not necessarily result in biased estimates. The presence of defiers acts to attenuate the estimated relationship between the instrument and the endogenous independent variable, ultimately resulting in underestimated causal relationships as long as the proportion of defiers does not exceed the proportion of compliers in the sample (Angrist & Pischke, 2009). Therefore, when considering the validity of an instrument in relation to A5b, a researcher must evaluate if there is a realistic expectation that the instrument will have a unidirectional impact or if the presence of heterogeneous treatment effects allows for defiers which will alter the estimates.

Moving on toward the estimation of our IV models, below we apply a number of tests of endogeneity to our empirical example to ensure that our Algebra II course taking variable is endogenously related to bachelor’s degree attainment and first- to second-year persistence. Then, we examine whether there is conceptual and/or empirical evidence in support of the five assumptions discussed above.

Tests of Endogeneity

Table 6.2 presents the results of a number of test statistics evaluating the endogeneity of our Algebra II variable in models of both bachelor’s degree attainment and first- to second-year persistence. The null hypothesis for each test is that the Algebra II variable is exogenous which would mean we need not be concerned about bias due to endogeneity and it would be unnecessary to employ IV methods. The robust χ ² test, robust F tests, and GMM C statistic are products of Stata’s estat endogenous postestimation commands available following the estimation of 2SLS and GMM IV models (to be discussed in greater detail below). Each of these tests of endogeneity approaches or exceeds conventional levels of statistical significance, suggesting that Algebra II course taking is endogenously related to persistence and degree attainment. The lower half of Table 6.2 presents coefficients and significance values estimated in two control function IV models estimated. In a control function approach, the residuals from the first stage model are inserted into the second stage model to “control” for the endogeneity between Algebra II course taking and the dependent variable. Whereas the control function approaches will be discussed more fully below, here it is important to note that the coefficients associated with the residuals in the second stage equation provide another test of the endogeneity assumption. If the coefficient on the residuals in the outcome equation is significantly related to the dependent variable, there is evidence that the Algebra II variable is endogenous. In all cases, these estimates approach or exceed conventional levels of statistical significance, providing evidence that the Algebra II variable is endogenously related to degree attainment and persistence.

Table 6.2 Tests of the endogeneity of Algebra II course taking

Given the evidence that Algebra II is endogenous, especially when estimating persistence, it is likely that traditional correlational techniques, such as OLS regression, will produce biased estimates. Therefore, we apply IV models as one potential means for reducing the bias in our estimates. However, we must first evaluate both our selection of instrumental variables and the specification of our model with respect to the five-assumption approach discussed above.

Selection of Instruments

Instrument selection is the key to and generally the largest obstacle when applying IV techniques. Many higher education studies use secondary datasets and the variables provided therein. Thus, our options for finding legitimate instruments are often limited due to at least two frequently occurring phenomena. First, the secondary data we often have access to is collected to study education issues. As such, many of the variables included in these datasets are highly correlated with each other, thereby mitigating the possibility of using any of these variables as instruments. Second, researchers may not have access to extant data, such as the unemployment data used in our study, that provide variables with sufficient exogenous variation that is needed for a valid instrument.

To determine whether an instrument is valid, both conceptual and empirical evidence should be provided in support of its application. Below, we discuss the conceptual foundations provided in defense of our instruments. Then, we consider how our empirical example holds up to the five assumptions when employing the counterfactual IV approach.

Conceptual Justification

From a conceptual point of view, our selection of instruments is based on a simplified two-period model of time allocation. We assume that students allocate their time between school, work, and leisure while enrolled in school (period one) and between work and leisure once they finish schooling (period two). We also assume that students who allocate more time to schooling while in high school take more difficult courses.

In our model, ${h}_{s}^{t}$denotes how much time a student devotes to school in a period, ${h}_{w}^{t}$denotes how much time is allocated to work in period t, l ^t denotes how much time is devoted to leisure activities in period t, and t can equal 1 or 2, depending on whether we are referencing time period one or time period two.⁸

To simplify, we assume that school, work, and leisure comprise all of a student’s time in period one and work and leisure take up all of their time in period two. Formally, we have

$$ {h}_{s}^{1}+{h}_{w}^{1}+{l}^{1}={T}^{1}$$

(6.12)

and

$$ {h}_{w}^{2}+{l}^{2}={T}^{2}$$

(6.13)

where T denotes the total amount of time available to a student in that period.

We also assume that a student’s overall utility (U) is a function of consumption, c, and leisure. Consumption is defined as a combination of wages, w, and hours worked, formally represented by

$$ {h_w^t}^{*}\text{w}^{t}={c}^{t}$$

(6.14)

Additionally, we assume that wages in period 2 increase with the amount of time allocated to schooling in period 1 $\left(f\left({h}_{s}^{1}\right)\right)$. So a student will attempt to maximize their utility, U, according to

$${\mathrm{max}}_{{h}_{w}^{1}{h}_{s}^{1}{h}_{w}^{2}}=U\left({w^1}^{*}\text{h}_{w}^{1},{T}^{1}-{h}_{w}^{1}-{h}_{s}^{1}\right)+\beta^*\text U\left(f\left({h}_{s}^{1}\right)^*\text{h}_{w}^{2},{T}^{2}-{h}_{w}^{2}\right)$$

(6.15)

Here, β represents a discount function that depreciates the value of future utilities with respect to current utilities. Therefore, individuals attempt to obtain the highest overall combined utility in period one and discounted utility in period two. However, the utility obtained in period two is a factor of both the discount rate and the amount of time allocated to schooling in period one.

While the above model can be understood to be driven strictly by student choice, where students allocate their time according to intrapersonal preferences and discount rates, there are also exogenous factors that drive time allocation, particularly with regard to work in period one. One of these is the availability of work. If students are unable to obtain employment in period one, then they will allocate less time to work and more time to school in period one, and they are likely to increase the quantity and/or difficulty of the courses that they take in high school. We operationalize the exogenous influence of availability of work in this model by using the unemployment rate (%) in the county where a student resides in the 10th grade.

Second, state policies often place limitations on the amount of time that students can allocate to work based on their age. For example, the state of California limits students who are under the age of 16 to working only 3 h per day and a total of 18 h per week, whereas 16- and 17-year-olds can work up to 4 h per day and 28 h per week. Similar laws exist in most other states and are expected to impact students’ allocation of time to both schooling and work. However, the degree to which the laws impact students’ allocation of time is expected to vary by state. We statistically control for this variation by including state-level fixed effects, which account for differences in policy impacts at the state level. This allows us to exploit the exogenous influence on the allocation of time to work by including an instrument that indicates whether a student is 16 years of age at the beginning of the 10th grade. We also provide an additional IV by including the interaction between the county-level unemployment IV and the 16 years of age instrument. This interaction term allows the influence of the county-level unemployment rate on Algebra 2 course taking to differ for students who are 16 years of age at the beginning of the 10th grade and those that are not. We hypothesize that changes in the unemployment rate will result in greater changes in Algebra 2 course taking among 16-year-olds who can allocate more time to work than their counterparts under the age of 16.

Evaluating Our Example with the Five-Assumption Approach

Below, we use our empirical example to discuss in detail how to evaluate a causal IV modeling approach with respect to the five assumptions from Angrist et al. (1996). We employ both empirical and conceptual evidence to assess whether our instruments and modeling approach meet each assumption. Then, once the assumptions are evaluated, we discuss a number of estimation approaches employing IV and compare results across the different approaches.

A1b. SUTVA

To satisfy assumption A1b, we must ensure that the effect of our treatment is consistent across all individuals in the sample. The treatment in our example is Algebra II course taking. So we must consider if the impact of Algebra II course taking on bachelor’s degree completion and first- to second-year persistence should be expected to be consistent across all students in our sample.

As was discussed above, the threat of spillover effects when treatments are administered in group settings has the potential to violate this assumption. In such cases, individuals within treatment and nontreatment groups may interact with each other (e.g., sharing information pertinent to the treatment), which might contaminate the treatment effect.

In our empirical example, the treatment is students taking an Algebra II course. The possibility of spillover would be unlikely in this case. In order for the Algebra II curriculum to spill over into other, non-Algebra II courses, contact between Algebra II instructors and non-Algebra II instructors would have to result in Algebra II concepts being taught in lower-level mathematics courses.

The other concern related to SUTVA is that the administration of the treatment is consistent across all treated groups. We expect the administration of the Algebra II curriculum to be consistent at the district level, though it may vary to some degree between districts. To account for this, we include state-level fixed effects in each of our models to control for such extraneous variation. Differences in administration between teachers within districts can be understood as a form of measurement error. Using national-level surveys, such as NELS and ELS, the values that we are actually able to measure (Algebra II course taking) and the actual treatment, what Algebra II curriculum students were exposed to, are going to be subject to some random variation. However, as long as this variation is approximately random, average treatment effects can still be estimated consistently. Given the structure of the administration and our included statistical controls, we believe the SUTVA assumption is satisfied.

A2b. Random Assignment

Next, we consider whether our instruments approximate random assignment, such that any individual in the sample has an equal probability of having any level of the instruments. More specifically, in our example, we need to determine whether county-level unemployment rates and/or whether a student is 16 years old at the beginning of 10th grade is determined in such a manner that they are randomly distributed across students.

First, we consider the county-level unemployment rate. The random nature of this variable is tied to the fact that it is driven by residence. It is unlikely that 10th grade students will travel across county lines for employment. Similarly, it is unlikely that parents will choose to move their students when they are in 10th grade to improve the quality of their educational environment, as residential mobility decreases as children get older, especially between counties (Long, 1972). Therefore, each student’s level of local unemployment is determined by their residence. Prior research has used the exogenous variation of a student’s residence as an instrument for a number of outcomes (Card, 1995). As local labor conditions, and other factors related to residence, change independently of both students’ course taking choices, their persistence in college, and eventual bachelor’s degree completion, we believe assumption A2b is satisfied.

Second, we need to examine whether a student’s age at the beginning of 10th grade is determined in such a manner that it is (basically) randomly distributed across the sample. We feel it is likely that a student’s birth month and year are determined by factors that approximate random assignment. Given the conceptual rationale provided above, we see no cause for serious concern about violations of assumption A2b.

A3b. Exclusion Restriction

Now we consider whether our instrumental variables’ only impact on the dependent variable is through their relationship with the endogenous independent variable of interest. Using our example, we must discern if the only impact that our instruments, county-level unemployment rates and being 16 years of age when a student enters 10th grade, have on our outcomes of interest (persistence and bachelor’s degree attainment) is through their influence on Algebra II course taking. Statistically, this can be stated as evaluating whether the instruments are correlated with the error term in the second stage equation (see Eq. 6.2 above). Empirically, this assumption can, in fact, never be tested (Angrist & Pischke, 2009; Porter, 2012) because the error in the second stage equation is a population parameter that we do not know the value of; thus, we can only make assumptions about its distribution. However, there are statistical tests (discussed below) that can provide evidence to support our conceptual argument for the validity of these instruments.

In order to discern if these instruments are (theoretically) correlated with the error term in the outcome equation, we must consider what the error term actually represents. While referred to as an error, this term in fact consists of any number of independent variables that influence our dependent variable of interest (persistence or bachelor’s degree attainment) but are either immeasurable or not included our model. Often such variables are referred to as “omitted” variables. A classic example of an omitted variable in many education research studies such as ours is student motivation. Observational data often include any number of demographic and academic characteristics about students, but measures of student motivation to succeed are often not available. Thus, measures of motivation are typically omitted from statistical models even though they are likely to be highly related to many of the educational outcomes we study. In order to conceptually evaluate whether the instruments we employ are correlated with the error term, we consider whether they are likely to be correlated with any variables that have been excluded from our model but are likely to have an impact on the outcomes of interest (persistence and bachelor’s degree attainment).

First, we consider county-level unemployment rates when students are in 10th grade. We expect that unemployment when a student is in 10th grade is likely to be correlated with unemployment when a student is in 12th grade, or even later, when they will be making decisions about college enrollment and persistence, which would ultimately influence degree attainment. However, we are actually able to include county-level unemployment rates when students are in 12th grade, which removes that variable from the error term and therefore removes the potential correlation. In doing so, we provide conceptual and some statistical support that our unemployment instrument meets assumption A3b.

Next, we consider whether students being age 16 at the beginning of 10th grade is correlated with the second stage error term. Research demonstrates that the age of a student when they begin school is often predictive of their subsequent academic performance (Angrist & Krueger, 1991). And one’s academic performance in high school affects one’s probability of achieving a bachelor’s degree (Astin & Oseguera, 2005; Camara & Echternacht, 2000). Therefore, if measures of academic performance are omitted from the model and subsumed into the error term, we might expect that age when beginning 10th grade will also be correlated with the error term. However, we include controls in our models for academic performance, using students’ scores on the NCES-standardized mathematics examination, therefore removing performance from the error term and decreasing the chances that age in 10th grade is endogenous.⁹ Including a control for academic performance provides us more confidence that this instrument meets assumption A3b.

If we are able to find at least two instruments for each endogenous regressor, then there are statistical tests available to examine whether this assumption is tenable. The most common of these tests is the overidentification (over-ID) test. An IV model is considered to be “just identified” if it includes one instrumental variable for each endogenous variable in the model. When the number of instruments exceeds the number of endogenous variables, the model is referred to as “overidentified.” If the number of endogenous variables exceeds the number of instruments, the model is “underidentified” and IV methods cannot be applied. When a model is overidentified, a Sargan-Hansen test of the overidentifying restrictions can be applied. In this test, the residuals from the second stage equation (6.6), y−ŷ, are regressed on the exogenous control variables from the model, x ₁. The test statistic is calculated by multiplying the number of observations in the model by the R-squared statistic. The over-ID statistic is distributed asymptotically as χ ² with degrees of freedom equal to the number of instruments minus the number of endogenous variables. The null hypothesis for this test is that the instruments are correctly excluded from the estimation of the dependent variable. However, this test does have its limitations as it still requires that we assume one instrumental variable is properly excluded from the second stage equation and then evaluates each additional IV with respect to the first. If the first IV does not in fact meet assumption A3b, then the over-ID test does not provide useful information. Stata provides a number of other similar over-ID tests for different IV models (see StataCorp, 2009, p. 757), the results of which we will discuss below.

Overidentification statistics for a number of the regressions we estimated are displayed in Table 6.3. Across the different IV models we estimated (to be discussed in detail below), none of the over-ID test statistics met conventional levels of significance. Again, we have to assume that the first IV, county-level unemployment in 10th grade, is properly excluded from second stage equation. Therefore, the over-ID tests provide statistical evidence that the additional IVs are properly excluded from the second stage equation. Given the empirical evidence and our conceptual evaluation of the instruments, we assert that assumption A3b is satisfied.

Table 6.3 Overidentification tests of instrumental variables

However, it is also important to note that significant overidentification statistics should not be the basis for fully rejecting the use of an instrument. The basis of the over-ID test is that the inclusion of a second instrument does not alter the estimates of an original model with only one instrument. However, it could be that two valid instruments could have differential impacts on individuals’ probability of treatment, and those differences could be even greater when considering the combined impact of the two instruments. While such differences would likely result in significant over-ID statistics, they would not justify the removal of either instrument from the IV model.

A4b. Nonzero Average Causal Effect of the Instrument on the Treatment

This assumption requires our instrument(s) to have a nonzero causal relationship with our endogenous treatment variable. In our example, the combined effect of our instruments on Algebra II course taking must be statistically significant. Tests for this assumption rely on the two-stage nature of many IV models. By evaluating the fit statistics of the first stage model, we are able to evaluate the correlation of the instrumental variables with the endogenous treatment variable. Using OLS in the first stage, the R ² statistic calculates the percentage of the variation in the endogenous treatment variable that is explained by all exogenous variables included in the first stage. The R ² statistic represents the strength of the relationship of all of the exogenous variables with the endogenous treatment variable; the primary concern of assumption A4b is the relationship of the instruments to the treatment variable. Partial-R ² statistics provide a measure of the proportion of the variance of the endogenous treatment variable that is explained by the instruments used as regressors in the first stage equation. Higher partial-R ² statistics represent a stronger relationship between the instruments and the endogenous treatment variable (i.e., Algebra II). Additionally, we can evaluate the F statistic, which provides a joint significance test of the relationship of the instruments to the endogenous treatment. This statistic should achieve and, researchers suggest, exceed conventional levels of statistical significance to demonstrate that instruments are properly specified (Hall, Rudebusch, & Wilcox, 1996). Each of these statistics can be obtained in Stata using the estatfirststage command following an IV modeling routine. Additionally, Wald tests of the joint significance of instruments can be computed for models where the first stage and second stage are estimated independently.

Test statistics evaluating the strength or relevance of our instrumental variables across the different models we estimated are displayed in Table 6.4. The R ² and adjusted R ² statistics for both samples indicate that our first stage models are accounting for between 23 and 25% of the variation in Algebra II course taking when all exogenous variables are included. The partial-R ² statistics suggest that our instruments are accounting for about 0.4–0.3% of the total variation in the models. This raises some concern about the strength of our instruments, but we can use a number of other test statistics to resolve those concerns. Stock, Wright and Yogo (2002) suggest that the F statistics should be larger than 10 to ensure against any bias induced because of weak instruments. The instruments in the first- to second-year persistence model, using the ELS:02 data, exceed this value, and therefore we accept that the instruments in that model satisfy assumption A4b. However, the F statistic for the bachelor’s degree completion model is only about six, suggesting that the relationship between our instruments and endogenous independent variable may be weaker than desired and could result in biased estimates (see Angrist & Pischke, 2009, p. 208).¹⁰ Although this is concerning, we are able to test for the potential for weak instrument bias in two ways suggested by Angrist and Pischke (also see Murray, 2006, for additional details of dealing with weak instrument problems). First, we estimate a two-stage least squares (2SLS) model (to be discussed in detail below) using only one instrument (the 16-year-old IV), because the 2SLS approach is nearly unbiased in the presence of weak instruments when the model is just identified (i.e., when the number of IVs equals the number of endogenous regressors). We then compare the coefficient estimates of the treatment effect (i.e., the coefficient on the Algebra II variable) from this model to the estimates produced by the 2SLS model that includes all of the instruments. When we include being 16 at the beginning of 10th grade as our instrument, we find that the just-identified model estimates an effect of 0.61 compared to the overidentified model estimates and effect of 0.55. We will discuss the substantive meaning of these results in the results section, but both models produce comparable estimates of the effects; therefore, we have some evidence that our treatment effect estimate from the bachelor’s degree attainment model is not severely biased due to a weak instrument problem.

Table 6.4 Tests of instrument relationships with Algebra II course taking

Angrist and Pischke (2009) also suggest that models estimated using limited information maximum likelihood (LIML) are less likely to be biased due to weak instruments than 2SLS models. Examining the estimates from each of these models in Table 6.6, the LIML model estimates an effect of 0.64 of Algebra II on bachelor’s degree attainment, which is very close to the estimate produced by both the just-identified and overidentified 2SLS models. Therefore, we are confident that there is a significant relationship between our instruments and our endogenous treatment variable and that A4b is satisfied.

A5b. Monotonicity

Next, we examine whether our instruments have a monotonic influence on high school mathematics course taking, such that increases in unemployment never result in decreases in mathematics course taking and that students who are 16 years of age in 10th grade are always less likely to take Algebra II. Our instrument is unlikely to satisfy this assumption fully, as there are assuredly students who decrease course taking levels in the face of increasing unemployment and 16-year-olds who are more likely to take Algebra II than younger students. However, we believe this set of students is likely to represent a very small portion of our sample; in which case, the presence of defiers simply places an upward bound on our estimate of the treatment effect (Angrist & Pischke, 2009; Porter, 2012). As defiers act in contradiction to the expected influence of the instrument, the estimated relationship between the instrument and the endogenous variable would be expected to be in the opposite direction to that of compliers (i.e., negative influence of unemployment on Algebra II and negative influence of being 16 on Algebra II). Mathematically, if we were to combine the estimated effects for each individual, the opposing signs would simply push the average effects of the instruments toward zero. As long as compliers outnumber defiers in our sample, we will be able to obtain at least a lower-bound estimate of the causal effect of mathematics course taking on postsecondary enrollment. Therefore, expecting that defiers are likely to account for only a very small portion of our sample, we believe that our instruments satisfy A5b.

We have evaluated the appropriateness of our IV approach for our empirical example, next we discuss a number of IV estimation strategies that can be employed to estimate causal treatment effects, and then we discuss the results using each of these estimation procedures.

Approaches to Modeling Causal Effects

Our empirical strategy is to estimate a number of different models testing the influence of high school-level mathematics course taking on first- to second-year persistence and bachelor’s degree attainment. Our estimation strategy is to begin by estimating a “naïve” statistical model using ordinary least squares (OLS) regression which does not account for the potential endogeneity of the regressor of interest (Algebra II). Next, two-stage least squares (2SLS) is employed, the first stage of which generates predicted probabilities of the Algebra II course taking using exogenous variation from the instruments and other controls. These predicted probabilities are then included as a regressor in the second stage equation. We then estimate a set of models that simultaneously estimate the IV model (limited information maximum likelihood (liml) and generalized method of moments (GMM)) and account for potential limitations of the basic 2SLS approach. We then employ a control function IV approach in which the residuals from the first stage regression are saved and then used as a regressor in the second stage. Doing so helps to “control” for the endogeneity of the instrumented variable (the Algebra II variable). Finally, we estimate another control function model which employs logistic regression in the second stage to account for the nonlinear relationship between the dichotomous dependent variable (i.e., persistence and degree attainment) and the included regressors. We employ these different methods to check the sensitivity of the results to the choice of method and pay particular attention to the estimates for the Algebra II variable for any differences that may emerge across the different model specifications.

Naïve Model: Using OLS Regression

The dependent variables of interest, persistence or degree attainment, are binary, and in such cases when OLS regression is applied, the model is referred to as a linear probability model (LPM). The LPM is formally represented by

$$ Y=\alpha +\beta X+\delta T+\epsilon $$

(6.16)

where Y, the dependent variable, is estimated as a function of a set of explanatory variables, X, and a treatment variable, T, that equals 1 when an observation (student) receives the treatment (takes Algebra II) and 0 when it does not. The traditional LPM regression framework does not account for any potential endogeneity that might exist between the treatment and the outcome variable (more accurately, between the treatment and the error). However, we might expect that there are excluded factors that directly relate to both the level of T and the level of Y. These excluded variables are absorbed into the error term, ε, which may be correlated with T. As was discussed above, an explanatory variable that is correlated with the error term is endogenous, and failure to adequately correct for this will result in a biased estimate of the coefficients for all explanatory variables included in the model.

We use the LPM model as a baseline model to evaluate the degree of bias in the point estimates that results from our failure to account for any endogeneity. As the LPM model assumes no endogeneity, the presence of endogeneity will result in biased estimates. When we apply other estimation procedures that account for endogeneity and reduce this source of bias, we expect that the estimates will differ from those produced by the LPM model. Using the LPM as a baseline, we will be able to clearly evaluate those differences by comparing the point estimate from the LPM to those obtained by employing the IV techniques.

The following set of statistical approaches employ a variety of instrumental variable techniques in order to account for endogeneity and in so doing provide less biased estimates of the “causal” relationship between the treatment and the outcomes of interest.

Two-Stage Least Squares

Two-stage least squares (2SLS) estimation, estimated using Stata’s ivregress 2sls command, is performed exactly according to its name. The estimation process occurs in two steps. The first stage is formally described below:

$$ \widehat{T}=\gamma +\beta X+\theta Z+\omega $$

(6.17)

The endogenous variable, Algebra II (T), is regressed on all of the exogenous variables, X, and a set of instruments, county-level unemployment, whether the student was 16 at the beginning of 10th grade, and the interaction of unemployment and age 16(Z), using a linear probability model (LPM). From this equation, estimates of T, denoted T, are produced. The initial values of T are understood to be composed of both endogenous and exogenous variations. When we use instruments to generate estimates of T, we decompose that variation into the exogenous portion, which is contained in the predicted values, $\widehat{T}$, and the endogenous portion, which is absorbed into the residuals, $T-\widehat{T}$. We then use the exogenous predicted values of T in the second stage model, formally displayed below:

$$ Y=\alpha +\beta X+\delta \widehat{T}+\epsilon $$

(6.18)

In this stage, the dependent variable of interest, Y (e.g., persistence or graduation), is regressed on the same set of exogenous variables, X, used in stage one, plus the predicted values of T produced by the first stage regression. Because the endogeneity in T has been reduced by replacing it with T, we expect that the estimate of δ will more closely approximate the causal influence of T on Y than when employing the naïve statistical model.

Simultaneous IV Models

Here, we discuss two simultaneous IV estimation procedures which build upon the 2SLS model: limited information maximum likelihood (LIML) and generalized method of moments (GMM). The LIML estimator is easy to estimate using the ivregressliml command in Stata; the results produced are robust to weak instrument problems (Rothenberg, 1983), and Monte Carlo simulations suggest the method is “less prone to bias and has more reliable standard errors” (Sovey & Green, 2011, p. 7). The GMM approach can be invoked in Stata with the ivregressgmm command. GMM provides a useful alternative to 2SLS when the independence assumption is violated (Baum, Schaffer, & Stillman, 2003). Given the possibility of an independence assumption violation due to the clustering of students within schools, this estimator is employed. Each of these commands is very simple to invoke by requiring the user to provide only the dependent variable and three sets of regressors: exogenous controls, endogenous independent variables, and the instruments.

Control Function Models

Another type of IV approach that produces equivalent estimates to the 2SLS approach is the control function technique (Card, 2001). However, the control function approach provides a greater degree of flexibility in the modeling of both the first and second stages, as will be discussed below. Here again, we estimate an OLS first stage model described formally as

$$ \widehat{T}=\gamma +\beta X+\theta Z+\omega $$

(6.19)

We retain the estimated residuals from this regression, $T-\widehat{T}$, rather than the predicted values, $\widehat{T}$, that were used in the 2SLS approach. These residuals are then inserted as a “control” in the second stage regression:

$$Y=\alpha +\beta X+\delta T+g(T-\widehat{T})+\epsilon$$

(6.20)

The inclusion of the residuals from the first stage controls for the endogenous variation in T, allowing δ to be interpreted as an estimate of the causal relationship between the treatment and the outcome variable of interest. In addition, the γ coefficient also provides a statistical test for the endogeneity of T. That is, if γ is statistically significant, then we are able to reject the null hypothesis that T is exogenously related to Y.

The control function approach suffers from improper standard errors due to the failure to account t for uncertainty introduced because of estimating the first stage regression. However, employing Stata’s bootstrapping procedure allows us to produce appropriate standard errors. By drawing a predetermined number of equally sized random samples from our data, with replacement, and then taking the average values of both point estimates and standard errors, bootstrapping provides a computationally intensive alternative to improve estimation.

Additionally, the control function approach allows for us to account for the nonlinearity of our dichotomous dependent variables. While each of the other procedures has relied on an OLS regression in the second stage, here we use a logistic regression which accounts for the dichotomous nature of both bachelor’s degree completion and first- to second-year persistence. While it has been argued that the linear probability model is suitable for dichotomous dependent variables, logit models may provide different estimates under some circumstances (Angrist & Pischke, 2009). Therefore, we include control function models employing both an LPM and logit regression in the second stage to evaluate any differences in point estimates due to the choice of regression method used.

Below, we provide a detailed discussion of the application of the IV approaches discussed above. We focus specifically on interpretation of the point estimates and marginal effects and when relevant discuss any important differences among these results.

Results

We discuss a number of descriptive statistics from each of our datasets to allow an introduction to the data and variables included in the multivariate models. Then, we move into a discussion of the estimates produced by the multivariate models. We first present the findings of our analysis modeling persistence from the first to second year of postsecondary education using the ELS:02 data. These models of student persistence serve as a proxy for our primary outcome of interest, bachelor’s degree attainment. This is due to a data limitation—students have not yet been followed long enough to determine whether they have completed a degree. We will then discuss the results of our degree attainment analysis using the NELS:88 data.

Descriptive Statistics

Table 6.1 presents descriptive statistics for the variables included in our models across the two samples: NELS, conducted from 1988 to 2000, and ELS, conducted from 2002 to 2006. The distribution of the dependent variables illustrates why policymakers are concerned about the consistently low educational attainment of students in the United States. Approximately one-third of students in the NELS sample attained a bachelor’s degree by the year 2000, 8 years after their expected high school graduation, and less than two-thirds of students in the ELS sample persisted to their second year of college by 2006. The distributions of other key variables are fairly similar between the two samples. For instance, despite educational stakeholders’ growing emphasis on providing a college preparatory curriculum for all students during the 1980s and 1990s, the sample statistics suggest that the percentage of students who take Algebra II remained at about 48–50% between the two surveys.

The mean unemployment in a student’s county of residence was lower for both NELS and ELS participants during their 10th grade years than in their 12th grade years. Specifically, the mean local unemployment rate was 5.77% when NELS participants were in the 10th grade (Fall 1989) and 7.51% when NELS participants were in the 12th grade (Spring 1992). ELS participants generally experienced more favorable economic conditions than NELS participants: The mean unemployment in a student’s county of residence was 4.96% in the 10th grade (2001) and 5.73% in the 12th grade (2004). Tenth grade unemployment rates had standard deviations of 2.39% and 1.68% in NELS and ELS, respectively, suggesting a relatively high level of variation in county-level unemployment in both samples. Our conceptual model suggests that the low local unemployment rates for students who were in the 10th grade in 1992 and 2001 may have induced students to enter the labor market and avoid intensive math coursework.

Additionally, there was a large shift in the proportion of students who were 16 years old in the 10th grade between the two surveys. In 1990, when NELS participants were in the 10th grade, 15.41% of sophomores were 16 years old. However, in 2002 when ELS students were in the 10th grade, 22.75% of sophomores were 16 years old. This means that fewer sophomores in the ELS sample than the NELS sample were impacted by policies that limit employment hours for youths aged 15 and under. Other explanatory variable sample statistics indicate that college students in the United States became increasingly racially diverse, but less socioeconomically diverse, in the decade between the two surveys.

Multivariate Models

A full table of results from both the NELS and ELS surveys is displayed in Tables 6.5 and 6.6. To allow comparisons across the models, all results are presented as marginal effects and may be interpreted as the percentage change in the probability of obtaining a bachelor’s degree (NELS) or persisting to the second year (ELS), given a one-unit change in the explanatory variable (ceteris paribus). For example, the coefficient for the male variable (−0.082) in the OLS column in Table 6.5 (the ELS results table) indicates that men have about an 8% lower probability of persisting from the first to second year than women. To foreshadow the results, across all of the models estimated, taking Algebra II increases the probability that students will earn a bachelor’s degree or persist to their second year of postsecondary education.

Table 6.5 Models of the impact of Algebra II course taking on first- to second-year persistence (ELS:02)

Table 6.6 Models of the impact of Algebra II course taking on bachelor’s degree attainment (NELS:88)

First- to Second-Year Persistence Results

Examining the results of the naïve OLS model, we find that students who take Algebra II have probabilities of persisting from the first to second year that are approximately 20% age points higher than students who did not take Algebra II. However, because this model does not account for the likelihood of selection bias, this estimate is likely biased. Therefore, we estimate a number of IV models that account for any endogeneity that may be present.

The naïve model of first- to second-year persistence presented in Table 6.5 underestimates the effect of the treatment, Algebra II course taking, on persistence. In fact, each of the instrumental variable models indicates that the treatment effect is nearly three times that of the OLS model. In the 2SLS, LIML, GMM, and control function (LPM) models, students who take Algebra II are estimated to have between a 59 and 60 percent higher probability of persisting to the second year than students who did not take Algebra II. The control function model using a logit approach in the second stage, accounting for the nonlinearity in our dependent variable, estimates a 52% increase in the probability of persisting when students take Algebra II as opposed to when they do not.

A number of other variables have consistent impacts on the probability of persisting from the first to the second year. Higher performance on the NCES-standardized mathematics exam is positively related to persistence: Those students in the 3^rd and 4th quartiles are, on average, about 12% and 22% (respectively) more likely to persist than students scoring in the lowest (1st) quartile. The effects of mathematics performance on persistence appear to decrease substantially between the OLS and the IV models, decreasing in magnitude in all cases. This suggests that the endogeneity in the OLS model is causing bias in the estimates not only of the Algebra II coefficients but also of many other regressors of interest.

Men are consistently less likely than women to persist to the second year, by about 6.5%. Students who identify as Asian or Pacific Islander are about 10% more likely to persist than Whites. Socioeconomic status has a consistent impact on persistence, such that individuals in higher SES quartiles are 15–20% more likely to persist than those in the lowest quartile. Finally, students whose mothers obtained either a bachelor’s or master’s degree are 4–6% more likely to persist than those whose mothers did not obtain a high school diploma.

Bachelor’s Degree Attainment Results

We find results comparable to those above when estimating models of bachelor’s degree completion using the NELS:88 data (see Table 6.6). The naïve model estimates about a 19% increase in the probability of completing a 4-year degree among students who have taken Algebra II, compared to their peers who have not. However, when accounting for the endogeneity of the Algebra II variable, our instrumental variable results suggest a much stronger relationship between Algebra II course taking and degree completion. Again, the 2SLS, LIML, GMM, and control function (LPM) models estimate an effect that is nearly three times larger than the estimate produced by the naïve OLS model, ranging from about a 55% increase in the probability of degree completion to a 67% increase. Further, our control function model that employs logistic regression in the second stage estimates a marginal effect of Algebra II course taking on bachelor’s degree attainment of.82—more than four times the size of that estimated produced by the OLS model.

Across all IV models, we find that male students are 5–7% less likely than female students to complete their bachelor’s degrees. Students who are of Asian or Pacific descent are 8–10% more likely than their White peers to complete a degree, whereas students of Native American descent are slightly less likely to graduate than Whites (holding all else equal). Higher-income students (SES quartiles 3 and 4) are between 10 and 26% more likely to earn a bachelor’s degree, relative to their peers who are of lower income.

Future Research, Implications for Policy, and Conclusions

This analysis employed an instrumental variables approach to determine the causal effect of high school courses on college completion. Specifically, we examined the impact of taking Algebra II or higher on a student’s probability of postsecondary attainment. In congruence with several prior studies (Adelman, 1999, 2006; Klopfenstein & Thomas, 2009; Rose & Betts, 2001), our “naïve” regression models indicate that students who take more intensive high school math courses have increased probabilities of degree completion compared to students who take less intensive math courses. Specifically, both the NELS and ELS naïve OLS analyses indicate that students who take Algebra II have a 19–20% higher probability of degree completion than students who do not take Algebra II. However, when we use local labor market conditions and student age in the 10th grade as instruments to account for the fact that student course taking is endogenous, we find that taking Algebra II has a much greater impact on a student’s probability of degree completion than the naïve model results indicate. The NELS and ELS IV models indicate that taking Algebra II can increase a student’s probability of degree attainment by as much as 50–80%. In sum, using the most recent course taking data available and accounting for endogeneity, we find that taking Algebra II in high school has a positive effect on a student’s likelihood of degree attainment. That the estimated positive effect of Algebra II course taking was larger in the IV estimates than the OLS estimates suggests that negative bias (the naïve estimates are lower that the “true” causal estimates) may be present in course taking effects studies that do not account for selection and omitted variable bias. Our naïve estimates obscure the fact that the students who are least likely to take intensive math coursework (marginal students) appear to benefit greatly from taking Algebra II while in high school.

These findings have implications for policies that aim to increase college completion. As noted in the introduction to this chapter, several states and school districts have implemented mandatory college preparatory requirements over the past several years. These requirements are an extension of state-mandated increases in the number of years of math coursework needed to earn a diploma that have occurred since the release of A Nation at Risk, the implementation of No Child Left Behind, and the publication of influential research from the US Department of Education (Adelman, 1999, 2006). Absent course taking effects research that strongly supports causal inference, policymakers who hope to improve student educational and labor market outcomes on a large scale have implemented these curriculum mandates on the basis of findings from correlational studies. Our study provides rigorous evidence that, at least for students who are at the margin of taking Algebra II or not, mandating them to take this course may indeed produce positive individual and maybe even societal benefits.

It is important to note that high school courses may have a causal impact not only on degree completion but on other outcomes that are of interest to state and federal policymakers. For instance, intensive high school courses may improve students’ critical thinking skills, high school graduation rates, access to college, or performance in college-level coursework. In a related study, Kim, Kim, DesJardins and McCall (2012, April) use the same IVs employed in this study on Florida student unit record data and find that taking Algebra II has a positive impact on the odds of enrolling in a 2- or 4-year college, as opposed to not enrolling in college at all. They also find that their IV model provides larger estimates of math course taking’s effects than a naïve statistical model, which suggests that the students who are least likely to take challenging courses appear to benefit from them the most in gaining access to postsecondary education.

To help inform policymakers, researchers should continue to explore how high school courses causally affect student educational attainment. Future studies could examine whether intensive courses in subjects other than math—such as science, English, or foreign languages—contribute to increased degree attainment. Additionally, it is important to determine if dropping out of the math course taking pipeline at different stages has different effects for students who attend different types of institutions. For example, it is possible that taking Algebra II has a positive effect on the degree attainment of students who attend 2-year and nonselective 4-year institutions but no effect on the attainment of students who attend selective 4-year colleges. It is possible that students who attend selective 4-year colleges may need to remain in the math pipeline through Trigonometry or Precalculus to improve their odds of degree attainment. Additionally, given the large disparities in course taking among disadvantaged and advantaged students, it is important that researchers determine whether the causal impact of coursework varies across student socioeconomic status and race/ethnicity (Dalton et al., 2007). If disadvantaged students benefit disproportionately from taking Algebra II and other intensive courses, eliminating de facto tracking may be a key step in reducing disparities in educational attainment between low- and high-SES students and underrepresented minority and majority students.

Above, we employ a local average treatment effect (LATE) approach using an IV framework. As noted, these approaches are often an improvement over the naïve approach that does not account for nonrandom assignment (i.e., endogeneity) issues. Although the IV approach is popular, it is not without its critics, some of whom believe it is somewhat a theoretical relative to other approaches. For example, structural models (as defined by economists at least) focus more on the description of a theoretical model of the process and mechanisms underlying the problem at hand and attempt to estimate the fundamental parameters of interest. As Heckman notes, “the problem that plagues the IV approach is that the questions it answers are usually defined as probability limits of estimators and not by well formulated economic problems. Unspecified ‘effects’ replace clearly defined economic parameters as the objects of empirical interest” (Heckman & Urzua, 2009, p. 3). Heckman and associates (Heckman & Vytlacil, 2005; Carneiro, Heckman, & Vytlacil, 2011) have bridged the IV and structural model literature using a local version of IV (which they dub local instrumental variables or LIV) which can be used to derive the effects estimable using standard IV methods (average treatment effects, average treatment on the treated, LATE) plus it allows for the estimation of a highly relevant policy effect which they call the marginal policy relevant treatment effect (MPRTE). This approach is designed to remedy some of the deficiencies of the standard IV approach, in particular problems when the instruments are not tightly linked to policy changes of interest, in which case IV estimates do “not answer well-posed policy questions” (Carneiro et al., 2011, p.2779). This approach seems to hold great promise in allowing researchers to identify and estimate the effects of policies on educational (and other) outcomes and in so doing allows us to inform policymakers so they can make better informed decisions.

Concerned scholars are becoming increasingly vocal about the need for higher education research to address selection bias and use statistical methods that allow for stronger causal inferences (Goldrick-Rab, Carter, & Wagner, 2007; Long, 2007; McCall & Bielby, 2012; Reynolds & DesJardins, 2009). This study helps address their concerns by providing researchers with a tool—instrumental variables estimation—for examining how an endogenous explanatory variable causally affects an outcome. We hope this example illustrates how important it is to employ statistical methods that account for nonrandom assignment into “treatments” in observational data, whether these treatments take the form of a course, scholarship, tutoring program, or any other intervention that may potentially facilitate educational attainment. Frankly, in many circumstances, the traditional “naïve” approach to studying educational policies, processes, and programs that are characterized by nonrandom assignment is often not rigorous enough. Higher education and institutional researchers need to become adept in using the latest tools that will allow us to make causal statements about what works in education and what needs to be improved. Hopefully, this chapter will be a valuable addition to the expanding literature in this area.

Appendix: Stata syntax

/*This file will run all analysis for the IV chapter on the ELS data. The file for the NELS data is nearly identical, simply replacing the dependent variable in each model from persistence to bachelor’s degree attainment*/

/*First create global macros for the models. This allows us to insert a large number of variables into our models without having to repeatedly type the variable names.*/

/***Becausethe data used for this analysis are restricted, we will not include actual variable names,but instead will provide alternate names for the variables used***/

/*Exogenous independent variables*/

global exog1 “mathquart2 mathquart3 mathquart4 male black asian_amhisp_amnative_ammixedoth ses_q2 ses_q3 ses_q4 mom_hs mom_att2yr mom_aa mom_att4yr mom_bamom_mamom_phd born_84 born_85 born_86 born_87 unemploy_rate2004 i.hsstate”

/*Endogenous independent variable*/

global endo1 “algebra_2”

/*Instrumental variables*/

global inst1 “unemploy_rate2001 age_16_urate age_16”

/*BIVARIATE CORRELATIONS AMONG ALL VARIABLES. Here we examine the bivariate relationships between each of our variables*/

corpse_att algebra_2 unemploy_rate2001 age_16_urate age_16 mathquart2 mathquart3 mathquart4 male black asian_amhisp_amnative_ammixedoth ses_q2 ses_q3 ses_q4 mom_hs mom_att2yr mom_aa mom_att4yr mom_bamom_mamom_phd unemploy_rate2004

spearmanpse_att algebra_2 unemploy_rate2001 age_16_urate age_16 mathquart2 mathquart3 mathquart4 male black asian_amhisp_amnative_ammixedoth ses_q2 ses_q3 ses_q4 mom_hs mom_att2yr mom_aa mom_att4yr mom_bamom_mamom_phd unemploy_rate2004

/*Multivariate models of first to second-year persistence*/

/***BASELINE OR NAIVE MODEL***/

/*Linear Probability Model (LPM)*/

reg persist $endo1 $exog1, robust

/*We use the ‘eststo’ command to save the estimates from each of our final modelswhich we use later to create a publication-ready table*/

eststo OLSpersist

/***INSTRUMENTAL VARIABLES ESTIMATORS***/

*Two Stage Least Squares (2SLS)

/*First we estimate the model, using the global macros from above*/

ivregress 2sls persist $exog1 ($endo1 = $inst1), vce(robust)

/*Here we examine the model fit statistics from the first stage model in the 2SLS approach. The ‘estatfirststage’ command provides R-squared and Adjusted R-squared statistics along with partial R-squared statistics for and F tests with significance levels for each endogenous variable*/

estat firststage

/*Here we examine the overidentification tests to evaluate the exclusion restriction for our instruments. To confirm our expectation that the variables are properly excluded from the second stage model. If that is the case these test statistics will not be statistically significant*/

estat overid

/*Next we examine tests of the endogeneity of our Algebra II variable. If our variable of interest is in factendogenous, then these statistics will be statistically significant*/

estat endogenous

/*Here we store the estimates from the 2SLS model to be used to create a publication-ready table which will also allow us to compare results across the estimated models.*/

eststo SLSpersist

*Limited Information Maximum Likelihood (LIML)

/*Estimating the model*/

ivregressliml persist $exog1 ($endo1 = $inst1), vce(robust)

/*Evaluatingthe first stage model statistics*/

estatfirststage

/*Overidentification tests*/

estat overid

/*Storing estimates*/

eststo LIMLpersist

*Generalized Method of Moments (GMM)

/*Running the model*/

ivregressgmm persist $exog1 ($endo1 = $inst1), vce(robust)

/*Againexamine the first stage statistics*/

estat firststage

/*Overidentification tests*/

estat overid

/*Tests for endogeneity*/

estat endogenous

/*Storing Estimates*/

eststo GMMpersist

/*Control function with LPM and Bootstrap*/

/*In order to bootstrap the standard errors for these estimates, we need to first write a program that will run the first stage regression, save the residuals, and then include those residuals as controls in the second stage regression */

capture program drop lpmcf

program lpmcf

 quietly {

/*estimate the first stage LPM*/

reg algebra_2 $exog1 $inst1, robust

/*just in case we already saved these variables we drop them*/

capture drop alg2_resid_els

/*store the residuals from the first stage */

predict alg2_resid_els, resid

/*estimate the second stage LPM*/

reg persist $endo1 $exog1 alg2_resid_els, robust

 }

end

/*Now we estimate a control function model with an LPM second stage on 250 bootstrapped samples and estimate our standard errors from that*/

bootstrap _b, seed(1) r(250): lpmcf

/*Store the estimates*/

eststo CFLPMpersist

*Control function with Logit and Bootstrap

/*This program estimates the first and second stages then we conduct a bootstrap to estimate the proper standard errors*/

capture program drop logitcf

program logitcf

 quietly{

/*estimate the first stage*/

reg algebra_2 $exog1 $inst1, robust

capture drop alg2_resid_els_logit

/*store residuals from first stage*/

predict alg2_resid_els_logit, resid

 /*estimate the second stage logit*/

logit persist $endo1 $exog1 alg2_resid_els_logit, vce(robust)

}

end

/*Now we estimate a control function model with a logit second stage on 250 bootstrapped samples and produce standard errors from that process*/

bootstrap _b, seed(1) r(250): logitcf

/*Because the coefficients produced through Stata’s logit routine are not directly comparable to those from each of the other models that are linear probability models in the second stage, we use Stata’s ‘margins’ command to convertlogit coefficients into comparable marginal effects*/

margins, dydx(*)

/*Store the results*/

eststo CFLogitpersist

/*Finally we employ the ‘esttab’ routine to create a publication-ready table of marginal effects (b) and significance measures (p)*/

esttabOLSpersistSLSpersistLIMLpersistGMMpersistCFLPMpersistCFLogitpersist, b(3) p(3) not wide plain