Reasoning in Uncertain Environments

Abstract

 Real-life propositions are neither fully true nor false, also there is always some uncertainty associated with them. Therefore, the reasoning using real-life knowledge should also be in accord. This chapter is aimed to fulfill the above objectives. The chapter presents the prerequisites—foundations of probability theory, conditional probability, Bayes theorem, and Bayesian networks which are graphical representation of conditional probability, propagation of beliefs through these networks, and the limitations of Bayes theorem. Application of Bayesian probability has been demonstrated for specific problem solutions. Another theory—the Dempster–Shafer theory of evidence—which provides better results as the evidences increase is presented, and has been applied on worked examples. Reasoning using fuzzy sets is yet another approach for reasoning in uncertain environments—a theory where membership of sets is partial. Inferencing using fuzzy relations and fuzzy rules has been demonstrated, followed by chapter summary, and a set of exercises at the end.

12.1 Introduction

The real-life propositions are neither fully true nor false, and there is uncertainty associated with them. Therefore, the reasoning drawn from these are also probabilistic. This requires probabilistic reasoning for decision-making. This chapter presents two approaches for probabilistic reasoning—the Bayes theorem and Dempster–Shafer theory. The first is implemented as Bayesian belief networks, where nodes (events) are connected using directed graph with edges of the graph representing cause–effect relationships; the beliefs propagate in a network as per the rules of Bayes conditional probability. The Dempster–Shafer (D-S) theory is based on evidential reasoning such that evidences are conjuncted, and as more and more evidences take part in the reasoning, the ignorance interval decreases. The classical probability theory is a special case of D-S theory of Evidential Reasoning.

In the case of Classical Logic, a proposition is always taken either as true or false. However, in a real-life scenario one cannot always say a proposition to be either 100% true or 100% false, but known to be true with a certain probability. For example, one can say that the proposition: “Moon rover will function alright,” may have a probability of being true as 30%, which is calculated based on the success rate of previous probes sent to the Moon. However, the proposition “Sun rover will function alright” has a probability of being true as 0%, due to extreme temperature at the Sun’s surface. Because such uncertainties are common in expert systems when they are deployed in real-life applications, the knowledge representation as well as the reasoning system of the expert system must be extended to work like in a real-life situation.

Fundamentally, there are two basic approaches to reasoning in uncertain domains: probabilistic reasoning and non-monotonic reasoning. The basis of probabilistic reasoning is to attach some probability value to each proposition to express the uncertainty of the event. These uncertainties may be derived from existing statistical information available as the database of a corpus, or these may be estimated by the experts.

Facilities for handling uncertainty have long been an integral part of knowledge based system. In the early days of rule-based programming, the predominant methods used variants on probability calculus to combine certainty factors associated with applicable rules. Although it was recognized that certainty factors did not conform to the well-established theory of probability, these methods were nevertheless favored because the probabilistic techniques available at the time required either specifying an intractable number of parameters or assumed an unrealistic set of independence of relationships.

The most important area, for understanding the uncertainties is medical diagnostics or troubleshooting of any system; in the first it is required to identify the patterns (diagnoses) on the basis of their properties (symptoms), while in the second it is common to recognize the faults on the basis of system behavior. However, there is no one-to-one mapping of symptoms and diagnoses, and the uncertainties of mapping symptoms with diagnoses prevail due to the following reasons:

• ascertaining of the symptoms,

• proper evaluation of symptoms, and

• insufficient criteria about reckoning the scheme.

Generally, the end user of an expert system identifies and ascertains about the symptoms and their uncertainties, while the uncertainties in the evaluation of symptoms are carried out by the experts. Because different people judge these uncertainties, they are likely to judge it differently, and there is no scope of normalization. Consequently, it is likely to be a large uncertainty. Often the reckoning methods are also simple, which are some “ad hoc representations”, on account of lack of theoretical foundations.

Many different methods for representing and reasoning with uncertain knowledge have been developed during the last three decades, including the certainty factor calculus, Dempster–Shafer theory, possibilistic logic, fuzzy logic, and Bayesian networks (also called belief networks and causal probabilistic networks).

Learning Outcomes of this Chapter:

• 1. Identify examples of knowledge representations for reasoning under uncertainty. [Familiarity]

• 2. Make a probabilistic inference in a real-world problem using Bayes theorem to determine the probability of a hypothesis given evidence. [Usage]

• 3. Apply Bayes rule to determine the probability of a hypothesis given evidence. [Usage]

• 4. Describe the complexities of temporal probabilistic reasoning. [Familiarity]

• 5. State the complexity of exact inference. Identify methods for approximate inference. [Familiarity]

• 6. Design and implement an HMM as one example of a temporal probabilistic system. [Usage]

• 7. Explain how conditional independence assertions allow for greater efficiency of probabilistic systems. [Assessment]

• 8. Make a probabilistic inference in a real-world problem using Dempster–Shafer’s theorem to determine the probability of a hypothesis given evidence. [Usage]

12.2 Foundations of Probability Theory

In the following, we list the commonly used terminology of the probability theory.

Considering an uncertain even E, the probability of its occurrence is a measure of the degree of likelihood of its occurrence.

A sample space S is the name given to the set of all possible events.

A probability measure is a function $P(E_i)$ that maps every event outcomes, $E_1, E_2, \ldots , E_n$ from event space S, to real numbers in the range [0, 1].

These outcomes satisfy the following axioms (basic rules) of probability:

• 1. for any event $E \subseteq S$, there is $0 \le P(E) \le 1$,

• 2. an outcome from space S that is certain is expressed as $P(S) = 1$, and

• 3. when events $E_i, E_j$ are mutually exclusive, i.e., for any events $E_i, E_j$, there is $E_i \cap E_j = \phi$, for all $i\ne j$. In that case, $P(E_1 \cup E_2 \cup \ldots \cup E_n) = P(E_1) + P(E_2) + \cdots + P(E_n) = 1$.

Using these three axioms, and the rules of set theory, the basic laws of probability can be derived. However, the axioms alone are not sufficient to compute the probability of an outcome, because it requires an understanding of the corresponding distribution of events. The distribution of events must be established using one of the following approaches:

• 1. Collection of experimental data to perform statistical estimates about the underlying distributions,

• 2. Characterization of processes using theoretical argument,

• 3. Understanding about the basic processes are helpful to assign subjective probability.

Some examples of computation of probability are given below. The upper case variable names represent the sets.

$$\begin{aligned} P(A) = \frac{count~of(All ~ A)}{count~of(all ~ events)} \end{aligned}$$

(12.1)

$$\begin{aligned} P(A \cap B) = \frac{count~of(All~A \text { and } B \text { together} )}{count~of(all ~B{\text {'}}s)} \end{aligned}$$

(12.2)

$$\begin{aligned} P(A \cap B)&= P(A \mid B)P(B)\nonumber \\&= P(B \mid A)P(A). \end{aligned}$$

(12.3)

Therefore,

$$\begin{aligned} P(A|B) = \frac{P(B\mid A)P(A)}{P(B)}. \end{aligned}$$

(12.4)

Most of the knowledge we deal with is uncertain, hence the conclusions based on available evidences and past experiences are incomplete. Many a time it is only possible to obtain partial knowledge about the outcomes.

12.3 Conditional Probability and Bayes Theorem

The Bayesian networks provide a powerful framework for modeling uncertain interactions between variables in any domain of concern. The interactions between the variables are represented in two ways: 1. Qualitative way, using directed acyclic graph, and 2. Quantitative way, which makes use of conditional probability distribution for every variable in the network. This probability distribution-based system allows to express the relationship between the variables, as functional, relational, or logical.

Along with the above, the dynamic probability theory provides a mechanism for revising the probabilities of events in a coherent way, as the evidences become available. We represent the conditional probability, i.e., the probability of occurrence of an event A, given that the event B has already occurred, as P(A|B). Note that, if the events A and B are totally independent, then P(A|B) and P(A) will have the same result, otherwise, due to its dependency, the occurrence of A will be effected, and accordingly the probability P(A|B). Here, occurrence of event A is called hypothesis and occurrence of event B is called as evidence. If we are counting the number of sample points, we are interested in the fraction of events B for which A is also true, i.e., $(B \cap A)$ is what fraction of B? The meaning of fraction is like the A and B are fractions of the universe set $\varOmega$. In $(B \cap A)$, both A and B are partly included, which is also represented as (A, B). From this it becomes clear that

$$\begin{aligned} P(A | B) = \frac{P(A, B)}{P(B)}. \end{aligned}$$

(12.5)

The above equation is often written as

$$\begin{aligned} P(A, B) = P(A | B)P(B). \end{aligned}$$

(12.6)

Equation (12.6) is also called “product rule” or simple form of Bayes theorem. It is important to note that this form of the rule is not often stated a definition, but a theorem, which can be derived from simpler assumptions. The term P(A|B) in the equation is called posterior probability.

The Bayes theorem is used to tell us how to obtain a posterior probability of a hypothesis A once we have observed some evidence B, given the prior probability P(A) of event A, and probability P(B|A)—the likelihood of observing B—were A to be given. The theorem is stated as

$$\begin{aligned} P(A|B) = \frac{P(B|A)P(A)}{P(B)}. \end{aligned}$$

(12.7)

The formula (12.7), though simple, has abundant practical importance in the area such as diagnosis, may it be patient or a fault diagnosis in software or an electric circuit, or any other similar situation. Note that it is often easier to conclude the probability of observing a symptom given a disease, than the reverse—that is, of a disease, given a symptom. Yet, in practice it is the latter (i.e., find out the disease or fault given the symptom), which is required to be computed. See what the doctors do, it is the disease (hypothesis) they try to find out given the symptom (evidence).

There are certain conditions under which the Bayes theorem is valid. Let us assume that there is only one symptom (S) and corresponding only one diagnosis (D), and having given this we will try to extend the formula of the Bayes theorem. The conditional probability for this is expressed as P(S|D), which says about relative frequency of occurrence of the symptom S when diagnosis D is true. The term P(S|D) can be expressed by

$$\begin{aligned} P(S|D) = \frac{|S\cap D|}{|D|}, \end{aligned}$$

(12.8)

where

• |S| is frequency of occurrence of symptom S,

• |D| is frequency of the occurrence of diagnosis D, and

• $|S\cap D|$ is frequency of simultaneous occurrence of both S and D.

The probability P(D|S), called posterior probability or conditional probability of diagnosis D, assuming a symptom S, is given by Bayes theorem as

$$\begin{aligned} P(D|S) = \frac{P(S|D)P(D)}{P(S)}. \end{aligned}$$

(12.9)

The term P(S|D) is called likelihood of symptom S when diagnosis is D, and P(D) is called prior probability.

The above can be proved as follows:

$$\begin{aligned} P(D|S)&= \frac{|S\cap D|}{|S|}\\&= \frac{|D|}{|D|} * \frac{|S\cap D|}{|S|}\\&= |D| * \frac{|S\cap D|}{|D| * |S|}\\&= |D| * \frac{|S\cap D|}{|D|}*\frac{1}{|S|}\\&= \frac{P(S|D)*P(D)}{P(S)};\text {using Eq.}~(12.8) \end{aligned}$$

The denominator terms P(S) is called the normalizing factor.

Example 12.1

Suppose that the following statistics hold for some disease:

• $P(tuberculosis) = 0.012$,

• $P(cough) = 0.10$, (for over 3 weeks)

• $P(cough \mid tuberculosis) = 0.90$, i.e., if a patient has tuberculosis, the coughing is found in 90% of the cases.

Given this, compute the probability of having tuberculosis, given that coughing exists in those persons, for over 3 weeks.

$$\begin{aligned} P(tuberculosis|cough)&= \frac{P(cough|tuberculosis)\times P(tuberculosis)}{P(cough)}\\&=\frac{0.9\times 0.012}{0.10}\\&=0.108. \end{aligned}$$

Hence, the relative probability that a patient who had a tuberculosis was found to be having also the cough is, 8.33 (= 0.9/0.108) times the probability of finding tuberculosis in the coughing patients. $\square$

Relative Probability

The Bayes theorem allows the determination of the most probable diagnosis, assuming the presence of symptoms $S_1 \ldots S_m$. The probability is determined using: 1. a priori probabilities $P(D_i)$ that belong to a set of diagnoses, and 2. likelihood $P(S_j / D_i)$. The latter is the relative frequency of the occurrence of a symptom $S_j$ given that the diagnosis is $D_i$. In the Bayes probability, an absolute probability is not important, but a relative probability $P_r$ is determined. $P_r$ is the probability of a diagnosis compared to the other diagnoses, which is computed as

$$\begin{aligned} P_r(D_i|S_1 \wedge S_2\wedge \ldots \wedge S_m) = \frac{P(D_i)~P(S_1|D_i) \ldots P(S_m|D_i)}{\varSigma _{j=1}^n P(D_j)~P(S_1|D_j) \ldots P(S_m|D_j)}. \end{aligned}$$

(12.10)

Note that in the above definition, the normalization factor of $P(S_1\wedge \ldots \wedge S_m)$, which is a common denominator, in the numerator and denominator terms, has been dropped.

When we are considering many symptoms, as in the above case, it is necessary that the correlation of every relevant combination of symptoms to disease be determined. However, if this happens, it would lead to a combinatorial explosion of diagnoses, e.g., with 100 all possible symptoms, there are $2^{100}$ different constellations of diagnoses. This figure is more that $10^{30}$!

Therefore, while using the Bayes theorem it is always assumed that the symptoms are independent of each other, i.e., for two symptoms, $S_i$ and $S_j$

$$\begin{aligned} P(S_i \wedge S_j | D) = P(S_i|D) P(S_j|D). \end{aligned}$$

(12.11)

The exception to the above is allowed when symptoms are caused directly by the same diagnosis.

From Eqs. (12.10) to  (12.11), it follows that

$$\begin{aligned} P(D|S_1 \wedge \ldots \wedge S_m)&= \frac{P(S_1\wedge \ldots \wedge S_m|D)}{P(S_1\wedge \ldots \wedge S_m)P(D)}\\&= \frac{P(S_1|D) \ldots P(S_m|D)}{P(S_1\wedge \ldots \wedge S_m)P(D)}. \end{aligned}$$

The Bayes theorem in the above form is correct, subject to the fulfillment of the following conditions:

• 1. The symptoms may depend only on the diagnoses, and must be independent of each other. This becomes a critical point, when more and more symptoms are ascertained.

• 2. The set of diagnoses is complete.

• 3. Single fault assumption or mutual exclusion of diagnoses—presence of any one diagnosis automatically excludes the presence of other diagnoses. This criteria is justified only in a relatively small set of diagnoses.

• 4. The requirement of correct and complete statistics of prior probabilities (P(D)) of the diagnoses, and conditional symptom-diagnosis probabilities(P(S|D)).

12.4 Bayesian Networks

The Bayesian network is a graphical representation of the Bayes theorem—a set of variables represented as cause–effect relations, where variables are nodes and edges represent the relevance or influence relation between variables. Absence of an edge between two variables indicates independence of the variables, i.e., nothing can be inferred about the state of one variable, having given the state of the other variable. A variable may assume the values from a collection such that this collection is a mutually exclusive as well as collectively exhaustive set. A variable is allowed to be discrete—having a finite countable number of states—or it may be continuous—infinitely many possible states.

The lowercase letters in Bayesian networks represent single variables, while uppercase letters represent sets of variables. To assign state k to variable x, we write as $x = k$. When the state of every variable is comprised in set X, then this set (an observation) is an instance of X. Set of all the instances is represented by a universal set U, which is the joint space of all the instances. A joint probability distribution over set U is the probability distribution over joint space U. Considering X,  and Y as sets, the expression P(X|Y) denotes the joint probability distribution over the set X, one for each conditional corresponding to every instance in the joint space of Y.

The Bayesian networks are good for structuring probabilistic information about a situation in a systematic way. This information is provided in localized and coherent way. These networks also provide a collection of algorithms, which help in deriving many information as implications of the conditionals, that can lead to important conclusions, and decisions about the given situation. These may be for example, in the area of genetics—mapping genes onto a chromosome, in message transmission and reception—finding the most likely message that was sent across a noisy channel, in system reliability—computing the overall reliability of a system, in online sales, e.g., to identify the most likely users who would respond to a given advertisement, in image processing, e.g., restoring a noisy image, and so on.

In more technical terms, a Bayesian network is a representation in a compact form of probability distribution using graphical method. The traditional methods were usually too large to handle probability and statistics computations, such as using tables and equations. Typically, a Bayesian network of 100s variables can be easily constructed and used for reasoning successfully about probability distribution [4].

12.4.1 Constructing a Bayesian Network

Though the definition of a Bayesian network is based on conditional independence, these networks are usually constructed using the notions of cause and effect. In simple words, for a given set of variables, we construct a Bayesian network by connecting every cause to its immediate effect using arrows in that direction. In almost all the cases, this results in Bayesian networks, whose conditional independence are implicit and accurate.

Fig. 12.1

Cause–effect Bayesian network

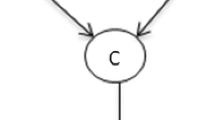
Figure 12.1 shows a Bayesian network with many causes ($c_1, c_2, \ldots , c_n$) and a single effect e. Due to this, specification of its local distribution can be quite onerous in the general case. As per the definition for a Bayesian network, it is necessary to compute the probability distribution of the node conditional on every instance of its parents. For example, if a node x has n number of parents, each is binary in nature (either 0 or 1 only), then we need to specify total $2^n$ probability distributions for the node x. We can reduce the complexity of this computation in such cases by adding more structures in the model. For example, we can convert our model into a n-way interaction model by associating with each cause node an inhibitory mechanism that prevents the cause from producing the effect. In such a model, the effect will be absent if and only if all the inhibiting mechanisms associated with the present cause node are active. And, if any of the inhibiting mechanism for this node is inactive, the cause node will produce the effect.

12.4.2 Bayesian Network for Chain of Variables

A problem domain is nothing but a set of variables. Thus, a Bayesian network for the domain $\{x_1, \ldots , x_n\}$ can represent a joint probability distribution over these variables. This distribution consists of a set of local conditional probability distribution, that when combined with a set of assertions of conditional independence, gives a joint global distribution.

Fig. 12.2

Chain of domain variables

The composition is based on the chain rule of probability (see Fig. 12.2), which dictates that

$$\begin{aligned} P(x_1, \ldots , x_n) = \prod _{i=1}^n P(x_i|x_1, \ldots , x_{i-1}). \end{aligned}$$

(12.12)

For each given variable $x_i$, let us assume that $S_i \subseteq \{x_1, \ldots , x_{i-1}\}$ is a set of variables which causes the variable $x_i$, and $\{x_1, \ldots , x_{i-1}\}$ to be conditionally independent. That is

$$\begin{aligned} P(x_i|x_1, \ldots , x_{i-1}) = P(x_i|S_i). \end{aligned}$$

(12.13)

The approach to this idea is that the distribution of $x_i$ can be represented as conditional on a parent set of $S_i$ which is substantially smaller than $\{x_1, \ldots , x_{i-1}\}$. Given these two sets, a Bayesian network can be represented as a directed acyclic graph such that each variables $x_1, \ldots , x_n$ corresponds to a node in that graph and the parents of the node corresponding to the variables in $S_i$. Note that since the graph coincides with the conditioning set $S_i$, the assertions of the conditional dependence are directly encoded by the Bayesian network structure. This is expressed in Eq. (12.13).

A conditional probability distribution $P(x_i|S_i)$ is associated with each node $x_i$, such that there is one distribution for each instance of $S_i$. By combining the Eqs. (12.12) and (12.13), we obtain a Bayesian network for $\{x_1, \ldots , x_n\}$ which uniquely determines a joint probability distribution for these variables. That is,

$$\begin{aligned} P(x_1, \ldots , x_n) = \prod _{i=1}^n P(x_i|S_i). \end{aligned}$$

(12.14)

Because the joint probability distribution for any network can be determined using Bayesian network for a given domain, this network can be used in principle to compute any probability of interest. Consider that we are given a simple Bayesian network, with structure $w \rightarrow x \rightarrow y \rightarrow z$, and we are interested to find out the probability “of occurrence of event w given that the event z has already occurred,” which can be expressed as P(w|z). From the Bayes rule, and making use of the above structure $w \ldots z$, the equation can be expressed as follows.

$$\begin{aligned} P(w|z) = \frac{P(w, z)}{P(z)}=\frac{\sum \limits _{x, y} P(w, x, y, z)}{\sum \limits _{w, x, y}P(w, x, y, z)}. \end{aligned}$$

(12.15)

In the above, P(w, x, y, z) is called the joint probability distribution computed for the Bayesian network $w \rightarrow x \rightarrow y \rightarrow z$. On observation of numerator and denominator terms of Eq. (12.15), we can understand that this approach is not feasible, due to the reason that it requires summing over exponential number of terms. However, we can exploit the conditional independence encoded in a Bayesian network to arrive at a more efficient computation. Using this feature, the network structure of Eq. (12.15) can be transformed to

$$\begin{aligned} P(w|z)&= \frac{\sum \limits _{x, y} P(w, x, y, z)}{\sum \limits _{w, x, y} P(w, x, y, z)}\nonumber \\&=\frac{P(w)\sum \limits _x P(x|w)\sum \limits _y P(y|x) P(z|y)}{\sum \limits _w P(w)\sum \limits _x P(w) P(x|w)\sum \limits _y P(y|x) P(z|y)}. \end{aligned}$$

(12.16)

Equation (12.16) indicates that using conditional independence (i.e., independence of conditional variable), we can often reduce the dimensions of an equation by rewriting the “sums over multiple variables as a product of sums over a single variable,” or at least to a lesser number of variables.

A probabilistic inference is a general problem of computing probabilities of interest from a joint probability distribution, which may be possibly implicit. It may be noted that all the exact algorithms for probabilistic inference using Bayesian networks exploit conditional independence in the manner described above.

For drawing probabilistic inferences, it is possible to exploit the conditional independence in a Bayesian network, however, the exact inference in an arbitrary Bayesian network is NP-hard.¹ But, actually, for many applications, the Bayesian networks are of small size, or they can be simplified sufficiently, such that the complexity issues are not important. For applications where usual inference are impracticable, there are equivalent applications existing which are particular network tailored or suited for specific queries.

12.4.3 Independence of Variables

The notions of independence and conditional independence are fundamentals notions of probability theory. It is the combination of quantitative information of numerical parameters and the qualitative information, that makes the probability theory so expressive. Consider x and y as two variables that are independent of each other. The corresponding probabilistic expression of occurrence of events corresponding to these variables is

$$\begin{aligned} P(x, y) = P(x) P(y). \end{aligned}$$

(12.17)

Given three variables x, y, z, the probability distribution of these can be decomposed into a joint probability distribution that comprises terms, each of two variables, as shown in Eq. 12.18 and Fig. 12.3.

$$\begin{aligned} P(x, y, z)&= P(x, y|z) P(z)\nonumber \\&= P(x|z) P(y|z) P(z). \end{aligned}$$

(12.18)

Fig. 12.3

Variables x and y are “Conditionally Dependent Given” z

For the situation shown in Fig. 12.3, the variables x and y are called marginally independent, but they are conditional dependent, for a given variable z. It is possible to convince ourselves using the following example. Let the first variable have the assignment x = “rain”, and the second is y = “sprinkler on”. When both are True, they will cause the lawn to become wet.

So far we have not made any observation about the lawn, and occurrence of x (rain) and y (sprinkler on) are independent. However, once it is observed that the lawn is wet, and it is confirmed that it raining, it automatically influences the probability of the sprinkler, that it is “on”. This probability distribution is therefore

$$\begin{aligned} P(x, y, z) = P(z|x, y) P(x) P(y). \end{aligned}$$

(12.19)

The next example shows the cause–effect relationships shown in Fig. 12.4. In this case, the probability distribution is given by

$$\begin{aligned} P(x, y, z) = P(y|z) P(z|x) P(x). \end{aligned}$$

(12.20)

Fig. 12.4

Variables x and y are conditionally independent given z

12.4.4 Propagation in Bayesian Belief Networks

The aim of constructing a Bayesian network is—for a given observation (evidence), answer a query about the probability distribution over the values of query variables. A Bayesian network having full specification contains all the information needed to answer all the queries of probability distribution over these variables. The propagation of evidence in these networks helps in drawing conclusions. Usually, we make use of the term “propagation” only, instead of propagation of evidence.

This kind of representation is called Bayesian belief network. The inference in this network amounts to the propagation of probabilities of a given and related information through the network to one or more conclusion nodes. If we consider representing the knowledge related to a set of variables, say, $x_1, x_2, \ldots , x_n$, using their point probability distribution, $P(x_1, x_2, \ldots , x_n)$, it will require a total of $2^n$ entries to store the entire distribution explicitly. Further, for the determination of probability say $x_i$ will require summing all the remaining $x_i$, which will make it prohibitively expensive in terms of computation.

However, once it is represented using causal relationships, the joint probability can be computed much faster. Figure 12.5 shows the cause and effect relationships between variables $x_1 \ldots x_5$, and the joint probability distribution can be given as

$$\begin{aligned} P(x_5|x_4 \wedge x_3) P(x_4|x_2 \wedge x_3) P(x_2|x_1) P(x_3|x_1) P(x_6|x_3) P(x_1). \end{aligned}$$

(12.21)

Fig. 12.5

Bayesian belief network

Example 12.2

Some examples of Bayesian belief networks.

Following are causal dependencies of variables, their corresponding belief networks, and probability distributions:

• (i) Let W = “Worn piston rings”, that causes O = “excessive oil consumption”, which in turn causes L = “low oil level in fuel tank”. Figure 12.6 shows the cause–effect relationships, and the joint probability distribution for this is given by

  $$\begin{aligned} P(W, O, L) = P(W)~P(O|W)~P(L| O). \end{aligned}$$

  (12.22)

• (ii) As another example, let W = “Worn piston rings” cause both B = “blue exhaust”, as well as, L = “low oil level” (see Fig. 12.7). The joint probability distribution is given by

  $$\begin{aligned} P(W, B, L) = P(W)~P(B|W)~P(L|W). \end{aligned}$$

  (12.23)

• (iii) Consider another example, with variables, L = “Low oil level”, which can be caused either by C = “excessive consumption” or by E = “oil leak” (see Fig. 12.8). The joint probability distribution is given by

  $$\begin{aligned} P(C, E, L) = P(C)~P(E)~P(L|C, E). \end{aligned}$$

  (12.24)

  $\square$

Fig. 12.6

Bayesian network-1

Fig. 12.7

Bayesian network-2

Fig. 12.8

Bayesian network-3

Fig. 12.9

Bayesian network-4

Based on the above discussions, we have the following steps for the construction of a Bayesian network:

• 1. Construct belief (event) nodes corresponding to the events,

• 2. For each node in belief network, make all links corresponding to the cause–effect relationships,

• 3. Compute probability at each nodes based on the probabilities of the premises nodes, and then,

• 4. Compute the joint probability distribution of the network.

Example 12.3

A Bayesian network for fire security system.

Figure 12.9 shows a small network of six binary variables given in Tables 12.1 and 12.2. The use of such network may be to compute answers to probabilistic queries, for example, we may like to know the probability of fire, given that people are reported to be leaving from the room, or answers for queries like what is the probability of smoke given that the alarm is off.

Table 12.1 Two-variable table

Table 12.2 Four-variable table

A Bayesian network has two components: a structure in the form of a directed acyclic graph, and a set of conditional probability tables. The acyclic graph’s nodes correspond to variables of interest (see Fig. 12.9), and the graphs edges have a formal interpretation in the form of direct causal influences. A Bayesian network must include the conditional probability tables (CPTs) for each variable quantifying the relationship between a variable and its parents in the network.

Consider that there are variables A = “Alarm”, F = “tempering”, and F = “Fire”, each of which may be True or False. Figure 12.9 shows the acyclic graph, and Table 12.2 shows the conditional probability distribution of A, given its parents as “Fire” and “Tempering”. As per this CPT, the probability of occurrence of the event $A = True$, given the evidence $F = True$ and $T = False$ (row 3), is $P(A = True | F = True, T = False) = 0.99$. This probability is called the network parameter.

The guaranteed consistency and completeness are the main features of Bayesian networks. The latter is possible because there is one and only one probability distribution, which satisfies the network constraints.

A Bayesian network with n binary variables will induce a unique probability distribution for over $2^n$ instantiations; such instantiations for the network shown in Fig. 12.9 are 64. This distribution provides sufficient information to predict probability for each and every event we can express using variables S, F, T, A, L, R, appearing in this network. An event may be a combination of these variables with True/False values. An example of an event may be to found out as “probability of an Alarm and Tempering, given no smoke, and a report has indicated people leaving the building.” $\square$

An important advantage of Bayesian networks is the availability of efficient algorithms for computing such probability distributions. In the absence of these networks, it would require explicit generation of required probability distributions. Generating such distributions explicitly is infeasible for a large number of variables. Interestingly, in areas such as genetics, reliability analysis, and information theory, the already existing algorithms are subsumed by the more general algorithms for Bayesian networks.

12.4.5 Causality and Independence

We will try to discover the central insight behind Bayesian networks, due to which it becomes possible to represent large probability distributions in a compact way. Consider Fig. 12.9 and the associated Conditional Probability Tables (CPTs), Tables 12.1 and 12.2. Each probability appearing in a CPT specifies a constraint which must be satisfied by the distribution induced by the network. Consider that a distribution must assign the probability of 0.1 to the event of “having smoke without fire”, i.e., $P(S = True|F = False)$, where S and F are variables, respectively for “smoke” and “fire”. These constraints, however, are insufficient to help in concluding a unique probability distribution. So, what additional information we need? This answer lies in the structure of a Bayesian network; as we know, that additional constraints are specified by the Bayesian network in the form of probabilistic conditional independence. As per that, once the parent of every variable is known, the variable in the structure is assumed to be independent of its non-descendent parents. Figure 12.9 shows that the variable L that stands for “leaving the premises” is taken as independent of its non-descendant parents T, F, and S, once its parent A becomes known. Put differently, as soon as the variable A becomes known, the probability distribution of variable L will not change on the availability of new information about the variables T, F, and S.

As a different case in Fig. 12.9, we assume that variable A has no dependence on variable S (a non-descendant parent of A). This assumption becomes true as soon as the parents F and T of variable A becomes known. These independence constraints, due to non-descendant parents are called Markovian assumptions of a Bayesian network [2].

From the above discussion, do we mean that whenever a Bayesian network is constructed, it is necessary to verify the conditional non-dependencies? This, in fact depends on the construction method adopted. There are three main approaches to the construction of Bayesian networks:

• 1. subjective construction,

• 2. a construction based on synthesis from other specifications, and

• 3. construction by learning from data.

The first method in the above approaches is somewhat less systematic, as one rarely thinks about the conditional independence while constructing a Bayesian network. Instead, one thinks about causality, i.e., adding an edge $E_i \rightarrow E_j$, from event $E_i$ to event $E_J$, whenever $E_i$ is recognized as a direct cause of $E_j$. This results in a causal structure where Markovian assumption is read as: “each variable becomes independent of its non-dependents, once direct causes are known.”

A distribution of probabilities induced due to a Bayesian network also satisfies additional independencies beyond the Markovian. All these independent variables can be identified using a graphical test, called d-separation.² As per this test, any two variables $E_i$ and $E_j$ shall be considered to be independent if every path between $E_i$ and $E_j$ is blocked by a third variable $E_k$. For instance, consider the path $\alpha$ as shown in Fig. 12.9.

$$\begin{aligned} \alpha : S \leftarrow F\rightarrow A \leftarrow T. \end{aligned}$$

(12.25)

Now, consider that alarm A is triggered. The path in Eq. (12.25) can be used to show a dependency between variables A and T as follows: we know that observing S (smoke as evidence) increases the likelihood that fire F has taken place. This is due to the direct cause–effect relation. Also, the increased likelihood that F has taken place explains away the tempering T as cause of the alarm, i.e., there are lesser chances that the alarm is due to tempering. Hence, a path in Eq. (12.25) can be used as a dependence between S and T. Therefore, the variables S and T are not independent due to the presence of unblocked path between them.

However, instead of variable A, if F is a given variable, this path cannot be used to show a dependency between S and T, and in that case the path will be blocked by F.

12.4.6 Hidden Markov Models

The  Hidden Markov Models (HMMs) are useful for modeling dynamic systems with some states not observable, and when it is required to make inferences about changing states, given the sequence of outputs they generate. The potential applications of HMMs are those that require temporal pattern recognition, like speech processing, handwriting recognition, recognizing gestures, and in bioinformatics [2].

Fig. 12.10

Hidden Markov model

Figure 12.10a shows an HMM—a model of a system with three states a, b, c, and with three outputs x, y, z, and possible transitions between the states. There is probability associated with each transition, e.g., there is a transition from state b to c with 20% probability. Each state can produce certain output, with some probability, e.g., state b can produce output z with probability 10%. An HMM of Fig. 12.10a has been represented by a Bayesian network as shown in Fig. 12.10b. There are two variables, $S_t$ (for state at time t), and $O_t$ (for system output at time t), with $t = 1, 2, \ldots , n$. The variable $S_t$ has three values a, b, c, and $O_t$ also has three values x, y, z. Using d-separation on this network, one can derive the characteristic properties of HMMs, i.e., once the system state at time t is known, its states and outputs are independent at time $> t$, and also independent at time $< t$. Figure 12.10b is a simple dynamic Bayesian network.

Fig. 12.11

Syntheizing a Bayesian network

12.4.7 Construction Process of Bayesian Networks

One approach for the construction of Bayesian networks is mostly subjective—reflecting on the available knowledge in the form of say, perceptions about causal influences. This knowledge is captured into a Bayesian network, e.g., the network shown in Fig. 12.9 we discussed earlier.

Automatic Synthesizing of networks

The second method for Bayesian networks construction synthesizes these networks automatically using some other type of formal knowledge. Many jobs, related to reliability and diagnosis, require system analysis. A Bayesian network can be automatically synthesized from the formal system design of such systems. We consider a job of reliability, where a reliability block diagram is used for reliability analysis, with system components being connected to effect their reliability and dependencies, as shown in Fig. 12.11a. The various components shown are power supply to power the Fan-1 and Fan-2, which collectively cool the processor-1 and 2, and these processors are interfaced to the a hard disk drive. The processor-1 requires the availability of either Fan-1 or 2, and each fan requires the availability of power supply. We are interested to compute the overall reliability of the system, i.e., probability of its availability, given the reliability of each of the components in the system. Figure 12.11b shows the systematic conversion of each block of the reliability block diagram into a Bayesian network fragment, where Subsystem-1, Subsystem-2, and Block-B are assumed to be available [2].

Figure 12.12 shows the corresponding Bayesian network constructed using reliability blocks. Using the reliability of individual components we can construct Conditional Probability Tables (CPTs) of this system. Consider the variables as follows: E is for power supply, $F_1$ and $F_2$ for fans, $P_1$, $P_2$ for processors, and D for hard disk. Let these variables represent the availability of the corresponding component. Let us assume that variable S represents the availability of the whole system. The variables $A_i$ and $O_j$ represent the logical AND and OR, respectively.

Fig. 12.12

A Bayesian network for reliability analysis

Network Constructing by learning from data

A third approach for the construction of Bayesian networks works on the principle of learning from data, like patients medical records, airline ticket records, or buying patterns of customers, etc. Such data sets can help the network to learn parameters given the structure of the network, or it can learn both the network and its parameters when the data set is complete. However, learning only the parameter is an easier task.

Since the learning itself is an inductive task, the learning process is guided using the induction principle. Two main principles of inductive-based learning are 1. maximum likelihood function, and 2. learning using the Bayesian approach. The first approach is suitable to those Bayesian networks that maximize the probability of observing the given data set, while the second approach uses some prior information that encodes preferences on a Bayesian network, along with the likelihood principle.

Let us assume that we are interested in learning the network parameters. Learning using the Bayesian approach allows to put a prior distribution on each network parameter’s possible values. The data set and the prior distribution together induce new distribution on the values of that parameter, called posterior distribution. This posterior distribution is then used to pick a value for that parameter, e.g. distribution mean. As an alternative, we can also use different parameter values while computing answers to queries. This can be done by averaging over to all possible parameter values according to their posterior probabilities.

Given a Bayesian network as in Fig. 12.12, we can find out the overall reliability of this system. Also, for example, given that the system is unavailable, we can find the most likely configuration of the two fans, or the processors. Further, given a Bayesian network, we can answer the questions such as What single component can be replaced to increase the system reliability by, say, 10%? These are the example questions which can be answered in these domains using the principles of Bayesian probability distributions.

12.5 Dempster–Shafer Theory of Evidence

The  Dempster–Shafer Theory (DST) of evidence can be used for modeling several single pieces of evidences within a single hypothesis relations,³ or a single piece of evidence in relations that are multi-hypotheses type. The DST is useful for the assessment of uncertainty of a system where actually only one hypothesis is true. Another approach to DST, called the reliability-oriented approach, contains the system with all hypotheses—pieces of evidence and data sources. The hypothesis is a collection of all possible states (e.g., faults) of the system, which is under consideration [5].

In DST, it is a precondition that all hypotheses are singletons (i.e., elements) of some frame of discernment—a finite universal set $\varOmega$, with $2^{|\varOmega |}$ subsets. However, we will write it simply as $2^\varOmega$ subsets. A subset of $\varOmega$ is a single hypothesis or a conjunction of hypotheses. The subsets $2^\varOmega$ are unique and not all of them disjoint, however, it is mandatory that all the hypotheses are disjoint and mutually exclusive, in addition to being unique.

The pieces of evidences above are symptoms or events. An example of a symptom or evidence is the failure that has occurred or may occur in the system. An evidence is always related to a single hypothesis or to a set of hypotheses (multi-hypothesis). Though theoretically it can be debated, it is not allowed in DST that many different evidences may lead to conclude the same hypothesis or the same collection of hypotheses. A relation between a piece of evidence and a hypothesis is qualitative, which correspond to a chain of cause–effect relations—an evidence implies an existence of hypothesis or hypotheses, like in the Bayes rule.

The DST represents a subjective viewpoint in the form of a computation for an unknown objective fact. The data sources used in DST are persons, organizations, or other entities that provide the information. Using a data source, the mapping in Eq. (12.26) assigns an evidential weight to a diagnosis set $A \subseteq \varOmega$. Since $A \in 2^\varOmega$, the set A contains a single hypothesis or a set of hypotheses. The probability of any diagnosis A is a function whose value is between 0 and 1, and is expressed by

$$\begin{aligned} m: 2^\varOmega \rightarrow [0, 1]. \end{aligned}$$

(12.26)

Note that the difference between DST with probability theory is that, the DST mapping clearly distinguishes between the evidence measures and probabilities.

Definition 12.1

(Focal Element) Each diagnosis set $A \subseteq \varOmega$, for which $m(A) > 0$, is called a focal element.

Definition 12.2

(Basic Probability Assignment) The function m is called a Basic Probability Assignment (BPA) that fulfills the condition:

$$\begin{aligned} \sum _{A \subseteq \varOmega }~m(A) = 1. \end{aligned}$$

(12.27)

Meaning of the above statement is that, for the evidences presented by each data source which are equal in weight, it is necessary that all statements of a single data source are normalized. In other words, no data source is more important than the others. We assume that if a data source is null, then its BPA should also be null, i.e., $m(\phi )=0$.

A belief measure is given by the function, which also ranges between 0 and 1,

$$\begin{aligned} bel: 2^\varOmega \rightarrow [0,1], \end{aligned}$$

(12.28)

such that

$$\begin{aligned} bel(A) = \sum _{B\subseteq A;~B \ne \phi }~m(B). \end{aligned}$$

(12.29)

Counterpart of belief (bel) is called plausibility measure pl, which again is a mapping $pl: 2^\varOmega \rightarrow [0, 1]$, and is defined as

$$\begin{aligned} pl(A) = \sum _{B \cap A \ne \phi }~m(B). \end{aligned}$$

(12.30)

It is important to note that pl(A) above is not be understood as a complement of bel(A). For a focal element $m(A) > 0$, and $A \subseteq \varOmega$, it always holds that $bel(A) \le pl(A)$. The difference between plausibility and belief is evidential interval range, called uncertainty interval. Thus,

$$\begin{aligned} uncertanty~interval = pl(A) - bel(A). \end{aligned}$$

(12.31)

As we add more and more evidences in the system, the uncertainty interval reduces, as will be seen in examples in the following. This is a natural and logical property of DST.

12.5.1 Dempster–Shafer Rule of Combination

The DST allows combination of evidences to predict the hypothesis with a stronger belief. It is called Dempster’s rule of combination, which aggregates two independent bodies of evidence, into one body of evidence, provided that they are defined within the same frame of discernment. The Dempster’s rule of combination combines two evidences and computes new basic probability assignment as

$$\begin{aligned} m(A) = m_1 \otimes m_2~(A) = \frac{\sum \limits _{A = B \cap C} m_1(B)*m_2(C)}{1-\sum \limits _{B \cap C = \phi } m_1(B)*m_2(C)}. \end{aligned}$$

(12.32)

In the above, $A \ne \phi$ and numerator part in the equation represent the accumulated evidences for the sets B and C, that supports the hypothesis A (since $A = B \cap C$), and the denominator is called the normalization factor [5].

12.5.2 Dempster–Shafer Versus Bayes Theory

The Dempster–Shafer Theory (DST) (also called theory of belief functions) is the generalization of the Bayes theory of conditional probability. To carry out the computation of probability, the Bayes theory requires actual probabilities for each question of interest. But in DST, the degree of belief of one question is based on the probabilities of the related questions. The “degree of belief” may or may not have real mathematical properties of probability, but, how much they actually differ from probabilities will depend on how closely the two questions are related.

The DST is based on two ideas: 1. obtaining degrees of belief for one question from subjective probabilities of related question, and 2. use Dempster’s rule for combining such degrees of belief when they are based on independent items of evidence.

The DST differs from the application of Bayes theorem in the following respects:

• 1. Unlike the Bayes theorem, the DST allows the representation of diagnoses in the form of classes and hierarchies, as shown in Fig. 12.13.

• 2. For a probability of $X\%$ for a diagnosis, the difference $(100-X)\%$ is not taken as against the diagnosis, but interpreted as an uncertainty interval. That is, the probability of diagnosis lies between $X\%$ and $100\%$, and as more and more evidence is added the diagnosis may tend toward $100\%$.

• 3. Probability against a diagnosis is considered as the probability of the complement of the diagnosis. For example, if an event set is $\{A, B, C, D\}$, the probability against the event “A” is probability of $\{B, C, D\}$, which will have further distribution.

Fig. 12.13

Hierarchy of evidences

In spite of many advantages of DST, evaluation of probabilities in DST is more complex than in the Bayesian probabilities. This is because, probabilities for a set of diagnoses are related to one another in DST, hence probability of a set of diagnoses needs to be calculated from the distribution of probabilities over all sets of diagnoses.

Example 12.4

Computing Probability distribution of a biased coin.

Consider a biased coin, where the probability of arriving at the head is $P(H)=0.5$. Since it is biased we do not know as to what the rest $50\%$ is attributed to. In the DS theory, this is called the ignorance level. Since we do not know where the rest of the probability goes, we assign it to the universe U = $\{H, T\}$. Which means that it can attribute to $\{T\}$ and $\{H, T\}$.

Now let us assume that there is an evidence, that probability for arriving at the tail is $46\%$. Due to this new evidence, the balance probability assignment is $1-0.45-0.46=0.09$, and this can be assigned to the set $\{H, T\}$, that cannot be attributed to $\{H\}$ or $\{T\}$, unless there is some further evidence available. Hence, 0.09 probability assigned stands for the coin standing vertical when it is tossed. $\square$

Example 12.5

Using DST for finding probabilities for certain diseases.

Let us assume that in a certain isolated island the universe set of disease is $\varOmega$ = $\{$malaria, typhoid, common cold$\}$. A team of Doctors visit this island and perform a laboratory test ($T_1$) on a patient, which shows that it is the case of $40\%$ for Malaria. Hence, as per the DS theory, the balance $60\%$ goes to the ignorance level for the entire universe $\{$malaria, typhoid, common cold$\}$.

Fearing lack of confidence, the Doctors ask the patient for a second laboratory test, for some other parameters; the evidence now shows a belief case of $30\%$ for Malaria. Hence, the rest $30\%$ goes to the entire universe $\{$malaria, typhoid, common cold$\}$. Thus ignorance is $30\%$.

The Doctor then asks for a third laboratory test, to further add to the evidences, and the finding shows that the belief for Typhoid is $20\%$. This makes the total belief of $90\%$, and the ignorance level reduces to $10\%$, which again is assigned to the universe set $\{$malaria, typhoid, common cold$\}$. $\square$

The above example shows that as more and more evidence is added, we get more and more strong belief about the distribution of probability on various diagnoses, and the ignorance level reduces. This, in fact, is what it should be, and the natural case of reasoning in a probability case.

Let us assume that the kind or errors which can occur in software testing is the set: $\{$data validation errors, computation errors, transmission errors, output error$\}$. In this case also we use DST, similar to the cases discussed above, and can compute the joint probability distribution of errors.

Example 12.6

Find out the distribution of probabilities for some diseases shown by a hierarchically structured diagnoses as shown in Fig. 12.13. Consider that the following are the probabilities of certain events: against $A=40\%$, and evidence for $Y=70\%$.

Let event $E_1$ correspond to against $A=40\%$, and event $E_2:$ correspond to $Y=70\%$. The evidence against A means evidence for the complement of A, which is the set of evidences $\{B, C, D\}$. From Fig. 12.13, the evidence for Y is evidence for set $\{A, B\}$.

In DST, when the evidences are combined, the probabilities get multiplied and the resultant set is the intersection of original sets. Table 12.3 shows the new distribution.

Table 12.3 Combination of evidences

The probability of an event or a set of events is expressed not as an absolute value but an uncertainty interval [a, b], where a and b are lower and upper probability limits, respectively. The value a is computed as the sum of the probabilities of the set and its subsets, while b is a value $100-c$, where c is the sum of the probabilities of complements of the set and complements of the subsets corresponding to a.

The probability range [a, b] for diagnoses $\{A\}$ and $\{B\}$ are computed as follows:

For diagnosis $\{A\}$:

$$\begin{aligned}{}[a, b]&= [\{A\}, 1-(\{B, C, D\} + \{B, C\} + \{B, D\} + \{C, D\} + \{B\} +\{C\}+\{D\} + \{\})]\\&=[0, 1-0.6] = [0, 0.4]. \end{aligned}$$

Hence, the probability of diagnosis $\{A\}$ lies between 0 and $40\%$.

We know that in DST, probabilities are multiplied and intersection is performed. Since probability for $\{A, B\}$ is 0.7 and for $\{B, C, D\}$ is 0.6, the probability for $\{B\}$ ($\{A, B\} \cap \{B, C, D\} = \{B\}$) is 0.42. Thus, the probability range for diagnosis B is

$$\begin{aligned}{}[a, b]&= [\{B\}, 1-(\{A, C, D\} + \{A, C\} + \{A, D\} + \{C, D\} + \{A\} +\{C\}+\{D\} + \{\})]\\&=[0.42, 1-0.0] = [0.42, 1]. \end{aligned}$$

Hence, the probability for $\{B\}$ lies between 42 and $100\%$.

If a further evidence $E_3$ of $20\%$ for D is added, the distribution of probabilities is changed as shown in Table 12.4.

Table 12.4 Combination of evidences after a new evidence $E_3$ is added

The empty bracket $\{\}$ shows that there is no diagnosis attributed to this fraction of probability. Since it is assumed that the set of diagnoses are complete, we can eliminate the empty set and the remaining sets of the probabilities can be taken as $100\%$. This can be done by dividing all probabilities of non-empty sets by a factor equal to $(1-s)$, where s is the sum of the probabilities of empty sets. For this example, $s=0.084 + 0.056 = 0.14$ and $1-s=1-0.14 = 0.86$. Now, the sum of probabilities without an empty set is 1.0. Next, we obtain the following results using Dempster’s rule of combination.

$$\begin{aligned} \{B\} = \frac{0.336}{0.86}=39.0\% \end{aligned}$$

$$\begin{aligned} \{D\} = \frac{0.06}{0.86} = 7.0\% \end{aligned}$$

$$\begin{aligned} \{A, B\} = \frac{0.224}{0.86}= 26.0\% \end{aligned}$$

$$\begin{aligned} \{B, C, D\} = \frac{0.144}{0.86}=16.8\% \end{aligned}$$

$$\begin{aligned} \{A, B, C, D\} = \frac{0.096}{0.86}=11.2\%. \end{aligned}$$

The probabilities for $\{A\}$ and $\{B\}$ are computed as follows:

• $\{A\}=[\{A\}, 1-(\{B, C, D\}+\ldots +\{B\}+\{D\})]=[0, 0.372]$, i.e., 0–$37.2\%$.

• $\{B\}=[\{B\}, 1-(\{A, C, D\}+\ldots +\{D\})]=[0.39, 0.93]$, i.e., 39–$93.0\%$.$\square$

From the above exercise, we note that the uncertainty interval (probability of $\{A, B, C, D\}$) has decreased after addition of new evidence $E_3$. In addition, the probabilities of A and B have turned out to be more precise, i.e., narrow.

However, we note that the computation required in DST is combinatorial, since with n diagnoses a total of $2^n$ number of sets need to be computed [7].

12.6 Fuzzy Sets, Fuzzy Logic, and Fuzzy Inferences

In  classical set theory, an element x of the universe U either absolutely belongs to a set $A \subseteq U$ or does not belong to it at all. This membership relation between the element x and set A is called crisp, i.e., either Yes/No (or On/Off). A fuzzy set is a generalization of a classical set by allowing the degree of membership, which is a real number [0, 1]. In extreme cases the degree is 0, i.e., the element does not belong to the set or 1, or the element fully belongs to the set.

To understand the idea of a fuzzy set, let us assume that people in an organization are the universe and consider a set of “young” people in this universe. The youngness is definitely not a step function from 1 to 0, as one attains a certain age, say 30 years. In fact, it would be natural if we associate a degree of youngness for each element of age, for example, ($\{ Anand/1, Babita/0.8, Choudhary/0.3\}$). That means, perhaps Anand is 23 years old, Babita is 27 years old, and Choudhary is in his 50s. The membership function of a set maps each element of the universe to some degree of association with the set.

The fuzzy set concept is somewhat similar to the concept of the set in the classical set theory. When we say, “Sun is a star”, it means the Sun belongs to the set of stars, and when we say, “Moon is a satellite”, it means the Moon belongs to the set of satellites of the Earth. At the same time, both these statements are true, hence, they both map to true or 1. The statement “the Sun is a black hole” is false as it does not belong to the set of blacks holes yet. Hence, the statement maps to false or 0. Thus, mapping of a statement in classical logic is either to 1 and 0, having crisp values. Since, with each statement in the classical set theory having logical value 0 or 1, the set of these statements is called a crisp set, and also, these sets have a logic associated, (T/F) due to the membership of their elements. Thus, sets and logic are two sides of the same coin, they go together. Various properties of fuzzy sets, like relations, logic, and inferences, have counterparts in the classical sets [1].

To propose a formal representation, a fuzzy set A is represented as $A=\{\frac{u}{a(u)} \mid u \in U\}$, where u is an element, and a(u) the membership function, called characteristic function, and represents the degree of belongingness; U is universe set. The notation $u \in U$ means “every $u \in U$”.

The Fuzzy operations have counterparts operations in classical set theory as union, intersection, complement, binary relation, and composition of relations.

The common definitions of fuzzy set operations are as follows.

$$\begin{aligned} A \cup B = \Big \{\frac{u}{max(a(u), b(u))} \mid u \in U\Big \} \end{aligned}$$

(12.33)

$$\begin{aligned} A \cap B = \Big \{\frac{u}{min(a(u), b(u))} \mid u \in U\Big \} \end{aligned}$$

(12.34)

and complement of A is expressed as

$$\begin{aligned} A^\prime = \Big \{\frac{u}{1 - a(u)} \mid u \in U\Big \}. \end{aligned}$$

(12.35)

It is possible to derive fuzzy versions of familiar properties of ordinary sets, such as commutative laws, associative laws, and De Morgan’s laws, based on the above definitions [6].

The definition of fuzzy logic has semantic issues also; as per that fuzzy logic it has two different senses: 1. It is a logical system, which is aimed to formalize the approximate reasoning, 2. It is rooted in a multivalued logic, but its objective is quite different from traditional multivalued logical system. It accounts for a concept of linguistic variables (large, small, big, old, cloudy, etc.), canonical form, fuzzy if-then rule, fuzzy quantifiers, etc. In a broad sense, fuzzy logic is governed by the fuzzy set theory.

The fuzzy arithmetic, fuzzy mathematical programming, fuzzy topology, fuzzy graph theory, and fuzzy data analysis are other branches of fuzzy set theory. It is indeed quite likely that most theories will be fuzzified in this way. The impetus for the transition from a crisp set theory to fuzzy theory results from the fact that both—the applicability to real-world problems and generality of the theory—are substantially enhanced when the concepts of a set are replaced by a fuzzy set.

The concept of a linguistic variable plays a central role in the applications of fuzzy logic. Consider the linguistic variable, say Age whose values are young, youth, and old, with “young” defined by a membership function $\mu$ as shown in Fig. 12.14. It is interesting to note that a numerical value such as 25 years is definitely simpler than a function like young. The value young represents a choice out of three values—young, youth, old—but 25 represents a choice, which is out of 100 values. Consequently, the linguistic variable young may be viewed as a method of data compression.

Fig. 12.14

Linguistic and numerical variable “young”

We achieve the same effect in quantization (conversion of an integer into a binary number), where the values are in intervals. In contrast to quantization, the values are overlapping in fuzzy sets. The advantage of granulation over quantizations are 1. granulation is more general, 2. it mimics the way humans interpret linguistic values (i.e., not as intervals), and 3. a transition from one linguistic value to the next higher and lower is gradual rather than abrupt. This results in a continuity and robustness of the system.

12.6.1 Fuzzy Composition Relation

Let us assume that A and B are fuzzy sets of universes U and V, respectively. The Cartesian product $U \times V$ is defined just like for ordinary sets. We define the Cartesian product $A \times B$ as follows,

$$\begin{aligned} \Big \{\frac{(u, v)}{min(a(u), b(v))} \mid u \in U, v \in V\Big \}. \end{aligned}$$

(12.36)

Every fuzzy binary relation (or a mapping relation or fuzzy relation), from fuzzy set U to fuzzy set V, is a fuzzy subset of relation R defined below. Here m(u, v) is called a membership function, having the range [0, 1].

$$\begin{aligned} R: U \times V = \Big \{\frac{(u, v)}{m(u, v)} \mid u \in U, v \in V\Big \}. \end{aligned}$$

(12.37)

A fuzzy relation R from set A to B can be defined as

$$\begin{aligned} R_{AB} = \Big \{\frac{(u, v)}{m(u, v)} \mid m(u, v) \le a(u), m(u, v) \le b(u), u \in U, v \in V\Big \}. \end{aligned}$$

(12.38)

Consider that a similar relation $R_{BC}$ exists from fuzzy set B to C. As in classical sets, a composition relation of relations $R_{AB}$ and $R_{BC}$, i.e., $R_{AB} \circ R_{BC}$ is obtained as

$$\begin{aligned} R_{AB} \circ R_{BC} = \bigcup \Big \{max\Big [\frac{(a,c)}{min(m_R(a, b), m_S(b, c))}\Big ]\Big \}. \end{aligned}$$

(12.39)

The fuzzy sets are extensions and more general forms of ordinary sets; accordingly, the fuzzy logic is an extension of the ordinary logic. Just as there are correspondences between ordinary sets and ordinary logic, there exists correspondence between fuzzy set theory and fuzzy logic. For example, the set operations of union (OR), intersection (AND), and complement (NOT) exists in classical set theory (classical logic) as well as in fuzzy system. The degree of belongingness of an element in a fuzzy set corresponds to the truth value of the proposition in fuzzy logic.

A fuzzy implication is viewed as describing a relation between two fuzzy sets. Using fuzzy logic we can represent a fuzzy implication such as $A \rightarrow B$, i.e., if “A then B”, where A and B are fuzzy sets. For example, if A is fuzzy set young, and B is fuzzy set small, then $A \rightarrow B$ may mean, if young then small. A simple definition is $A \rightarrow B = A \times B$, where $A \times B$ is the Cartesian product of fuzzy sets A and B.

12.6.1.1 Inferencing in Fuzzy Logic

Let R be a fuzzy relation from set U to V (i.e., $R: U \rightarrow V$), X be a fuzzy subset of U, and Y be a fuzzy subset of V. Given these, we can define a composition rule of fuzzy inference as

$$\begin{aligned} Y = X \circ R \end{aligned}$$

(12.40)

where Y is said to be induced by X and R. A fuzzy inference is based on fuzzy implication and the compositional rule of inference. A fuzzy inference is defined as follows:

• Given:

• Implication: “If A then B”

• Premise: “X is true”,

• Derive:

• Conclusion Y.

To derive a fuzzy inference, we perform the following steps:

• 1. Given, “if A then B”, compute the fuzzy implication as a fuzzy relation, $R = A \times B$,

• 2. Induce Y by $Y = X \circ R$.

12.6.2 Fuzzy Rules and Fuzzy Graphs

We  have noted that linguistic variable in fuzzy logic behaves as a source of data compression, as a linguistic variable may stand for a large number of values. The fuzzy logic, in addition, provides fuzzy if-then rule or simply the fuzzy rule, and a fuzzy-graph. The fuzzy rule and fuzzy graph bear the same relation to numerical value dependencies that the linguistic variable has with numerical values [8].

Fig. 12.15

A function and corresponding fuzzy graph

Figure 12.15 shows a fuzzy graph $f^*$ of a function dependence $f: X \rightarrow Y$, where $X \in U$, $Y \in V$, are linguistic variables. Let the set of values in linguistic variables X and Y be $A_i$, $B_i$, respectively. This graph is an approximate compressed representation of f in the form of $f^*$ as

$$\begin{aligned} f^* = A_1 \times B_i + A_2 \times B_2 + \ldots + A_n \times B_n, \end{aligned}$$

(12.41)

which is equal to

$$\begin{aligned} f^* = \sum _{i=1}^n A_i \times B_i. \end{aligned}$$

(12.42)

$A_i$, $B_i$ (for $i=1 \ldots n$) are called contiguous fuzzy subsets of sets U and V, respectively. Also, $A_i \times B_i$ is the Cartesian product of $A_i, B_i$, and “$+$” in Eq. (12.41) represents the operation of disjunction—a union operation. When expressed more explicitly in the form of membership functions, we have

$$\begin{aligned} \mu _{f^*}(u, v) = V_i(\mu _{A_i} \wedge \mu _{B_i}). \end{aligned}$$

(12.43)

where $\mu$ is the membership function. The operation of $\wedge$ is min, $\vee$ is max, $u \in U$, and $v \in V$.

A fuzzy graph can also be represented as a fuzzy relation $f^*$, as shown in Table 12.5.

Table 12.5 Fuzzy relation $f^*$

Also, a fuzzy graph can be represented as a collection of if-then rules as follows:

$$\begin{aligned} f^*:~&if~X~is~A_1~then~Y~is~B_1\nonumber \\&if~X~is~A_2~then~Y~is~B_2\nonumber \\&~~~~~~~\ldots \nonumber \\&if~X~is~A_n~then~Y~is~B_n. \end{aligned}$$

(12.44)

In other words, “(X, Y) is $A_i \times B_i$”. Given a fuzzy if-then rule set as follows,

$$\begin{aligned} f^*:~&if~X~is~small~then~Y~is~large\nonumber \\&if~X~is~medium~then~Y~is~medium\nonumber \\&~~~~~~~\ldots \nonumber \\&if~X~is~large~then~Y~is~small. \end{aligned}$$

(12.45)

This rule can be represented equivalently as a fuzzy graph (see Fig. 12.16) using the fuzzy expression for $f^*$,

$$\begin{aligned} f^* = small \times large + medium \times medium + \cdots + large \times small. \end{aligned}$$

(12.46)

Fig. 12.16

Fuzzy graph for a fuzzy relation (Eq. 12.46)

An important concept in a fuzzy graph is any type of function (or relation) that can be approximated by a fuzzy graph. For example, a normal distribution for probability is represented as a fuzzy graph, as shown in Fig. 12.17. This representation is useful in decision-making and fault diagnosis. Here, the probability P is represented by

$$\begin{aligned} P = small \times medium + medium \times large + large \times small. \end{aligned}$$

(12.47)

The constraint for probability is that it sums to 1, i.e., $\varSigma _i P_i = 1$.

Fig. 12.17

Fuzzy graph for a probability distribution

12.6.3 Fuzzy Graph Operations

The interesting point in fuzzy calculus is that it aims to develop computational procedures for basic operations on fuzzy graphs. These operations are generalizations of basic operations on crisp sets and functions, and can be defined as follows: The required computations can be simplified if the operation of “$*$” is taken as monotonically increasing. That is, if $a, b, a^\prime$, and $b^\prime$ are real numbers, then the following holds:

$$\begin{aligned} a^\prime \ge a, b^\prime \ge b \Rightarrow a^\prime * b^\prime \ge a*b\nonumber \\ a^\prime \le a, b^\prime \le b \Rightarrow a^\prime * b^\prime \le a*b. \end{aligned}$$

(12.48)

From these operations, it can be easily deduced that “$*$” is a distributive operator over “$\vee$ (max)” and “$\wedge$ (min)”. Accordingly,

$$\begin{aligned} a * (b \vee c) = a * b \vee a * c\nonumber \\ a * (b \wedge c) = a * b \wedge a * c. \end{aligned}$$

(12.49)

From the above, we conclude that if

$$\begin{aligned} f^* = \sum _i A_i \times B_i \end{aligned}$$

(12.50)

is a fuzzy graph and C is a fuzzy set, then

$$\begin{aligned} C * \big (\sum _i A_i \times B_i \big ) = \sum _i C * (A_i \times B_i). \end{aligned}$$

(12.51)

Consider finding the intersection of fuzzy graphs (Fig. 12.18) $f^*$ and $g^*$, where

$$\begin{aligned} f^* = \sum _i A_i \times B_i \end{aligned}$$

(12.52)

and

$$\begin{aligned} g^* = \sum _j C_j \times D_j. \end{aligned}$$

(12.53)

From $f^*$ and $g^*$, we obtain the fuzzy intersection as

$$\begin{aligned} f^* \cap g^* = \sum _{i, j} (A_i \times B_i) \cap (C_j \times D_j) \end{aligned}$$

(12.54)

and, the view of distributivity of “$\cap$” ultimately reduces to

$$\begin{aligned} f^* \cap g^* = \sum _{i, j} (A_i \cap C_j) \times (B_i \cap D_j). \end{aligned}$$

(12.55)

These operations on fuzzy functions and fuzzy relations are shown in Fig. 12.18.

Fig. 12.18

Basic operations on functions and relations of fuzzy sets

12.6.4 Fuzzy Hybrid Systems

Different forms of hybrid systems are designed as combinations of Fuzzy Logic, Neural Networks, and Genetic Algorithms. The fundamental concepts of such hybrid systems is to complement each other’s weaknesses, that creates a new approach to solving problems. For example, in fuzzy logic systems, there is no learning capability, there is no memory, and there is no capability of pattern recognition. Fuzzy systems combined with neural networks will have all these three capabilities.

Fuzzy systems are extensively used for control, like fuzzy controllers, specially fuzzy PID (proportional, integral and derivative) controllers.

In spite of their wider applicability, the fuzzy systems have the following limitations: The stability is a major issue in their control. There is no formal theory guaranteeing their stability. Fuzzy systems have no memory and lack the learning capabilities. Determining good membership functions and tuning fuzzy systems are not always easy. In addition, verification and validation of fuzzy systems require extensive testing. In light of these limitations, the fuzzy systems are being used more and more, and they become better suited when combined with the neural networks and genetic algorithms.

12.7 Summary

Probability and Bayes theorem

In classical logic, a proposition is always taken as either true or false, while in real life, truth value of a proposition may be known only with a certain probability. This requires probabilistic reasoning. Two basic approaches for reasoning are probabilistic reasoning and non-monotonic reasoning.

Many different methods exist for representing and reasoning with uncertain knowledge, these include Bayesian networks, Dempster–Shafer theory, possibilistic logic, and fuzzy Logic.

Bayesian networks offer a powerful framework for the modeling of uncertainties. These networks are represented in two different ways: (1) Qualitative approach, by means of directed acyclic graphs, and (2) Quantitative approach, by specifying a conditional probability distribution for every variable present in the network. The conditional probability is represented by

$$\begin{aligned} P(A | B) = \frac{P(A, B)}{P(B)} \end{aligned}$$

(12.56)

where comma denotes the conjunction of events.

The Bayes theorem is used to find out conditional probability. The theorem is stated as

$$\begin{aligned} P(A|B) = \frac{P(B|A) P(A)}{P(B)}. \end{aligned}$$

(12.57)

In a Bayesian network, a node corresponds to a variable, which assumes values from a collection of mutually exclusive and collective exhaustive states, and the edges represent relevance or influences between variables. As per the definition of Bayesian networks, it is required to access the probability distribution of the node conditional on every instance of its parents. Thus, if a node has n-binary-valued parents, there are $2^n$ probability distributions for that node. A probabilistic inference is nothing but computing probabilities of interest from a (possibly implicit) joint probability distribution. All exact algorithms for probabilistic inference in Bayesian networks exploit the criteria of conditional independence.

Solving the problem of finding the exact inference in an arbitrary Bayesian network is NP-hard.

The inferencing in a network amounts to propagation of probabilities of a given and related information through the network to one ore more conclusion nodes.

The subjective approach for the construction of Bayesian networks reflects on the available knowledge (typically, perceptions about causal influences). Other method for Bayesian networks is based on automatically synthesizing these networks for the purpose of reliability and diagnosis. This approach is used to synthesize a Bayesian network automatically with the help of formal knowledge of system design.

The third method for constructing Bayesian networks is based on learning from data, such as medical records, customers’ purchases data, or data records of customers applied for finances. These data sets are used to learn the network parameters, given their structures, or can learn both the structure and network parameters.

Dempster–Shafer Theory

The Dempster–Shafer Theory (DST) of evidence is used to model several single pieces of evidence within a single hypothesis relations, or a single piece of evidence within multi-hypotheses relations.

The combination rule of DST aggregates two independent bodies of evidence into one body of evidence, provided that they are defined within the same frame of discernment.

The DST is based on two ideas: 1. to obtain the degree of belief for one question using the subjective probabilities of a related question, and 2. making use of Dempster’s rule to combine degrees of two belief which are based on independent items of evidence.

In DST, the difference $(100-X)\%$ with respect to a probability of $X\%$ for a diagnosis is not valued against the diagnosis, but interpreted as an uncertainty interval, i.e., the probability of a diagnosis is not $X\%$, but lies between X and $100\%$.

Evaluation of probabilities in DST is more complicated than in Bayes theorem, because the probabilities for a set of diagnoses must be related to one another, and the probability of a particular set of diagnoses must be calculated from the distribution of probabilities over all sets of diagnoses.

Fuzzy logic, sets, and reasoning

A fuzzy set is a generalization of ordinary set by allowing the degree of membership a real number [0, 1], in contrast to the membership of 0 and 1 in ordinary set theory. The fuzzy operations that have counterparts in classical set theory are union, intersection, complement, binary relation, and composition of relations.

Other branches of fuzzy set theory are fuzzy mathematical programming, fuzzy arithmetic, fuzzy topology, fuzzy graph theory, and fuzzy data analysis.

In fuzzy logic systems, there is no learning capability, no memory, and no capability of pattern recognition. Fuzzy systems combined with neural networks will have all these three capabilities.

Different forms of hybrid systems are constructed using a combination of fuzzy logic and other areas. These are Fuzzy-neuro systems, Fuzzy-GA (fuzzy and genetic algorithms), and Fuzzy-neuro-GA. They help to complement each other’s weaknesses, and create new systems that are more robust to solving problems.

Fig. 12.19

Membership functions: Small, Medium, Tall

Exercises

• 1. We assume a domain of 5-card poker hands out of a deck of 52 cards. Answer the following under the assumption that it is a fair deal.

  • a. How many 5-card hands can be there (i.e., number of atomic events in joint probability distribution).

  • b. What is the probability of an atomic event?

  • c. What is the probability that a hand will comprise four cards of the same rank?

• 2. Either prove it is true or give a counterexample in each of the following statements.

  • a. If $P(a \mid b, c) = P(a)$, then show that $P(b \mid c) = P(b)$.

  • b. If $P(a \mid b, c) = P(b \mid a, c)$, then show that $P(a \mid c) = P(b \mid c)$.

  • c. If $P(a \mid b) = P(a)$, then show that $P(a \mid b, c) = P(a \mid c)$.

• 3. Consider that for a coin, the probability that when tossed the head appears up is x and for tails it is $1 - x$. Answer the following:

  • a. Given that the value of x is unknown, are the outcomes of successive flips of this coin independent of each other? Justify your answer in the case of head and tail.

  • b. Given that we know the value of x, are the outcomes of successive flips of the coin independent of each other? Justify.

• 4. Show that following statements of conditional independence,

  $$P(X \mid Z) P(Y | Z) = P(X, Y \mid Z)$$

  are also equivalent to each of the following statements,

  $$ P(Y \mid Z) = P(Y \mid X, Z),$$

  and

  $$P(X \mid Z) = P(X \mid Y, Z).$$

• 5. Out of two new nuclear power stations, one of them will give an alarm when the temperature gauge sensing the core temperature exceeds a given threshold. Let the variables be Boolean types: A = alarm sounds, FA =alarm be faulty, and FG = gauge be faulty. The multivalued nodes are G = reading of gauge, and T = actual core temperature.

  • a. Given that the gauge is more likely to fail when the core temperature goes too high, draw a Bayesian network for this domain.

  • b. Assume that there are just two possible temperatures: actual and measured, normal and high. Let the probability that the gauge gives the correct reading be x when it is working, and y when it is faulty. Find out the conditional probability associated with G.

  • c. Assume that the alarm and gauge are correctly working, and the alarm sounds. Find out an expression for the probability in terms of the various conditional probabilities in the network, that the temperature of the core is too high.

  • d. Let the alarm work correctly unless it is faulty. In case of being faulty, it never sounds. Give the conditional probability table associated with A.

• 6. Compute the graphical representation of the fuzzy membership in the graph 12.19 for following set operations:

  • a. $Small \cap Tall$

  • b. $(Small \cup Medium)$–Tall

• 7. Given the fuzzy sets $A = \{\frac{a}{0.5}, \frac{b}{0.9}, \frac{e}{1}\}$, $B=\{\frac{b}{0.7}, \frac{c}{0.9}, \frac{d}{0.1}\}$, Compute $A \cup B$, $A \cap B, A^\prime , B^\prime$.

• 8. Let $X = \{ a, b, c, d, e\}$, $A = \{\frac{a}{0.5}, \frac{c}{0.3}, \frac{e}{1}\}$. Compute:

  • a. $\bar{A}$

  • b. $\bar{A} \cap A$

  • c. $\bar{A} \cup A$