Keywords

1 Introduction

Picture languages generated by grammars or recognized by automata have been advocated since the seventies for problems arising in the framework of pattern recognition and image analysis [1–8]. In syntactic approaches to generation of picture patterns, several two-dimensional grammars have been proposed. Array rewriting grammars [6], controlled tabled L-array grammars [5], and pure 2D context-free grammars [8] are some of the picture generating devices. Applications of these models to the generation of “kolam” patterns [9] and in clustering analysis [10] are found in the literature. Oliver Matz’s context-free grammars [2] rely on the motion of row and column catenation. The concept of tiling systems (TS) is used as a device of recognizing picture languages [1]. Tile rewriting grammar (TRG) combines Rosenfeld’s isometric rewriting rules with the tiling system of Giammarresi [7].

On the other hand, a Petri net is an abstract formal model of information flow [11]. Petri nets have been used for analyzing systems that are concurrent, asynchronous, distributed, parallel, nondeterministic, and/or stochastic. Tokens are used in Petri nets to simulate dynamic and concurrent activities of the system. A string language can be associated with the execution of a Petri net. By defining a labeling function for transitions over an alphabet, the set of all firing sequences, starting from a specific initial marking leading to a finite set of terminal markings, generates a language over the alphabet [11]. The tokens of such a Petri net are just black dots. All the tokens are alike, and the firing rule depends only on the existence of these tokens and the number available in the input places for the transition to fire.

Petri net structure to generate rectangular arrays is found in [12–15]. In [12] column row catenation petri net system has been defined. A transition with several input places having different arrays is associated with a catenation rule as label. The label of the transition decides the order in which the arrays are joined (column-wise or row-wise) provided the condition for catenation is satisfied. In column row catenation petri net system [12], a transition with a catenation rule as label and different arrays in the different input places is enabled to fire. On the contrary in array token Petri nets [13–15], the catenation rule involves an array language. All the input places of the transition with a catenation rule as label should have the same array as token, for the transition to be enabled. The size of the array language to be joined to the array in the input place depends on the size of the array in the input place. Applications of these models to generation of “kolam” patterns [15] and in clustering analysis [13] are found in the literature.

In this paper, we examine the generative capacity of the two different array-generating models. Array token Petri net is able to generate only the regular languages [14]. To control the firing sequence, inhibitor arcs are introduced. The introduction of inhibitor arcs increases the generative capacity. Array token Petri nets with inhibitor arcs generate the context-free and context-sensitive languages [14].

The paper is organized as follows: Sect. 2 and Sect. 3 give the preliminary definitions. Section 4 recalls the concept of array token Petri net structure and column row catenation Petri net system, the language associated with the structure and explains with some examples. Section 5 compares the languages generated by the two different models.

2 Preliminaries

Let Σ be a finite alphabet.

Definition 2.1

A two-dimensional array [6] over Σ is a two-dimensional rectangular array of elements of Σ. The set of all two-dimensional arrays over Σ is denoted by \( \Sigma ^{{\text{**}}} \). A two-dimensional language over Σ is a subset of \( \Sigma ^{{\text{**}}} \).

Two types of catenation operations are defined between two arrays. Let A of size (m, n) and B of size (p, q) be two arrays over an alphabet Σ. The column catenation A 

figure a

 B is defined only when m = p, and the row catenation A ⊝ B is defined only when n = q \( (x)^{n} \) denotes a horizontal sequence of n “\( x \)” and \( (x)_{n} \) denotes a vertical sequence of n “\( x \).” \( (x)^{n + 1} = (x)^{n} \) 

figure b

 x and \( (x)_{n + 1} = (x)_{n} \) ⊝ \( x \) where \( x\,\,\varepsilon \,\,\Sigma ^{{\text{**}}} \).

3 Petri Nets

In this section, the preliminary definitions of Petri Net [11] and notations used are recalled. A Petri net is one of several mathematical models for the description of distributed systems. A Petri net is a directed bipartite graph, in which the bars represent transitions and circles represent places. The directed arcs from places to a transition denote the pre-condition, and the directed arcs from the transition to places denote the post-conditions. Graphically, places in a Petri net may contain a discrete number of marks called tokens. Any distribution of tokens over the places will represent a configuration of the net called a marking. A transition of a Petri net may fire whenever there are sufficient tokens at all the input places. When a transition fires, it consumes these tokens and places tokens at all its output places. When a transition fires, marking of the net changes. Arcs include a “weight” property that can be used to determine the number of tokens consumed or produced when a transition fires. Marking changes according to the firing rules which are given below. In the graph, the weight of an arc is written on the arc.

Definition 3.1

A Petri Net structure is a four-tuple C = (P, T, I, O) where P = {P 1, P 2,…, P n } is a finite set of places, n ≥ 0, T = {t 1, t 2,…, t m } is a finite set of transitions; m ≥ 0, P ∩ T = Ø, I:P × T → N is the input function from places to transitions with weight w(p, t) being a natural number, and O: T × P → N is the output function from transitions to places with weight w(t, p) being a natural number.

Note

The number of tokens required in the input place, for the transition to be enabled, will depend on the weight of the arc from the place to the transition. The number of tokens put in the output place will depend on the weight of the arc from the transition to the place.

Definition 3.2

A Petri Net marking is an assignment of tokens to the places of a Petri Net. The tokens are used to define the execution of a Petri Net. The number and position of tokens may change during the execution of a Petri Net.

The marking at a given time is shown as a n-tuple, where n is the number of places. The Petri net can be easily represented by a graph. The places are represented by circles, and transitions are represented by rectangular bars. Input and output functions are shown by directed arcs. The weight of an arc is written on the arc in the graph. The weight is assumed to be one if no weight is specified on the arc.

Definition 2.3

An inhibitor arc from a place p i to a transition t j has a small circle in the place of an arrow in regular arcs. This means the transition t j is enabled only if p i has no tokens. A transition is enabled only if all its regular inputs have tokens and all its inhibitor inputs have zero tokens.

A string language [11] can be associated with the execution of a Petri net. Transitions are labeled with elements of an alphabet. Only the firing sequences that start from a given initial marking and reaching a specific final marking are considered. In this sequence, all the transitions are replaced by their label. This will correspond to a string over the alphabet. Thus, a labeled Petri net generates a string language. Hack [16] and Baker [17] can be referred for Petri net string languages.

4 Petri Net Generating Rectangular Arrays

With labeled Petri net generating string languages as a motivating factor, two models for generating arrays have been introduced. In string generating Petri nets, the tokens are all black dots. A transition is enabled if all the input places have the required number of tokens. In array-generating models, the tokens are arrays over a given alphabet. The firing rules of transition depend not only on the number of the arrays available but also on the size of the array which is residing in the input places of the transition. In Sect. 4.1, the definition of array token Petri net structure [14] is recalled with examples. The definition of column row catenation Petri net [12] is recalled and explained with examples in Sect. 4.2.

4.1 Array Token Petri Net Structure

Array token Petri net structure is defined [14] in such a way that it generates an array language. This structure retains the four components of the traditional Petri net structure C = (P, T, I, O). This Petri net model has places and transitions connected by directed arcs. The marking of the net is just not black dots but arrays over a given alphabet. Rectangular arrays over an alphabet are taken as tokens to be distributed in places. Variation in marking, labels, and firing rules of the transition are listed out below.

Array Language:

Array languages are used in the catenation rules. An array language contains an infinite set of arrays. The arrays are having either a fixed number of columns with varying number of rows or having a fixed number of rows with varying number of columns.

Catenation rule as label for transitions:

Column catenation rule is in the form A \( {\ominus } \) B. The array A denotes the array in the input place of the transition. B is an array language whose number of rows will depend on “m” the number of rows of A. For example, if \( B = (x\,\,x)_{m} \) ,then the catenation adds two columns of \( x \) after the last column of the array A. B \( {\ominus } \) A would add two columns of \( x \) before the first column of A. The number of rows of B is determined by the number of rows of A to enable the catenation.

Row catenation rule is in the form A Ө B. The array A denotes the array in the input place of the transition. B is an array language whose number of columns will depend on “n” the number of columns of A. For example, if \( B = \left[ {\begin{array}{*{20}c} x \\ x \\ \end{array} } \right]^{n} \), then the catenation A Ө B adds two rows of \( x \) after the last row of the array A. But B Ө A would add two rows of \( x \) before the first row of the array A. The number of columns of B is determined by the number of columns of A to enable the catenation.

Firing rules in array token Petri net

We define the different types of enabled transition in array token Petri net structure. The pre- and post-condition for firing the transition in all the cases are given below:

  1. 1.

    When all the input places of a transition t have the same array as token

    1. (i)

      When the transition t does not have label

      1. (a)

        Each input place should have at least the required number of arrays (dependent on the weight of the arc from the input place to the transition).

      2. (b)

        Firing t consumes arrays from all the input places and moves the array to all its output places

    2. (ii)

      When the transition t has a catenation rule as label

      1. (a)

        Each input place should have at least the required number of arrays (dependent on the weight of the arc from the input place to the transition).

      2. (b)

        The catenation rule is either of the form A \( {\ominus } \) B or

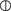
        figure c

        . The array A denotes the array in the input place. If B is involved in column catenation, then B will be an array language defined with variable row size. If B is involved in row catenation, then B will be an array language defined with variable column size. The variable size of the array B takes a particular value so that the condition for catenation is satisfied.

      3. (c)

        Firing t consumes arrays from all the input places p, and the catenation is carried out in all its output places.

  2. 2.

    When the input places of t have different arrays as token

    1. (a)

      The label of t designates one of its input places.

    2. (b)

      The designated input place has the same array as tokens.

    3. (c)

      The input places have sufficient number of arrays (depends on the weight of the arc from the input place to the transition).

    4. (d)

      Firing t consumes arrays from all the input places and moves the array from the designated input place to all its output places.

Definition 4.1.1

An array token Petri net N is a 8-tuple N = (P, T, I, O, Σ, σ, μ 0, F), where P = {P 1,…, P n } is a finite set of places; T = {t 1, t 2,…, t m } is a finite set of transitions; I : P × T → N, the input function; O : P × T → N, the output function; Σ a finite alphabet; σ : T → R U P is a partial function which associates label to certain transitions of the net; R is a set of catenation rules; μ 0 : P → \( \Sigma ^{{\text{**}}} \) is a partial function which gives an initial marking of arrays in certain places of the net; F \( \subseteq \) P is the subset of final places.

Definition 4.1.2

The language generated by an array token Petri net N, L(N), is the set of all rectangular arrays which reach the places belonging to F.

Arrays over a given alphabet are residing in certain places of the net structure. All possible firing sequences are fired in such a way that the arrays move from the initial place to any one of the final places. While the transitions fire either the array just moves from the input place to the output place or it catenates with another array and then moves into the output place. An example is given to explain the concepts.

Definition 4.1.3

An array token Petri net structure with at least one inhibitor arc is defined as array token Petri net with inhibitor arc and is denoted by the N I .

Definition 4.1.4

The family of array languages generated by array token Petri net is denoted by L(N), and the family of array languages generated by array token Petri net with inhibitor arc is denoted by L(N 1).

Example 4.1.1

The array token labeled Petri net N I (1) = (P, T, I, O, Σ, σ, μ 0, F), where P = {P 1, P 2, P 3, P 4, P 5, P 6, P 7}, T = {t 1, t 2, t 3, t 4, t 5, t 6}. The input and output arrows are seen from the figure. The labels are shown in the figure. Σ = {a}. μ 0(p 1) = μ 0(p 2) = µ 0(p 7) = s is the initial marking. F = {P 7} is the final place (Fig. 1).

Fig. 1
figure 1

Petri net to generate square array of side 2n

Full size image

The arrays used are \( S = \begin{array}{*{20}c} a & a \\ a & a \\ \end{array} ,\,\,\,B_{1} = \left( {\begin{array}{*{20}c} a & a \\ \end{array} } \right)_{m} ,\,\,B_{2} = \left( {\begin{array}{*{20}c} a \\ a \\ \end{array} } \right)^{n} \). To start with t 1 is enabled. Firing t 1 pushes the 2 × 2 array S in P 2 to P 3. Firing t 2 adds two columns and firing t 3 adds two rows.

Firing the sequence t 1 t 2 t 3 generates the array

$$ \begin{array}{*{20}c} a & a & a & a \\ a & a & a & a \\ a & a & a & a \\ a & a & a & a \\ \end{array} $$

in P 2 and P 5. At this stage, there is no array in P 1, and so both t 4 and t 6 are enabled. Firing t 6 pushes the 4 × 4 array into P 7 and P 2. Firing t 4 enables t 5. Since weight of the arc from t 5 to P 1 is two, firing t 5 pushes two 4 × 4 arrays into P 1. Now, the sequence t 1 t 2 t 3 has to be fired two times for both t 4 and t 6 to be enabled. Then, the array in P 2 can be pushed into P 7. Thus, t 1 t 2 t 3 t 7 t 4 t 5 (t 1 t 2 t 3)2 t 6 generates the array of size 8 × 8. The language generated is squares of side 2n, n ≥ 1.

4.2 Column Row Catenation Petri Net Structure

Column row catenation Petri net system [12] also generates an array language. This structure retains the eight components N = (P, T, I, O, Σ, σ, μ 0, F) of array token Petri net structure. When the input places have different arrays, the transition only shifts the array that is specified by the label of the transition in the previous model. But in column row catenation Petri net, the transition consumes the different arrays and catenates them (condition for catenation has to be satisfied). This variation in labels and firing rules of the new model are listed out below.

In this model, a variation is made in the catenation rule when the transition consumes different arrays from the input places. The label of the transition could be a catenation rule. Let A and B be two different arrays with same number of columns in the two input places P 1 and P 2 of a transition t. Then, the catenation rule P 1 

figure d

 P 2 can be given as a label of the transition t. The transition t, on firing, will join A and B row-wise in the same order. Similarly, if C and D are two different arrays with same number of rows in the two input places P 1 and P 2 of a transition t. Then, the catenation rule P 1  \( {\ominus } \) P 2 can be given as a label of the transition t. The transition t, on firing, will join C and D column-wise in the same order. The number of input places is not restricted. The catenation rule specifies the order in which the arrays are joined (row-wise or column-wise). P 1 ⊝ P 2 ⊖ … ⊖ P k joins the arrays in P 1, P 2,…, P k row-wise in that order.

Firing rules in Column row catenation Petri net structure

Both the pre- and post-condition of the firing rules enlisted 1(i) and 1(ii) in array token Petri net structure holds in this model. The firing rules are the same when all the input places of a transition have the same array as token. When the input places have different arrays as tokens, then the firing rules differ.

Input places having different arrays as tokens can be classified as follows:

  1. (i)

    Within one input place different arrays can reside.

  2. (ii)

    Different input places have different arrays but within one input place only copies of the same array is found.

Firing rules when the input places have different arrays as token.

  1. 1.

    When at least one input place of t has different arrays as token and if label of t is one of the input places

    1. (a)

      The input place, designated by the label, should have the same array as tokens.

    2. (b)

      The input places have sufficient number of arrays (depends on the weight of the arc from the input place to the transition).

    3. (c)

      Firing t consumes arrays from the input places and moves the array from the designated input place to all its output places.

  2. 2.

    When different input places of t have different arrays, but within one input place only copies of the same array is found and if label of t is a catenation rule

    1. (a)

      The input places have sufficient number of arrays (depends on the weight of the arc from the input place to the transition).

    2. (b)

      The catenation rule is either of the form P 1 \( {\ominus } \) P 2 \( {\ominus } \)…\( {\ominus } \) P k or P 1 ϴ P 2 ϴ…ϴ P k .

    3. (c)

      The arrays should satisfy the condition for catenation.

    4. (d)

      Firing t consumes arrays from all the input places and joins the arrays in the order stated and puts in all its output places.

Definition 4.2.1

A column row catenation Petri net structure N CR is an 8-tuple N CR = (P, T, I, O, Σ, σ, μ 0, F), where P = {p 1,…, p n } is a finite set of places; T = {t 1, t 2,…, t m } is a finite set of transitions; I : P × T → N, the input function; O : P × T → N, is the output function; Σ a finite alphabet; σ : T → R U P is a partial function which associates label to certain transitions of the net, R is a set of catenation rules; μ 0 : P → \( \Sigma ^{{\text{**}}} \) is a partial function which gives an initial marking of arrays in certain places of the net; F \( \subseteq \) P is the subset of final places.

Definition 4.2.2

The language generated by a column row catenation Petri net structure N CR, L(N CR), is the set of all rectangular arrays which reach the places belonging to F.

Definition 4.2.3

The family of such array languages generated by column row catenation Petri net structure is denoted by L(N CR)

Example 4.2.1

The column row catenation Petri net structure is the 8-tuple N CR(1) = (P, T, I, O, Σ, σ, μ 0, F) with P = {P 1, P 2, P 3, P 4, P 5, P 6, P 7, P 8, P 9}, T = {t 1, t 2, t 3, t 4, t 5, t 6, t 7, t 8, t 9}. The input and output function are seen from the graph given in Fig. 2. \( {\varSigma = \{ *, \bullet \} } \). The labels are seen in the graph. μ 0(P 1) = μ 0(P 4) = S is the initial marking. F = {P 9} is the final place. The arrays involved are

$$ s\,\,\text{ = }\,\,\begin{array}{*{20}c} { \bullet } \\ \text{*} \\ { \bullet } \\ \end{array} \,\,\text{,}\,\,B_{\text{1}} \text{ = (*)}_{m} \text{,}\,\,B_{\text{2}} { = ( \bullet )}^{n} $$

Firing the sequence of transition t 1 t 2 t 3, say three times puts the array given in Fig. 3a in P 7 and firing the sequence t 5 t 5 t 6 puts the array given in Fig. 3b in P 8, and firing the transition generates the diamond of size 9 × 9 given Fig. 3c in P 9, t 9 the final place. The language generated by N CR(1) is the set of all diamonds of odd size length.

Fig. 2
figure 2

Petri net to generate diamonde of odd side length

Full size image
Fig. 3
figure 3

The arrays reaching the places P 7, P 8, P 9 respectively

Full size image

5 Generative Capacity of the Models

In this section, comparison of the generative capacity of the two models is done with the other array language generating models. For the definition of array rewriting grammar refer to [6], extended controlled table L-array grammar refer to [5], and pure 2D context-free grammar refer to [8].

Theorem 5.1

The family of array languages generated by array token Petri net structure is a proper subset of the family of such array languages generated by array token Petri net structure with inhibitor arc. \( \mathcal{L}( \mathcal{N} ) \) is a proper subset of \( \mathcal{L}( \mathcal{N}_{\mathcal{I}} ) \).

Proof

The families of (R : Y)AL, where Y is either regular, context-free or context-sensitive can be generated by array token Petri net structure. (R : Y)AL is a proper subset of \( \mathcal{L}( \mathcal{N} ) \) [14]. Any member of the family (R)P2DCFL can be generated by array token Petri net structure [14]. Any member of the family (R)T0LAL can be generated by array token Petri net structure [14]. Any language generated by a Table 0L-array grammar with context-free or context-sensitive can be generated by array token Petri net structure with inhibitor arcs [14]. The families of (X : Y)AL, where X is either context-free or context-sensitive and Y is either regular, context-free, or context-sensitive can be generated by array token Petri net structure with inhibitor arcs [14]. Since (R : Y)AL is a proper subset of (X : Y)AL, where X is either context-free or context-sensitive and (R)T0LAL is a proper subset of (CF)T0LAL, it follows that \( \mathcal{L}( \mathcal{N} ) \) is a proper subset of \( \mathcal{L}( \mathcal{N}_{\mathcal{I}} ) \).

Theorem 5.2

The family of array languages generated by array token Petri net structure (with or without inhibitor arc) is a proper subset of the family of such array languages generated by column row catenation Petri net structure. Both \( \mathcal{L}( \mathcal{N} ) \) and \( \mathcal{L}( \mathcal{N}_{\mathcal{I}} ) \) are proper subsets of \( \mathcal{L}( \mathcal{N}_{\mathcal{CR}} ) \).

Proof

The two models have different firing rules when two different input places do not have the same array. In array token Petri net structure, if a transition is labeled with a catenation rule and its input places have different arrays as token, then the transition is not enabled. But in column row catenation Petri net structure, a transition labeled with a catenation rule, its input places having different arrays as token, is enabled if the condition for catenation is satisfied. The array language generated in Example 4.2.1 cannot be generated by any array token Petri net structure. On the other hand, all transitions which are enabled in array token Petri net structure are also enabled in column row catenation Petri net structure. Hence, every language generated by array token Petri net structure can also be generated by column row catenation Petri net structure. Therefore, it follows that both \( \mathcal{L}( \mathcal{N} ) \) and \( \mathcal{L}( \mathcal{N}_{\mathcal{I}} ) \) are proper subsets of \( \mathcal{L}( \mathcal{N}_{\mathcal{CR}} ) \).

6 Conclusion

Examples have been given to analyze the differences in the firing rules and the generative capacity of the two models. The generative capacity of the array token Petri net structure with inhibitor arc is more than the generative capacity of array token Petri net structure. It has been proved that the column row catenation structure has more generative capacity than the array token Petri net structure.