Vibration Analysis of Laminated Composite Beam with Transverse Cracks

Abstract

The present study deals with the effect of transverse cracks on the dynamical characteristics of laminated composite beam based on first order shear deformation theory (FSDT) is investigated. The cracks formulation is derived from the fracture mechanics theory as the inverse of the compliance matrix calculated with the proper stress intensity factors and strain energy release rate expressions. The various parameters such as fiber orientation, volume fraction of fiber, crack depth and crack location in the presence of cracks on the natural frequency are studied in detail. The frequencies of vibration of a cracked beam is computed and compares with the results of other investigators. A program is developed in MATLAB environment to study the effects of various parameters on the natural frequencies of composite beam with transverse cracks.

1 Introduction

The beam is one of the most fundamental structural components, used frequently used in many structures to carry and transfer loads in the machine and civil structures. In recent years, the use of fiber reinforced composite in weight-sensitive structures, such as the aerospace constructions, turbine blades, robot arm etc. have been increased because of their high specific stiffness, high specific modulus and tailor-ability. The problem related to strength degradation and structural integrity is a major problem in such type of construction due to the presence of crack whose investigations present a considerable importance. These cracks cause an increase in amplitude of vibration level and finally lead to catastrophic failures. This may also cause changes in the structural parameters (e.g., the stiffness of a structural member such as beam elements), which can change the dynamic properties (such as natural frequencies and mode shapes). A good numbers of research works related to the dynamic behavior of composite beam without crack are available in the literature. But very few literatures are available on dynamic analysis of composite beam with cracks. Krawczuk et al. [1] modeled and presented an algorithm for the creation of characteristic matrices for the composite beam with single transverse fatigue crack. They used finite element method for the analysis. Song et al. [2] investigated the effects of multiple cracks on composite beam subjected to coupled bending-torsion loading based on Timoshenko beam theory. Wang et al. [3] presented free vibration analysis of cracked composite beams under coupled bending–torsion loading based on a classical theory. Sridhar et al. [4] used pseudo spectral finite element method for the wave propagation analysis in anisotropic and inhomogeneous un-cracked and cracked structures. Kumar et al. [5] investigated free vibration analysis of the cracked composite beam using experimental setup. Ghoneam [6] investigated numerical and experimental analysis of Eigen parameters of laminated composite beam with transverse open crack. Sung and Kim [7] investigated effect of a crack due to rotating speed of composite beam based on Timoshenko Beam theory using finite element method. Kisa [8] studied free vibration analysis of a cantilever composite beam with multiple cracks using finite element and component mode synthesis method. Loya et al. [9] found natural frequencies for bending vibration of Timoshenko cracked beams using perturbation method. Krawczuk [10] studied the static and dynamic analysis of the cracked composite beam using finite element method. Krawczuk and Ostachowicz [11] investigated the Eigen frequencies of a cracked cantilever composite beam. They presented two models of the beam. In the first model, the crack was modeled by a mass-less spring and in the second model the cracked part of the beam replaced by a cracked element.

In the present work, finite element method is used for the free vibration of generally laminated composite beams with a transverse crack on the basis of first order shear deformation theory (FSDT). The various parameters such as fiber orientation, volume fraction of fiber, crack depth and crack location in the presence of cracks on the natural frequency are studied in detail by selecting some numerical examples and results of which has been compared with the results of other investigators. A program is developed in MATLAB environment to study the effects of various parameters on the natural frequencies of composite beam with transverse cracks .

2 Mathematical Formulation

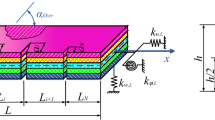
Considering a cantilever composite model of uniform cross section having transverse open cracks of depth ‘a’ and located at a distance ‘x’ from fixed end as shown in Fig. 1. The length, width and height of the beam are L, B and H respectively. The laminated composite beam is assumed to be made of unidirectional laminate composite.

Fig. 1

Geometry of cantilever composite beam with single cracked composite beam

For laminated composite beam, the assumed displacement field based on FOST can be written as

$$ u(x,z,t) = u_{0} (x,t) + z\uptheta(x,t) $$

(1a)

$$ w(x,z,t) = w_{0} (x,t) $$

(1b)

where u₀ and w₀ are mid-plane axial and transverse displacements in x and z-directions, $\theta$ is the rotation of the normal to the mid-plane about the y-axis and t is the time.

The strain-displacement relationships are given by

$$ \upvarepsilon_{x} =\upvarepsilon_{x}^{0} + zk_{x} $$

(2a)

$$ \gamma_{xz} = \frac{{\partial w_{0} }}{\partial x} . $$

(2b)

Applying the finite element method in the beam vibration analysis , we obtained the mass matrix M and a stiffness matrix K as

$$ \left[ K \right] = \int\limits_{V} {\left[ {\mathop B\nolimits^{T} } \right] \, \left[ D \right]\left[ B \right]dV} $$

(3)

$$ \left[ M \right] = \int\limits_{V} {\mathop {[N]}\nolimits^{T} [\uprho][N]dV} $$

(4)

where [N] denotes the shape function and the matrix [D] can be written as

$$ \left[ D \right] = \left[ {\begin{array}{*{20}c} {\mathop A\nolimits_{11} } & {\mathop B\nolimits_{11} } & 0 \\ {\mathop B\nolimits_{11} } & {\mathop D\nolimits_{11} } & 0 \\ 0 & 0 & {\mathop S\nolimits_{55} } \\ \end{array} } \right] \, $$

(5)

2.1 Crack Modeling

The most convenient method to determine the stiffness matrix of crack is to obtain first flexibility matrix and then take the inverse of it. Derivation of a total flexibility matrix of crack consists of two parts—first flexibility matrix due to crack, which leads to energy release and additional deformation of the structure and second consists of a flexibility matrix of intact beam. The stress intensity factors in the fracture mechanics were used to model the crack. The beam has a uniform depth along z-axis and is loaded with axial force P₁; shear force P₂ and bending moment P₃. The flexibility coefficient due to presence of crack can be obtained from Castiglione’s theorem in the following form.

$$ C_{ij} = \frac{{\partial^{2} U}}{{\partial P_{i} \partial P_{j} }} $$

(6)

where U is the additional elastic strain energy of the element by the crack, while P_i and P_j denote the independent nodal forces of the finite element. The additional elastic strain energy in the case of cracks existing in unidirectional composite materials is equal to

$$ U = \int\limits_{A} {\left( {D_{1} \sum\limits_{i = 1}^{i = N} {K_{{\text{I}}i}^{2} } + D_{12} \sum\limits_{i = 1}^{i = N} {K_{{\text{I}}i} } \sum\limits_{i = 1}^{i = N} {K_{{\text{II}}i} } + D_{2} \sum\limits_{i = 1}^{i = N} {K_{{\text{I}}i}^{2} } } \right){\text{dA}}} $$

(7)

where A is the surface crack, K _ij (j = I, II, i = 1, 2 …n) are the stress intensity factors and D₁, D₁₂ and D₂ are coefficients depending on the material parameters are taken from Krawczuck et al. [1].

The stress intensity factors for a composite beam with a crack are taken from Tada et al. [12] are expressed as

$$ K_{ij} = \sigma_{i} \sqrt {\pi a} Y_{j} F_{ji} \left( \frac{a}{H} \right) $$

(8)

where, $\sigma_{i}$ is the stress for the corresponding fracture mode, a is crack depth, H is the height of the beam, $F_{ji} (\frac{a}{H})$ (j = I, II, i = 1, 2, 3) is the correction factor for the finite specimen size, Yj(ξ) (j = I, II) is the correction factor for the anisotropic material are taken from Kisa [8].

As a result $C_{ij}$ can be written as

$$ C_{ij} = \left[ {\begin{array}{*{20}c} {C_{11} } & {C_{12} } & {C_{13} } \\ {C_{21} } & {C_{22} } & {C_{23} } \\ {C_{31} } & {C_{32} } & {C_{33} } \\ \end{array} } \right] . $$

(9)

Total flexibility matrix C_Total of the cracked beam element can now be obtained by

$$ C_{total} = C_{intact} + C_{ij} $$

(10)

where $C_{intact}$ is the flexibility matrix of intact beam are taken from Sung and Kim [7].

Finally, stiffness matrix of the beam element with crack can be written as

$$ K_{crack} = TC_{total}^{ - 1} T^{t} $$

(11)

where T is the transformation matrix are taken from Sung and Kim [7].

3 Result and Discussion

The convergence study is first done for first non-dimensional frequencies of the cracked composite beam as a function of angle of fibers for different mesh division and is shown in Table 1. As observed, a mesh of 10 elements shows good convergence of the numerical solutions for the free vibration and this mesh is employed throughout for study in the subsequent vibration analysis of composite beam. For intact beam the non-dimensional natural frequencies are normalized according to the following relation [8].

Table 1 Convergence of non-dimensional free vibration frequencies of cracked composite beam for different angle of fibers

$$ \upomega_{i} = L\sqrt {\upomega\sqrt {\frac{{12\uprho}}{{S_{11} H^{2} }}} } . $$

(12)

For cracked beam the non-dimensional natural frequencies are normalized according to the following relation [8].

$$ \mathop\upomega\nolimits_{j} = \frac{{\mathop\upomega\nolimits_{crack} (\alpha )}}{{\mathop\upomega\nolimits_{nc} (\alpha )}} $$

(13)

where, $\omega_{crack}$ and $\omega_{nc}$ denote the natural frequency of the cracked and non-cracked cantilever composite beam as a function of the angle of the fiber $(\alpha )$, respectively.

After convergence study, the accuracy and efficiency of present formulation are checked through comparison with previous studies. First three non-dimensional frequencies of the non-cracked beam for different angles of fibers obtained by present formulation is compared with those obtained by Kisa [8] using finite element method as shown in Fig. 2. First three non-dimensional frequencies of the cracked beam for different angles of fibers with different crack ratio obtained by present formulation is compared with those obtained by Kisa [8] as shown in Fig. 3. The geometrical characteristics and material properties of the beam were chosen as the same of those used in [9]. The present results show good agreement with previous results.

Fig. 2

Comparison of first three non-dimensional frequencies of the non-cracked composite beam as a function of the angle of fibers α, value of V = 0.30

Fig. 3

Comparison of effect of angle of fiber on non-dimensional natural frequency of the cracked composite beam for different the crack depth a/H = 0.0, 0.2, 0.4 and 0.6, values of V = 0.30

After the convergence study and comparison of formulation with the existing literature, the studies extend to the investigation of the vibration analysis of laminated composite beam with transverse crack including shear deformation effects using finite element method. The geometrical properties of the beam were chosen as the same of those used in Krawczuck et al. [11] and geometrical characteristics of the beam are L = 381 mm, B = H = 25.4 mm. The numerical results are presented below to show the effects of various parameters like crack ratio, crack depth, fiber orientation and volume fraction of fibers on the natural frequency. The shear correction factor to be used is 5/6.

In Fig. 3, it is clear from the results that as the angle of the fiber increases from 0° to 90°, the non-dimensional natural frequency decrease. The variation of angle of fiber with a volume of fraction of fiber 0.50 on the frequencies of vibration of composite beam of varying crack depth is shown in Fig. 4. As observed, from the results the decreases in natural frequencies become more with increasing crack depth. When crack is perpendicular to fiber orientation decreases in natural frequencies are higher as the angle of the fiber increases, the changes in the first frequency reduce. For the value of the angle of fiber is greater than 30 these changes are very low and nearly same to that of non-cracked beam. The effect of variation in the angle of the fibers on the frequencies of vibration of composite beam with varying crack location, constant crack depth ratio 0.2 and volume fraction of fibers 0.50 is shown in Fig. 5. As observed, from the results that crack near the free end will have a smaller effect on the fundamental frequency than the closer end. The first and second natural frequencies are changed when the cracks are located at the near fixed end and middle of the beam respectively. The effect of variation of volume fraction of fibers on the frequencies of vibration of composite beam of varying crack depth is shown in Fig. 6. As observed, from the results the decreases in natural frequencies become more with increasing crack depth. It also shows that the reduction in frequency highest takes place in between the volume of fibers 0.2 and 0.8.

Fig. 4

Effect of angle of fiber on non-dimensional natural frequency of the cracked composite beams for different the crack depth a/H = 0.0, 0.2, 0.4 and 0.6: a relative first frequency, b relative second frequency

Fig. 5

Effect of angle of fiber on non-dimensional natural frequency of the cracked composite beams for different the crack location at constant depth a/H = 0.2: a relative first frequency, b relative second frequency

Fig. 6

Effect on non-dimensional fundamental natural frequencies of the cracked composite beam as a function of the volume fraction of fibers for several values of the crack depth a/H = 0.2, 0.4 and 0.6

4 Conclusion

In this paper, the free vibration analysis composite beam with transverse open crack based on first order shear deformation theory (FSDT ) using finite element method is investigated. The effect of these parameters crack locations, crack depth, angle of fiber and volume fraction of fiber on natural frequencies is studied. The stiffness matrix of cracked beam element is derived using stress intensity factors in the fracture mechanics. The presented procedure can be used to identify cracks by linking the variation in service of the composite structural beam natural frequencies to the structural changes due to cracks.