Keywords

1 Introduction

Molecular spin qubits based on extremely stable open shell compounds [1, 2] are the latest arrival among physically realized matter qubits [2, 3]. Such molecular spin qubits – composed of unpaired spins and nuclei with non-zero nuclear spin quantum numbers in the electronic spin network of molecular frames – are intrinsically synthetic matter spins [4], because the need for molecular optimization to make functioning matter spin qubits requires testing with actual, open shell chemical entities. We emphasize that the molecular optimization has to fulfill all of DiVincenzo’s five criteria [5] and additionally to provide material uniformity and stability under strong microwave and RF irradiation. An additional requirement is to establish appropriate crystal engineering for quantum computing and quantum information processing (QC/QIP) [2, 3]. This is important for controlling decoherence of the spin qubits in ensemble, which is partly governed by intermolecular spin-spin interactions and symmetry of the crystal lattice.

Molecular optimization by synthetic chemistry is advantageous to generate scalable spin qubits such as electron spin versions of a Lloyd model system [6, 7], in which three non-equivalent g-tensors, A, B, and C are arranged in a 1D periodic (ABC)n backbone. A synthetic approach to the Lloyd model has been a materials challenge, but now molecular units for a prototypical Lloyd model have been isolated and chemically identified by X-ray structural analysis and electron magnetic resonance spectroscopy, as described below. Alternative approaches to Lloyd model systems are also briefly described. Molecular spins as qubits resources are composed of both electron spins as bus qubits and nuclear spins as client qubits. This is due to the intrinsic nature of unpaired electron spins, whose molecular wavefunctions are extended and delocalized in such a manner that the electronic structures are governed by both group-theoretical and topological symmetry of the electron network [1, 4]. Thus, gate operations with electron spin qubits only can be achieved by utilizing anisotropic electron spin dipolar interactions between the spin qubits, as shown below. The electron spin qubits connect the client spin qubits via hyperfine (A) interactions, and we emphasize that molecular information about the principal axes of hyperfine qubit A-tensors is important to implement quantum computing in anisotropic media such as solid-state materials, as shown in a later section herein.

2 Synthetic Approaches to Lloyd Model Electron Spin Scalable Qubit Systems

We have extended the original Lloyd model – in which qubits resources are nuclear spin-1/2 systems, later extended to high spin systems with nuclear-nuclear interactions assumed to be usable for gate operations – to the corresponding electron spin versions. Our idea has been underlain by the feasibility of molecular optimization in terms of synthetic strategy for scalability and facile initialization processes compared with the nuclear spin qubit based versions. A remarkable advantage relevant to the Lloyd model is that one needs to prepare only three kinds of addressable spin qubits, say A, B and C, as a one-dimensional array in an (ABC)n periodic manner. The periodic boundary conditions are strict and relevant to the materials uniformity required for the accuracy of any gate operations in the frequency domain during QC/QIP processes. Materials control of periodicity with uniformity is important in crystal engineering for ensemble solid-state QC/QIP. The issues can be met by molecular optimization with specific chemical bonding schemes like a DNA-based approach described below.

In an electron spin version of the Lloyd model, the g-tensors of molecular spins play an essential role in building up the (ABC)n periodic spin chain, in which A, B and C have different g-tensors that are addressable in the frequency domain of current microwave technology. We emphasize that for an electron spin Lloyd model system in isotropic media, the use of significantly non-equivalent isotropic g-values (termed genuine g-tensor approach-2) or a pseudo g-tensor (hyperfine A-tensor) approach is essential to differentiate between the three molecular spin qubits. The genuine g-tensor approach-2 requires particular molecular optimization in which the g-tensor of each molecular spin is tuned by introducing hetero-atoms at a radical site. This is termed electronic tuning of the g-tensor. In molecular spin based solid-state QC/QIP, the spatial orientation of each g-tensor provides non-equivalence of the resonance frequency with respect to an applied static magnetic field, with differentiation of the three molecular spins if the molecular optimization is properly achieved, as described below (genuine g-tensor approach-1). The pseudo g-tensor (hyperfine A-tensor) approach utilizes nuclear spins with sizable hyperfine couplings to a particular electron spin site (e.g., a radical moiety). The hyperfine coupling gives rise to significant additional splitting of the resonance line, which differentiates between two g-tensors having the same principal values and axes. Such A-tensor engineering is a workable method to lift inversion symmetry induced degeneracy of two g-tensors. Isotopic labeling at one radical site in biradical systems having inversion symmetry is one of the applications of this method.

The electronic tuning approach above is also applicable to solid-state QC/QIP. A promising application of this approach is to utilize DNA-like double-stranded structures capable of incorporating non-equivalent open-shell metal ligands at complementary hydrogen bonding sites. This is termed DNA based supramolecular crystal engineering. In the electron spin version of the Lloyd model, anisotropic electron dipolar interactions between neighboring molecular spins are utilized to execute quantum gate operations. This contrasts with the use of small exchange interactions in the case of nuclear spin Lloyd model qubits with closed shell molecular frames, for two main reasons: (1) precise control of exchange interactions to order of MHz is a still-intractable problem in open shell chemical entities [1, 2]; (2) experimental limitations of current microwave spin technology mean that presently available excitation bandwidth cannot cope with sizable exchange couplings. The latter will be sorted out by emerging microwave technology, if the corresponding frequency is not very high (less than 100 GHz).

In this section, we describe the g-tensor-orientation approach to the electron spin version of the Lloyd model, from the viewpoint of materials challenges (genuine g-tensor approach-1) [8], focusing on molecular optimization for a prototypical Lloyd model of the electron spin version. Figure 28.1 shows a prototypical spin chain of electron spin version Lloyd model, in which supramolecular ligands play dual roles in building up 1D spin chains of the proposed periodicity. One is that the ligands are able to incorporate either open or closed shell transition metal cations, and the other is that the ligands can yield triple-stranded 1D structures of metal-ligation to give triple-stranded helical symmetry (see the caption of Fig. 28.1 for the dual roles). The metals are located in a pseudo-octahedral symmetry of the local structures. The departure from octahedral symmetry matters in terms of establishing the g-tensor orientation approach. This is because octahedral symmetry cannot generate a non-equivalency of magnetic tensors in the triple-stranded helical environment, so the three molecular spins units would not be distinguishable. One of the crucial points in the supramolecular approach, where the ligands play dual roles, is how to control the magnitude of the deviation from strict octahedral symmetry and to increase the axial nature of the relevant magnetic tensors at the transition metal cation sites. Another crucial, practical point is the synthetic feasibility of length extension of the periodicity while strictly keeping the other structural boundary conditions. The present supramolecular approach is subject to two apparent weaknesses that should be improved from the viewpoint of molecular optimization. One is the fact that the method is not applicable for materials syntheses using the genuine g-tensor approach-2 with electronic tuning of the g-tensors in a straight forward manner. To our knowledge, current supramolecular chemistry cannot afford subtle synthetic differentiation between metal cations having non-equivalence of their g-tensors. In this context, a novel molecular optimization strategy requires functioning modification of ligands combined with control of their metal binding selectivity in terms of theoretical considerations of the contribution to their g-tensors from spin-orbit interactions. The other is the broadened linewidth of electron spin resonance (ESR) transitions compared with those from organic-only open-shell spin qubits. This arises from nuclear electric quadrupolar interactions of transition metal ions. This issue is not intrinsic but relevant to the excitation strength of pulsed microwave irradiation at resonance.

Fig. 28.1
figure 1

A prototypical model of the electron spin version of the Lloyd model (supramolecular approach). Molecular optimization is based on the g-tensor orientation approach-1. The strength of ligand-metal self-association should be strong enough to keep the triple-stranded helical structure unfolded even in solution at ambient temperature [8]. The supramolecular ligands bind transition metal cations in a pseudo octahedral symmetry with a robust global structure to suppress decoherency of ensemble electron spin qubits when incorporated into crystal lattices with diamagnetic host molecules. Use of various metal cations also allows preparation of magnetically-diluted, mixed single crystals with desired concentration ratios of guest/host molecules. Supramolecular functionality also allows triple-stranded structures, in which the orientations of electron spin qubit g-tensors and other magnetic tensors are governed by the global molecular symmetry

Full size image

In this context, g-tensor engineering approaches based on the DNA double-stranded (ABC)n architecture have the advantage of utilizing electronic tuning of the g-tensor, in which the complementary hydrogen bonding scheme can afford 1D periodic chains of non-equivalent g-tensors for molecular spin qubits [9]. The DNA-based approach to g-tensor engineering was tested by introducing molecular spins at mismatched sites of the complementary hydrogen bonds in the DNA oligonucleotides. Both the global and local molecular structures were probed by Q-band pulsed ELectron-electron-DOuble-Resonance (pulsed ELDOR) spectroscopy and by computational molecular mechanics modeling. In DNA-based g-tensor engineering, the molecular rigidity of molecular spin qubits introduced at desired sites of the hydrogen bonding is crucial, and this approach utilizing organic molecular spins is not subject to the two weaknesses for the metal cation approach described above.

3 Controlled-NOT Gate Operations by Molecular Spin Qubits

Molecular spins for qubits usage are composed of both electron spins as bus qubits and nuclear spins as client qubits. The client qubits are useful in many aspects of qubits usage (particularly as quantum spin memory), but nuclear spin qubits giving cross-talk in g-tensor engineered molecular spin qubits are an obstacle in executing gate operations composed of electron spin qubits, because they give so many unwanted nuclear sublevels. Toward avoiding this problem, the biradical 1 depicted in Fig. 28.2a is the first synthetic electron spin qubit system which allows Controlled-NOT (CNOT) gate operations by the use of molecular electron spins [10].

Fig. 28.2
figure 2

Biradical 1 as a spin qubit that makes Controlled-NOT gate operations implemented in molecular systems. (a) Molecular structure: The two nitrogen nuclei are 15N-labeled and all the protons of the two radical fragments deuterium-labeled. There is no inversion symmetry between the two radical sites, so orientation g-tensor engineering is achieved. (b) The exchange interaction between the radical sites is <0.2 MHz owing to molecular optimization, in which the two central benzene rings bridging the two radicals govern the relative orientation of the g-tensors. The Controlled-NOT gate operations by electron spin qubits in molecular systems were implemented by utilizing anisotropic spin-dipolar interactions (−9.5 MHz for the zero-field splitting parameter) [10]

Full size image

In the biradical 1, orientation g-tensor engineering is achieved using the two radical sites with non-equivalent g-tensors denoted by molecular fragments in blue and red in Fig. 28.2. The two radical sites are not related by inversion symmetry, so hyperfine A-tensor engineering is not necessary in the molecular optimization. The two nitrogen nuclei and thirty-four hydrogen atoms in the fragments are 15 N- and fully deuterium-labeled, respectively. The isotope labeling enormously enhances the spectral resolution. Particularly, the nitrogen labeling is crucial to identify the magnetic field orientation suitable for QC/QIP experiments. The biradical 1 is diluted to a desired concentration in a diamagnetic host lattice of the related bisketone molecule whose molecular structure is approximately the same as that of 1. The central benzene rings play an important role to allow a large angle between the two radical fragments, allowing effective orientation g-tensor engineering. After the measurements of angular dependence of fine-structure hypefine-split ESR spectra with respect to crystal coordinate or molecular principal axis orientation, we can identify orientations of the static magnetic field with respect to the crystal and fully determine the magnetic tensors in the spin Hamiltonian. This identification provides conditions for QC/QIP experiments such as initialization, CNOT gate operation, or quantum teleportation between molecular spin qubits, so long as appropriate rf and microwave frequency pulse energies and sequences can be achieved. Obviously, two microwave frequencies with their phases controlled in currently available coherent-dual pulsed ELDOR [3b] are not enough, so Nuclear Magnetic Resonance (NMR) paradigm, pulsed-ESR spin technology using conventional microwave frequencies has been implemented in our laboratory (Osaka City University). This emerging spin technology can afford realistic QC/QIP experiments in which both electron spin bus and nuclear client qubits can be manipulated/controlled in the Bloch sphere in an equal manner. This new spin technology is not subject to limitations of the number of irradiation pulses, their relative phase and amplitudes. This was demonstrated by first CNOT gate operation in the molecular spin qubits of 1, which were been implemented in the magnetic field direction in which the eigenstates of the nuclear spins are not affected during the electron spin transitions on resonance. Thus, only the four electron spin sublevels are involved in the QC experiments, and the gate operations are achieved by utilizing anisotropic electron spin dipolar interactions (−9.5 MHz for the zero-field splitting parameter). In biradical 1, the molecular structure optimization gave effective suppression of the exchange interaction (less than 0.2 MHz). The molecular optimization for shortening the distance between two molecular spin qubits also gives faster gate operations than those for the longer distance, as expected.

4 Adiabatic Quantum Computation on a Molecular Spin QC

A molecular spin quantum computer utilizes electron spins as bus qubits which are manipulated by electron spin resonance (ESR) based magnetic resonance techniques in open shell molecules, in which nuclear spins topologically connected play the role of client qubits. In this section, we focus on adiabatic quantum (AQ) computation [11] by utilizing both electron spin bus qubits and nuclear client qubits in as fully controlled a manner as possible using current levels of spin resonance technology. The molecular spin AQ computation is underlain by the recent implementation of NMR-paradigm pulsed ESR technology from the experimental side. A factorization of 21 was chosen for the adiabatic algorithm in order to illustrate the essence of the approach, for comparison with NMR molecular systems. We present for the first time pulse sequences required for ESR QC experiments using molecular spin systems, and possible problems to be encountered in molecular spin AQ computation are pointed out for further development.

Since Shor’s algorithm appeared, attempts at realistic QC/QIP have been made from the experimental side [12, 13], with the first experiment performed by utilizing pulsed NMR techniques [14] without invoking quantum entanglement. An experiment proposed by Peng and coworkers factorizes 21 by an Adiabatic Quantum Computer (AQC) with rather small numbers of qubit resources such as three qubits. They performed this QC experiment using solution NMR conditions in which C, H and F nuclear spin states in a dimethylfluoromalonate molecule were manipulated [15]. AQC is one of the computation models of QCs, which processes information in the ground states of a quantum system with variation of the corresponding Hamiltonian [11]. Although AQC has been defined as different from standard QC, it is important that: (1) AQC has the same computational ability as standard QC [16]; (2) AQC can allow performance of error correction [17].

From the viewpoint of spin resonance, it is interesting to identify the difference between NMR and ESR qubit systems in terms of AQC. As already described in the preceding section, in the ESR system molecular spins with open shell electronic structures are utilized in QC/QIP, and electron spins play the role of bus qubits while nuclear spins are client qubits. Particular magnetic interactions involving electron spins are utilized for computational operations, and thus generally shorter overall computational time is anticipated [18]. Here, we describe the theoretical study of an adiabatic factorization problem, illustrating how a molecular spin AQC works when AQC is implemented in real molecular spin qubits. This gives a foundation to build the implementation of molecular spin based AQC.

AQC requires definition of an adiabatic Hamiltonian path in an algorithm. The initial Hamiltonian, Ĥ i and the final Hamiltonian, Ĥ f are adopted as Eqs. (28.1) and (28.2) in this study, respectively.

$$ {\widehat{H}}_{\mathrm{i}}=a{\displaystyle \sum_{i=1}^n{\sigma}_x^i} $$
(28.1)
$$ {\widehat{H}}_{\mathrm{f}}={\left(N-xy\right)}^2 $$
(28.2)

where, \( a=30 \), \( N=21 \), \( n=3 \), \( x=\left(I-{\sigma}_z^1\right)+I \), \( y=2\left(I-{\sigma}_z^2\right)+\left(I-{\sigma}_z^3\right)+I \) in the factorization of 21 [15]. In this algorithm, there are unsolvable problems when the solution of (x, y) has the same bit size because the two ground states have the same energy. Nevertheless, there are two advantages to this algorithm: (1) the algorithm easily compares ESR systems (i.e., molecular spins) to NMR systems; (2) this approach requires only a small number of qubits for execution. Applied to molecular spins using pulsed ESR techniques, the time evolution operator of the adiabatic process is approximated in finite time steps and defines the needed, adiabatic path as Eq. (28.3).

$$ \begin{array}{ll}U={\displaystyle \prod_{m=1}^5 \exp \left(-i{\widehat{H}}_m\varDelta t\right)},\hfill & {\widehat{H}}_m={\left(m/5\right)}^2{\widehat{H}}_{\mathrm{f}}+\left\{1-{\left(m/5\right)}^2\right\}{\widehat{H}}_{\mathrm{i}}\hfill \end{array} $$
(28.3)

The time evolution operator U is a non-commutative operator in Eq. (28.3). Therefore, U was transformed by the Trotter expansion to commutable operators in the pulse sequences of calculations (see Appendices at the end of this chapter): the theoretical fidelity of this approach is 0.91 [15].

Generally the spin Hamiltonian in a molecular spin QC with the static magnetic field along the z-direction can be written by Eq. (28.4) in the Schrödinger picture.

$$ \begin{aligned}\hfill {\widehat{H}}_{\mathrm{MSQC}}&={\displaystyle \sum_{i=1}^N{S}^i{g}^i{\beta}^iB}-{\displaystyle \sum_{j=1}^M{I}^j{g}^j{\beta}^jB}+{\displaystyle \sum_{i<j}^{N,N}{S}^i{\left(J+D\right)}^{ij}{S}^j}\\ &\quad +{\displaystyle \sum_{i=j=1}^{N,M}{S}^i{A}^{ij}{I}^j}+{\displaystyle \sum_{i<j}^{M,M}{I}^i{\left(J+D\right)}^{ij}{I}^j}\end{aligned} $$
(28.4)

The first and second terms are Zeeman interactions for electron and nuclear spins, and g i is a second rank tensor which is related to the Larmor frequency ω i0 of an ith spin (\( {\omega}_0^i={g}_{zz}^i{\beta}^i{B}_z/\hslash \) where B z is the static magnetic field in the ESR system). The interactions between spins are written by second rank tensors of J, D and A which correspond to electron exchange interaction, anisotropic fine-structure (mainly spin-dipolar interaction in organic molecular high spins) and hyperfine interaction, respectively.

The effective Hamiltonian in the time evolution operator is calculated by transforming to an interaction picture of the spin Hamiltonian. Following the common procedure, the unperturbed Hamiltonian is selected for Zeeman terms by assuming the secular approximation with small anisotropy in the g-tensor. This approach is equivalent to adopting the rotational frame in quantum mechanics. Since most experiments of a molecular spin QC have been carried out in single crystal systems incorporating open shell molecules such as radicals or multi-radicals, in this study for designing pulse sequences, either a three-electron system (3e system) or one-electron plus two-nuclear system (1e + 2n system) is adopted, as exemplified in Fig. 28.3. In transforming to the interaction picture, the principal axes of the hyperfine tensors are assumed to be parallel to the static magnetic field, to simplify by eliminating effects from anisotropic terms. We have known that this assumption is special for most of real molecular spin qubits, and that non-linearity of the quantization axes is crucial to acquire better fidelity to the model. Overall, Eqs. (28.5) and (28.6) are obtained as perturbation Hamiltonians in the time evolution operator of the 3e system and 1e + 2n system, respectively,

$$ {\widehat{H}}_{\mathrm{int}}^{3\mathrm{e}}={S}_z^1{\left(J+D\right)}^{12}{S}_z^2+{S}_z^2{\left(J+D\right)}^{23}{S}_z^3+{S}_z^3{\left(J+D\right)}^{31}{S}_z^1 $$
(28.5)
$$ {\widehat{H}}_{\mathrm{int}}^{1\mathrm{e}+2\mathrm{n}}={S}_z^1{A}^{12}{I}_z^2+{I}_z^2{\left(J+D\right)}^{23}{I}_z^3+{I}_z^3{A}^{31}{S}_z^1 $$
(28.6)

where (J + D)ij and A ij are the zz-components of the corresponding tensor. In solution, only the D tensor will vanish on the basis of its traceless character.

Fig. 28.3
figure 3

Molecular structures of a phthalocyanine system (four electron (4e) system, left) and an isotope-labeled diphenylnitroxide (DPNO) (one-electron and two nuclear-spin (1e + 2n) system without counting 15N nucleus, right). In the calculation described in the text, only three electron qubits of the phalocyanine system are treated, so one of the four radical sites should be closed shell. Any nuclear effects mainly arising from the nitrogen nuclei are neglected in the present treatment, for simplicity

Full size image

Pulse sequences were calculated using two pulse operations (arbitrary angle operations of the x- and y-directions) for each qubit with time evolution (arbitrary time). A phthalocyanine derivative for the 3e system and a diphenyl nitroxide (DPNO) for the 1e + 2n system were adopted as real molecular examples of these (see Fig. 28.3 for the molecules). There are four electron spins in the phtalocyanine system, so we assumed a three-qubit system in which one radical site is chemically reduced. These systems have strong enough isotropic interactions that are needed for establishing constant time in any orientation, and they are workable molecular spin QCs from the previous study [19, 20]. Considering the experimental restrictions, e.g. selecting the axis for the g-tensor while keeping co-linearity of the hyperfine tensors, the average time for an adiabatic calculation can approximately equal the isotropic coupling case (J 12 = J 23 = −22.8 MHz, J 31 = −40.8 MHz, A 12 = −5.56 MHz and A 31 = −37.9 MHz) [19, 20]. By this assumption, the obtained pulse sequences are the same as those in the solution state of these systems. The 3-qubit interaction on the adiabatic time evolution is replaced by reducing 2-qubit interactions [21]. In the case of the 1e + 2n system, the interactions between nuclei are too weak to manipulate, therefore the interactions are replaced by 3-qubits interactions and the other 2-qubits interactions. We replaced the pulses only when we need to connect two pulses. The pulse sequences were lined up in the 3-qubit interaction, 2-qubit interactions and 1-qubit operations as shown in Fig. 28.4.

Fig. 28.4
figure 4

The pulse sequences for the factorization problem of 21. (a) The sequence of the 3e-system. The time, t i and the green character indicate the pulse time interval and the operation of the adiabatic Hamiltonian, respectively. The pulse in blue including the number is for an arbitrary operation of the x- or y-direction. In the adiabatic process, the pulse sequences need to loop five times (n = 1 to 5). (b) The sequences of the 1e + 2n system. In this case, the pulse sequence basically similar to (a) but replace A-block of (a) to nuclear cases for (b). (c) Denotes the types of pulse for easier identifications. Black and red blocks indicate the x- and y-direction, and narrow and wide blocks indicate π/2 and π pulses, respectively. The numbered pulses are the x- or y- operations in a certain angle. The details of the operation time and angle are calculated

Full size image

The estimated, calculated time and the total operation angles for each spin are shown in Table 28.1. For comparison to a three-nuclear system, we have calculated the time for the NMR system to be approximately 50 ms and for the ESR system to be about 0.23 μs. Thus, using a three-electron (3e) system can be about 105 faster. This is because the nuclear spin system has exchange couplings of the magnitude of 50–200 Hz. On the other hand, in the 3e system couplings are on the order of 20–40 MHz. As expected, an important result is that the calculation speed is not simply proportional to the gyromagnetic ratio between the two systems, but to the interaction strength. From the experimental point of view, if one tries to perform the same adiabatic algorithms in molecular electron spin systems as for the NMR systems, the short time operations (e.g., 0.2 ns) for 2-qubit interactions could be a problem. Even under this condition, we can perform the adiabatic calculation by scaling up the problem Hamiltonian, but the required time proportionally increases for the Hamiltonian. Alternatively, one can treat the electron spin systems using accurate and short time operations (below 0.2 ns), which is a technical issue for current microwave technology. We emphasize that this problem appears only in AQC not in a standard QC.

Table 28.1 Operation angles and required times in the 3e system and 1e + 2n system are shown
Full size table

In the 1e + 2n system the required time when ignoring the pulse manipulation time is about 1.57 μs, therefore this system also is faster than for NMR system methodology. In this molecular spin system, the same problem for the short operation time occurs. Another problem with the 1e + 2n system is the manipulation of nuclear spins. Because of the absolute value of the g factor, the Rabi operation for nuclei (e.g., π pulse) in the molecular spin system takes much more time than for electrons (about few μs for nuclear spins) [20], so the time required for this algorithm would depend on the operation time of the nuclear spins. In this case, the hyperfine interactions which are larger than or as the same order of magnitude as the Rabi frequency need to be taken into account in the pulse formulation.

In terms of operation angles, our pulse sequence requires a larger number of pulses than in the NMR method [15]. The operation angles in the 1e + 2n system need approximately twice the number of pulse operations than the 3e system, due to the replacements of the 2-qubit operation. This difficulty of this adiabatic algorithm mostly arises from the three qubit interaction (Fig. 28.4).

In this section, we have illustrated the factorization problem of 21 treated by AQC by utilizing molecular spin qubits and presented the difference between the NMR and ESR systems. In the 3e system, increased speed depending on the interaction strength has been proven and shorter time operations in the molecular spin systems are suggested. Also, the 1e + 2n system has the possibility for increased speed, although appropriate treatment of the nuclear spin operations is needed. The difficulties in applying the present adiabatic algorithm to molecular spin qubits are identified, and mostly arise from three-qubit interactions. Overall, we have introduced experiments for AQC that utilize molecular spin qubits in which appropriate molecular optimization has been made to solve the problems for correct adiabatic operations in ESR systems.

5 Multi-Spin Quantum Control Through Single Spin Manipulation

5.1 Theoretical Background

Toward the realization of quantum computing, it suffices if we could fully control a given many-body quantum system. By full control, we mean the implementation of any unitary operation on the system, maintaining its quantum coherence throughout the operation. The system that is the subject of our control typically comprises a number of qubits, and high-fidelity applications of single- and two-qubit operations to arbitrary qubits have been a much-coveted goal for physicists.

Aiming at the implementation of a small number of elementary qubit operations appears to be convenient, since any unitary transformations on many-qubit systems can be decomposed into a sequence of simple operations, or quantum logic gates. Yet, performing a multi-qubit operation usually requires control of inter-qubit interactions. In order to switch interactions between qubits, we would need an extra control probe for every qubit pair; it may be a physical electrode to control voltage, or additional electromagnetic waves to induce interactions between degrees of freedom, or even a measurement on auxiliary qubits to cause an effective state change.

Here we primarily focus on the systems of spin-1/2 particles, as they are a naturally very good two-state system, i.e., qubit, and, in many cases they have advantages in terms of scalability and longer coherence times. Although spin-spin interactions, such as the Heisenberg-type exchange interactions, are capable of realizing useful two-qubit operations, it is hard to switch such inter-spin interactions at will, as described in the earlier sections.

Luckily, the difficulty in performing two-qubit operations in the presence of constant coupling between qubits is not a crucial problem for quantum computing, since the decomposition of a unitary transformation into elementary gates is just for descriptive convenience. All we need to do is to seek the right modulation of external field parameters, where time evolution becomes equal to the desired unitary transformation. We employ this approach here to find a feasible field modulation (pulse sequence) for nontrivial quantum operations using multi-spin systems.

The most generic form of the system Hamiltonian is described as

$$ H(t)={H}_0+{\displaystyle \sum_m{f}_m(t){H}_m}, $$
(28.7)

where H 0 represents an unmodulable interaction and H m represents external fields that can be controlled experimentally by a modulation function f m (t). For example, if the system is a one-dimensional chain of spins-1/2: H 0 describes the inter-spin couplings, such as H 0 = ∑ n J n σ n  · σ n+1; H m represents the Zeeman interaction between the m-th spin and the local magnetic field b m , i.e., H m  = b m σ m ; and f m (t) denotes the field intensity at time t. Here, b m is the unit vector in the direction of the field at the m-th site. As we want to control the entire system by modulating a small number of parameters, we would consider that the number m of controllable Hamiltonians H m is small, e.g., two or three.

The Schrödinger equation for the time evolution operator under the Hamiltonian Eq. (28.8) is

$$ \begin{array}{ll}i\frac{d}{dt}U(t)=H\left[\mathbf{f}(t)\right]U(t),\hfill & U(0)=I,\hfill \end{array} $$
(28.8)

where f(t) stands for the set {f m (t)}. This equation can formally be integrated as

$$ U(t)=\mathsf{T} \exp \left(-i{\displaystyle {\int}_0^tH\left[\mathbf{f}\left(\tau \right)\right]d\tau}\right), $$
(28.9)

where T is the time-ordering operator.

We are interested in the set {U(t)} with a finite t, each element of which is obtainable by varying the pulse sequence f(t). Let us define the reachable set R to be the unitaries that can be arbitrarily close to the unitary transform U(T) in Eq. (28.9) with a finite T and a right pulse sequence f(t)(t ε [0,T]). That is,

$$ \begin{array}{lllll}\forall \varLambda \in \mathcal{R},\hfill & \forall \varepsilon \in 0,\hfill & \exists \mathrm{f}(t)\in, \hfill & \exists T<0,\hfill & \mathrm{such}\ \mathrm{that}\ \left|\right|V-U(t)\left|\right|<\varepsilon .\hfill \end{array} $$
(28.10)

If R is equal to U(2N) or SU(2N) for an N spin system, then any unitary operation for this system can be realized within a finite time by designing the pulse sequence appropriately, and hence is fully controllable.

Then, how can we characterize R, given a set of Hamiltonians {H m }(m ε {0,1,…,M}). A famous theorem of quantum control gives a concise answer to this question [22].

Theorem 28.1

The reachable set R is the connected Lie group associated with the Lie algebra L that is generated by taking commutators of elements in {H m } repeatedly, i.e.,

$$ \mathrm{R}={e}^{\mathrm{L}}. $$
(28.11)

In the Lie algebra U(n) (or SU(n)), each element in the algebra is skew-Hermitian. Thus, precisely speaking, L contains {iH m } and their repeated commutators.

The algebra L is often called dynamical Lie algebra, and its elements take the form [A 1 ,[A 2 ,[…,[A k  − 1, A k ]…]]], where A 1 ,A 2 ,…,A k ε {H m }. The linearly independent ones form the basis of the dynamical Lie algebra. Because we are considering a finite dimensional system, this process of taking commutators eventually stops generating a new basis that is linearly independent with respect to those generated before. The maximum number of the independent bases, i.e., the rank, is n 2 or n 2 − 1, when H m are n × n matrices in U(n) or SU(n), respectively.

Therefore, in the context of quantum control, where we disregard the effect of the global phase, if the rank of the dynamical Lie algebra L is equal to n 2 − 1, R is equal to SU(n), and hence the system is fully controllable through {H m }. Even if R does not coincide with SU(n), any unitary in R can be implemented, thus partially controllable. The simplest case of this theorem is the control of a single spin-1/2. If the magnetic field can be controlled in two (orthogonal) directions, say x and y, the modulable Hamiltonians are σ x and σ y (through the Zeeman interaction). The commutator of these, [σ x ,σ y ], gives σ z (apart from the i factor). This means that we can effectively control σ z as well, so the rank of L is three. Since SU(2) is three dimensional, the single spin is fully controllable by field control in two directions. This particular simplistic case corresponds to the Euler decomposition of arbitrary rotations, such that any rotation in three dimensions can be expressed as a product of rotations around the two fixed directions.

While Theorem 28.1 is very powerful in judging the controllability of the system, it does not tell anything about how we should design the control pulse sequences, let alone the necessary time duration for a pulse sequence to implement a specific unitary operation. Although some partial results have been obtained to reduce the complexity of this problem [23], finding optimal control pulses is a computationally hard task in general. Thus we still need to rely on some algorithms of numerical calculations that have been developed for these purposes, such as the one developed by Macnes and coworkers [24].

Knowing that all parameters (including the inter-qubit interactions) do not necessarily have to be controlled, one can implement some nontrivial quantum operations on a real system in the lab. Molecular spins in molecules, which are the subject of our study, are a good basis for which Theorem 28.1 can be applied nicely; they are constantly interacting with each other, and in electron-spin-only mediated systems each spin typically has a different g-factor from others if appropriate molecular optimization is made as described in the previous sections, and thus it is not very hard to control a few electron spins or nuclear ones selectively. In the following section, we describe attempts to achieve indirect quantum control practically, using a three-spin system consisting of one electron spin and two nuclear spins, which is termed a bus spin qubit system. Here the electron spin and nuclear spins act as a bus qubit and client qubits, respectively, in the molecular frame.

5.2 Indirect Application of a Quantum Gate on a Three-Spin System

Typically, in a hybrid molecular system of an electron spin plus nuclear spins, a single electron spin has been used for state preparation, readout and control while the nuclear spins act as qubits for storing and processing information. It has been shown that in such systems, the nuclear spins can be indirectly fully controllable through an electron spin as a spin actuator via hyperfine interactions [25, 26]. In this study, we designed a control pulse sequence numerically to implement a high fidelity gate operating on nuclear spins. Using the pulse sequence, we are currently attempting to implement multi-qubit operations with systems of three and more spins, and we will verify the result of quantum operations (under limited access) using well-established electron nuclear multiple resonance methods. We emphasize that pulse techniques composed of only microwave frequencies to manipulate nuclear spins under certain conditions are novel spin technology that is still under development. This spin technology enables us to rotate nuclear spins faster than pulsed ENDOR based techniques.

We consider a three-spin system composed of an electron spin and two nuclear ones in the presence of an external static magnetic field. For simplicity, the spin Hamiltonian of the system in frequency units is given by Eq. (28.12),

$$ \begin{aligned}{H}_0&=\frac{g_{zz}{\beta}_e{B}_0}{h}{S}_z-\frac{\gamma_{n_1}}{2\pi }{B}_0{I}_z^1-\frac{\gamma_{n_2}}{2\pi }{B}_0{I}_z^2\hfill \\ &\quad +{A}_{zx}^1{S}_z{I}_x^1+{A}_{zy}^1{S}_z{I}_y^1+{A}_{zz}^1{S}_z{I}_z^1+{A}_{zx}^2{S}_z{I}_x^2+{A}_{zy}^2{S}_z{I}_y^2+{A}_{zz}^2{S}_z{I}_z^2,\hfill \end{aligned} $$
(28.12)

where β e is the Bohr magneton, γ ni/2π = 42.576 MHz /T as the gyromagnetic ratio of a hydrogen atom, and B 0 is the external static magnetic field which is applied along the z-direction of the g-tensor, respectively. A zz is the zz component of the hyperfine coupling tensor, while A zx and A zy denote the anisotropic hyperfine coupling coefficients. S and I are the electron spin and nuclear spin operators, respectively. The nuclear spin-dipolar interactions between two nuclear spins is neglected since its strength is almost 1000 times smaller than the hyperfine interactions between electron and nucleus.

If all transitions between the eight states of a 1e + 2n system are accessible, universal control in the system is possible. For different values of the hyperfine coupling coefficients, the probabilities of transitions between all the states can be varied, depending on the direction of the static magnetic field with respect to the molecular principal-axis system in the solid state. In order to control the system efficiently and to realize high fidelity quantum gate behavior, the hyperfine coefficients must carefully be designed to ensure that all the transitions can be accessed with significant transition probabilities. We emphasize that in terms of conventional electron magnetic resonance spectroscopy complex experimental conditions are required in addition to appropriate molecular optimization for molecular spins. Microwave irradiation on the single electron makes it work as an actuator to perform an entangling gate between the two nuclear spins. The Hamiltonian of control can then simply be described by Eq. (28.13), as

$$ {H}_{control}=\frac{g_{zz}{\beta}_e{B}_e(t)}{h}{S}_x $$
(28.13)

where B e is the amplitude of the oscillating microwave magnetic field which is applied on the electron on the x-direction. Thus g zz β ε Β ε(t)/h corresponds to the strength of the microwave magnetic field.

The actual spin system employed here is a diphenylaminoxyl (DPNO = diphenylnitroxide) derivative, whose molecular structure is given in Fig. 28.5. We emphasize that spin manipulation technology should be based on pulsed electron-nuclear multiple resonance technique with controlled phase of each spin by coherence microwave frequency.

Fig. 28.5
figure 5

Experimental qubit spin system, diphenylaminoxyl (DPNO). The nitrogen labeling simplifies hyperfine ESR spectra with significantly enhanced spectral resolution. Red, blue, gray and white balls denote oxygen, nitrogen-15, carbon, and proton and deutron atoms, respectively. The principle-axis alignments are shown with corresponding arrows in the figure. The molecular structure is assumed if it is incorporated in a diamagnetic host lattice having a similar molecular structure to diphenylaminoxyl

Full size image

The hyperfine and g-tensors of DPNO are given by Yoshino [27]. The principal values of the proton hyperfine tensors and g-factor in their principal-axis coordinate system of Fig. 28.5, are summarized in Eqs. (28.14) to (28.15) as follows:

$$ g=\left(\begin{array}{ccc}\hfill 2.0097\hfill & \hfill 0\hfill & \hfill 0\hfill \\ {}\hfill 0\hfill & \hfill 2.0053\hfill & \hfill 0\hfill \\ {}\hfill 0\hfill & \hfill 0\hfill & \hfill 2.0024\hfill \end{array}\right) $$
(28.14)
$$ \begin{array}{ll}{e}^{-1}H:\left(\begin{array}{ccc}\hfill -8.63\hfill & \hfill 0\hfill & \hfill 0\hfill \\ {}\hfill 0\hfill & \hfill -5.56\hfill & \hfill 0\hfill \\ {}\hfill 0\hfill & \hfill 0\hfill & \hfill -2.22\hfill \end{array}\right)\hfill & {e}^{-2}H:\left(\begin{array}{ccc}\hfill -8.82\hfill & \hfill 0\hfill & \hfill 0\hfill \\ {}\hfill 0\hfill & \hfill -5.76\hfill & \hfill 0\hfill \\ {}\hfill 0\hfill & \hfill 0\hfill & \hfill -2.34\hfill \end{array}\right)\hfill \end{array} $$
(28.15)

The hyperfine couplings can be adjusted by varying the orientation of the static magnetic field with respect to a single crystal doped with DPNO. Transforming the tensors from the principal-axis system to the laboratory-axis reference, the orientation that can differentiate between transitions with suitable transition probabilities between all the states can be chosen for QC experiments. Any rotation of the frame can generally be described by Eq. (28.16) and (28.17), where

$$ {T}_{\mathrm{lab}}=R{T}_{\mathrm{diag}}{R}^t $$
(28.16)

with

$$ R=\left(\begin{array}{l} \cos {\theta}_{ax} \cos {\theta}_{ay} \cos {\theta}_{az}\hfill \\ {} \cos {\theta}_{bx} \cos {\theta}_{by} \cos {\theta}_{bz}\hfill \\ {} \cos {\theta}_{cx} \cos {\theta}_{cy} \cos {\theta}_{cz}\hfill \end{array}\right) $$
(28.17)

where (x,y,z) and (a,b,c) denote the laboratory-axis and principal-axis references, respectively. The g-factor terms of the electron spin and the hyperfine couplings of the hydrogen atoms for the chosen orientation are typically as given below in Eq. (28.18):

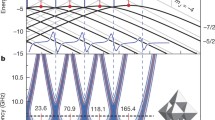
$$ \begin{array}{l}{g}_{zz}=2.00253;\hfill \\ {}{A}_{zx}^1=-0.12158\kern0.5em \mathrm{MHz};{A}_{zy}^1=1.15564\kern0.5em \mathrm{MHz};{A}_{zz}^1=-8.37156\kern0.5em \mathrm{MHz};\hfill \\ {}{A}_{zx}^2=-0.91001\kern0.5em \mathrm{MHz};{A}_{zy}^2=1.33327\kern0.5em \mathrm{MHz};{A}_{zz}^2=-7.25018\kern0.5em \mathrm{MHz}.\hfill \end{array} $$
(28.18)

We have designed numerically a pulse sequence which can performs a C-NOT gate on two nuclei with 1H’ being the control qubit and 2H being the target qubit of the gate. Choosing the values B = 0.35 T and g zz β e B e/h = 10 MHz for the intensity of the static magnetic field and the energy of the microwave to be employed, the gate can be performed in 5 μs with fidelity 0.81. Since in our experimental setup, the excitation bandwidth is on the order of 100 MHz, we fixed ∆t = 0.005 ns in our numerical calculation, which yields the excitation bandwidth = 200 MHz. In order to get higher fidelity, we need a longer time duration: in the present molecular spin t =11 μs leads to a fidelity of 0.99. However, we emphasize that shorter pulse durations are better from the viewpoint of quantum information processing, so QC experiments may be better performed at L-band frequencies. By setting B 0 = 0.1 T, the fidelity can be as high as 0.94 for t = 5 μs, and 0.99 for t = 6 μs. The numerically computed pulse sequences are shown in Fig. 28.6. One can extend this method to any number of nuclear spins that have resolvable anisotropic hyperfine interactions.

Fig. 28.6
figure 6

Pulse sequences which perform a C-NOT gate with fidelity 0.99 as a function of time. In the left/right panels, the magnetic field is chosen as B =0.35 T/B =0.1 T. The former corresponds to QC experiments at X-band and the latter at L-band

Full size image

6 Conclusions

In order to manipulate or control both bus and client qubits in an equivalent manner, the implementation of sophisticated microwave pulse technology is essential. Novel microwave pulse technology that enables full control of both the amplitudes and phases of multiple microwave frequencies has already been emerging, indicating that new spin technology based on arbitrary wave generators (AWGs) can be powerful in manipulating ensemble molecular spin systems. The problems described in Sect. 28.5 are relevant to enable appropriate molecular optimizations of spin behavior. We also emphasize that the three-electron spin system under study imposes limitations in terms of its molecular optimization but sophisticated quantum chemical calculations of D tensors are available, which will enable us to design more appropriate three- or multi-electron spin molecular systems. In this quest of achieving practical molecular spin QCs or QIP systems, pulse-based advanced microwave spin technology combined with molecular optimization is essential.