Keywords

1 Introduction

Origami, the traditional paper craft and art, is well-known all over the world today. In recent years, scientists, designers, and engineers from around the world have been inspired to produce three-dimensional shapes by folding flat sheets. Origami generated by mathematical interpretation and computation is called mathematical origami and has led to the modeling of numerous novel origami-based structures beyond the aspect of the arts. Furthermore, mathematical origami provides important ideas for the design of new structures and mechanisms in engineering. In the decade since Nojima [20] proposed origami engineering—the scientific study of the origami techniques and their application to engineering—the scope of practical applications to which origami has been applied has expanded. Current applications include space-efficient structure designs , robot designs, medical devices, and automobile components.

This paper serves as an introduction to mathematical origami and origami engineering for readers who are not familiar with this research field. First, mathematics used in the design of origami-based foldable models is presented. Next, representative mathematical origamis and recent applications to engineering studied by us are demonstrated.

2 Mathematical Origami

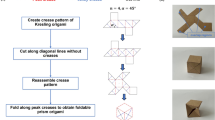
Origami-based models are geometrically designed with the assumption that the material to be folded has ideally zero thickness, and is not stretchable but flexible enough to allow bending. Paper is often used as the material to satisfy these prerequisites. One field of origami-based structure designs focuses on designing foldable models that change shape dramatically when pulled and compressed in accordance with given direction(s). For example, Fig. 1 shows a fundamental foldable model inspired from the twist buckling pattern of a cylinder [3, 8, 18, 19]. The model is constructed by folding according to the pattern shown in Fig. 1d. The solid and broken lines correspond to mountain and valley folds, respectively. After folding, the boundaries on the right and the left are glued to make a closed cylinder. Thus, it can be folded compactly or flat-foldable to the height direction of the cylinder.

Fig. 1
figure 1

Folding behaviors of the foldable cylindrical structure: a Initial spatial state; b folding/expanding state; c folded state; d folding pattern for the structure. This figure was extracted from Ishida et al. [10]

Full size image

Kawasaki’s theorem specifies how such flat-foldable models are designed [7, 13]. Let \(\alpha _1, \alpha _2, \ldots , \alpha _{2n-1}, \alpha _{2n}\) be successive angles around a single vertex. To be flat-foldable around the single vertex, it is necessary and sufficient that the sum of the angles skipped one turn is equal to the other sum of the angles:

$$\begin{aligned} \alpha _1+ \alpha _3+ \cdots + \alpha _{2n-1} = \alpha _2+ \alpha _4+ \cdots + \alpha _{2n}. \end{aligned}$$
Fig. 2
figure 2

Kawasaki’s Theorem for four fold lines around a vertex

Full size image

For the case in which the sum of all the angles, \(\alpha _1+ \alpha _2+ \alpha _3+ \cdots + \alpha _{2n}\), is equal to \(2\pi \) or the vertex is positioned on a developable surface, Kawasaki’s condition can be reduced to

$$\begin{aligned} \alpha _1+ \alpha _3+ \cdots + \alpha _{2n-1} = \alpha _2+ \alpha _4+ \cdots + \alpha _{2n}=\pi . \end{aligned}$$

This condition can be obtained as follows. Consider four fold lines around a vertex, as shown in the example in Fig. 2. The sum of the angles around a vertex O is equal to \(2\pi \) in the unfolded state. The angle goes forward and back in turn with the folding of lines OA, OB, OC, and OD. To be flat-foldable, it must return to the initial position or the sum of the angles must be zero in the folded state. Kawasaki’s theorem for four fold lines around a vertex, \(\alpha _1+ \alpha _3 = \alpha _2+ \alpha _4 = \pi \), is thus obtained. The structure shown in Fig. 1 satisfies Kawasaki’s theorem for six fold lines around every vertex because of the symmetric design, and therefore, the whole structure is flat-foldable. For generalized designs, Tachi [22] provides a software application called Freeform Origami that facilitates control of the coordinates of vertices on the pattern independently for asymmetric designs, while still keeping the flat-foldability.

To form a closed tube such as a cylinder, another constraint must be applied in order that the position of the left boundary is identical to that of the right boundary when it is folded. For simple symmetric designs such as that shown in Fig. 1, the mountain and valley folds rotate the line segments by \(2(\alpha +\beta )\) and \(-2\alpha \), respectively (Fig. 3). The sum of the rotation angles produced by N-time foldings, \(2N\beta \), must be equal to \(2\pi \) [19]. Thus, the constraint of the angle, \(2N\beta = 2\pi \), is obtained to form a cylinder. In this example, \(N = 6\) so that \(\beta \) is determined as \(\pi /6\).

Fig. 3
figure 3

Constraint of the angle to form the cylinder with thetorsional buckling pattern

Full size image
Fig. 4
figure 4

Folding behaviors of the foldable S-shaped tube

Full size image
Fig. 5
figure 5

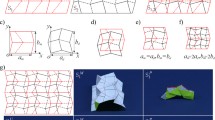
Flat-folding of the foldable circular disks: a Circular disk pattern to form a triangular prism; b folding process of the circular disk shown in (a); c variety of physical models. A part of the figure was extracted from Ishida et al. [11]

Full size image

Considering these conditions, a variety of origami-based structures have been studied around the world. Studies have been published, for example, in the book \(Origami^5\), the post proceeding of the fifth meeting of origami science, mathematics, and education [23]. The next post proceeding, \(Origami^6\), will be on the market soon.

Let us now look at some examples of flat-foldable structures. Ishida et al. [9] demonstrated the patterns for folding toroidal tubes with regular folding patterns and connected those patterns with different main curvatures while still maintaining the flat-foldability. Thus, suppose that arbitrary winding tubes are approximated to a combination of toroidal tubes with different main curvatures, it was clarified that not only straight cylinders but also even winding tubes, shown in Fig. 4, are flat-foldable.

Further, the flat-folding of circular disks, shown in Fig. 5, is an interesting example. Those structures, designed by Nojima [18, 19], were folded as if they were wrapped around the center of the disk to form polygonal pillars. For example, the circular disk with three spirals from the circumference to the center of the disk was designed in accordance with Kawasaki’s condition at every vertex (Fig. 5a). The disk was folded along the three spirals and formed a triangular prism, as shown in Fig. 5b. The cross-sectional shapes can be varied by changing the number of spirals, such as a square prism from four spirals and a hexagonal prism from six spirals. However, those were only regular polygonal prisms. Ishida et al. [11] widened the variation and produced prisms with unequal sides, such as a rectangular prism, and prisms with unequal angles, such as a rhombic prism, by arranging the positions and the angles of the spirals (Fig. 5c).

3 Origami Engineering

The application of origami-based structures to engineering devices, such as medical devices [14], self-assembling robots [2] and folding structures [1, 16], has been extensively researched globally. In this section, some recent examples studied by us are introduced.

3.1 Origami-Based Vibration Isolators

The foldable cylindrical model shown in Fig. 1 is known as a bi-stable structure; it is stable at the initial spatial state and the folded state, but unstable between both states [17]. Hagiwara et al. [5] noticed that adding linear springs to the bi-stable structure results in a zero-stiffness spring. This is a key idea that led to the development of a novel origami-based vibration isolator that does not transmit any excitation to the other side of the structure around the region where the stiffness is ideally zero [10, 12]. Figure 6a shows the computational model of the isolator, which comprises metallic truss elements connecting each other by ball joints. If a linear spring is implemented in the spring-mass-damper system shown in Fig. 6b, the system will have a strong resonant frequency resulting from the eigen frequency of the spring that corresponds to 2 Hz in Fig. 6c. However, if the proposed isolator is used instead of the linear spring, the system will not have a strong peak because it is a nonlinear spring designed not to transmit excitation, and therefore, the amplification of the vibration can be reduced. To verify these computational results, experimental evaluation of the prototype models is currently in progress.

Fig. 6
figure 6

Computational model for the origami-based vibration isolator and its vibration response: a Computational truss model consisting of horizontal bar elements, longitudinal bar elements, and diagonal bar elements, which are connected by ball joints; b vibration system consisting of the origami-based foldable model with linear springs, a damper, and a mass; c vibration response of the systems. This figure was extracted from Ishida et al. [10]

Full size image
Fig. 7
figure 7

Comparison of conventional energy absorbers and the proposed energy absorber. The figure was extracted from Hagiwara [4]

Full size image

3.2 Origami-Based Energy Absorbers

Tubular shell structures are widely used as energy absorbers in passenger cars to save the lives of passengers when crushes occur. On the conventional absorbers with rectangular cross-sectional shells (upper left image in Fig. 7), small grooves called beads can be arranged in such a manner so as to prevent the absorber from bending to the outside and to efficiently absorb energy under axial loading [6]. However, these conventional absorbers with beads can deform only up to 70 % of their initial height and the other 30 % of the height remains because of the volume of the buckled absorber. Furthermore, they cannot mitigate peak shocks at the instant of the crush and so passengers can be severely injured. To solve these problems, tubular shell structures with foldable cylinders have been studied [15, 21, 24]. Numerical investigations have shown that optimization of the design parameters, such as the angles of fold lines, results in the proposed absorbers (upper right image in Fig. 7) being able to reduce the initial shock and also to buckle by up to 90 % of their initial height [4]. The optimized absorbers can also absorb 1.5 times more energy than the conventional ones. In addition, the hydro forming fabrication method that is currently used to mass produce various industrial parts can be applied to develop and produce the proposed absorbers.

Thus, the advantages of using foldable cylindrical models in absorber designs are clear. However, the proposed absorbers have not yet been adopted for actual use in cars because of the high forming cost incurred by the hydro forming method. Consequently, cost reduction is a challenge for the future.

4 Conclusion

To be flat-foldable around a vertex, it is necessary to satisfy the condition that the sum of angles skipped one turn is equal to the other sum of the angles (Kawasaki’s theorem). To form a foldable tube, another constraint also has to be considered; the position of the left boundary should be identical to that of the right boundary when it is folded.

To date, numerous flat-foldable structures have been designed in accordance with the above-mentioned conditions. They are not limited to straight structures such as cylinders but also winding tubes and wrappable disks, for example. The varieties of foldable structure designs have expanded the applications to engineering. Although the remarkable characteristics of the foldable structures are the dramatic changes in the shapes through folding and deploying motions, the application is not only linked with the characteristics, but also with the mechanical characteristics that the folding patterns possess, such as bi-stability of vibration isolators. Further, foldable designs yield new solutions to practical problems, as exemplified by the case of energy absorbers . There is virtually no limit to the ideas for new applications using foldable structures. We hope that this paper stimulates the creativity of readers and helps them to produce new ideas in their research fields.