Keywords

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Introduction

In Chap. 1, we consider the mechanism of regional agglomeration and dispersion with core–periphery model constructed by Ottaviano, Tabuchi, and Thisse [5]. This model is an extremely powerful model to explain how regional agglomeration and dispersion occur endogenously under the influence of economic activities. Because we assumed that full employment was established in Chap.1, we did not take account of unemployment in the model. However, unemployment is an extremely important issue to be resolved in many countries regardless of developing countries or developed countries. Some developing countries experience urban unemployment during economic development.

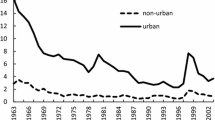
Recently China has played the role of the “World’s Factory” and has also achieved rapid economic growth, becoming a country with economic power. The Chinese government has strictly classified types of households as urban or rural laborer attributable to “domiciliary register registration regulations” established in 1958. The government prohibited rural laborers without domiciliary register to migrate from rural areas to urban areas. In the 1990s, these migrant rural laborers played the role of workers to support China’s manufacturing and export industry. Consequently, the Chinese economy experienced rapid economic growth and recorded the second highest GDP in the world. However, in China, regional disparity came to be actualized with economic growth. China also faces some severe social issues, which other developed countries have already experienced, such as environmental issues, unemployment, and social security. As explained in Chap. 1, the Chinese government introduced market mechanisms into the Chinese economy in the 1980s. Then, the Chinese economy achieved rapid economic growth. Regarding Chinese economic policies, the central government in China put east coast regions before other regions. Consequently, economic disparity occurred. This differential gave rural people a stark incentive to migrate from rural areas to urban areas. Figure 3.1 describes urban unemployment and the urban unemployment rate during 1993–2003. As one might understand from Fig. 3.1, the urban unemployment rate including layoffs, worsened in the latter half of the 1990s.

Fig. 3.1
figure 1

Urban unemployment and the urban unemployment rate in China (Source: http://www.meti.go.jp/report/tsuhaku2005/2005honbun)

Full size image

Particularly, unemployment is a severe issue irrespective of where it occurs. Many economists have been interested in unemployment problems and have sought prescriptions for its improvement. Herein, we present a dualistic economy model in which sectors of two kinds exist attributable to different wage systems in the economy. Lewis [3] conducts pioneering studies of dualistic economy issues. Because Lewis [3] assumes that an unlimited labor supply is available at subsistence wage, he does not describe a mechanism for urban unemployment.

Harris and Todaro [2] conceive a mechanism by which urban unemployment occurred endogenously in the framework of a dualistic economy. The economic model constructed in the study, called the Harris and Todaro model , is as important to studies in this area as that by Lewis [3] is for development economics. Many economists have extended Harris and Todaro model from various viewpoints. For example, although Harris and Todaro [2] regard capital as the fixed specific capital in each sector, Corden and Findlay [1] relax this assumption, and analyze a model with free mobility of capital between the urban area and the rural area. Although Corden and Findlay [1] are not explicit about the stability of equilibrium, Neary [4] refers to the stability of equilibrium in the Corden and Findlay model.

We overview Harris and Todaro [2] to describe a dualistic economy and to explain urban unemployment endogenously. The model presented in this chapter is applied in the models of Chaps. 10 and 14. In next section, we refer to Harris and Todaro [2] as a basic dualistic economy model. Section 3.3 derives equilibrium of model and analyzes the effects of some parameters on equilibrium using comparative statics. In Sect. 3.4, some policy parameters are introduced into the model; we consider the effects of some economic policies on the urban unemployment rate and other endogenous variables. Finally we conclude the analysis of this chapter.

2 The Model

We consider a dualistic economy model constructed by Harris and Todaro [2]. The dualistic economy in this section consists of urban and rural areas.Footnote 1 The population in this economy is denoted by L. Although a manufactured goods sector is located in the urban area, an agricultural goods sector is located in the rural area. Now X and Y respectively denote the manufactured goods sector and the agricultural sector. We assume that the urban wage is fixed above the labor market-clearing level, as do Harris and Todaro [2], and that it has downward rigidity attributable to the minimum wage system, and so on. Particularly, let \(\bar{w}_{X}\) represent the minimum wage in the urban area, which is higher than the rural wage.

Here we normalize the price of agricultural goods to one because we deal with the agricultural goods as numeraire. Presuming that this economy is a small open economy, then the price of manufactured goods is given exogenously.Footnote 2 Moreover, we consider that both sectors face a competitive market.

2.1 Production

Because we assume a small open economy , we define p as the price of manufactured goods. Similarly to Harris and Todaro [2], both sectors require labor and capital as inputs for production. Although labor is mobile between the urban area and rural area, capital is immobile between them. We regard the capital used in each sector as a sector-specific input.

Manufactured Goods Sector

Manufactured goods are produced in the urban area. They require two factors to produce the manufactured goods: labor and capital. Following Harris and Todaro [2], we also deal with capital as fixed input. Consequently, the manufactured goods sector determines only labor input to maximize their profit. Here we define the production function of manufactured goods as follows.

$$\displaystyle{ X = X(L_{X},\bar{K}_{X}), }$$
(3.1)

Therein, L X and \(\bar{K}_{X}\) respectively indicate the amount of labor input and fixed capital input into the manufactured goods production. We assume that the marginal product of labor and capital is positiveFootnote 3 and that the production function is concave, continuous, and differentiable, i.e.,

$$\displaystyle{X_{L} \equiv \frac{\partial X} {\partial L_{X}}> 0,\ \ X_{K} \equiv \frac{\partial X} {\partial \bar{K}_{X}}> 0,\ \ X_{LL} \equiv \frac{\partial ^{2}X} {\partial L_{X}^{2}} <0,\ \ X_{KK} \equiv \frac{\partial ^{2}X} {\partial \bar{K}_{X}^{2}} <0}$$

The manufactured goods market is competitive, and the price of manufactured goods is denoted by p. Consequently, the first order condition with respect to labor is given by

$$\displaystyle{ pX_{L} -\bar{ w}_{X} = 0 }$$
(3.2)

Agricultural Goods Sector

Next we consider the behavior of the agricultural goods sector. Whereas the manufactured goods are produced in the urban area, the agricultural goods are produced in the rural area, and also require two kinds of input factors for production as does the manufactured goods sector. Because the agricultural goods sector also deals with sector-specific capital as fixed input, an agricultural goods sector determines only labor input. Consequently, the production function of agricultural goods sector is given as

$$\displaystyle{ Y = Y (L_{Y },\bar{K}_{Y }), }$$
(3.3)

where L Y and \(\bar{K}_{Y }\) respectively denote labor input and fixed capital input of the agricultural goods sector.

$$\displaystyle{Y _{L} \equiv \frac{\partial Y } {\partial L_{Y }}> 0,\ \ Y _{K} \equiv \frac{\partial Y } {\partial \bar{K}_{Y }}> 0,\ \ Y _{LL} \equiv \frac{\partial ^{2}Y } {\partial L_{Y }^{2}} <0,Y _{KK} \equiv \frac{\partial ^{2}Y } {\partial \bar{K}_{Y }^{2}} <0}$$

Because the price of agricultural goods is normalized, the first-order condition to maximize the profit of agricultural goods sector is the following.

$$\displaystyle{ Y _{L} - w_{Y } = 0, }$$
(3.4)

Therein, w Y is the wage in the rural area. Finally we assume that the following inequality helds in both production functions.

$$\displaystyle{ X_{LL}X_{KK} - X_{LK}X_{KL}> 0 }$$
(3.5)
$$\displaystyle{ Y _{LL}Y _{KK} - Y _{LK}Y _{KL}> 0 }$$
(3.6)

2.2 Households

We refer to the behavior of households in the economy presented in this chapter. Particularly, index X, U, and Y respectively signify households employed in the manufactured goods sector, households unemployed in the urban area, and households employed in the agricultural goods sector. All households have common preferences and the same utility function. Let U i represent the utility function of household i( = X, Y, U). We define the following quasi-linear utility function of household i.

$$\displaystyle{ U_{i}(C_{X}^{i},C_{ Y }^{i}) = u(C_{ X}^{i}) + C_{ Y }^{i} }$$
(3.7)

Therein, C X i and C Y i respectively denote consumption of manufactured goods and agricultural goods. Moreover, the property of sub-utility function u(C X i) satisfies u′ > 0, and \(u^{{\prime\prime}} <0\). The budget constraint of each household is given by

$$\displaystyle{ w_{i} + I = pC_{X}^{i} + C_{ Y }^{i}, }$$
(3.8)

where w i and I respectively represent the wage income of household i and a lump sum redistribution.Footnote 4 Maximizing (3.7) subject to (3.8), we derive the indirect utility function V i (p, w i ). Here, no income effect is attributable to (3.7). Consequently, the difference among households depends on the wage income. The minimum wage with downward rigidity in the urban area is higher than the rural wage. Here we define \(\lambda\) as the urban unemployment rate.

$$\displaystyle{ \lambda \equiv \frac{L_{U}} {L_{X} + L_{U}} }$$
(3.9)

Nobody has incentive to move to the other region because the expected wage in urban area is equal to the wage in rural area in equilibrium. Therefore, the migration equilibrium condition is given as

$$\displaystyle{ (1-\lambda )\bar{w}_{X} = w_{Y } }$$
(3.10)

Presuming that population in the economy is given by L, the population constraint is the following.

$$\displaystyle{ L_{X} + L_{U} + L_{Y } = L }$$
(3.11)

Combining (3.9) with (3.11), we rewrite the population constraint as follows.

$$\displaystyle{ L_{X} + (1-\lambda )L_{Y } = (1-\lambda )L }$$
(3.12)

3 Equilibrium and Comparative Statics

3.1 Equilibrium

We explained the behaviors of production sectors and households and derived some equilibrium conditions in the previous section. L X , L Y , L U , and \(\lambda\) are determined by the system comprising (3.2), (3.4), (3.9), and (3.12). Arranging these conditions, the system in our model is described using the following three equations:

$$\displaystyle{ pX_{L} =\bar{ w}_{X} }$$
(3.13)
$$\displaystyle{ Y _{L} = (1-\lambda )\bar{w}_{X} }$$
(3.14)
$$\displaystyle{ L_{X} + (1-\lambda )L_{Y } = (1-\lambda )L }$$
(3.15)

We describe the equilibrium of this system in Fig. 3.2. The horizontal axis shows the population in this economy. The vertical axis shows wages in each region. The value of marginal products of manufactured goods sector is the decreasing function with respect to labor. Without the downward rigidity of wage, the equilibrium wage is determined by w ∗, in which the value of marginal products of manufactured goods sector is equal to the marginal products of the agricultural goods sector. The employment of the urban area and the rural area are given respectively as O X B and BO Y . No urban unemployment exists under these circumstances.

Fig. 3.2
figure 2

Equilibrium in Harris and Todaro model

Full size image

However, urban employment is described by O X A because we assume that the wage in the urban area has downward rigidity and that it is fixed on \(\bar{w}_{X}\). The marginal products of agricultural goods are also the decreasing function with respect to labor. Next we define the following function ϕ to derive equilibrium under the Harris and Todaro model.

$$\displaystyle{ \phi \equiv \frac{L_{X}\bar{w}_{X}} {L_{X} + L_{U}} }$$
(3.16)

Because L X is constant because of the downward rigidity of wages, ϕ is the decreasing function with respect to L U . Migration equilibrium is achieved at point C, in which the expected wage in urban area is equal to the marginal product of the agricultural goods sector. Consequently, w Y ∗ becomes an equilibrium wage in rural area. Although labor in urban area is described by O X C in Fig. 3.2, urban employment is given as O X A. Consequently, urban unemployment is described by AC.

3.2 Comparative Statics

Next we consider comparative statics given by the system described above. Differentiating (3.13)–(3.15) completely and expressing them with the matrix, they are as follows.

$$\displaystyle\begin{array}{rcl} \left (\begin{array}{ccc} pX_{LL}& 0 & 0 \\ 0 &Y _{LL}& \bar{w}_{X} \\ 1 & 1-\lambda &L - L_{Y }\\ \end{array} \right )\left (\begin{array}{c} L_{X} \\ L_{Y }\\ \lambda \\ \end{array} \right ) = \left (\begin{array}{c} - X_{L}dp \\ 0 \\ (1-\lambda )dL\\ \end{array} \right )& &{}\end{array}$$
(3.17)

If | Δ | is defined as the determinant of coefficient matrix in (3.17), then | Δ | is given as

$$\displaystyle{ \vert \varDelta \vert = pX_{LL}Y _{LL}(L - L_{Y }) - pX_{LL}(1-\lambda )\bar{w}_{X}> 0 }$$
(3.18)

We analyze the effect of each exogenous variables on endogenous variables, which are L X , L Y , and \(\lambda\). First, we consider the effect of manufactured goods prices on each endogenous variables in equilibrium. Results of comparative statics by consideration of (3.17), (3.18), and by Cramer’s formula show the effect of manufactured goods prices on each endogenous variable as

$$\displaystyle{ \frac{dL_{X}} {dp} = \frac{-X_{L}Y _{LL}(L - L_{y}) + X_{L}(1-\lambda )\bar{w}_{X}} {\vert \varDelta \vert }> 0 }$$
(3.19)
$$\displaystyle{ \frac{dL_{Y }} {dp} = \frac{-X_{L}\bar{w}_{X}} {\vert \varDelta \vert } <0 }$$
(3.20)
$$\displaystyle{ \frac{d\lambda } {dp} = \frac{-X_{L}Y _{LL}} {\vert \varDelta \vert }> 0 }$$
(3.21)

From comparative statics from (3.19)–(3.21), the increase of manufactured goods price is known to aggravate the urban unemployment rate , although it increases employment in the manufactured goods sector. For the urban unemployment rate, we derive the following theorem.

Theorem 3.1.

The increase of manufactured goods price aggravates the urban unemployment rate although it increases urban employment.

Second, we consider the effect of total population in the economy on endogenous variables, which are L X , L Y , and \(\lambda\). Using Cramer’s formula to (3.17) and (3.18), we derive the following results of comparative statics, which show the effects of population L on L X , L Y , and \(\lambda\).

$$\displaystyle{ \frac{dL_{X}} {dL} = \frac{0} {\vert \varDelta \vert } = 0 }$$
(3.22)
$$\displaystyle{ \frac{dL_{Y }} {dL} = \frac{-pX_{LL}\bar{w}_{X}} {\vert \varDelta \vert }> 0 }$$
(3.23)
$$\displaystyle{ \frac{d\lambda } {dL} = \frac{pX_{LL}Y _{LL}} {\vert \varDelta \vert }> 0 }$$
(3.24)

Because the increase of population in the economy does not affect the value of marginal products of manufactured goods sector, the value of marginal products curve is not shifted by it. Moreover, the minimum wage in urban area is unaffected by it. Therefore, urban employment does not change because of the increase of population in the economy. Although the increase of population in the economy does not increase urban employment, it increases rural employment because no downward rigidity occurs in the rural area and full employment is achieved by wage adjustment, in which the equilibrium wage in rural area is equal to the value of marginal products of agricultural goods sector. Because urban employment does not change with increasing population, the agricultural goods sector absorbs part of the surplus labor. Consequently, rural employment increases because of the increase of population in the economy. However, this increase in rural employment causes the equilibrium wage in the rural area to decrease for achievement of full employment in the agricultural goods sector. When the equilibrium wage in the rural area promotes labor to have incentive to migrate from the rural area to the urban area because the difference between the expected wage in the urban area and the wage in the rural area increases. Therefore, the urban unemployment rate also aggravates the urban unemployment rate. Regarding the effect of increasing population in the economy on the urban unemployment rate, we derive the following theorem.

Theorem 3.2.

The increase of labor in the economy aggravates the urban unemployment rate although it engenders increased rural employment.

This section presents analysis of the effects of exogenous variables, which are p and L, on endogenous variables, which are L X , L Y , and \(\lambda\). However, we have to note that we deal with capital as a fixed input because we consider capital as a sector-specific factor.

4 Policy Effects in a Dualistic Economy

We have reviewed the mechanism of simple dualistic economy model constructed by Harris and Todaro [2] and analyzed the properties of equilibrium in the previous section. Although we analyzed the effects of some parameters on equilibrium, this model did not include policy parameters. In this section, we introduce some policies into the model in the previous section to analyze their effects on equilibrium in the dualistic economy. Specifically we introduce subsidy policy of two kinds into a dualistic model: a subsidy for manufactured goods sector, and a subsidy for agricultural goods sector. Similarly to Harris and Todaro [2], we assume that the capital input for each sector is sector-specific input. Therefore, we deal with capital input of both sectors as fixed inputs. Each sector can determine only the labor input because each sector deals with capital input as a fixed input. Let s X and s Y represent the subsidy per unit of labor for manufactured goods sector and agricultural goods sector, respectively. Introducing those subsidies into the model, we can revise (3.2) and (3.4) as follows.

$$\displaystyle{ pX_{L} -\bar{ w}_{X} + s_{X} = 0 }$$
(3.25)

and

$$\displaystyle{ Y _{L} - w_{Y } + s_{Y } = 0. }$$
(3.26)

Substituting (3.4) for (3.10), the revised migration equilibrium condition is given as shown below.

$$\displaystyle{ (1-\lambda )\bar{w}_{X} = Y _{L} + s_{Y } }$$
(3.27)

Because L X , L Y , L U , and \(\lambda\) are endogenous variables, they are determined by the following system, which consists of (3.9), (3.12), (3.25), (3.26) and (3.27).

$$\displaystyle{ pX_{L} =\bar{ w} - s_{X} }$$
(3.28)
$$\displaystyle{ Y _{L} = (1-\lambda )\bar{w} - s_{Y } }$$
(3.29)
$$\displaystyle{ L_{X} + (1-\lambda )L_{Y } = (1-\lambda )L }$$
(3.30)

Completely differentiating (3.28)–(3.30), we describe them with the following matrix.

$$\displaystyle\begin{array}{rcl} \left (\begin{array}{ccc} pX_{LL}& 0 & 0 \\ 0 &Y _{LL}& \bar{w}_{X} \\ 1 & 1-\lambda &L - L_{Y }\\ \end{array} \right )\left (\begin{array}{c} dL_{X} \\ dL_{Y } \\ d\lambda \\ \end{array} \right ) = \left (\begin{array}{c} - ds_{X} - X_{L}dp \\ - ds_{Y } \\ (1-\lambda )dL\\ \end{array} \right )& &{}\end{array}$$
(3.31)

We define \(\vert \bar{\varDelta }\vert\) as the determinant of the coefficient matrix in (3.31), \(\vert \bar{\varDelta }\vert\) is given as presented below

$$\displaystyle{ \vert \bar{\varDelta }\vert \equiv pX_{LL}Y _{LL}(L - L_{Y }) - (1-\lambda )\bar{w}_{X}pX_{LL}> 0 }$$
(3.32)

Applying Cramer’s formula to (3.31) and (3.32), the effect of each subsidy on endogenous variables is analyzed. First, we refer to the effect of a subsidy for manufactured goods sector on equilibrium. Results of comparative static analyses are as follows.

$$\displaystyle{ \frac{dL_{X}} {ds_{X}} = \frac{-Y _{LL}(L - L_{Y }) + (1-\lambda )\bar{w}} {\vert \bar{\varDelta }\vert }> 0 }$$
(3.33)
$$\displaystyle{ \frac{dL_{Y }} {ds_{X}} = \frac{-\bar{w}} {\vert \bar{\varDelta }\vert } <0 }$$
(3.34)
$$\displaystyle{ \frac{d\lambda } {ds_{X}} = \frac{Y _{LL}} {\vert \bar{\varDelta }\vert } <0 }$$
(3.35)

According to the results of comparative statics from (3.33)–(3.35), we know that a subsidy for manufactured goods sector increases labor demand of manufactured goods sector although it decreases that of agricultural goods sector. Moreover, it is known that a subsidy for manufactured goods sector improves the urban unemployment rate.

Next we analyze the effect of a subsidy for agricultural goods sector on endogenous variables. Similar to above analysis, we apply Cramer’s formula to (3.31) and (3.32) and derive the following results of comparative statics.

$$\displaystyle{ \frac{dL_{X}} {ds_{Y }} = 0 }$$
(3.36)
$$\displaystyle{ \frac{dL_{Y }} {ds_{Y }} = \frac{-(L - L_{Y })pX_{LL}} {\vert \bar{\varDelta }\vert }> 0 }$$
(3.37)
$$\displaystyle{ \frac{d\lambda } {ds_{Y }} = \frac{(1-\lambda )pX_{LL}} {\vert \bar{\varDelta }\vert } <0 }$$
(3.38)

Because a subsidy for agricultural goods sector does not affect the marginal product of labor in the manufactured goods sector, the labor demand of manufactured goods sector is constant in spite of subsidy s Y . Finally, we refer to the effect of a subsidy for agricultural goods sector on the urban unemployment rate. As a consequence of (3.38), we know that a subsidy for agricultural goods sector as well as that for manufactured goods sector also improves the urban unemployment rate. Therefore, we derive the following theorem based on results of the comparative statics described above.

Theorem 3.3.

A subsidy for sector i(= X,Y ) increases the required labor input of sector i and improves urban unemployment rate.

Moreover, we consider the effect of a subsidy for the manufactured goods sector or the agricultural goods sector on urban unemployed labor. Because we define (3.9) as the urban unemployment rate, urban unemployment labor shown by L U is given as presented below.

$$\displaystyle{ L_{U} = \left ( \frac{\lambda } {1-\lambda }\right )L_{X} }$$
(3.39)

Differentiating (3.39) with respect to s X , we derive the effect of s X on L U as follows.

$$\displaystyle\begin{array}{rcl} \frac{dL_{U}} {ds_{X}} & =& \frac{d\lambda } {ds_{X}} \cdot \frac{dL_{U}} {d\lambda } \\ & =& \frac{d\lambda } {ds_{X}} \cdot \frac{1} {(1-\lambda )^{2}} + \left ( \frac{\lambda } {1-\lambda }\right )\frac{dL_{X}} {ds_{X}}{}\end{array}$$
(3.40)

Taking account of (3.33) and (3.35), the sign of (3.40) is known not to be determined uniquely. Although a subsidy for manufactured goods sector improves the urban unemployment rate, it is possible that labor increases more than improvement of the urban employment with a subsidy for urban sector migration from the rural area to the urban area. Consequently, urban unemployed labor increases, although a subsidy for manufactured goods sector improves the urban unemployment rate. Next we consider the effect of a subsidy for agricultural goods sector on urban unemployed labor. Similarly to analyzing the effect of a subsidy for manufactured goods sector on urban employed labor, we differentiate (3.39) with respect to s Y .

$$\displaystyle\begin{array}{rcl} \frac{dL_{U}} {ds_{Y }} & =& \frac{d\lambda } {ds_{Y }} \cdot \frac{dL_{U}} {d\lambda } \\ & =& \frac{d\lambda } {ds_{Y }} \cdot \frac{1} {(1-\lambda )^{2}} + \left ( \frac{\lambda } {1-\lambda }\right )\frac{dL_{X}} {ds_{Y }} <0{}\end{array}$$
(3.41)

Although a subsidy for agricultural goods sector increases the required labor of the agricultural goods sector, it does not affect the employment of the manufactured goods sector, i.e., \(\frac{dL_{X}} {ds_{Y }}\) is equal to zero. Consequently, we know that sign of (3.41) is negative because the improvement of employment in rural area with a subsidy for agricultural goods sector engenders an increase in rural employment, although it does not increase the employment of the manufactured goods sector. Therefore, urban unemployment rate are improved because the total urban labor decreases with this subsidy. Therefore, we can derive the following theorem.

Theorem 3.4.

Although a subsidy for agricultural goods sector decreases unemployed labor in the urban area, that for manufactured goods does not necessarily decrease unemployed labor in the urban area.

5 Concluding Remarks

We reviewed a dualistic economy model in this chapter. Particularly, we examined a model constructed by Harris and Todaro [2] to explain a dualistic economy. This model, called the Harris and Todaro model, is extremely useful to analyze a dualistic economy. Many researchers have extended the Harris and Todaro model in many directions after Harris and Todaro [2]. As we stated in Sect. 3.2, although Harris and Todaro [2] consider that each production sector requires labor and capital for production, they assume that the capital in each region is sector-specific and that it is not mobile among regions. However, this assumption lacks authenticity. Corden and Findlay [1] and Neary [4] extend the Harris and Todaro model by relaxing the assumption of immobile capital. They discussed the stability of equilibrium in the model. Although we do not deal with the model, in which capital is mobile between urban and rural areas, in detail, it is important to analyze a dualistic economy model with mobile capital between them.

We analyze the effects of some economic policies on equilibrium using comparative statics. As referred in Sect. 3.3, a subsidy for the manufactured goods sector increases unemployed labor in the urban area, although it improves the urban unemployment rate. These results are always known as the “Todaro Paradox” . Even if the government conducted a subsidy policy for manufactured goods sector to increase urban employment, it is possible that it would engender increased unemployed labor in urban areas. Therefore, the government should take account of the effects of any policy on labor migration among regions when it enacts any policy improving urban unemployment rates. However, a subsidy for agricultural goods sector improves the urban unemployment rate and decreases unemployed labor in urban areas. Consequently, a subsidy for agricultural goods sector is more effective than that for the manufactured goods sector. In fact, although Lewis [3] emphasized that development in urban area resolves a dualistic economy, Harris and Todaro [2] emphasized that development in rural areas is more important than in urban areas.

Although Harris and Todaro [2] is an important study in the field of development economics, their model includes some points to be revised. For instance, they do not address how unemployed laborers (households) make their living because they do not receive wage income. Moreover, in fact, they consider other points, which are environment, social security, and so on, although Harris and Todaro [2] assume that households are interested in the difference between expected wages in urban areas and wages in rural areas. Consequently, it is necessary to resolve those issues using the extended model.