Keywords

1 Introduction

A mathematical billiard is a continuous-time dynamical system describing the motion of a massless point particle, the billiard ball, moving freely with constant speed in the interior of a connected compact Riemannian manifold P with piecewise smooth boundary, the billiard table. The billiard ball moves along geodesics of P until it hits its boundary \(\partial P\). If the collision with \(\partial P\) occurs at a smooth boundary point, the billiard ball reflects according to a prespecified rule, the reflection law. Otherwise, if the collision with \(\partial P\) occurs at a non-smooth boundary point, a corner, the forward dynamics may not be well-defined. The most commonly considered reflection law is the elastic reflection: the tangential component of the billiard ball velocity remains the same, while the normal component changes its sign. However, as we will see below, there exist equally reasonable alternative reflection laws with relevant mathematical implications.

Interesting questions concerning the dynamical properties of mathematical billiards include, among others, the existence and number of periodic orbits or more general invariant sets, the existence and number of dense orbits in phase space, the existence of non-trivial invariant measures, or the positivity of Lyapunov exponents. Note that all these properties depend solely on the geometry of \(\partial P\), the metric on P and the precise reflection law under consideration. See the survey paper [13] for a recent overview of the field with a focus on open problems.

It is worth remarking that mathematical billiards are not just mathematical abstractions, but are also models for important problems in optics, acoustics or classical mechanics. A notable example is the Boltzmann gas of elastically colliding hard balls in a box in statistical mechanics [25, 28]. A second interesting example, which may also be reduced to the study of a billiard, is provided by a mechanical system consisting of a fixed number of point particles constrained to move with no friction on a line segment, bouncing off the segment ends and each other without loss of kinetic energy [29].

2 Planar Billiards

In this section we will restrict our attention to planar billiards, i.e. the special case when the billiard table P is a connected compact subset of \({\mathbb {R}}^2\) with piecewise smooth closed curve as boundary. Before proceeding, we note that the dynamics of a billiard flow is completely determined by the dynamics of a discrete time map – the billiard map \(\varPhi \). Indeed, the billiard flow may be seen as the suspension flow over such map. Very roughly, the billiard map gives the next impact point \(s'\in \partial P\) and angle of reflection \(\theta '\in (-\pi /2,\pi /2)\) as a function of the previous impact \((s,\theta )\in \partial P\times (-\pi /2,\pi /2)\). Notice that at a point where the boundary \(\partial P\) is not smooth, the billiard map may not be defined and its domain of definition is only a subset of \(\partial P\times (-\pi /2,\pi /2)\).

One of the most interesting features of billiard dynamics is that it exhibits a whole range of dynamical behaviours, from integrable to chaotic. Let us restrict our attention for the time being to the case of billiards with the standard elastic reflection law. Billiards in tables with smooth and strictly convex boundaries exhibit regular dynamics in some parts of the phase space. These are known as Birkhoff billiards. The corresponding billiard map is an area preserving twist map. Moreover, if the table is an ellipse, the billiard is integrable [4]. Indeed, Birkhoff’s conjecture states that elliptic tables provide the only example of integrable billiards among the class of Birkhoff billiards. In what concerns the opposite side of the regularity spectrum, chaotic behaviour may be found in hyperbolic billiards, i.e. billiards with non-zero Lyapunov exponents. Key examples of this family of billiards include Sinai’s table [26] and the Bunimovich stadium [6]. Both exhibit strong ergodic properties, but while the billiard map associated with Sinai’s table is uniformly hyperbolic, the one associated with Bunimovich stadium is non-uniformly hyperbolic. This difference appears in the speed of the decay of correlations: Sinai’s table has exponential decay of correlations, whereas the Bunimovich stadium has subexponential decay of correlations. These properties are due to dispersive effects caused by the boundary, formed by the disk and the square, in the case of Sinai’s table, and to the interplay between boundary segments, formed by the semi-circles and the rectangle, for the Bunimovich stadium. Other billiards with hyperbolic behaviour were discovered by Wojtkowski [30], Markarian [20] and Donnay [9]. There is an extensive literature in this topic, see e.g. [7, 8, 15] for further details.

We are particularly interested in the case when the billiard table is a polygon: a polygonal billiard. For the standard elastic reflection law, these billiards are never hyperbolic since their topological entropy vanishes and thus, their Lyapunov exponents are zero [12, 14]. Its dynamical properties depend heavily on the angles of the table. If all angles of the table are a rational multiple of \(\pi \), the polygonal billiard is called rational, otherwise it is called irrational. We provide next a quick overview of the main properties of polygonal billiards, but see the surveys [11–13, 27] for a rather complete overview of the topic.

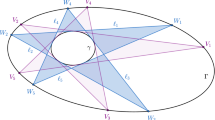
Rational billiards are reasonably well understood: any orbit has only a finite number of different angles of reflection and their dynamics can be viewed as the geodesic flow on a translation surface. Flat two-dimensional tori are the only translation surfaces of genus one and correspond to integrable billiard tables, the only ones being rectangles, equilateral triangles, right isosceles triangles and right triangles with an angle \(\pi /6\). If the translation surface has higher genus, then the phase space is foliated by invariant surfaces of genus higher than one. Moreover, Kerckhoff et al. [17] proved that the billiard flow on these translation surfaces is uniquely ergodic for almost all surfaces. Other properties worth mentioning include:

  1. (i)

    periodic orbits exist and are dense in the phase space [5, 10, 22];

  2. (ii)

    for all but countably many directions, all infinite semi-orbits are dense in configuration space, i.e. a rational polygonal billiard is minimal [16].

In what concerns the dynamical properties of irrational billiards, most of what is known is based on typical properties:

  1. (i)

    arbitrarily close to a given polygon there is an irrational polygon, with vertices as close as desired, whose billiard map is ergodic with respect to the standard invariant measure. More precisely, for every \(n\ge 3\), in the space of n-gons there is a dense \(G_\delta \)-subset of ergodic tables [17].

  2. (ii)

    the set of topologically transitive polygons is a dense \(G_\delta \)-subset of the space of n-gons [16].

  3. (iii)

    given an arbitrary polygon, any orbit on the corresponding billiard table is either periodic or its closure contains at least one vertex [14].

While rational billiards are never mixing and their periodic orbits forms a dense set in the phase space, it is not know whether irrational billiards can be mixing and have periodic orbits.

The dynamics of billiards with the standard elastic reflection law discussed so far is conservative, i.e. they admit an invariant measure that is absolutely continuous with respect to the phase space volume. Markarian, Pujals and Sambarino [21] studied a class of non-conservative billiards, which they call pinball billiards, with a non-elastic reflection law according to which the angle of reflection is a contraction of the angle of incidence. Under a set of mild assumptions, they proved that the billiard map associated with a large family of contractive reflection laws has dominated splitting, i.e. the tangent bundle splits into two invariant directions such that the growth rate along one direction dominates uniformly the growth rate along the other direction. A particular consequence of their result is that all pinball billiards on polygonal tables have dominated splitting. Further results for particular choices of billiard table shapes with a contractive reflection law were obtained for non-polygonal billiards [1, 2], the equilateral triangle billiard [3] and the square billiard [18].

3 Polygonal Billiards with a Contractive Reflection Law

We will now provide an overview of the setup considered in [19]. We consider planar polygonal billiard tables with a contractive general reflection law, that we will describe in a moment. Let P be a non self-intersecting n-gon, which we do not always assume to be convex. Denote by \(|\partial P|\) the length of \(\partial P\) and define M to be the subset of \(\mathbb {R}^2\) given by

$$M=(0,|\partial P|) \times \left( -\frac{\pi }{2},\frac{\pi }{2}\right) .$$

Let \(0 = \tilde{s}_{1}< \cdots< \tilde{s}_{n} < \tilde{s}_{n+1}= |\partial P|\) be the values of the arclength coordinate \(s\in (0,|\partial P|)\) corresponding to vertices of the polygon P. Denote by V the set

$$ V = \{\tilde{s}_{0},\ldots ,\tilde{s}_{n+1}\} \times \left( -\frac{\pi }{2},\frac{\pi }{2}\right) $$

and by \(S_1^+\) the closure of the set of all \(x_0\in M\) such that the billiard flow starting from \(x_0\) reaches a corner of P in its first collision with \(\partial P\). Finally, define the set \(N_1^+\) to be given by \(N_1^+= \partial M \cup V \cup S_1^+\) and for \( n \ge 1 \), define

$$ N^{+}_{n+1} = N^{+}_{n} \cup \varPhi ^{-1}_{f}(N^{+}_{n}) $$

and \( N^{+}_{\infty } = \bigcup _{n \ge 1} N^{+}_{n}\).

Denote by \( \bar{\varPhi } :M \setminus N^{+}_{1} \rightarrow M \) the billiard map on P with the standard elastic reflection law. The billiard map \(\varPhi \) is given by

$$ \bar{\varPhi }(x_{0}) = (s(x_{0}),\theta (x_{0})), $$

where \((s(x_{0}),\theta (x_{0}))\in M\) are, respectively, the coordinate of the first collision point with \(\partial P\) for an orbit of the billiard flow starting at \(x_0\in M\setminus N_1^+\) and the corresponding angle of reflection. To define a billiard map with a general reflection law, we note that a reflection law is simply given by a function \( f :(-\pi /2,\pi /2) \rightarrow (-\pi /2,\pi /2) \) and define \(R_f:M\rightarrow M\) to be the map given by

$$R_{f}(s,\theta )=(s,f(\theta )). $$

Then, the billiard map on P with the general reflection law f, \(\varPhi _{f}:M \setminus N^{+}_{1} \rightarrow M\), is given by

$$ \varPhi _{f} = R_{f} \circ \bar{\varPhi }.$$

We will consider a class of general reflection laws that are contractive in the sense that we now pass to explain. Let \(f :(-\pi /2,\pi /2) \rightarrow {\mathbb {R}}\) be a differentiable function and define

$$ \lambda (f) = \sup _{\theta \in (-\pi /2,\pi /2)} |f'(\theta )|. $$

For each \( k \ge 1 \), define \(\mathcal{R}^k_1\) to be the set of all \( C^{k} \) embeddings \( f:(-\pi /2,\pi /2) \rightarrow {\mathbb {R}}\) with \(f(0)=0\) and \(\lambda (f) < 1\). Note that if \(f \in \mathcal{R}^{k}_{1}\), then f is a strict contraction and \(\theta =0\) is its unique fixed point. Moreover, note that requiring f to be strictly increasing and such that \(f \in \mathcal{R}^{k}_{1}\) leads to a reflection law satisfying Condition A1b of [21]. The simplest example of such a reflection law is given by the family of linear reflection laws \(f(\theta ) = \sigma \theta \) with \(0< \sigma < 1\), previously studied in [2, 3, 18, 21].

A invariant set \( \varSigma \subset M \) is hyperbolic if there exist a non-trivial measurable splitting \( T_{\varSigma } M = E \oplus F \) and two measurable functions \( 0< \mu < 1 \) and \( A > 0 \) on \(\varSigma \) such that for all \( x \in \varSigma \) and \( n \ge 1\), we have

$$\begin{aligned} \begin{aligned} \Vert D\varPhi _f^{n}|_{E(x)}\Vert&\le A(x) \mu (x)^{n} \\ \Vert D\varPhi _f^{-n}|_{F(\varPhi _f^{n} x)}\Vert&\le A(x) \mu (x)^{n}. \end{aligned} \end{aligned}$$

If the functions \(\mu \) and A can be replaced by constants and the splitting is continuous, then \(\varSigma \) is called uniformly hyperbolic, otherwise it is called non-uniformly hyperbolic.

Let D be the set defined by

$$ D = \bigcap _{n \ge 0} \varPhi ^{n}_{f} (M \setminus N^{+}_{\infty }) $$

and note that every element of D has infinite positive and negative semi-orbits. Indeed, D is the largest invariant subset of M under \(\varPhi _f\). Following the terminology introduced by Pesin in [23], we call the set

$$ A=\overline{\bigcap _{n\ge 0}\varPhi _f^n(M \setminus N^{+}_{\infty })}, $$

the attractor of \(\varPhi _{f}\). If D is uniformly hyperbolic, then we say that the attractor A is hyperbolic.

We are now ready to provide an overview of the main results in [19]. These concern properties such as hyperbolicity of the invariant sets and the existence of hyperbolic attractors with finitely many ergodic SRB (Sinai-Ruelle-Bowen) measures for the class of billiards described above, i.e. billiards in polygonal tables P with contractive reflection laws \(f\in \mathcal{R}^k_1\), for \(k\ge 1\).

3.1 Hyperbolicity

In this section we will discuss hyperbolicity of the invariant sets of the billiard map \(\varPhi _f\). Markarian, Pujals and Sambarino proved in [21] that any invariant set \(\varSigma \) of \(\varPhi _f\) has dominated splitting. Their results hold for a large class of billiards, which includes the polygonal ones. Note that this is in striking contrast with what is observed for conservative polygonal billiards, which exhibit parabolic dynamics.

We start with the following simple characterization for the periodic orbits of the billiard map \(\varPhi _f\).

Proposition 1

The periodic points of \( \varPhi _f\) have the following properties:

  1. 1.

    every periodic point of period two is parabolic,

  2. 2.

    the set \( \mathcal{P}\) of all periodic points of period two of \( \varPhi _f\) is attracting,

  3. 3.

    every periodic point of period greater than two is hyperbolic.

From the previous result, we conclude that if a polygon has parallel sides, then its billiard map \(\varPhi _f\) has \(\mathcal{P}\) as an attracting set. However, even when \(\mathcal{P}\) is non-empty, uniformly hyperbolic invariant subsets \(\varSigma \) may exist.

Proposition 2

Suppose \( \varSigma \) is an invariant set with the property that there exists \( m>0 \) such that no positive semi-orbit of points in \(\varSigma \) contains sequences of consecutive collisions between parallel sides of P consisting of more than m collisions. Then \( \varSigma \) is uniformly hyperbolic.

We remark that the proposition above holds for every \(f \in \mathcal {R}^{k}_{1} \), thus improving a previous result by Markarian, Pujals and Sambarino, stating that for any convex polygon without parallel sides, the map \(\varPhi _{f}\) is hyperbolic as long as \( \lambda (f) \) is sufficiently close to zero [21, Corollary 4 and Theorem 23].

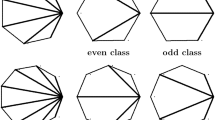
As a consequence of the proposition above, we obtain that any invariant subset of the billiard map \(\varPhi _f\) associated with any regular polygon with an odd number of sides is uniformly hyperbolic.

3.2 Existence of Hyperbolic Attractors with Finitely Many Ergodic SRB Measures

An invariant measure \(\mu \) for a diffeomorphism f on a manifold is SRB if \(\mu \) is hyperbolic and the conditional measures of \(\mu \) on unstable manifolds are absolutely continuous with respect to the Riemannian measures on these leaves. The relevance of SRB measures is due to the fact that ergodic SRB measures are physical.

In what follows, we will provide conditions for the existence of a hyperbolic attractor for \(\varPhi _f\) with finitely many ergodic SRB measures. This implies that the hyperbolic periodic points are dense. Our approach is based on the use of a general theorem, due to Pesin [23], providing conditions for the existence of countably many ergodic SRB measures for hyperbolic attractors of piecewise smooth maps. This result was later improved to a finite number of ergodic SRB measures by Sataev in [24]. It is known that the conditions of such theorem are satisfied for the Lorenz, generalized Lozi and Belykh families of maps.

Recall the definition of the set A given in the beginning of this section. The following result gives us a criterium for A to be a hyperbolic attractor for \(\varPhi _f\).

Proposition 3

A is a hyperbolic attractor if and only if the polygon does not have parallel sides facing each other.

Define the sequence of sets \(S_n^+\) through the recursion

$$S^{+}_{n+1} = S^{+}_{n} \cup \varPhi ^{-1}_{f}(S^{+}_{n}), \qquad n\ge 1. $$

Let \(p(S_n^+)\) be the maximum number of smooth components of \(S_n^+\) intersecting at one point. This quantity is well defined, since for any reflection law \(f \in \mathcal {R}^{k}_{1} \), \(S_n^+\) is a union of finitely many \(C^k\) curves. Moreover, for the particular case of a convex polygonal billiard, we have \(p(S_1^+)=2\), while for a non-convex polygonal billiard one must have \(p(S_1^+)\ge 2\). Let \(\alpha (\varPhi _f^n)\) denote the smallest expansion rate of the nth iterate of the billiard map along the unstable direction. Finally, denote by \(\mathcal{B}\) the subset of contractive \(C^2\) reflection laws f in \(\mathcal{R}_1^2\) such that f and its inverse \(f^{-1}\) have bounded second derivatives.

The following theorem provides us with a condition for a hyperbolic attractor of \(\varPhi _f\) to have finitely many ergodic SRB measures.

Theorem 1

Consider a polygon without parallel sides facing each other and suppose that \(f\in \mathcal{B}\). If there is \(m\ge 1\) such that

$$ p(S_m^+)<\alpha (\varPhi _f^m), $$

then A has finitely many ergodic SRB measures.

The existence of a hyperbolic attractor with finitely many ergodic SRB measures is indeed a robust property under small changes in the reflection law.

Theorem 2

Consider a polygon without parallel sides facing each other, \(f_0\in \mathcal{R}_1^1\) or \(f_0=0\), and

$$ n>\frac{\log p(S_1^+)}{\log \alpha (\varPhi _{f_0})} $$

such that

$$\begin{aligned} \varPhi _{f_0}^k(S_1^+)\cap S_1^+=\emptyset \quad \text {for}\quad 1\le k\le n-1. \end{aligned}$$

Then there is \(\delta >0\) such that for \(f\in \mathcal{B}\) satisfying \(\lambda (f-f_0)<\delta \), the billiard map \(\varPhi _f\) has a hyperbolic attractor with finitely many ergodic SRB measures.

The existence of a hyperbolic attractor with finitely many ergodic SRB measures is a generic property among the space of n-gons with strongly contractive reflection laws.

Theorem 3

There exists an open, dense and full measure subset of the space of n-gons such that for every polygon P in such set, there is \(\lambda _0>0\) such that if \(\lambda (f)<\lambda _0\) and \(f\in \mathcal{B}\), then \(\varPhi _f\) has a hyperbolic attractor with finitely many ergodic SRB measures.

3.3 Some Special Polygons

We will now specialize the results above concerning hyperbolicity and the existence of hyperbolic attractors with finitely many ergodic SRB measures to billiard tables with particular shapes.

We start by considering the case of regular polygons, for which we have obtained the following result.

Theorem 4

Consider a regular polygon with an odd number of sides. There is \(\lambda _0>0\) such that if \(\lambda (f)<\lambda _0\) and \(f\in \mathcal{B}\), then the billiard map \(\varPhi _f\) has a hyperbolic attractor with finitely many ergodic SRB measures.

The techniques used in the proof of the theorem above do not apply to the case of regular polygons with an even number of sides though. However, in this last case we are still able to provide a set of conditions on the reflection law f under which any invariant set not intersecting the attracting set \(\mathcal{P}\) is uniformly hyperbolic.

Proposition 4

Consider a regular polygon with an even number \(N\ge 6\) of sides and let \(f\in \mathcal{R}^k_1\) be an odd function such that \(f'>0\), \(\lambda (f)\le 1/2\) and \(f(\delta \frac{2\pi }{N})\le \delta f(\frac{2\pi }{N})\) for every \(0\le \delta \le 1\). Then there exists a positive constant C such that every orbit of \(\varPhi _f\) having more than C collisions between parallel sides belongs to the basin of attraction of \(\mathcal{P}\). In particular, every invariant set \( \varSigma \) of \( \varPhi _{f} \) not intersecting the basin of attraction of \( \mathcal{P}\) is uniformly hyperbolic.

We will now consider the case of acute triangles. Recall that a triangle is called acute if all its internal angles \(\phi _i\) are less than \(\pi /2\). The following theorem generalizes a result in [3] for equilateral triangles (\(\phi _i=\pi /3\)) and reflection laws of the form \(f(\theta )=\sigma \theta \) with \(\sigma <1/3\).

Theorem 5

For any acute triangle and \(f\in \mathcal{B}\) satisfying

$$ \lambda (f) < \frac{2}{\pi }\min _i\left( \frac{\pi }{2}-\phi _i\right) , $$

the billiard map \(\varPhi _f\) has a hyperbolic attractor with finitely many ergodic SRB measures.

Finally, we consider the case of rectangular billiard tables P. Note that in this case the attracting set \(\mathcal{P}\) is never empty. Despite this fact, we are still able to prove that every invariant set \(\varSigma \) not intersecting the basin of attraction of \(\mathcal{P}\) is hyperbolic.

Recall the definition of the set D given in the beginning of this section and note that \( D \setminus B(\mathcal {P}) \) is invariant. Indeed, \( D \setminus B(\mathcal {P}) \) is always hyperbolic, being uniformly hyperbolic if the hypothesis of Proposition 2 holds.

Proposition 5

The set \( D \setminus B(\mathcal {P}) \) is hyperbolic.

We note that the previous proposition holds also for polygonal tables that are finite unions of rectangles with sides parallel to two fixed orthogonal axes such as, for instance, L-shaped polygons.

It is possible to check that \( B(\mathcal {P}) = M \setminus N^{+}_{\infty } \) for every \( f \in \mathcal {R}^{k}_{1} \) with \( f'<0\). Therefore, we restrict ourselves to the case \(f'>0\) from now on. By rescaling P, we may assume without loss of generality that the sides of P have length 1 and \( 0 < h \le 1\). Define

$$ f_{1}(\theta ) = - f(\theta ) \quad \text {for } \theta \in [-\pi /2,\pi /2], $$

and

$$ f_{2}(\theta ) = f\left( {\text {sgn}}(\theta )\frac{\pi }{2}-\theta \right) \quad \text {for } \theta \in [-\pi /2,0) \cup (0,\pi /2]. $$

The geometrical meaning \( f_{1} \) and \( f_{2} \) is the following. If \( (s_{0},\theta _{0}) \) and \( (s_{1},\theta _{1}) \) are two consecutive collisions, then \( \theta _{1} = f_{1}(\theta _{0}) \) when the two collisions occur at parallel sides of P, and \( \theta _{1}= f_{2}(\theta _{0}) \) when the two collisions occur at adjacent sides of P.

From the properties of f, one can easily deduce that i) \( f_{2} \) is strictly decreasing, ii) the restriction of \( f_{2} \) to each interval \( (-\pi /2,0) \) and \( (0,\pi /2) \) is a strict contraction with Lipschitz constant less than \( \lambda (f) \), and iii) \( f_{2} \) has two fixed points \( \theta ^{-}< 0 < \theta ^{+}\).

Let \( \theta ^{-}_{*}< 0 <\theta ^{+}_{*} \) be the two solutions of

$$ \mathcal {F}(\theta ):=\sum ^{\infty }_{n=0} \tan \left( \left| f^{n}_{1}(\theta )\right| \right) = \frac{1}{h}, \quad \theta \in (-\pi /2,\pi /2) $$

and let \(\tilde{\theta }\) be the quantity given by

$$ \tilde{\theta } : = \min \left\{ f_{2}\left( f\left( \frac{\pi }{2}\right) \right) ,-f_{2}\left( f\left( -\frac{\pi }{2}\right) \right) \right\} . $$

Let T be the subset of \( M \setminus N^{+}_{\infty } \) consisting of elements whose positive semi-trajectory bounces between two parallel sides of the rectangle P. Note that T is a forward invariant set containing \( \mathcal{P}\).

Finally, let

$$ \hat{M} = M \setminus (T \cup N^{+}_{\infty }).$$

The set \( \hat{M} \) consists of elements with infinite positive semi-trajectory having at least a pair of consecutive collisions at adjacent sides of P.

We state below a sufficient condition for the existence of uniform hyperbolic invariant sets.

Proposition 6

Suppose that \( f'>0 \) and

$$\begin{aligned} \tilde{\theta } > \max \{-\theta ^{-}_{*},\theta ^{+}_{*}\} \nonumber \ . \end{aligned}$$

We have that

  1. 1.

    \( \hat{M} \) is a forward invariant set,

  2. 2.

    every invariant subset of \( \hat{M} \) is uniformly hyperbolic,

  3. 3.

    \( B(\mathcal {P}) = T\).

Finally, we give sufficient conditions for the basis of attraction of \(\mathcal{P}\) to be the whole set of points in M for which every iterate of \(\varPhi _f\) is well defined.

Proposition 7

Suppose that \( f'> 0 \) and

$$\begin{aligned}\begin{gathered} h \le \tan \tilde{\theta } \nonumber \\ f_{1}(\theta ^{+}_{*})< \theta ^{-} \quad \text {and} \quad \theta ^{+} < f_{1}(\theta ^{-}_{*}). \nonumber \end{gathered}\end{aligned}$$

Then \( B(\mathcal {P}) = M \setminus N^{+}_{\infty }\).