Keywords

1 Introduction

Time series classification is widely used in many domains such as medicine, finance, and science [1–4]. One nearest neighbor (1-NN) classifier with Dynamic Time Warping (DTW) distance function is one of the most popular time series classifiers that has been demonstrated to work extremely well and is difficult to beat [5]. Although 1-NN with DTW is quite effective, it still has the known weaknesses in its high computational time and its sensitivities to noises in the training set. Figure 1 illustrates a 2-class problem with six training data sequences, one of which contains noises (candidate sequence 3). When we want to classify a new sequence (with the real class B label), the 1-NN with DTW could wrongfully classify it to class A, as it matches the best to sequence 3 that is contaminated by noises.

Fig. 1.
figure 1figure 1

One-nearest neighbor classification with noisy training data

Full size image

To mitigate this problem, many approaches have been proposed, including Longest Common Subsequence (LCSS) [22] and variation of edit distances [23, 24]. However, they still suffer from high computational cost and difficulty in parameter selection. Some other researchers have proposed Support Vector Machine (SVM) that combined together the benefits of DTW by using DTW distance as the feature [6] to solve time series classification problems [7–9]. SVM is a powerful algorithm that can be applied in many domains because it builds a classifier from a hyperplane that separates features of input or exploits mapping of features into higher dimensional space through kernel function in non-linearly separable problems. It can also ignore some noisy data points that may lead to wrong classification. Recently, some research works have attempted to establish a kernel for DTW [7, 8] or have attempted to use other features together with DTW to increase the accuracy of SVM [9]. However, complexity and computational time for feature construction are still their weaknesses. In this work, we therefore mainly focus on reducing computational time, especially in the feature vector construction step, while being able to maintain high accuracies, comparing with the real DTW distance being used as a feature for SVM. Specifically, we take both the advantages of a lower bound function for DTW and robustness of SVM to build a faster yet accurate time series classifier.

The rest of the paper is organized as follows. The next section gives brief details on background and related works. Section 3 explains our proposed work with details on our experiment setup. Section 4 provides the experiment results and discussion, and the last section concludes our work.

2 Background and Related Works

In this section, we briefly give some details about Dynamic Time Warping (DTW), global constraint, Lower bound function for DTW, and Support Vector Machine (SVM).

2.1 Dynamic Time Warping (DTW)

Dynamic Time Warping (DTW) is a similarity measure for time series data that has gained its popularity over Euclidean distance metric due to its higher accuracy and more flexibility in non-linear alignments between two data sequences. Given two time series sequences, Q and C of length m and n, respectively, as follows.

$$ Q = \left\{ {q_{1} ,q_{2} ,q_{3} , \ldots , q_{i} , \ldots ,q_{m} } \right\} $$
(1)
$$ C = \left\{ {c_{1} ,c_{2} ,c_{3} , \ldots , c_{j} , \ldots ,c_{n} } \right\} $$
(2)

To align the two time series, an m by nmatrix is constructed to hold cumulative distances (γ(i th, j th)) between all pairs of data points from these two time series sequences. The cumulative distance in each cell is calculated from a sum of the distance of the current element, \( d\left( {q_{i} ,c_{j} } \right) = \left( {q_{i} - c_{j} } \right)^{2} \), and the minimum of the cumulative distance of the three adjacent elements:

$$ \gamma \left( {i,j} \right) = d\left( {q_{i} ,c_{j} } \right) + { \hbox{min} }\left\{ {\gamma \left( {i - 1,j} \right),\gamma \left( {i,j - 1} \right),\gamma \left( {i - 1,j - 1} \right)} \right\} $$
(3)

Dynamic programming is used to obtain optimal alignment and cumulative distance from the elements (1, 1) to \( \left( {m, n} \right) \). The optimal warping path is obtained by backtracking. However, in most time series mining tasks, we often are interested in only the distance value, contained in \( \left( {m, n} \right) \). So, backtracking can be omitted. The DTW distance is calculated by Eq. (4). Note that the squared root can also be omitted to speed up the calculation.

$$ DTW\left( {Q,C} \right) = \sqrt {\gamma \left( {q_{m} ,c_{n} } \right)} $$
(4)

2.2 Global Constraint

To improve the performance of DTW, a global constraint is often applied to prevent unreasonable warping, which in turn increases the accuracy. While any shapes and sizes of the global constraints can be utilized, Sakoe-Chiba Band [10] is one of the simplest global constraints [11] that restricts the warping path to stay within specific boundary (r), as shown in Fig. 2. Equation (3) with the Sakoe-Chiba constraint can be rewritten as follows:

Fig. 2.
figure 2figure 2

The Sakoe-Chiba band restricts the warping path to stay within the boundary.

Full size image
$$ {\gamma \left( {i, j} \right) = d\left( {q_{i} , c_{j} } \right) + { \hbox{min} } \left\{ {\gamma \left( {i - 1, j} \right), \gamma \left( {i, j - 1} \right), \gamma \left( {i - 1, j - 1} \right)} \right\};\,i + r \ge j\,and\,i - r \le j} $$
(5)

2.3 Lower Bound of DTW

Due to its O(n 2) time complexity, DTW is considered too expensive for large time series data. In the past decade, various lower bound functions for DTW have been proposed to speed up the DTW calculation for data mining tasks [12–14]. The main idea of lower bound function is to approximate the real DTW distance with the crucial property that the computed lower bound will never exceed the real DTW distance. Such property will allow us to skip many expensive DTW calculations when the lower bound value is greater than the best-so-far distance. Regardless of many well proposed lower bounds [25, 26], we consider LB_Keogh [14] in this work due to its simplicity and tightness of the bound. However, LB_Keogh requires a DTW global constraint (r) to construct an upper (U) and lower (L) envelopes around any sequence Q, as follows:

$$ U_{i} = max\left( {q_{i - r}\,:\,q_{i + r} } \right) $$
(6)
$$ L_{i} = min\left( {q_{i - r}\,:\,q_{i + r} } \right) $$
(7)

Once the envelope is constructed, the lower bound value between a sequence C and the envelope is computed using Eq. (8). Any part of the sequence beyond the envelope (above or below) will be included as part of the lower bound, as shown in Fig. 3.

Fig. 3.
figure 3figure 3

An illustration of the upper and lower envelope in LB_Keogh function. The lower bound value is computed by the sum of the squared distance between the upper or lower envelope and the sequence C that are outside the envelope area.

Full size image
$$ LB\_Keogh\left( {Q,C} \right) = \mathop \sum \limits_{i = 1}^{n} \left\{ {\begin{array}{*{20}c} {\left( {U_{i} - c_{i} } \right)^{2} if\,c_{i} > U_{i} } \\ {\left( {L_{i} - c_{i} } \right)^{2} if\,c_{i} < L_{i} } \\ {0 otherwise} \\ \end{array} } \right. $$
(8)

2.4 Support Vector Machine (SVM)

SVM is a powerful classification algorithm that has been applied to a variety of problems and domains, including finance and medicine [15, 16]. SVM is based on the idea of constructing a hyperplane to separate the data that may be mapped to higher dimensional feature space using a kernel function. In the other words, if the data can be linearly separated, a hyperplane is constructed from input data, which gives a maximum margin called support vector as shown in Fig. 4. Otherwise, a kernel function is applied to map the input space into higher dimensional feature space that can be linearly separated by a hyperplane [17] as shown in Fig. 5.

Fig. 4.
figure 4figure 4

Support vector machine with linearly separable data.

Full size image
Fig. 5.
figure 5figure 5

Support vector machine uses a kernel function to map non-linearly separable data from input space into higher dimensional space that can be separated by a hyperplane.

Full size image

2.5 Related Works

Some works have used DTW distance as an SVM’s feature for time series classification problem [7–9]. Gudmundsson, S. et al. used DTW as a feature and concentrated on designing a complex SVM kernel so called ppfSVM [8], but the results turned out that it still could not beat 1-NN with DTW even though their SVM achieved better results over other existing SVM approaches. Most recently, Kate, R. J. found that employing a simple polynomial kernel function is sufficient with no need to design a complex kernel function [9]. Together with the use of other features such as Symbolic Aggregate approximation (SAX) [18], Euclidean distance, and DTW with global constraint, the results have showed to even outperform 1-NN using DTW with global constraint. However, regardless of its winning performance on accuracies, the time complexity is still its drawback. Therefore, this motivates us to aim at building a faster time series classifier while maintaining its robustness in achieving high classification accuracies.

3 Proposed Work and Experiment Setup

In this section, we provide details of our proposed work, which creates features based on LB_Keogh values that will be used in SVM classifier. Then, we also provide information about datasets and tools used in the experiments.

3.1 LB_Keogh Feature Construction

As discussed in Sect. 2.5, instead of using DTW with global constraint distance as a feature, which is extremely expensive, LB_Keogh with a global constraint is used to construct the feature. For each training data sequence, LB_Keogh feature vector is constructed by computing lower bound values from that data sequence to every single sequence in the training set. Testing is done very similarly; LB_Keogh feature vector is obtained from computing lower bound values from each of the test data to every training data sequence. More concretely, given a training dataset C with k time series sequences, a feature vector of any sequence Q that will be used in a classifier is defined as follows.

$$ {LB\_Keogh\_Feature\left( Q \right) = \left\{ {LB\_Keogh\left( {Q,C_{1} } \right), LB\_Keogh\left( {Q,C_{2} } \right), \ldots ,LB\_Keogh\left( {Q,C_{k} } \right)} \right\}} $$
(9)

3.2 Making a Classifier

Once the LB_Keogh feature is obtained, LIBSVM [20] was used to build an SVM classifier with the following parameters: SVM type = C-SVC, Penalty parameter C = 1, and Kernel type = polynomial with coefficient and gamma = 1. We also perform 10-fold cross validation on each training set to determine the polynomial degree that fits the best to the problem. After the classifier is built for each dataset, its performance is tested using its corresponding unseen test data.

3.3 Datasets and Experiment Setup

In this work, we employ the whole 47 benchmark datasets from the UCR Time Series Classification Archive [19]. The information about the datasets (e.g., the number of classes, sequence length, train/test split) can be found on the archive. For each dataset, the DTW’s global constraint parameter r is set according to what is reported on the UCR Time Series Mining webpage [19]. The performance is evaluated by comparing classification error rates as well as the computational time in feature vector construction of our proposed work (LB_Keogh_Feature) with the state-of-the-art SVM classifier with DTW-R distance as the feature proposed by [9]. All of the experiments were carried out using Weka (v.3.6.12) software [21] on core i7-3770 3.40 GHz CPU with 16 GB of RAM.

4 Experiment Results and Discussion

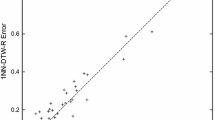
Figure 6 visually compares the classification error rates between our proposed SVM using LB_Keogh_Feature and the most recently proposed SVM using DTW-R_Feature. Note that the points above the diagonal line denote the datasets on which the rival method DTW-R_Feature performs better (with lower error rate), and the points below the diagonal line denote the datasets on which our proposed LB_Keogh_Feature performs better, achieving lower error rate. The red triangular points (7 out of 47 datasets) denote the discrepancies in the error rates that are statistically significant at 5 % level. We can see that the error rates between the two approaches are mostly very comparable, with the exception of the following six datasets, Cricket_Y, FaceAll, FacesUCR, Lighting2, OSULeaf, and Two_Patterns, where DTW-R_Feature is better, and one dataset, CinC_ECG_torso, where DTW-R_Feature is worse.

Fig. 6.
figure 6figure 6

A comparison between the classification error rates using our proposed LB_Keogh_Feature and the state-of-the-art DTW-R_Feature on all 47 datasets. The red triangular points indicate the discrepancies in the error rates that are statistically significant at 5 % level (Color figure online).

Full size image

LB_Keogh_Feature generally works very well on most datasets. However, we have looked into the feature vector of the six datasets where it performed statistically worse than DTW-R_Feature. In particular, for each dataset, we sum up all the feature vectors in the training data and compare between the feature vectors from our proposed LB_Keogh_Feature and the rival DTW-R_Feature. Figure 7 shows some snippets of the feature vectors in each class of three datasets, i.e., Car, Cricket_Y, and Lighting2; the blue lines represent the LB_Keogh_Feature, and the red lines represent the DTW-R_Feature. Note that both algorithms have the same error rate in Car dataset, as it shows very similar feature vectors, whereas DTW-R_Feature outperforms in the other two datasets. In the latter case, we can see that since the features from LB_Keogh are essentially lower bounds or approximation to the real DTW-R distance, the blue lines show that the LB_Keogh_Feature generally underestimates the distance, i.e., achieving not very tight lower bounds, which could in essence affect the classification accuracy.

Fig. 7.
figure 7figure 7

Some snippets of the sum of the feature vectors within each class of the three training data, comparing between those from our proposed LB_Keogh_Feature in blue and those from the rival DTW-R_Feature in red (Color figure online).

Full size image
Fig. 8.
figure 8figure 8

The speedups of our proposed LB_Keogh_Feature over the rival method on all 47 datasets

Full size image

The computational time in feature vector construction of both approaches are recorded. The speedups of our proposed LB_Keogh_Feature over the rival method are shown in Fig. 8. We can see that LB_Keogh_Feature vector is faster to be constructed in almost all datasets, except for 12 datasets whose global constraint values are zero (i.e., Euclidean distance is performed instead of DTW), where both approaches consume similar time complexity. The average speedup of all 47 datasets is 19.79 (26.24 speedup if 12 Euclidean datasets are excluded).

5 Conclusion

In this work, we propose a fast time series classification based on SVM that used LB_Keogh distance as a feature. The experiment results show that our proposed work can speed up the classification tasks by a large margin, while being able to maintain high accuracies, comparing with the state-of-the-art approach where the real DTW-R distance is used as a feature. It is also observed that our proposed feature can achieve comparable classification accuracies (little lower in some and little higher in some, with no statistical significance). However, in some datasets where the error rates drop down a little, statistically differing at 5 % significant level, good speedups on all the datasets are achieved, indicating the tradeoff between the classification accuracies and the running time it could save.