Keywords

1 Introduction

Deployable structure has the characteristics of small size, large space, which can be expanded into a preset contracted state and maintain a steady configuration. Therefore, it has a broad application prospects in the fields of aviation, aerospace, and construction. The scissor deployable structure in the paper is a kind of bar deployable structures, the scissor unit is the basic unit consisting of scissor deployable structures, which is connected by two links to form “X”-type structure through the hinge with the movement contraction function. The scissor hinge units can be composed of a variety of specific deployable forms using different ways, such as flat stretch arm, spherical grid system, and quadrilateral cross-sectional stretching arms.

In recent years, with the increasing of the competition of the international aerospace engineering, the demanding for dynamic behavior of deployable structures [1–3] in the motion process becomes more intense, the need to accurately predict the dynamics of deployable structures grows more urgent. Cambridge University Professor Pellegrino [4] together with the European Space Agency carried out the design and structure optimization of the two-dimensional and three-dimensional scissor structure as the basic unit consisting of deployable structure; Gantes [5, 6] completed the geometric design of the hemispherical deployable structures through symbols operation method and made sure the advantage of symbolic operation method in the geometric design of deployable structures; Langbecker [7] made an in-depth research on the motion characteristics and expanding conditions of deployable scissor-type mechanism and established a folding equations to analyze translation, cylindrical and the expanding process of ball deputy agencies; Oxford University Chen et al. [8] and Gan and Pellegrino [9] studied the bifurcation phenomenon in the kinematic analysis of deployable structures and thus may explain the emergence of mutations of hexagonal ring. Huang et al. [10, 11] carried out the simulation analysis of dynamics of the deployable structures with clearance after the expansion lock structure through clearance collision hinge model; Chen et al. [12] carried out structure design study for six prism unit deployable antenna; Ji et al. [13] analyzed and simulated the expanding process of the asymmetrical planar deployable structure, the expanding conditions of asymmetrical bodies were discussed, and the dynamics acceleration, velocity, and other physical quantities were carried out using the numerical simulation, but the impact of reaction force on institutions was not made a full discussion. In the engineering field, symmetry deployable structures can be applied to a broader field [14]; the symmetrical array deployable institutions were regarded as objects in the paper; Lagrange multipliers were used to build a dynamic model; the Baumgarte stabilization method was used to avoid numerical divergence; the dynamic characteristics of the reaction force, acceleration, and other physical dynamics during the expanding process of the deployable structures were made a thorough study, as opposed to asymmetrical bodies, which shows a specificity of symmetrical institutions during motion process.

2 Dynamics Model and Equations of Symmetrical Deployable Structures

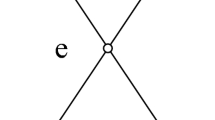
The scissor unit was arrayed along a straight line, and the adjacent units were connected by joints, the linear array combination deployable structures can be obtained, shown in Fig. 1. Scissor unit consists of two bars (d 1, d 2), which was connected by joint \( o_{3} \). A unit was made up with five nodes, including a hinge point and four endpoints which were equaled by hinged point.

Fig. 1
figure 1

Linear array deployable mechanism-based SLE

Full size image

2.1 Constraint Equation of Scissor Mechanism

Constraint equation is a prerequisite for dynamics analysis. Due to the symmetry of scissor mechanism, a detailed analysis of constraint equations for unit mechanism was in favor of considering the overall organization of the constraint equations. Figure 2 shows the plane mathematical model of any scissor unit. The bar ij and bar kl rely on hinge o to connect and transmit motion, achieving scalability. Due to the design needs, the distance between the endpoint of each rod and the hinge o can be changed.

Fig. 2
figure 2

Unit scissor hinge constraints

Full size image

According to the basic constraint equations between the rigid bodies, the constraint equation of any plane scissor unit can be established as follows:

$$ \varvec{\varPhi}_{\varvec{q}} = \frac{b}{a + b}x{}_{i} + \frac{a}{a + b}x_{j} - \frac{d}{c + d}x_{k} - \frac{c}{c + d}x_{l} = 0 $$
(1)

where a, b, c, d refer to the distance from endpoints i, j, k, l to the pin o.

The constraint equations of scissor units obtained can be assembled; then, the whole constraint equations of the mechanism can be obtained. For the unit symmetry deployable mechanism shown in Fig. 1, its constraint equation can be written as follows:

$$ \varvec{\varPhi}= \left[ \begin{aligned} \begin{array}{*{20}c} {x_{a} } \\ {y_{a} } \\ {y_{h} } \\ {x_{a} + x_{g} - x_{b} - x_{h} } \\ {y_{a} + y_{g} - y_{b} - y_{h} } \\ {x_{c} + x_{g} - x_{b} - x_{f} } \\ {y_{c} + y_{g} - y_{b} - y_{f} } \\ {x_{c} + x_{e} - x_{d} - x_{f} } \\ {y_{c} + y_{e} - y_{d} - y_{f} } \\ {(x_{a} - x_{g} )^{2} + (y_{a} - y_{g} )^{2} - l_{ag}^{2} } \\ {(x_{b} - x_{h} )^{2} + (y_{b} - y_{h} )^{2} - l_{bh}^{2} } \\ {(x_{b} - x_{f} )^{2} + (y_{b} - y_{f} )^{2} - l_{bf}^{2} } \\ {(x_{c} - x_{g} )^{2} + (y_{c} - y_{g} )^{2} - l_{cg}^{2} } \\ {(x_{c} - x_{e} )^{2} + (y_{c} - y_{e} )^{2} - l_{ce}^{2} } \\ \end{array} \hfill \\ (x_{d} - x_{f} )^{2} + (y_{d} - y_{f} )^{2} - l_{df}^{2} \hfill \\ \end{aligned} \right] = 0 $$
(2)

the constraint Eq. (2) can be represented as a matrix form.

$$ \varvec{\varPhi}(\varvec{q},t) = \left[ {\begin{array}{*{20}c} {\varvec{\varPhi}_{{\mathbf{1}}} (\varvec{q},t)} & {\varvec{\varPhi}_{{\mathbf{2}}} (\varvec{q},t)} & \cdots & {\varvec{\varPhi}_{{\mathbf{i}}} (\varvec{q},t)} \\ \end{array} } \right]^{\text{T}} = 0\quad i = 15 $$
(3)

2.2 Dynamic Equation of Scissor Mechanism

The speed and acceleration equation of the system can be obtained after the constraint equations were calculated first- and second-order derivative:

$$ \dot{\phi} (q,\dot{q} ,t) = \phi_{q} (q,t)\dot{q} + \phi_{t} (q,t) = 0 $$
(4)
$$ \ddot{\phi} (q,\dot{q} ,{\ddot q} ,t) = \phi_{q} (q,t){\ddot q} + (\phi_{q} \dot{q} )_{q} \dot{q} + 2\phi_{qt} \dot{q} + \phi_{tt} = 0 $$
(5)

where \( \varvec{\varPhi}_{\varvec{q}} (\varvec{q,t}) \) is the Jacobian matrix order:

$$ \eta = - (\phi_{q} \dot{q} )_{q} - 2\phi_{qt} \dot{q} -\phi_{tt} $$
(6)

Then, Eq. (5) can be converted to

$$ \ddot{\phi} (q,\dot{q} ,{\ddot q} ,t) = \phi_{q} (q,t){\ddot q} - \eta = 0 $$
(7)

Mass matrix of the scissor mechanism in Fig. 1 can be assembled as follows:

$$ \varvec{M} = \frac{\rho Al}{6}\left[ {\begin{array}{*{20}c} {2{\varvec{I}}_{2} } & {{\varvec{I}}_{2} } \\ {{\varvec{I}}_{2} } & {2{\varvec{I}}_{2} } \\ \end{array} } \right] $$
(8)

where \( \rho \), A, l, respectively, represent rod density, cross-sectional area and unit rod length, \( {\mathbf{\rm I}}_{2} \) is the 2 × 2 unit matrix.

The scissor mechanism variation equation can be obtained according to Newton’s law:

$$ \delta q^{T} (M{\ddot q} - Q) = 0 $$
(9)

where M, Q stand mass matrix and generalized force matrix respectively.

The variation equations can be obtained from constraint equations:

$$ \varvec{\varPhi}_{\varvec{q}} \delta q = 0 $$
(10)

The Lagrange motion differential equations can be obtained through arranging formula (9) and (10):

$$ M{\ddot q} + \phi_{Q}^{T} \lambda = Q $$
(11)

where \( \lambda \) is the Lagrange multiplier.

The Lagrange augmented matrix can be combined with motion differential equations and acceleration constraint equations:

$$ \left[ {\begin{array}{*{20}c} M & {\phi_{Q}^{T} } \\ {\phi_{q} } & 0 \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {\ddot q} \\ \lambda \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} Q \\ \eta \\ \end{array} } \right] $$
(12)

Formula (12) only introduced an acceleration constraint equation, the velocity, and position obtained will not necessarily meet the position constraint equations and velocity constraint equations; the constraint violation phenomenon would occur during the solving process. To avoid the constraint violation problem, this paper used a constraint violation stabilization method Baumgarte [15] proposed, namely the correction factors were introduced to correct the system

$$ \phi {\ddot q} - \eta - 2\alpha \dot{\phi} - \beta^{2} \phi = 0 $$
(13)

where \( \eta \) is acceleration right item which includes velocity, displacement, time. \( \alpha \) and \( \beta \) are the correction coefficient greater than 0, usually it would have a good stability when \( \alpha \) and \( \beta \) equal each other. \( \alpha \) and \( \beta \) are taken as 5 in the paper during the process of simulation and calculation.

Stable dynamics equation can be obtained after constraint correction:

$$ \left[ {\begin{array}{*{20}c} M & {\phi_{q}^{T} } \\ {\phi_{q} } & 0 \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {\ddot q} \\ \lambda \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} Q \\ {\eta - 2\alpha \dot{\phi} - \beta^{2} \phi } \\ \end{array} } \right] $$
(14)

Although the correction coefficient introduced which destroyed the initial dynamics equation of the system has some influence on acceleration time history, it has small impact on coordinate time history and avoiding the divergence of the results in a large part. Meanwhile, the stability of the equation even can reach about 75 % when \( \alpha \) and \( \beta \) are equal.

3 Numerical Simulation of Scissor Array Symmetrical Deployable Mechanisms

According to the geometric model shown in Fig. 1, each bar is in uniform quality, density \( \rho = 2840\;{\text{kg}}/{\text{m}}^{3} \), each bar length is \( l = 2\;{\text{m}} \), the expansion rod cross section is rectangular, the cross-sectional width is \( b = 0.02\;{\text{m}} \), height is \( h = 0.05\;{\text{m}} \), the axial force \( F = - 50\;{\text{N}} \) was applied to point H. The initial values \( \dot{q}(t_{0} ) \) and \( q(t_{0} ) \) have been known at the initial time, the integration step is taken as 0.02 s, and the constraint force of the scissor deployable mechanism can be obtained according to \( R = - {\varvec{\Phi}}_{q}^{\text{T}} \lambda \). Also, the multi-step Runge–Kutta method was used to solve the kinetic equation, the changing curve of displacement, velocity, acceleration, and reaction forces of endpoint of each rod for the scissor array deployable structures with time can be obtained during deploying process, which is shown in Figs. 3, 4, 5, and 6.

Fig. 3
figure 3

Changing curve of the node displacement with time

Full size image
Fig. 4
figure 4

Changing curve of the node velocity with time

Full size image
Fig. 5
figure 5

Changing curve of the node acceleration with time

Full size image
Fig. 6
figure 6

Changing curve of the node constraint force with time

Full size image

It can be concluded from all the figures shown above that the movement of each node is very complex, but which presents the unique symmetry properties that the array structure owns during the expansion process that the freedom of y direction of endpoint H is constrained and the node H suffers the reverse force of x-axis. As shown in Figs. 3, 4, and 5 that the displacement, velocity, and acceleration of node A, B, C, D converge to 0 in the x direction during the kinematic process. The acceleration and velocity of node E, F, G, H along x direction are gradually increasing, the displacement of node approaches zero simultaneously. The displacement, velocity, and acceleration of node A, H, node B, G, node C, F, node D, E along the y-axis show the symmetry property. It is shown in three figures, when t = 0.8 s, the mechanism reached a critical state; after more than 0.8 s, the geometry properties of the scissor mechanism will be damaged. During the process of 0–0.8 s, velocity and displacement gradually increased with the changing of acceleration. The similar situation is shown in Fig. 6, and the movement of the mechanism will be damaged after the time beyond 0.8 s. At this moment, the constraint force of the corresponding node along the y-axis still maintained symmetry. Meanwhile, the symmetrical characteristic of each node in the x direction was not obvious since the force was along the x-axis.

4 Conclusions

  1. 1.

    As shown in Fig. 5, the change of the acceleration of node in x direction is relatively stable before 0.4 s and the acceleration increased rapidly after 0.4 s. In order to ensure the mechanism can slowly deploy, a reasonable strategy can be made according to Figs. 5 and 6;

  2. 2.

    During the deployment process of the scissor array deployable mechanism, the dynamics of the each node along x direction on the force side changed more obviously. However, the dynamics of x direction of the each node on the non-force side changed slightly, which was caused by constraints, and symmetry properties of the scissor mechanism;

  3. 3.

    It can be seen from the figures above that the scissor mechanism along y-axis has a uniform variation in displacement, velocity, acceleration, and force, which shows the symmetry of the scissor linear array deployable structure along y-axis is more obvious. Due to the impact of the external force in x-axis, the symmetry properties of the constraint force for the node in x direction do not turn out.