The Smaller (SALI) and the Generalized (GALI) Alignment Indices: Efficient Methods of Chaos Detection

Skokos, Charalampos (Haris); Manos, Thanos

doi:10.1007/978-3-662-48410-4_5

Charalampos (Haris) Skokos¹⁸ &
Thanos Manos^19,20,21

Part of the book series: Lecture Notes in Physics ((LNP,volume 915))

2626 Accesses
14 Citations

Abstract

We provide a concise presentation of the Smaller (SALI) and the Generalized Alignment Index (GALI) methods of chaos detection. These are efficient chaos indicators based on the evolution of two or more, initially distinct, deviation vectors from the studied orbit. After explaining the motivation behind the introduction of these indices, we sum up the behaviors they exhibit for regular and chaotic motion, as well as for stable and unstable periodic orbits, focusing mainly on finite-dimensional conservative systems: autonomous Hamiltonian models and symplectic maps. We emphasize the advantages of these methods in studying the global dynamics of a system, as well as their ability to identify regular motion on low dimensional tori. Finally we discuss several applications of these indices to problems originating from different scientific fields like celestial mechanics, galactic dynamics, accelerator physics and condensed matter physics.

The original version of this chapter was revised. An erratum to this chapter can be found at DOI 10.1007/978-3-662-48410-4_9

An erratum to this chapter can be found at http://dx.doi.org/10.1007/978-3-662-48410-4_9

Access provided by Autonomous University of Puebla. Download chapter PDF

Second-Order Chaos Indicators MEGNO2 and OMEGNO2: Theory

Article 08 February 2018

A multi-arc approach for chaotic orbit determination problems

Article 08 November 2018

Classifying orbits in the classical Hénon–Heiles Hamiltonian system

Article 31 October 2014

Keywords

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

5.1 Introduction and Basic Concepts

A fundamental aspect in studies of dynamical systems is the identification of chaotic behavior, both locally, i.e. in the neighborhood of individual orbits, and globally, i.e. for large samples of initial conditions. The most commonly used method to characterize chaos is the computation of the maximum Lyapunov exponent (mLE) $\lambda _{1}$. In general, Lyapunov exponents (LEs) are asymptotic measures characterizing the average rate of growth or shrinking of small perturbations to orbits of dynamical systems. They were introduced by Lyapunov [55] and they were applied to characterize chaotic motion by Oseledec in [70], where the Multiplicative Ergodic Theorem (which provided the theoretical basis for the numerical computation of the LEs) was stated and proved. For a recent review of the theory and the numerical evaluation of LEs the reader is referred to [81]. The numerical evaluation of the mLE was achieved in the late 1970s [11, 32, 69] and allowed the discrimination between regular and chaotic motion. This evaluation is performed through the time evolution of an infinitesimal perturbation of the orbit’s initial condition, which is described by a deviation vector from the orbit itself. The evolution of the deviation vector is governed by the so-called variational equations [32].

In practice, $\lambda _{1}$ is evaluated as the limit for $t \rightarrow \infty$ of the finite time maximum Lyapunov exponent

$$\displaystyle{ \varLambda _{1}(t) = \frac{1} {t}\ln \frac{\|\mathbf{w}(t)\|} {\|\mathbf{w}(0)\|}, }$$

(5.1)

where t denotes the time and $\|\mathbf{w}(0)\|$, $\|\mathbf{w}(t)\|$ are the Euclidean norms^{Footnote 1} of the deviation vector $\mathbf{w}$ at times t = 0 and t > 0 respectively. Thus

$$\displaystyle{ \lambda _{1} =\lim _{t\rightarrow \infty }\varLambda _{1}(t). }$$

(5.2)

The computation of the mLE was extensively used for studying chaos and it is still implemented nowadays for this purpose. Nevertheless, one of its major practical disadvantages is the slow convergence of the finite time Lyapunov exponent (5.1) to its limit value (5.2). Since $\varLambda _{1}(t)$ is influenced by the whole evolution of the deviation vector, the time needed for it to converge to $\lambda _{1}$ is not known a priori, and in many cases it may become extremely long. This delay can result in CPU-time expensive computations, especially when the study of many orbits is required for the global investigation of a system. In order to overcome this problem several other fast chaos detection techniques have been developed over the years; some of which are presented in this volume.

Throughout this chapter we consider finite-dimensional conservative dynamical systems and in particular, autonomous Hamiltonian models and symplectic maps (except from Sect. 5.4.3 where a time dependent Hamiltonian system is studied). In these systems regular motion occurs on the surface of a torus in the system’s phase space and is characterized by $\lambda _{1} = 0$. Any deviation vector $\mathbf{w}(0)$ from a regular orbit eventually falls on the tangent space of this torus and its norm will approximately grow linearly in time, i.e. eventually becoming proportional to t, $\|\mathbf{w}(t)\| \propto t$. Consequently, $\varLambda _{1}(t) \propto \ln t/t$, which practically means that $\varLambda _{1}(t)$ tends asymptotically to zero following the power law t ⁻¹ because the values of $\ln t$ change much slower than t as time grows (see for example [11, 26] and Sect. 5.3 of [81]). On the other hand, in the case of chaotic orbits the use of any initial deviation vector in (5.1) and (5.2) practically leads to the computation of the mLE $\lambda _{1}> 0$ because this vector eventually is stretched towards the direction associated to the mLE, assuming of course that $\lambda _{1}>\lambda _{2}$, with $\lambda _{2}$ being the second largest LE. We note here that, from the first numerical attempts to evaluate the mLE [11, 32] it became apparent that a random choice of the initial deviation vector $\mathbf{w}(0)$ leads with probability one to the computation of $\lambda _{1}$. This means that, the choice of $\mathbf{w}(0)$ does not affect the limiting value of $\varLambda _{1}(t)$, but only the initial phases of its evolution. This behavior introduces some difficulties when we want to evaluate the whole spectrum of LEs of chaotic orbits because any set of initially distinct deviation vectors eventually end up to vectors aligned along the direction defined by the mLE. It is worth-noting that even in cases where we could theoretically know the initial choice of deviation vectors which would lead to the evaluation of LEs other than the maximum one, the unavoidable numerical errors in the computational procedure will lead again to the computation of the mLE [15]. This problem was bypassed by the development of a procedure based on repeated orthonormalizations of the evolved deviation vectors [10, 12–15, 78, 95].

Although the eventual coincidence of distinct initial deviation vectors for chaotic orbits with $\lambda _{1}>\lambda _{2}$ was well-known from the early 1980s, this property was not directly used to identify chaos for about two decades until the introduction of the Smaller Alignment Index (SALI) method in [79]. In the 1990s some indirect consequences of the fact that two initially distinct deviation vectors eventually coincide for chaotic motion, while they will have different directions on the tangent space of the torus for regular ones, were used to determine the nature of orbits, but not the fact itself. In particular, in [91] the spectra of what was named the ‘stretching number’, i.e. the quantity

$$\displaystyle{ \alpha = \frac{\ln \left (\frac{\left \|\mathbf{w}(t+\varDelta t)\right \|} {\left \|\mathbf{w}(t)\right \|} \right )} {\varDelta t}, }$$

(5.3)

where Δ t is a small time step, were considered. The main outcome of that paper was that ‘the spectra for two different initial deviations are the same for chaotic orbits, but different for ordered orbits’, as was stated in the abstract of Voglis et al. [91]. This feature was later quantified in [92] by the introduction of a quantity measuring the ‘difference’ of two spectra, the so-called ‘spectral distance’. In [92] it was shown that this quantity attains constant, positive values for regular orbits, while it becomes zero for chaotic ones. It is worth noting that in [91] it was explained that the observed behavior of the two spectra was due to the fact that the deviation vectors eventually coincide for chaotic orbits, producing the same sequences of stretching numbers, while they remain different for regular ones resulting in different spectra of stretching numbers. Nevertheless, instead of directly checking the matching (or not) of the two deviation vectors the method developed in [91, 92] requires unnecessary, additional computations as it goes through the construction of the two spectra and the evaluation of their ‘distance’. Naturally, this procedure is influenced by the whole time evolution of the deviation vectors, which in turn results in the delay of the matching of the two spectra with respect to the matching of the two deviation vectors.

Apparently, the direct determination of the possible coincidence (or not) of the deviation vectors is a much faster and more efficient approach to reveal the regular or chaotic nature of orbits than the evaluation of the spectral distance, as it requires less computations (see [79] for a comparison between the two approaches). This observation led to the introduction in [79] of the SALI method which actually checks the possible coincidence of deviation vectors, while the later introduced Generalized Alignment Index (GALI) [84] extends this criterion to more deviation vectors. As we see in Sect. 5.3 this extension allows the correct characterization of chaotic orbits also in the case where the spectrum of the LEs is degenerate and the second, or even more, largest LEs are equal to $\lambda _{1}$.

In order to illustrate the behaviors of both the SALI and the GALI methods for regular and chaotic motion we use in this chapter some simple models of Hamiltonian systems and symplectic maps.

In particular, as a two degrees of freedom (2D) Hamiltonian model we consider the well-known Hénon-Heiles system [43], described by the Hamiltonian

$$\displaystyle{ H_{2} = \frac{1} {2}(p_{1}^{2} + p_{ 2}^{2}) + \frac{1} {2}(q_{1}^{2} + q_{ 2}^{2}) + q_{ 1}^{2}q_{ 2} -\frac{1} {3}q_{2}^{3}. }$$

(5.4)

We also consider the 3D Hamiltonian system

$$\displaystyle{ H_{3} =\sum _{ i=1}^{3} \frac{\omega _{i}} {2}(q_{i}^{2} + p_{ i}^{2}) + q_{ 1}^{2}q_{ 2} + q_{1}^{2}q_{ 3}, }$$

(5.5)

initially studied in [15, 32]. Note that ω _i in (5.5) are some constant coefficients. As a model of higher dimensions we use the ND Hamiltonian

$$\displaystyle{ H_{N} = \frac{1} {2}\sum _{i=1}^{N}p_{ i}^{2} +\sum _{ i=0}^{N}\left [\frac{1} {2}(q_{i+1} - q_{i})^{2} + \frac{1} {4}\beta (q_{i+1} - q_{i})^{4}\right ], }$$

(5.6)

which describes a chain of N particles with quadratic and quartic nearest neighbor interactions, known as the Fermi–Pasta–Ulam β model (FPU-β) [36], where $q_{0} = q_{N+1} = 0$. In all the above-mentioned ND Hamiltonian models, q _i, p _i, i = 1, 2, … N are respectively the generalized coordinates and the conjugate momenta defining the 2N-dimensional (2Nd) phase space of the system.

As a symplectic map model we consider in our presentation the 2M-dimensional (2Md) system of coupled standard maps studied in [51]

$$\displaystyle\begin{array}{rcl} \begin{array}{ccl} x'_{j}& =&x_{j} + y'_{j}\\ && \\ y'_{j} & =&y_{j} + \frac{K_{j}} {2\pi } \sin \left (2\pi x_{j}\right ) - \frac{\gamma } {2\pi }\left \{\sin \left [2\pi \left (x_{j+1} - x_{j}\right )\right ] +\sin \left [2\pi \left (x_{j-1} - x_{j}\right )\right ]\right \},\end{array} & &{}\end{array}$$

(5.7)

where j = 1, 2, …, M is the index of each standard map, K _j and γ are the model’s parameters and the prime (′) denotes the new values of the variables after one iteration of the map. We note that each variable is given modulo 1, i.e. 0 ≤ x _j < 1, 0 ≤ y _j < 1 and also that the conventions x ₀ = x _M and $x_{M+1} = x_{1}$ hold.

In order to make this chapter more focused and easier to read we decided not to present any analytical proofs for the various mathematical statements given in the text; we prefer to direct the reader to the publications where these proofs can be found. Nevertheless, we want to emphasize here that all the laws describing the behavior of the SALI and the GALI have been obtained theoretically and they are not numerical estimations or fits to numerical data. Indeed, these laws succeed to accurately reproduce the evolution of the indices in actual numerical simulations, some of which are presented in the following sections.

The chapter is organized as follows. In Sect. 5.2 the SALI method is presented and the behavior of the index for regular and chaotic orbits is discussed. Section 5.3 is devoted to the GALI method. After explaining the motivation that led to the introduction of the GALI, the definition of the index is given and its practical computation is discussed in Sect. 5.3.1. Then, in Sect. 5.3.2 the behavior of the index for regular and chaotic motion is presented and several example orbits of Hamiltonian systems and symplectic maps of various dimensions are used to illustrate these behaviors. The ability of the GALI to identify motion on low dimensional tori is presented in Sect. 5.3.3, while Sect. 5.3.4 is devoted to the behavior of the index for stable and unstable periodic orbits. In Sect. 5.4 several applications of the SALI and the GALI methods are presented. In particular, in Sect. 5.4.1 we explain how the SALI and the GALI can be used for understanding the global dynamics of a system, while specific applications of the indices to various dynamical models are briefly discussed in Sect. 5.4.2. The particular case of time dependent Hamiltonians is considered in Sect. 5.4.3. Finally, in Sect. 5.5 we summarize the advantages of the SALI and the GALI methods and briefly discuss some recent comparative studies of different chaos indicators.

5.2 The Smaller Alignment Index (SALI)

The idea behind the SALI’s introduction was the need for a simple, easily computed quantity which could clearly identify the possible alignment of two multidimensional vectors. As has been already explained, it was well-known that any two deviation vectors from a chaotic orbit with $\lambda _{1}>\lambda _{2}$ are stretched towards the direction defined by the mLE, eventually becoming aligned having the same or opposite directions. Thus, it would be quite helpful to devise a quantity which could clearly indicate this alignment.

Since we are only interested in the direction of the two deviation vectors and not in their actual size, we can normalize them before checking their alignment. This process also eliminates the problem of potential numerical overflow due to vectors’ growth in size, which appears especially in the case of chaotic orbits. So in practice, we let the two deviation vectors evolve under the system’s dynamics (according to the variational equations for Hamiltonian models, or the so-called tangent map for symplectic maps) normalizing them after a fixed number of evolution steps to a predefined norm value. For simplicity in our presentation we consider the usual Euclidean norm (denoted by $\|\,\cdot \,\|$) and renormalize the evolved vectors to unity.

In the case of chaotic orbits this procedure is schematically shown in Fig. 5.1 where the two initially distinct unit deviation vectors^{Footnote 2} $\hat{\mathbf{w}}_{1}(0)$, $\hat{\mathbf{w}}_{2}(0)$ converge to the same direction. We emphasize that Fig. 5.1 is just a schematic representation on the plane of the real deviation vectors which are objects evolving in multidimensional spaces. Since the mLE $\lambda _{1}> 0$ denotes the mean exponential rate of each vector’s stretching, they are elongated at some later time t > 0,^{Footnote 3} becoming $\mathbf{w}_{1}(t)$, $\mathbf{w}_{2}(t)$, while the corresponding unit vectors are $\hat{\mathbf{w}}_{1}(t)$, $\hat{\mathbf{w}}_{2}(t)$. Then the diagonals of the parallelograms defined by $\hat{\mathbf{w}}_{1}(t)$, $\hat{\mathbf{w}}_{2}(t)$, both for t = 0 and t > 0, depict the sum and the difference of the two unit vectors.

In the particular case shown in Fig. 5.1 the two unit vectors tend to align by becoming equal. This means that $\|\hat{\mathbf{w}}_{1}(t) -\hat{\mathbf{ w}}_{2}(t)\| \rightarrow 0$ and $\|\hat{\mathbf{w}}_{1}(t) +\hat{\mathbf{ w}}_{2}(t)\| \rightarrow 2$. Of course the dynamics could have led the vectors to become opposite. In that case we get $\|\hat{\mathbf{w}}_{1}(t) -\hat{\mathbf{ w}}_{2}(t)\| \rightarrow 2$ and $\|\hat{\mathbf{w}}_{1}(t) +\hat{\mathbf{ w}}_{2}(t)\| \rightarrow 0$. Since we are not interested in the particular orientation of the deviation vectors, i.e. whether they become equal or opposite to each other, when we check their possible alignment, a rather natural choice is to define the minimum of norms $\|\hat{\mathbf{w}}_{1}(t) +\hat{\mathbf{ w}}_{2}(t)\|$, $\|\hat{\mathbf{w}}_{1}(t) -\hat{\mathbf{ w}}_{2}(t)\|$ as an indicator of the vectors’ alignment. This is the reason of the appellation, as well as of the definition of the SALI in [79] as

$$\displaystyle{ \mbox{ SALI}(t) =\min \left \{\|\hat{\mathbf{w}}_{1}(t) +\hat{\mathbf{ w}}_{2}(t)\|,\|\hat{\mathbf{w}}_{1}(t) -\hat{\mathbf{ w}}_{2}(t)\|\right \}, }$$

(5.8)

with $\hat{\mathbf{w}}_{i}(t) = \frac{\mathbf{w}_{i}(t)} {\|\mathbf{w}_{i}(t)\|}$, i = 1, 2 being unit vectors.

Naturally, in order for the SALI to be efficiently used as a chaos indicator it should exhibit distinct behaviors for chaotic and regular orbits. As explained before the SALI becomes zero for chaotic orbits. On the other hand, in the case of regular orbits deviation vectors fall on the tangent space of the torus on which the motion occurs, having in general different directions as there is no reason for them to be aligned [82, 91]. This behavior is shown schematically in Fig. 5.2. Thus, in this case the index should be always different from zero. In practice, the values of the SALI exhibit bounded fluctuations around some constant, positive number.

Thus, in order to compute the SALI we follow the evolution of two initially distinct, random, unit deviation vectors $\hat{\mathbf{w}}_{1}(0)$, $\hat{\mathbf{w}}_{2}(0)$. Choosing these vectors to be also orthogonal sets the initial SALI to its highest possible value (SALI$(0) = \sqrt{2}$) and ensures that they are considerably different from each other, which has proved to be a very good computational practice. Then, every t = τ time units we normalize the evolved vectors $\mathbf{w}_{1}(i\tau )$, $\mathbf{w}_{2}(i\tau )$, i = 1, 2, …, to $\hat{\mathbf{w}}_{1}(i\tau )$, $\hat{\mathbf{w}}_{2}(i\tau )$ and evaluate the SALI(i τ) from (5.8). This algorithm is described in pseudo-code in Table 5.1 of the Appendix. A MAPLE code for this algorithm, developed specifically for the Hénon-Heiles system (5.4) can be found in Chap. 5 of [20].

The completely different behaviors of the SALI for regular and chaotic orbits are clearly seen in Fig. 5.3,^{Footnote 4} where some representative results are shown for the 2D Hamiltonian system (5.4) and the 6d symplectic map

$$\displaystyle\begin{array}{rcl} \begin{array}{ccl} x'_{1} & =&x_{1} + y'_{1} \\ y'_{1} & =&y_{1} + \frac{K} {2\pi } \sin \left (2\pi x_{1}\right ) - \frac{\gamma } {2\pi }\left \{\sin \left [2\pi \left (x_{2} - x_{1}\right )\right ] +\sin \left [2\pi \left (x_{3} - x_{1}\right )\right ]\right \} \\ x'_{2} & =&x_{2} + y'_{2} \\ y'_{2} & =&y_{2} + \frac{K} {2\pi } \sin \left (2\pi x_{2}\right ) - \frac{\gamma } {2\pi }\left \{\sin \left [2\pi \left (x_{3} - x_{2}\right )\right ] +\sin \left [2\pi \left (x_{1} - x_{2}\right )\right ]\right \} \\ x'_{3} & =&x_{3} + y'_{3} \\ y'_{3} & =&y_{3} + \frac{K} {2\pi } \sin \left (2\pi x_{3}\right ) - \frac{\gamma } {2\pi }\left \{\sin \left [2\pi \left (x_{1} - x_{3}\right )\right ] +\sin \left [2\pi \left (x_{2} - x_{3}\right )\right ]\right \},\end{array} & &{}\end{array}$$

(5.9)

obtained by considering M = 3 coupled standard maps with $K_{1} = K_{2} = K_{3} = K$ in (5.7). From the results of Fig. 5.3 we see that for both systems the SALI of regular orbits (black, solid curves) remains practically constant and positive, i.e.

$$\displaystyle{ \mbox{ SALI} \propto \mbox{ constant}. }$$

(5.10)

On the other hand, the SALI of chaotic orbits (black, dashed curve in Fig. 5.3a and grey, solid curve in Fig. 5.3b) exhibits a fast decrease to zero after an initial transient time interval, reaching very small values around the computer’s accuracy (10⁻¹⁶). Actually, it was shown in [83] that the SALI tends to zero exponentially fast in such cases, following the law

$$\displaystyle{ \mbox{ SALI}(t) \propto \exp \left [-(\lambda _{1} -\lambda _{2})t\right ], }$$

(5.11)

where $\lambda _{1}$, $\lambda _{2}$ ($\lambda _{1} \geq \lambda _{2}$) are the first (i.e. the mLE) and the second largest LEs respectively. As an example demonstrating the validity of this exponential-decay law we plot in Fig. 5.4 the evolution of the SALI (solid curve) of the chaotic orbit of Fig. 5.3a using a linear horizontal axis for time t. Since for 2D Hamiltonian systems $\lambda _{2} = 0$, (5.11) becomes

$$\displaystyle{ \mbox{ SALI}(t) \propto \exp \left (-\lambda _{1}t\right ), }$$

(5.12)

For this particular orbit the mLE was found to be $\lambda _{1} \approx 0.047$ in [83]. From Fig. 5.4 we see that (5.12) with $\lambda _{1} = 0.047$ (dashed line) reproduces correctly the evolution of the SALI.^{Footnote 5}

Thus, the completely different behavior of the SALI for regular (5.10) and chaotic (5.11) orbits permits the clear and efficient distinction between the two cases. In [79, 83] a comparison of the SALI’s performance with respect to other chaos detection techniques was presented and the efficiency of the index was discussed. A main advantage of the SALI method is its ability to detect chaotic motion faster than other techniques which depend on the whole time evolution of deviation vectors, like the mLE and the spectral distance, because the SALI is determined by the current state of these vectors and is not influenced by their evolution history. Hence, the moment the two vectors are close enough to each other the SALI becomes practically zero and guarantees the chaotic nature of the orbit beyond any doubt. In addition, the evaluation of the SALI is simpler and more straightforward with respect to other methods that require more complicated computations. Such aspects were discussed in [83] where a comparison of the index with the Relative Lyapunov Indicator (RLI) [77] and the so-called ‘0–1’ test [39] was presented. Another crucial characteristic of the SALI is that it attains values in a given interval, namely SALI$(t) \in [0,\sqrt{2}]$, which does not change in time as is for example the case for the Fast Lyapunov Indicator (FLI) [37]. Thus, setting a realistic threshold value below which the SALI is considered to be practically zero (and the corresponding orbit is characterized as chaotic), allows the fast and accurate discrimination between regular and chaotic motion. Due to all these features the SALI became a reliable and widely used chaos indicator as its numerous applications to a variety of dynamical systems over the years prove. Some of these applications are discussed in Sect. 5.4.

5.3 The Generalized Alignment Index (GALI)

A fundamental difference between the SALI and other, commonly applied chaos indicators, is that it uses information from the evolution of two deviation vectors instead of just one. A consequence of this feature is the appearance of the two largest LEs in (5.11). After performing this first leap from using only one deviation vector, the question of going even further arises naturally. To formulate this in other words: why should we stop in using only two deviation vectors? Can we extend the definition of the SALI to include more deviation vectors? Assuming that this extension is possible, what will we gain from it? Will the use of more than two deviation vectors lead to the introduction of a new chaoticity index which will permit the acquisition of a deeper understanding of the system’s dynamics, exhibiting at the same time a better numerical performance than the SALI? For instance, from (5.11) we realize that in the case of a chaotic orbit with $\lambda _{1} \approx \lambda _{2}$ the convergence of the SALI to zero will be extremely slow. As a result long integrations would be required in order for the index to distinguish this orbit from a regular one for which the SALI remains practically constant. Although the existence of such chaotic orbits is not very probable the drawback of the SALI remains. An alternative way to state this problem is the following: can we construct a new index whose behavior in the case of chaotic orbits will depend on more LEs than the two largest ones so that it can overcome the discrimination problem for $\lambda _{1} \approx \lambda _{2}$?

Indeed, such an index can be constructed. The key point to its development is the observation that the SALI is closely related to the area of the parallelogram defined by the two deviation vectors.^{Footnote 6} From the schematic representation of the deviation vectors’ evolution in Fig. 5.1 we see that when the SALI vanishes one of the diagonals of the parallelogram also vanishes, and consequently its area becomes zero. The area A ₂ of a usual 2d parallelogram is equal to the norm of the exterior product of its two sides $\mathbf{v}_{1}$, $\mathbf{v}_{2}$, and also equal to the half of the product of its diagonals’ lengths

$$\displaystyle{ A_{2} =\|\mathbf{ v}_{1} \times \mathbf{ v}_{2}\| = \frac{\|\mathbf{v}_{1} +\mathbf{ v}_{2}\| \cdot \|\mathbf{ v}_{1} -\mathbf{ v}_{2}\|} {2}. }$$

(5.13)

In a similar way, the area A of the parallelogram of Fig. 5.1 is given by the generalization of the exterior product of vectors to higher dimensions, i.e. the so-called wedge product denoted by (∧),^{Footnote 7} so that

$$\displaystyle{ A =\|\hat{\mathbf{ w}}_{1} \wedge \hat{\mathbf{ w}}_{2}\| = \frac{\|\hat{\mathbf{w}}_{1} +\hat{\mathbf{ w}}_{2}\| \cdot \|\hat{\mathbf{ w}}_{1} -\hat{\mathbf{ w}}_{2}\|} {2}. }$$

(5.14)

Note the analogy of this equation to (5.13).^{Footnote 8}

Based on the fact that the SALI is related to the area of the parallelogram defined by two unit deviation vectors, the extension of the index to include more vectors is straightforward: the new quantity is defined as the volume of the parallelepiped formed by more than two deviation vectors. This volume is computed as the norm of the wedge product of these vectors. These arguments led to the introduction in [84] of the Generalized Alignment Index of order k (GALI_k) as

$$\displaystyle{ \mbox{ GALI}_{k}(t) =\|\hat{\mathbf{ w}}_{1}(t) \wedge \hat{\mathbf{ w}}_{2}(t) \wedge \ldots \wedge \hat{\mathbf{w}}_{k}(t)\|, }$$

(5.15)

where $\hat{\mathbf{w}}_{i}$ are unit vectors as in (5.8). In this definition the number of used deviation vectors should not exceed the dimension of the system’s phase space, because in this case the k vectors will become linearly dependent and the corresponding volume will be by definition zero, as is for example the area defined by two vectors having the same direction. Thus, for an ND Hamiltonian system with N ≥ 2 or a 2Nd symplectic map with N ≥ 1, we consider only GALIs with 2 ≤ k ≤ 2N.

By its definition the GALI_k is a quantity clearly indicating the linear dependence (GALI_k = 0) or independence (GALI_k > 0) of k deviation vectors. The SALI has the same discriminating ability as SALI = 0 indicates that the two vectors are aligned, i.e. they are linearly dependent, while SALI > 0 implies that the vectors are not aligned, which means that they are linearly independent. Actually, the connection between the two indices can be quantified explicitly. Indeed, it was proved in the Appendix B of [84] that

$$\displaystyle{ \mbox{ GALI}_{2} = \mbox{ SALI} \cdot \frac{\max \left \{\|\hat{\mathbf{w}}_{1}(t) +\hat{\mathbf{ w}}_{2}(t)\|,\|\hat{\mathbf{w}}_{1}(t) -\hat{\mathbf{ w}}_{2}(t)\|\right \}} {2}. }$$

(5.16)

Since the $\max \left \{\|\hat{\mathbf{w}}_{1}(t) +\hat{\mathbf{ w}}_{2}(t)\|,\|\hat{\mathbf{w}}_{1}(t) -\hat{\mathbf{ w}}_{2}(t)\|\right \}$ is a number in the interval $[\sqrt{2},2]$ we conclude that

$$\displaystyle{ \mbox{ GALI}_{2} \propto \mbox{ SALI}, }$$

(5.17)

which means that the GALI₂ is practically equivalent to the SALI. This is another evidence that the GALI definition (5.15) is a natural extension of the SALI for more than two deviation vectors.

5.3.1 Computation of the GALI

Let us discuss now how one can actually calculate the value of the GALI_k for an ND Hamiltonian system (N ≥ 2) or a 2Nd symplectic map (N ≥ 1). For this purpose we consider the k × 2N matrix

$$\displaystyle{ \mathbf{A}(t) = \left [\begin{array}{cccc} w_{11}(t) & w_{12}(t) &\cdots &w_{1\,2N}(t) \\ w_{21}(t) & w_{22}(t) &\cdots &w_{2\,2N}(t)\\ \vdots & \vdots & & \vdots \\ w_{k1}(t)&w_{k2}(t)&\cdots &w_{k\,2N}(t) \end{array} \right ] }$$

(5.18)

having as rows the 2N coordinates of the k unit deviation vectors $\hat{\mathbf{w}}_{i}(t)$ with respect to the usual orthonormal basis $\hat{\mathbf{e}}_{1} = (1,0,0,\ldots,0)$, $\hat{\mathbf{e}}_{2} = (0,1,0,\ldots,0)$, …, $\hat{\mathbf{e}}_{2N} = (0,0,0,\ldots,1)$. We note that the elements of A(t) satisfy the condition $\sum _{j=1}^{2N}w_{ij}^{2}(t) = 1$ for i = 1, 2, …, k as each deviation vector has unit norm.

We can now follow two routes for evaluating the GALI_k(t). According to the first one we compute the GALI_k by evaluating the norm of the wedge product of k vectors as

$$\displaystyle\begin{array}{rcl} \mbox{ GALI}_{k}(t) = \left \{\sum _{1\leq i_{1}<i_{2}<\cdots <i_{k}\leq 2N}\left (\det \left [\begin{array}{cccc} w_{1i_{1}}(t) & w_{1i_{2}}(t) &\cdots &w_{1i_{k}}(t) \\ w_{2i_{1}}(t) & w_{2i_{2}}(t) &\cdots &w_{2i_{k}}(t)\\ \vdots & \vdots & & \vdots \\ w_{ki_{1}}(t)&w_{ki_{2}}(t)&\cdots &w_{ki_{k}}(t) \end{array} \right ]\right )^{2}\right \}^{1/2},& &{}\end{array}$$

(5.19)

where the sum is performed over all the possible combinations of k indices out of 2N (a proof of this equation can be found in [84]). In practice this means that in our calculation we consider all the k × k determinants of A(t). Equation (5.19) is particularly useful for the theoretical description of the GALI’s behavior (actually expressions (5.22) and (5.23) below were obtained by using this equation), but not very efficient from a practical point of view. The reason is that the number of determinants appearing in (5.19) can increase enormously when N grows, leading to unfeasible numerical computations.

A simpler, straightforward and computationally more efficient approach to evaluate the GALI_k was developed in [85], where it was proved that the index is equal to the product of the singular values z _i, i = 1, 2, …, k of A ^T(t) (the transpose of matrix A(t)), i.e.

$$\displaystyle{ \mbox{ GALI}_{k}(t) =\prod _{ i=1}^{k}z_{ i}(t). }$$

(5.20)

We note that the singular values of A ^T(t) are obtained by performing the Singular Value Decomposition (SVD) procedure to A ^T(t). According to the SVD method (see for instance Sect. 2.6 of [74]) the 2N × k matrix A ^T is written as the product of a 2N × k column-orthogonal matrix U (U ^T ⋅ U = I _k, with I _k being the k × k unit matrix), a k × k diagonal matrix Z having as elements the positive or zero singular values z _i, i = 1, …, k, and the transpose of a k × k orthogonal matrix V (V ^T ⋅ V = I _k), i.e.

$$\displaystyle{ \mathbf{A}^{\mathrm{T}} = \mathbf{U} \cdot \mathbf{Z} \cdot \mathbf{V}^{\mathrm{T}}. }$$

(5.21)

In practice, in order to compute the GALI of order k we follow the evolution of k initially distinct, random, orthonormal deviation vectors $\hat{\mathbf{w}}_{1}(0)$, $\hat{\mathbf{w}}_{2}(0)$, …, $\hat{\mathbf{w}}_{k}(0)$. Similarly to the computation of the SALI, choosing orthonormal vectors ensures that all of them are sufficiently far from linear dependence and gives to the GALI_k its largest possible initial value GALI_k = 1. Afterwards, every t = τ time units we normalize the evolved vectors $\mathbf{w}_{1}(i\tau )$, $\mathbf{w}_{2}(i\tau )$, …, $\mathbf{w}_{k}(i\tau )$, i = 1, 2, …, to $\hat{\mathbf{w}}_{1}(i\tau )$, $\hat{\mathbf{w}}_{2}(i\tau )$, …, $\hat{\mathbf{w}}_{k}(i\tau )$ and set them as rows of a matrix A(i τ) (5.18). Then, according to (5.20) the GALI_k(i τ) is computed as the product of the singular values of matrix A ^T(i τ). This algorithm is described in pseudo-code in Table 5.2 of the Appendix. A MAPLE code computing all the possible GALIs (i.e. GALI₂, GALI₃ and GALI₄) for the 2D Hamiltonian (5.4) can be found in Chap. 5 of [20].

5.3.2 Behavior of the GALI for Chaotic and Regular Orbits

After defining the new index and explaining a practical way to evaluate it, let us discuss its ability to discriminate between chaotic and regular motion. As we have already mentioned, in the case of a chaotic orbit all deviation vectors eventually become aligned to the direction defined by the largest LE. Thus, they become linearly dependent and consequently the volume they define vanishes, meaning that the GALI_k, 2 ≤ k ≤ 2N, will become zero. Actually, in [84] it was shown analytically that in this case the GALI_k(t) decreases to zero exponentially fast with an exponent which depends on the k largest LEs as

$$\displaystyle{ \mbox{ GALI}_{k}(t) \propto \exp \left \{-\left [(\lambda _{1} -\lambda _{2}) + (\lambda _{1} -\lambda _{3}) + \cdots + (\lambda _{1} -\lambda _{k})\right ]t\right \}. }$$

(5.22)

Note that for k = 2 we get the exponential law (5.11) in agreement with the equivalence between the GALI₂ and the SALI (5.17).

Let us now consider the case of regular motion in a ND Hamiltonian system or a 2Nd symplectic map with N ≥ 2. In general, this motion occurs on an Nd torus in the system’s 2Nd phase space. As we discussed in Sect. 5.2, in this case any deviation vector eventually falls on the Nd tangent space of the torus (Fig. 5.2). Consequently, the k initially distinct, linearly independent deviation vectors we follow in order to compute the evolution of the GALI_k eventually fall on the Nd tangent space of the torus, without necessarily having the same directions. Thus, if we do not consider more deviation vectors than the dimension of the tangent space (k ≤ N) we end up with k linearly independent vectors on the torus’ tangent space and consequently the volume of the parallelepiped they define (i.e. the GALI_k) will be different from zero. As we see later on, numerical simulations show that in this case the GALI_k exhibits small fluctuations around some positive value. If, on the other hand, we consider more deviation vectors than the dimension of the tangent space (N < k ≤ 2N) the deviation vectors eventually become linearly dependent, as we end up with more vectors in the torus’ tangent space than the space’s dimension. Thus, the volume that these vectors define will vanish and the GALI_k will become zero. Specifically, in [84] it was shown analytically that in this case the GALI_k tends to zero following a power law whose exponent depends on the torus dimension and on the number k of deviation vectors considered, i.e. GALI$_{k} \propto t^{-2(k-N)}$. In summary the behavior of the GALI_k for regular orbits is

$$\displaystyle{ \mbox{ GALI}_{k}(t) \propto \left \{\begin{array}{ll} \mbox{ constant}&\mbox{ if $2 \leq k \leq N$ } \\ \frac{1} {t^{2(k-N)}} & \mbox{ if $N <k \leq 2N.$}\\ \end{array} \right. }$$

(5.23)

From this equation we see that $\mbox{ SALI} \propto \mbox{ GALI}_{2} \propto \mbox{ constant}$, in accordance to (5.10).

5.3.2.1 Some Illustrative Paradigms

In what follows we illustrate the different behaviors of the GALI_k by computing its evolution for some representative chaotic and regular orbits of various ND autonomous Hamiltonians and 2Nd symplectic maps. Before doing so let us note that for these systems the LEs comes in pairs of values having opposite signs

$$\displaystyle{ \lambda _{i} = -\lambda _{2N-i+1},\,\,\,\,i = 1,2,\ldots,N, }$$

(5.24)

while, moreover

$$\displaystyle{ \lambda _{N} =\lambda _{N+1} = 0 }$$

(5.25)

for Hamiltonian systems [14, 41, 81].

5.3.2.1.1 Hamiltonian Systems

Initially, we consider the 2D Hamiltonian (5.4) which has a 4d phase space. For this system we can define the GALI_k for k = 2, 3 and 4. Then, according to (5.24) and (5.25), the LEs satisfy the conditions $\lambda _{1} = -\lambda _{4}$, $\lambda _{2} =\lambda _{3} = 0$. Thus, according to (5.22) the evolution of the GALIs for a chaotic orbit is given by

$$\displaystyle{ \mbox{ GALI}_{2}(t) \propto e^{-\lambda _{1}t},\,\,\,\mbox{ GALI}_{ 3}(t) \propto e^{-2\lambda _{1}t},\,\,\,\mbox{ GALI}_{ 4}(t) \propto e^{-4\lambda _{1}t}. }$$

(5.26)

On the other hand, for a regular orbit (5.23) indicates that

$$\displaystyle{ \mbox{ GALI}_{2}(t) \propto \mbox{ constant},\,\,\,\mbox{ GALI}_{3}(t) \propto \frac{1} {t^{2}},\,\,\,\mbox{ GALI}_{4}(t) \propto \frac{1} {t^{4}}. }$$

(5.27)

From the results of Fig. 5.5, where the time evolution of the GALI₂, the GALI₃ and the GALI₄ for a chaotic orbit (actually the one considered in Figs. 5.3a and 5.4) and a regular orbit are plotted, we see that the laws (5.26) and (5.27) describe quite accurately the obtained numerical data.

For a 3D Hamiltonian like (5.5) the theoretical prediction (5.22) gives

$$\displaystyle{ \begin{array}{c} \mbox{ GALI}_{2}(t) \propto e^{-(\lambda _{1}-\lambda _{2})t},\,\,\,\mbox{ GALI}_{3}(t) \propto e^{-(2\lambda _{1}-\lambda _{2})t},\,\,\,\mbox{ GALI}_{4}(t) \propto e^{-(3\lambda _{1}-\lambda _{2})t}, \\ \mbox{ GALI}_{5}(t) \propto e^{-4\lambda _{1}t},\,\,\,\mbox{ GALI}_{6}(t) \propto e^{-6\lambda _{1}t},\end{array} }$$

(5.28)

for a chaotic orbit, because, according to (5.24) and (5.25), $\lambda _{1} = -\lambda _{6}$, $\lambda _{2} = -\lambda _{5}$ and $\lambda _{3} =\lambda _{4} = 0$. On the other hand, a regular orbit lies on a 3d torus and according to (5.23) the GALIs should behave as

$$\displaystyle{ \begin{array}{c} \mbox{ GALI}_{2}(t) \propto \mbox{ constant},\,\,\,\mbox{ GALI}_{3}(t) \propto \mbox{ constant},\,\,\,\mbox{ GALI}_{4}(t) \propto \frac{1} {t^{2}}, \\ \mbox{ GALI}_{5}(t) \propto \frac{1} {t^{4}},\,\,\,\mbox{ GALI}_{6}(t) \propto \frac{1} {t^{6}}. \end{array} }$$

(5.29)

In Fig. 5.6 we plot the time evolution of the various GALIs for a chaotic (Fig. 5.6a) and a regular (Fig. 5.6b) orbit of the 3D Hamiltonian (5.5). From the plotted results we see that the behaviors of the GALIs are very well approximated by (5.28) and (5.29). We note here that the constant values that the GALI₂ and the GALI₃ eventually attain in Fig. 5.6b are not the same. Actually, the limiting value of GALI₃ is smaller than the one of GALI₂.

As an example of evaluating the GALIs for multidimensional Hamiltonians we consider model (5.6) for N = 8 particles. This corresponds to an 8D Hamiltonian system H ₈, having a 16d phase space, which allows the definition of several GALIs: starting from GALI₂ up to GALI₁₆. In Fig. 5.7 the time evolution of several of these indices are shown for a chaotic (Fig. 5.7a, b) and a regular (Fig. 5.7c, d) orbit. From these results we again conclude that the laws (5.22) and (5.23) are quite accurate in describing the time evolution of the GALIs.

The first seven indices, GALI₂ up to GALI₈, exhibit completely different behaviors for chaotic and regular motion: they tend exponentially fast to zero for a chaotic orbit (Fig. 5.7a, b), while they attain constant, positive values for a regular one (Fig. 5.7c). This characteristic makes them ideal numerical tools for discriminating between the two cases, as we see in Sect. 5.4.1.1 where some specific numerical examples are discussed in detail.

Although the constancy of the GALI_k, k = 1, …, 8 for regular orbits is predicted from (5.23), nothing is yet said about the actual values of these constants. It is evident from Fig. 5.7c that these values decrease as the order k of the GALI_k increases, something which was also observed in Fig. 5.6b for the 3D Hamiltonian (5.5). For the regular orbit of Fig. 5.7c we see that GALI₈ ≈ 10⁻⁷. One might argue that this very small value could be considered to be practically zero and that the orbit might be (wrongly) classified as chaotic. The flaw in this argumentation is that the possible smallness of GALI₈ ≈ 10⁻⁷ is of relative nature as this value should be compared with the values that the index reaches for actual chaotic orbits. For instance, the chaotic orbit of Fig. 5.7b has GALI₈ ≈ 10⁻⁴⁰, after only t ≈ 160 time units! At the same time we get GALI₈ ≈ 10⁻¹ for the regular orbit (Fig. 5.7c). In addition, extrapolating the results of GALI₈ for the chaotic orbit in Fig. 5.7b to e.g. t ≈ 10⁵ we would obtain values extremely smaller than the value GALI₈ ≈ 10⁻⁷ archived for the regular orbit in Fig. 5.7c.

The necessity to determine an appropriate threshold value for the GALI_k, 2 ≤ k ≤ N, below which orbits will be securely classified as chaotic, becomes evident from the above analysis. Since a theoretical, or even an empirical (numerical) relation between the order k of the GALI_k and the constant value it reaches for regular orbits is still lacking, one efficient way to determine this threshold value is by computing the GALI_k for some representative chaotic and regular orbits of each studied system. Then, a safe policy is to define this threshold to be a few orders of magnitude smaller than the minimum value obtained by the GALI_k for the tested regular orbits. For example, based on the results of Fig. 5.6 for the 3D Hamiltonian (5.5) this threshold value for the GALI₃ could be set to be ≤ 10⁻⁸, while for the system of Fig. 5.7 a reliable threshold value for the GALI₈ could be ≤ 10⁻¹⁶.

The results of Fig. 5.7 verify the predictions of (5.22) and (5.23) that the GALIs of order 8 < k ≤ 16 tend to zero both for chaotic and regular orbits. Nevertheless, the completely different way they do so, i.e. they decay exponentially fast for chaotic orbits, while they follow a power law decay for regular ones, allows us again to develop a well-tailored strategy to discriminate between the two cases. The different decay laws result in enormous differences in the time the indices need to reach any predefined low value. Thus, the measurement of this time can be used to characterize the nature of the orbits, as we see in Sect. 5.4.1.2. For example, for the chaotic orbit of Fig. 5.7b GALI₁₆ ≈ 10⁻³⁰ after about t ≈ 25 time units, while it reaches the same small value after about t ≈ 10⁵ time units for the regular orbit of Fig. 5.7d; a time interval which is larger by a factor ≈ 4000 with respect to the chaotic orbit!

5.3.2.1.2 Symplectic Maps

Although up to now our discussion concerned the implementation of the GALIs to Hamiltonian systems, the indices follow laws (5.22) and (5.23) also for symplectic maps (with the obvious substitution of the continuous time t by a discrete one which counts the map’s iterations n) as the representative results of Figs. 5.8 and 5.9 clearly verify. In particular, in Fig. 5.8 we see the behavior of the GALIs for a chaotic (Fig. 5.8a) and a regular (Fig. 5.8b) orbit of the 4d map

$$\displaystyle{ \begin{array}{ccl} x'_{1} & =&x_{1} + y'_{1} \\ y'_{1} & =&y_{1} + \frac{K} {2\pi } \sin \left (2\pi x_{1}\right ) - \frac{\gamma } {2\pi }\sin \left [2\pi \left (x_{2} - x_{1}\right )\right ] \\ x'_{2} & =&x_{2} + y'_{2} \\ y'_{2} & =&y_{2} + \frac{K} {2\pi } \sin \left (2\pi x_{2}\right ) - \frac{\gamma } {2\pi }\sin \left [2\pi \left (x_{1} - x_{2}\right )\right ], \end{array} }$$

(5.30)

obtained from (5.7) for M = 2 and $K_{1} = K_{2} = K$, while in Fig. 5.9 a chaotic (Fig. 5.9a) and a regular (Fig. 5.9b) orbit of the 6d map (5.9) are considered.

These results illustrate the fact that the GALI_k has the same behavior for Hamiltonian flows and symplectic maps. For instance, even by simple inspection we conclude that the GALIs behave similarly in Figs. 5.5 and 5.8, which refer to a 2D Hamiltonian and a 4d map respectively, as well as in Figs. 5.6 and 5.9, which refer to a 3D Hamiltonian and a 4d map respectively.

5.3.2.2 The Case of 2d Maps

Equations (5.22) and (5.23) describe the behavior of the GALIs for ND Hamiltonian systems and 2Nd symplectic maps with N ≥ 2. What happens if N = 1? The case of an 1D, time independent Hamiltonian is not very interesting because such systems are integrable and chaos does not appear. But, this is not the case for 2d maps, which can exhibit chaotic behavior.

In 2d maps only the GALI₂ (which, according to (5.17) is equivalent to the SALI) is defined. For chaotic orbits the GALI₂ decreases exponentially to zero according to (5.22), which becomes

$$\displaystyle{ \mbox{ GALI}_{2}(n) \propto \mbox{ SALI}(n) \propto \exp \left (-2\lambda _{1}n\right ), }$$

(5.31)

in this particular case, since, according to (5.24) $\lambda _{1} = -\lambda _{2}> 0$. Note that in (5.31) we have substituted the continuous time t of (5.22) by the number n of map’s iterations. The agreement between the prediction (5.31) and actual, numerical data can be seen for example in Fig. 5.10a where the evolution of the SALI ($\propto \mbox{ GALI}_{2}$) is plotted for a chaotic orbit of the 2d standard map

$$\displaystyle{ \begin{array}{ccl} x'_{1} & =&x_{1} + y'_{1} \\ y'_{1} & =&y_{1} + \frac{K} {2\pi } \sin \left (2\pi x_{1}\right ),\end{array} }$$

(5.32)

obtained from (5.7) for M = 1. Thus, we conclude that (5.22) is also valid for 2d maps.

But what happens in the case of regular orbits? Is (5.23) still valid for k = 2 and N = 1? First of all let us note that for these particular values of k and N only the second branch of (5.23) is meaningful, and it provides the prediction that the GALI₂ tends to zero as n ⁻². This result is interesting, as this is the first case of regular motion for which no GALI remains constant. But actually the vanishing of the GALI₂ in this case is not surprising. Regular motion in 2d maps occurs on 1d invariant curves. So, any deviation vector from a regular orbit eventually falls on the tangent space of this curve, which of course has dimension 1. Thus, the two deviation vectors needed for the computation of the GALI₂ eventually becomes collinear and consequently GALI$_{2} \rightarrow 0$. Actually the prediction obtained by (5.23), that for regular orbits of 2d maps

$$\displaystyle{ \mbox{ GALI}_{2}(n) \propto \mbox{ SALI}(n) \propto \frac{1} {n^{2}}, }$$

(5.33)

is correct, as for example the results of Fig. 5.10b show.

In conclusion we note that the behavior of the SALI/GALI₂ for chaotic and regular orbits in 2d maps is respectively given by (5.31) and (5.33), which are obtained from (5.22) and (5.23) for k = 2 and N = 1. The different behaviors of the index for chaotic (exponential decay) and regular motion (power law decay) were initially observed in [79], although the exact functional laws (5.31) and (5.33) were derived later [83, 84]. As was pointed out even from the first paper on the SALI [79], these differences allow us to use the SALI/GALI₂ to distinguish between chaotic and regular motion also in 2d maps (see for instance [65, 79]).

5.3.3 Regular Motion on Low Dimensional Tori

An important feature of the GALIs is their ability to identify regular motion on low dimensional tori. In order to explain this capability let us assume that a regular orbit lies on an sd torus, 2 ≤ s ≤ N, in the 2Nd phase space on an ND Hamiltonian system or a 2Nd map with N ≥ 2. Then, following similar arguments to the ones made in Sect. 5.3.2 for regular motion on an Nd torus, we conclude that the GALI_k eventually remains constant for 2 ≤ k ≤ s, because in this case the k deviation vectors will remain linearly independent when they eventually fall on the sd tangent space of the torus. On the other hand, any s < k ≤ 2N deviation vectors eventually become linearly dependent as there will be more vectors on the torus’ tangent space than the space’s dimension, and consequently the GALI_k will vanish. In this case, the way the GALI_k tends to zero depends not only on k and N, as in (5.23), but also on the dimension s of the torus. Actually, it was shown analytically in [27, 85] that for regular orbits on an sd torus the GALI_k behaves as

$$\displaystyle{ \mbox{ GALI}_{k}(t) \propto \left \{\begin{array}{ll} \mbox{ constant}&\mbox{ if $2 \leq k \leq s$} \\ \frac{1} {t^{k-s}} & \mbox{ if $s <k \leq 2N - s$} \\ \frac{1} {t^{2(k-N)}} & \mbox{ if $2N - s <k \leq 2N.$}\\ \end{array} \right. }$$

(5.34)

It is worth noting that for s = N we retrieve (5.23) as the second branch of (5.34) becomes meaningless, while by setting k = 2, s = 1 and N = 1 we get (5.33).

The validity of (5.34) is supported by the results of Fig. 5.11 where two representative regular orbits of the H ₈ Hamiltonian, obtained by setting N = 8 in (5.6), are considered (we note that Fig. 5.7 refers to the same model). The first orbit (Fig. 5.11a, b) lies on a 2d torus as the constancy of only GALI₂ indicates. The decay of the remaining GALIs is well reproduced by the power laws (5.34) for N = 8 and s = 2. The second orbit (Fig. 5.11c, d) lies on a 4d torus and consequently the GALI₂, the GALI₃ and the GALI₄ remain constant, while all other indices follow power law decays according to (5.34) for N = 8 and s = 4.

In Fig. 5.12 we see the evolution of some GALIs for regular motion on low dimensional tori of the 40d map obtained by (5.7) for M = 20. The results of Fig. 5.12a denote that the orbit lies on a 3d torus in the 40d phase space of the map, while in the case of Fig. 5.12b the motion takes place on a 6d torus. The plotted straight lines help us verify that for both orbits the behaviors of the decaying GALIs are accurately reproduced by (5.34) for N = 20, s = 3 (Fig. 5.12a) and N = 20, s = 6 (Fig. 5.12b).

5.3.3.1 Searching for Regular Motion on Low Dimensional Tori

Equation (5.34), as well as the results of Figs. 5.11 and 5.12 imply that the GALIs can be also used for identifying regular motion on low dimensional tori. From (5.34) we deduce that the dimension of the torus on which the regular motion occurs coincides with the largest order k of the GALIs for which the GALI_k remains constant. Based on this remark we can develop a strategy for locating low dimensional tori in the phase space of a dynamical system. The GALI_k of initial conditions resulting in motion on an sd torus eventually will remain constant for 2 ≤ k ≤ s, while it will decay to zero following the power law (5.34) for k > s. So, after some relatively long time interval, all the GALIs of order k > s will have much smaller values than the ones of order k ≤ s. Thus, in order to identify the location of sd tori, 2 ≤ s ≤ N, in the 2Nd phase space of a dynamical system we evaluate at first various GALIs for several initial conditions and then find the initial conditions which result in large GALI_k values for k ≤ s and small values for k > s.

As was mentioned in Sect. 5.3.2.1, the constant, final values of the GALIs for regular motion decrease with the order of the GALI (see Figs. 5.6b, 5.7c, 5.9b, 5.11c and 5.12). Since this decrease has not been quantified yet, a good computational approach in the quest for low dimensional tori is to ‘normalize’ the values of the GALIs for each individual orbit by dividing them by the largest GALI_k value, $\max \left (\mbox{ GALI}_{k}\right )$, obtained by all orbits in the studied ensemble at the end time t = t _e of the integration. In this way we define the ‘normalized GALI_k’

$$\displaystyle{ g_{k}(t) = \frac{\mbox{ GALI}_{k}(t)} {\max \left [\mbox{ GALI}_{k}(t_{e})\right ]}. }$$

(5.35)

Then, by coloring each initial condition according to its g _k(t _e) value we can construct phase space charts where the position of low dimensional tori is easily located.

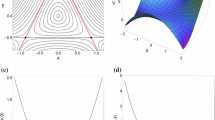
To illustrate this method we present (following [38]) the search for low dimensional tori in a subspace of the 8d phase space of the 4D Hamiltonian system H ₄ obtained by setting N = 4 and β = 1. 5 in (5.6). In order to facilitate the visualization of the whole procedure we restrict our search in the subspace (q ₃, q ₄) by setting the other initial conditions of the studied orbits to $q_{1} = q_{2} = 0.1$, $p_{1} = p_{2} = p_{3} = 0$, while p ₄ > 0 is evaluated so that H ₄ = 0. 010075. In Fig. 5.13 we color each permitted initial condition in the (q ₃, q ₄) plane according to its g ₂, g ₃ and g ₄ value at $t = t_{e} = 10^{6}$ time units (panels (a), (b) and (c) respectively).

For this particular Hamiltonian we can have regular motion on 2d, 3d and 4d tori. Let us see now how we can exploit the results of Fig. 5.13 to locate such tori. Motion on 2d tori results in large final g ₂ values and to small g ₃ and g ₄. So, such tori should be located in regions colored in yellow or light red in Fig. 5.13a and in black in Fig. 5.13b, c. A region which satisfies these requirements is located at the upper border of the colored areas in Fig. 5.13. The evolution of the GALIs of an orbit with initial conditions in that region (denoted by a triangle in Fig. 5.13) is shown in Fig. 5.14a and it verifies that the motion takes place on a 2d torus, as only the GALI₂ remains constant.

Extending the same argumentation to higher dimensions we see that motion on a 3d torus can occur in regions colored in yellow or light red in both Fig. 5.13a, b and in black in Fig. 5.13c. The initial condition of an orbit of this kind is marked by a small square in Fig. 5.13. The evolution of this orbit’s GALIs (Fig. 5.14b) verifies that the orbit lies on a 3d torus, because only the GALI₂ and the GALI₃ remain constant. Orbits on 4d tori is the most common situation of regular motion for this 4D Hamiltonian system. This is evident from the results of Fig. 5.13 because most of the permitted area of initial conditions correspond to high g ₂, g ₃ and g ₄ values. A randomly chosen initial condition in this region (marked by a circle in Fig. 5.13) results indeed to regular motion on a 4d torus as the constancy of its GALI_k, k = 2, 3, 4 in Fig. 5.14c clearly indicates.

We note that initial conditions leading to chaotic motion in this system would correspond to very small g ₂, g ₃ and g ₄ values (due to the exponential decay of the associated GALIs) and consequently would be colored in black in all panels of Fig. 5.13. The lack of such regions in Fig. 5.13 signifies that all considered initial conditions lead to regular motion. This happens because regions of chaotic motion occupy a tiny fraction of the system’s phase space, because its nonlinearity strength is very small. Therefore, chaotic motion is not captured by the grid of initial conditions of Fig. 5.13.

5.3.4 Behavior of the GALI for Periodic Orbits

Let us now discuss the behavior of the GALIs for periodic orbits of period T; i.e. orbits satisfying the condition $\mathbf{x}(t + T) =\mathbf{ x}(t)$, with $\mathbf{x}(t)$ being the coordinate vector in the system’s phase space. In the presentation of this topic we mainly follow the analysis performed in [67]. The linear stability of periodic orbits is defined by the eigenvalues of the so-called monodromy matrix, which is obtained by the solution of the variational equations (for Hamiltonian systems) or by the evolution of the tangent map (for symplectic maps) for one period T (see for example [22, 80] and Sect. 3.3 of [53]). When all eigenvalues lie on the unit circle in the complex plane the orbit is characterized as elliptic, while otherwise it is called hyperbolic (unstable). For a detailed presentation of the various stability types of periodic orbits the reader is referred for example to [22, 40, 44, 45, 80].

The presence of periodic orbits influence significantly the dynamics. In most systems we observe that the majority of non-periodic orbits in the vicinity of an elliptic one are regular. So, although initial conditions near an elliptic orbit can lead to chaos, regular orbits exhibiting a time evolution similar to the elliptic orbit itself prevail. If one assumes that the elliptic orbit is integrable and in its vicinity the Kolmogorov–Arnold–Moser (KAM) theorem (see for example Sect. 3.2 of [53] and references therein) can be applied (for which one needs to check a non-degeneracy condition which is typically satisfied), then there is large measure of orbits on KAM tori nearby. In Hamiltonian systems of dimension larger than 2 the phenomenon of Arnold diffusion (see for example Chap. 6 of [53] and references therein) typically would lead to an escape of orbits from the neighborhood of the elliptic orbit. However, it is generally believed that Arnold diffusion occurs on a slow time scale, and we do not expect interference with the GALI method. Of course, regular behavior on nearby KAM tori does not imply that the elliptic orbit itself is stable (e.g. Appendix of [34]). On the other hand, in chaotic Hamiltonian systems and symplectic maps orbits in the vicinity of an unstable periodic orbit typically behave chaotically and diverge from the periodic one exponentially fast. This divergence is characterized by LEs (with at least one of them being positive) which are determined by the eigenvalues of the monodromy matrix (e.g. [13, 84] and Sect. 5.2b of [53]). Thus, following arguments similar to the ones developed in Sect. 5.3.2 for chaotic orbits, we easily see that the GALI_k of unstable periodic orbits decreases to zero following the exponential law (5.22), i. e.

$$\displaystyle{ \mbox{ GALI}_{k}(t) \propto \exp \left \{-\left [(\lambda _{1} -\lambda _{2}) + (\lambda _{1} -\lambda _{3}) + \cdots + (\lambda _{1} -\lambda _{k})\right ]t\right \}, }$$

(5.36)

where $\lambda _{i}$, i = 1, …, k are the periodic orbit’s k largest LEs.

In Fig. 5.15a we see that the evolution of the GALIs for an unstable periodic orbit of the 2D Hamiltonian (5.4) is well approximated by (5.36) for $\lambda _{1} = 0.084$. This value is the orbit’s mLE determined by the eigenvalues of the corresponding monodromy matrix (see [67] for more details). We also note that according to (5.24) and (5.25) we set $\lambda _{1} = -\lambda _{4}$, and $\lambda _{2} =\lambda _{3} = 0$ in (5.36). The agreement between the numerical data and the theoretical prediction (5.36) is lost after about t ≈ 350 time units. This happens because the numerically computed orbit eventually deviates from the unstable periodic one due to unavoidable computational inaccuracies and enters the chaotic region around the periodic orbit. In general, this region is characterized by different LEs with respect to the ones of the periodic orbit. The effect of this behavior on the orbit’s finite time mLE $\varLambda _{1}$ (5.1) is seen in Fig. 5.15b. The computed $\varLambda _{1}$ deviates from the value $\lambda _{1} = 0.084$ (marked by a horizontal dotted line) at about the same time the GALI₂ changes its decreasing rate in Fig. 5.15a. Eventually, $\varLambda _{1}$ stabilizes at another positive value, which characterizes the chaoticity of the region around the periodic orbit.

On the other hand, the case of stable periodic orbits is a bit more complicated, because the GALIs behave differently for Hamiltonian flows and symplectic maps. In [67] it was shown analytically that for stable periodic orbits of ND Hamiltonian systems, with N ≥ 2, the GALIs decay to zero following the following power laws

$$\displaystyle{ \mbox{ GALI}_{k}(t) \propto \left \{\begin{array}{ll} \frac{1} {t^{k-1}} & \mbox{ if $2 \leq k \leq 2N - 1$} \\ \frac{1} {t^{2N}} & \mbox{ if $k = 2N.$}\\ \end{array} \right. }$$

(5.37)

We observe that this equation can be derived from (5.34), which describes the behavior of the GALIs for motion on an sd tori, by setting s = 1. We note that the first branch of (5.34) is meaningless for s = 1, while the other two branches take the forms appearing in (5.37). The connection between (5.34) and (5.37) is not surprising if we notice that a periodic orbit is nothing more than an 1d closed curve in the system’s phase space, having the some dimension with an 1d torus.

Small, random perturbations from the stable periodic orbit generally results in regular motion on an Nd torus. So, the GALIs of the perturbed orbit will follow (5.23). Thus, in general, the GALIs of regular orbits in the vicinity of a stable periodic orbit behave differently with respect to the indices of the periodic orbit itself (except from the GALI_2N and the GALI_2N−1, which respectively follow the laws $\propto t^{-2N}$ and $\propto t^{-(2N-2)}$ in both cases). The most profound change happens for the GALIs of order 2 ≤ k ≤ N because, according to (5.23), they remain constant in the neighborhood of the periodic orbit, while they decay to zero following the power law (5.37) for the periodic orbit.

The correctness of (5.37) becomes evident from the results of Fig. 5.16a, where the time evolution of the GALIs of a stable periodic orbit of the 2D Hamiltonian (5.4) is shown. In particular, we see that the indices decay to zero following the power laws GALI$_{2} \propto t^{-1}$, GALI$_{3} \propto t^{-2}$, GALI$_{4} \propto t^{-4}$ predicted from (5.37). According to (5.23) the GALIs of regular orbits in the neighborhood of the stable periodic orbit should behave as GALI$_{2} \propto \mbox{ constant}$, GALI$_{3} \propto t^{-2}$ and GALI$_{4} \propto t^{-4}$. Thus, only the GALI₂ is expected to behave differently for regular orbits in the vicinity of the periodic orbit of Fig. 5.16a. The results of Fig. 5.16b show that this is actually true. The GALI₂ of the neighboring regular orbits initially follows the same power law decay of the periodic orbit (GALI$_{2} \propto t^{-1}$), but later on it stabilizes to a constant positive value. We see that the further the orbit is located from the periodic one the sooner the GALI₂ deviates from the power law decay.

These differences of the GALI₂ values can be used to identify the location of stable periodic orbits in the system’s phase space, although the index was not developed for this particular purpose.^{Footnote 9} This becomes evident from the result of Fig. 5.17 where the values of the GALI₂ at t = 10⁵ for several orbits of the Hénon-Heiles system (5.4) are plotted as a function of the q ₂ coordinate of the orbits’ initial conditions. The remaining coordinates are $q_{1} = p_{2} = 0$, while p ₁ > 0 is set so that H ₂ = 0. 125. Actually these initial conditions lie on the symmetry line of the subspace defined by q ₁ = 0, p ₁ > 0, i.e. the horizontal line p ₂ = 0 in Figs. 5.19 and 5.20 below. This line passes through the initial condition of some periodic orbits of the system. For the construction of Fig. 5.17 we considered an ensemble of 7 000 orbits whose q ₂ coordinates are equally distributed in the interval − 0. 1 ≤ q ₂ ≤ 0. 6. The data points are line connected, so that the changes of the GALI₂ values become easily visible.

In Fig. 5.17 regions of relatively large GALI₂ values ($\gtrsim 10^{-4}$) correspond to regular (periodic or quasiperiodic) motion. Chaotic orbits and unstable periodic orbits have very small GALI₂ values ($\lesssim 10^{-12}$), while domains with intermediate values ($10^{-12} \lesssim \mbox{ GALI}_{2} \lesssim 10^{-4}$) correspond to sticky chaotic orbits. An interesting feature of Fig. 5.17 is the appearance of some relatively narrow regions where the GALI₂ decreases abruptly obtaining values $10^{-4} \lesssim \mbox{ GALI}_{2} \lesssim 10^{-1}$; the most profound one being in the vicinity of q ₂ ≈ 0. 3. These regions correspond to the immediate neighborhoods of stable periodic orbits, with the periodic orbit itself been located at the point with the smallest GALI₂ value.

The creation of these characteristic ‘pointy’ shapes is due to the behavior depicted in Fig. 5.16b: the GALI₂ has relatively small values on the stable periodic orbit, for which it decreases as $\propto t^{-1}$, while it attains constant, positive values for regular orbits in the vicinity of the periodic orbit. These constant values increase as the orbit’s initial conditions depart further away from the periodic orbit. So, more generally, the appearance of such ‘pointy’ formations in GALI_k plots (2 ≤ k ≤ N) provide good indications for the location of stable periodic orbits.

Let us now turn our attention to maps. In 2Nd symplectic maps stable periodic orbits of period l correspond to l distinct points (the so-called stable fixed points of order l). Any deviation vector from the periodic orbit rotates around each fixed point. This behavior can be easily seen in the case of 2d maps where the tori around a stable fixed point correspond to closed invariant curves which can be represented, through linearization, by ellipses (see for example Sect. 3.3b of [53]). Thus, any k initially distinct deviation vectors needed for the computation of the GALI_k will rotate around the fixed point keeping on average the angles between them constant. Consequently the volume of the parallelepiped they define, i.e. the value of the GALI_k, will remain practically constant. Thus, in the case of stable periodic orbits of 2Nd maps, with N ≥ 1 we have

$$\displaystyle{ \mbox{ GALI}_{k}(t) \propto \mbox{ constant},\,\,\,\,\mbox{ for $2 \leq k \leq 2N$}. }$$

(5.38)

This behavior is clearly seen in Fig. 5.18a where the evolution of the GALI₂, the GALI₃ and the GALI₄ for a stable periodic orbit of period 7 of the 4d map (5.30) is plotted.

Again small perturbations of the periodic orbit’s initial conditions generally result in motion on an Nd tori. Then, the evolution of the corresponding GALIs is provided by (5.23) for N ≥ 2, while the GALI₂ will decrease to zero according to (5.33) for 2d maps. So, the most striking difference between the behavior of the GALI_k of a stable periodic orbit and of a neighboring, regular orbit appears for k > N, because in this case the GALI_k remains constant for the periodic orbit, while it decays to zero for the neighboring one. Differences of this kind can be observed in Fig. 5.18b.

5.4 Applications

The ability of the SALI and the GALI methods to efficiently discriminate between chaotic and regular motion was described in detail in the previous sections, where some exemplary Hamiltonian systems and symplectic maps were considered. In what follows we present applications of this ability to various dynamical systems originating from different research fields.

5.4.1 Global Dynamics

In Sect. 5.3.2 we discussed how one can use the various GALIs to reveal the chaotic or regular nature of individual orbits in the 2Nd phase space of a dynamical system. Additionally, in Sect. 5.3.4 we saw how the measurement of the GALI₂ values for an ensemble of orbits can facilitate the uncovering of some dynamical properties of the studied system, in particular the pinpointing of stable periodic orbits (Fig. 5.17), while in Sect. 5.3.3.1 we described how a more general search can help us locate motion on low dimensional tori.

Now we see how one can use the GALIs in order to study the global dynamics of a system. For simplicity we use in our analysis the 2D Hamiltonian system (5.4), but the methods presented below can be (and actually have already been) implemented to higher-dimensional systems.

5.4.1.1 Investigating Global Dynamics by the GALI_k with 2 ≤ k ≤ N

According to (5.22) and (5.23) the GALI_k, with 2 ≤ k ≤ N, behaves in a completely different way for chaotic (exponential decay) and regular (remains practically constant) orbits. Thus, by coloring each initial condition of an ensemble of orbits according to its GALI_k value at the end of a fixed integration time we can produce color plots where regions of chaotic and regular motion are easily seen. In addition, by choosing an appropriate threshold value for the GALI_k, below which the orbit is characterized as chaotic (see Sect. 5.3.2.1 on how to set up this threshold), we can efficiently determine the ‘strength’ of chaos by calculating the percentage of chaotic orbits in the studied ensemble. Then, by performing the same analysis for different parameter values of the system we can determine its physical mechanisms that increase or suppress chaotic behavior.

A practical question arises though: which index should one use for this kind of analysis? The obvious advantage of the GALI₂/SALI is its easy computation according to (5.8), which requires the evolution of only two deviation vectors. On the other hand, evaluating the GALIs of order up to k = N is more CPU-time consuming as the computation of the index from (5.20) requires the evolution of more deviation vectors, as well as the implementation of the SVD algorithm. An advantage of these higher order indices is that they tend to zero faster than the GALI₂/SALI for chaotic orbits. So, reaching their threshold value which characterizes an orbit as chaotic, requires in general, less computational effort. This feature is particularly useful when we want to estimate the percentage of chaotic orbits, as there is no need to continue integrating orbits which have been characterized as chaotic (see Sect. 5.2 of [84] for an example of this kind). Thus, we conclude that the reasonable choices for such global studies are the GALI₂/SALI and the GALI_N.

In order to illustrate this process, let us consider the 2D Hénon-Heiles system (5.4), for which GALI_N ≡ GALI₂, since N = 2. In Fig. 5.19 we see color plots of its Poincaré surface of section defined by q ₁ = 0 (a concise description of the construction of a surface of section can be found for instance in Sect. 1.2b of [53]). The remaining initial conditions of each orbit are its coordinates on the (q ₂, p ₂) plane of Fig. 5.19, while p ₁ > 0 is set so that H ₂ = 0. 125. For each panel of Fig. 5.19 a 2d grid of approximately 350, 000 equally distributed initial conditions is considered. Each point on the (q ₂, p ₂) plane is colored according to its $\log (\mbox{ GALI}_{2})$ value at t = 2000, while white regions denote not permitted initial conditions. Regions colored in yellow or light red correspond to regular orbits, while dark blue and black domains contain chaotic ones. Intermediate colors at the borders between these two regions indicate sticky chaotic orbits.

This kind of color plots can reveal fine details of the underlying dynamics, like for example the small yellow ‘islands’ of regular motion inside the large, black chaotic ‘sea’, as well as allow the accurate estimation of the percentage of chaotic or regular orbits in the studied ensemble. Naturally the denser the used grid is, the finer the uncovered details become, but unfortunately the higher the needed computational effort gets. In an attempt to speed up the whole process the following procedure was followed in [3] where the dynamics of the Hénon-Heiles system (5.4) was studied. The final GALI₂/SALI value and the corresponding color was assigned not only to the initial condition of the studied orbit, but also to all intersection points of the orbit with the surface of section. This assignment can be extended even further by additionally taking into account the symmetry of Hamiltonian (5.4) with respect to the q ₂ variable, which results in structures symmetric with respect to the p ₂ = 0 axis in Fig. 5.19. Consequently, points symmetric to this axis should have the same GALI₂/SALI value. So, orbits with initial conditions on grid points to which a color has already been assigned, as they were intersection points with the surface of section of previously computed orbits, are not computed again and so the construction of color plots like the ones of Fig. 5.19 is speeded up significantly. In [3] it was shown that this approach achieves very accurate estimations of the percentages of chaotic orbits with respect to the ones obtaining by coloring each and every initial condition according to the index’s value at the end of the integration time (this is actually how Fig. 5.19 was produced).

Let us now discuss the differences between panels (a) and (b) of Fig. 5.19. In both figures the chaotic regions are practically the same. Nevertheless, in the yellow and light red colored domains, where regular motion occurs, some ‘spurious’ structures appear in Fig. 5.19a, which are not present in Fig. 5.19b. For example, inside the large stability island with $0 \lesssim q_{2} \lesssim 0.5$ at the right side of Fig. 5.19a we observe an almost horizontal formation colored in light red, while similar colored ‘arcs’ appear inside many other islands of regular motion. These artificial features emerge when one uses exactly the same set of orthonormal, initial deviation vectors for every studied orbit, as we did in Fig. 5.19a. The appearance of such features in color plots of other chaos detection methods has already been reported in the literature [9]. A simple way to avoid them is to use a different, random set of initial, orthonormal vectors for the computation of the GALI₂, as we did in Fig. 5.19b. By doing so, these spurious features disappear and only structures related to the actual dynamics of the system remain, like for instance the cyclical ‘chain’ of the light red colored, elongated regions inside the big stability island at the right side of Fig. 5.19b. This structure indicates the existence of some higher order stability islands, which are surrounded by an extremely thin chaotic layer. This layer is not visible for the resolution used in Fig. 5.19b. A magnification, and a much finer grid would reveal this tiny chaotic region.

5.4.1.2 Investigating Global Dynamics by the GALI_k with N < k ≤ 2N

As was clearly explained in Sect. 5.3.2.1 the GALIs of order N < k ≤ 2N tend to zero both for chaotic and regular orbits, but with very different time rates as (5.22) and (5.23) state. This deference can be also used to investigate global dynamics, but following an alternative approach to the one developed in Sect. 5.4.1.1. Since these GALIs decay to zero exponentially fast for chaotic orbits, but follow a much slower power law decay for regular ones, the time t _th they need to reach an appropriately chosen, small threshold value will be significantly different for the two kinds of orbits. We note that both the exponential and the power law decays become faster with increasing order k of GALI_k. Consequently, the creation of huge differences in the GALI_k values, which allow the discrimination between chaotic and regular motion, will appear earlier for larger k values. So, in general, the overall required computational time decreases significantly by using a higher order GALI_k, despite the integration of more deviation vectors, since this integration will be terminated earlier. Thus, the best choice in investigations of this kind is to use the GALI_2N.

Let us illustrate this approach by computing the GALI₄ for the 2D Hénon-Heiles system (5.4), at a grid in its q ₁ = 0 surface of section. The outcome of this procedure is seen in Fig. 5.20, where each initial condition is colored according to the time t _th needed for its GALI₄ to become ≤ 10⁻¹². Each orbit is integrated up to t = 500 time units and if its GALI₄ value at the end of the integration is larger than the threshold value 10⁻¹² the corresponding t _th value is set to t _th = 500 and the initial condition is colored in blue according to the color scales seen below the panel of Fig. 5.20. Regions of regular motion correspond to large t _th values and are colored in blue, while all the remaining colored domains contain chaotic orbits. Again, white regions correspond to forbidden initial conditions. This approach yields a very detailed chart of the dynamics, analogous to the one seen in Fig. 5.19.

An advantage of the current approach is its ability to clearly reveal various ‘degrees’ of chaotic behavior in regions not colored in blue. Strongly chaotic orbits are colored in red and yellow as their GALI₄ becomes ≤ 10⁻¹² quite fast. Orbits with larger t _th values correspond to chaotic orbits which need more time in order to show their chaotic nature, while the ‘sticky’ chaotic regions are characterized by even higher t _th values and are colored in light blue. We note that for every initial condition we used a different, random set of orthonormal deviation vectors in order to avoid the appearance of possible ‘spurious’ structures, like the ones seen in Fig. 5.19a.

5.4.2 Studies of Various Dynamical Systems

The SALI and the GALI methods have been used broadly for the study of the phase space dynamics of several models originating from different scientific fields. These studies include the characterization of individual orbits as chaotic or regular, as well as the consideration of large ensembles of initial conditions along the lines presented in Sect. 5.4.1, whenever a more global understanding of the underlying dynamics was needed.

In this section we present a brief, qualitative overview of such investigations. For this purpose we focus mainly on the outcomes of these studies avoiding a detailed presentation of mathematical formulas and equations for each studied model.

5.4.2.1 An Accelerator Map Model

Initially, let us discuss two representative applications of the SALI. The first one concerns the study of a 4d symplectic map which describes the evolution of a charged particle in an accelerator ring having a localized thin sextupole magnet. The specific form of this map can be found in [19] where the SALI method was used for the construction of phase space color charts where regions of chaotic and regular motion were clearly identified, as well as for evaluating the percentage of chaotic orbits.

Later on, in [16, 17] this map was used to test the efficiency of chaos control techniques for increasing the stability domain (the so-called ‘dynamic aperture’) around the ideal circular orbit of this simplified accelerator model. These techniques turned out to be quite successful, as the addition of a rather simple control term, which potentially could be approximated by real multipole magnets, increased the stability region of the map as can be seen in Fig. 5.21.

5.4.2.2 A Hamiltonian Model of a Bose-Einstein Condensate

Let us now turn our attention to a 2D Hamiltonian system describing the interaction of three vortices in an atomic Bose-Einstein condensate, which was studied in [52]. By means of SALI color plots the extent of chaos in this model was accurately measured and its dependence on physically important parameters, like the energy and the angular momentum of the vortices, were determined.

In real experiments, from which the study of this model was motivated, the life time of Bose-Einstein condensates is limited. For this reason the time in which the chaotic nature of orbits is uncovered played a significant role in the analysis presented in [52]. Actually, different ‘degrees of chaoticity’ are revealed by registering the time t _th that the SALI of a chaotic orbit requires in order to become ≤ 10⁻¹² (Fig. 5.22). This approach is similar to the one presented in Sect. 5.4.1.2, and allows the identification of regions with different strengths of chaos.

The chaotic orbits of Fig. 5.22a are decomposed in Figs. 5.22b–e in four different sets according to their t _th value: t _th ∈ [140, 500] (Fig. 5.22b), t _th ∈ (500, 1000] (Fig. 5.22c), t _th ∈ (1000, 1500] (Fig. 5.22d) and t _th ∈ (1500, 2000] (Fig. 5.22e), where time is measured in some appropriate units (see [52] for more details). From these results we see that, as the initial conditions move further away from the center of the x-shaped region of Fig. 5.22a the orbits need more time to show their chaotic nature and consequently, some of them can be considered as regular from a practical (experimental) point of view. For instance, in real experiments one would expect to detect chaotic motion in regions shown in Fig. 5.22b where orbits have relatively small t _th values. Thus, an analysis of this kind can provide practical information about where one should look for chaotic behavior in actual experimental set ups.

5.4.2.3 Further Applications of the SALI and the GALI Methods

The SALI and the GALI methods have been successfully employed in studies of various physical problems and mathematical toy models, as well as for the investigation of fundamental aspects of nonlinear dynamics (e.g. see [30]). In what follows we briefly present some of these studies

In [65] the SALI/GALI₂ method was used for the global study of the standard map (5.32). By considering large ensembles of initial conditions the percentage of chaotic motion was accurately computed as a function of the map’s parameter K. This work revealed the periodic re-appearance of small (even tiny) islands of stability in the system’s phase space for increasing values of K. Subsequent investigations of the regular motion of the standard map in [62] led to the clear distinction between typical islands of stability and the so-called accelerator modes, i.e. motion resulting in an anomalous enhancement of the linear in time orbits’ diffusion. Typically, this motion is highly superdiffusive and is characterized by a diffusion exponent ≈ 2.

In [21] the GALI was used for the detection of chaotic orbits in many dimensions, the prediction of slow diffusion, as well as the determination of quasiperiodic motion on low dimensional tori in the system (5.7) of many coupled standard maps. Additional applications of the SALI in studying maps can be found in [73], where the index was used for shedding some light in the properties of accelerator models, while in [76] a coupled logistic type predator-prey model describing population growths in biological systems was considered. Further studies of 2d and 4d maps based on the SALI method were performed in [35].

Models of dynamical astronomy and galactic dynamics are considered to be the spearhead of the chaos detection methods [31]. Actually, many of these methods have been used, or often even constructed, to investigate the properties of such systems. Several applications of the SALI to systems of this kind can be found in the literature. In [18, 88, 89] the stability properties of orbits in a particular few-body problem, the so-called the Sitnikov problem, were studied, while in [94] the long term stability of two-planet extrasolar systems initially trapped in the 3:1 mean motion resonance was investigated. The SALI was also used to study the dynamics of the Caledonian symmetric four-body problem [90], as well as the circular restricted three-body problem [75].

In systems modeling the dynamics of galaxies special care should be taken with respect to the determination of the star motion’s nature, because this has to be done as fast as possible and in physically relevant time intervals (e.g. smaller than the age of the universe). Hence, in order to check the adequacy of a proposed galactic model, in terms of being able to sustain structures resembling the ones seen in observations of real galaxies, the detection of chaotic and regular motion for rather small integration times is imperative. The SALI and the GALI methods have proved to be quite efficient tools for such studies, as they allow the fast characterization of orbits. This ability reduces significantly the required computational burden, as in many cases the determination of the orbits’ nature is achieved before the predefined, final integration time.

In particular, the SALI method has been used successfully in studying the chaotic motion and spiral structure in self-consistent models of rotating galaxies [93], the dynamics of self-consistent models of cuspy triaxial galaxies with dark matter haloes [23], the orbital structure in N body models of barred-spiral galaxies [42], the secular evolution of elliptical galaxies with central masses [50], the chaotic component of cuspy triaxial stellar systems [25], as well as the chaoticity of non-axially symmetric galactic models [97] and of models with different types of dark matter halo components [96].

The SALI was used in [65] for investigating the dynamics of 2D and 3D Hamiltonian models of rotating bared galaxies. This work was extended in [60] by using the GALI for studying the global dynamics of different galactic models of this type. In particular, the effects of several parameters related to the shape and the mass of the disk, the bulge and the bar components of the models, as well as the rotation speed of the bar, on the amount of chaos appearing in the system were determined. Moreover, the implementation of the GALI₃ in the 3D Hamiltonians allowed the detection of regular motion on low (2d) dimensional tori, although these systems support, in general, 3d orbits. The astronomical significance of these orbits was discussed in detail in [60].

Implementations of the SALI to nuclear physics systems can be found in [56–58, 86, 87] where the chaotic behavior of boson models is investigated, as well as in [5] where the dynamics of a Hamiltonian model describing a confined microplasma was studied. Recently the SALI and the GALI methods, together with other chaos indicators, were reformulated in the framework of general relativity, in order to become invariant under coordinate transformation [54].

The SALI and the GALI have been also used to study the dynamics of nonlinear lattice models. Applications of these indices to the Fermi–Pasta–Ulam model can be found in [1, 2, 4, 27–29, 71, 85] where the properties of regular motion on low dimensional tori, the long term stability of orbits, as well as the interpretation of Fermi–Pasta–Ulam recurrences were studied. In [63] the GALI method managed to capture the appearance of a second order phase transition that the Hamiltonian Mean Field model exhibits at a certain energy density. The index successfully verified also other characteristics of the system, like the sharp transition from weak to strong chaos. Further applications of the SALI method to other models of nonlinear lattices can be found in [4, 72].

In addition, the SALI was further used in studying the chaotic and regular nature of orbits in non-Hamiltonian dynamical systems [6, 47], some of which model chaotic electronic circuits [46, 48, 49].

5.4.3 Time Dependent Hamiltonians

The applications presented so far concerned autonomous dynamical systems. However, there are several phenomena in nature whose modeling requires the invocation of parameters that vary in time. Whenever these phenomena are described according to the Hamiltonian formalism, the corresponding Hamiltonian function is not an integral of motion as its value does not remain constant as time evolves.

The SALI and the GALI methods can be also used to determine the chaotic or regular nature of orbits in time dependent systems as long as, their phase space does not shrink ceaseless or expand unlimited, with respect to its initial volume, during the considered times. This property allows us to utilize the time evolution of the volume defined by the deviation vectors, as in the case of the time independent models, and estimate accurately its possible decay for time intervals where the total phase space volume has not changed significantly.

In conservative time independent Hamiltonians orbits can be periodic (stable or unstable), regular (quasiperiodic) or chaotic and their nature does not change in time. Sticky chaotic orbits may exhibit a change in their orbital morphologies from almost quasiperiodic to completely chaotic behaviors, but in reality their nature does not change as they are weakly chaotic orbits. On the other hand, in time dependent models, individual orbits can display abrupt transitions from regular to chaotic behavior, and vice versa, during their time evolution. This is an intriguing characteristic of these systems which should be captured by the used chaos indicator. Such transitions between chaotic and regular behaviors can be seen for example in N body simulations of galactic models. For this reason, time dependent analytic potentials trying to mimic the evolution of N body galactic systems, are expected to exhibit similar transitions.

An analytic time dependent bared galaxy model consisting of a bar, a disk and a bulge component, whose masses vary linearly in time was studied in [68]. The time dependent nature of the model influences drastically the location and the size of stability islands in the system’s phase space, leading to a continuous interplay between chaotic and regular behaviors. The GALI was able to capture subtle changes in the nature of individual orbits (or ensemble of orbits) even for relatively small time intervals, verifying that it is an ideal diagnostic tool for detecting dynamical transitions in time dependent systems.

Although both 2D and 3D time dependent Hamiltonian models were studied in [68], we further discuss here only the 3D model in order to illustrate the procedure followed for detecting the various dynamical epochs in the evolution of an orbit. The main idea for doing that is the re-initialization of the computation of the GALI_k, with 2 ≤ k ≤ N, whenever the index reaches a predefined low value (which signifies chaotic behavior) by considering k new, orthonormal deviation vectors resetting GALI_k = 1.

Let us see this procedure in more detail. In [68] the evolution of the GALI₃ was followed for each studied orbit. The three randomly chosen, initial orthonormal deviation vectors set GALI₃ = 1 in the beginning of the numerical simulation (t = 0). These vectors were evolved according to the dynamics induced by the 3D, time dependent Hamiltonian up to the time t = t _d that the GALI₃ became smaller than 10⁻⁸ for the fist time. At that point the time t = t _d was registered and three new, random, orthonormal vectors were considered resetting GALI₃ = 1. Afterwards, the evolution of these vectors was followed until the next, possible occurrence of GALI₃ < 10⁻⁸. Then the same process was repeated.

Why was this procedure implemented? What is the reason behind this strategy? In order to reveal this reason let us assume that an orbit initially behaves in a chaotic way and later on it drifts to a regular behavior. The volume formed by the deviation vectors will shrink exponentially fast, becoming very small during the initial chaotic epoch and will remain small throughout the whole evolution in the regular epoch, unless one re-initializes the deviation vectors and the volume they define. In this way the deviation vectors will be able to ‘feel’ the new, current dynamics.

An example case of this kind is shown in Fig. 5.23. In particular, in Fig. 5.23a we see that the evolution of the finite time mLE $\varLambda _{1}$ is not able to provide valid information about the different dynamical epochs that the studied orbit experiences. This is due to the index’s averaging nature which takes into account the whole history of the evolution. On the other hand, the re-initialized GALI₃ (whose time evolution is shown in Fig. 5.23b) clearly succeeds in depicting the transitions between regular epochs, where it oscillates around positive values (such time intervals are denoted by I and III in Fig. 5.23a, b), and chaotic ones, where it exhibits repeated exponential decays to very small values (epoch II). From the results of Fig. 5.23a it becomes evident that the computation of the mLE cannot be used as a reliable criterion for determining the chaotic or regular nature of the orbit in these three time intervals.

Another way to visualize the results of Fig. 5.23b is through the measurement of the time t _d needed for the repeated re-initializations of the GALI₃, or in other words, of the time needed for the GALI₃ to decrease from GALI₃ = 1 to GALI₃ ≤ 10⁻⁸. In Fig. 5.23c we present t _d as a function of the evolution time of the orbit. From the results of this figure we see that during the time interval $7500 \lesssim t \lesssim 14,000$ the value of t _d is rather small, indicating strong chaotic motion. For smaller times, $t \lesssim 7500$, the GALI₃ takes a long time to become small, suggesting the presence of regular motion or of (relatively) weaker chaotic motion. The upwardly pointing arrow, after $t \gtrsim 15,000$, shows that the GALI₃ no longer falls to zero, which again indicates the appearance of a regular epoch.

After the first, successful application of the GALIs to time dependent Hamiltonians in [68], the same approach was followed for the study of a more sophisticated time dependent galactic model in [61]. This analytic Hamiltonian model succeeded to incorporate the evolution of the basic morphological features of an actual N body simulation, by allowing all the relevant parameters of its dynamical components to vary in time.

5.5 Summary

In this chapter we presented how the SALI and the various GALIs can be used to study the chaotic behavior of dynamical systems.

Following the history of the evolution of these indices, we initially presented in Sect. 5.2 the underlying idea behind the introduction of the SALI: the index actually quantifies the possible alignment of two initially distinct deviation vectors. The natural generalization of this idea, by considering more than two deviation vectors and checking if they become linearly dependent, led later on, to the introduction of the GALI, as we explained in Sect. 5.3. The close relation between the two indices was also pointed out, as according to (5.17) the GALI₂ and the SALI practically coincide

$$\displaystyle{\mbox{ GALI}_{2} \propto \mbox{ SALI}.}$$

Avoiding the presentation of mathematical proofs (which the interested reader can find in the related references), we formulated in Sect. 5.3 the laws that the indices follow for chaotic and regular orbits, providing also several numerical results which demonstrate their validity.

In particular, for ND Hamiltonian systems (N ≥ 2) and 2Nd symplectic maps (N ≥ 1) the GALI_k tends exponentially to zero for chaotic orbits and unstable periodic orbits following (5.22)

$$\displaystyle{\mbox{ GALI}_{k}(t) \propto \exp \left \{-\left [(\lambda _{1} -\lambda _{2}) + (\lambda _{1} -\lambda _{3}) + \cdots + (\lambda _{1} -\lambda _{k})\right ]t\right \},}$$

while for regular motion on as sd torus, with 2 ≤ s ≤ N, the evolution of the GALI_k is given by (5.34)

$$\displaystyle{\mbox{ GALI}_{k}(t) \propto \left \{\begin{array}{ll} \mbox{ constant}&\mbox{ if $2 \leq k \leq s$} \\ \frac{1} {t^{k-s}} & \mbox{ if $s <k \leq 2N - s$} \\ \frac{1} {t^{2(k-N)}} & \mbox{ if $2N - s <k \leq 2N.$}\\ \end{array} \right.}$$

The latter formula is quite general as (a) for s = N it provides (5.23), which describes the behavior of the GALI_k for motion on an Nd torus, i.e. the most common situation of regular motion in the 2Nd phase space of the system, (b) for k = 2, s = 1 and N = 1 it gives (5.33), which describes the power law decay of the GALI₂ in the case of a 2d map (the GALI₂ is the only possible GALI in this case), and (c) for s = 1 it becomes (5.37), which provides the power law decay of the GALI_k for stable periodic orbits of Hamiltonian systems (we remind that in the case of stable periodic in maps all the GALIs remain constant (5.38)).

In our presentation, we paid much attention to issues concerning the actual computation of the indices. In Sect. 5.3.1 we explained in detail an efficient way to evaluate the GALI_k, which is based on the SVD procedure (5.20), while in the Appendix we provide pseudo-codes for the computation of the SALI and the GALI. In Sect. 5.3.3.1 we discussed a numerical strategy for the detection of regular motion on low dimensional tori (see Figs. 5.13 and 5.14), while in Sect. 5.3.4 we showed how the evaluation of the GALI for an ensemble of orbits can lead to the location of stable periodic orbits (see Figs. 5.17 and 5.18). In addition, the effect of the choice of the initial deviation vectors on the color plots depicting the global dynamics of a system, was discussed in Sect. 5.4.1.1, where specific strategies to avoid the appearance of spurious structures in these plots were presented (see Fig. 5.19).

One of the main advantages of the SALI and the GALI methods is their ability to discriminate between chaotic and regular motion very efficiently. The GALI_k with 2 ≤ k ≤ N tends exponentially fast to zero for chaotic orbits, while it attains positive values for regular ones. Due to these different behaviors these indices, and in particular the GALI₂/SALI and the GALI_N, can reveal even tiny details of the underlying dynamics, if one follows the procedure presented in Sect. 5.4.1.1. Implementing the numerical strategies developed in Sect. 5.4.1.2 we can also use the completely different time rates with which the GALI_k with N < k ≤ 2N, tends to zero (exponentially fast for chaotic orbits and power law decay for regular ones) in order to study the dynamics globally. Finally, in Sect. 5.4.3 a particular numerical method, the re-initialization of the GALI_k, proved to be the suitable approach to reveal even brief changes in the dynamical nature of orbits in time dependent Hamiltonians.

The SALI and the GALI have already proven their usefulness in chaos studies as their many applications to a variety of dynamical systems show (see Sect. 5.4.2). Nevertheless, several other chaos indicators have been developed over the years. A few, sporadic comparisons between some of these methods have been performed in studies of particular dynamical systems (e.g. [9, 75, 79, 83]). Recently, detailed and systematic comparisons between many chaos indicators based on the evolution of deviation vectors were conducted [33, 59], and the SALI method was added in the software package LP-VIcode [24], which includes several of these indicators. The main outcome of these comparative studies was that the use of more than one chaos indicators is useful, if not imperative, for revealing the dynamics of a system.

Notes

1.
We note that the value of $\lambda _{1}$ is independent of the used norm.
2.
We note that throughout this chapter we use the hat symbol ($\,\hat{}\,$) to denote a unit vector.
3.
For Hamiltonian systems the time is a continuous variable, while for maps it is a discrete one counting the map’s iterations.
4.
We note that throughout this chapter the logarithm to base 10 is denoted by $\log$.
5.
We note that here, as well as in several, forthcoming figures in this chapter, the evaluation of the LEs is done only for confirming the theoretical predictions for the time evolution of the SALI (Eq. (5.12) in the current case) and later on of the GALIs, and it is not needed for the computation of the SALI and the GALIs.
6.
Note that this parallelogram is not the usual 2d parallelogram on the plane because its sides (the deviation vectors) are not 2d vectors.
7.
For a brief introduction to the notion of the wedge product the reader is referred to the Appendix A of [84] and the Appendix of [81].
8.
A proof of the second equality of (5.14) can be found in the Appendix B of [84].
9.
It is worth mentioning here that other chaos indicators, like the Orthogonal Fast Lyapunov Indicator (OFLI) and its variations [7, 8], are quite successful in performing this task as they were actually designed for this purpose.

References

Antonopoulos, Ch., Bountis, T.: Detecting order and chaos by the Linear Dependence Index (LDI) method. ROMAI J. 2(2), 1–13 (2006)
MATH MathSciNet Google Scholar
Antonopoulos, Ch., Christodoulidi, H.: Weak chaos detection in the Fermi-Pasta-Ulam-α system using q-Gaussian statistics. Int. J. Bifurcat. Chaos 21, 2285 (2011)
Article Google Scholar
Antonopoulos, Ch., Manos, A., Skokos, Ch.: SALI: an efficient indicator of chaos with application to 2 and 3 degrees of freedom Hamiltonian systems. In: Tsahalis, D.T. (ed.) From Scientific Computing to Computational Engineering. Proceedings of the 1st International Conference, vol. III, pp. 1082–1088. Patras University Press, Patras (2005)
Google Scholar
Antonopoulos, Ch., Bountis, T., Skokos, Ch.: Chaotic dynamics of N-degree of freedom Hamiltonian systems. Int. J. Bifurcat. Chaos 16, 1777–1793 (2006)
Article MATH MathSciNet Google Scholar
Antonopoulos, Ch., Basios, V., Bountis, T.: Weak chaos and the ‘Melting Transition’ in a confined microplasma system. Phys. Rev. E 81, 016211 (2010)
Article ADS Google Scholar
Antonopoulos, C., Basios, V., Demongeot, J, Nardone, P., Thomas, R.: Linear and nonlinear arabesques: a study of closed chains of negative 2-element circuits. Int. J. Bifurcat. Chaos 23, 1330033 (2013)
Article MATH Google Scholar
Bario, R.: Sensitivity tools vs. Poincaré sections. Chaos Solitons Fractals 25, 711–726 (2005)
Article ADS MathSciNet Google Scholar
Bario, R.: Painting chaos: a gallery of sensitivity plots of classical problems. Int. J. Bifurcat. Chaos 16, 2777–2798 (2006)
Article MATH MathSciNet Google Scholar
Barrio, R., Borczyk, W., Breiter, S.: Spurious structures in chaos indicators maps. Chaos Solitons Fractals 40, 1697–1714 (2009)
Article ADS MATH MathSciNet Google Scholar
Benettin, G., Galgani, L.: Lyapunov characteristic exponents and stochasticity. In: Laval, G., Grésillon, D. (eds.) Intrinsic Stochasticity in Plasmas, pp. 93–114. Edit. Phys., Orsay (1979)
Google Scholar
Benettin, G., Galgani, L., Strelcyn, J.M.: Kolmogorov entropy and numerical experiments. Phys. Rev. A 14, 2338–2344 (1976)
Article ADS Google Scholar
Benettin, G., Galgani, L., Giorgilli, A., Strelcyn, J.M.: Tous les nombres caractéristiques sont effectivement calculables. C. R. Acad. Sc. Paris Sér. A 286, 431–433 (1978)
ADS MATH MathSciNet Google Scholar
Benettin, G., Froeschlé, C., Scheidecker, J.P.: Kolmogorov entropy of a dynamical system with an increasing number of degrees of freedom. Phys. Rev. A 19, 2454–2460 (1979)
Article ADS MathSciNet Google Scholar
Benettin, G., Galgani, L., Giorgilli, A., Strelcyn, J.M.: Lyapunov characteristic exponents for smooth dynamical systems and for Hamiltonian systems; A method for computing all of them. Part 1: theory. Meccanica (March) 9–20 (1980)
Google Scholar
Benettin, G., Galgani, L., Giorgilli, A., Strelcyn, J.M.: Lyapunov characteristic exponents for smooth dynamical systems and for Hamiltonian systems; A method for computing all of them. Part 2: Numerical application. Meccanica (March) 21–30 (1980)
Google Scholar
Boreux, J., Carletti, T., Skokos, Ch., Vittot, M.: Hamiltonian control used to improve the beam stability in particle accelerator models. Commun. Nonlinear Sci. Numer. Simul. 17, 1725–1738 (2012)
Article ADS MATH MathSciNet Google Scholar
Boreux, J., Carletti, T., Skokos, Ch., Papaphilippou, Y., Vittot, M.: Efficient control of accelerator maps. Int. J. Bifurcat. Chaos 22(9), 1250219 (2012)
Article MathSciNet Google Scholar
Bountis, T., Papadakis, K.E.: The stability of vertical motion in the N-body circular Sitnikov problem. Celest. Mech. Dyn. Astron. 104, 205–225 (2009)
Article ADS MATH MathSciNet Google Scholar
Bountis, T., Skokos, Ch.: Application of the SALI chaos detection method to accelerator mappings. Nucl. Instrum. Methods Phys. Res. A 561, 173–179 (2006)
Article ADS Google Scholar
Bountis, T.C., Skokos, Ch.: Complex Hamiltonian Dynamics. Springer, Berlin (2012)
Book MATH Google Scholar
Bountis, T., Manos, T., Christodoulidi, H.: Application of the GALI Method to localization dynamics in nonlinear systems. J. Comp. Appl. Math. 227, 17–26 (2009)
Article ADS MATH MathSciNet Google Scholar
Broucke, R.A.: Periodic orbits in the elliptic restricted three–body problem. NASA, Jet Propulsion Laboratory, Tech. Rep. 32-1360 (1969)
Google Scholar
Capuzzo-Dolcetta, R., Leccese, L., Merritt, D., Vicari, A.: Self-consistent models of cuspy triaxial galaxies with dark matter haloes. Astrophys. J. 666, 165–180 (2007)
Article ADS Google Scholar
Carpintero, D.D., Maffione, N., Darriba, L.: LP–VIcode: a program to compute a suite of variational chaos indicators. Astron. Comput. 5, 19–27 (2014)
Article ADS Google Scholar
Carpintero, D.D., Muzzio, J.C., Navone, H.D.: Models of cuspy triaxial stellar systems –III. The effect of velocity anisotropy on chaoticity. Mon. Not. R. Astron. Soc. 438, 2871–2881 (2014)
Article ADS Google Scholar
Casati, G., Chirikov, B.V., Ford, J.: Marginal local instability of quasi-periodic motion. Phys. Lett. A 77, 91–94 (1980)
Article ADS MathSciNet Google Scholar
Christodoulidi, H., Bountis, T.: Low-dimensional quasiperiodic motion in Hamiltonian systems. ROMAI J. 2(2), 37–44 (2006)
MATH MathSciNet Google Scholar
Christodoulidi, H., Efthymiopoulos, Ch.: Low-dimensional q-tori in FPU lattices: dynamics and localization properties. Physica D 261, 92 (2013)
Article ADS MATH MathSciNet Google Scholar
Christodoulidi, H., Efthymiopoulos, Ch., Bountis, T.: Energy localization on q-tori, long-term stability, and the interpretation of Fermi-Pasta-Ulam recurrences. Phys. Rev. E 81, 016210 (2010)
Article ADS Google Scholar
Cincotta, P.M., Efthymiopoulos, C., Giordano, C.M., Mestre, M.F.: Chirikov and Nekhoroshev diffusion estimates: bridging the two sides of the river. Physica D 266, 49–64 (2014)
Article ADS MATH MathSciNet Google Scholar
Contopoulos, G.: Order and Chaos in Dynamical Astronomy. Springer, Berlin, Heidelberg (2002)
Book MATH Google Scholar
Contopoulos, G., Galgani, L., Giorgilli, A.: On the number of isolating integrals in Hamiltonian systems. Phys. Rev. A 18, 1183–1189 (1978)
Article ADS Google Scholar
Darriba, L.A., Maffione, N.P., Cincotta, P.M., Giordano, C.M.: Comparative study of variational chaos indicators and ODEs’ numerical integrators. Int. J. Bifurcat. Chaos 22, 1230033 (2012)
Article MATH MathSciNet Google Scholar
Dullin, H.R., Meiss, J.D., Sterling, D.: Generic twistless bifurcations. Nonlinearity 13, 203–224 (2000)
Article ADS MATH MathSciNet Google Scholar
Faranda, D., Mestre, M.F., Turchetti, G.: Analysis of round off errors with reversibility test as a dynamical indicator. Int. J. Bifurcat. Chaos 22, 1250215 (2012)
Article MATH MathSciNet Google Scholar
Fermi, E., Pasta, J., Ulam, S.: Studies of nonlinear problems. I. Los Alamos Rep LA-1940 (1955)
Google Scholar
Froeschlé, C., Gonczi, R., Lega, E.: The fast Lyapunov indicator: a simple tool to detect weak chaos. Application to the structure of the main asteroidal belt. Planet. Space Sci. 45, 881–886 (1997)
Google Scholar
Gerlach, E., Eggl, S., Skokos, Ch.: Efficient integration of the variational equations of multi–dimensional Hamiltonian systems: application to the Fermi–Pasta–Ulam lattice. Int. J. Bifurcat. Chaos 22, 1250216 (2012)
Article MATH MathSciNet Google Scholar
Gottwald, G.A., Melbourne, I.: A new test for chaos in deterministic systems. Proc. R. Soc. Lond. A 460, 603–611 (2004)
Article ADS MATH MathSciNet Google Scholar
Hadjidemetriou, J.: The stability of periodic orbits in the three-body problem. Celest. Mech. 12, 255–276 (1975)
Article ADS MATH MathSciNet Google Scholar
Haken, H.: At least one Lyapunov exponent vanishes if the trajectory of an attractor does not contain a fixed point. Phys. Lett. A 94, 71–72 (1983)
Article ADS MathSciNet Google Scholar
Harsoula, M., Kalapotharakos, C.: Orbital structure in N-body models of barred-spiral galaxies. Mon. Not. R. Astron. Soc. 394, 1605–1619 (2009)
Article ADS Google Scholar
Hénon, M., Heiles, C.: The applicability of the third integral of motion: Some numerical experiments. Astron. J. 69, 73–79 (1964)
Article ADS MathSciNet Google Scholar
Howard, J.E., Dullin, H.R.: Linear stability of natural symplectic maps. Phys. Lett. A 246, 273–283 (1998)
Article ADS MATH MathSciNet Google Scholar
Howard, J.E., MacKay, R.S.: Linear stability of symplectic maps. J. Math. Phys. 28, 1036–1051 (1987)
Article ADS MATH MathSciNet Google Scholar
Huang, G., Cao, Z.: Numerical analysis and circuit realization of the modified LÜ chaotic system. Syst. Sci. Control Eng. 2, 74–79 (2014)
Article Google Scholar
Huang, G-Q, Wu, X.: Analysis of Permanent-Magnet Synchronous Motor Chaos System. Lecture Notes in Computer Science, vol. 7002, pp. 257–263. Springer, Berlin, Heidelberg (2011)
Google Scholar
Huang, G.Q., Wu, X.: Analysis of new four-dimensional chaotic circuits with experimental and numerical methods. Int. J. Bifurcat. Chaos 22, 1250042 (2012)
Article Google Scholar
Huang, G., Zhou, Y.: Circuit simulation of the modified Lorenz system. J. Inf. Comput. Sci. 10, 4763–4772 (2013)
Article MathSciNet Google Scholar
Kalapotharakos, C.: The rate of secular evolution in elliptical galaxies with central masses. Mon. Not. R. Astron. Soc. 389, 1709–1721 (2008)
Article ADS Google Scholar
Kantz, H., Grassberger, P.: Internal Arnold diffusion and chaos thresholds in coupled symplectic maps. J. Phys. A 21, L127–133 (1988)
Article ADS MATH MathSciNet Google Scholar
Kyriakopoulos, N., Koukouloyannis, V., Skokos, Ch., Kevrekidis, P.: Chaotic behavior of three interacting vortices in a confined Bose-Einstein condensate. Chaos 24, 024410 (2014)
Article ADS MathSciNet Google Scholar
Lichtenberg, A.J., Lieberman, M.A.: Regular and Chaotic Dynamics, 2nd edn. Springer, Berlin (1992)
Book MATH Google Scholar
Lukes-Gerakopoulos, G.: Adjusting chaotic indicators to curved spacetimes. Phys. Rev. D 89, 043002 (2014)
Article ADS Google Scholar
Lyapunov, A.M.: The general problem of the stability of motion. Taylor and Francis, London (1992) (English translation from the French: Liapounoff, A.: Problème général de la stabilité du mouvement. Annal. Fac. Sci. Toulouse 9, 203–474 (1907). The French text was reprinted in Annals Math. Studies vol. 17. Princeton University Press (1947). The original was published in Russian by the Mathematical Society of Kharkov in 1892)
MATH Google Scholar
Macek, M., Stránský, P., Cejnar, P., Heinze, S., Jolie, J., Dobeš, J.: Classical and quantum properties of the semiregular arc inside the Casten triangle. Phys. Rev. C 75, 064318 (2007)
Article ADS Google Scholar
Macek, M, Dobeš, J., Cejnar, P.: Occurrence of high-lying rotational bands in the interacting boson model. Phys. Rev. C 82, 014308 (2010)
Article ADS Google Scholar
Macek, M, Dobeš, J., Stránský, P., Cejnar, P.: Regularity-induced separation of intrinsic and collective dynamics. Phys. Rev. Lett. 105, 072503 (2010)
Article ADS Google Scholar
Maffione, N.P., Darriba, L.A., Cincotta, P.M., Giordano, C.M.: A comparison of different indicators of chaos based on the deviation vectors: Application to symplectic mappings. Celest. Mech. Dyn. Astron. 111, 285–307 (2011)
Article ADS MathSciNet Google Scholar
Manos, T., Athanassoula, E.: Regular and chaotic orbits in barred galaxies - I. Applying the SALI/GALI method to explore their distribution in several models. Mon. Not. R. Astron. Soc. 415, 629–642 (2011)
Google Scholar
Manos, T., Machado, R.E.G.: Chaos and dynamical trends in barred galaxies: bridging the gap between N-body simulations and time-dependent analytical models. Mon. Not. R. Astron. Soc. 438, 2201–2217 (2014)
Article ADS Google Scholar
Manos, T., Robnik, M.: Survey on the role of accelerator modes for the anomalous diffusion: The case of the standard map. Phys. Rev. E 89, 022905 (2014)
Article ADS Google Scholar
Manos, T., Ruffo, S.: Scaling with system size of the Lyapunov exponents for the Hamiltonian mean field model. Transp. Theory Stat. Phys. 40, 360–381 (2011)
Article ADS MATH MathSciNet Google Scholar
Manos, T., Skokos, Ch., Bountis, T.: Application of the Generalized Alignment Index (GALI) method to the dynamics of multi-dimensional symplectic maps. In: Chandre C., Leoncini, X., Zaslavsky, G. (eds.) Chaos, Complexity and Transport: Theory and Applications. Proceedings of the CCT 07, pp. 356–364. World Scientific, Singapore (2008)
Chapter Google Scholar
Manos, T., Skokos, Ch., Athanassoula, E., Bountis, T.: Studying the global dynamics of conservative dynamical systems using the SALI chaos detection method. Nonlinear Phenomen. Complex Syst. 11(2), 171–176 (2008)
MathSciNet Google Scholar
Manos, T., Skokos, Ch., Bountis, T.: Global dynamics of coupled standard maps. In: Contopoulos, G., Patsis, P.A. (eds.) Chaos in Astronomy, Astrophysics and Space Science Proceedings, pp. 367–371. Springer, Berlin, Heidelberg (2009)
Google Scholar
Manos, T., Skokos, Ch., Antonopoulos, Ch.: Probing the local dynamics of periodic orbits by the generalized alignment index (GALI) method. Int. J. Bifurcat. Chaos 22, 1250218 (2012)
Article MATH MathSciNet Google Scholar
Manos, T., Bountis, T., Skokos, Ch.: Interplay between chaotic and regular motion in a time-dependent barred galaxy model. J. Phys. A Math. Theor. 46, 254017 (2013)
Article ADS MATH MathSciNet Google Scholar
Nagashima, T., Shimada, I.: On the C-system-like property of the Lorenz system. Prog. Theor. Phys. 58, 1318–1320 (1977)
Article ADS Google Scholar
Oseledec, V.I.: A multiplicative ergodic theorem. Ljapunov characteristic numbers for dynamical systems. Trans. Moscow Math. Soc. 19, 197–231 (1968)
MathSciNet Google Scholar
Paleari, S., Penati, T.: Numerical Methods and Results in the FPU Problem. Lecture Notes in Physics, vol. 728, pp. 239–282. Springer, Berlin (2008)
Google Scholar
Panagopoulos, P., Bountis, T.C., Skokos, Ch.: Existence and stability of localized oscillations in 1-dimensional lattices with soft spring and hard spring potentials. J. Vib. Acoust. 126, 520–527 (2004)
Article Google Scholar
Petalas,, Y.G., Antonopoulos, C.G., Bountis, T.C., Vrahatis, M.N.: Evolutionary methods for the approximation of the stability domain and frequency optimization of conservative maps. Int. J. Bifurcat. Chaos 18, 2249–2264 (2008)
Article MATH MathSciNet Google Scholar
Press, W.H., Teukolsky, S.A., Vetterling, W.T., Flannery, B.P.: Numerical Recipes in Fortran 77, 2nd edn. The Art of Scientific Computing. Cambridge University Press, Cambridge (1992)
MATH Google Scholar
Racoveanu, O.: Comparison of chaos detection methods in the circular restricted three-body problem. Astron. Nachr. 335, 877–885 (2014)
Article ADS Google Scholar
Saha, L.M., Sahni, N.: Chaotic evaluations in a modified coupled logistic type predator-prey model. Appl. Math. Sci. 6(139), 6927–6942 (2012)
MathSciNet Google Scholar
Sándor, Zs., Érdi, B., Széll, A., Funk, B.: The relative Lyapunov indicator: an efficient method of chaos detection. Celest. Mech. Dyn. Astron. 90, 127–138 (2004)
Google Scholar
Shimada, I., Nagashima, T.: A numerical approach to ergodic problem of dissipative dynamical systems. Prog. Theor. Phys. 61, 1605–1615 (1979)
Article ADS MATH MathSciNet Google Scholar
Skokos, Ch.: Alignment indices: a new, simple method for determining the ordered or chaotic nature of orbits. J. Phys. A 34, 10029–10043 (2001)
Article ADS MATH MathSciNet Google Scholar
Skokos, Ch.: On the stability of periodic orbits of high dimensional autonomous Hamiltonian systems. Physica D 159, 155–179 (2001)
Article ADS MATH MathSciNet Google Scholar
Skokos, Ch.: The Lyapunov Characteristic Exponents and their Computation. Lecture Notes in Physics, vol. 790, pp. 63–135. Springer, Berlin, Heidelberg (2010)
Google Scholar
Skokos, Ch., Antonopoulos, Ch., Bountis, T.C., Vrahatis, M.N.: How does the smaller alignment index (SALI) distinguish order from chaos? Prog. Theor. Phys. Suppl. 150, 439–443 (2003)
Article ADS Google Scholar
Skokos, Ch., Antonopoulos, Ch., Bountis, T.C., Vrahatis, M.N.: Detecting order and chaos in Hamiltonian systems by the SALI method. J. Phys. A 37, 6269–6284 (2004)
Article ADS MathSciNet Google Scholar
Skokos, Ch., Bountis, T.C., Antonopoulos, Ch.: Geometrical properties of local dynamics in Hamiltonian systems: the generalized alignment index (GALI) method. Physica D 231, 30–54 (2007)
Article ADS MATH MathSciNet Google Scholar
Skokos, Ch., Bountis, T.C., Antonopoulos, Ch.: Detecting chaos, determining the dimensions of tori and predicting slow diffusion in Fermi-Pasta-Ulam lattices by the generalized alignment index method. Eur. Phys. J. Spec. Top. 165, 5–14 (2008)
Article Google Scholar
Stránský, P., Cejnar, P., Macek, M.: Order and chaos in the Geometric Collective Model. Phys. At. Nucl. 70(9), 1572–1576 (2007)
Article Google Scholar
Stránský, P., Hruška, P., Cejnar, P.: Quantum chaos in the nuclear collective model: classical-quantum correspondence. Phys. Rev. E 79, 046202 (2009)
Article ADS Google Scholar
Soulis, P., Bountis, T., Dvorak, R.: Stability of motion in the Sitnikov 3-body problem. Celest. Mech. Dyn. Astron. 99, 129–148 (2007)
Article ADS MATH MathSciNet Google Scholar
Soulis, P.S., Papadakis, K.E., Bountis, T.: Periodic orbits and bifurcations in the Sitnikov four-body problem. Celest. Mech. Dyn. Astron. 100, 251–266 (2008)
Article ADS MATH MathSciNet Google Scholar
Széll, A., Érdi, B., Sándor, Z., Steves, B.: Chaotic and stable behavior in the Caledonian Symmetric Four-Body problem. Mon. Not. R. Astron. Soc. 347, 380–388 (2004)
Article ADS MATH Google Scholar
Voglis, N., Contopoulos, G., Efthymiopoulos, C.: Method for distinguishing between ordered and chaotic orbits in four-dimensional maps. Phys. Rev. E 57, 372–377 (1998)
Article ADS Google Scholar
Voglis, N., Contopoulos, G., Efthymiopoulos, C.: Detection of ordered and chaotic motion using the dynamical spectra. Celest. Mech. Dyn. Astron. 73, 211–220 (1999)
Article ADS MATH MathSciNet Google Scholar
Voglis, N., Harsoula, M., Contopoulos, G.: Orbital structure in barred galaxies. Mon. Not. R. Astron. Soc. 381, 757–770 (2007)
Article ADS Google Scholar
Voyatzis, G.: Chaos, order, and periodic orbits in 3:1 resonant planetary dynamics. Astrophys. J. 675, 802–816 (2008)
Article ADS Google Scholar
Wolf, A., Swift, J.B., Swinney, H.L., Vastano, J.A.: Determining Lyapunov exponents from a time series. Physica D 16, 285–317 (1985)
Article ADS MATH MathSciNet Google Scholar
Zotos, E.E.: Classifying orbits in galaxy models with a prolate or an oblate dark matter halo component. Astron. Astrophys. 563, A19 (2014)
Article ADS Google Scholar
Zotos, E.E., Caranicolas, N.D.: Order and chaos in a new 3D dynamical model describing motion in non-axially symmetric galaxies. Nonlinear Dyn. 74, 1203–1221 (2013)
Article MathSciNet Google Scholar

Download references

Acknowledgements

Many of the results described in this chapter were obtained in close collaboration with Prof. T. Bountis, Dr. Ch. Antonopoulos and Dr. E. Gerlach. This work was partially supported by the European Union (European Social Fund - ESF) and Greek national funds through the Operational Program “Education and Lifelong Learning” of the National Strategic Reference Framework (NSRF)—Research Funding Program: ‘THALES’. Ch. S. would like to thank the Research Office of the University of Cape Town for the Research Development Grant which funded part of this study, as well as the Max Planck Institute for the Physics of Complex Systems in Dresden for its hospitality during his visit in December 2014–January 2015, when part of this work was carried out. In addition, Ch. S. thanks T. van Heerden for the careful reading of the manuscript and for his valuable comments. We are also grateful to the three anonymous referees whose constructive remarks helped us improve the content and the clarity of the chapter.

Author information

Authors and Affiliations

Department of Mathematics and Applied Mathematics, University of Cape Town, Rondebosch, 7701, South Africa
Charalampos (Haris) Skokos
Center for Applied Mathematics and Theoretical Physics (CAMTP), University of Maribor, Krekova 2, SI-2000, Maribor, Slovenia
Thanos Manos
School of Applied Sciences, University of Nova Gorica, Vipavska 11c, SI-5270, Ajdovščina, Slovenia
Thanos Manos
Institute of Neuroscience and Medicine Neuromodulation (INM-7), Research Center Jülich, 52425, Jülich, Germany
Thanos Manos

Authors

Charalampos (Haris) Skokos
View author publications
You can also search for this author in PubMed Google Scholar
Thanos Manos
View author publications
You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Charalampos (Haris) Skokos .

Editor information

Editors and Affiliations

University of Cape Town, Department of Mathematics and Applied Ma, Rondebosch, South Africa
Charalampos (Haris) Skokos
School of Mathematics and Statistics, University of Sydney, Sydney, Australia
Georg A. Gottwald
Observatoire de Paris, IMCCE, Paris, France
Jacques Laskar

Appendix: Pseudo-Codes for the Computation of the SALI and the GALI k

We present here pseudo–codes for the numerical computation of the SALI (Table 5.1) and the GALI_k (Table 5.2) methods, according to the algorithms presented in Sects. 5.2 and 5.3.1 respectively.

Table 5.1 Numerical computation of the SALI

Full size table

Table 5.2 Numerical computation of the GALI_k

Full size table

Rights and permissions

Reprints and permissions

Copyright information

About this chapter

Cite this chapter

Skokos, C.(., Manos, T. (2016). The Smaller (SALI) and the Generalized (GALI) Alignment Indices: Efficient Methods of Chaos Detection. In: Skokos, C., Gottwald, G., Laskar, J. (eds) Chaos Detection and Predictability. Lecture Notes in Physics, vol 915. Springer, Berlin, Heidelberg. https://doi.org/10.1007/978-3-662-48410-4_5

Download citation

DOI: https://doi.org/10.1007/978-3-662-48410-4_5
Published: 04 March 2016
Publisher Name: Springer, Berlin, Heidelberg
Print ISBN: 978-3-662-48408-1
Online ISBN: 978-3-662-48410-4
eBook Packages: Physics and AstronomyPhysics and Astronomy (R0)

Publish with us

Policies and ethics

The Smaller (SALI) and the Generalized (GALI) Alignment Indices: Efficient Methods of Chaos Detection

Abstract

Similar content being viewed by others

Second-Order Chaos Indicators MEGNO2 and OMEGNO2: Theory

A multi-arc approach for chaotic orbit determination problems

Classifying orbits in the classical Hénon–Heiles Hamiltonian system

Keywords

5.1 Introduction and Basic Concepts

5.2 The Smaller Alignment Index (SALI)

5.3 The Generalized Alignment Index (GALI)

5.3.1 Computation of the GALI

5.3.2 Behavior of the GALI for Chaotic and Regular Orbits

5.3.2.1 Some Illustrative Paradigms

5.3.2.1.1 Hamiltonian Systems

5.3.2.1.2 Symplectic Maps

5.3.2.2 The Case of 2d Maps

5.3.3 Regular Motion on Low Dimensional Tori

5.3.3.1 Searching for Regular Motion on Low Dimensional Tori

5.3.4 Behavior of the GALI for Periodic Orbits

5.4 Applications

5.4.1 Global Dynamics

5.4.1.1 Investigating Global Dynamics by the GALI k with 2 ≤ k ≤ N

5.4.1.2 Investigating Global Dynamics by the GALI k with N < k ≤ 2N

5.4.2 Studies of Various Dynamical Systems

5.4.2.1 An Accelerator Map Model

5.4.2.2 A Hamiltonian Model of a Bose-Einstein Condensate

5.4.2.3 Further Applications of the SALI and the GALI Methods

5.4.3 Time Dependent Hamiltonians

5.5 Summary

Notes

References

Acknowledgements

Author information

Authors and Affiliations

Corresponding author

Editor information

Editors and Affiliations

Appendix: Pseudo-Codes for the Computation of the SALI and the GALI k

Appendix: Pseudo-Codes for the Computation of the SALI and the GALI k

Rights and permissions

Copyright information

About this chapter

Cite this chapter

Download citation

Share this chapter

Publish with us

Search

Navigation

5.4.1.1 Investigating Global Dynamics by the GALI_k with 2 ≤ k ≤ N

5.4.1.2 Investigating Global Dynamics by the GALI_k with N < k ≤ 2N

Appendix: Pseudo-Codes for the Computation of the SALI and the GALI_k