Keywords

17.1 Introduction

It is well known that disturbances exist in all practical processes [1–5]. In recent years, disturbance observer based control (DOBC) strategies have been successfully used in various systems, such as robot manipulators [6–8], high speed direct-drive positioning tables [9], permanent magnet synchronous motors [10] and magnetic hard drive servo systems [11] etc. However, the exogenous disturbances in most DOBC results [12, 13] are supposed to be generated by linear exogenous system, while there are always irregular and nonlinear disturbances in practical systems, which will no longer be effective by using the present model-based disturbance observer design methods.

On the other hand, Takagi-Sugeno (T-S) fuzzy model becomes very popular since it is a powerful tool for approximating a wide class of nonlinear systems, such as descriptor systems [14], networked control systems [15, 17], stochastic systems [16] and time-delay systems [15]. Furthermore, some typical control problems, including dynamic tracking control [18], fault estimation and detection [19], sliding-mode control [20] and filter design [21] have also been considered through T-S fuzzy modeling.

This paper discusses the anti-disturbance tracking control for the T-S fuzzy models with parametric uncertainties and irregular disturbances. Following the T-S fuzzy modeling for unknown irregular disturbances, the composite anti-disturbance controller are designed by combining PI control structure and disturbance observer design method. It is shown that the stability and the favorable tracking performance of augmented systems can achieved by using convex optimization algorithm and Lyapunov analysis method. Finally, simulation results in flight control system are given to show the efficiency of the proposed approach.

17.2 Model Description with Fuzzy Disturbance Modeling

Considering the following T-S fuzzy model with parametric uncertainties and exogenous disturbances

Plant Rule a: If \(\vartheta _{1}\) is \(M_{1}^{a}\), and \(\cdots \) and \(\vartheta _{q}\) is \(M_{q}^{a}\), then

$$\begin{aligned} \left\{ \begin{aligned} \dot{x}(t)&=(A_{0a}+\varDelta A_{0a})x(t)+(B_{0a}+\varDelta B_{0a})[u(t)+d_{1}(t)]+d_{2}(t)\\ y(t)&=C_{0a}x(t)\\ \end{aligned} \right. \end{aligned}$$
(17.1)

where \(\vartheta =[\vartheta _{1},\ldots ,\vartheta _{q}]\) and \(M_{g}^{a}(a=1,2,\ldots ,p)\) are the premise variables and the fuzzy sets, respectively. p, q are the numbers of If-Then rules and premise variables, respectively. \(x(t)\in R^{n},u(t)\in R^{m}, d_{1}(t)\in R^{m},d_{2}(t)\in R^{n}\) and \(y(t)\in R^{p_{1}}\) are the control input, modeled disturbance, unmodeled disturbance with bounded peaks and the measurement output, respectively. \(A_{0a}, B_{0a}, C_{0a}\) are the coefficient matrices with appropriate dimensions. \(\varDelta A_{0a}\) and \(\varDelta B_{0a}\) represent parametric uncertainties.

The overall fuzzy model can be inferred as follows

$$\begin{aligned} \left\{ \begin{aligned} \dot{x}(t)&=\sum _{a=1}^{p}h_{a}(\vartheta )\left\{ (A_{0a}+\varDelta A_{0a})x(t)+(B_{0a}+\varDelta B_{0a})[u(t)+d_{1}(t)]\right\} +d_{2}(t)\\ y(t)&=\sum _{a=1}^{p}h_{a}(\vartheta )C_{0a}x(t) \end{aligned} \right. \end{aligned}$$
(17.2)

where \(\sigma _{a}(\vartheta )=\prod _{g=1}^{q}M_{g}^{a}(\vartheta _{g}),h_{a}(\vartheta )=\sigma _{a}(\vartheta )/\sum _{a=1}^{p}\sigma _{a}(\vartheta ) \), in which \(M_{g}^{a}(\vartheta _{g})\) is the grade of membership of \(\vartheta _{g}\) in \(M_{g}^{a}\) and \(h_{a}(\vartheta )\ge 0,\sum _{a=1}^{p}h_{a}(\vartheta )=1\).

Moreover, the nonlinear disturbances \(d_{1}(t)\) can be generated by the following T-S fuzzy model with r plant rules.

Plant Rule j: If \(\theta _{1}\) is \(A_{1}^{j}\), and \(\cdots \) and \(\theta _{n}\) is \(A_{n}^{j}\), then

$$\begin{aligned} \left\{ \begin{aligned} \dot{w}(t)&=W_{j}w(t) \\ d_{1}(t)&=V_{j}w(t) \end{aligned} \right. \end{aligned}$$
(17.3)

where \(W_{j}\) and \(V_{j}\) are known coefficient matrices. \(\theta _{i}(i=1,\ldots ,n)\) and \(A_{i}^{j}(j=1,2,\ldots ,r)\) are the premise variables and the fuzzy sets, respectively. r is the number of If-Then rules, while n is the number of the premise variables.

By fuzzy blending, the overall fuzzy model can be defined as follows

$$\begin{aligned} \left\{ \begin{aligned} \dot{w}(t)&=\sum _{j=1}^{r}h_{j}(\theta )W_{j}w(t) \\ d_{1}(t)&=\sum _{j=1}^{r}h_{j}(\theta )V_{j}w(t) \\ \end{aligned} \right. \end{aligned}$$
(17.4)

where \( \omega _{j}(\theta )=\prod _{i=1}^{n}A_{i}^{j}(\theta _{i}), h_{j}(\theta )=\omega _{j}(\theta )/\sum _{j=1}^{r}\omega _{j}(\theta ) \), \(\theta =[\theta _{1},\ldots ,\theta _{n}], j=1,\ldots ,r\) is the membership function of the system with respect to plant rule j, and \(h_{j}(\theta )=\omega _{j}(\theta )/\sum _{j=1}^{r}\omega _{j}(\theta )\).

The uncertainties in T-S fuzzy model (1) are assumed to be of the form

$$\begin{aligned} \varDelta A_{0a}=HF(t)E_{1a},\; \varDelta B_{0a}=HF(t)E_{2a} \end{aligned}$$
(17.5)

where \(H,E_{1a}\) and \(E_{2a}\) are constant matrices with corresponding dimensions. F(t) is an unknown, real and possibly time-varying matrix with Lebesgue measurable elements satisfying

$$\begin{aligned} F^{T}(t)F(t)\le I,\forall t. \end{aligned}$$
(17.6)

Lemma 1

Assume that X and Y are vectors or matrices with appropriate dimension. The following inequality

$$\begin{aligned} X^{T}Y+Y^{T}X\le \alpha X^{T}X+\alpha ^{-1}Y^{T}Y \end{aligned}$$
(17.7)

holds for any constant \(\alpha >0\).

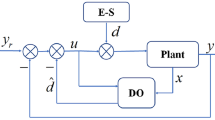
17.3 Design of DOB PI Composite Controller

In this section, we construct a composite full-state observer to estimate the state x(t) and the disturbance \(d_{1}(t)\) simultaneously.

Based on the above-mentioned T-S fuzzy model (2), we introduce a new state variable

$$\begin{aligned} \bar{x}(t):=\left[ x^{T}(t),\int _{0}^{t}e^{T}(\tau )d\tau \right] ^{T} \end{aligned}$$
(17.8)

where the tracking error e(t) is defined as \(e(t)=y(t)-y_{d}\), \(y_{d}\) is the reference output. Then the augmented system can be established as

$$\begin{aligned} \dot{\bar{x}}(t)=\sum _{a=1}^{p}h_{a}(\vartheta )\{A_{a}\bar{x}(t)+B_{a}[u(t)+d_{1}(t)]\}+Cy_{d}+Jd_{2}(t) \end{aligned}$$
(17.9)

where \(A_{a} = \left[ \begin{array}{cc} A_{0a}+HFE_{1a} &{} 0 \\ C_{0a} &{} 0 \\ \end{array} \right] , B_{a}=\left[ \begin{array}{c} B_{0a}+HFE_{2a} \\ 0 \\ \end{array} \right] , C=\left[ \begin{array}{c} 0 \\ -I \\ \end{array} \right] , J=\left[ \begin{array}{c} I \\ 0 \\ \end{array} \right] \).

By combining the exogenous disturbance model (4) with T-S fuzzy model (2), the augmented system can be further constructed by

$$\begin{aligned} \left\{ \begin{aligned} \dot{z}(t)&=\sum _{a=1}^{p}\sum _{j=1}^{r}h_{a}(\vartheta )h_{j}(\theta )\{\bar{A}_{0aj}z(t)+\bar{B}_{0a}u(t)\}+\bar{J}d_{2}(t)\\ y(t)&=\sum _{a=1}^{p}h_{a}(\vartheta )\bar{C}_{0a}z(t) \\ \end{aligned} \right. \end{aligned}$$
(17.10)

where \(z(t)=[x^{T}(t),w^{T}(t)]^{T}\), \({} \bar{A}_{0aj}=\left[ \begin{array}{cc} A_{0a}+HFE_{1a} &{} (B_{0a}+HFE_{2a})V_{j} \\ 0 &{} W_{j} \\ \end{array} \right] , \bar{B}_{0a}=\left[ \begin{array}{c} B_{0a}+HFE_{2a} \\ 0 \\ \end{array} \right] , \bar{C}_{0a}=\left[ \begin{array}{cc} C_{0a} &{} 0 \\ \end{array} \right] , \bar{J}=\left[ \begin{array}{cc} I &{} 0 \\ \end{array} \right] ^{T} \).

The composite observer for both x(t) and w(t) is designed as

$$\begin{aligned} \left\{ \begin{aligned} \dot{\hat{z}}(t)&=\sum _{a=1}^{p}\sum _{j=1}^{r}h_{a}(\vartheta )h_{j}(\theta )\{\bar{A}_{0aj}\hat{z}(t)+\bar{B}_{0a}u+L(\hat{y}(t)-y(t))\}\\ \hat{y}(t)&=\sum _{a=1}^{p}h_{a}(\vartheta )\bar{C}_{0a}\hat{z}(t) \\ \end{aligned} \right. \end{aligned}$$
(17.11)

where \(\hat{z}(t)=[\hat{x}^{T}(t),\hat{w}^{T}(t)]^{T}\), \(L=[L^{T}_{1},L^{T}_{2}]^{T}\) is the observer gain to be determined later. Moreover, the full-state estimation error \(\tilde{e}=z(t)-\hat{z}(t)\) can be expressed as

$$\begin{aligned} \dot{\tilde{e}}(t)=\sum _{a=1}^{p}\sum _{j=1}^{r}h_{a}(\vartheta )h_{j}(\theta )(\bar{A}_{0aj}+L\bar{C}_{0a})\tilde{e}(t)+\bar{J}d_{2}(t) \end{aligned}$$
(17.12)

The composite-observer-based (COB) PI-type controller with fuzzy rules is refined as

$$\begin{aligned} u(t)=-\hat{d}_{1}(t)+\sum _{b=1}^{p}h_{b}(\vartheta )\left( K_{Pb}\hat{x}+K_{Ib}\int _{0}^{t}e(\tau )d\tau \right) , K_{b}=\left[ \begin{array}{cc} K_{Pb} &{} K_{Ib} \\ \end{array} \right] \end{aligned}$$
(17.13)

where \( \hat{d}_{1}(t)=\sum _{j=1}^{r}h_{j}(\theta )\left[ \begin{array}{cc} 0 &{} V_{j} \\ \end{array} \right] \hat{z}(t) \).

Substituting (13) into (9) yields

$$\begin{aligned} \dot{\bar{x}}(t)=\sum _{a,b=1}^{p}\sum _{j=1}^{r}h_{a}(\vartheta )h_{b}(\vartheta )h_{j}(\theta )\left[ (A_{a}+B_{a}K_{b})\bar{x}(t)+D_{abj}\tilde{e}+Cy_{d}+Jd_{2}(t)\right] \end{aligned}$$
(17.14)

where \(D_{abj}=[-B_{a}K_{Pb},B_{a}V_{j}]\).

Combining the estimation error model (12) with the closed-loop model (14) yields

$$\begin{aligned} \left[ \begin{array}{c} \dot{\bar{x}}(t) \\ \dot{\tilde{e}}(t) \\ \end{array} \right] =&\sum _{a,b=1}^{p}\sum _{j=1}^{r}h_{a}(\vartheta )h_{b}(\vartheta )h_{j}(\theta ) \left\{ \left[ \begin{array}{cc} A_{a}+B_{a}K_{b} &{} D_{abj} \\ 0 &{} \bar{A}_{0aj}+L\bar{C}_{0a} \\ \end{array} \right] \left[ \begin{array}{c} \bar{x}(t) \\ \tilde{e}(t) \\ \end{array} \right] \right. \nonumber \\&+ \left. \left[ \begin{array}{c} C \\ 0 \\ \end{array} \right] y_{d} \right\} \end{aligned}$$
(17.15)

17.4 Theorem Proof via Convex Optimization Algorithm

Theorem 1

For the augmented system (15) consisting of PI control input and the disturbance observer, if there exist \(Q_{1}=P_{1}^{-1}>0\) and \(R_{1b}\) satisfying

$$\begin{aligned} \varTheta _{aa}<0,a=1,2\ldots ,p;\;\varTheta _{ab}+\varTheta _{ba}<0,a<b,a,b=1,2\ldots ,p \end{aligned}$$
(17.16)

and \(P_{2}>0\) and \(R_{2}\) satisfying

$$\begin{aligned} \sum _{a=1}^{p}\sum _{j=1}^{r}\varXi _{aj}<0 \end{aligned}$$
(17.17)

where

$$\begin{aligned} \varTheta _{ab}=\left[ \begin{array}{ccccccc} sym(\tilde{A}_{a}Q_{1}+\tilde{B}_{a}R_{1b}) &{} C &{} J &{} G_{1}H &{} G_{2}H &{} Q_{1}G_{1}E_{1a} &{} R_{1b}^{T}E_{2a}^{T}\\ C^{T} &{} -\mu _{1}^{2}I &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 \\ J^{T} &{} 0 &{} -\mu _{3}^{2}I &{} 0 &{} 0 &{} 0 &{} 0 \\ H^{T}G_{1}^{T} &{} 0 &{} 0 &{} -\alpha _{1}^{-1}I &{} 0 &{} 0 &{} 0 \\ H^{T}G_{2}^{T} &{} 0 &{} 0 &{} 0 &{} -\alpha _{2}^{-1}I &{} 0 &{} 0 \\ E_{1a}G_{1}^{T}Q_{1} &{} 0 &{} 0 &{} 0 &{} 0 &{} -\alpha _{1}I &{} 0 \\ E_{2a}R_{1b} &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} -\alpha _{2}I \\ \end{array} \right] \end{aligned}$$
(17.18)
$$\begin{aligned} \varXi _{aj}=\left[ \begin{array}{cccccc} sym(P_{2}\tilde{A}_{0aj}+R_{2}\bar{C}_{0a}) &{} P_{2}G_{3}H &{} G_{3}E_{1a}^{T} &{} P_{2}G_{4}H &{} G_{5}^{T}V_{j}^{T}E_{2a}^{T} &{} P_{2}\bar{J}\\ H^{T}G_{3}^{T}P_{2} &{} -\beta _{1}^{-1}I &{} 0 &{} 0 &{} 0 &{} 0 \\ E_{1a}G_{3}^{T} &{} 0 &{} -\beta _{1}I &{} 0 &{} 0 &{} 0 \\ H^{T}G_{4}^{T}P_{2} &{} 0 &{} 0 &{} -\beta _{2}^{-1}I &{} 0 &{} 0 \\ E_{2a}G_{5} &{} 0 &{} 0 &{} 0 &{} -\beta _{2}I &{} 0 \\ \bar{J}^{T}P_{2} &{} 0 &{} 0 &{} 0 &{} 0 &{} -\mu _{2}^{2}I \\ \end{array} \right] \end{aligned}$$
(17.19)

and \(\mu _{1}>0, \mu _{2}>0, \mu _{3}>0, \alpha _{1}>0, \alpha _{2}>0, \beta _{1}>0, \beta _{2}>0\) are known parameter. Then the augmented system (15) under the composite controller (13) is stable and the tracking error e(t) convergent to zero. The gains are given by \(K_{b}=R_{1b}Q_{1}^{-1}\) and \(L=P_{2}^{-1}R_{2}\).

Please noted that due to the limitation of the paper length, the corresponding proof of Theorem 1 is omitted.

17.5 Simulation Example

Similarly with [22], the following T-S fuzzy models are introduced to describe the simple airplane plant

$$A_{01}=\left[ \begin{array}{cc} -0.833 &{} 1.000\\ -2.175 &{} -1.392\\ \end{array} \right] , A_{02}=\left[ \begin{array}{cc} -1.134 &{} 1.000\\ -4.341&{} -2.003\\ \end{array} \right] , A_{03}=\left[ \begin{array}{cc} -1.644 &{} 1.000\\ -22.547 &{} -3.607\\ \end{array} \right] $$

\(B_{01}=[-0.1671,-10.9160]^{T}, B_{02}=[-0.2128,-19.8350]^{T}, B_{03}=[-0.2110,-32.08 13]^{T}, C_{01}=C_{02}=C_{03}=[1,1], d_{2}(t)=[0.1,0.1]^{T}sin(0.1\pi t), E_{21}=E_{22}=E_{23}=[0.1,0.1]^{T}, H=\left[ \begin{array}{cc} 1 &{} 0 \\ 0 &{} 1 \\ \end{array} \right] , F=\left[ \begin{array}{cc} sin(t)/2 &{} 0 \\ 0 &{} cos(t)/2 \\ \end{array} \right] , E_{11}=E_{12}=E_{13} =\left[ \begin{array}{cc} 0.2 &{} 0 \\ 0 &{} 0.2 \\ \end{array} \right] \).

The member functions are chosen as

$$M_{1}^{a}=exp\left( \frac{-(y-s_{a})^{2}}{2\sigma _{1}^{2}}\right) / \left[ exp(\frac{-(y+1)^{2}}{2\sigma _{1}^{2}})+exp(\frac{-(y-1)^{2}}{2\sigma _{2}^{2}})+exp(\frac{-y^{2}}{2\sigma _{3}^{2}})\right] $$

where \(\sigma _{1}=\sigma _{2}=\sigma _{3}=0.8,s_{1}=-1,s_{2}=1,s_{3}=0\).

The nonlinear irregular exogenous disturbance is described by two T-S fuzzy rules, and \(W_{1}=\left[ \begin{array}{cc} -1 &{} 2 \\ -5 &{} 0 \\ \end{array} \right] , V_{1}=\left[ \begin{array}{cc} 0 &{} 4 \\ \end{array} \right] , W_{2}=\left[ \begin{array}{cc} 0 &{} -6 \\ 4 &{} 0 \\ \end{array} \right] , V_{2}=\left[ \begin{array}{cc} 0 &{} 4 \\ \end{array} \right] \).

The member functions are chosen as

$$A_{1}^{1}=\frac{exp(\frac{-(w_{1}-1.2)^{2}}{2\sigma _{1}^{2}})}{exp(\frac{-(w_{1}-1.2)^{2}}{2\sigma _{1}^{2}})+exp(\frac{-(w_{1}-1)^{2}}{2\sigma _{2}^{2}})}, A_{1}^{2}=\frac{exp(\frac{-(w_{1}-1)^{2}}{2\sigma _{2}^{2}})}{exp(\frac{-(w_{1}-1.2)^{2}}{2\sigma _{1}^{2}})+exp(\frac{-(w_{1}-1)^{2}}{2\sigma _{2}^{2}})}$$

where \(\sigma _{1}^{2}=0.5, \sigma _{2}^{2}=1\).

Supposed that the initial values in augmented system (10)–(11) are taken to be \(x_{0}=\left[ \begin{array}{cc} 2 &{} 3 \\ \end{array} \right] ^{T}\), \(\hat{x}_{0}=\left[ \begin{array}{cc} -2 &{} -2 \\ \end{array} \right] ^{T}\), \(w_{0}=\left[ \begin{array}{cc} 2 &{} 1 \\ \end{array} \right] ^{T}\), \(\hat{w}_{0}=\left[ \begin{array}{cc} 1 &{} 1 \\ \end{array} \right] ^{T}\).

Fig. 17.1
figure 1

Disturbance and its estimation

Full size image
Fig. 17.2
figure 2

The trajectory of system output

Full size image

The desired tracking objective is design as \(y_{d}=5\). Figure 17.1 displays the response of nonlinear disturbance and its observation value, which illustrates the tracking performance of the disturbance observer is satisfactory. Figure 17.2 is the trajectory of system output and the good performance dynamic tracking performance can be embodied.

17.6 Conclusion

This paper studies the anti-disturbance tracking control framework for T-S fuzzy models by using T-S disturbance modeling and disturbance observer design. The DOB PI composite controller is designed based on T-S fuzzy models and T-S fuzzy disturbance models simultaneously. As a result, a convex optimization approach is adopted to ensure the augmented closed-loop systems stable and convergence of the tracking error to zero.