A Coupled Method of Meshfree Poly-Cell Galerkin and Finite Element for Elasticity Problems

Abstract

This paper developed a new method named as MPG/FEM method which is constructed by coupling the meshfree poly-cell Galerkin method (MPG) with the finite element method (FEM) for the analysis of elasticity problems. The present MPG/FEM method synthesizes the advantages of both FEM and MPG. MPG/FEM method not only simplifies the implementation of essential boundary conditions like FEM, but also inherits good accuracy from MPG. The numerical tests in the present work demonstrate that the results obtained by MPG/FEM method show an excellent agreement with the theoretical results. The coupled method is very accurate and has a promising potential for the analyses of more complicated elasticity problems.

1 Introduction

The finite element method (FEM) has been widely applied to solve various types of problems in science and engineering in the past several decades [1]. However, due to its strong reliance on element mesh, it is always difficult (or even impossible) to simulate some problems such as large deformation problems with severe element distortions, crack growth problems with arbitrary and complex paths which do not coincide with original element interfaces, and the problems of breakage of material with large number of fragments [2]. In order to eliminate these shortcomings, the meshfree methods (MMs) have been developed and achieved remarkable progress in the recent years. They include the smoothed particle hydrodynamic method (SPH) [3, 4], the element-free Galerkin method (EFG) [5], the reproducing kernel particle method (RKPM) [6], the meshless local Petrov-Galerkin method (MLPG) [7, 8], etc.

As elements are necessary in FEM, the integration cells based on background mesh are also required in EFG regardless of the actual geometrics. Compared with FEM, MMs have more difficulties in accurate integration, for the boundaries of integration domains do not align with shape function supports [9]. Then, MLPG is developed to waive the background cells [7], however, it resulted in an unsymmetrical stiffness matrix and obviously led to additional difficulties and extra expenses for analysis. The stabilized conforming nodal integration method is presented thereafter, but the nodal volume is not easy to evaluate [10], especially for 3D problems with complex geometries. To evaluate the volume of nodal support, the Voronoi diagram [11, 12] and other meshfree methods based on it [3, 13, 14] are adopted, nevertheless, the generation of Voronoi diagram is much more time-consuming and expensive than Delaunay triangulation which is widely used in standard FEM [15, 16].

The meshfree poly-cell Galerkin method (MPG) [17] employed the ploy-cell which is the local support domain surrounding the node and it can make sure of the alignment of integration domains with shape functions supports. Moreover, unlike the standard moving least-square approximation (MLS) applied in EFG and MLPG, an improved MLS is introduced in MPG which can avoid the frequent matrix inversion and improve the computation efficiency. However, like other MMs, the shape functions of MPG do not satisfy the Kronecker delta property, and the treatment of essential boundary conditions is not as straightforward as that in meshbased methods.

In order to tackle these problems, a coupled method has developed. The present work introduces a new simulation method called MPG/FEM method, it couples MPG with FEM to synthesize their advantages and overcome their shortcomings. In MPG/FEM method, the research domain is divided into two types of sub-domains: the first type of sub-domain which needs to impose essential boundary conditions is simulated by FEM, the other type of sub-domain is simulated by MPG, and these two parts are connected by transition domain which is the subdomain of the second sub-domain. The transition domain of MPG and FEM are discretized by interface elements, and a hybrid displacement approximation is defined to make sure that the shape functions of these interface elements can satisfy the delta Kronecker property.

This paper is organized as follows. Section 2 gives a brief description of MPG including the construction of poly-cell local support domain, MLS approximation and discrete equations for elasticity problems. Section 3 presents the coupled method of MPG and FEM and briefs the coupling technique. Section 4 gives two typical numerical examples of the present MPG/FEM method. Finally, some conclusions are drawn in Sect. 5.

2 Improved Poly-Cell Galerkin Method

In the construction of MPG trail function, the influenced domain is confirmed by poly-cell, and the moving least-squares approximation (MLS) method is widely used to construct shape functions.

2.1 Poly-Cell Support Construction

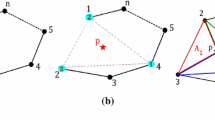
In the construction of MPG trial function, the influenced domain possessed by an interested node should be confirmed firstly. Unlike the traditional MMs, whose influenced domain is usually a circular domain centered by the interested node, the influenced domain of MPG is confirmed by poly-cell, as shown in Fig. 1. In the poly-cell local domain, a background mesh is firstly generated that may cover the whole research domain. The background mesh can be either Voronoi diagram or regular mesh [15], and the regular mesh is preferred in this paper. For an arbitrary node, its host cell needs to be found firstly, and then the local support domain can be obtained by extending the size of its host cell in four directions ($x_+$, $x_-$, $y_+$, $y_-$) [17]. The extending distance in direction $x_+$ of the given node can be expressed as: $d_{eI}^{x_{+}}=n_e c_x,$ where $c_x$ is the size of host cell in the $x$ direction, $n_e$ is a constant integer ($n_e=1$ in this work). The extending distances in other directions are obtained in the similar way.

Fig. 1

Schematic of constructing poly-cell local support based on regular background mesh

After obtaining the local support, the weight function requires to be defined based on this poly-cell local domain. Suppose a node $I$ has a local support shown in Fig. 2, then the weight function of node $I$ is defined by $w_I(x,y)=f(x)g(y),$ in which

$$\begin{aligned} f(x)=\left\{ \begin{array}{ll} e^{-\beta \left[ \frac{x-x_I}{0.5(x^{\max }_{I}-x^{\min }_{I})}\right] ^2},&{}\text {if}~x^{\min }_{I}\le x \le x^{\max }_{I}\\ 0,&{}\text {else}, \end{array} \right. \end{aligned}$$

(1)

$$\begin{aligned} g(y)=\left\{ \begin{array}{ll} e^{-\beta \left[ \frac{y-y_I}{0.5(y^{\max }_{I}-y^{\min }_{I})}\right] ^2},&{}\text {if}~y^{\min }_{I}\le y \le y^{\max }_{I}\\ 0,&{}\text {else}, \end{array} \right. \end{aligned}$$

(2)

where $\beta$ is a constant parameter, which will be studied in Sect. 4.

Fig. 2

A sampling local support of interested node $I$. Note This node may not be at the center of the support domain

2.2 Moving Least-Squares Approximation

Lancaster and Salkauskas [18] presented moving least-squares approximation (MLS), which is widely applied to form trial functions in MMs. Consider a field $u(x)$ defined in the 2D domain $\varOmega$ with boundary $\varGamma$, which can be approximated in the following form:

$$\begin{aligned} u^h(x)&=\sum \limits _{i=1}^{m}p_i(x)a_i(x)=p^T(x)a(x),\end{aligned}$$

(3)

$$\begin{aligned} p(x)&=\big [p_1(x),p_2(x),\ldots ,p_m(x)\big ]^T,\end{aligned}$$

(4)

$$\begin{aligned} a(x)&=\big [a_1(x),a_2(x),\ldots ,a_m(x)\big ]^T, \end{aligned}$$

(5)

where $p(x)$ is the vector of basis functions $p_i(x)$ built by the Pascal’s triangles, $a(x)$ is the vector of unknown nodal parameter of the field $u(x)$, $x$ is the space coordinates, and $m$ is the number of basis functions.

To determine $a(x)$, a quadratic function $J(x)$ is constructed by the value of approximation function $u^h(x)$ and field function $u(x)$ at arbitrary node $i$:

$$\begin{aligned} J(x)&=\sum \limits _{i=1}^{n}w_i(x)\big [u^h(x_i)-u(x_i)\big ]^2\\ \nonumber&=\sum \limits _{i=1}^{n}w_i(x)\bigg [\sum \limits _{i=1}^{n}p_j(x_i)a_j(x_i)-u_i\bigg ]^2, \end{aligned}$$

(6)

where $n$ is the number of nodes inside and on the boundary line of the local support, and $w_i(x)$ is the value of the weight function. The partial derivative of $J(x)$ with respect to $a(x)$ leads to the following equation:

$$\begin{aligned} A(x)a(x)=B(x)u, \end{aligned}$$

(7)

where the moment matrix $A$ and basic matrix $B$ are expressed by

$$\begin{aligned} A(x)&=\sum \limits _{i=1}^{n}w_i(x)p(x_i)p^T(x_i),\end{aligned}$$

(8)

$$\begin{aligned} B(x)&=\big [w_1(x)p(x_1), w_2(x)p(x_2), \ldots , w_n(x)p(x_n)\big ], \end{aligned}$$

(9)

$$\begin{aligned} u&=(u_1,u_2,\ldots ,u_n)^T. \end{aligned}$$

(10)

Solving Eq. (7) yields:

$$\begin{aligned} a(x)=A^{-1}(x)B(x)u. \end{aligned}$$

(11)

Substituting Eq. (11) back into Eq. (3) leads to:

$$\begin{aligned} u^h(x)&=p^T(x)A^{-1}(x)B(x)u=N(x)u,\end{aligned}$$

(12)

$$\begin{aligned} N(x)&=p^T(x)A^{-1}(x)B(x), \end{aligned}$$

(13)

where $N(x)$ is the vector of MLS shape functions.

In the improved MLS approximation, the Schmidt orthogonalizing formulas is imported to orthogonalize the vector of basis functions $r(x)$. Substituting $r(x)$ as $p(x)$ into equations of the standard MLS. A similar form of equations will be obtained as follows:

$$\begin{aligned} A(x)&=\sum _{i=1}^{n}w_i(x)r(x_i)r^T(x_i),\end{aligned}$$

(14)

$$\begin{aligned} B(x)&=\big [w_1(x)r(x_1), w_2(x)r(x_2), \ldots , w_n(x)r(x_n)\big ]. \end{aligned}$$

(15)

Since the vector $r$ is an orthonormalized vector, matrix $A$ will be an identical matrix, and then the modified shape functions simplified as:

$$\begin{aligned} N(x)=r^T(x)B(x). \end{aligned}$$

(16)

The advantage of using orthogonalized basis functions is that it not only reduces the computational cost, but also improves the accuracy of interpolation [19].

2.3 Discrete Equations

Consider a solid problem defined in domain $\varOmega$ bounded by $\varGamma (\varGamma =\varGamma _t+\varGamma _u)$, the governing equations of the problems can be expressed as follows:

$$\begin{aligned}&\nabla \sigma +b=0~~(\text {in}~~\varOmega ),\end{aligned}$$

(17)

$$\begin{aligned}&\sigma \times n=\bar{t}~~(\text {on}~~\varGamma _t),\end{aligned}$$

(18)

$$\begin{aligned}&u=\bar{u}~~(\text {on}~~\varGamma _u), \end{aligned}$$

(19)

where $\nabla$ is the divergence operator, $\sigma =[\sigma _x,\sigma _y,\sigma _{xy}]^T$ is the stress vector, $u=[u,v]^T$ is the displacement field, $b=[b_x, b_y]^T$ is the body force vector, $\bar{t}$ is the prescribed traction on natural boundary, $\bar{u}$ is the prescribed displacement on essential boundary, and $n$ is the vector of unit outward normal at a point on the natural boundary.

Liu [20] presented the unconstrained Galerkin weak form for elasticity problems as Eq. (20).

$$\begin{aligned} \int _{\varOmega }(L\delta u)^{T}DLud\varOmega -\int _{\varOmega }\delta u^Tbd\varOmega -\int _{\varGamma t}\delta u^Ttd\varGamma =0, \end{aligned}$$

(20)

where $L$ is the differential operator.

In linear elasticity, the material matrix $D$ for plane stress problem and plane strain problem are expressed respectively as Eqs. (21) and (22):

$$\begin{aligned} D=&\frac{E}{1-v^2}\left[ \begin{array}{lll} 1&{}v&{}0\\ v &{} 1 &{} 0\\ 0 &{} 0 &{} \frac{1-v}{2} \end{array}\right] ,\end{aligned}$$

(21)

$$\begin{aligned} D=&\frac{E(1-v)}{(1+v)(1-2v)}\left[ \begin{array}{lll} 1&{}\frac{v}{1-v}&{}0\\ \frac{v}{1-v}&{}1&{}0\\ 0&{}0&{}\frac{1-2v}{2(1-v)} \end{array}\right] , \end{aligned}$$

(22)

where $E$ is Young’s modules and $v$ is possion’s ratio.

Like FEM, MPG uses the similar global weak form given in Eq. (20). Substituting the approximation equations into Galerkin weak form leads to $Ku=f,$ where

$$\begin{aligned} K_{ij}&=\int _\varOmega B_{i}^TDB_{j}d\varOmega ,\end{aligned}$$

(23)

$$\begin{aligned} f_i&=\int _{\varGamma _{t}}N_{i}^{T}\bar{t}d\varGamma +\int _{\varOmega }N_{i}^Tbd\varOmega ,\end{aligned}$$

(24)

$$\begin{aligned} B_{i}&=\left[ \begin{array}{lll} \frac{\partial N_{i}}{\partial x}&{}0&{}\frac{\partial N_{i}}{\partial y}\\ 0&{}\frac{\partial N_{i}}{\partial y}&{}\frac{\partial N_{i}}{\partial x} \end{array}\right] . \end{aligned}$$

(25)

3 Coupling of MPG and FEM

In order to couple MPG and FEM, the displacement compatibility and the force equilibrium conditions on interface boundary should be satisfied. The hybrid displacement approximation and hybrid shape functions are proposed in MPG/FEM method.

1. Transition Condition

Consider a 2D solid problem whose problem domain can be divided into two parts $\varOmega _1$ and $\varOmega _2$, and these two sub-domains are connected by the interface boundary $\varGamma _I$. FEM is used in $\varOmega _1$ and MPG is used in $\varOmega _2$ as shown in Fig. 3. In the coupling of MPG and FEM, the displacement compatibility and the force equilibrium conditions on $\varGamma _I$ should be satisfied.

Fig. 3

Interface elements used in MPG/FEM method

Thus, the nodal displacements $U_I^{(1)}$ and $U_I^{(2)}$ of node I on $\varGamma _I$ for $\varOmega _1$ and $\varOmega _2$ should be equal.

$$\begin{aligned} U_I^{(1)}=U_I^{(2)}=U_I. \end{aligned}$$

(26)

And the summation of the nodal forces $F_I^{(1)}$ and $F_I^{(2)}$ of node $I$ on $\varGamma _I$ for $\varOmega _1$ and $\varOmega _2$ should be zero.

$$\begin{aligned} F_I^{(1)}+F_I^{(2)}=0. \end{aligned}$$

(27)

In the coupled methods, it is ideal to satisfy the both two requirements. The displacement compatibility is more important and must be satisfied precisely, while the force equilibrium condition could be satisfied approximately by using the method of weighted residuals in some coupled methods [21].

2. Coupling Technique

Due to the shape functions of MPG lacking delta Kronecker property, it is impossible to couple MPG and FEM directly. So, the transition domain is introduced in MPG domain [21], in which the interface elements are discretized and the MLS shape functions are constructed near the interface boundary $\varGamma _I$. In these interface elements, a hybrid displacement approximation is defined to make sure that the MLS shape functions in the MPG domain along $\varGamma _I$ can satisfy the delta Kronecker property. Figure 3 shows the transition domain $\varOmega _I$ which is a layer of sub-domain along the interface boundary $\varGamma _I$ within MPG domain $\varOmega _2$. The new displacement approximation in MPG domain $\varOmega _2$ can be rewritten as

$$\begin{aligned} u^h(x)=\sum \limits _{i=1}^{n}\tilde{N_i}(x)u_i, \end{aligned}$$

(28)

where the hybrid shape functions of the interface elements are defined as

$$\begin{aligned} \tilde{N_i}(x)=\left\{ \begin{array}{ll} \big [1-R(x)\big ]N_i(x)+R(x)\varphi (x),&{}x\in \varOmega _I\\ N_i(x),&{}x\in \varOmega _2-\varOmega _I, \end{array} \right. \end{aligned}$$

(29)

where $\varphi (x)$ is the FEM shape functions of an interface element, $R(x)$ is a ramp function and it is performed as

$$\begin{aligned} R(x)=\sum \limits ^{k}_{j=1}\varphi (x),x\in \varGamma _I, \end{aligned}$$

(30)

where $k$ is the number of nodes located on the interface boundary $\varGamma _I$ for an interface element. According to the property of FEM shape functions, $R(x)$ will be unity along $\varGamma _I$ and vanish outside of the interface domain:

$$\begin{aligned} R(x)=\left\{ \begin{array}{ll} 1,&{}x\in \varGamma _I\\ 0,&{}\varOmega _2-\varOmega _I. \end{array}\right. \end{aligned}$$

(31)

Therefore, the modified interface shape functions can satisfy both FEM interpolation and MPG approximation, and it means that the coupling of MPG and FEM can satisfy displacement consistency and interpolate a linear field precisely.

4 Numerical Examples

Two cases of 2D Elasticity problems have been studied in order to examine the properties of the presented MPG/FEM. The variable units used in this paper are based on international standard unit system unless specially denoted.

4.1 Cantilever Beam

A 2D cantilever beam with length $L$, height $D$ and unit thickness is studied as a benchmark problem here. The beam is fixed at the left end and subjected to a parabolic traction $P$ at the free end as shown in Fig. 4. Timoshenko and Goodier [22] calculated the theoretical solutions in stress for the plain strain case as follows.

$$\begin{aligned} \left\{ \begin{array}{l} \sigma _{xx}=-\frac{P}{I}(L-x)(y-\frac{D}{2})\\ \sigma _{yy}=0\\ \sigma _{xy}=-\frac{Py}{2I}(y-D), \end{array}\right. \end{aligned}$$

(32)

where $I$ is the moment of inertia of $D^3/12$.

The parameters in the computation are taken as: $L=8$, $D=1$, $P=-1$, $v=0.25$, $E=3.0\times 10^7$, and the plane strain condition is assumed.

Fig. 4

A 2D cantilever beam subjected to parabolic traction on the right end

Fig. 5

Discretized model of the cantilever beam

As shown in Fig. 5, the beam is divided into two parts. FEM using the four-node quadrilateral elements is used in the left part where the essential boundary condition is included, and MPG is used in the right part where the traction boundary condition is included. These two parts are connected by the transition region which is a sub-domain of MPG domain and discretized by 10 regularly distributed transition particles. Figure 6 illustrates the error of stress in $x$ direction at the cross-section of $x = L/2$ with different value of $\beta$ between calculated value and theoretical value. The figure shows the error is smaller with a larger value of $\beta$ , and $\beta$ is selected to be 0.8 as the optimal parameter.

Fig. 6

Comparison for error of stress in $x$ direction at the cross-section of $x=L/2$ with different value of $\beta$

4.2 Hollow Cylinder Under Internal Pressure

A hollow cylinder with an internal radius $a$, an external radius $b$ and unit thickness is considered as another typical problems to validate the MPG/FEM. As shown in Fig. 7, the uniform pressure $p$ is applied to the inner surface $(r =a)$, while the outer surface $(r =b)$ is free of traction. Due to the symmetry of the problem, only one-quarter of the cylinder is modeled. Also, Young and Budynas [23] gave the theoretical solution.

$$\begin{aligned} \left\{ \begin{array}{l} \sigma _{r}=\frac{a^2p}{b^2-a^2}(1-\frac{b^2}{r^2})\\ \sigma _{\theta }=\frac{a^2p}{b^2-a^2}(1+\frac{b^2}{r^2})\\ \sigma _{r\theta }=0. \end{array}\right. \end{aligned}$$

(33)

In the numerical computations, the following parameters are chosen: $a=1$, $b=5$, $p=1$, and the plane stress conditions are assumed. The material used is linear elastic with Young’s modules $E =1\times 10^3$ and $v=0.25$ unless specially denoted.

Fig. 7

A hollow cylinder subjected to internal pressure $p$ and its quarter model

Fig. 8

Discretized model of the hollow cylinder

Fig. 9

Comparison of solutions for stress

As shown in Fig. 8, the hollow cylinder is also divided into several sub-domains. FEM is used in the sub-domain where the essential boundary condition is included, MPG is used in anther sub-domain, and these two sub-domains are connected by transition domain. Figure 9 contrasts the solution for stress in radial direction and circumferential direction between theoretical and calculated value by the coupled method with $\beta$ equals 0.8, and they both show an excellent alignment between the theoretical results and numerical results.

4.3 Results and Analysis

Numerical examples have shown an excellent consistency between the theoretical and numerical results, and the following can be seen clearly:

• (1) The improved poly-cell local support domain guarantees the alignment of integration domain and support of the shape functions, which can significantly improve the accuracy of numerical integration.

• (2) Comparing with FEM, the MPG/FEM method is more flexible in dealing with the geometrical boundary, only the essential boundary which is limited in the studied boundary is simulated with the same way to FEM.

• (3) Comparing with MPG, the shape functions of MPG/FEM method can satisfy the Kronecker delta property, so it is easier to impose essential boundary conditions.

• (4) An excellent agreement has presented by comparing the solutions for stress between the theoretical and numerical results, and it shows the MPG/FEM method has a high precision in dealing with elasticity problems.

5 Conclusions

Formulations of a coupled method named as MPG/FEM method are presented in this paper. Numerical examples such as hollow cylinder under internal pressure, shows an excellent agreement between the theoretical and numerical results. The advantages of MPG/FEM are as follows:

• (1) The poly-cell local support domain guarantees the alignment of integration domain and support of the shape functions, which can significantly improve the accuracy of numerical integration.

• (2) Comparing with FEM, the MPG/FEM method is more flexible in dealing with the geometrical boundary, only the essential boundary which is limited in the studied boundary is simulated with the same way to FEM.

• (3) Comparing with MPG, the shape functions of MPG/FEM method can satisfy the Kronecker delta property, so it is easier to impose essential boundary conditions.

• (4) An excellent agreement has presented by comparing the solutions for stress between the theoretical and numerical results, and it shows the MPG/FEM method has a high precision in dealing with elasticity problems.