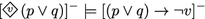Abstract
This paper presents a novel semantics for deontic modals which provides a uniform solution to prominent puzzles in the literature. The paper focuses on deontic conflicts, discussing them using the Dr. Procrastinate puzzle as an example. The focus lies on the Dr. Procrastinate puzzle as it combines an upward monotonicity puzzle with a conflict of obligations, allowing an explanation of the solutions to both types of puzzle in detail.
The semantics is an extension of radical inquisitive semantics, and it modifies Andersonian deontic modals as it introduces quantification over alternatives. The solution to deontic conflicts is made possible by the semantics allowing permission and prohibition statements to introduce multiple violations. Each rule is assigned a different violation, allowing for reasoning with rules also in cases where it is impossible to avoid violating all rules.
I am grateful to Jeroen Groenendijk, Stefan Hinterwimmer, Floris Roelofsen, Mandy Simons, Carla Umbach, and Matthijs Westera for extensive discussion of the ideas presented here and closely related topics, to two anonymous reviewers for constructive criticism, and to the Estonian Research Council for their support.
Access provided by Autonomous University of Puebla. Download conference paper PDF
Similar content being viewed by others
Keywords
These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.
1 Introduction
This paper aims to unravel conflicts between deontic modal auxiliaries such as may and must. We will represent permission as \(\Diamond \varphi \) and obligation as \(\Box \varphi \) as is standard.
A deontic conflict is a situation in which every state of affairs results in the violation of a rule. For example, imagine a teenager whose mother and father are both cross with her. The mother thinks she spends too much time in her room and the father thinks she has stayed out too late. The two issue the following punitive rules.

The salient reading of the modals in (1) is deonticFootnote 1 - (1-a) says that, according to the rules which now apply to the teenager, if she does not leave her room, she breaks these rules, and (1-b) says that leaving the room breaks rules. Naturally, the two rules together are unfair, as she does not have any way to avoid displeasing both the mother and father. This situation is an example of a deontic conflict as all choices for the teenager result in a violation of some rule. Such deontic conflicts have been at the center of a number of prominent puzzles for standard deontic logic.
Standard modal logic (SML) [29] and theories that extend it, such as Kratzer semantics [23, 24], express modals as quantification over possible worlds. Permission is represented as existential quantification and obligation (and thus prohibition) as universal quantification. Kratzer adds two contextual features for deontic modals. First, the modal base, which is a function \(f\) such that \(f(w)\) represents the content of a body of laws in a world \(w\). Secondly, an ordering on worlds according to how close they are to the ideal world.
Deontic conflicts such as the one in (1) are regrettably commonplace and their existence poses a problem for the standard account. In SML, (1-a) is the case when all accessible worlds are \(p\) worlds and (1-b) is the case when none of the accessible worlds are \(p\) worlds. Obviously, these statements cannot both be the case, so in each non-absurd state of evaluation, at least one of the rules in (1) will be predicted to be false. But that’s counter-intuitive. The situation is a deontic conflict precisely because both of those rules hold simultaneously, leading to unavoidable trouble for the teenager.Footnote 2
There are a number of well known puzzles for standard theories of deontic modals: puzzles which include deontic conflicts such as the Dr. Procrastinate puzzle,Footnote 3 other puzzles such as Ross’s paradox,Footnote 4 the free choice puzzleFootnote 5 and the conditional oughts puzzle,Footnote 6 This paper will focus on the deontic conflicts and Dr. Procrastinate.
Jackson’s Dr. Procrastinate puzzle focuses on an expert who, when asked to write a review, will not write it. This fact is represented by (2-a). As experts are expected to write reviews, intuitively, the obligationFootnote 7 in (2-b) holds. As not writing a review will delay the entire process of a review actually being written, (2-c) holds as well.

In the literature on the puzzle it is agreed that there are two predictions to be made. First, one should not be able to infer (3) from (2-b) as that leads to an intuitive contradiction between (2-c) and (3).

Intuitively, (2-b) and (2-c) coexisting is not absurd as both can be the case simultaneously. This is the case because the obligation in (2-b) requires one to bring about both \(p\) and \(q\), and not \(p\) alone. In fact, accepting without writing is going to delay the entire process. Unfortunately, standard accounts of deontic modals are upward monotonic, which means that any entailment between propositions holds also when those propositions are embedded under a modal operator, so whenever \(\varphi \models \psi \) then \(O \varphi \models O \psi \). As standardly the entailment in (4-a) holds, so does the entailment in (4-b).

According to the standard treatment of modals, the entailment in (4-b) holds, so whenever (2-b) holds, so does (3). Immediately, a solution suggests itself on how to avoid this part of the puzzle - the semantics for deontic modals should not be upward monotonic. This approach has been adopted by many recent authors, including Lassiter, Cariani and others. [11, 25]. The treatment of deontic modals presented here is also non-monotonic, but the lack of upward monotonicity is motivated independently.
Looking ahead, we will consider the addition of multiple violations to the semantics, so that different deontic rules can refer to separate violations. By doing so, we wish to demonstrate that non-monotonicity is not a necessary component for solving the deontic conflict described in the story.
Regarding the deontic conflict part of the puzzle, despite the fact that Dr. Procrastinate will necessarily violate the obligation in (2-b), she could avoid violating the second obligation in (2-c). The semantics ought to also predict that her behaviour is more reproachable when she chooses to violate both obligations, i.e., to accept the request to write the review, despite (2-a) being the case. This fact does not concern monotonicity.
This paper will present the deontic semantics \(\textsc {madris}\),Footnote 8 which provides a uniform solution to these prominent puzzles of deontic modals. \(\textsc {madris}\) stands for Modified Andersonian Deontic Radical Inquisitive Semantics as it is in the spirit of the current most prominent alternative to SML, which expresses modals as Andersonian [7] implications to violations.Footnote 9
Anderson introduced a distinguished proposition \(v\) to stand for sentences of the kind “some rule has been violated.” When some \(\varphi \) is obligatory, when you do not do \(\varphi \) then you have violated the obligation. This can be represented as \(\Box \varphi := \lnot \varphi \rightarrow v\). Similarly, if some \(\varphi \) is permitted then it would be odd to find out that by doing \(\varphi \) you have incurred a violation. This intuition can be represented as \(\Diamond \varphi := \varphi \rightarrow \lnot v\).
A violation is not exactly a state of affairs or an unfortunate consequence but rather the observation that some rules have not been followed. Anderson [7, p.347] provides a useful analogy with chess to explain violations. According to the rules of chess, a pawn may move at most two squares at a time. So, playing e5 which moves the pawn three squares violates that rule. See the illustration on the following page.Footnote 10

Naturally, nothing stops a player from lifting the pawn from e2 to e5, nor will a punishment necessarily follow. Yet, anyone that opens with e5 is not playing chess according to its rules. And \(v\) records the fact some rule is violated.
Anderson’s treatment of deontic modals via material implication or relevant implication suffers from a number of puzzles besides deontic conflicts, most importantly, it does not account for the strengthening the antecedent puzzle [8]. We will demonstrate in Sect. 3.8 that madris avoids the strengthening the antecedent puzzle.
Implication plays an important role in an Andersonian treatment of deontics, so for a modern treatment of implication, consider the conditional in (5).

In the current prominent theory on conditionals by Kratzer [22, 23], the antecedent becomes the restrictor of a modal operator in the consequent that’s evaluated with respect to a modal base and an ordering source. If no modal is found in the consequent, it is assumed to be a covert epistemic necessity operator.Footnote 11 (5) is analyzed in Kratzer semantics with a covert necessity modal over the consequent we will both be wrong and (5) is the case when, after restricting the modal base for this necessity modal to all worlds where antecedent, I agree with you, holds, the consequent, it must be that we will both be wrong, is the case as well.
In madris, conditionals are designed to make similar predictions to Kratzer semanticsFootnote 12 but there is the option to go with a stronger clause for negation than in Kratzer semantics, which is still weaker than classical negation for material implication. The treatment accounts for Ramsey’s intuition that the conditional question if p, then q? has two contrary answers if p, then q and if p, then not q. This paper will illustrate the stronger clauses but is not committed to either the stronger or weaker negation of conditionals.
We will be focusing on the crucial feature of inquisitive semantics that its treatment of disjunction formalizes the intuition that or sentences serve to offer alternatives. This has been suggested in the literature as a solution to the free choice puzzle by, for example, Aloni [5]. Unlike previous accounts in which universal quantification over alternatives was a part of only the support-conditions of a sentence, we also quantify universally over alternatives in the rejection-conditions of deontic modals.
madris is an extension of radical inquisitive semantics, and it modifies Andersonian deontic modals by introducing quantification over alternatives. This has a significant effect on the treatment of the negation of modals. In madris, deontic modals are related to implications, but due to different negation conditions between the two, deontic modals cannot be defined via implication.
This account provides intuitive predictions for both modal sentences and their negations, while offering a solution to the puzzles of SML.Footnote 13
2 Semantics
Consider a propositional language with negation \((\lnot )\), conjunction \((\wedge )\) and implication \((\rightarrow )\) as its basic connectives, to which we add a class of special atoms (\(v_{_1},v_{_{2}},...\)) that state that a specific rule has been violated.
We introduce deontic sentential operators (

), read as permission. We add a second deontic operator (obligation) standardly:

. The \(v ... v_n\) within the diamond and box symbols refers to the particular rule which grants the permission or sets an obligation. Depending on the rule, modals can refer to different violations, and we assume that each rule does generally refer to a different violation.
Disjunction is defined in the usual way: \(\varphi \vee \psi :=\lnot (\lnot \varphi \wedge \lnot \psi )\). As in basic inquisitive semantics (See [13–15]), an interrogative sentential operator is introduced in the language by definition: \({?\varphi } := \varphi \vee \lnot \varphi \), but it will not be utilized here.
A world is a binary valuation of the atomic sentences in the language, including the designated atoms that state that a specific rule has been violated. Let \(\mathcal {A}\) be the set of atomic sentences. We represent a world \(w\) as a set which for each \(a\in \mathcal {A}\) contains either \(a\) or \(\overline{a}\), meaning that \(a\) holds in \(w\), and that \(a\) doesn’t hold in \(w\), respectively. \(\sigma \) and \(\tau \) are variables that range over states, which are sets of worlds, and we use \(\omega \) to denote the set of all worlds, which corresponds to the ignorant state.
In our recursive semantics we define when a state supports (\(\models ^+\)) and rejects (\(\models ^-\)) a sentence.Footnote 14 We denote the set of states that supports a sentence by \([\varphi ]^+\) and states that reject a sentence by \([\varphi ]^-\). The recursive semantics that we will state guarantees that \([\varphi ]^+\) and \([\varphi ]^-\) are downward closed. i.e. if \(\sigma \in [\varphi ]^+\) and \(\tau \subseteq \sigma \), then \(\tau \in [\varphi ]^+\) and same for \([\varphi ]^-\). The meaning of a sentence is determined by the pair \(\langle [\varphi ]^+, [\varphi ]^-\rangle \).
For the propositional case there are always one or more maximal supporting/rejecting states for a sentence called alternatives.
Definition 1
Alternatives
-
Support-alternatives: \(\textsc {alt}[\varphi ]^+ :=\{\sigma \in [\varphi ]^+\mid \lnot \exists \tau \in [\varphi ]^+:\tau \supset \sigma \}\)
-
Rejection-alternatives: \(\textsc {alt}[\varphi ]^- :=\{\sigma \in [\varphi ]^-\mid \lnot \exists \tau \in [\varphi ]^-:\tau \supset \sigma \}\)
The key notions of inquisitiveness and informativeness are defined standardly for inquisitive semantics (see, e.g., Ciardelli et al. [13, p. 9)]). But unlike in basic inquisitive semantics, a sentence \(\varphi \) can be inquisitive or informative both on the support-side and rejection-side, which is mirrored in the definition.
Definition 2
Inquisitiveness and informativeness
-
\(\varphi \) is support-inquisitive iff at least two alternatives support \(\varphi \).
-
\(\varphi \) is rejection-inquisitive iff at least two alternatives reject \(\varphi \).
-
\(\varphi \) is inquisitive iff \(\varphi \) is support-inquisitive or rejection-inquisitive.
-
\(\varphi \) is support-informative iff \(\bigcup [\varphi ]^+\not =\omega \).
-
\(\varphi \) is rejection-informative iff \(\bigcup [\varphi ]^-\not =\omega \).
-
\(\varphi \) is informative iff \(\varphi \) is support-informative or rejection-informative.
According to the clause for support-informativeness, a sentence \(\varphi \) is informative if the union of all its supporting states does not include all worlds, and likewise for rejection-informativeness.
When the set of support-alternatives for \(\varphi \), \(\textsc {alt}[\varphi ]^+\), contains more than one element then \(\varphi \) is (support-) inquisitive, and when the set of rejection-alternatives for \(\varphi \), \(\textsc {alt}[\varphi ]^-\), contains more than one element then \(\varphi \) is (rejection-) inquisitive. This plays a crucial role in explaining free choice phenomena concerning deontic modals.
Since meanings are determined by the pair of supporting and rejecting states, entailment should also be stated relative to both components of meaning. Classically this would be a correct, but redundant formulation as the support and reject perspective on entailment would coincide.
Definition 3
Entailment
-
Support-entailment: \(\varphi \models _+ \psi \) iff \([\varphi ]^+\subseteq [\psi ]^+\)
-
Rejection-entailment: \(\varphi \models _- \psi \) iff \([\psi ]^-\subseteq [\varphi ]^-\)
-
Entailment: \(\varphi \models \psi \) iff \(\varphi \) support-entails \(\psi \) and \(\varphi \) rejection-entails \(\psi \).
According to Definition 3, a sentence \(\varphi \) support-entails the sentence \(\psi \) if every state that supports \(\varphi \) also supports \(\psi \), and likewise for rejection. The dual nature of entailment plays an important role in the explanation of various deontic puzzles.Footnote 15
The recursive statement of the semantics is as follows.
Definition 4
(MADRIS).
-
Atomic sentences:
-
\(\sigma \models ^+ p\) iff \(\forall w\in \sigma :p\in w\)
-
\(\sigma \models ^- p\) iff \(\forall w\in \sigma :\overline{p} \in w\)
-
Negation:
-
\(\sigma \models ^+ \lnot \varphi \) iff \(\sigma \models ^- \varphi \)
-
\(\sigma \models ^- \lnot \varphi \) iff \(\sigma \models ^+ \varphi \)
-
Conjunction:
-
\(\sigma \models ^+\varphi \wedge \psi \) iff \(\sigma \models ^+\varphi \) and \(\sigma \models ^+\psi \)
-
\(\sigma \models ^-\varphi \wedge \psi \) iff \(\sigma \models ^-\varphi \) or \(\sigma \models ^-\psi \)
-
Implication:
-
\(\sigma \models ^+ \varphi \rightarrow \psi \) iff \(\forall \tau \in \textsc {alt}[\varphi ]^+:\tau \cap \sigma \models ^+\psi \)
-
\(\sigma \models ^- \varphi \rightarrow \psi \) iff \(\exists \tau \in \textsc {alt}[\varphi ]^+:\tau \cap \sigma \models ^-\psi \)
-
Deontic permission:
-
\(\sigma \models ^+\)
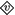
\(\varphi \quad iff\ \ \forall \tau \in \textsc {alt}[\varphi ]^+:\tau \cap \sigma \models ^-v\)
-
\(\sigma \models ^-\)
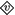
\(\varphi \quad iff\ \ \forall \tau \in \textsc {alt}[\varphi ]^+:\tau \cap \sigma \models ^+v\)
3 Illustrating the Semantics
The clauses of \(\textsc {madris}\) are illustrated below with examples.Footnote 16
3.1 Atomic Sentences
Consider the natural language example in (6).

The treatment of atomic sentences is standard, but as is characteristic of the radical approach to inquisitive semantics, the semantics specifies both the support and rejection conditions for a sentence. According to clause 1 of Definition 4, an atomic sentence \(p\) is supported by a state \(\sigma \) if \(p\) holds in every world \(w\) in \(\sigma \); and \(p\) is rejected in \(\sigma \) if \(p\) holds in no world \(w\) in \(\sigma \).
This means that there is a unique maximal state \(\sigma \) that supports \(p\), a unique element of \(\textsc {alt}[p]^+\), which consists of all worlds where \(p\) holds; and a unique maximal state \(\sigma \) that rejects \(p\), a unique element of \(\textsc {alt}[p]^-\), which consists of all worlds where p does not hold. The fact that there is a single maximal state means that atoms are neither support-inquisitive nor rejection-inquisitive.
As the maximal supporting state does not include worlds where \(\lnot p\) holds, and the maximal rejecting state does not include worlds where \(p\) holds, \(p\) is both support informative and rejection informative. We will generally omit discussion of informativeness below, unless a sentence is not informative.
The meaning of the atomic sentences \(p\) and \(q\) is depicted in Figs. 1 and 2, respectively, where the circles correspond to worlds that concern only the value of these two atomic sentences. Maximal states that support a sentence are indicated by solid lines; maximal states that reject a sentence are indicated by dashed lines.
3.2 Negation
Negation is illustrated by the negative response to the atomic sentence in (6). According to clause 2 of Definition 4, negation flips between support and rejection, so that a sentence \(\lnot \varphi \) is supported by a state \(\sigma \) if \(\sigma \) rejects \(\varphi \) and conversely for the rejection of \(\lnot \varphi \). This means that \(\lnot \varphi \) is support-inquisitive when \(\varphi \) is rejection-inquisitive, and vice versa. Consider the simple example \(\lnot p\), whose meaning is depicted in Fig. 3.
3.3 Conjunction
Consider the illustrating natural language example in (7).

According to clause 3 of Definition 4, a state \(\sigma \) supports a conjunction \(\varphi \wedge \psi \) if \(\sigma \) supports both \(\varphi \) and \(\psi \); and \(\sigma \) rejects this conjunction if \(\sigma \) rejects \(\varphi \) or \(\sigma \) rejects \(\psi \).
Consider the simple example \(p \wedge q\). A state \(\sigma \) supports \(p\wedge q\) if \(\sigma \) supports both \(p\) and \(q\). This means that \(\textsc {alt}[p\wedge q]^+\) consists of a single element, the state that consists of all worlds where both \(p\) and \(q\) hold, and is thus not support-inquisitive.
A state \(\sigma \) rejects \(p \wedge q\) if it rejects either \(p\) or it rejects \(q\). As \(\textsc {alt}[p \wedge q]^-\) consists of two elements, a state consisting of all worlds where \(p\) does not hold and a state consisting of all worlds where \(q\) does not hold, \(p \wedge q\) is rejection-inquisitive. The meaning of \(p \wedge q\) is depicted in Fig. 4.
3.4 Disjunction
\(\varphi \vee \psi \) is defined in the standard way as \(\lnot (\lnot \varphi \wedge \lnot \psi )\) and is illustrated by Fig. 5. As disjunction corresponds to the negation of conjunction, it is support-inquisitive but not rejection-inquisitive.
3.5 Implication
Implication directly utilizes the notion of alternatives as the universal quantification in the support clause and the existential quantification in the reject clause both concern the alternatives for the antecedent. According to clause 4 of Definition 4, a state \(\sigma \) supports \(\varphi \rightarrow \psi \) if every alternative (i.e., maximal supporting state) for the antecedent \(\varphi \), restricted to the information contained in \(\sigma \), supports the consequent \(\psi \). A state \(\sigma \) rejects \(\varphi \rightarrow \psi \) only when some maximal supporting state for \(\varphi \), restricted to the information contained in \(\sigma \), rejects \(\psi \). Consider the simple example \(p \rightarrow q\), illustrated by the natural language example (8).

As explained above, there is only one maximal supporting state for an atomic sentence \(p\), consisting of all worlds where \(p\) is the case. This means that the universal and existential quantification in the support and rejection clauses do not play a crucial role with this example. A state \(\sigma \) supports \(p \rightarrow q\) if the maximal substate of \(\sigma \) where \(p\) is the case supports \(q\). So, in all worlds in \(\sigma \) where \(p\) is the case, \(q\) should be the case as well. A state \(\sigma \) rejects \(p\rightarrow q\) if the maximal substate of \(\sigma \) where \(p\) is the case rejects \(q\). So, in all the worlds in \(\sigma \) where \(p\) is the case, \(q\) should not be the case. Figure 6 shows the meaning of \(p \rightarrow q\). The quantification over alternatives in the clauses comes into play when the antecedent or consequent is support-inquisitive. These effects are discussed in the Subsect. 3.7 which compares implication and deontic permission.
3.6 Violation-Based Deontic Modals
According to the clause for permission, the state \(\sigma \) supports a permission statement

if every maximal supporting state for the prejacent \(\varphi \), restricted to the information contained in \(\sigma \), rejects the violation \(v\).
A state \(\sigma \) rejects

if every maximal supporting state for \(\varphi \), restricted to the information contained in \(\sigma \), supports \(v\). So, a state that rejects permission for \(\varphi \) supports the statement that \(\varphi \) is prohibited.
Consider the simple exaple

illustrated by example (9).

There is only one maximal supporting state for an atomic sentence \(p\), consisting of all worlds where \(p\) is the case. The universal quantification in the support and rejection clause concerns only this state. A state \(\sigma \) supports

if the maximal substate of \(\sigma \) where \(p\) is the case supports \(\lnot v\). So, in all worlds in \(\sigma \) where \(p\) is the case, the violation \(v\) must not be the case. A state \(\sigma \) rejects

if the maximal substate of \(\sigma \) where \(p\) is the case supports \(v\). So, in all worlds in \(\sigma \) where \(p\) is the case, the violation \(v\) should be the case as well. The simple example is structurally similar to implication and, in madris when the antecedent/prejacent of

is not inquisitive, it can be expressed via implication.
Proposition 1
If \(\varphi \) is not support-inquisitive, then

.
This holds e.g. when \(\varphi \) is the atom \(p\). As is evident, we follow Anderson’s intuition that the meaning of deontic operators is connected to implication. Unlike implication, though, permission does not have an arbitrary sentence \(\psi \) as its consequent, instead, permission always refers to a specific violation \(v\). Furthermore, the rejection clause for permission differs from the clause for implication, which will be discussed in Subsect. 3.7 where we compare modals and implication.
Figure 7 illustrates

, and the three deontic statuses: permission, prohibition and neutrality. For convenience, non-violation worlds (\(\overline{v}\)) are indicated in green and violation worlds (\(v\)) in red.Footnote 17 The illustrative picture allows one to determine the deontic status of a state of affairs by seeing whether worlds that support a state of affairs \(p\) are within, outside or both with respect to the maximal state that supports the deontic statement in the figure.
-
Permission. The state where p is permitted has no \(pv\) world in the maximal supporting state,Footnote 18 so looking at \(p\) worlds, \(\lnot v\) is also the case. The maximal state for
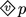
is illustrated by using a continuous line in Fig. 7.
-
Prohibition. The state where p is prohibited, has no \(p\overline{v}\) world. The state which supports

is illustrated by using a dashed line in Fig. 8.
-
Neutral. Both of these states are deontically neutral towards \(\lnot p\) as the maximal supporting states include both a \(\overline{p} v\) and a \(\overline{p} \overline{v}\) world.
3.7 Comparing Implication and Permission
The differences between implication and permission concern their rejection conditions and inquisitiveness. In the simple implication \(p \rightarrow q\) quantification over the alternatives for the antecedent play no significant role due to the antecedent only having one maximal supporting state. This, however, is not the case for \((p \vee q)\rightarrow r\), where the antecedent is a support-inquisitive disjunction for which there are two maximal supporting states: the set of all worlds where \(p\) is the case and the set of all worlds where \(q\) is the case (see Fig. 5).
The natural language example in (10) illustrates \((p \vee q)\rightarrow r\).

For a state \(\sigma \) to support \((p \vee q)\rightarrow r\), what should hold is that for each of the two maximal supporting states for \(p \vee q\), when \(\sigma \) is restricted to it, the resulting substate of \(\sigma \) supports \(r\). So, in each world in \(\sigma \) where \(p\) is the case, \(r\) should also be the case; and in each world in \(\sigma \) where \(q\) is the case, \(r\) should also be the case.
For a state \(\sigma \) to reject \((p \vee q)\rightarrow r\), what should hold is that for one (or both) of the two maximal supporting states for \(p \vee q\): the maximal supporting state for \(p\) and the maximal supporting state for \(q\), when \(\sigma \) is restricted to it, the resulting substate of \(\sigma \) rejects \(r\).
Consider \((p \rightarrow r) \wedge (q \rightarrow r)\). The first conjunct \(p \rightarrow r\) is supported in \(\sigma \) if the maximal state where \(p\) is supported, restricted to \(\sigma \), also supports \(r\). Likewise for \(q\rightarrow r\). According to the clause for conjunction, the state \(\sigma \) supports \((p \rightarrow r) \wedge (q \rightarrow r)\) if both conjuncts are supported. So both the maximal supporting states for \(p\) and for \(q\), restricted to \(\sigma \), also support \(r\).
According to the rejection clause for conjunction, a state \(\sigma \) rejects \((p \rightarrow r) \wedge (q \rightarrow r)\) if it rejects either conjunct: \(p \rightarrow r\) or \(q \rightarrow r\). A state \(\sigma \) rejects \(p \rightarrow r\) if all maximal supporting states for \(p\), restricted to \(\sigma \), reject \(r\). Likewise for \(q \rightarrow r\).
This means that \((p \vee q)\rightarrow r\) is supported and rejected in the same states as \((p \rightarrow r) \wedge (q \rightarrow r)\) and hence that the two sentences are equivalent.
Proposition 2
\((p \vee q)\rightarrow r \equiv (p \rightarrow r)\wedge (q \rightarrow r)\)
Classically this equivalence also holds and neither of the sentences is support-inquisitive. The maximal supporting state for \((p \vee q)\rightarrow r\) is illustrated in Fig. 9. \(\textsc {madris}\) also produces the result that both sentences are rejection-inquisitive. As we discussed with regard to \(p\wedge q\) above, illustrated by Fig. 4, this conjunction is rejected when either \(p\) or \(q\) is rejected. The conjunction between \(p\rightarrow r\) and \(q\rightarrow r\) should also be rejected when either conjunct is rejected. madris obtains this result as illustrated by Fig. 10 showing the two maximal rejecting states for \((p\vee q)\rightarrow r\).Footnote 19
In madris the free choice effect of

receives a straightforward semantic treatment, as

is support-equivalent to \(\varphi \rightarrow \lnot v\).
Proposition 3
\([\)

\((p\vee q)]^{+}\equiv [(p\vee q)\rightarrow \lnot v]^{+}\equiv [(p\rightarrow \lnot v)\wedge (q\rightarrow \lnot v)]^{+}\)
The solution to the free choice problem in madris has been extensively discussed in earlier work,Footnote 20 so it is not repeated here. But it is helpful to use free choice examples to illustrate the difference between the behaviour of implication and permission under negation.
According to an Andersonian analysis of permission as an implication,

is support-inquisitive, but intuitively it is not.

The salient reading of (11) says that both disjuncts are prohibited. We refer to this as the no choice reading, in that choosing to establish either a research center or a laboratory will break the rule in (11). This is because the drafters of a law or rule establish which permissions and obligations hold, which leaves no room for inquisitiveness. This leads to the standard non-inquisitiveness intuition regarding the interpretation of free choice examples and their negation (see example (11)):

, which the semantics predicts.
Unlike implication, both the support and reject clause for permission has universal quantification scoping over the prejacent, guaranteeing that even with an inquisitive prejacent \(\varphi \),

is not rejection-inquisitive. For a state \(\sigma \) to support

, what should hold is that for each of the two maximal supporting states for \(p \vee q\), \(p\) and \(q\), restricting \(\sigma \) to them results in a substate of \(\sigma \) which supports \(v\). So, in each world in \(\sigma \) where \(p\) is the case, \(v\) should also be the case, and in each world in \(\sigma \) where \(q\) is the case, \(v\) should also be the case. This results in a single maximal rejecting state illustrated in Fig. 11. As we saw earlier, due to the existential quantifier in the rejection clause for implication, when the antecedent is support-inquisitive, an implication is rejection-inquisitive. As illustrated by Fig. 12, \([(p \vee q)\rightarrow \lnot v]^-\) contains two maximal rejecting states. One rejecting state corresponds to \([p\rightarrow v]^+\) and is shaped like an ‘L’ while the other rejecting state corresponds to \([q\rightarrow v]^+\) and is rectangle-shaped. Due to not being rejection-inquisitive,

is stronger than \([(p \vee q)\rightarrow \lnot v]^-\).Footnote 21 The only way modals can be inquisitive is when an inquisitive connective scopes over modals.
3.8 Strengthening the Antecedent
Besides deontic conflicts, an Andersonian treatment of deontic modals standardly suffers from the strengthening the antecedent puzzle. The modified Andersonian treatment of modals allows madris to avoid this puzzle.
Andersonian modals which reduce deontic modals to implication inherit the properties of implication; for example, material implication is downward monotonic (DM). The property of DM shown in (12).

Downward monotonicity is generally regarded an unwanted property of deontic modals due to the strengthening the antecedent puzzle that we will discuss presently.
Strengthening the antecedent is a puzzle for material implication and other DM implications. The problem lies in the fact that in a material implication account an implication entails the implication where the antecedent has been strengthened with a conjunct: (14).
In the following, we will distinguish between the clauses in \(\textsc {madris}\) and material implication by representing the latter with \(\rightarrow _{m}\). In propositional logic, a conjunction entails its conjuncts:

We will make use of this entailment as in (14), the antecedent of the premise is \(p\) and the antecedent of the conclusion is \(p\wedge q\).

As discussed by Lewis [26, p.80] and others, the entailment in (14) leads to counter-intuitive examples such as (15).

Intuitively, we can accept (15-a) without accepting (15-b), but a material implication account of condtionals predicts that when (15-a) is the case, (15-b) cannot be false. This is not to say that there do not exist natural language examples in which the inference is more plausible. Consider (16).

Intuitively, we accept both (16-a) and (16-b). In fact, we can add any arbitrary conjunct in (16-b), such as whistling, because it does not change the outcome. But the existence of examples such as (15) demonstrates that the plausibility of the inference in (16) cannot be a general inference rule for implication.
Strengthening the antecedent is also relevant for deontic modals. Recall that Anderson defined a permission utterance as relevant implication from the prejacent to the negation of a violation \(v\). Anderson used relevant implication but we will adopt material implication for brevity’s sake. If the modal is defined using material implication, then whenever (17-a) holds, (17-b) holds as well.

This leads to examples such as the following.

Intuitively, no-one would accept that when permission is granted to walk the dog, this also grants permission to kill the president. So, strengthening the antecedent should not to be valid for neither implication nor modals in \(\textsc {madris}\). Because (13) holds, if \(\textsc {madris}\) modals were DM, whenever (18-a) is the case, so would be (18-b).
In \(\textsc {madris}\), strengthening the antecedent is not valid for implication or modals, which means deontic modals are not DM in \(\textsc {madris}\). We will demonstrate how strengthening the antecedent fails in \(\textsc {madris}\). The modal and implication case are parallel.
Consider the maximal supporting and rejecting states for the premise and conclusion in (18-a). A state \(\sigma \) supports \(p \rightarrow r\) if the maximal supporting state for \(p\), restricted to \(\sigma \), supports \(r\). Such a state cannot contain worlds where \(p\) and \(q\) hold, but \(r\) does not, nor worlds where \(p\) holds but \(q\) and \(r\) do not. On the other hand, a state \(\sigma \) supports \((p\wedge q) \rightarrow r\) if the maximal supporting state for \(p\wedge q\), restricted to \(\sigma \), supports \(r\). The only worlds incompatible with such a state are those where both \(p\) and \(q\) hold but \(r\) does not. We thus conclude that every state that supports \(p\rightarrow r\) also supports \((p\wedge q)\rightarrow r\) so that \(p\rightarrow r\) support-entails \((p \wedge q)\rightarrow r\).
This fact is illustrated in Figs. 13 and 14.
The support-entailment explains the intuitiveness of the inference in (16). When the additional information in the second conjunct does not have an effect on the implication, we do end up at only worlds in which \((p \wedge q)\rightarrow r\) also holds.
It is only when we begin to consider how one might reject the two sentences that the we see a difference. Recall that entailment looks at both supporting and rejecting states, such that when \(\varphi \) entails \(\psi \), every state that supports \(\varphi \) must also support \(\psi \) and every rejecting state for \(\psi \) must be a rejecting state for \(\varphi \).
Consider the maximal rejecting state for \((p \wedge q)\rightarrow r\) compared to the maximal rejecting state for \(p\rightarrow r\). A state \(\sigma \) rejects \((p\wedge q)\rightarrow r\) if the maximal supporting state for \(p\wedge q\), restricted to \(\sigma \), rejects \(r\). As we are interested only in worlds where both conjuncts hold, the only worlds that annot be in the state are those where \(p\), \(q\) and \(r\) hold. So it is possible to reject \((p\wedge q)\rightarrow r\) with relatively little information.
Conversely, a state rejects \(p\rightarrow r\) if the maximal supporting state for \(p\), restricted to \(\sigma \), rejects \(r\). Such a state cannot include both worlds where \(p\), \(q\) and \(r\) hold and also worlds where \(p\) and \(r\) hold but \(q\) does not hold. As we can see in Figs. 15 and 16, the maximal rejecting state for \((p \wedge q)\rightarrow r\) is not a rejecting state for \(p\rightarrow r\).
As \((p\wedge q)\rightarrow r\) only concerns the situation in which both \(p\) and \(q\) are the case, it does not provide as much information regarding when \(r\) follows as \(p \rightarrow r\) which also concerns itself with \(p\overline{q}\) worlds. This means that \(p\rightarrow r\) does not rejection-entail \((p \wedge q)\rightarrow r\).
Recall that entailment requires both support-entailment and rejection-entailment. As \(p\rightarrow r\) does not rejection-entail \((p \wedge q)\rightarrow r\), it also does not entail it. Due to the weaker rejection-conditions of the conclusion, strengthening the antecedent is not a valid inference pattern, which explains the counter-intuitive examples in the literature.
Also consider the deontic case. As with implication, the maximal supporting state for

supports

so

support-entails

. This can be determined by looking at Figs. 17 and 18. A state \(\sigma \) supports

if the maximal supporting state for \(p \wedge q\), restricted to \(\sigma \), rejects \(v\). As the maximal supporting state in Fig. 18 illustrates, the only world incompatible with

is the one where \(p\), \(q\) and \(v\) all hold. This world is also incompatible with

because a state \(\sigma \) supports

if the maximal supporting state for \(p\), restricted to \(\sigma \), rejects \(v\). So, for

is incompatible with all \(p\) worlds where \(v\) is the case. So the world where \(p\) and \(v\) are the case but \(q\) isn’t is also incompatible with

.
From this we can conclude that

grants less permission than

. It only grants permission for those situations in which both \(p\) and \(q\) are the case, and does not say whether a violation is incurred or not in those worlds where \(q\) is not the case. So it does not grant permission for cases where someone brings about \(p\) without bringing about \(q\). In this sense,

is a weaker permission statement than

that does grant permission to bring about \(p\) without bringing about \(q\).
On the other hand, as we can see in Figs. 19 and 20, the maximal rejecting state for

is not a rejecting state for

as it includes the world where \(p\) is the case but \(q\) and \(v\) are not the case.

is weaker than

as it only concerns the situation in which both \(p\) and \(q\) are the case. As such, for a state to reject

, the state cannot be such that it includes the worlds where both \(p\) and \(q\) are the case and no violation is incurred.
The world where \(p\) holds but \(q\) and \(v\) do not does not concern the conjunction example. Yet, the inclusion of this world does not satisfy the requirements for a state to reject

. For a state to reject

, when \(p\) is the case, a violation must occur. A state with the world where \(p\) is the case, but a violation does not occur, is not a rejecting state for

. This means that

does not rejection-entail

, and then it also does not entail it.
\(\textsc {madris}\) provides a semantic solution to the puzzle of strengthening the antecedent for implication and deontic modals in parallel fashion.Footnote 22 So madris correctly predicts that deontic modals are not DM.
3.9 Multiple Violations
The semantics allows the designation of \(v_{_1},\) \(v_{_2}\), etc for each specific violation. Unlike Anderson’s original conceptualization, now \(v_n\) stands for “rule\(_n\) has been violated” where \(n\) indexes each rule to a specific violation. Violations can be reasoned about in the same manner as any other information but there is no guarantee that every set of rules allows one to avoid all violations as there exist inherently conflicted sets of rules. Multiple violations will allow one to still determine the state with least violations.
Consider again the deontic conflict in (1), but this time we distinguish the two deontic statements by mother and father as two separate rules.

This distinction is sufficient for \(\textsc {madris}\) to provide the tools required to state that each alternative for the teenager results in a violation. Furthermore, \(\textsc {madris}\) allows for a more fine-grained analysis of such a deontic conflict through the introduction of multiple violations.
One way to conceptualize multiple violations is to differentiate deontic authorities. We will not use this conceptualization but it is useful to consider it briefly to see its shortcomings.
In the above example, mother and father can be taken to represent different deontic authorities: each provides rules they enforce largely independently of the other. We could then say that there exists a violation for mother: \(v_{_1}\) and a violation for father: \(v_{_2}\).
What the analysis gains from such a treatment is that we can now differentiate between different consequences of the inevitable breaking of the rules. The teenager can reason from the fact that mother’s violation results in a stern look (\(v_{_1}\rightarrow q\)) and father’s violation results in a more severe punishment (\(v_{_2}\rightarrow r\)) that, wishing to avoid \(r\), it is advantageous to stay in the room (\(\lnot p\)), even though doing so also violates a rule.
But such a conceptualization is problematic as rules set by one authority, for example by mother, can be inconsistent and deontic conflicts can still occur. For reasons of forgetfulness, malice, etc. people create situations of deontic conflicts. So, it could easily be the case that mother uttered both (19-a) and (19-b) in which case the conceptualization does not allow us to reason about the consequences of choosing \(p\) and \(\lnot p\) in the same manner as before.
It is possible to reason that some rules are more important to follow than others, even when they come from the same authority. A single law can specify that the violation of one article is followed by a harsher punishment than another. Consider different degrees of murder: manslaughter receives fewer years in prison than murder even though the violations are considered from the perspective of one authority - the state.
So, as is generally accepted in law, it is more plausible to assume that each rule has its own violation associated with it, such that the statement (19-a) being distinct from (19-b) would be the basis for associating (19-a) with \(v_{_1}\) and (19-b) with \(v_{_2}\).
A standard example of this in legal discourse, illustrated in (20), is a case when a court deems someone guilty of violating one article of a law, but judges that the defendant did not violate other articles of the same law.Footnote 23

Were the conceptualization of multiple violations authority-based, the judgment would be inconsistent: the defendant both incurs and does not incur the same violation. But this is not plausible.Footnote 24
Returning to the deontic conflict in (19), \(v_1\) refers to the rule (19-a) and \(v_2\) refers to the rule (19-b), so when the teenager chooses to leave the room, \(\lnot p\) holds, and via rule

, \(v_2\) holds as well. This violation says that the rule in (19-b) has been violated.
Further Work on Suppositions. A prevalent intuition regarding deontic statements says that sentences such as

should not provide information regarding whether \(p\) or \(\lnot p\) is the case. This intuition is straightforwardly accounted for in \(\textsc {madris}\) but it reappears with regard to certain deontic conflicts. Consider the conjunction in (21) on the assumption that both permission statements refer to the same violation.

The conjunction in (21) is supported by a state \(\sigma \) if both conjuncts, (21-a) and (21-b) are supported in the state. The first conjunct is supported by a state \(\sigma \) if the maximal supporting state for \(p\), restricted to \(\sigma \), supports \(\lnot v\). The second conjunct, (21-b), is supported by a state \(\sigma \) if the maximal supporting state for \(p\), restricted to \(\sigma \), supports \(v\). The conjunction is supported by \(\sigma \) only if there exist no worlds that support \(p\), i.e., the prejacent is not the case.
It is problematic that the conjunction of two permission statements, neither of which alone provides information regarding whether \(p\) or \(\lnot p\) is the case, provides the information that \(\lnot p\) is the case. This is because both

and

share the same prejacent \(p\) but the conjuncts provide contrary deontic information. The first states that no violation is incurred, and the other than a violation is incurred, which makes the two statements intuitively inconsistent.
\(\textsc {madris}\) does not yet have the tools to account for this type of an inconsistency, as it allows the prejacent to be vacuously supported by the empty state. The maximal supporting state for (21) where the prejacent \(p\) is rejected is illustrated in Fig. 21. Intuitively, this is a case of supposition failure as the supposition that the prejacent \(p\) is the case fails in all cases.
Not all deontic conflicts result in supposition failure. This paper focuses on the majority of deontic conflicts which can be intuitively avoided in case the permission and violation statements refer to different violations. But where such interpretations are infelicitous, and we have to assume that both deontic statements refer to the same violation, a deontic conflict results in supposition failure.
Groenendijk and Roelofsen have recently developed an extension of radical inquisitive semantics called suppositional inquisitive semantics [17] which adds suppositional content as a third component of meaning next to informative and inquisitive.Footnote 25 In the extension, the rejection of the antecedent of a conditional or the rejection of the prejacent of a modal no longer vacuously supports the implication or modal statement as a whole. To more accurately account for examples such as (21), ongoing work extends suppositional inquisitive semantics in the spirit of madris to also account for such cases.Footnote 26
4 Solving Puzzles
Alongside deontic conflicts as a whole, this paper demonstrates how introducing multiple violations solves the Dr. Procrastinate puzzle that combines an upward monotonicity puzzle with a deontic conflict. This puzzle allows us to demonstrate the finer workings of this non-monotonic semantics for deontic modals with multiple violations.
4.1 Dr. Procrastinate
Recall the Dr. Procrastinate puzzle in example (2) repeated here as (22).

According to the literature, there are two predictions to make: i) the conjunction of (22-b) and (22-c) is not intuitively absurd as they can be the case simultaneously; ii) we know that Dr. Procrastinate will violate the obligation in (22-b) but could avoid violating the second violation in (22-c), so if Dr. Procrastinate accepts, despite the fact that she will not finish writing the review, the semantics should predict that her behaviour is more reproachable than when she does not accept.
Upward Monotonicity. A standard approach to the puzzle concerns upward monotonicity as (22-b) is generally represented by an embedded conjunction. In SML and Kratzer semantics obligation is upward monotonic, so the embedded conjunction

in (22-b) entails the embedded conjunct

, which contradicts

in (22-c).
For the sake of argument, assume that the obligations in (22-b) and (22-c) refer to the same violation. \(\textsc {madris}\) captures that the obligations in (22-b) and (22-c) are not contradictory because the semantics is not upward monotonic.
Recall that because madris specifies both support and rejection conditions, entailment also concerns both support and rejection such that for \(\varphi \) to entail \(\psi \) every state which supports \(\varphi \) must also support \(\psi \) and, also, every state which rejects \(\psi \) must also reject \(\varphi \). This two-fold requirement is classically the case, but with the specified rejection conditions for permission and obligation, it makes the semantics non-monotonic.
Consider

and

. For

to entail

, the definition of entailment specifies two conditions: a) every state which supports

must also support

, and b) every state which rejects

must also reject

.
Consider requirement (a) first. Figure 22 shows the maximal supporting state for

. A state \(\sigma \) supports

if every rejection-alternative for \((p\wedge q)\), restricted to \(\sigma \), supports \(v\). \(\textsc {alt}[p\wedge q]^-\) consists of two elements, one consisting of all the worlds where \(p\) does not hold, and the other consisting of all the worlds where \(q\) does not hold. Due to universal quantification over these alternatives, \(\sigma \) supports

when all worlds in \(\sigma \) where either \(p\) or \(q\) does not hold are such that \(v\) does hold.
Figure 23 shows the maximal supporting state for

. A state \(\sigma \) supports

if every alternative for \(\lnot p\), restricted to \(\sigma \), supports \(v\). \(\textsc {alt}[p]^-\) consists of a single element consisting of all the worlds where \(p\) does not hold, so \(\sigma \) supports

when all worlds in \(\sigma \) where \(p\) does not hold are such that \(v\) does hold.
As Figs. 22 and 23 illustrate, every state which supports

also supports

, so

support-entails

. To determine whether entailment also holds, we also need to consider rejection-entailment.
Consider the rejection-entailment requirement that every state which rejects

must also reject

. A state \(\sigma \) rejects

if every alternative for \(\lnot p\), restricted to \(\sigma \), rejects \(v\). \(\textsc {alt}[p]^-\) consists of a single element consisting of all the worlds where \(p\) does not hold, so \(\sigma \) supports

when all worlds in \(\sigma \) where \(p\) does not hold are such that \(v\) does not hold. The maximal rejecting state for

is shown on Fig. 24.
Also consider that a state \(\sigma \) rejects

if every rejection-alternative for \((p\wedge q)\), restricted to \(\sigma \), rejects \(v\). \(\textsc {alt}[p\wedge q]^-\) consists of two elements, one consisting of all the worlds where \(p\) does not hold, and the other consisting of all the worlds where \(q\) does not hold. Due to universal quantification over these alternatives, \(\sigma \) rejects

when all worlds in \(\sigma \) where either \(p\) or \(q\) does not hold are such that \(v\) also does not hold. The maximal rejecting state for

is shown on Fig. 25.
Figures 24 and 25 illustrate that the maximal rejecting state for

is not a rejecting state for

as it contains the world \(\{p\overline{q} v\}\) which is not contained in the maximal rejecting state for

. Using this world, one can easily provide a counterexample.
Consider the state \(\{p\overline{q} v,\overline{pqv}\}\) in which not writing the review can lead to a violation. The state rejects

because in the only world in the state where \(p\) does not hold, \(v\) does not hold. But the state does not reject

because in the world \(p\overline{q} v\) where \(q\) does not hold, \(v\) does hold. As demonstrably every state which rejects

does not reject

, then

does not rejection-entail

and thus, it also does not entail it. This also demonstrates that \(\textsc {madris}\) is non-monotonic.
The non-monotonicity of madris arises from the rejection conditions specified in the semantics and motivated independently of the puzzle. Yet, non-monotonicity alone is insufficient to account for the second intuition in the Dr. Procrastinate puzzle. Introducing multiple violations accounts for both the intuition that (22-b) does not contradict (22-c) and also for the second intuition.
Reasoning with Multiple Violations. The second intuition which needs to be covered concerns the possibility that Dr. Procrastinate can avoid making the situation worse by fulfilling (22-c), despite violating (22-b). To allow reasoning in such a contrary to duty situation, the obligations will need to refer to different violations. Introducing multiple violations provides a basic way to quantitatively compare better and worse states by determining states with less violations.Footnote 27

(23-a) can be dubbed the expert rule as it says that when you are an expert in your field you have an obligation to accept requests to write reviews. If you accept the request to write, you also ought to fulfill the request, which is to say that one ought to write. For convenience, accepting a request and writing have been combined into a single rule.
The procrastinate rule in (23-b) is also necessary because Dr. Procrastinate will not write the book review, so (22-a) holds. Despite always failing to abide by the expert rule, she can make things even worse by accepting and not writing. The rule in (23-b) says that if you will not fulfill the request, you ought not to accept it. In this case, not accepting the request delays the entire reviewing process. As this ought to be avoided, the rule in (23-b) holds.
In what follows, \(v_1\) says that the expert rule has been violated, and \(v_2\) says that the procrastinate rule has been violated.
Intersecting (23-a), (23-b) and (22-a) and the maximal supporting state is shown in Fig. 26. The worlds factively eliminated by \(\lnot q\) are left gray. Green worlds contain no violations, orange worlds only one and red worlds two violations.
The maximal supporting state for the story contains three worlds, so the representation of the situation in madris is not absurd. Each of the worlds is a \(v_{{1}}\) world, which correctly captures the intuition that as long as Dr. Procrastinate does not write the review, she is doing something wrong, i.e., she incurs a violation of the expert rule.
Furthermore, only one \(p\) world remains and in that world \(v_{{2}}\) occurs which says that Dr. Procrastinate is also in violation of the procrastinate rule. This means that \(\textsc {madris}\) predicts that in case Dr. Procrastinate does accept to write a review, despite not writing it, then she will incur a second violation on top of \(v_{{1}}\). Yet, the two remaining \(\lnot p\) worlds differ in that one is a \(v_{{2}}\) world and the other is a \(\lnot {v_{{2}}}\) world (coloured orange because it contains only one violation). When both a violation and a non-violation follows \(\lnot p\), we say that this state is deontically neutral with respect to \(\lnot p\). Thus, Dr. Procrastinate - barring additional information - can avoid the second violation by not accepting to write the review. And this is the second intuition for the semantics to capture.
5 Conclusions
\(\textsc {madris}\) is an alternative semantics for deontic modals that provides a uniform semantic solution to puzzles of standard modal logic and Kratzer semantics. \(\textsc {madris}\) utilizes the radical inquisitive semantics account of conditionals and provides a strong treatment of deontic permission. This non-monotonic semantics for modals was developed to provide an intuitive account of the free choice effect and monotonicity puzzles. The modification of the Andersonian treatment of deontic modals by introducing quantification over alternatives, and especially universal quantification in the rejection-clause for permission, \(\textsc {madris}\) also makes intuitive predictions concerning the behaviour of modals under negation.
Furthermore, deontic conflicts and contrary to duty situations are common in deontic contexts. \(\textsc {madris}\) allows one to reason with multiple violations that not only avoid the problematic inferences in puzzles such as Dr. Procrastinate but also give an intuitive characterizations of such situations.
The work in this article has recently been developed in the framework of suppositional inquisitive semantics which adds suppositional content to the semantics. For further information, see [2].
Notes
- 1.
May and must can also receive, among others, epistemic readings. For a related treatment of epistemic modals, see [2].
- 2.
This simple version of a deontic conflict does not pose a problem for Kratzer semantics which also considers an ordering of worlds. See for example Lassiter [25, p. 151] for discussion on deontic conflicts which also cause problems for Kratzer semantics.
- 3.
See [19].
- 4.
See [27].
- 5.
- 6.
See [19].
- 7.
In this paper, ought is used interchangeably with must because distinctions between the two do not play a role in the presented treatment.
- 8.
- 9.
Anderson introduced relevant implication instead of material implication, but a full discussion of this logic is outside of the scope of this paper.
- 10.
The image is taken from the popular online chess site chess.com.
- 11.
- 12.
- 13.
We are constrained to deontic modals. See work in progress on suppositional inquisitive semantics [2] on how to treat epistemic modals in a structurally similar manner.
- 14.
There is a further extension of the system [17] which distinguishes a third relation between states and sentences which concerns a state dismissing a supposition of a sentence. In the semantics presented here, when a state rejects \(p\), it both supports and rejects \(p \rightarrow q\), and \(\Diamond p\). In the suppositional extension such states are characterized as neither supporting nor rejecting them, but as dismissing a supposition of theirs.
- 15.
Equivalence is defined as mutual entailment.
- 16.
The natural language examples are for illustration only. The actual picture of positive and negative responses is naturally more complicated. See for example Brasoveanu et al. [10].
- 17.
If you are reading this in gray-scale, violation worlds are darker and non-violation worlds are lighter.
- 18.
SML treats permission as weaker, so
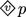
does not guarantee that when you bring about \(p\), no violation occurs.
- 19.
- 20.
See [4], especially for discussion on how to also attain disjunctive readings under permission.
- 21.
Stronger is understood through entailment:
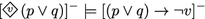
.
- 22.
Strengthening the antecedent also doesn’t hold for obligation for the same reason as it does not hold for implication and permission, but we do not have the space to go through the calculations here.
- 23.
This example is a simplification of a World Trade Organization panel report from case DSU 344. For further details see [4, p. 104].
- 24.
This is not to say that further work should not focus on more fine-grained conceptualizations.
- 25.
Such an approach is not to be confused with work on presuppositions which, as far as the author is aware, is an entirely disconnected phenomenon.
- 26.
See [2].
- 27.
More involved scenarios will likely require a more fine-grained approach which compares violations.
References
Aher, M.: Deontic contexts and the interpretation of disjunction in legal discourse. Canadian Journal of Linguistics/Revue Canadienne de Linguistique 58(1), 13–42 (2013). http://bit.ly/15FfFdB
Aher, M., Groenendijk, J.A.G.: Searching for directions: epistemic and deontic modals in InqS. Presented at the Tenth International Tbilisi Symposium on Language, Logic and Computation (TbiLLC), 26 September 2013 (2014). http://bit.ly/1pA0kin
Aher, M.: Free Choice in Deontic Inquisitive Semantics (DIS). In: Aloni, M., Kimmelman, V., Roelofsen, F., Sassoon, G.W., Schulz, K., Westera, M. (eds.) Logic, Language and Meaning. LNCS, vol. 7218, pp. 22–31. Springer, Heidelberg (2012). http://bit.ly/UzirsR
Aher, M.: Modals in legal language. Ph.D. thesis, University of Osnabrück (2013). http://bit.ly/1ca9Ru4
Aloni, M.: Free choice, modals, and imperatives. Nat. Lang. Semant. 15, 65–94 (2007). http://bit.ly/Zdh8k9
Alonso-Ovalle, L.: Disjunction in alternative semantics. Ph.D. thesis, University of Massachusetts, Amherst (2006)
Anderson, A.R.: Some nasty problems in the formal logic of ethics. Nous 1, 345–360 (1967). http://bit.ly/NcSlZG
Asher, N., Bonevac, D.: Free choice permission is strong permission. Synthese 145(3), 303–323 (2005). http://bit.ly/RswjTm
Barker, C.: Free choice permission as resource-sensitive reasoning. Semant. Pragmat. 3, 1–38 (2010). http://bit.ly/16goZPL
Brasoveanu, A., Farkas, D., Roelofsen, F.: N-words and sentential negation: evidence from polarity particles and VP ellipsis. Semant. Pragmat. 6, 1–33 (2013). http://bit.ly/11wY2e0
Cariani, F.: Ought and resolution semantics. Noûs (2011). doi:10.1111/j.1468-0068.2011.00839.x. http://bit.ly/LRCsJQ
Cariani, F., Kaufmann, M., Kaufmann, S.: Deliberative modality under epistemic uncertainty. Linguist. Philos. 36(3), 225–259 (2011)
Ciardelli, I., Groenendijk, J.A.G., Roelofsen, F.: Inquisitive Semantics: NASSLLI 2012 lecture notes (2012) Unpublished manuscript. http://bit.ly/V6uWy6
Ciardelli, I., Roelofsen, F.: Inquisitive logic. J. Philos. Log. 40(1), 55–94 (2011). http://bit.ly/NlCcRF
Groenendijk, J.A.G., Roelofsen, F.: Inquisitive Semantics and Pragmatics. Presented at the Stanford workshop on Language, Communication and Rational Agency, 30–31 May 2009. http://bit.ly/MoWgAx
Groenendijk, J.A.G., Roelofsen, F.: Radical Inquisitive Semantics. presented first at Osnabrueck University Institute of Cognitive Science Colloquium on the 13th of January 2010. Unpublished http://bit.ly/NFO9zn
Groenendijk, J.A.G., Roelofsen, F.: Suppositional Inquisitive Semantics. In: Proceedings of the Tenth International Tbilisi Symposium on Language, Logic and Computation (2014). Submitted
Frank, A.: Context dependence in modal constructions. Ph.D. thesis, University of Stuttgart (1996)
Jackson, F.: On the semantics and logic of obligation. Mind, New Series 94(374), 177–195 (1985). http://bit.ly/OQSwx9
Kamp, H.: Free choice permission. In: Aristotelian Society Proceedings N.S 74, pp. 57–74 (1973). http://bit.ly/Rb1cxb
Kaufmann, S., Schwager, M.: A unified analysis of conditional imperatives. In: Cormany, E., Ito, S., Lutz, D. (eds.) Proceedings of semantics and linguistic theory(SALT), vol. 19, pp. 239–259 (2011). eLanguage
Kratzer, A.: Conditional necessity and possibility. In: Bäuerle, R., Egli, U., von Stechow, A. (eds.) Semantics from Different Points of View, vol. 6, pp. 117–147. Springer, Heidelberg (1979)
Kratzer, A.: Modals and Conditionals: New and Revised Perspectives. Oxford studies in Theoretical Linguistics. Oxford University Press, Oxford (2012)
Kratzer, A.: What “Must" and “Can" must and can mean. Linguist. Philos. 1, 337–355 (1977). http://bit.ly/ZhvZtR
Lassiter, D.: Measurement and modality: the scalar basis of modal semantics. Ph.D Dissertation, Department of Linguistics, New York University (2011). http://bit.ly/OYyCji
Lewis, D.: Counterfactuals. Basil Blackwell, Oxford (1973)
Ross, A.: Imperatives and logic. Theoria 7, 53–71 (1941). Reprinted in Philosophy of Science 11(1), 30–46 (1944). http://bit.ly/QPYk73
Sano, K.: A Note on Support and Rejection for Radical Inquisitive Semantics (2010). Unpublished manuscript
von Wright, G.H.: Deontic logic. Mind, New Series 60(237), 1–15 (1951)
Zimmermann, T.E.: Free choice disjunction and epistemic possibility. Nat. Lang. Seman. 8, 255–290 (2000)
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2015 Springer-Verlag Berlin Heidelberg
About this paper
Cite this paper
Aher, M. (2015). Deontic Conflicts and Multiple Violations. In: Aher, M., Hole, D., Jeřábek, E., Kupke, C. (eds) Logic, Language, and Computation. TbiLLC 2013. Lecture Notes in Computer Science(), vol 8984. Springer, Berlin, Heidelberg. https://doi.org/10.1007/978-3-662-46906-4_3
Download citation
DOI: https://doi.org/10.1007/978-3-662-46906-4_3
Published:
Publisher Name: Springer, Berlin, Heidelberg
Print ISBN: 978-3-662-46905-7
Online ISBN: 978-3-662-46906-4
eBook Packages: Computer ScienceComputer Science (R0)