Motion Planning and Decision Making for Underwater Vehicles Operating in Constrained Environments in the Littoral

Abstract

This paper seeks to enhance the mission and motion-planning capabilities of autonomous underwater vehicles (AUVs) operating in constrained environments in the littoral zone. The proposed approach automatically plans low-cost, collision-free, and dynamically-feasible motions that enable an AUV to carry out missions expressed as formulas in temporal logic. The key aspect of the proposed approach is its use of roadmap abstractions in configuration space to guide the expansion of a tree of feasible motions in the state space. This makes it possible to effectively deal with challenges imposed by the vehicle dynamics and the need to operate in the littoral zone, which is characterized by confined waterways, shallow water, complex ocean floor topography, varying currents, and miscellaneous obstacles. Experiments with accurate AUV models carrying out different missions show considerable improvements over related work in reducing both the running time and solution costs.

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Introduction

As maritimePlaku, Erion McMahon, James operations shift from deep waters to the littoral, it becomes increasingly important to enhance the mission and motion-planning capabilities of AUVs. Operating in the littoral brings new challenges which are not adequately addressed by existing approaches. As the littoral is characterized by highly-trafficked zones, the AUV must operate near the ocean floor in order to avoid collisions with medium- to small-sized ships. Operations are further complicated when tankers are present, which often cause large drafts, or when fishing vessels are trawling, which could cause the AUV to get entangled. Additional complications arise from boulders, wreckage, and other objects found at the bottom of the ocean, sudden changes in elevation of the ocean floor, and varying ocean currents associated with tides and weather patterns. Dealing with these challenges requires efficient motion-planning approaches that take into account the vehicle dynamics and quickly plan feasible motions that enable the AUV to operate close to the ocean floor while avoiding collisions.

The demand to enhance the capabilities of AUVs operating in the littoral becomes more pressing when coupled with critical missions, such as monitoring harbors or searching for mines and other objects of interest. AUV operations, however, are currently limited to simple missions given in terms of following a set of predefined waypoints or covering an area of interest by following specific motion patterns. Conventional approaches to motion planning for AUVs based on potential fields, numeric optimizations, A*, or genetic algorithms [1–5] have generally focused on largely unobstructed and flat environments where dynamics and collision avoidance do not present significant problems. As a result, while conventional approaches are able to plan optimal paths in 2D environments, they become inefficient when dealing with the challenges arising from dynamics and the need to operate close to the ocean floor in constrained 3D environments. The restrictions to follow predefined waypoints or motion patterns and to operate in essentially flat environments greatly limits the feasibility of such approaches being used for complex missions in constrained 3D environments.

To enhance the mission and motion-planning capabilities of AUVs, this paper develops an approach that makes it possible to express maritime operations in Linear Temporal Logic (LTL) and automatically plan collision-free and dynamically-feasible motions to carry out such missions. As missions are characterized by events occurring across a time span, LTL allows for the combination of these events with logical ($\wedge$ and, $\vee$ or, $\lnot$ not) and temporal operators ($\Box$ always, $\Diamond$ eventually, $\cup$ until, $\bigcirc$ next). As an illustration, the mission of inspecting several areas of interest while avoiding collisions can be expressed in LTL as

$$\begin{aligned} \Box \pi _{{\small {\textit{safe}}}} \wedge \Diamond \pi _{A_1} \wedge \ldots \wedge \Diamond \pi _{A_n}, \end{aligned}$$

(1)

where $\pi _{\small {\textit{safe}}}$ denotes the proposition “no collisions” and $\pi _{A_i}$ denotes “searched area $A_i$.” As another example, searching $A_1$ or $A_2$ before $A_3$ or $A_4$ is written as

$$\begin{aligned} \Box \pi _{{\small {\textit{safe}}}} \wedge \left( (\lnot \pi _{A_3} \wedge \lnot \pi _{A_4}) \cup ((\pi _{A_1} \vee \pi _{A_2}) \wedge \bigcirc (\pi _{A_3} \vee \pi _{A_4}))\right) . \end{aligned}$$

(2)

The expressive power of LTL makes it possible to consider sophisticated missions, making planning even more challenging. Motions need to be coupled with decision making to determine the best course of action to accomplish a given mission. The discrete aspects, which relate to determining the propositions that need to be satisfied to obtain a discrete solution, are intertwined with the continuous aspects, which need to plan collision-free and dynamically-feasible motions in order to implement the discrete solutions.

As a result, approaches that compute discrete solutions without taking into account the intertwined dependencies with the continuous aspects have been limited in scope and capability [6, 7]. Such approaches rely on the limiting assumption that a motion controller would be available to implement any discrete solution. However, due to dynamics, obstacles, complex ocean floor topography, and drift caused by currents, only some discrete solutions could be feasible. Indeed, determining which discrete solutions are feasible is one of the major challenges when dealing with the combined planning problem. As a result of such strong requirement on the availability of motion controllers to implement any discrete solution the applicability of these approaches is limited to 2D environments, disk robot shapes, low-dimensional state spaces, and simplified dynamics.

To address the challenges imposed by the intertwined dependencies of the discrete and continuous aspects of the combined planning problem, the proposed approach simultaneously conducts the search in the discrete space of LTL sequences and the continuous space of feasible motions. The proposed approach builds on our recent framework [8, 9], which combined discrete search with sampling-based motion planning to compute collision-free and dynamically-feasible trajectories that satisfy LTL specifications.

The proposed approach significantly enhances our previous framework [8, 9] by (i) improving the computational efficiency; (ii) generating lower cost solutions; and (iii) enhancing the application from ground vehicles to AUVs, taking into account drift caused by ocean currents and complex ocean floor topography. A key aspect of the technical contribution is the introduction of roadmap abstractions in configuration space to guide a sampling-based exploration of the state space. The roadmap is constructed by sampling collision-free configurations and connecting neighboring configurations with simple collision-free paths. The roadmap represents solutions to a simplified motion-planning problem that does not take into account the vehicle dynamics. These solutions are converted into heuristic costs and heuristic paths to guide sampling-based motion planning as it expands a tree of feasible motions in the state space, taking into account the vehicle dynamics, drift caused by ocean currents, and collision avoidance. The roadmap abstraction also facilitates the decision-making mechanism by providing estimates on the feasibility of reaching intermediate goals as part of the overall mission specified by the LTL formula. Simulation experiments with accurate AUV models carrying out different missions show considerable improvements over related work in reducing both the running time and solution costs.

2 Problem Formulation

AUV Simulator: This paper uses the MOOS-IvP framework [10], which provides a 3D AUV simulator that accurately models the vehicle dynamics. The simulator propagates the dynamics based on a set of control inputs and external drift forces caused by the ocean currents, i.e., $s_{\small {\textit{new}}} \leftarrow {\small \textsc {simulator}}(s, u, {\small {\textit{drift}}}, dt),$ where $s_{{\small {\textit{new}}}}$ is the new state obtained by applying the control input $u$ and the external forces ${\small {\textit{drift}}}$ to the current state $s$ and propagating the dynamics for $dt$ time steps. The MOOS-IvP vehicle model has a state space which consists of the vehicles position and orientation, the actuator values (thrust, rudder, elevator), and the vehicle dynamics (speed, depth rate, buoyancy rate, turn rate, acceleration, etc.). The model represents a second-order dynamical system that has been tested in many applications and shown to be robust and accurate [10].

From Co-Safe LTL to Finite Automata: As mentioned, LTL formulas are composed by combining propositions with logical ($\wedge$ and, $\vee$ or, $\lnot$ not) and temporal operators ($\Box$ always, $\Diamond$ eventually, $\cup$ until, $\bigcirc$ next). The temporal semantics are as follows: $\Box \phi$ indicates that $\phi$ is always true; $\Diamond \phi$ indicates that $\phi$ will eventually be true; $\phi \cup \psi$ indicates that $\phi$ will be true until $\psi$ becomes true; $\bigcirc \phi$ indicates that $\phi$ will become true in the next time step.

Since LTL planning is PSPACE-complete [11], as in prior work [8, 9], this paper considers co-safe LTL, which is satisfied by finite sequences. Co-safe LTL formulas are converted into Deterministic Finite Automata (DFA) [12], which is more amenable for computation. Figure 1 shows an example.

Fig. 1.

The mission “visit any two of the areas $p_1, p_2, p_3, p_4$” encoded as a finite automaton and as a co-safe LTL formula $\bigvee _{i\ne j} (\Diamond p_i \wedge \Diamond p_j)$

Let $\varPi$ denote the set of propositions. A DFA is a tuple $\mathcal {A}= (Z, Q, \delta , z_{\small {\textit{init}}}, {\small {\textit{Accept}}})$, where $Z$ is a finite set of states, $Q = 2^\varPi$ is the input alphabet corresponding to the discrete space, $\delta : Z \times Q \rightarrow Z$ is the transition function, $z_{\small {\textit{init}}} \in Z$ is the initial state, and ${\small {\textit{Accept}}} \subseteq Z$ is the set of accepting states.

To facilitate presentation, let $\mathcal {A}(\left[ q_i\right] _{i=1}^n, z)$ denote the state obtained by running $\mathcal {A}$ on $[q_i]_{i=1}^n$, $q_i \in Q$, starting from the state $z$. Then, $[q_i]_{i=1}^n$ is accepted iff $\mathcal {A}(\left[ q_i\right] _{i=1}^n, z_{\small {\textit{init}}}) \in {\small {\textit{Accept}}}$. Moreover, let ${\small {\textit{Reject}}}$ denote the states that cannot reach an accepting state. Let $\delta (z)$ denote all the non-rejecting states connected by a single transition from $z$, i.e., $\delta (z) = \{\delta (z, q) : q \in Q\} - {\small {\textit{Reject}}}.$ Let ${\small {\textit{props}}}(z_{\small {\textit{from}}}, z_{\small {\textit{to}}})$ denote all the propositions $\pi _{i_1}, \ldots , \pi _{i_k}$ labeling the transition from $z_{\small {\textit{from}}}$ to $z_{\small {\textit{to}}}$. As an example, referring to Fig. 1, ${\small {\textit{props}}}(4, 6) = \{p_1, p_2, p_3\}$.

Discrete Semantics in the Continuous State Space: The semantics of a proposition $\pi \in \varPi$ is defined over the continuous state space $S$ by a function ${\small \textsc {holds}}_\pi : S \rightarrow \{\small \mathtt{true }, \small \mathtt{false }\}$, which indicates if a continuous state satisfies $\pi$. This interpretation provides a mapping from $S$ to $Q$, i.e.,

$$ {\small {\textit{qstate}}}(s) = \{\pi : \pi \in \varPi \wedge {\small \textsc {holds}}_\pi (s) = \small \mathtt{true }\}. $$

Moreover, as the continuous state changes according to a trajectory $\zeta : [0, T] \rightarrow S$, parametrized by time, the discrete state ${\small {\textit{qstate}}}(\zeta (t))$ may also change. In this way, $\zeta$ maps to a sequence of discrete states, ${\small {\textit{qstates}}}(\zeta ) = [q_i]_{i=1}^{n}$, $q_i \ne q_{i+1}$. As a result, $\zeta$ satisfies a specification given by $\mathcal {A}$ iff $\mathcal {A}$ accepts ${\small {\textit{qstates}}}(\zeta )$.

The objective is then to compute a dynamically-feasible trajectory $\zeta : [0, T] \rightarrow S$ that enables the AUV to carry out the mission, i.e., $\mathcal {A}$ accepts ${\small {\textit{qstates}}}(\zeta )$, while avoiding collisions and operating close to the ocean floor.

3 Method

3.1 Roadmap Abstraction

The approach uses solutions to a simplified version of the problem which ignores the vehicle dynamics to guide the overall search. The vehicle motions in this simplified version are defined over the vehicle’s configuration space, denoted as $C$, which accounts for translations and rotations, but not for velocities, accelerations, curvature, and other constraints related to dynamics.

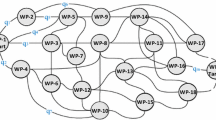
Roadmap Construction: Motivated by the success of the Probabilistic RoadMap (PRM) [13] in dealing with motion-planning problems in configuration spaces, the proposed approach constructs a roadmap $RM =(V_{RM}, E_{RM})$ to capture the connectivity of the free configuration space. The roadmap is constructed by sampling collision-free configurations and connecting neighboring configurations via local paths, where a distance metric $\rho : C \times C \rightarrow R^{\ge 0}$ defines the distance between two configurations. Any PRM variant [13–15] can be used for the roadmap construction. Since the roadmap will be used to define heuristic costs based on shortest paths it is important to allow cycles during roadmap construction. Since $C$ is of lower dimensionality than $S$ and the motions are less constrained in $C$, the roadmap construction takes only a fraction of the overall running time.

Implicit Partition of the State Space Induced by the Roadmap: The roadmap and the distance metric $\rho$ induce an implicit partition of $S$ into equivalence classes where roadmap configurations act as centers of Voronoi sites. In particular, let ${\small {\textit{cfg}}}(s) \in C$ denote the configuration corresponding to $s \in S$. For example, ${\small {\textit{cfg}}}(s)$ could correspond to position and orientation. The state $s$ is then associated with the configuration $c \in V_{RM}$ closest to ${\small {\textit{cfg}}}(s)$ according to $\rho$, i.e.,

$$ {\small {\textit{NearestCfgRM}}}(s) = \arg \min _{c\in V_{RM}} \rho ({\small {\textit{cfg}}}(s), c). $$

This partition, as described later in the section, is particularly useful when determining the region from which to expand the search in the state space $S$.

Mapping Roadmap Configurations to Propositions: Each configuration $c \in V_{RM}$ is mapped to a discrete state based on the propositions it satisfies, i.e.,

$$ {\small {\textit{qstate}}}(c) = \{\pi : \pi \in \varPi \wedge {\small \textsc {holds}}_{\pi }(c) = \small \mathtt{true }\}. $$

The inverse map from propositions to configurations is defined as

$$ {\small {\textit{cfgs}}}(\pi ) = \{c : c \in V_{RM} \wedge {\small \textsc {holds}}_{\pi }(c) = \small \mathtt{true }\}. $$

Additional sampling may take place during roadmap construction to ensure ${\small {\textit{cfgs}}}(\pi )$ is nonempty. Based on the problem under consideration, it may be easier to sample directly from the regions associated with the propositions. For example, propositions in the experiments in this paper correspond to areas of interest in the environment. As such, a configuration can be generated by sampling a position inside the area and then a random orientation.

Heuristic Costs Based on Shortest Paths: The roadmap is used to define heuristic costs of the form ${\small {\textit{hcost}}}(c, \pi _{i_1}, \ldots , \pi _{i_k})$ as the length of the shortest path from $c$ to a roadmap configuration $c'$ satisfying one of the propositions $\pi _{i_1}, \ldots , \pi _{i_k}$, i.e., $c' \in \cup _{j = 1}^k {\small {\textit{cfgs}}}(\pi _{i_j})$. This heuristic cost serves as an estimate on the difficulty of expanding the motion tree $\mathcal {T}$ from tree vertices associated with the Voronoi site defined by $c$ to reach states that satisfy one of the propositions $\pi _{i_1}, \ldots , \pi _{i_k}$. Dijkstra’s shortest-path algorithm is used for the computation of the heuristic cost, where $\rho (c_i, c_j)$ defines the weight of an edge $(c_i, c_j) \in E_{RM}$.

3.2 Overall Search

The roadmap abstraction in conjunction with the automaton $\mathcal {A}$ guides the search in $S$. A tree data structure $\mathcal {T}$ is used as the basis for conducting the search in $S$. The tree starts at the initial state $s_{{\small {\textit{init}}}}$ and is incrementally expanded by adding new collision-free and dynamically-feasible trajectories as branches.

The tree vertices are partitioned according to their corresponding automaton states. More specifically, let ${\small {\textit{traj}}}(v)$ denote the trajectory obtained by concatenating the trajectories associated with the edges connecting the root of $\mathcal {T}$ to $v$. The vertex $v$ keeps track of the automaton state obtained by running ${\small {\textit{qstates}}}({\small {\textit{traj}}}(v))$ on $\mathcal {A}$, denoted as ${\small {\textit{astate}}}(v)$. The computation of ${\small {\textit{astate}}}(v)$ is done incrementally when checking for collisions the trajectory from the parent of $v$ to $v$, as described in Sect. 3.2. The partition induced by $\mathcal {A}$ is then defined as

$$ {\small {\textit{TreeVertices}}}(z) = \{v : v \in \mathcal {T}\wedge z \in Z\wedge z = {\small {\textit{astate}}}(v)\}. $$

To speed up computation, the approach keeps track of the automaton states reached by $\mathcal {T}$, referred to as active automaton states and defined as

$$ {\small {\textit{ActiveAStates}}} = \{z : z \in Z \wedge |{\small {\textit{TreeVertices}}}(z)| > 0\}. $$

A solution is obtained if $\mathcal {T}$ reaches an accepting automaton states, i.e., ${{\small {\textit{ActiveAStates}}}}\,\cap \,{{\small {\textit{Accept}}}} \ne \emptyset$. The search proceeds incrementally at each iteration as follows:

• 1. an automaton state $z_{\small {\textit{from}}}$ is selected from ${\small {\textit{ActiveAStates}}}$;

• 2. an automaton state $z_{\small {\textit{to}}}$ is selected from $\delta (z_{\small {\textit{from}}})$;

• 3. attempts are made to expand $\mathcal {T}$ from ${\small {\textit{TreeVertices}}}(z_{\small {\textit{from}}})$ toward $z_{\small {\textit{to}}}$.

These steps are repeated until a solution is obtained or an upper bound on computational time is exceeded. A description of each of these steps follows.

Selecting Automaton States: The selection of $z_{\small {\textit{from}}}$ from ${\small {\textit{ActiveAStates}}}$ determines the tree vertices from which to expand the search. Since the overall objective is to compute a trajectory that reaches an accepting automaton state, the selection is biased toward states that are close to an accepting state, i.e., ${\small {\textit{prob}}}(z_{\small {\textit{from}}}) = 2^{-d(z_{\small {\textit{from}}})} / \sum \nolimits _{z' \in {\small {\textit{ActiveAStates}}}} 2^{-d(z')},$ where $d(z)$ denotes the minimum number of transitions to reach an accepting state in $\mathcal {A}$ from $z$.

The selection of $z_{\small {\textit{to}}}$ aims to promote expansion toward unreached automaton states ($|{\small {\textit{TreeVertices}}}(z_{\small {\textit{to}}})| = 0$) in order to explore new regions. Similar to the bias in the selection of $z_{\small {\textit{from}}}$, preference is given to those unreached automaton states that are close to accepting states. Taking these into account, $z_{\small {\textit{to}}}$ is selected from the neighbors of $z_{\small {\textit{from}}}$ according to the probability distribution ${\small {\textit{prob}}}(z_{\small {\textit{to}}}) = 2^{-d(z_{\small {\textit{to}}})} / \sum \nolimits _{z' \in \delta (z_{\small {\textit{from}}}) - {\small {\textit{ActiveAStates}}}} 2^{-d(z')}.$

Tree Expansion: The tree expansion from ${\small {\textit{TreeVertices}}}(z_{\small {\textit{from}}})$ adds new collision-free and dynamically-feasible trajectories aiming to reach $z_{\small {\textit{to}}}$. Since $z_{\small {\textit{to}}} \in \delta (z_{\small {\textit{from}}})$ the automaton transition from $z_{\small {\textit{from}}}$ to $z_{\small {\textit{to}}}$ determines the propositions that need to be satisfied in order to reach $z_{\small {\textit{to}}}$, which, as described in Sect. 2, are denoted as ${\small {\textit{props}}}(z_{\small {\textit{from}}}, z_{\small {\textit{to}}})$. Recalling again the example in Fig. 1, the automaton state $z_6$ can be reached from $z_4$ by satisfying one of the propositions $p_1$, $p_2$, $p_3$. Then, the objective is to expand ${\small {\textit{TreeVertices}}}(z_{\small {\textit{from}}})$ towards states $s \in S$ such that ${\small \textsc {holds}}_{\pi }(s) = \small \mathtt{true }$ for some $\pi \in {\small {\textit{props}}}(z_{\small {\textit{from}}}, z_{\small {\textit{to}}})$.

In this way, the expansion from ${\small {\textit{TreeVertices}}}(z_{\small {\textit{from}}})$ toward $z_{\small {\textit{to}}}$ gives rise to a motion-planning problem. The roadmap abstraction is used to effectively guide the tree expansion. To speed up computation, ${\small {\textit{TreeVertices}}}(z)$ are further grouped according to the nearest configuration in the roadmap $RM$, i.e.,

$$\begin{aligned} {\small {\textit{TreeVertices}}}(z, c)&= \{v : v \in {\small {\textit{TreeVertices}}}(z) \wedge c = {\small {\textit{NearestCfgRM}}}({\small {\textit{sstate}}}(v))\}, \end{aligned}$$

where ${\small {\textit{sstate}}}(v)$ denotes the state in $S$ associated with $v$. The approach also keeps track of all the active roadmap configurations, i.e.,

$$ {\small {\textit{ActiveCfgs}}}(z) = \{c : c \in V_{RM} \wedge |{\small {\textit{TreeVertices}}}(z, c)| > 0\}. $$

From an implementation perspective, each time a vertex $v$ is added to $\mathcal {T}$, it is also added to the corresponding ${\small {\textit{TreeVertices}}}(z, c)$. Moreover, $c$ is added to ${\small {\textit{ActiveCfgs}}}(z)$ if not already there.

The tree expansion proceeds incrementally for several iterations. During each iteration, a roadmap configuration $c$ is selected from ${\small {\textit{ActiveCfgs}}}(z_{\small {\textit{from}}})$. The selection is based on ${\small {\textit{hcost}}}(c, \pi _1, \ldots , \pi _k)$ where $\{\pi _1, \ldots , \pi _k\} = {\small {\textit{props}}}(z_{\small {\textit{from}}}, z_{\small {\textit{to}}})$. In particular, the procedure selects the configuration $c$ in ${\small {\textit{ActiveCfgs}}}(z_{\small {\textit{from}}})$ with the lowest ${\small {\textit{hcost}}}(c, \pi _1, \ldots , \pi _k)$. As described in Sect. 3.1, ${\small {\textit{hcost}}}(c, \pi _1, \ldots , \pi _k)$ is initially computed as the length of the shortest-path in the roadmap from $c$ to a configuration satisfying one of the propositions $\pi _1, \ldots , \pi _k$. As such, the selection strategy provides a greedy component necessary to effectively expand the search toward $z_{\small {\textit{to}}}$. To balance the greedy exploitation with methodical exploration, ${\small {\textit{hcost}}}(c, \pi _1, \ldots , \pi _k)$ is increased after each selection. Increasing the heuristic cost, for example, by doubling it, promotes selection of other configurations in future iterations. In this way, the tree expansion has the flexibility to make rapid progress toward $z_{\small {\textit{to}}}$ while effectively discovering new ways to reach it. A hash map keep tracks of the heuristic costs using $\langle c, \pi _1, \ldots , \pi _k\rangle$ as keys.

After selecting $c$ from ${\small {\textit{ActiveCfgs}}}(z_{\small {\textit{from}}})$, a vertex $v$ is selected from vertices in ${\small {\textit{TreeVertices}}}(z_{\small {\textit{from}}}, c)$. A simple strategy that has worked well in practice is to select $v$ at random. A collision-free and dynamically-feasible trajectory is then obtained by applying control inputs for several time steps starting from ${\small {\textit{sstate}}}(v)$ and running the AUV simulator to obtain the new state. The approach uses motion controllers to generate the control inputs. In particular, PID controllers are used to adjust the heading and steer the AUV toward selected target positions. To expand the search toward $z_{\small {\textit{to}}}$, the target is often selected near configurations associated with the roadmap path from $c$ to configurations satisfying propositions in ${\small {\textit{props}}}(z_{\small {\textit{from}}}, z_{\small {\textit{to}}})$. At other times, the target is selected uniformly at random from the entire workspace to expand the search along new directions. After selecting the target position, the PID controllers are invoked until the trajectory comes close to the target, a collision is found, or a maximum number of steps is exceeded. Intermediate states along the generated trajectory and the final state are added to $\mathcal {T}$. Bookkeeping information is updated accordingly.

4 Experiments and Results

The approach is tested on a simulated environment using an accurate and robust AUV simulator, as described in Sect. 2. Several LTL formulas are used to specify different missions.

4.1 Experimental Setup

Ocean Floor: A simulated ocean floor map is created by adding random peaks. A uniform grid is imposed over $(x, y)$ and the center of each peak is sampled at random. The height of each grid cell is determined based on the distance to the closest peak. The height map is then converted to a triangular mesh. As shown in Fig. 2, this setting provides a challenging environment due to changes in topography. In the experiments, the dimensions of the grid are set to $1.5\,\mathrm{km} \times 1.5\,\mathrm{km}$, which correspond to realistic settings for AUV missions.

Fig. 2.

One of the environments used in the experiments. The ocean floor and the obstacles are shown in gold. The areas of interest are shown as red boxes. The AUV in its initial state is shown in red. A zoomed-in illustration is shown below the environment (Color figure online).

The AUV is $4.93\,\mathrm{m}$ long and has a diameter of $0.53\,\mathrm{m}$. The AUV moves at a maximum speed of $1.5\,\mathrm{m/s}$. The AUV is restricted to an altitude of $2\,\mathrm{m}$ to $8\,\mathrm{m}$ from the ocean floor. Operation this close to the ocean floor is required in order to provide high quality acoustic bathymetric data along with detecting objects of interest. The environment is populated with 100 obstacles placed at random positions to test the ability of the approach to avoid collisions.

Ocean Currents: The drift caused by ocean currents is modeled as vector fields. The drift magnitude becomes smaller as the depth increases since the ocean currents are stronger closer to the surface. For the experiments, we used publicly-available data from the National Data Buoy Center [16] describing the ocean currents for the Chesapeake Bay Channel (see Fig. 3(a)). From this data, the vector field was extracted and then scaled to match the area dimensions used in the experiments (see Fig. 3(b)).

LTL Mission Specifications: Each area of interest $A_i$ defines a proposition $\pi _i$. The function ${\small \textsc {holds}}_{\pi _i}(s)$ is $\small \mathtt{true }$ iff the AUV is in area $A_i$ when its state is $s$. An area $A_i$ is defined as a box, placed at random inside the test environment. The inspection mission, which requires the AUV to visit each area of interest, is defined by the following LTL formula:

$$ \phi _1 = \bigwedge _{i=1}^n \Diamond \pi _{A_i}. $$

Note that the mission specification leaves it up to the approach to determine an appropriate order in which to visit the areas. Experiments were also conducted with a mission that requires visiting the areas of interest in a predefined order $A_1, \ldots , A_n$. This mission, referred to as “sequencing,” is given by

$$ \phi _2 = \beta \cup (\pi _{A_1} \wedge ((\pi _{A_1} \vee \beta ) \cup (\pi _{A_2} \wedge ( \ldots (\pi _{A_{n-1}} \vee \beta ) \cup \pi _{A_n})))),\;\text{ where }\; \beta = \wedge _{i=1}^n \lnot \pi _{A_i}. $$

Fig. 3.

(left) Ocean currents for the Chesapeake Bay Channel. Data obtained from National Data Buoy Center [16]. (right) Current field with the missing data filled in and scaled to fit each area used in the experiments. See Sect. 4.1 for more details.

Computational Time and Normalized Solution Cost: Due to the probabilistic nature of sampling-based motion planning, results are based on 30 different runs for each problem instance. The five worst and the five best runs are discarded to avoid the influence of outliers. Results report on average computational time and normalized solution costs. Standard deviations are also included as bars in the plots. To understand how good a trajectory cost is, we normalize it with respect to the cost of the shortest-path in the roadmap abstraction from ${\small {\textit{config}}}(s_{\small {\textit{init}}})$ that satisfies the LTL mission specification. Such shortest path is computed by running the graph search over the product graph formed by combining the roadmap with the automaton [9]. The roadmap cost provides a lower bound as it is over the configuration space and does not take dynamics into account. Experiments are run on an Intel Core i7 machine (CPU: 1.90 GHz, RAM: 4 GB) using Ubuntu 12.10. Code is compiled with GNU g++-4.7.2.

4.2 Results

The proposed approach is compared to our prior framework [8]. Figure 4 summarizes the results when varying the number $n$ of areas of interest.

Fig. 4.

Results when comparing the proposed approach (labeled as new) to prior work [8]. Bars indicate one standard deviation. A missing data point in the graph indicates the method timed out before obtaining a solution. Results include the time to construct the DFAs from the LTL formulas (in the order of milliseconds). For the proposed approach, results also include the time to construct the roadmap abstraction, which took between $0.1$ s–$0.4$ s. Solution costs are normalized with respect to those obtained by the roadmap abstraction, which provides a lower bound as it is over the configuration space and does not take the vehicle dynamics into account.

Results show considerable improvements both in reducing the running time and the solution cost. The approach in prior work has difficulty solving the problem instances as $n$ is increased. In contrast, the proposed approach effectively solves the problem instances. Prior work relies on a workspace decomposition to guide the tree expansion, which, as the problems become more challenging, can lead the exploration along infeasible discrete paths. The lead will eventually be corrected, but it may take the approach in considerable time to do so and find other more feasible leads. In contrast, the proposed approach relies on a roadmap abstraction to capture the connectivity of the free configuration space, which more effectively guides the tree expansion in the state space.

The results show that in addition to computational time the proposed approach effectively computes low-cost, dynamically-feasible, solution trajectories. The costs of these solutions are comparable to those obtained by the roadmap abstraction, which provides a lower bound as it is over the configuration space and does not account for the motion dynamics (recall that the plots show the normalized solution cost over the roadmap abstraction solution cost). By using the roadmap abstraction as a guide, and the expansion heuristics, the proposed approach is able to effectively find low-cost solutions.

5 Discussion

This paper focused on enhancing the mission and motion-planning capabilities of AUVs operating in the littoral zone, which is characterized by confined waterways, shallow waters, complex ocean floor topography, varying currents, and miscellaneous obstacles. The proposed approach can take into account maritime operations expressed in LTL and automatically plans collision-free and dynamically-feasible motions to carry out such missions. The key aspect of the approach is the introduction of roadmap abstractions to capture the connectivity of the free configuration space and, in conjunction with an automaton representing the LTL formula, to effectively guide the expansion of a tree of feasible motions in the state space.

In future work, we plan to enhance the approach so that it can be applied to real AUVs operating in the littoral. This would require adaptations to fit a replanning framework, building the map from sensory information, and quickly responding to unanticipated obstacles, changes in elevation, or other events.