Accelerating String Matching on MIC Architecture for Motif Extraction

Abstract

Identifying repeated factors that occur in a string of letters or common factors that occur in a set of strings represents an important task in computer science and biology. Such patterns are called motifs, and the process of identifying them is called motif extraction. In biology, motifs may correspond to functional elements in DNA, RNA, or protein molecules. In this article, we orchestrate MoTeX, a high-performance computing tool for MoTif eXtraction from large-scale datasets, on Many Integrated Core (MIC) architecture. MoTeX uses state-of-the-art algorithms for solving the fixed-length approximate string-matching problem. It comes in three flavors: a standard CPU version; an OpenMP version; and an MPI version. We compare the performance of our MIC implementation to the corresponding CPU version of MoTeX. Our MIC implementation accelerates the computations by a factor of ten compared to the CPU version. We also compare the performance of our MIC implementation to the corresponding OpenMP version of MoTeX running on modern Multicore architectures. Our MIC implementation accelerates the computations by a factor of two compared to the OpenMP version.

1 Introduction

Identifying repeated factors that occur in a string of letters or common factors that occur in a set of strings represents an important task in computer science and biology. Such patterns are called motifs, and the process of identifying them is called motif extraction. Motif extraction has numerous direct applications in areas that require some form of text mining, that is, the process of deriving reliable information from text [5]. Here we focus on its application to molecular biology.

In biological applications, motifs correspond to functional and/or conserved DNA, RNA, or protein sequences. Alternatively, they may correspond to (recently, in evolutionary terms) duplicated genomic regions, such as transposable elements or even whole genes. It is mandatory to allow for a certain number of mismatches between different occurrences of the same motif since both, single nucleotide polymorphisms, as well as errors introduced by wet-lab sequencing platforms might have occurred. Hence, molecules that encode the same or related functions do not necessarily have exactly identical sequences.

A DNA motif is defined as a sequence of nucleic acids that has a specific biological function (e.g., a DNA binding site for a regulatory protein). The pattern can be fairly short, 5 to 20 base-pairs (bp) long, and is known to occur in different genes [7], or several times within the same gene [9]. The DNA motif extraction problem is the task of detecting overrepresented motifs as well as conserved motifs in a set of orthologous DNA sequences. Such conserved motifs may, for instance, be potential candidates for transcription factor binding sites.

A single motif is a string of letters (word) on an alphabet $\varSigma$. Given an integer error threshold $e$, a motif on $\varSigma$ is said to $e$ -occur in a string $s$ on $\varSigma$, if the motif and a factor (substring) of $y$ differ by a distance of $e$. In accordance with the pioneering work of Sagot [10], we formally define the common motifs problem as follows:

The common motifs problem takes as input a set $s_1,\ldots ,s_N$ of strings on $\varSigma$, where $N \ge 2$, the quorum $1 \le q \le N$, the maximal allowed distance (error threshold) $e$, and the length $k$ for the motifs. It consists in determining all motifs of length $k$, such that each motif $e$-occurs in at least $q$ input strings. Such motifs are called valid. The values for $k$, $e$, and $q$ are determined empirically.

In accordance with [3], motif extraction algorithms can be divided into two major classes: (1) word-based (string-based) methods that mostly rely on exhaustive enumeration, that is, counting and comparing oligonucleotide sequence ($k$-mer) frequencies; and (2) probabilistic sequence models, where the model parameters are estimated using maximum-likelihood or Bayesian inference methods.

Here, we focus on word-based methods for motif extraction. A plethora of word-based tools for motif extraction, such as RISO [6, 10], YMF [11], Weeder [7], and RISOTTO [1], have already been released. The comprehensive study by Tompa et al. [12] compared thirteen different word-based and probabilistic methods on real and synthetic datasets, and identified Weeder and YMF—which are both word-based—as the most effective methods for motif extraction.

Very recently, we have introduced MoTeX, the first word-based HPC tool for MoTif eXtraction from large-scale datasets [8]. It can be used to tackle the common motifs problem by making a stricter assumption on motif validity, which we will elaborate later on. MoTeX is based on string algorithms for solving the so-called fixed-length approximate string-matching problem under the edit distance model [4] and under the Hamming distance model [2]. Given that $k \le w$, where $w$ is the size of the computer word (in practice, $w$ = 64 or $w$ = 128), the time complexity of this approach is $\mathcal {O}(N^2 n^2)$ for the common motifs problem, where $n$ is the average sequence length. The analogous parallel time complexity is $\mathcal {O}(N^2 n^2 / p)$, where $p$ is the number of available processors.

Hence, MoTeX exhibits the following advantages: under the realistic assumption that $k \le w$, time complexity does not depend on (i) the length $k$ for the motifs (ii) the size $|\varSigma |$ of the alphabet, or (iii) the maximal allowed distance $e$. Given the stricter assumption on motif validity, it is guaranteed to find globally optimal solutions. Furthermore, the size of the output is linear with respect to the size of the input. In addition, MoTeX can identify motifs either under the edit distance model or the Hamming distance model. Finally, apart from the standard CPU version, MoTeX comes in two HPC flavors: the OpenMP-based version that supports the symmetric multiprocessing programming (SMP) paradigm; and the MPI-based version that supports the message-passing programming (MPP) paradigm.

In [8], we demonstrated that MoTeX can alleviate the shortcomings of current state-of-the-art tools for motif extraction from large-scale datasets. We showed how the quadratic time complexity of MoTeX can be slashed, in theory and in practice, by using parallel computations. The extensive experimental results presented in [8] are promising, both in terms of accuracy under statistical measures of significance as well as efficiency; a fact that suggests that further research and development of MoTeX is desirable. For instance, the MPI version of MoTeX requires about one hour to process the full upstream Homo sapiens genes dataset using 1056 processors, for any value of $k$ and $e$, while current sequential programmes require more than two months for this task.

Our contribution. Many Integrated Core (MIC) architecture combines many cores onto a single chip, the coprocessor. One can write parallel programs, using the SMP paradigm, that can offload sections of code to run on the coprocessor—or alternatively, that run natively on the coprocessor. The compiler provides the language extensions to facilitate programming for MIC architecture such as pragmas to control the data transfer between the host CPU and the coprocessor. In this article, we orchestrate MoTeX on MIC architecture. We compare the performance of our MIC implementation, running on a single chip of MIC architecture, to the corresponding CPU version of MoTeX running on the host CPU. Our MIC implementation, using the full single-chip potential, accelerates the computations by a factor of ten compared to the CPU version. We also compare the performance of our MIC implementation to the corresponding OpenMP version of MoTeX running on a single chip of modern Multicore architectures. Our MIC implementation accelerates the computations by a factor of two compared to the OpenMP version, both using the full single-chip potential.

2 Definitions and Notation

In this section, in order to provide an overview of the algorithms used later on, we give a few definitions.

An alphabet $\varSigma$ is a finite non-empty set whose elements are called letters. A string on an alphabet $\varSigma$ is a finite, possibly empty, sequence of elements of $\varSigma$. The zero-letter sequence is called the empty string, and is denoted by $\varepsilon$. The length of a string $x$ is defined as the length of the sequence associated with the string $x$, and is denoted by $|x|$. We denote by $x[i]$, for all $1 \le i \le |x|$, the letter at index $i$ of $x$. Each index $i$, for all $1 \le i \le |x|$, is a position in $x$ when $x \ne \varepsilon$. It follows that the $i$th letter of $x$ is the letter at position $i$ in $x$, and that $x = x[1\mathinner {.\,.}|x|]$.

A string $x$ is a factor of a string $y$ if there exist two strings $u$ and $v$, such that $y=uxv$. Let the strings $x,y,u$, and $v$, such that $y=uxv$. If $u=\varepsilon$, then $x$ is a prefix of $y$. If $v=\varepsilon$, then $x$ is a suffix of $y$.

Let $x$ be a non-empty string and $y$ be a string. We say that there exists an (exact) occurrence of $x$ in $y$, or, more simply, that $x$ occurs (exactly) in $y$, when $x$ is a factor of $y$. Every occurrence of $x$ can be characterised by a position in $y$. Thus we say that $x$ occurs at the starting position $i$ in $y$ when $y[i\mathinner {.\,.}i+|x|-1]=x$. It is sometimes more suitable to consider the ending position $i+|x|-1$.

The edit distance, denoted by $\delta _E(x,y)$, for two strings $x$ and $y$ is defined as the minimum total cost of operations required to transform string $x$ into string $y$. For simplicity, we only count the number of edit operations and consider that the cost of each edit operation is $1$. The allowed operations are the following:

• ins: insert a letter in $y$, not present in $x$; $(\varepsilon , b),~b \ne \varepsilon$;

• del: delete a letter in $y$, present in $x$; $(a, \varepsilon ),~a \ne \varepsilon$;

• sub: substitute a letter in $y$ with a letter in $x$; $(a,b),~a \ne b,~a,b \ne \varepsilon$.

The Hamming distance $\delta _H$ is only defined on strings of the same length. For two strings $x$ and $y$, $\delta _H(x, y)$ is the number of positions in which the two strings differ, that is, have different letters.

3 Algorithms

In this section, we first formally define the fixed-length approximate string-matching problem under the edit distance model and under the Hamming distance model. We then provide a brief description and analysis of the sequential algorithms to solve it. Finally, we show how the common motifs problem can be reduced to the fixed-length approximate string-matching problem, by using a stricter assumption than the one in the initial problem definition for the validity of motifs.

Problem 1 (Edit distance)

Given a string $x$ of length $m$, a string $y$ of length $n$, an integer $k$, and an integer $e < k$, find all factors of $y$, which are at an edit distance less than, or equal to, $e$ from every factor of fixed length $k$ of $x$.

Problem 2 (Hamming distance)

Given a string $x$ of length $m$, a string $y$ of length $n$, an integer $k$, and an integer $e < k$, find all the factors of $y$, which are at a Hamming distance less than, or equal to, $e$ from every factor of fixed length $k$ of $x$.

Let $\mathsf D [0\mathinner {.\,.}n, 0 \mathinner {.\,.}m]$ be a dynamic programming (DP) matrix, where $\mathsf D [i, j]$ contains the edit distance between some factor $y[i'\mathinner {.\,.}i]$ of $y$, for some $1 \le i' \le i$, and factor $x[\max \{1, j - k + 1\} \mathinner {.\,.}j]$ of $x$, for all $1 \le i \le n$, $1 \le j \le m$. This matrix can be obtained through a straightforward $\mathcal {O}(k m n)$-time algorithm by constructing DP matrices $\mathsf D ^s [0 \mathinner {.\,.}n, 0 \mathinner {.\,.}k]$, for all $1 \le s \le m - k + 1$, where $\mathsf D ^s[i, j]$ is the edit distance between some factor of $y$ ending at $y[i]$ and the prefix of length $j$ of $x[s \mathinner {.\,.}s + k - 1]$. We obtain $\mathsf D$ by collating $\mathsf D ^1$ and the last row of $\mathsf D ^s$, for all $2 \le s \le m - k + 1$. We say that $x[\max \{1, j - k + 1\} \mathinner {.\,.}j]$ $e$-occurs in $y$ ending at $y[i]$ iff $\mathsf D [i, j] \le e$, for all $1 \le j \le m$, $1 \le i \le n$.

Example 1

Let the string $x:=\mathtt{GGGTCTA }$, the string $y:=x$, and $k:=3$. Table 1a illustrates matrix $\mathsf D$. Consider, for instance, the case where $j=6$. Column $6$ contains all $e$-occurrences of factor $x[4\mathinner {.\,.}6]=\mathtt{TCT }$, that is the factor of length $k=3$ ending at position $6$ of $x$, in $y$. Cell $\mathsf D [4,6]=2$, tells us that there exists some factor $y[i'\mathinner {.\,.}4]$ of $y$, such that, for $i'=2$, $\delta _E(y[2\mathinner {.\,.}4],x[4 \mathinner {.\,.}6])=2$.

Table 1. Matrix $\mathsf D$ and matrix $\mathsf M$

Iliopoulos, Mouchard, and Pinzon devised MaxShift [4], an algorithm with time complexity $\mathcal {O}(m\lceil k/w \rceil n)$, where $w$ is the size of the computer word. By using word-level parallelism MaxShift can compute matrix $\mathsf D$ efficiently. The algorithm requires constant time for computing each cell $\mathsf D [i, j]$ by using word-level operations, assuming that $k \le w$. In the general case it requires $\mathcal {O}(\lceil k/w \rceil )$ time. Hence, algorithm MaxShift requires time $\mathcal {O}(mn)$, under the assumption that $k \le w$. The space complexity is $\mathcal {O}(m)$ since each row of $\mathsf D$ only depends on the immediately preceding row.

Theorem 1

([4]). Given a string $x$ of length $m$, a string $y$ of length $n$, an integer $k$, and the size of the computer word $w$, matrix $\mathsf D$ can be computed in time $\mathcal {O}(m\lceil k/w\rceil n)$.

Let $\mathsf M [0\mathinner {.\,.}n, 0 \mathinner {.\,.}m]$ be a DP matrix, where $\mathsf M [i, j]$ contains the Hamming distance between factor $y[\max \{1, i - k + 1\}\mathinner {.\,.}i]$ of $y$ and factor $x[\max \{1, j - k + 1\} \mathinner {.\,.}j]$ of $x$, for all $1 \le i \le n$, $1 \le j \le m$. Crochemore, Iliopoulos, and Pissis devised an analogous algorithm [2] that solves the analogous problem under the Hamming distance model with the same time and space complexity.

Theorem 2

([2]). Given a string $x$ of length $m$, a string $y$ of length $n$, an integer $k$, and the size of the computer word $w$, matrix $\mathsf M$ can be computed in time $\mathcal {O}(m\lceil k/w\rceil n)$.

Example 2

Let the string $x:=\mathtt{GTGAACT }$, the string $y:=\mathtt{GTCACGT }$, and $k:=3$. Table 1b illustrates matrix $\mathsf M$. Consider, for instance, the case where $j=7$. Column $7$ contains all $e$-occurrences of factor $x[5\mathinner {.\,.}7]=\mathtt{ACT }$, that is, the factor of length $k=3$ ending at position $7$ of $x$, in $y$. Cell $\mathsf M [6,7]=1$, tells us that $\delta _H(y[4\mathinner {.\,.}6],x[5 \mathinner {.\,.}7])=1$.

By making the following stricter assumption for motif validity, the common motifs problem can be directly and efficiently solved using the above algorithms.

Definition 1

A valid motif is called strictly valid iff it occurs exactly, at least once, in (any of) the input strings.

Consider, for instance, the DNA alphabet $\varSigma =\{\mathtt{{A,C,G,T}}\}$. The number of possible DNA motifs of length $k:=10$ is $|\varSigma |^k=1,048,576$. Given a dataset with a size of ${\approx }1$ MB, the possibility that there exists a motif that is valid, but not strictly valid, is rather unlikely. In other words, given such a dataset, the possibility that there exists a pattern which does not occur exactly, at least once, in the dataset and it also satisfies all the restrictions imposed by the input parameters, is rather unlikely.

The common motifs problem (detecting strictly valid motifs) can be directly solved by solving the fixed-length approximate string-matching problem for all $N^2$ pairs of the $N$ input strings. Consider, for example, the common motifs problem under the Hamming distance model. We use an array $u_r$ for each input string $s_r$, such that for all $1 \le r \le N$, $k \le j \le |s_r|$, $u_r[j]$ contains the total number of strings in which motif $s_r[j - k + 1 \mathinner {.\,.}j]$ $e$-occurs; we set $u_r[j]:= 0$, for all $0 \le j < k$. Array $u_r$, for all $1 \le r \le N$, can easily be computed, by computing matrix $\mathsf M$ for pair $(s_r, s_t)$, for all $1 \le t \le N$. While computing matrix $\mathsf M$, we increment $u_r[j]$ only once iff $\mathsf M [i,j] \le e$, for some $k \le i \le |s_t|$; as soon as we have computed the $N$ different matrices $\mathsf M$ for $s_r$, it suffices to iterate over array $u_r$ and report $s_r[j - k + 1 \mathinner {.\,.}j]$, for all $k \le j \le |s_r|$, as a strictly valid motif iff $u_r[j] \ge q$. An array $v_r$, such that $v_r[j]$, for all $1 \le j \le |s_r|$, denoting the total number of $e$-occurrences of motif $s_r[j - k + 1 \mathinner {.\,.}j]$ in $s_1,\ldots ,s_N$ can also be maintained. Maintaining arrays $u_r$ and $v_r$ does not induce additional costs. Therefore, the common motifs problem can be solved in time $\mathcal {O}(n^2)$ per matrix, where $n$ is the average length of the $N$ strings, thus $\mathcal {O}(N^2n^2)$ in total.

Example 3

Let the input strings $s_r:=\mathtt{GTGAACT }$, $s_t:=\mathtt{GTCACGT }$, $e:=1$, $q:=2$, and $k:=3$. Further, let the current state of arrays $u_r$ and $v_r$ be:

$$ \begin{array}{rcccccccc} j: &{} \scriptstyle 0 &{} \scriptstyle 1 &{} \scriptstyle 2 &{} \scriptstyle 3 &{} \scriptstyle 4 &{} \scriptstyle 5 &{} \scriptstyle 6 &{} \scriptstyle 7 \\ u_r[j] : &{} 0 &{} 0 &{} 0 &{} 0 &{} 1 &{} 0 &{} 1 &{} 0 \\ v_r[j] : &{} 0 &{} 0 &{} 0 &{} 0 &{} 2 &{} 0 &{} 2 &{} 0 \\ \end{array} $$

Table 1b illustrates matrix $\mathsf M$. Arrays $u_r$ and $v_r$ are:

$$ \begin{array}{rcccccccc} j: &{} \scriptstyle 0 &{} \scriptstyle 1 &{} \scriptstyle 2 &{} \scriptstyle 3 &{} \scriptstyle 4 &{} \scriptstyle 5 &{} \scriptstyle 6 &{} \scriptstyle 7 \\ u_r[j] : &{} 0 &{} 0 &{} 0 &{} 1 &{} 2 &{} 0 &{} 2 &{} 1 \\ v_r[j] : &{} 0 &{} 0 &{} 0 &{} 1 &{} 3 &{} 0 &{} 3 &{} 1 \\ \end{array} $$

and so the strictly valid motifs are $s_r[2 \mathinner {.\,.}4]=\mathtt{TGA }$ and $s_r[4 \mathinner {.\,.}6]=\mathtt{AAC }$.

4 Implementation

MoTeX is implemented as a programme that solves the common motifs problem for strictly valid motifs. MoTeX was implemented in the C programming language under a GNU/Linux system. It is distributed under the GNU General Public License (GPL). The open-source code and documentation are available at http://www.exelixis-lab.org/motex. The mandatory input parameters are:

• a file with the $N$ input strings in FASTA format (sequences);

• the length $k$ for the motifs;

• the distance $d$ ($d:=0$ for Hamming distance or $d:=1$ for edit distance);

• the maximal allowed distance $e$;

• the quorum $q' \le 100$ (%) as the ratio of quorum $q$ to $N$.

Given these parameters, MoTeX outputs a text file containing the strictly valid motifs. For each reported motif, it also outputs the total number of sequences in which the motif $e$-occurs at least once and the total number of its $e$-occurrences.

Apart from the standard CPU version, MoTeX comes in two HPC flavors: the OpenMP version for shared memory systems and the MPI version for distributed memory systems. The user can choose the best-suited version depending on: the total size of the input sequences; the nature of the input dataset, for instance, a few very long sequences or many relatively short sequences; the available HPC architecture; and the number $p > 1$ of available processors.

Here we focus on the case when $p \le N$, where $N$ is the number of input sequences; that is, we have a large number of relatively short sequences. The user can choose any of the two HPC versions. MoTeX evenly distributes the computation of the $N^2$ distinct DP matrices for the $N$ input sequences in a straightforward manner across the $p$ processors. Therefore, if $p \le N$, the common motifs problem for strictly valid motifs can be solved in parallel in time $\mathcal {O}(N^2n^2/p)$.

4.1 MIC Implementation

Our MIC implementation is a parallel program that uses the SMP paradigm by offloading sections of the code to run on the coprocessor. First, we used the compiler option offload-attribute-target to flag every global routine and global data object in the source file with the offload attribute target(mic).

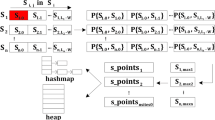
The compiler supports two programming models: a non-shared memory model and a virtual-shared memory model. In our implementation, we used the non-shared memory model which is appropriate for dealing with flat data structures such as scalars, arrays, and structures that are bit-wise copyable. Data in this model is copied back and forth between the host CPU and the coprocessor around regions of the offloaded code. The data selected for transfer is a combination of variables implicitly transferred because they are lexically referenced within offload constructs, and variables explicitly listed in clauses in the pragma. Only pointers to non-pointer types are supported—pointers to pointer variables are not supported. Arrays are supported provided the array element type is a scalar or bitwise copyable structure or class—so arrays of pointers are not supported. We therefore defined the following flat data structures:

• Sequence $\mathsf S = s_1s_2\ldots s_N$ of size $nN$, where $s_i$ is an input sequence, for all $1 \le i \le N$, and $n$ is the average sequence length;

• Array $\mathsf L$ of size $N$, such that $\mathsf L [i]$ stores the length of $s_{i+1}$, for all $0 \le i < N$;

• Array $\mathsf I$ of size $N$, such that $\mathsf I [i]$ stores the starting position of $s_{i+1}$ in $\mathsf S$, for all $0 \le i < N$;

• Array $\mathsf U$ of size $nN$, such that $\mathsf U [\mathsf I [i]\mathinner {.\,.}\mathsf L [i]-1]$ stores array $u$ (see Sect. 3 for details) of $s_{i+1}$, for all $0 \le i < N$;

• Array $\mathsf V$ of size $nN$, such that $\mathsf V [\mathsf I [i]\mathinner {.\,.}\mathsf L [i]-1]$ stores array $v$ (see Sect. 3 for details) of $s_{i+1}$, for all $0 \le i < N$.

Then we placed the offload pragma before the code block computing the $N^2$ distinct DP matrices for the $N$ input sequences. While the instruction sets for the host CPU and the coprocessor are similar, they do not share the same system memory. This means that the variables used by the code block must exist on both the host CPU and coprocessor. To ensure that they do, the pragmas use specifiers to define the variables to copy between the host CPU and coprocessor:

• in specifier defines a variable as strictly an input to the coprocessor. The value is not copied back to the host CPU. $\mathsf S$, $\mathsf L$, and $\mathsf I$ were defined by in;

• out specifier defines a variable as strictly an output of the coprocessor. $\mathsf U$ and $\mathsf V$ were defined by out.

Therefore it becomes obvious that $\mathsf S$, $\mathsf L$, $\mathsf I$, $\mathsf U$, and $\mathsf V$ are copied either back or forth between the host CPU and the coprocessor at most once.

Finally, the code-block statement following the offload pragma is converted into an outlined function that runs on the coprocessor. This code is permitted to call other functions. In order to ensure that these called functions are also available on the coprocessor, we marked the functions to be called by the offloaded code block with the special function attribute _ _declspec(target (mic)).

5 Experimental Results

The following experiments were conducted on a GNU/Linux system running on:

• Multicore architecture I: a single AMD Opteron 6174 Magny-Cours CPU at 2.20 GHz with 12 cores;

• Multicore architecture II: a single Intel Xeon CPU E5-2630 0 at 2.30 GHz with 6 cores;

• MIC architecture: a single Intel Xeon host CPU E5-2630 0 at 2.30 GHz with a single Intel Xeon Phi 5110P coprocessor at 1.053 GHz with 60 cores.

We evaluated the time performance of our MIC implementation, denoted by MoTeX-MIC (Xeon-Phi), running on the host CPU and the coprocessor against: (i) the standard CPU version of MoTeX, denoted by MoTeX-CPU (Opt), and (ii) the OpenMP version with 12 threads, denoted by MoTeX-OMP -t 12 (Opt), both running on the Multicore architecture I; and (iii) the standard CPU version of MoTeX, denoted by MoTeX-CPU (Xeon), and (iv) the OpenMP version with 6 threads, denoted by MoTeX-OMP -t 6 (Xeon), both running on the Multicore architecture II. As input datasets for the programmes, we used $1062$ upstream sequences of Bacillus subtilis genes of total size $240$ KB and $200$ and $1200$ upstream sequences of Homo sapiens genes of total size $240$ KB and $1.2$ MB, respectively, obtained from the ENSEMBL database. We measured the elapsed time for each programme for different combinations of input parameters. In particular, we provided different values for the motif length $k$, the distance $d$ used, the maximal allowed distance $e$, and the quorum $q'$ as a proportion of sequences in the input dataset.

Fig. 1.

Elapsed-time comparisons for the common motifs problem

Fig. 2.

Elapsed-time comparison for the common motifs problem using $1200$ sequences of Homo sapiens

As depicted in Figs. 1 and 2, our MIC implementation accelerates the computations by a factor of ten compared to the corresponding CPU version and by a factor of two compared to the OpenMP version. We observe that, similar to other architectures such as GPGPU, for the same input dataset, the speedup gained from our MIC implementation increases as the ratio of the workload to the size of the data transferred between the host CPU and the coprocessor increases. For instance, notice that in Fig. 2, while the time efficiency of MoTeX-OMP -t 12 (Opt), MoTeX-OMP -t 6 (Xeon), and MoTeX-MIC (Xeon-Phi) is similar for Hamming distance, the later programme becomes faster by a factor of two with the same dataset for edit distance, which is computationally more intensive.