Self-Attraction and Loading of Oceanic Masses

Abstract

When attempting to simulate sea-level variations precisely, the gravitational potential of the moving water masses themselves and their capability of modifying the Earth’s shape have to be considered. Self-attraction and loading (SAL) describes said effects. We describe SAL theoretically, deriving equations that allow to compute SAL either with spherical harmonic functions or with a convolution integral, and show how the equations can be modified to reduce computational demands of the calculation. Key questions of past and ongoing research on the topic include a quantification of SAL at periods from days to years and generated by different processes, the possibility of dynamical feedbacks, and the question of how SAL can be adequately represented in various modeling applications. Gravitation being a body force of infinite range, investigations of SAL include a wide range of processes connected to mass redistribution. For instance, this includes the fast tidal variability, but also atmospherically induced ocean dynamics, or mass redistribution on land and in the atmosphere. Future research is expected to be focused on tidal applications and to consider SAL on longer time scales as an equilibrium response.

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Introduction

The distribution of water masses in the world ocean varies permanently on multiple time scales and is forced by multiple processes. Melting land ice generates water input into the ocean, changing wind patterns induce ocean currents which in turn move water masses, and atmospheric pressure fields lead to relocated oceanic water masses. Additionally, tides induced by the combination of gravitational attraction by celestial bodies and Earth rotation are superimposed and lead to mass variations on periods spanning from a few hours to months or years.

All of these mass variations are induced by non-oceanic forces. Yet the image of water masses and solid Earth reacting passively to these forces oversimplifies things in several ways: First, it neglects the gravitational attraction that additional water masses at one location on the Earth exert on water throughout the remainder of the world ocean. A second reason is the elastic deformation of the seafloor when being exposed to an additional load. And third, a yielding seafloor entails a mass redistribution in the Earth’s interior, changing its gravitational potential. The collection of these phenomena is summarized under the name self-attraction and loading (SAL) and is not only of interest when simulating tides that repeat within a couple of hours or days, but is also crucial for projections on time scales of centuries.

Furthermore, the same processes are also at work when masses redistribute on the continents or in the atmosphere, be it due to the buildup and melting of ice sheets, the formation of cyclones and anticyclones, or the depletion and replenishment of groundwater reservoirs. In all cases, the mass distribution can be transformed into an equivalent two-dimensional field of surface mass density akin to the field of ocean bottom pressure (OBP) and subsequently be treated with the same mathematical formalism that was initially developed for tidal applications.

This formalism can be implemented into ocean models either interactively, modifying the hydrodynamic equations with a changed potential, or as a correction to sea-level fields in the post-processing. In both cases, the calculations are computationally intensive as the water at each point reacts to modified masses at all other points throughout the ocean. The infinite range of gravitational attraction and the linkage of distant points through crustal deformation make the full calculations cumbersome, so adequate simplifications of the formalism are needed in many applications.

SAL cannot be directly measured since it is merely a secondary force acting on oceanic water masses, masked by a variety of other forces that influence ocean dynamics more strongly. It is specifically of interest for modeling applications in which all relevant forces need to be implemented in order to come up with geographically heterogeneous sea-level time series. These can, in turn, be validated with observations.

This chapter is structured as follows: We will begin by formulating the SAL problem in terms of spherical harmonic functions, then reformulate it as a convolution of the generating field with Green’s functions, and discuss the reasoning behind various attempts of parameterizing the problem. We will then raise the key questions for the topic, concerning the magnitude of SAL, the different possibilities of implementing SAL in numerical applications, and the question of computational efficiency. The discussion of fundamental results in the field of SAL investigations will be split into a part focussed on tides and a part focussed on nontidal variations. It will mainly concentrate on the ocean but also touch other subsystems. Future research directions will be discussed before drawing conclusions from this review.

2 Theory

2.1 Derivation of Spherical Harmonic Equations

We derive the change in gravitational potential induced by self-attraction and loading following Hendershott (1972), Ray (1998), Müller (2007), and Kuhlmann et al. (2011). Certain assumptions are made: First, we assume a spherically symmetrical Earth, neglecting both geometrical deviations due to oblateness and asymmetries in the density distribution when computing the elastic response, which is reasonable to first order. Second, we neglect anelastic behavior, which would result in a time delay in the solid Earth’s response to loading. Elasticity is generally an adequate assumption when time scales shorter than decades are considered. Third, we assume that the loads considered are distributed on a spherical shell of zero thickness. For an extension of the calculations beyond the limitations of these assumptions, see Klemann et al. (2013, this volume).

Ocean, land hydrology, and atmosphere generate the bulk of their combined mass variations within a thin shell on the order of 10 km, which is negligibly small compared to the Earth’s radius of > ​​ 6, 000 km, so we assume that all variable masses are concentrated on the Earth’s surface.

The gravitational potential V (p) at a location p induced by a point mass m at location q (see Fig. 1 for the notation) can be written as

$$\displaystyle{ V (\mathbf{p}) =\gamma \frac{m} {\overline{\mathbf{p}\mathbf{q}}} }$$

(1)

with γ being the gravitational constant and $\overline{\mathbf{p}\mathbf{q}}$ the distance between p and q. The contributions from all masses on the sphere need to be summed up in order to obtain the total potential at point p. We do this by integrating over the surface mass density $\sigma (\mathbf{q})$, i.e., the mass per unit area:

$$\displaystyle{ V (\mathbf{p}) =\gamma \int _{\lambda ^{{\prime}}}\int _{\phi ^{{\prime}}}\frac{\sigma (\mathbf{q})} {\overline{\mathbf{p}\mathbf{q}}}\cos \phi ^{{\prime}}\,d\phi ^{{\prime}}\,d\lambda ^{{\prime}} =\gamma \iint _{ S^{{\prime}}}\frac{\sigma (\mathbf{q})} {\overline{\mathbf{p}\mathbf{q}}}dS^{{\prime}} }$$

(2)

We now rewrite the distance $\overline{\mathbf{p}\mathbf{q}}$ in a way that makes spherical harmonic functions appear, thereby making it possible to insert solid Earth properties into the calculations via Love numbers . With $\Omega$ the central angle between p and q and R the sphere’s radius, we can specify the distance between the two points as (Abramowitz and Stegun 1972, p. 72)

$$\displaystyle{ \overline{\mathbf{p}\mathbf{q}} = 2R\sin \left (\frac{\Omega } {2} \right ) = 2R\sqrt{\frac{1 -\cos \Omega } {2}} = R\sqrt{2 - 2\cos \Omega }\,. }$$

(3)

The series of Legendre polynomials, on the other hand, which will lead toward a description with spherical harmonics, can be written as

$$\displaystyle{ \sum _{n=0}^{\infty }P_{ n}(\cos \Omega ) = \frac{1} {\sqrt{2 - 2\cos \Omega }} = \frac{R} {\overline{\mathbf{p}\mathbf{q}}}\,. }$$

(4)

This expression for the distance $\overline{\mathbf{p}\mathbf{q}}$ can be inserted into Eq. (2), obtaining for the gravitational potential

$$\displaystyle\begin{array}{rcl} V (\mathbf{p})& =& \frac{\gamma } {R}\iint _{S^{{\prime}}}\sigma (\lambda ^{{\prime}},\phi ^{{\prime}})\sum _{ n=0}^{\infty }P_{ n}(\cos \Omega )dS^{{\prime}}{}\end{array}$$

(5)

$$\displaystyle\begin{array}{rcl} & =& \frac{\gamma } {R}\sum _{n=0}^{\infty }\iint _{ S^{{\prime}}}\sigma (\lambda ^{{\prime}},\phi ^{{\prime}})P_{ n}(\cos \Omega )dS^{{\prime}}\,.{}\end{array}$$

(6)

Note that the spatial dependence of $\sigma$ reduces to the angles $\lambda ^{{\prime}}$ and $\phi ^{{\prime}}$, taking into account that the masses are distributed on a spherical shell of zero thickness. Since $\sigma (\lambda ^{{\prime}},\phi ^{{\prime}})$ does not depend on n, the integration and the summation could be interchanged in the second step.

Fig. 1

Notations for the distances and angles describing two points on a sphere

We now consider the decomposition of the surface mass density $\sigma$ into spherical harmonics . The n-th degree coefficient, implying a sum over all orders $m = 0,\ldots,n$ which we omit here for brevity, writes down

$$\displaystyle{ \sigma _{n}(\lambda,\phi ) = \frac{2n + 1} {4\pi R^{2}} \iint _{S^{{\prime}}}\sigma (\lambda ^{{\prime}},\phi ^{{\prime}})P_{ n}(\cos \Omega )dS^{{\prime}}\,. }$$

(7)

A derivation of this equation for the special case of R = 1 can be found in Smirnow (1955, p. 427). The integral in Eq. (7) is precisely the one we found in Eq. (6). This lets us express the potential V (p) as a sum of spherical harmonic coefficients of the surface mass density:

$$\displaystyle{ V (\mathbf{p}) =\gamma 4\pi R\sum _{n=0}^{\infty } \frac{\sigma _{n}(\lambda,\phi )} {2n + 1}\,. }$$

(8)

Netwon’s law of universal gravitation reads

$$\displaystyle{ \left \vert \mathbf{F}\right \vert =\gamma \frac{m_{1}m_{2}} {r^{2}} \,\text{,} }$$

(9)

which makes the gravitational constant on the Earth’s surface g equal to

$$\displaystyle{ g = \frac{\gamma M_{e}} {R^{2}} }$$

(10)

with M _e being the Earth’s mass and R its radius. Inserting this into Eq. (8) leads to a new expression for the spherical shell’s potential:

$$\displaystyle{ V (\mathbf{p}) = \frac{4\pi R^{3}g} {M_{e}} \sum _{n=0}^{\infty } \frac{\sigma _{n}(\lambda,\phi )} {2n + 1}\,. }$$

(11)

Inserting the mean density of the Earth $\rho _{e} = 3M_{e}/(4\pi R^{3})$ yields

$$\displaystyle{ V (\mathbf{p}) = \frac{3g} {\rho _{e}} \sum _{n=0}^{\infty } \frac{\sigma _{n}(\lambda,\phi )} {2n + 1}\,. }$$

(12)

In applications, especially when ocean models are used, OBP anomalies are more common than surface mass densities as input fields for SAL calculations. OBP being the gravitational force exerted by $\sigma$ per area,

$$\displaystyle{ p_{B,n}^{{\prime}}(\lambda,\phi ) =\int \frac{F_{\sigma,n}(\lambda,\phi )} {dS^{{\prime}}} \,\text{,} }$$

(13)

the area element canceling out when rewriting in terms of surface mass density,

$$\displaystyle{ p_{B,n}^{{\prime}}(\lambda,\phi ) =\int \frac{g \cdot m_{n}(\lambda,\phi )} {dS^{{\prime}}} =\int \frac{g \cdot \sigma _{n}(\lambda,\phi ) \cdot dS^{{\prime}}} {dS^{{\prime}}} \,\text{,} }$$

(14)

we can replace

$$\displaystyle{ p_{B,n}^{{\prime}}(\lambda,\phi ) = g \cdot \sigma _{ n}(\lambda,\phi )\,. }$$

(15)

Therefore, the additional potential on a water parcel at location p due to gravitational attraction by the spherical harmonic functions of bottom pressure anomalies $p_{B,n}^{{\prime}}$ turns out as

$$\displaystyle{ V (\mathbf{p}) = \frac{3} {\rho _{e}}\sum _{n=0}^{\infty }\frac{p_{B,n}^{{\prime}}(\lambda,\phi )} {2n + 1} \,. }$$

(16)

Additionally to this gravitational potential, two terms arise for loading effects. First, the additional mass lowering the seafloor deforms the Earth elastically by an amount of $h_{n}^{{\prime}}V _{n}/g$; second, the mass redistribution within the Earth shifts the gravitational potential by $k_{n}^{{\prime}}V _{n}/g$. These two shifts in fact define the Love numbers $h_{n}^{{\prime}}$ and $k_{n}^{{\prime}}$ (Munk and MacDonald 1960, p. 24; see also Klemann et al. 2013, this volume). The degree dependence of the Love numbers takes into account that the elastic properties of the Earth are a function of the spatial scale of the applied force. The complete potential due to SAL therefore adds up to

$$\displaystyle{ V (\mathbf{p}) =\sum _{ n=0}^{\infty }(1 + k_{ n}^{{\prime}}- h_{ n}^{{\prime}})\alpha _{ n}^{{\prime}}p_{ B,n}^{{\prime}}(\lambda,\phi )\;\;\;\text{with}\;\;\;\alpha _{ n}^{{\prime}} = \frac{3} {\rho _{e}(2n + 1)}\,. }$$

(17)

The generating field $p_{B}^{{\prime}}$ is not necessarily limited to bottom pressure anomalies caused by oceanic water masses, but can also include mass distributions from other sources, such as land hydrology, atmosphere, or cryosphere, restated in pressure units. The attractive and deformational effects are identical as long as the assumption of an infinitely thin spherical shell remains sensible.

2.2 Reformulation with Green’s Functions

The decomposition of the generating field into spherical harmonic functions is cumbersome. Alternatively, one can re-substitute the analogous expression to the definition of the spherical harmonic coefficient from Eq. (7) for the bottom pressure into Eq. (17), obtaining

$$\displaystyle\begin{array}{rcl} V (\mathbf{p})& =& \sum _{n=0}^{\infty }(1 + k_{ n}^{{\prime}}- h_{ n}^{{\prime}})\alpha _{ n}^{{\prime}}\frac{2n + 1} {4\pi R^{2}} \iint _{S^{{\prime}}}p_{B}(\lambda ^{{\prime}},\phi ^{{\prime}})P_{ n}(\cos \Omega )dS^{{\prime}}{}\end{array}$$

(18)

$$\displaystyle\begin{array}{rcl} & =& \iint _{S^{{\prime}}}p_{B}(\lambda ^{{\prime}},\phi ^{{\prime}}) \frac{R} {M_{e}}\sum _{n=0}^{\infty }(1 + k_{ n}^{{\prime}}- h_{ n}^{{\prime}})P_{ n}(\cos \Omega )dS^{{\prime}}\,.{}\end{array}$$

(19)

None of the factors before the integral sign depended on the angles $\lambda ^{{\prime}}$ or $\phi ^{{\prime}}$, and $\alpha _{n}^{{\prime}}$ could be merged with the fraction. Now, the Green’s function of the problem can be defined as

$$\displaystyle{ \mathcal{G}(\Omega ) = \frac{R} {M_{e}}\sum _{n=0}^{\infty }(1 + k_{ n}^{{\prime}}- h_{ n}^{{\prime}})P_{ n}(\cos \Omega )\,\text{,} }$$

(20)

so the potential can be rewritten as

$$\displaystyle{ V (\mathbf{p}) =\iint _{S^{{\prime}}}p_{B}(\lambda ^{{\prime}},\phi ^{{\prime}})\mathcal{G}(\Omega )dS^{{\prime}}\,. }$$

(21)

Due to the spherical symmetry, the Green’s function depends only on the central angle $\Omega$ between the points p and q as well as on constant factors, so it can be computed once and for all before input data for the generating field is even considered. This convolution approach can save computing time by eliminating the need for a decomposition of the generating field into spherical harmonics. It comes however at the price of an integration over the entire sphere once for the potential at each point p and again at every time step. It also brings an additional problem: What is the limit of $\mathcal{G}(\varOmega )$ as Ω approaches 0? In Eq. (4), this comes down to a division by zero. A work-around is to distribute the mass onto an extended area of approximately gridbox size (Stepanov and Hughes 2004). For this distributed mass, an approximate mean distance to the gridbox center can be calculated, so the case of Ω = 0 is avoided. A second option is to iteratively subdivide the identical grid cell, thereby reducing the mass for which the distance $\overline{\mathbf{p}\mathbf{q}}$ is zero. For all other subdivisions of the grid cell, SAL can be computed. When a large enough part of the grid cell mass is taken into account with this method, the remainder at zero distance may be neglected. In effect, this approach is equivalent to calculating an effective distance of a grid cell to itself. Since grid cell shapes on a regular grid are latitude dependent, this effective distance needs to be latitude dependent as well.

2.3 Extension with the Sea-Level Equation

The approaches described above assume that a mass distribution invokes a potential which then needs to be applied to the hydrodynamic equations from which ocean currents arise. In certain applications, no interactive ocean model is available, but it is rather attempted to correct available sea-level fields for SAL effects. In this context, the geoid change induced by the present water masses needs to be calculated in a gravitationally consistent way, i.e., the ocean mass itself needs to be considered as a source of gravitation and crustal deformation modifying the geoid to which it adjusts. The new sea level, adjusted to the modified geoid, is described by the sea-level equation (Farrell and Clark 1976).

$$\displaystyle{ \zeta (\lambda,\phi ) = \frac{\rho _{w}} {g} (\mathcal{G}{\ast}\zeta )(\lambda,\phi ) +\zeta _{e} - \frac{\rho _{w}} {gS_{\text{oc}}^{{\prime}}}\iint _{S_{\text{oc}}^{{\prime}}}(\mathcal{G}{\ast}\zeta )(\lambda,\phi )dS^{{\prime}}\,. }$$

(22)

The sea level ζ in an ocean of constant water density ρ _w is described as the sum of a convolution of itself with the Green’s function $\mathcal{G}(\Omega )$, i.e., the sea level’s contribution as loading described above, and a eustatic contribution ζ _e to account for additional masses from, e.g., melting ice caps. The last term ensures mass conservation and can also be seen as a eustatic contribution. The sea-level equation can also be extended by permitting the surface of the ocean $S_{\text{oc}}^{{\prime}} = S_{\text{oc}}^{{\prime}}(t)$, i.e., allowing for migrating shorelines . This description has the desired property of being gravitationally self-consistent, i.e., resulting in a sea-level field that coincides with the geoid induced by all preceding mass redistributions. The drawback to this approach is that it is an integral equation that can only be solved iteratively: $\zeta (\lambda,\phi )$ occurs on both sides. Fortunately it turns out that, in most applications, it converges quickly. Interpreting the meaning of the iterative process, one could say that the sea level does not simply adjust to the induced potential and thereby reaches a new equilibrium state. Rather, the adjusting water masses modify the gravitational potential, which induces new water mass distributions, which modifies the potential, and so on.

Computing SAL with the sea-level equation becomes necessary mostly for processes on geological time scales, when melting ice caps, migrating shorelines, and changes in Earth rotation become relevant. For these processes, a simulation with a time-stepping model that interactively simulates ocean circulation and implements SAL as an additional force to which the ocean can react is not feasible, but it is necessary to compute approximate equilibrium solutions which rely on the assumption of an ocean at rest adjusted to the geoid. Numerical implementations of the solution commonly rely on a pseudo-spectral approach (corresponding to the formulation with spherical harmonics in Sect. 2.1; see Kendall et al. 2005) or on spectral finite elements (corresponding to the formulation with Green’s functions in Sect. 2.2; see Wu 2004).

2.4 Parameterization and Simplification

Implementations of SAL in ocean models, either in the spectral domain with spherical harmonics or in the spatial domain with Green’s functions, are numerically intensive. The decomposition of the generating field into spherical harmonics at every model time step and the back-transformation into the spatial domain after the gravitational potential has been modified increases in complexity when model grids of higher resolution are considered, since then the spherical harmonics have to be computed up to a higher degree and order. The alternative of convolving the generating field with a Green’s function is not necessarily more efficient either, since the convolution requires $\mathcal{O}(N^{2})$ operations when a grid of N points is considered. Therefore, various ways of simplifying the problem have been explored.

A radical but commonly used approach of simplification is to set the term

$$\displaystyle{ \alpha _{n}^{{\prime}}(1 + k_{ n}^{{\prime}}- h_{ n}^{{\prime}}) =\beta = \text{const.} }$$

(23)

in Eq. (17). This does away with the entire decomposition into spherical harmonics as the induced potential becomes linearly dependent on the generating surface mass density and goes back to a suggestion by Accad and Pekeris (1978). It implies approximating the curve in Fig. 2 with a degree-independent constant, which is a crude assumption, and neglects all far-field effects of distant masses attracting each other. In effect, it is a local approximation of the elastic response.

Fig. 2

The loading Love number combination $\gamma _{n}^{{\prime}}\alpha _{n} =\beta _{n}$ as a function of spherical harmonic degree n based on the Earth model used by Farrell (1972) (Figure taken from Ray 1998). Here, $\gamma _{n}^{{\prime}} = 1 + k_{n}^{{\prime}}- h_{n}^{{\prime}}$ and α _n correspond to $\alpha _{n}^{{\prime}}$ from Eq. (17) multiplied with the mean seawater density ρ _w ≈ 1,025 kg/m³

A different method of simplification consists in cutting off the series in Eq. (17) at a certain degree n _max, mostly high enough to make use of the full resolution of the grid the input data is provided on. Choosing a lower n _max reduces the computational cost. Lower n _max is equivalent to applying a spatial low-pass filter, but if the bulk of the spectral power is concentrated on long wavelengths, this approach is useful.

Considering Eq. (21), a reduction in computational cost can also be made by replacing the area of integration, which was the entire surface of the sphere $S^{{\prime}}$, by a subset of this surface. This might be done by choosing an upper limit to the angle $\Omega$ until the contribution to the potential, which according to Eq. (1) is inversely proportional to the distance between the points p and q, becomes negligible. Taking into account only the near-field is particularly tempting when regional model simulations or data sets are used.

Other attempts of simplification have been more heuristic. For instance, Stepanov and Hughes (2004) suggested to make β in Eq. (23) a function of the local depth or latitude, exploiting the observational evidence that the spatial scales of mass anomalies within the ocean are smaller in shallow shelf areas and in higher latitudes. The degree dependence of β shown in Fig. 2 can be translated into one factor β _n corresponding to one spatial scale, determined by its degree n. Even if far-field effects are still neglected, such varying β values can be adequate if characteristic length scales of mass variations can be estimated a priori. These approaches come with drawbacks: If depth- or latitude-dependent length scales are unknown, they need to be determined with help of the generating fields. For mass variations on a different time scale or from a different source, say atmospheric instead of oceanic masses, the dependence needs to be established anew. Different models also weigh the contributions of superposed effects differently, and different measurement systems resolve different phenomena in space and time.

3 Key Questions

3.1 Magnitude of SAL on Different Frequencies

Is SAL worth simulating at all, considering the high computational demands? We are dealing here with a problem that is extraordinarily well understood on a theoretical level – Newtonian gravitation – but that adds considerable numerical complexity to the calculation of ocean currents in a model. The initial question in each application of SAL in an ocean model is therefore directed at the magnitude of the effect: Is it negligible in view of remaining uncertainties, or not?

This question does not have a simple yes-or-no answer. Depending on temporal and spatial scale of the generating mass fields as well as level of scientific understanding and modeling capabilities concerning other processes, answers may vary. Generally speaking, SAL becomes important when large mass variations occur over short time periods. An implementation used for tides is not necessarily appropriate in an application concerned with melting ice caps.

3.2 Dynamical or Equilibrium Response?

Ocean models typically run at a temporal resolution that is much higher than the resolution of the desired output fields. In order to appropriately account for wave propagation or eddy dynamics, internal time steps on the order of minutes may be necessary, even if, for climatological studies, only daily or monthly mean output fields are needed. If SAL can be approximated as an equilibrium response to an additional gravitational potential, inducing only negligibly small additional currents and not significantly altering the distribution of heat and salt, it can be computed as a correction to the model output fields. This approach reduces the computational expenses by orders of magnitude. If, on the other hand, the response of water masses to the altered potential takes longer than one time step of the model output, feedback loops make it essential to implement SAL dynamics into the model code at the point where horizontal currents are computed. The same goes for cases in which additionally induced currents redistribute, for instance, the oceanic heat content in a way that alters convection.

3.3 How to Improve Computational Efficiency

Gravitation acts as a body force over an infinite spatial range. Unlike in computations of frictional effects or pressure gradients, it is not sufficient to have an exchange of information between neighboring grid cells, but at least in principle, the entire global mass distribution is needed to compute self-attraction and, equally, loading effects. This approach consumes a lot of computing time, which is always one of the bottlenecks in modeling applications. The creation and evaluation of methods to reduce the computational enormity of the SAL calculations is a recurring research endeavor.

4 Fundamental Results

4.1 Tidal Variations

Investigations of SAL effects on tides began with Hendershott (1972), who solved Laplace’s tidal equations with and without accounting for SAL and thereby laying much of the theoretical groundwork described in Sect. 2. His model of the ocean was very basic, neglecting crucial phenomena such as dissipation, but his results concerning SAL are noteworthy nonetheless: SAL modifications to tidal amplitudes turned out to be of the same order of magnitude as the astronomical forcing potential itself. Farrell (1972) followed a similar approach, calculating solutions to Laplace’s tidal equations iteratively. He considered the M ₂ tide only and separated the influence of deformational and gravitational potential variations. After convolving the Green’s function with the M ₂ tide, he attributed about half of the changes to nearby (i.e., distances below 3^∘) elastic deformation and the other half to the Newtonian effect integrated over all distances. Within the elastic deformation, the h _n part caused by vertical surface deformation dominates over the k _n part stemming from a modified Earth gravity field. This led him to suggest the use of local models for the near-field Earth structure and standard, radially symmetric, Earth models such as the Gutenberg-Bullen model for the far-field contribution.

Gordeev et al. (1977) reconsidered the problem, computing SAL-affected tides and accounting for dissipation at the coasts in their ocean model. They concluded that SAL does not produce a major alteration of the tides’ spatial structure, but that modifications are important in specific regions of the world’s ocean. In particular, tidal amplitudes increased in the low and mid-latitudes in the Pacific while decreasing in the Indian Ocean and in the North Atlantic. Generally, modifications remained below 20 %, but in some regions they surpassed a factor 1.5 or 2. This is understandable when considering the far-field impact: Calm regions of the oceans are influenced by neighboring regions of vigorous tides. Gordeev et al. (1977) observed modifications particularly of tidal phases amounting to 30^∘ or more, a shifting of amphidromes and a turning of nodal zones. Even if, at the time, observations of open-ocean tides were sparse, it became clear that SAL is an effect important enough not to be neglected in the computation of tides for applications where more than an order-of-magnitude accuracy is aimed for.

A groundbreaking advancement came from Accad and Pekeris (1978). They first calculated SAL as an iterative correction to both the initial M ₂ and S ₂ tide. In light of the mathematical complications that this approach brings along, Accad and Pekeris (1978) looked at the improved solution (Fig. 3) and noted a marked proportionality between the uncorrected and the corrected fields of amplitudes, while phase shifts in their model were minor. They therefore calculated the constant of proportionality between the two fields. For the M ₂ tide, this factor β was approximately equal to 0.085. The simplicity of this approach is tempting: Instead of a cumbersome convolution, spherical harmonic analysis, or even iterative solutions, the effect of SAL on tidal amplitudes could be computed by multiplying the generating field with a constant factor and adding it to the initial solution. The correction of roughly 10 % would be worth the effort, especially since it comes at virtually no computational cost.

Fig. 3

M ₂ tide in a 2^∘ model without (top) and with (bottom) SAL considered. Solid lines: Cotidal lines in Greenwich hours. Dashed lines: Corange lines in centimeters (From Accad and Pekeris 1978)

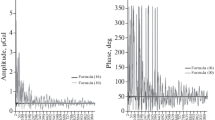
Later research generally considered SAL to be crucial for an accurate determination of tidal amplitudes, frequencies, and phases. For example, Zahel (1991) simulated tides with and without data assimilation and compared solutions with no SAL, parameterized SAL following Accad and Pekeris (1978), or full SAL. He particularly noticed an increase in tidal periods when SAL is incorporated that had heretofore been overlooked. The advent of satellite altimetry in the early 1990s sparked additional interest in tidal phenomena, as open-ocean tides became observable for the first time and speculations about their characteristics could be held against measurements. Certain authors attempted to remove tides from the altimetry data and needed estimates of SAL in order to remove oscillations of the correct amplitude, frequency, and phase (Egbert et al. 1994). Other authors used TOPEX/Poseidon satellite altimetry to come up with precise estimates of tidal amplitudes and phases and to reinvestigate how well the scalar approximations of SAL would approximate the calculation with the full integral (Ray 1998). The result is indeed sobering: Ray (1998) concluded that “none is recommended in general, and most serious applications should use the full integral formulations”. Especially in shelf areas, the scalar approximation turned out to perform weakly, since here contributions to sea level from local and open-ocean tides often cancel out (Fig. 4). When not only the amplitudes but also the phases are considered, the scalar approximation performed worst in the open ocean. The errors made by applying it exceed 25 mm, which is roughly a third of the amplitude caused by SAL in total. The general problem Ray (1998) found was that the optimal β value changes dramatically from the coast to the open ocean.

Fig. 4

Errors made when simulating the M ₂ tide with the scalar approximation with β = 0. 085 (top) and β = 0. 12 (bottom). Units are millimeters. Note the improvement in open-ocean regions at the expense of shelf areas when increasing β (From Ray 1998)

In contrast to the conclusions made by Ray (1998) and Stepanov and Hughes (2004) made another attempt at parameterization of SAL . They noted that, while omission of SAL would introduce an error of around 4 cm, a parameterized inclusion of the effects would at least reduce this error by 50 %. They also suggested an incremental improvement of the parameterization, defining β as a function of local depth. The optimal global parameter they computed for their model amounted to β = 0. 12, the same value that (Ray 1998) had determined for the M ₂ tide in the open ocean.

Müller (2008) approached the problem from the theoretical side. He considered tides to be a superposition of free oscillations , i.e., eigenmodes of the world’s ocean basins. The expansion coefficient that would define the weight of a particular eigenmode depends on the resonance depth (the similarity between the forcing period and the eigenperiod) as well as on the shape factor (the similarity between the forcing vector and the eigenvector, i.e., the shape of the oscillatory pattern). Müller (2008) solved the eigenproblem for periods between 9 and 40 h and attempted to analyze the importance of SAL by computing these eigenmodes once with and once without accounting for SAL. As earlier authors had noted, frequencies of particular modes decreased when SAL was applied. The explanation Müller (2008) gave for this phenomenon is based on the parameterized approximation of SAL which can be reframed as a modification of gravitational acceleration ($g_{\mathrm{new}} = (1 - 0.085)g_{\mathrm{old}}$). In the idealized case of a square basin, it can be shown that the eigenfrequency of the free oscillation is proportional to $\sqrt{g}$, and the same effect – slightly modified – rules more complex basins as well. Tides furthermore turned out to be delayed by SAL. This phase shift between eigenmodes with and without SAL can be formulated analytically; it is largest if both modes are near-resonant and if the frequency shift due to SAL is large. In order to simulate, for instance, the maximum tidal elevation at a certain coastal tide gauge at the correct time, SAL needs to be implemented in the model.

4.2 Nontidal Variations

Two major developments have led to increased interest in the impact of SAL on nontidal ocean variations during the past 10 years: First, increased computing power allows for more complex ocean models, running at higher resolutions and accounting for more physical processes. Second, the Gravity Recovery and Climate Experiment (GRACE, Chambers et al. 2004; Schmidt et al. 2006) provides an unprecedented data set of OBP variations, which is the variable that causes SAL effects in the first place.

Stepanov and Hughes (2004) started by implementing SAL into the purely barotropic OCCAM model and simulating 1 month worth of both tidal and nontidal ocean dynamics, calculating SAL effects anew at each time step with a Green’s function approach. The shortness of the simulation was required by the limited availability of computing time and justified by the assumption that SAL effects of periods longer than 7 days were supposed to yield an equilibrium response, which could more easily be computed in the post-processing. Since their implementation slowed the model by a factor of 10, they investigated the capability of various parameterizations to emulate the SAL effect. Unfortunately, the evaluated parameterizations turned out to be less capable than in the case of tides. The underlying problem is the multitude of spatial scales and associated wave speeds in nontidal ocean variations, which reach from barely resolved mesoscale turbulences to Rossby waves of planetary scale. If a parameter had to be chosen nevertheless, Stepanov and Hughes (2004) suggested a value of β = 0. 10 which, in their model, reduced the errors made when SAL is omitted by 30 % on average. In calm oceanic regions, however, errors due to an inadequate computation of SAL (or none at all) turned out to be of the same amplitude as the local OBP signals themselves. The reason lies in the remote action of gravitation and crustal deformation: Distant but large OBP variations impact calm regions and produce larger mass variations here than any other process.

Kuhlmann et al. (2011) investigated possible feedbacks on ocean currents and density distributions. They implemented SAL into a baroclinic nontidal ocean model in a way that computing time was increased by merely 16 % and could show that the dynamical and hydrographic feedbacks are present but small – a result that justifies correcting sea-level fields in the post-processing. Kuhlmann et al. (2011) were less optimistic about scalar approximations of the SAL effect, showing that the process is highly nonlinear both in space, as others had noted, and in time, where the optimal parameter β turned out to vary by approximately ± 20 % on a multitude of time scales.

Tamisiea et al. (2010) followed a different approach. They did not compute SAL effects at every time step during the model run, but rather afterward in the post-processing, thereby neglecting feedbacks and possibly misrepresenting fast oscillations. The paper was focussed, however, on the annual cycle. An additional advantage of their method is the ease with which influences from other subsystems can be considered. The authors computed the gravito-elastodynamical impacts of continental, atmospheric, and oceanic masses on sea-level fields, using mass allocations from respective models or measurements. It was not necessary to couple the models interactively, nor was input data necessary for every internal model time step. Since only the equilibrium response of the ocean was to be investigated, monthly mean fields for all three systems provided enough information.

Figure 5 shows the annual cycle’s amplitude and phase that gravitation and Earth elasticity impose on their model ocean. Both are dominated by the hydrological signal. A prominent hydrological annual cycle in Southern Asia (monsoon climate) and Western Africa attracts water masses toward these regions. Tamisiea et al. (2010) explained the minimum amplitudes in the Northern Hemisphere by a cancelation of the regional and global annual cycles: The local mass load is 180^∘ phase-shifted with respect to the global water mass in the oceans, so at times of the year when a maximum snowpack attracts ocean water, the global mean sea level is at a minimum since the amount of water in the ocean is minimal. These two impacts cancel out. The effect of atmospheric load on sea level turned out to account for only a third of the hydrological loads’ amplitude, SAL due to OBP is even smaller. The globally integrated signal has an amplitude of 9.1 mm and a phase of 268^∘.

Fig. 5

Effect of SAL caused by hydrology on sea-level annual cycle amplitude (top) and phase (bottom) (From Tamisiea et al. 2010)

Vinogradova et al. (2010) followed up on this work, focussing on SAL effects modifying the annual cycle of OBP rather than sea-surface height. They used an ocean state estimate from the ECCO project, enhanced by SAL effects which were in turn driven by hydrological, atmospheric, and dynamic mass fields. Comparing the three forcing fields, land hydrology turned out to be most important, similar to what (Tamisiea et al. 2010) had found. The hydrological signature of Southern Asia caused the most prominent deviations of the OBP field, followed by atmospherically induced mass variations. The least impact on OBP annual cycles was the contribution due to dynamically varying ocean water masses themselves. Vinogradova et al. (2010) also provided a comparison of their model OBP with in situ measurements at certain points in the ocean. Accounting for SAL effects improved the agreement between model and data, but even in the improved model version, large residuals between model and observation remained. The explained variance did not exceed 32 %, indicating a large mismatch between the two data sets. The authors suggested that the coarse model resolution of 1^∘ in longitude and latitude as well as the smoothed bathymetry might be responsible for the discrepancy.

In the following, Vinogradova et al. (2011) broadened the scope of their investigations of SAL effects on sea-surface height caused by land hydrology, atmospheric pressure, and ocean dynamics. While using the same data as Tamisiea et al. (2010), they investigated the significance of SAL on subannual, annual, and interannual time scales. They came to the conclusion, however, that the effects are strongest on annual periods. Comparing the different subsystems, hydrological fields turned out to cause the largest sea-surface height variations, followed by ocean dynamics.

The most recent work on SAL comes from Richter et al. (2013), who considered a special phenomenon: A warming deep ocean entails an expansion of the water column and, therefore, an upward shift of the water column’s center of mass. This creates a pressure gradient in the upper layers of the ocean, causing water to flow toward the shelf areas. The emerging mass redistribution leads to the known processes of SAL, even though Richter et al. (2013) chose to compute them with the sea-level equation (Farrell and Clark 1976), thereby incorporating secondary effects of changed Earth rotation and migrating shore lines. Since this iterative calculation is not performed during the model run, dynamical feedbacks are neglected once again. The input data for the calculation of SAL effects on sea-surface height and OBP came from three scenarios for the twenty-first-century projections of global warming, simulated with a coupled atmosphere-ocean general circulation model.

Richter et al. (2013) found the effect to vary strongly in space. It produced an additional + 3 cm of sea-level rise on the North American Atlantic coast and + 2 cm in the Arctic, around Asia, South America, and Australia. These gains were compensated by − 2 cm throughout the central Atlantic, the Indian Ocean, and less so the Southern Ocean (Fig. 6). All in all, SAL caused a redistribution of water masses from the southern to the northern hemisphere where the larger shelf areas are located. The shift of water masses onto shelves increased coastal sea-level rise by 3–5 % on global average compared to the rise computed from thermal expansion alone.

Fig. 6

Modification of steric and eustatic sea-level rise due to SAL effects in a twenty-first-century projection of global warming due to Representative Concentration Pathway (RCP) 8.5, which estimates an additional 8.5 W/m² of radiative forcing by the end of the twenty-first century (From Richter et al. 2013)

5 Future Directions

Future research concerned with SAL will likely cease efforts of parameterizing an effect that has repeatedly been shown to escape linearization. Certain nontidal applications will neglect SAL outright, as it has shown to bring only minor improvements to ocean currents and density distributions. Other applications will account for SAL in its full complexity, especially in view of increasing availability of high-capacity computing resources.

One such application is the simulation of tides , where models of higher resolution and better understanding of various physical processes in the ocean need to account for SAL changing amplitudes, frequencies, and phases significantly. But also when projecting regional distributions of sea-level rise on decadal time scales, SAL and possibly viscoelastic extensions thereof need to be considered, most likely in the post-processing of the data such as it is often done with the inverse-barometer correction for changing air pressure. For instance, the reports by the Intergovernmental Panel on Climate Change (IPCC) have heretofore focussed on global mean sea-level rise, but projections of regional distributions become more and more important as climate change leaves the purely scientific arena and sparks the interest of policymakers concerned with adaptation efforts on the regional and local level.

Regarding modeling efforts on shorter time scales, the focus on SAL-related research should lie on the impact of land hydrology on sea-level patterns. Better measurements of continental water masses, be it with the gravity mission GRACE, with the soil-moisture satellite SMOS, or with in situ stations and feeding into hydrological models, can be used to correct sea-level fields. Coupling models of the various subsystems can lead to further insights on possible interactions.

6 Conclusion

Coming back to the key questions posed in Sect. 3, it can be noted that SAL is an effect modifying sea level and ocean bottom pressure by roughly 10 %. The precise magnitude depends, however, on various factors: Since the effects are scale dependent, different models resolving different processes come up with different results. The effect varies strongly in space and time, and the relative corrections due to SAL in calm ocean regions are immense. When tides are concerned, SAL does not only modify amplitudes but also frequencies and phases.

The dynamical component of SAL corrections needs to be taken into account predominantly when fast variations, roughly below 1 week, are concerned. Tidal applications fulfill this criterion, climate studies mostly do not. The mechanisms shaping the characteristics of tides could not be understood properly without implementing the physics of SAL. On the other hand, various authors have successfully applied SAL in climate studies as a correction in the post-processing, thereby making it easy to handle numerically. While SAL needs to be included in the post-processing of ocean models to produce precise sea-level patterns, the computational expenses of an implementation at every time step are too high to be justified in most climate-related applications.

Attempts to approximate SAL physics in order to reduce the numerical cost of its consideration have largely failed. The process is too variable in space and time, and approximations have repeatedly missed the target of reducing the error by at least an order of magnitude.

SAL is expected to play an important role in the further investigation of tidal patterns . These are not only of intrinsic interest but are also needed for the correction of gravitational measurements or altimetry data; thus a better understanding of the underlying processes can produce benefits across a wide range of applications. For nontidal ocean mass variations, mostly hydrology showed impacts of a magnitude that makes further research promising.