Keywords

1 Introduction

In the past several decades, the stock option was one of the most popular financial derivatives, which was widely and successfully used to hedge risk in the financial world. To develop a model for the price of a stock option, Black and Scholes (1973) and Merton (1973) derived a parabolic second order partial differential equation (PDE) for the value V(S,t) of an option on stokes in 1973. This equation is known as the Black-Scholes equation, and can be solved exactly by transforming the equation into a diffusion one, when the coefficients are constant or space independent. However, when a problem is space-dependent, this transformation is impossible, numerical solution is a natural way to solve the problem. In the real financial market, numerical solutions are normally sought. Hence, efficient and accurate numerical algorithms are essential for solving this problem accurately. Options research methods are mainly binarytree (Boyle and Lau 1994), Monte Carlo methods (Shahbandarzadeh et al. 2013) and finite difference method (Han and Wu 2003; Tavella and Randall 2000; During et al. 2003).

Standard discretization schemes break down for the Black-Scholes equation for high interest rate and low volatility. For these parameters, the problem becomes singly-perturbed, which means that coefficient of the diffusion term becomes very small, the Black-Scholes equation becomes a convection-dominated operator. Hence, standard schemes like the second-order central difference introduce spurious oscillations around the true solution. The central difference method will lead to nonphysical oscillations in the computed solution. This is due to a loss in stability (Hundsdorfer and Verwer 2003). To overcome this disadvantage, the convection term needs to be discretized using proper upwind finite difference schemes to avoid oscillations in convection dominated problems. However, if the sign of convection coefficient changes over the solution domain, the direction of the upwind scheme must also be changed accordingly. On the other hand, the order of accuracy of the upwind schemes is usually lower than the central schemes on the same stencil. To eliminate the affection of the convection term, we must introduce a variable substitution in the convection diffusion equation to transform into the diffusion equation (Hua Huang 2011; Liao and Khaliq 2009). Our goal is to obtain an unconditionally stable high-order compact finite difference scheme for solving Black-Scholes equation with variable coefficients. Another distinct feature of our method is that the option price and the derivatives-hedge delta can be solved, simultaneously.

This paper is organized as follows. A continuous model of Black-Scholes equation is introduced in Sect. 2, The high order compact scheme for solving linear convection-diffusion equation with variable coefficient are outlined, an unconditional stability is also proved, improvement of accuracy both in time and space can be achieved by applying Richardson extrapolation algorithm in Sect. 3. Two numerical examples are presented in Sect. 4 for verifying the accuracy and the efficiency of the new algorithms. In the end, we give some concluding remarks.

2 Black-Scholes Equation

Assume V(S,t) is the option price at time t and stock value S ∈ [0, ∞) ⊂ R, t ∈ [0,T], respectively with T denote the terminal expiry time of the option, σ is the volatility, r is the risk-free interest rate, D is dividend yield. It is well known that V satisfies the following Black-Scholes equation (Black and Sholes 1973);

$$ \begin{array}{c}\displaystyle\frac{\partial V}{\partial t}+\frac{1}{2}{\sigma}^2(t){S}^2\frac{\partial^2V}{\partial {S}^2}+\left(r\right(t\left)-D\right(S,t\left)\right)S\frac{\partial V}{\partial S}-r(t)V=0 \quad for\kern0.5em \left(S,t\right)\in Q\end{array} $$
(1)

For a call option, the most common final and boundary conditions are defined as:

$$ V\left(S,T\right)= \max \left(S-E,0\right),S\in \Omega $$
(2)
$$ \begin{aligned}[b] & V\left(0,t\right)=0,\\ {}&\underset{S\to \infty }{ \lim }V\left(S,t\right)=S-E{e}^{-r\left(T-t\right)}\end{aligned} $$
(3)

where Q = Ω × (0,T), Ω = [0, ∞), D(S,t) = Sd(S,t).

Both the solution V and its derivative V S are desired. V S is called the hedge delta which represents the sensitivity of the option value to the change of the underlining stock price. The instantaneously riskless portfolio at time t consists of one long position in the derivative and a short position of exactly V S shares of the underlying stock (Liao and Khaliq 2009).

The value of this portfolio is given by;

$$ \prod =V-S{V}_S $$
(4)

One must employ a change of variables

$$ S=E{e}^x,t=T-\tau, V= Eu\left(x,\tau \right) $$
(5)

These formulas are substituted into the (1), we get a forward convection diffusion equation

$$ \frac{\partial u}{\partial \tau }=\frac{1}{2}{\sigma}^2\left(\tau \right)\frac{\partial^2u}{\partial {x}^2}+c\left(x,\tau \right)\frac{\partial u}{\partial x}-r\left(\tau \right)u $$
(6)

where \( a\left(\tau \right)=\frac{1}{2}{\sigma}^2\left(\tau \right),c\left(x,\tau \right)= Er(t){e}^x-D\left(x,t\right) \), which is a viable coefficient equation.

This change of variables gives initial conditions for the call

$$ u\left(x,0\right)=g(x)= \max \left({e}^x-1,0\right), $$
(7)

Boundary conditions

$$ \begin{array}{l}\underset{x\to -\infty }{ \lim }u\left(x,\tau \right)=0,\kern1em t>0\\ {}\underset{x\to \infty }{ \lim }u\left(x,\tau \right)={e}^x-{e}^{-\lambda \tau},\kern1em t>0\end{array} $$
(8)

Let c(x,τ) depends on r, σ, high interest rate and low volatility result to the convection dominated flow. The solution of (6) u and u x must be obtained, for the riskless portfolio, simultaneously.

3 New Compact Finite Difference

3.1 Description of the New Method

We introduce the notations

$$ {A}_i^n=A\left({x}_i,{t}{_{n+1/2}}\right),{B}_i^n=B\left({x}_i,{t}_{n+{_{n+1/2}}}\right) $$
$$ {\delta}_t{u}^n=\raisebox{1ex}{$\left({u}^{n+1}-{u}^n\right)$} \left/ \raisebox{-1ex}{$\tau $}\right.,{\mu}_t{u}^n=\raisebox{1ex}{$\left({u}^{n+1}+{u}^n\right)$} \left/ \raisebox{-1ex}{$2$}\right. $$
$$ {\delta}_x^2{U}_i=\frac{U_{i+1}-2{U}_i+{U}_{i-1}}{\Delta {x}^2} $$

Differentiating both sides of (6) with respect to x leads to

$$ {\left({u}_{\tau}\right)}_x=a\left(\tau \right){\left({u}_{xx}\right)}_x+{c^{\prime}}_x(x){u}_x+c(x){u}_{xx}-\lambda {u}_x $$
(9)

Let v = u x in (9), then

$$ {v}_t=a\left(\tau \right){v}_{xx}+{c^{\prime}}_x(x)v+c(x){u}_{xx}-\lambda v $$
(10)

(9) and (10) now form a system of equations for u and v

$$ \left(\begin{array}{l}{u}_{\tau}\\ {}{v}_{\tau}\end{array}\right)=\left(\begin{array}{cc}\hfill a\hfill & \quad 0\hfill \\ {}\hfill c(x)\hfill & \quad a\hfill \end{array}\right)\left(\begin{array}{l}{u}_{xx}\\ {}{v}_{xx}\end{array}\right)+\left(\begin{array}{cc}\hfill -\lambda \hfill & \quad c(x)\hfill \\ 0\hfill & \quad {c^{\prime}}_x(x)-\lambda \hfill \end{array}\right)\left(\begin{array}{c}\hfill u\hfill \\ {}\hfill v\hfill \end{array}\right) $$
(11)

Setting U = (u,v)T, Eq. (11) can be written as

$$ {U}_{\tau }=A\left(x,\tau \right){U}_{xx}+B\left(x,\tau \right)U $$
(12)

where

$$ A\left(x,\tau \right)=\left(\begin{array}{cc}\hfill a\hfill & \quad 0\hfill \\ {}\hfill c(x)\hfill & \quad a\hfill \end{array}\right),B\left(x,\tau \right)=\left(\begin{array}{cc}\hfill -\lambda \hfill & \quad c(x)\hfill \\ 0\hfill & \quad {c^{\prime}}_x(x)-\lambda \hfill \end{array}\right). $$

(12) is the common reaction–diffusion equation, the Padé approximation for the special derivative can be used to achieve fourth-order accuracy on the 3-points stencil (You 2006), Crank-Nicolson scheme used to handle the time derivative

$$ {\delta}_t{U}_i^n={A}_i^n{\mu}_t{\left({U}_{xx}\right)}_i^n+{B}_i^n{\mu}_t{U}_i^n+{\tau}^2{\left({s}_1\right)}_i^n+{\tau}^4{\left({s}_2\right)}_i^n+O\left({\tau}^6\right) $$

where s 1(x,t), s 2(x,t) are given by

$$ \begin{aligned}[b]{s}_1&=\frac{1}{24}\left(\frac{\partial^3U}{\partial {\tau}^3}-3A\left(x,\tau \right)\frac{\partial^4U}{\partial {x}^2\partial {\tau}^2}-3B\left(x,\tau \right)\frac{\partial^2U}{\partial {\tau}^2}\right)\\ {}{s}_2&=\frac{1}{1920}\left(\frac{\partial^5U}{\partial {\tau}^5}-5A\left(x,\tau \right)\frac{\partial^6U}{\partial {x}^2\partial {\tau}^4}-5B\left(x,\tau \right)\frac{\partial^4U}{\partial {\tau}^4}\right)\end{aligned} $$
(13)

Regarding the second derivative,

$$ {\delta}_x^2{U}_i=\left(1+\frac{h^2}{12}{\delta}_x^2\right){U}_{xx}-\frac{h^4}{240}\frac{\partial^6U}{\partial {x}^6}+O\left({h}^6\right) $$

Defining difference operator M x

$$ {M}_x{U}_i:=\left(1+\frac{\Delta {x}^2}{12}{\delta}_x^2\right){U}_i=\frac{1}{12}\left({U}_{i+1}+10{U}_i+{U}_{i-1}\right) $$

Multiplying (12) τM x and substituting (13),

$$ \begin{array}[b]{l}\displaystyle\frac{M_x}{\tau }{\delta}_t{U}_i^n={A}_i^n{\mu}_t{\delta}_x^2{U}_i^n+{M}_x{B}_i^n{\mu}_t{U}_i^n+\frac{A_i^n{h}^4}{240}{\left(\frac{\partial^6U}{\partial {x}^6}\right)}_i^{n+\frac{1}{2}}\\ {}\qquad \qquad \quad +{M}_x\left({\tau}^2{\left({s}_1\right)}_i^{n+\frac{1}{2}}+{\tau}^4{\left({s}_2\right)}_i^{n+\frac{1}{2}}\right)+O\left({\tau}^6+{\tau}^2{h}^4+{h}^6\right)\end{array} $$
(14)

Then, we can obtain

$$ \left( \left( 1-\frac{B_i^n\tau }{2} \right){M}_x-\frac{A_i^n\tau }{2}{\delta}_x^2 \right){U}_i^{n+1}=\tau {\varepsilon}_i^{n+1/2}+\left( \left( 1+\frac{B_i^n\tau }{2} \right){M}_x+\frac{A_i^n\tau }{2}{\delta}_x^2 \right){U}_i^n $$

where

$$ \varepsilon ={\tau}^2{M}_x\left({s}_1+{\tau}^2{s}_2\right)+\frac{A_i^n{h}^4}{240}\left(\frac{\partial^6U}{\partial {x}^6}\right)+O\left({\tau}^6+{\tau}^2{h}^4+{h}^6\right) $$

Omitting the small term, we obtain

$$ \begin{aligned}[b] &\left(I-{C}_i\right){U}_{i+1}^{n+1}+10\left(I-{D}_i\right){U}_i^{n+1}+\left(I-{C}_i\right){U}_{i-1}^{n+1}\\ {}& \qquad \ =\left(I+{C}_i\right){U}_{i+1}^n+10\left(I+{D}_i\right){U}_i^n+\left(I+{C}_i\right){U}_{i-1}^n\end{aligned} $$
(15)

where \( {r}_1=\frac{\tau }{h^2},\kern1em {C}_i=\frac{\tau {B}_i^{n+\frac{1}{2}}}{2}+6{r}_1{A}_i^n,\kern1em {D}_i=\frac{\tau {B}_i^n}{2}-12{r}_1{A}_i^n \)

The discretized equations form a system of block tridiagonal algebraic equation. Scheme (15) is fourth-order accurate in space and second order in time. We can get U = [u,u x ]T through solving the (15).

3.2 Initial and Boundary Conditions

The initial condition for v can be obtained by differentiating g(x)

$$ v\left(x,0\right)={u}_x\left(x,0\right)={g}_x(x) $$
(16)

When the approximation at the boundary has one-order lower accuracy than at inner points, the overall accuracy of the solution is kept at the higher order (Gustaffon 1975). The boundary conditions for v are less straight forward. In order to guarantee the fourth accuracy in scheme (15). We should generate boundary conditions for v at the spatial grid point i = 0 and i = M at least under the third accuracy.

The direct application of Taylor’s expansion with Maclaurin reminder derives

$$ \frac{u_2-{u}_0}{2h}=\left(1+\frac{h^2}{6}{\delta}_x^2\right)\frac{\partial u}{\partial x}\left|{}_{x={x}_1}\right.-\frac{h^4}{360}\frac{\partial^5u}{\partial {x}^5}\left|{}_{x={x}_1}\right.+O\left({h}^6\right) $$

Omitting small term, we have

$$ \frac{u_2-{u}_0}{2h}=\left(1+\frac{h^2}{6}{\delta}_x^2\right){v}_1=\frac{1}{6}{v}_2+\frac{4}{6}{v}_1+\frac{1}{6}{v}_0+\tilde{s} $$

Then, we obtain the boundary condition

$$ {v}_0=\frac{3\left({u}_2-{u}_0\right)}{\Delta x}-{v}_2-4{v}_1 $$
(17)

Considering the other end point i = M, the boundary condition can be got from the (8)

$$ {v}_M=\frac{3\left({u}_M-{u}_{M-2}\right)}{\Delta x}-4{v}_{M-1}-{v}_{M-2} $$
(18)

3.3 Stability Analysis

Theorem 1

Suppose u(x,τ) ∈ C 4,2 (R × [0,T]) is the solution of the convection diffusion equation with constant para-meter λ, then for any λ ≥ 0, the difference scheme ( 15 ) is unconditional stable.

Proof

We conduct Von Neumann stability analysis (Balsara 1995) for the new compact scheme. Assume that the solution is of the form \( {u}_j^n={\widehat{u}}^n{e}^{ikjh} \) the exponential represents the spatial dependence. In the exponential jh represents the position along the grid and k is the spatial wave number

Taking the discrete Fourier transform of the difference scheme (15), we have

$$ M\left(\begin{array}{c} {\widehat{u}}^{n+1} \\ {\widehat{v}}^{n+1} \end{array}\right)=N\left(\begin{array}{c}{\widehat{u}}^n \\ {\widehat{v}}^n\end{array}\right) $$

where

$$ M=\left(\arraycolsep3pt\begin{array}{cc} B\left(1+\frac{\lambda \tau}{2}\right)+H& -\dfrac{ c\tau}{2}B\\[10pt] {}cH& B\left(1+\frac{\lambda \tau}{2}\right)+H\end{array}\right), $$
$$ N=\left[\arraycolsep3pt\begin{array}{cc}B\left(1-\frac{\lambda \tau}{2}\right)-H& \dfrac{ c\tau}{2}B\\[10pt] {}- cH& B\left(1-\frac{\lambda \tau}{2}\right)-H\end{array}\right] $$

with θ = kh, \( B=1-\frac{1}{3}{ \sin}^2\frac{\theta }{2}, \) \( H=2{r}_1{ \sin}^2\frac{\theta }{2}, \)

\( R=B \left(1+\frac{\lambda \tau}{2}\right)+H \), obviously, R ≥ B > 0, H ≥ 0, for any λ ≥ 0.

Thus

$$ \left(\begin{array}{c}\hfill {\widehat{u}}^{n+1}\hfill \\ {}\hfill {\widehat{v}}^{n+1}\hfill \end{array}\right)={M}^{-1}N\left(\begin{array}{c}\hfill {\widehat{u}}^n\hfill \\ {}\hfill {\widehat{v}}^n\hfill \end{array}\right) $$
(19)

Here M − 1 N is the amplification matrix at each time-step. In order for the numerical algorithm to be stable, the modulus of the eigenvalues of M − 1 N must be less than or equal to unity for all possible values of θ.

The eigenvalues of M − 1 N can be calculated as

$$ {\lambda}_{1,2}=\frac{B^2-{\left(\raisebox{1ex}{$ B\lambda \tau $} \left/ \raisebox{-1ex}{$2$}\right.+H\right)}^2-\raisebox{1ex}{${c}^2\tau BH$} \left/ \raisebox{-1ex}{$2$}\right.\pm icB\sqrt{2 BH\tau}}{R^2+\raisebox{1ex}{${c}^2\tau BH$} \left/ \raisebox{-1ex}{$2$}\right.} $$

assume \( {\left|{\lambda}_{1,2}\right|}^2=\frac{P}{Q} \), then we have

$$ P-Q=-4B\left(\frac{ B\lambda \tau}{2}+H\right)\left({R}^2+\raisebox{1ex}{${c}^2\tau BH$} \left/ \raisebox{-1ex}{$2$}\right.\right)\le 0 $$

So, |λ 1,2|2 ≤ 1, for any λ ≥ 0.

Theorem 2

Zhi Zhong Sun ( 2001 ) suppose u(x,t) ∈ C 4,2 (R × [0,T]) is the solution of the linear parabolic equations with variable coefficients, the difference scheme ( 15 ) is convergent with the convergence order O(τ 2 + h 4 ) in the L ∞ norm.

3.4 Richardson Extrapolation

Let the solution of the scheme (15) with conditions (16, 17, and 18) is U k i (h,τ)

Theorem 3

Let v n i , w n i are the solutions of the equations

$$ \left\{\begin{array}{c}\hfill \dfrac{\partial v}{\partial t}-A\left(x,t\right)\dfrac{\partial^2v}{\partial {x}^2}+B\left(x,t\right)v={s}_1\left(x,t\right),x\in R,t\in \left(0,T\right],\hfill \\ \hspace*{-12pt}v\left(x,0\right)=0, \qquad\qquad\qquad\qquad\qquad x\in R\hfill \end{array}\right. $$
$$ \left\{\begin{array}{c}\hfill \dfrac{\partial w}{\partial t}-A\left(x,t\right)\dfrac{\partial^2w}{\partial {x}^2}+B\left(x,t\right)w={s}_2\left(x,t\right),x\in R,t\in \left(0,T\right]\hfill \\ \hspace*{-12pt}w\left(x,0\right)=0,\qquad\qquad\qquad\qquad\qquad x\in R\hfill \end{array}\right. $$

with homogeneous Dirichlet boundary, and

$$ \left\{\begin{array}{c}\hfill \dfrac{\partial \tilde{u}}{\partial t}-A\left(x,t\right)\dfrac{\partial^2\tilde{u}}{\partial {x}^2}+B\left(x,t\right)\tilde{u}=p\left(x,t\right),x\in R,t\in \left(0,T\right]\hfill \\[6pt] \hspace*{-36pt}\tilde{u}\left(x,0\right)=0,\qquad\qquad\qquad\qquad\qquad\qquad x\in R\hfill \\ {}\hfill \underset{x\to -\infty }{ \lim}\tilde{u}\left(x,t\right)={\left[0,\tilde{s}\right]}^T,\underset{x\to \infty }{ \lim}\tilde{u}\left(x,t\right)={\left[0,\tilde{s}\right]}^T,t\in \left(0,T\right]\hfill \end{array}\right. $$

are smooth enough, where s 1, s 2 is given in(13)

$$ p\left(x,t\right)=\frac{A(x)}{240}\frac{\partial^6U}{\partial {x}^6},\kern1em \tilde{s}=\frac{h^4}{360}\frac{\partial^5u}{\partial {x}^5} $$

Then

$$ \begin{aligned}{U}_i^k\left(h,\tau \right)&=U\left({x}_i,{\tau}_k\right)-{\tau}^2v\left({x}_i,{\tau}_k\right)-{\tau}^4w\left({x}_i,{\tau}_k\right)-{h}^4\tilde{u}\left({x}_i,{\tau}_k\right)\\ &\quad+O\left({\tau}^6+{\tau}^2{h}^4+{h}^6\right)\end{aligned} $$

Proof

The error equation of the difference (15) is

$$ \begin{aligned} &{M}_x{\delta}_{\tau }{e}_i^n-{A}_i^n{\mu}_t{\delta}_x^2{e}_i^n+{M}_x{A}_i^n{\mu}_t{e}_i^n={M}_x{\left({s}_1\right)}_i^{n+1/2}{\tau}^2\\ {}& \quad +{M}_x{\left({s}_2\right)}_i^{n+\frac{1}{2}}{\tau}^4+{M}_x{p}_i^{n+\frac{1}{2}}{h}^4+O\left({\tau}^6+{\tau}^2{h}^4+{h}^6\right),\\ {}&{e}_i^0=0,{e}_0^k=0,{e}_m^k={\left[0,{\tilde{s}}_m^k\right]}^T{h}^4+O\left({h}^6\right),\end{aligned} $$
(20)

Similar with (15), we also construct the difference scheme

$$ \left\{\begin{array}{l}{M}_x{\delta}_{\tau }{v}_i^n-{A}_i^n{\mu}_t{\delta}_x^2{v}_i^n+{M}_x{B}_i^n{\mu}_t{v}_i^n={M}_x{\left({s}_1\right)}_i^{n+1/2}\\ {}{v}_i^0=0,\kern1em {v}_0^k=0,\kern1em {v}_m^k=0\end{array}\right. $$
(21)
$$ \left\{\begin{array}{l}{M}_x{\delta}_{\tau }{w}_i^n-{A}_i^n{\mu}_t{\delta}_x^2{w}_i^n+{M}_x{B}_i^n{\mu}_t{w}_i^n={M}_x{\left({s}_2\right)}_i^{n+1/2}\\ {}{w}_i^0=0,\kern1em {w}_0^k=0,\kern1em {w}_m^k=0\end{array}\right. $$
(22)

and

$$ \left\{\begin{array}{l}{M}_x{\delta}_{\tau }{\tilde{u}}_i^n-{A}_i^n{\mu}_t{\delta}_x^2{\tilde{u}}_i^n+{M}_x{B}_i^n{\mu}_t{\tilde{u}}_i^n={M}_x{p}_i^{n+1/2}\\ {}{\tilde{u}}_i^0=0,\kern1em {\tilde{u}}_0^k=0,\kern1em {\tilde{u}}_m^k=0\end{array}\right. $$
(23)

Let

$$ {r}_i^k={e}_i^k-{\tau}^2{v}_i^k-{\tau}^4{w}_i^k-{h}^4{\tilde{u}}_i^k $$

Let (20) − τ 2 × (21) − τ 4 × (22) − h 4 × (23), we have

$$ \left\{\begin{array}{l}{M}_x{\delta}_t{r}_i^n-{A}_i^n{\mu}_t{\delta}_x^2{r}_i^n+{M}_x{B}_i^n{\mu}_t{r}_i^n=O\left({\tau}^6+{\tau}^2{h}^4+{h}^6\right)\\ {}{e}_i^0=0,{e}_0^k=0,{e}_m^k=0,\end{array}\right. $$

According to Theorem 2, we can obtain

$$ {\left\Vert {r}^k\right\Vert}_{\infty }=O\left({\tau}^6+{\tau}^2{h}^4+{\tau}^6\right) $$

Let R = O(τ 6 + τ 2 h 4 + h 6)

$$ U\left({x}_i,{t}_k\right)-{U}_i^k\left(h,\tau \right)-\left[{\tau}^2{v}_i^k+{\tau}^4{w}_i^k+{h}^4{\tilde{u}}_i^k\right]=R $$
(24)

Let τ = O(h), we obtain the sixth-order accurate approximation both in time and space. The detailed approach to extrapolation is described as follows.

Step 1. Replace τ by \( {\tau/2} \) in (24) yield

$$ U\left({x}_i,{t}_k\right)-{U}_i^k\left(h,\frac{\tau }{2}\right)-\left[\frac{\tau^2}{4}{v}_i^k+\frac{\tau^4}{16}{w}_i^k+{h}^4{\tilde{u}}_i^k\right]=R $$
(25)

Then 4 × (25) − (24), we can get

$$ u\left({x}_i,{t}_k\right)-{\widehat{U}}_i^k\left(h,\tau \right)=\frac{\tau^4}{4}{w}_i^k\left(h,\tau \right)+{h}^4{\tilde{u}}_i^k\left(h,\tau \right)+R $$
(26)

with \( {\widehat{U}}_i^k\left(h,\tau \right)=\frac{4}{3}{u}_i^k\left(h,\frac{\tau }{2}\right)-\frac{1}{3}{u}_i^k\left(h,\tau \right) \)

Step 2. Replace h, τ by \( {h/2} \), \( {\tau/2} \) in (26)

$$ u\left({x}_i,{t}_k\right)-{\widehat{U}}_i^k\left(\frac{h}{2},\frac{\tau }{2}\right)=\frac{1}{4}\frac{\tau^4}{16}{w}_i^k\left(\frac{h}{2},\frac{\tau }{2}\right)+\frac{h^4}{16}{\tilde{u}}_i^k\left(\frac{h}{2},\frac{\tau }{2}\right)+R$$

Then, we have

$$ u\left({x}_i,{t}_k\right)-{W}_i^j\left(h,\tau \right)=O\left({\tau}^6+{\tau}^2{h}^4+{h}^6\right) $$

with \( {W}_i^k\left(h,\tau \right)=\frac{16}{15}{\widehat{U}}_i^k\left(\frac{h}{2},\frac{\tau }{2}\right)-\frac{1}{15}{\widehat{U}}_i^k\left(h,\tau \right) \)

Step 3. Compute the extrapolation W k i (h,τ) by

$$ {\widehat{U}}_i^k\left(h,\tau \right)=\frac{4}{3}{u}_i^k\left(h,\frac{\tau }{2}\right)-\frac{1}{3}{u}_i^k\left(h,\tau \right) $$
(27)
$$ {W}_i^k\left(h,\tau \right)=\frac{16}{15}{\widehat{U}}_i^k\left(h,\tau \right)-\frac{1}{15}{\widehat{U}}_i^k\left(h,\tau \right) $$
(28)

4 Solution of the Black-Scholes Equation

Case 1. Linear Convection-Diffusion Equation

To show both the time and space accuracy of the new algorithm, we must verify the new scheme by solving a 1D convection-diffusion equation. Considering the follow equation:

$$ \left\{\arraycolsep4pt\begin{array}{ll}\hfill \dfrac{\partial u}{\partial t}=\dfrac{1}{2}\dfrac{\partial^2u}{\partial {x}^2}+\frac{1}{2}\frac{\partial u}{\partial x},\hfill & \hfill x\in \left(0,1\right),t\in \left(0,T\right]\hfill \\[10pt] {}\hfill u\left(x,0\right)={e}^x,\hfill & x\in \left(0,1\right)\hfill \end{array}\right. \vspace*{-3pt} $$

which exact solution is u(x,t) = e x + t, the boundary conditions are obtained for the exact solution.

error 1 , error 2 , error 3 denote the maximum errors of the high order compact scheme (15), extrapolation scheme (27), extrapolation scheme (28), respectively. The data in Table 1 show the errors between the numerical and exact solutions at T = 1.0 for a fixed h = 0.0001, while ∆t is varying.

Table 1 Maximal error and convergence order in time when H is fixed
Full size table

One can see that the error from the extrapolation scheme (28) is smaller than which from the others.

The data in Table 2 shows that the error of solution by the extrapolation scheme (28) at T = 1 with ∆t = h, it is a sixth-order algorithm.

Table 2 Maximal error and convergence order of the scheme (27)
Full size table

Case 2. Variable Coefficient Problem

To verify the efficiency of the compact scheme (15) and extrapolation schemes (28) for the nonlinear Black Scholes equation, we construct the problem as follows (Lifeng Xi et al. 2008);

$$ \begin{array}{l}\displaystyle-\frac{\partial u}{\partial t}-2{x}^2\frac{\partial^2u}{\partial {x}^2}-\left(1+ xt\right)x\frac{\partial u}{\partial x}+{e}^tu=f\left(x,t\right),\left(x,t\right)\in \varOmega \\ {}u\left(0,t\right)=u\left(1,t\right)=0,t\in \left[0,1\right]\\ {}u\left(x,1\right)=\left(1-{x}^3\right)\left({e}^x-1\right)+x\left(1-x\right),x\in \left[0,1\right]\end{array} \vspace*{-3pt} $$

Chosen f(x,t) such that

$$ u\left(x,t\right)=t\left(1-{x}^3\right)\left({e}^x-1\right)+{t}^3x\left(1-x\right) \vspace*{-3pt} $$

The data in Table 3 shows the high order compact (15) is second-order accurate in time and fourth-order accurate in space with respect to L ∞-norms.

Table 3 Maximal error and convergence order of the scheme (15) (∆t = h2)
Full size table

The data in Table 4 shows the extrapolation scheme (28) is sixth-order accurate both in time and space with respect to L ∞-norms.

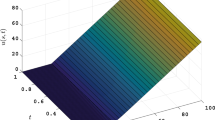
Table 4 Maximal error and convergence order of the scheme (28) (∆t = h)
Full size table

Figures 1 and 2 show the option prices and the hedge delta of the European call at the 3 month and the half year. We can solve the Black-Scholes equation through the high order compact (15) or the extrapolation scheme (28), simultaneously.

Fig. 1
figure 1

Option prices for different maturity time. *Denote the numerical solution. The horizontal axis indicates the normalized stoke price

Full size image
Fig. 2
figure 2

Hedge delta for different maturity time. *Denote the numerical solution. The horizontal axis indicates the normalized stoke price

Full size image

5 Conclusion

An efficient fourth-order compact scheme and Richardson’s extrapolation scheme have been proposed in this paper. These methods combine the Crank-Nicolson method in the time discretization and the fourth-order Padé approximation to the second spatial derivatives in the space discretization. An unconditionally stable of the compact scheme is also proved, and is particularly suitable for problems which require calculations of both the solutions and their derivatives, such as, Black-Scholes equation. The option price and hedge delta are obtained, simultaneously. Then, a riskless portfolio is also obtained. A three-grid stencil extrapolation algorithm has been established to make the final solution sixth-order accurate in both time and space. As a result, by the use of a coarser temporal grid, we can obtain the numerical solution of acceptable accuracy with low time cost. Numerical results coincide with our theoretical analysis very well, and demonstrate the high accuracy and efficiency of the extrapolation algorithm.