Land Surface Hydrological Models

Abstract

The details of land-surface models (LSMs) are presented here from the perspective of providing the proper boundary condition to and interaction with a “parent” atmospheric model. Topics include atmospheric forcing to LSMs, land data sets, surface-layer turbulence, surface fluxes and energy and water budgets, land-surface physics, and the role of the land states and surface fluxes in local land-atmosphere interaction. Connections of LSMs with hydrological models (e.g., saturated zone or groundwater, and streamflow or river-routing) and land data assimilation are outside the scope of this chapter.

1 Introduction

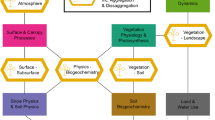
Traditionally, from the perspective of a Numerical Weather Prediction (NWP) or a coupled atmosphere-ocean-land-ice seasonal and longer time-scale climate model, the role of a land-surface model (LSM) is to provide surface quantities as boundary conditions to the atmosphere, which includes the surface fluxes and land states (and other land-surface properties) needed to calculate the surface fluxes. In providing these necessary surface boundary conditions, the land model closes the surface energy and water budgets. The land provides predictability in weather and climate models, where land states, especially soil moisture, vegetation, and snow, can provide predictability in the window between deterministic (weather) and seasonal and longer climate (e.g., ocean-atmosphere) time scales (Fig. 1). The Noah land model (Ek et al. 2003) is described here as a useful example of those classes of land models developed in conjunction with atmospheric numerical prediction models (Fig. 2). Although not covered in this chapter, the LSM also provides the upper boundary conditions in the form of runoff that is passed to a hydrology model that accounts for the movement of water deeper into the groundwater and lateral connections that end up as stream/riverflow with an ultimate connection to the ocean.

Fig. 1

Land predictability lies between atmosphere and ocean-atmosphere interaction. (Courtesy Paul Dirmeyer, George Mason University.)

Fig. 2

Noah land-surface model . See text for details

To provide proper boundary conditions, a land model must have atmospheric forcing to drive the LSM; appropriate physics to represent land-surface processes (for the relevant temporal and spatial scales, including the correct land-atmosphere interactions) and associated LSM parameters; corresponding land data sets, e.g., land use/land cover (vegetation type), soil type, surface albedo, snow cover, surface roughness, etc.; and proper initial land states, analogous to initial atmospheric conditions, though land states may carry more memory, especially, e.g., in deep soil moisture, similar to ocean temperatures and corresponding ocean heat content.

2 Atmospheric Forcing Data

A land model is forced by incoming solar and longwave radiation; precipitation; pressure; and wind, temperature, and humidity. Atmospheric forcing may be from a parent atmospheric model (analysis or reanalysis) and/or from in situ or remotely sensed observations, where precipitation is quite important for LSMs since this affects soil moisture which in turn affects both heat and moisture flux, with solar radiation incident at the surface an additional important forcing as this drives the available energy for surface fluxes. The downward longwave radiation can be important especially during the night when small changes in this radiative forcing may affect the surface energy budget such that the surface may become “decoupled” from the atmosphere, especially over snow cover which may be “insulated” from energy from the soil beneath the snowpack. This will be affected by patchy snow cover, where the soil may then more properly “communicate” with the surface. The near-surface atmospheric variables (wind, temperature, and humidity) affect the vegetation response as well as near-surface gradients in these quantities, thereby affecting surface fluxes. This forcing data set (e.g., Fig. 3) may be spatial in manner at a particular time for an LSM run “offline” in 2-D mode, or coupled with a parent atmospheric model. Alternately, a time series of a forcing data set for a particular point can be used to provide a location-specific LSM run, i.e., 1-D offline, thereby allowing for long runs of the LSM for analysis and land model development, with minimal compute cost. Inclusion of a land data assimilation feature to ingest some or all of these forcing terms constitute a land data assimilation system, whether in an offline LSM-only or coupled with a parent atmospheric model mode.

Fig. 3

Example atmospheric forcing to LSM. See text for details

3 Land Data Sets

Land models depend on a number of land data sets in order to properly specify the surface characteristics necessary for the execution of the LSM physics. Land-use class (or vegetation type) and soil type (or soil texture class) may be specified for a given site, and generally come from global data sets, often from a satellite product (e.g., Fig. 4; Hansen et al. 2000 for land-use, and Schwarz and Alexander 1995, and USDA Soil Survey 1995 for soils). These quantities are generally treated as static, especially soil type, but for land-use, there may be year-to-year changes (and on even shorter time scales, especially at higher resolution), e.g., in the case of urbanization, deforestation, and desertification.

Fig. 4

(a) 1-km IGBP-MODIS land-use class/vegetation type, (b) 1-km STATSGO-FAO soil type

Albedo is a diurnally and seasonally varying quantity, where we make use of monthly climatologies of mid-day albedo based on remotely sensed Moderate Resolution Imaging Spectroradiometer (MODIS) data for snow-free albedo (Friedl et al. 2010; Fig. 5a). Over deep snow, the albedo of the surface is higher and in LSMs previously was often set to some uniformly large value (e.g., 0.70), however, this can vary greatly depending on the surface character. For example, a conifer forest may have a lower albedo due to darker treetops sticking through a brighter (deep) snowpack (depending on the vegetation fraction), compared with a higher albedo for a completely snow-covered grassland. Maximum snow albedo may be given as a function of the land-use class and vegetation fraction, or again from MODIS data as annual maximum snow albedo climatology (e.g., Barlage et al. 2005; Fig. 5b). Note the differences between the North American boreal forests with lower maximum snow albedos due to more shading of the snowpack under the canopy, compared to the U.S. Great Plains grasslands with higher maximum snow albedos due to more open ground and exposed snow cover. Albedo may also be a calculated quantity by the LSM which depends on soil moisture and texture/color, as well as solar zenith angle (as determined by, e.g., a solar elevation calculation or from a radiation code from a coupled parent atmospheric model to adjust the mid-day albedo to a value for a particular time of day).

Fig. 5

(a) 1-km monthly, Boston Univ.-MODIS monthly snow-free albedo, (b) 5-km Univ. Arizona-MODIS maximum snow albedo

The initial inclusion of seasonally and spatially varying vegetation climatology in LSMs was an important feature in order to more properly represent the surface energy partition (including the calculation of evapotranspiration). Unless the LSM has a prognostic calculation of vegetation phenology (vegetation cover (green vegetation fraction or GVF) and vegetation density (leaf area index or LAI)), these quantities are provided in the form of 2-D maps or given as functions of the vegetation type, or scaled based on the seasonal phenology of GVF in the case of LAI . These quantities may come from remotely sensed data sets, e.g., long-term climatology data sets (Fig. 6a–b; Gutman 1999 for GVF) or via near-realtime observations (e.g., Fig. 6c). These data sets were generated from Advanced Very-High-Resolution Radiometer (AVHRR), MODIS , and Visible Infrared Imager Radiometer Suite (VIIRS) satellite imagery.

Fig. 6

(a) 16-km green vegetation fraction (GVF) multi-year climatology from AVHRR, (b) 4-km leaf area index (LAI) climatology from MODIS, (c) 4-km near-realtime (15 May 2016) GVF from VIIRS

Snow cover is a seasonal feature for many high-latitude regions, and more ephemeral in nature at locations equatorward during the cold season. Snow data sets are often updated daily (e.g., Fig. 7) or even subdaily depending on availability of remotely sensed and in situ data. LSMs determine the onset, evolution, and ablation of snowpacks, but updating snow information based on observations is necessary, again to determine the proper surface energy and water budgets, and especially important for numerical weather prediction models that are run multiple times in a day. Snowpack physics will be discussed further below.

Fig. 7

(a) 4-km snow cover from the National Ice Center, (b) 16-km snow depth and cover from the US Air Force 557th Weather Wing (formerly Air Force Weather Agency, AFWA)

Longwave surface emissivity is another land data set that can be determined from remotely sensed data or specificed from other land data sets, e.g., vegetation and soil type. Fresh snow may have a surface emissivity approaching unity (1.0), while a sandy soil with high quartz content may be less than 0.9. Surface emissivity is included in equations for solving the surface energy budget, and as a general approximation is often set to 1.0.

Other surface characteristics include soil depth and slope, all important for vegetation processes and the movement of water in the soil, with connections to runoff and groundwater hydrology.

4 Land-Surface Model

The Noah LSM has many features that are similar to other LSMs and has been previously described in Mahrt and Pan (1984) and Pan and Mahrt (1987), with updates described in Chen et al. (1996), and Ek et al. (2003). More recent updates to the Noah LSM are described in Niu et al. (2011) and Yang et al. (2011), and among these include an explicit vegetation layer and subcanopy (requiring separate energy budgets), CO₂-based photosynthesis (for canopy conductance in the calculation of transpiration, mentioned further below), a prognostic calculation of vegetation phenology (cover and density), and a multilayer snowpack, with this updated Noah LSM called “Noah-MP.” Our focus here is on the “classic” Noah LSM.

4.1 Surface Fluxes

The land-surface model determines the surface fluxes for the surface and water budgets, and the surface momentum flux, i.e.,:

$$ {R}_n=H+ LE+G, $$

(1)

$$ \Delta S=P-R-E, $$

(2)

$$ \tau =\rho {C}_m{U}_a^2, $$

(3)

where Eqs. (1) and (2) are the surface energy and water budgets, respectively, and Eq. (3) is the surface momentum flux. In the surface energy budget, the net radiation (R_n) is partitioned between the turbulent sensible (H) and latent heat (LE) fluxes to or from the surface, respectively, and the soil heat flux (G), the flux into or out of the soil.

The latent heat flux (or evapotranspiration) is composed of evaporation of canopy-intercepted water, soil, or direct (non-vegetative) evaporation and plant transpiration, and in the presence of snowpack, an additional latent heat flux associated with snow phase change. The L in the LE may be the latent heat of vaporization (L_v) or of sublimation (L_s), depending on a liquid or frozen surface (Evapotranspiration is discussed further below).

In the surface water budget, ΔS includes the change in land-surface water, i.e., soil moisture, snowpack (cold season), and canopy water (dewfall or frostfall and intercepted precipitation, that are small, but not always negligible) and is balanced by precipitation (P), runoff (R), and evapotranspiration (E), where P − R is infiltration of moisture into the soil.

Finally, the surface momentum flux (3) is a function of wind speed and surface drag that depends on surface characteristics and the near-surface turbulent exchange (discussed further below). Surface characteristics include the land-use or vegetation type, vegetation density, and cover (e.g., patchy grassland vs. a dense forest canopy, presence of snow, etc.), while the surface turbulent exchange is in the form of a surface drag coefficient depends on the near-surface atmospheric stability, where unstable (stable) conditions are characterized by stronger (weaker) turbulent exchange with the near surface atmosphere, and U_a is the horizontal wind speed at some reference height in the atmosphere, (z_a) defined as

$$ {U}_a=\sqrt{u_a^2+{v}_a^2}, $$

(4)

where u_a and v_a are the horizontal wind components at z_a, e.g., as determined from a parent atmospheric model, or alternately via observations. Note that the grid-averaged wind speed in a model may vanish, but surface heat and moisture fluxes can be non-zero (due to subgrid horizontal motions), hence the surface flux parameterizations needs to account for free-convection conditions, e.g., by adding a minimum wind speed (<1 ms⁻¹) or the convective velocity scale (w_∗) to the mean wind speed.

The surface energy budget may be broken down further as:

$$ {\displaystyle \begin{array}{l}{R}_n=S\downarrow -S\uparrow +L\downarrow -L\uparrow, \\ {}\ =S\downarrow \left(1-{\alpha}_s\right)+L\downarrow -{\epsilon}_s\sigma {T}_s^4,\end{array}} $$

(5)

$$ H=\rho {c}_p{C}_h{U}_a\left({T}_s-{T}_a\right), $$

(6)

$$ LE=\rho {L}_v{C}_q{U}_a\left({q}_s-{q}_a\right), $$

(7)

where R_n is comprised of the incoming solar radiation (S ↓), outgoing or reflected solar radiation (S ↑), incoming atmospheric longwave radiation (L ↓), and emitted longwave radiation (L ↑). The reflected solar radiation can be expressed as the incoming solar radiation multiplied by a surface albedo (α_s, a function of surface properties such as vegetation and soil type, soil moisture, snow cover, etc.), while the emitted longwave radiation is a function of the surface emissivity (ϵ_s, also a function of surface properties, with a value near unity), the Stefan-Boltzmann constant (σ = 5.67 × 10⁻⁸), and the surface skin temperature (T_s). The sensible and latent heat fluxes depend on U_a, and the near-surface gradients in the temperature (T_s − T_a) and specific humidity (q_s − q_a), respectively, specific heat (c_p, 1004.5 J kg⁻¹ K⁻¹) and latent heat (L_v, assumed constant as 2.5 × 10⁶ J kg⁻¹, or L_s as noted further above), respectively, and the surface turbulent exchange coefficients for heat (C_h) and moisture (C_q), respectively. (Here we adopt the usual convention that C_q = C_h.) Note that the approach of a single effective surface temperature, encompassing surface, canopy, and snow, has been adopted which is then used in the calculation of surface fluxes. See Fig. 8.

Fig. 8

Surface fluxes for different surfaces in Noah LSM

4.2 Surface Turbulent Exchange Coefficients

Surface exchange coefficients (and thus surface fluxes) are calculated by iterating an implicit formula of the Monin-Obukhov stability-dependent profile functions based on surface-layer similarity theory. This is an alternative to using the explicit approach by Louis (1979) and Louis et al. (1982) based on the near-surface bulk Richardson number. There are limitations in the Louis formulations for cases where the ratio of the momentum to heat roughness is large, as demonstrated in Holtslag and Ek (1996). These limitations have been further addressed in van den Hurk and Holtslag (1997), who suggest more accurate explicit functions based on the bulk Richardson number. We present both implicit and explicit approaches here; see Beljaars and Holtslag (1991) for a more detailed comparison.

4.2.1 Implicit Exchange Coefficients Calculation

The surface exchange coefficients for momentum and heat (and moisture) using the implicit formulations are (respectively)

$$ {C}_m=\frac{k^2}{{\left[\ln \left({z}_a/{z}_{0m}\right)-{\Psi}_m\left({z}_a/L\right)+{\Psi}_m\left({z}_{0m}/L\right)\right]}^2}, $$

(8)

$$ {C}_h=\frac{k^2}{\left[\ln \left({z}_a/{z}_{0m}\right)-{\Psi}_m\left({z}_a/L\right)+{\Psi}_m\left({z}_{0m}/L\right)\right]\left[\ln \left({z}_a/{z}_{0h}\right)-{\Psi}_h\left({z}_a/L\right)+{\Psi}_h\left({z}_{0h}/L\right)\right]}, $$

(9)

where k is the von Kármán constant (taken as 0.40), z_a is the atmospheric reference height (e.g., first atmospheric model level height), z_0m and z_0h are the roughness lengths for momentum and heat, respectively, L is the Obukhov length, and Ψ_m,h are the stability profile functions for momentum and heat. (As with the exchange coefficient, we assume that Ψ_q = Ψ_h.) The profile functions for unstable conditions (following Paulson 1970) are

$$ {\Psi}_m=2\ln \left[\left(1+x\right)/2\right]+\ln \left[\left(1+{x}^2\right)/2\right]-2{\tan}^{-1}(x)+\pi /2, $$

(10)

$$ {\Psi}_h=2\ln \left[\left(1+{x}^2\right)/2\right], $$

(11)

where

$$ x={\left(1-16z/L\right)}^{1/4}, $$

(12)

and for stable conditions (following Webb 1970) are

$$ {\Psi}_m={\Psi}_h=-5z/L. $$

(13)

The Webb (1970) profile functions are fairly consistent with most data for 0 < z/L < 0.5 (see Beljaars and Holtslag 1991). Alternate profile functions for stable conditions follow Holtslag and De Bruin (1988) for up to z/L ≈ 7

$$ -{\Psi}_m=a\frac{z}{L}+b\left(\frac{z}{L}-\frac{c}{d}\right)\exp \left(-d\frac{z}{L}\right)+\frac{bc}{d}, $$

(14)

$$ {\Psi}_h={\Psi}_m, $$

(15)

where a = 0.7, b = 0.75, c = 5, and d = 0.35. This expression behaves like (13) for small z/L values and approaches −Ψ_m ≈ a(z/L) for large z/L (very stable conditions).

Typically, z_0m ≈ 0.01 − 0.10m and z_0m ≫ z_0h for bare soil and short vegetation (e.g., croplands, grasslands), while z_0m ≈ 1.0m and z_0m/z_0h ≈ O(1–10) for taller vegetation (e.g., forests) and is affected by vegetation cover, e.g., weighted in some manner by the fraction of vegetation versus bare soil.

4.2.2 Explicit Exchange Coefficients Calculation

Following Louis (1979) and Louis et al. (1982), the surface exchange coefficients for momentum and heat (and moisture) using the explicit formulations are (respectively)

$$ {C}_m={k}^2\frac{F_m}{{\left[\ln \left({z}_a/{z}_{0m}\right)\right]}^2}, $$

(16)

$$ {C}_h=\left(\frac{k^2}{R}\right)\frac{F_h}{\ln \left({z}_a/{z}_{0m}\right)\ln \left({z}_a/{z}_{0h}\right)}, $$

(17)

where R, estimated as 1.0, is the ratio of the drag coefficients for momentum and heat in the neutral limit and is taken from Businger et al. (1971). Here, C_m and C_h are functions of F_m,h instead of Ψ_m,h. For unstable condition (modified by Holtslag and Beljaars 1989), F_m,h are defined as

$$ {F}_m=1-\frac{10{Ri}_b}{1+75\;{k}^2{\left[\ln \left({z}_a/{z}_{0m}\right)\right]}^{-2}{\left[-{Ri}_b\left({z}_a/{z}_{0m}\right)\right]}^{1/2}}, $$

(18)

$$ {F}_h=1-\frac{15{Ri}_b}{1+75\;{k}^2{\left[\ln \left({z}_a/{z}_{0m}\right)\right]}^{-1}{\left[\ln \left({z}_a/{z}_{0h}\right)\right]}^{-1}{\left[-{Ri}_b\left({z}_a/{z}_{0m}\right)\right]}^{1/2}}, $$

(19)

and for stable conditions (modified by Holtslag and Beljaars 1989)

$$ {F}_m={F}_h=\frac{1}{1+10{Ri}_b\left(1+8{Ri}_b\right)}, $$

(20)

where Ri_b is the near-surface bulk Richardson number, defined as

$$ {Ri}_b=\frac{gz_a\left({\theta}_{av}-{\theta}_{sv}\right)}{\theta_{av}{U}_a^2}, $$

(21)

where g is gravity, θ_av − θ_sv is the virtual potential temperature gradient between the air θ_av at z_a, and the surface θ_sv.

By itself, the usual similarity theory under stable conditions leads to a significant overestimation of surface cooling. This is due to (a) failure to consider subgrid-scale spatial variability where vertical fluxes can occur in part of the grid even with large (bulk) Richardson number (Ri_b) based on grid averaged variables (Mahrt 1987), (b) poor vertical resolution where turbulence may occur in thinner layers, perhaps intermittently, even when Ri_b over the model layer is large, (c) neglect of clear air radiative cooling, (d) neglect of gravity wave momentum transport, and (e) use of a surface skin temperature from the surface energy balance (as is done, instead of temperature at the roughness height) to compute the near-surface bulk Richardson number.

To compensate for such inadequacies, various mechanisms have been employed (and are often unreported) which include capping the allowable value of the Richardson number or specifying a minimum wind speed. An alternative to Eq. (20) that leads to noted improvement in model performance in the nocturnal boundary layer is the area-averaged exchange coefficient relationship of Mahrt (1987) where for stable conditions F_m,h are defined as

$$ {F}_m={F}_h=\exp \left(-{\alpha}_m{Ri}_b\right), $$

(22)

where α_m is nominally set equal to 1.0. However, α_m is expected to depend on, e.g., (a) model vertical resolution, (b) wind speed, and (c) subgrid characteristics such as standard deviation of subgrid surface skin temperature, terrain height, or some other measure of the surface inhomogeneity.

4.3 Prognostic Land States

The prognostic variables that must be determined in order to calculate surface fluxes are the volumetric soil moisture content (${\Theta}_{soil_n}$, for soil layer n), and soil temperature (${T}_{soil_n}$), and the canopy water content (C_w).

4.3.1 Soil Moisture Tendency

Soil moisture is modeled with the prognostic equation for the volumetric water content (Θ) as

$$ \frac{\mathrm{\partial \Theta }}{\partial t}=\frac{\partial {K}_{\Theta}}{\partial z}+\frac{\partial }{\partial z}\left({D}_{\Theta}\frac{\mathrm{\partial \Theta }}{\partial z}\right)+F\left(\Theta \right), $$

(23)

where K_Θ is hydraulic conductivity and D_Θ is the soil water diffusivity, both highly nonlinear functions of the soil water content (Θ), varying by several orders of magnitude from dry to wet soil conditions, and F(Θ) is the soil water source/sink term representing evapotranspiration, infiltration, and runoff. Infiltration is the ability of a soil of a given wetness to absorb water at a given rate, and runoff is amount of soil moisture that leaves the soil column, at the surface due to precipitation in excess of the infiltration rate, laterally due to soil moisture in excess of saturation for a given layer, and through the bottom due to gravitational drainage, where infiltration and runoff are functions of soil type and soil water content (see Chen et al. 1996, Schaake et al. 1996, and Koren et al. 1999 for further details). Evapotranspiration is discussed further in Sect. 4.4.4, and K_Θ and D_Θ in Sect. 4.6.

4.3.2 Soil Temperature Tendency

Soil heat transfer is treated with a prognostic equation for soil temperature (T) such that

$$ {C}_{\Theta}\frac{\partial T}{\partial t}=\frac{\partial }{\partial z}\left({\lambda}_T\frac{\partial T}{\partial z}\right), $$

(24)

where C_Θ is the volumetric heat capacity of moist soil and λ_T is the soil thermal conductivity, both functions of the soil water content (Θ). C_Θ is linearly related to Θ, whereas λ_T is a nonlinear function of Θ and increases by several orders of magnitude from dry to wet soil conditions; C_Θ and λ_T are discussed further in Sect. 4.7.

4.3.3 Canopy Water Tendency

The canopy water content (C_w) changes as

$$ \frac{\partial {C}_w}{\partial t}={\sigma}_f PD\downarrow -{E}_c, $$

(25)

where σ_f is the plant shading factor (0 ≤ σ_f ≤ 1). PD↓ is precipitation + dewfall which increases C_w, while canopy water evaporation (E_c) decreases C_w. (Precipitation is a forcing quantity provided to the land model from e.g., observations or from a parent atmospheric model.)

4.4 Solution of Surface Energy Budget

In order to determine the surface values of temperature and moisture necessary to calculate surface heat and moisture fluxes, it is necessary to solve the surface energy balance where we begin by evaluating the surface energy balance for the reference state of the surface that is in a saturated condition in order to determine the potential evaporation. We determine the potential evaporation closely following the derivation in Mahrt and Ek (1984), except that the usual Penman (1948) potential evaporation relationship is modified (as discussed below) since the surface temperature is needed to compute net radiation. This surface energy balance for a saturated surface condition is:

$$ \left(1-\alpha \right)S\downarrow +L\downarrow -{\epsilon}_s\sigma {T}_s^4=H+{LE}_p+G, $$

(26)

where potential evaporation (LE_p) and the other terms have been previously defined. Here T_s and H are their values corresponding to the potential evaporation LE_p. (The left hand side of Eq. (26) is simply the net radiation under this saturated condition.) In determining potential evaporation, G is determined using variables from the previous model time step and is updated later. The outgoing longwave radiation, $\sigma {T}_s^4$, is linearized as

$$ \sigma {T}_s^4\approx \sigma {T}_a^4\left[1+4\left(\frac{T_s-{T}_a}{T_a}\right)\right], $$

(27)

where T_a is the air temperature at the first model level in the atmosphere. Here the sensible heat flux uses a saturated surface temperature appropriate for the potential evaporation and is defined as

$$ H=\rho {c}_p{C}_hU\left({T}_s-{T}_a\right), $$

(28)

where T_s is the saturated surface temperature, and the other terms have been previously defined.

4.4.1 Soil Heat Flux

Soil heat flux (G) is formulated (e.g., described in McCumber and Pielke 1981) as

$$ G=-{\lambda}_T\frac{\partial {T}_{s_1}}{\partial z}, $$

(29)

where λ_T is the soil thermal conductivity and $\partial {T}_{s_1}/\partial z$ is the soil temperature gradient in the upper soil layer. The finite difference form of Eq. (29) is

$$ G=-{\lambda}_T\frac{T_s-{T}_{s_1}}{\Delta z}, $$

(30)

where T_s and ${T}_{s_1}$ are the surface and upper soil layer temperatures, respectively, and Δz is the mid-point of the upper soil layer. As with the sensible heat flux (28), for the purpose of calculating potential evaporation, G is determined using values (e.g., actual T_s, etc.) from the previous model time step, but is updated later.

In the presence of a vegetation layer, soil heat flux is reduced because of reduced heat conductivity through vegetation (see Fig. 8). This has been demonstrated by Viterbo and Beljaars (1995) in the ECMWF model land-surface scheme (TESSEL, van den Hurk et al. 2000). They suggest a simple parameterization to deal with this effect where G is computed as the product of an empirical coefficient (appropriate to the surface concerned) and the temperature difference between the surface and the center of the upper soil layer (3.5 cm in the TESSEL scheme, at that time), i.e.,

$$ G={\Lambda}_T\Delta T, $$

(31)

where Λ_T is a fixed constant thermal conductivity function (e.g., 7 W m⁻² K⁻¹ for a grassland site at Cabauw, Netherlands). This formulation draws upon earlier work by van Ulden and Holtslag (1985), and implicitly accounts for the reduction of soil heat flux in the presence of vegetation. Van den Hurk et al. (1995), van den Hurk and Beljaars (1996), and van den Hurk et al. (2000) describe refinements to this approach where the value of Λ_T varies depending on land-surface classification, e.g., bare ground, sparse vegetation, etc. λ_T and alternatives to the soil heat flux formulation in the TESSEL scheme are discussed further in Sect. 4.7.

4.4.2 Linearized Surface Energy Balance

We further define

$$ {F}_n=\left(1-\alpha \right)S\downarrow +L\downarrow -{\epsilon}_s\sigma {T}_a^4-G, $$

(32)

and substitute into Eq. (26) to obtain

$$ {F}_n-4\sigma {T}_a^4\left(\frac{T_s-{T}_a}{T_a}\right)=H+{L}_v{E}_p. $$

(33)

Substituting Eq. (28) into Eq. (33) we obtain

$$ {F}_n-4\sigma {T}_a^4\left(\frac{T_s-{T}_a}{T_a}\right)=\rho {c}_p{C}_hU\left[\left({T}_s-{T}_a\right)-\left({\theta}_a-{T}_a\right)\right]+{L}_v{E}_p. $$

(34)

4.4.3 Potential Evaporation

To determine the surface evapotranspiration, we begin by calculating the Penman (1948) potential evaporation that is defined as evaporation from a surface with no “resistance” to evaporation (e.g., free evaporation from an open water surface) and formulated as

$$ {\displaystyle \begin{array}{l}{L}_v{E}_p=\rho {c}_p{C}_qU\left({q}_{s, sat}-{q}_a\right)\\ {}\ =\rho {c}_p{C}_hU\left[\frac{dq_s}{dT}\left({T}_s-{T}_a\right)+\left({q}_{a, sat}-{q}_a\right)\right],\end{array}} $$

(35)

where we make the usual assumption that the exchange coefficients for moisture and heat are equal (C_q = C_h). dq_s/dT is the slope of the saturation specific humidity with temperature, q_s,sat is the surface saturation specific humidity, and q_a,sat and q_a are the saturation and actual specific humidities at the first atmospheric model level, respectively. To explicitly eliminate T_s in our expression for potential evaporation, we solve for T_s − T_a in Eq. (35), where

$$ {T}_s-{T}_a=\left[\frac{L_v{E}_p}{\rho {L}_v{C}_hU}-\left({q}_{a, sat}-{q}_a\right)\right]{\left(\frac{dq_s}{dT}\right)}^{-1}. $$

(36)

Substituting for T_s − T_a in Eq. (34) using Eq. (36), and after some rearranging, we solve for potential evaporation

$$ {L}_v{E}_p=\rho {c}_p{C}_hU\left(\frac{\Delta \left[\frac{F_n}{\rho {c}_p{C}_hU}+\left({\theta}_a-{T}_a\right)\right]+A\left(r+1\right)}{\Delta +r+1}\right), $$

(37)

where

$$ {\displaystyle \begin{array}{l}\Delta =\frac{dq_s}{dT}\frac{L_v}{c_p},\\ {}A=\frac{L_v}{c_p}\left({q}_{a, sat}-{q}_a\right),\\ {}r=\frac{4\sigma {T}_a^4{R}_d}{p_s{c}_p{C}_hU}.\end{array}} $$

4.4.4 Surface Evapotranspiration

The total surface moisture flux, or evapotranspiration (E), has contributions from five sources: evaporation of water from an open water source (E_w) (e.g., lakes), plant canopy (E_c), direct evaporation from the soil (E_d), plant transpiration (E_t), and sublimation from the snow or ice surfaces (E_s; see Sect. 4.8.4 under Cold Season Processes), e.g., Fig. 9, so the total is

$$ E={E}_w+{E}_d+{E}_c+{E}_t+{E}_s. $$

(38)

The total evaporation cannot exceed the potential evaporation (E_p) defined in Eq. (37). Evaporation from an open water source, E_w, is simply the potential evaporation (E_p). The sum of the evaporative terms is aggregated into a single flux that is then passed to the atmosphere (Fig. 9).

Fig. 9

Example model grid box showing (left) surface fluxes from a number of sources, i.e., open water, canopy water, plant transpiration, direct evaporation, and snow/ice sublimation, and (right) the aggregated flux that is passed to the atmosphere, e.g., a parent atmospheric model

4.4.5 Canopy Evaporation

The canopy evaporation of free water (E_c) is formulated as

$$ {E}_c={\sigma}_f{\left(\frac{C_w}{S_w}\right)}^n{E}_p, $$

(39)

where σ_f is the vegetation fraction (or plant shading factor, a fraction between 0 and 1), C_w and S_w are the actual and saturated water contents, respectively, for a canopy surface (a function of plant type), and n = 0.5, following Pan and Mahrt (1987) who cite earlier studies. The canopy water is filled by precipitation or dewfall, and when saturated, all additional water is assumed to fall through to the ground surface.

4.4.6 Direct Soil Evaporation

To determine direct evaporation (E_d) at the air-soil interface, it is necessary to determine the rate at which the soil can provide moisture to the surface to evaporate. We assume that evaporation may proceed at the potential rate until the surface soil moisture content decreases to an “air-dry” value, Θ_d (see Mahrt and Pan 1984, Chang et al. 1999, and references therein). As a first step, we demand that the evaporation be at the potential rate in which case

$$ {E}_p=\left[{D}_{\Theta}\left(\frac{\mathrm{\partial \Theta }}{\partial z}\right)+{K}_{\Theta}\right]\left(1-{\sigma}_f\right), $$

(40)

where D_Θ is the soil water diffusivity and K_Θ is the soil hydraulic condictivity (D_Θ and K_Θ will be discussed further below). The finite-difference form of Eq. (40) is

$$ {E}_p=\left[{D}_{\Theta}\left(\frac{\Theta_s-{\Theta}_1}{\Delta z/2}\right)+{K}_{\Theta}\right]\left(1-{\sigma}_f\right), $$

(41)

where D_Θ and K_Θ are the values averaged between the surface and upper soil layer, Θ_s and Θ₁ are the volumetric soil moisture contents at the surface and upper soil model layer, respectively, and Δz/2 is the mid-point of the upper soil layer. The direct soil evaporation can proceed at a potential rate when the apparent soil moisture at the surface (obtained by solving for Θ_s in Eq. (41)) is greater than the air-dry value (Θ_d), that is, when the soil is sufficiently wet (demand control stage). When the soil dries out, the evaporation can only proceed at the rate by which the soil can diffuse water upward from below (flux control stage) in which case Θ_s = Θ_d and E_d < E_p. Then the direct soil evaporation (in finite difference form) is

$$ {E}_d=\left[{D}_{\Theta}\left(\frac{\Theta_d-{\Theta}_1}{\Delta z/2}\right)+{K}_{\Theta}\right]\left(1-{\sigma}_f\right). $$

(42)

4.4.7 Plant Transpiration and Canopy Resistance

Plant transpiration (E_t) is calculated as

$$ {E}_t={\sigma}_f{k}_v\left[1-{\left(\frac{C_w}{S_w}\right)}^n\right]{E}_p, $$

(43)

where k_v is the “plant coefficient” (a fraction between 0 and 1) and can be related to the commonly used expression of “canopy resistance,” r_c (sometimes called “surface resistance” if the surface is not fully covered with vegetation). The canopy resistance (r_c) accounts for the reduction in transpiration due to plant stomatal control and has been often expressed in the meteorological land-surface modeling community as a function of environmental variables, most commonly: incoming solar radiation, air temperature, specific humidity deficit of the air, and soil moisture availability. The plant coefficient (k_v) may be related to r_c by equating the expression for transpiration used in the Noah LSM (43) with the usual Penman-Monteith expression for transpiration (Monteith 1965). The following relation is then obtained for k_v

$$ {k}_v=\frac{\left(r+1+\Delta +{\delta}_{\theta}\right)}{\left(r+1+{\delta}_{\theta}\right)\;\left(1+{r}_c{C}_hU\right)+\Delta}, $$

(44)

where terms have been defined above. The canopy resistance itself may follow the Jarvis-Stewart “big leaf” approach (Jarvis 1976; Stewart 1988), where (r_c) is a function of a number of empirical coefficient based on environmental conditions (atmospheric and soil); r_c is then given as

$$ {r}_c={r}_{c\;\mathit{\min}}{\left({r}_{cs}{r}_{cT}{r}_{cq}{r}_{cs oil}\right)}^{-1}, $$

(45)

where r_cmin is the minimum canopy resistance, and r_cs, r_cT, r_cq, and r_csoil are the irradiance, temperature, specific humidity deficit, and soil moisture availability factors, respectively, all affecting the canopy resistance, where all terms here are a function of vegetation type and time of year. (An additional factor is the soil temperature, i.e., r_csT, that could affect the canopy resistance, especially in the spring with “vegetation green-up” and seed germination when soil temperatures are increasing.) The description here closely follows the canopy resistance formulation described in Noilhan and Planton (1989), i.e.,

$$ {r}_{cs}=\frac{a_{s1}S\downarrow {a}_{s2} LAI+\frac{r_{smin}}{r_{smax}}}{a_{s3}+{a}_{s1}S\downarrow {a}_{s2} LAI}, $$

(46)

where LAI is the leaf area index , a_s1, a_s2, and a_s3 are coefficients, and r_smin is the minimum stomatal resistance (r_smin = r_cmin LAI), and S↓ is the incoming solar radiation.

$$ {r}_{cT}=1-{a}_{T1}{\left({T}_{cr\mathrm{e}f}-{T}_a\right)}^2, $$

(47)

where a_T1 is a coefficient, T_cref is a reference temperature, and T_a is the air temperature at the first model level in the atmosphere.

$$ {r}_{cq}=1-{a}_{q1}\left({q}_{a, sat}-{q}_a\right), $$

(48)

where a_q1 is a coefficient, and q_a,sat and q_a are the saturation and actual specific humidities, respectively, at the first model level in the atmosphere.

$$ {r}_{csoil}\left({\Theta}_i\right)=\left\{\begin{array}{ll}\ 0,& {\Theta}_i\le {\Theta}_{wilt}\\ {}\frac{\Theta_i-{\Theta}_{wilt}}{\Theta_{fc}-{\Theta}_{wilt}},& {\Theta}_{wilt}<{\Theta}_i\le {\Theta}_{fc}\\ {}\ 1,& {\Theta}_{fc}<{\Theta}_i\end{array}\right\}, $$

(49)

where r_csoil(Θ_i) is for a given soil layer Θ_i. Θ_fc is the field capacity, the volumetric soil moisture content above which plants are no longer water stressed, while Θ_wilt is the permanent wilting point, the volumetric soil moisture content at which transpiration ceases. The total r_csoil is then

$$ {r}_{csoil}=\sum \limits_{i=1}^n{r}_{csoil}\left({\Theta}_i\right){g}_i\frac{\Delta {z}_i}{\Delta z}, $$

(50)

where n is the number of soil layers, g_i is the root density function for the ith soil layer, and Δz_i and Δz are the thicknesses of the ith soil layer and total soil column, respectively. (g_i is nominally set to unity for each soil layer in the Noah LSM, that is, an equal root density with depth. However, observations suggest that the root density varies with depth, perhaps higher nearer the surface or in a soil layer with episodically higher soil moisture content.)

Alternates to “Jarvis-Stewart,” e.g., following Niu et al. (2011) and Yang et al. (2011) in the “Noah-MP” use the more physically based Ball-Berry CO₂-based photosynthesis approach to describe canopy conductance and how this depends on environmental factors. See Niu et al. (2011) and Yang et al. (2011) for further details.

4.5 Surface Temperature

To determine surface temperature (T_s) we start with the surface energy balance similar to Eq. (26) except now we use the actual evaporation E calculated from Eq. (38) instead of the potential evaporation E_p. Note that actual evaporation can be expressed as E = βE_p where β is a factor multiplied by the potential evaporation to get the actual evaporation; β absorbs all influences that reduce the potential evaporation to the actual. The surface energy balance then becomes

$$ \left(1-\alpha \right)S\downarrow +L\downarrow -{\epsilon}_s\sigma {T}_s^4=H+\beta {L}_v{E}_p+G. $$

(51)

Using Eqs. (27) and (28), we can rewrite this surface energy balance as

$$ F-4\sigma {T}_a^4-4\sigma {T}_a^4\left(\frac{T_s-{T}_a}{T_a}\right)=\rho {c}_p{C}_hU\left[\left({\theta}_s-{T}_a\right)-\left({\theta}_a-{T}_a\right)\right]+\beta {L}_v{E}_p+G, $$

(52)

where F = (1 − α)S↓ + L↓. Using the definition of the soil heat flux (G) from Eq. (30), and r from Eq. (38), we can solve for T_s as

$$ {T}_s=\frac{\Delta z\rho {c}_p{C}_hU\left[{T}_a\left(r+1\right)+\left({\Theta}_a-{T}_a\right)\right]+\Delta z\left(F-\sigma {T}_a^4-\beta {L}_v{E}_p\right)+{\lambda}_T{T}_{s_1}}{\Delta z\rho {c}_p{C}_hU\left(r+1\right)+{\lambda}_T}. $$

(53)

After updating the soil moisture content, and soil and surface temperatures, an updated soil heat flux (G) can be found by re-evaluating Eq. (29). Similarly, the sensible heat flux (H) is updated using Eq. (6).

4.6 Soil Hydraulics

4.6.1 Clapp and Hornberger

Hydraulic conductivity (K_Θ) and soil water diffusivity (D_Θ) used in Eq. (23) are nonlinear functions of soil moisture (Θ) and change by several orders of magnitude from dry to wet soil conditions (see Ek and Cuenca 1994). They follow Clapp and Hornberger (1978) (and Cosby et al. 1984) and are defined as

$$ {K}_{\Theta}={K}_{\Theta {}_s}{\left(\frac{\Theta}{\Theta_s}\right)}^{2b+3}, $$

(54)

$$ {D}_{\Theta}=\left(\frac{bK_{\Theta_s}{\psi}_s}{\Theta_s}\right){\left(\frac{\Theta}{\Theta_s}\right)}^{b+2}, $$

(55)

where ${K}_{\Theta_s}$ is the saturation hydraulic conductivity, Θ_s is the saturation volumetric soil moisture content, b is an empirically derived coefficient, and ψ_s is the saturation soil moisture potential (all a function of soil type), where the actual soil moisture potential, ψ, is defined as

$$ \psi ={\psi}_s{\left(\frac{\Theta}{\Theta_s}\right)}^{-b}, $$

(56)

where Eq. (56) is also from Clapp and Hornberger (1978).

4.6.2 van Genuchten

An alternate to Clapp and Hornberger is the approach by van Genuchten (1980) where

$$ {K}_{\Theta}={K}_{\Theta_s}{S}_e^l{\left[1-{\left(1-{S}_e^{1/m}\right)}^m\right]}^2, $$

(57)

$$ {D}_{\Theta}={K}_{\Theta}\left(\mathrm{\partial \Theta }/\partial \psi \right), $$

(58)

where l and m are fitting parameters (functions of soil type and soil density), and S_e is the effective soil moisture saturation fraction defined as

$$ {S}_e=\left(\Theta -{\Theta}_r\right)/\left({\Theta}_s-{\Theta}_r\right), $$

(59)

where the Θ_r is the residual volumetric soil moisture content and the other terms have been defined above. The soil moisture potential is defined as

$$ \psi =\frac{1}{\alpha_s}{\left[{S}_e^{-1/m}-1\right]}^{1/n}, $$

(60)

where α_s and n are also fitting parameters, and m = 1 − 1/n. See Cuenca et al. (1996) and Beljaars and Bosveld (1997) for further information on the van Genuchten formulation.

4.7 Soil Thermodynamics

The thermal conductivity (λ_T) used in Eq. (24) is a nonlinear function of the soil moisture content (Θ), changing by a few orders of magnitude from dry to wet soil conditions, and in the absence of vegetation is the “bare soil” thermal conductivity λ_T0. Following Al Nakshabandi and Kohnke (1965), λ_T0 is expressed as

$$ {\lambda}_{T0}=\left\{\begin{array}{rr}420\;\exp \left(\left[-{\log}_{10}\left(100|\psi |\right)\right]+2.7\right),& {\log}_{10}\left(100|\psi |\right)\le 5.1\\ {}0.1722,& {\log}_{10}\left(100|\psi |\right)>5.1\end{array}\right\}, $$

(61)

where ψ is soil moisture potential.

An alternative to Al Nakshabandi and Khonke is the formulation by Johansen (1975) described in Peters-Lidard et al. (1998), where λ_T0 is a less nonlinear function of soil moisture content and yields more (less) thermal conductivity for drier (moister) soils. As noted in Marshall et al. (2003) and Ek et al. (2003), this then yields greater (lesser) soil heat flux, that in turn leads to a more damped (amplified) diurnal signal in the surface skin and near-surface (e.g., 2-m) air temperatures, and was found to improve the land-surface response in mesoscale model performance.

Soil heat flux is reduced in the presence of a vegetation canopy because of reduced heat conductivity through vegetation and is included implicitly in the soil heat flux formulation in the ECMWF TESSEL land-surface scheme (van den Hurk et al. 2000). An alternative is described in Peters-Lidard et al. (1997) where the effect of vegetation is explicitly included, so that soil thermal conductivity is reduced by an exponential function of vegetation as

$$ {\lambda}_T={\lambda}_{T0}{\mathrm{e}}^{-\beta LAI}, $$

(62)

where LAI is the leaf area index , and β is an empirical coefficient equal to 0.5. Alternatively, the vegetation fraction (0 ≤ σ_f ≤ 1) may be used instead of LAI, where

$$ {\lambda}_T={\lambda}_{T0}{\mathrm{e}}^{-{\beta}^{\prime }{\sigma}_f}, $$

(63)

and β′ is an empirical coefficient, nominally equal to 2.0 (Ek et al. 2003). See Fig. 10.

Fig. 10

Ratio of soil thermal conductivity under vegetation to bare soil thermal conductivity (K_veg/K_s1) as a function of green vegetation fraction

The volumetric heat capacity of moist soil (C_Θ) used in Eq. (24) includes contributions from the mineral soil itself, as well as from air, water, and ice in the soil and is linearly related to soil moisture (Θ) as

$$ {C}_{\Theta}=\left(1-{\Theta}_{sat}\right){c}_{soil}+\left({\Theta}_{sat}-\Theta \right){c}_a+\left(\Theta -{\Theta}_{ic\mathrm{e}}\right){c}_w+{\Theta}_{ic\mathrm{e}}{c}_{ic\mathrm{e}}, $$

(64)

where c_soil is the soil heat capacity (a function of soil type, but chosen as 1.26 × 10⁶ J m⁻³ K⁻¹), c_a is the heat capacity of air in the soil (1250 J m⁻³ K⁻¹, which assumes an air density of ≈1.24 kg m⁻³), c_w is the heat capacity of water in the soil (4.2 × 10⁶ J m⁻³ K⁻¹), and c_i is the heat capacity of ice in the soil (2.1 × 10⁶ J m⁻³ K⁻¹), and Θ_ice is the frozen soil moisture (discussed in Cold Season Processes below).

4.8 Cold Season Processes

Cold season processes are important in the evolution of the land-surface for a large portion of the earth during many cold season months. In the presence of snow cover, albedo increases, surface roughness is often reduced, and the exchange of heat and moisture between land-surface and atmosphere is diminished, while subsurface freezing reduces the movement of heat and moisture within the soil. All of these processes affect the surface energy budget and thus the surface fluxes (and snow melting), so it is necessary to include these effects in LSMs used in weather and climate models, i.e., in the Noah and other LSMs (e.g., Viterbo et al. 1999; Smirnova et al. 2000; Boone et al. 2000; Boone and Etchevers 2001). These processes are described further below. Refer also to Koren et al. (1999) and Ek et al. (2003).

4.8.1 Snowpack Evolution

Snowpack accumulates due to falling snow, with the depth determined by the precipitation amount (the snow water equivalent), and the density of the snow which uses a parameterization based on air temperature. Snow density may be as high as 10:1 (snow depth:snow water equivalent) or higher for newly fallen cold, dry snow, or may have a much smaller ratio approaching 2.5:1 in the Noah LSM after compaction, important in the seasonal snowpack evolution, where the compaction is determined by snow temperature and snow age. The Noah LSM has a single-layer bulk snowpack, where newly-fallen snow is added to the snowpack, increasing depth, and then the density is “homogenized” into single value for the snowpack. On the otherhand, the Noah-MP has a multilayer (up to 3) snowpack (See Niu et al. 2011; Yang et al. 2011) and carries separate temperatures and densities in each snow layer.

4.8.2 Fractional Snow Cover

A fractional snow cover treatment allows for patchy snow cover if the snow depth is below some threshold, and hence allows exposed ground, a lower albedo, more energy absorption, and the aggregate (e.g., model gridbox) surface skin temperature may rise above freezing. As such the surface sensible heat flux may be greater than a completely snow-covered surface, with a corresponding increase in low-level air temperature. The subgrid patchiness is related to the depth of the snow and surface characteristics, e.g., for a “smoother” surface such as grassland, a smaller snow depth threshold is required for 100% snow cover compared to a forest (Fig. 11).

Fig. 11

Snow cover fraction as a function of snow water equivalent (SWE) for forest (thick solid line) and grassland (thick dashed line) vegetation classes

4.8.3 Albedo over Snow

In the presence of snow cover, the surface albedo may be markedly increased due to the high albedo of snow (depending on vegetation cover). Even over deep snow, however, the albedo can vary greatly depending on the surface characteristics. For example, a conifer forest may have a lower albedo due to darker treetops sticking through a brighter (deep) snowpack, compared with a higher albedo for completely snow-covered grassland. In conditions of shallow snowpack when snow first accumulates at the start of snowfall or diminishes due to snow sublimation or snow melt, there will be patchy snow-covered areas, e.g., in a model gridbox. To account for this patchiness effect, the surface albedo is formulated as a composite of a snow-covered and non-snow-covered surface as

$$ \alpha ={\alpha}_0+\left(1-{\sigma}_f\right){\sigma}_s\left({\alpha}_s-{\alpha}_0\right) $$

(65)

where α, α₀, and α_s are the actual, snow-free, and maximum snow surface albedo (from Sect. 3), respectively, σ_f is the green vegetation fraction (0 ≤ σ_f ≤ 1), and σ_s is the snow cover fraction, as illustrated in Fig. 12. As snow depth becomes zero, the albedo becomes the snow-free albedo (α = α₀). When the snow depth exceeds a threshold value (dependent on land-use class, e.g., vegetation type), snow cover is 100% (σ_s = 1) and α = α_s, the maximum snow albedo.

Fig. 12

Surface albedo contours as a function of snow cover fraction versus green vegetation fraction with “typical” forest (grassland) values for snow-free albedo, α₀ = 0.15 (α₀ = 0.20) and maximum snow albedo, α_s = 0.60 (α_s = 0.70)

4.8.4 Snow Sublimation

Snow sublimation is calculated from the potential evaporation, except that the latent heat of sublimation rather than latent heat of vaporization is used in calculating the surface moisture flux in energy terms. For patchy snow cover, the snow sublimation is simply proportionally weighted by the snow cover fraction (snow sublimation, E_s) and the non-snow-covered fraction (a sum of the other evaporative terms, E_w + E_d + E_c + E_t), similarly proportionally weighted, i.e.,

$$ E={\sigma}_s{E}_s+\left(1-{\sigma}_s\right)\left({E}_w+{E}_d+{E}_c+{E}_t\right). $$

(66)

The depth of the snowpack is then decreased by the loss of snow mass (SWE) corresponding to E_s.

4.8.5 Snow Melt

The solution of the surface energy budget yields a surface temperature, and when that temperature remains below freezing, if any snowpack is present, no melting takes place. When that temperature is above freezing, then the surface energy budget is reevaluated, but holding the surface temperature at freezing, with the residual energy then used to melt snow, where the depth of the snowpack is then decreased by the loss of snow mass (SWE) corresponding to the snow melt. In the case of a fractional snow cover, a portion of this residual energy is used to melt snow, with the remaining portion heating the non-snow-covered fraction of the surface, hence yielding an aggregate (e.g., model gridbox) surface skin temperature above freezing. In the Noah LSM, any melted snow is immediately added to the soil water, while the Noah-MP can carry melted snow liquid water in the snowpack, including the re-freezing of this liquid water (e.g., at night when temperatures drop).

4.8.6 Soil Heat Flux Under Snow

As the snowpack becomes very thin, it is difficult to estimate the large near-surface temperature gradients in the snow and upper soil layer. As such, the soil heat flux formulation in the Noah LSM includes the effect of heat flow through thin patchy snow cover by considering the thermal conductivity of a snowpack-plus-upper-soil layer following a method described in Lunardini (1981), where heat flow can be in parallel, in series, or intermediate between the two. Here parallel heat flow through the snowpack-plus-upper-soil-layer is assumed which yields a larger thermal conductivity (than say, series), implicitly accounting for the nonuniform nature of snowpack cover. The effective thermal conductivity for the surface is then determined via a linear weighting between the snow-covered and non-snow-covered fractions (e.g., of a model gridbox), where

$$ {\displaystyle \begin{array}{c}{K}_T=\Delta {Z}_s{K}_s+\Delta {Z}_{s1}{K}_{s1},\\ {}\ {K}_{\mathrm{e} ff}={\sigma}_s{K}_T+\left(1-{\sigma}_s\right){K}_{s1},\end{array}} $$

(67)

where K_s1, K_T, K_eff are the thermal conductivities of the upper soil layer, snow-plus-upper-soil-layer, and patchy snow-covered surface (Fig. 13), respectively, ΔZ_s1 is the upper soil layer depth, and σ_s is the snow cover fraction (0 ≤ σ_s ≤ 1). The soil heat flux through the patchy snow-covered surface is then formulated as

$$ G=\frac{K_{\mathrm{e} ff}\left({T}_s-{T}_{s1}\right)}{\Delta {Z}_s+\Delta {Z}_{s1}} $$

(68)

Fig. 13

Thermal conductivity (K_eff) through patchy snow cover versus snow water equivalent (SW E) for forest (thick solid line) and grassland (thick dashed line) vegetation classes, with the same patchiness corresponding to Fig. 11

In this formulation, the thermal conductivity remains robustly defined even in the extremes of vanishing snow cover (ΔZ_s = 0, σ_s = 0, K_eff = K_s1), or for a very deep snowpack (ΔZ_s ≫ ΔZ_s1, σ_s = 1, K_eff → K_s), which is quite important for numerical stability. Patchy snow cover must be accounted for since it increases the heat flux between the surface and atmosphere (especially at smaller snow cover fractions) because of the typically larger thermal conductivity of soil compared to snow.

4.8.7 Frozen Soil Thermodynamics and Hydraulics

In freezing conditions, a portion of the soil moisture may undergo freezing, that is,

$$ \Theta ={\Theta}_{liq}+{\Theta}_{ic\mathrm{e}} $$

(69)

where Θ is the total soil moisture, Θ_liq is the liquid soil moisture, and Θ_ice is the soil ice (frozen soil moisture, a function of both soil temperature and soil moisture), and soil physics must accommodate this condition. Soil moisture can be super-cooled such that not all water is frozen even if the soil layer is below freezing, so that the flow of liquid water portion in the soil follows the soil moisture tendency equation (23). Also, to account for the phase change of soil moisture, an additional source/sink term, ρ_wL_s∂Θ_ice/∂t, is added to the soil temperature tendency equation (24), where ρ_w is water density, and L_s is latent heat of fusion. Additionally, the thermal conductivity for frozen soil is adjusted, depending on soil type and soil moisture content; similarly there is a reduction in the infiltration of water (from unfrozen precipitation or snowmelt) into frozen soils. The impact of freezing soils provides a thermal inertia at the freezing point due to freezing and thawing of soils, reducing the amplitude of diurnal and seasonal temperature cycle in the soil.

5 Land-Atmosphere Interaction

Land-atmosphere coupling involves the interactions between the land-surface and the atmospheric boundary layer (ABL), and in turn with the free atmosphere above. The role of soil moisture in the evolution of surface fluxes and atmospheric boundary layer (ABL) development, including ABL clouds (i.e., fair-weather cumulus) involves a complex interaction of surface and atmospheric processes (see Fig. 14). We examine local land-atmosphere interaction or coupling in a “two-legged” approach (see Dirmeyer et al. 2018; Santanello et al. 2017) by inspecting the soil moisture-surface flux (“terrestrial leg”) and surface flux-ABL (“atmospheric leg”) relationships.

Fig. 14

Important interactions between the land-surface and atmospheric boundary layer for conditions of daytime surface heating. Solid arrows indicate the direction of feedbacks that are normally positive (leading to an increase of the recipient variable). Dashed arrows indicate negative feedbacks. Two consecutive negative feedbacks make a positive feedback

5.1 Near-Surface Land-Atmosphere Interaction (NSLAI)

The terrestrial leg of land-atmospheric interaction determines the coupling between soil moisture and the evolution of surface fluxes and is posed in terms of soil moisture changes and the effect on the surface evaporative fraction. Evaporative fraction is the fraction of available energy at the surface that goes into surface moisture flux (versus the energy that goes into surface sensible heat flux, soil or ground heat flux, and outgoing longwave radiation), and is a combination of plant transpiration, bare soil (direct) evaporation, and evaporation of canopy-intercepted water. The change in evaporative fraction with changing soil moisture is an indicator of the strength of coupling between the surface and the atmosphere and depends on a number of different processes. These include to what degree the surface is vegetated, how plant transpiration and soil hydraulic and thermal processes change with changing soil moisture, as well as the low-level surface-layer turbulence. For strong (weak) near-surface land-atmosphere coupling, a given change in soil moisture yields a large (small) change in evaporative fraction.

5.1.1 NSLAI: Potential Evaporation

We begin with the potential evaporation (LE_p) since it has a role in calculating the total surface moisture flux. Theoritically, LE_p is the evaporation from a well-watered or wet surface with unstressed vegetation (Penman 1948) (and has also been applied to evaporation from open water and bare soil). The corresponding evaporative fraction for potential evaporation (ef_p) is

$$ {\displaystyle \begin{array}{c}{LE}_p=\frac{s\left({R}_n-G\right)+\rho {c}_p{g}_a\delta e}{s+\gamma },\\ {}{ef}_p=\frac{s+\frac{\rho {c}_p{g}_a\delta \mathrm{e}}{R_n-G}}{s+\gamma },\end{array}} $$

(70)

where s is the slope of the saturation vapor pressure (with temperature), R_n is net radiation, G is soil heat flux, ρ is air density, c_p is specific heat of air, g_a is aerodynamic conductance (a measure of atmospheric turbulence), δe is the atmospheric vapor pressure deficit (a measure of atmospheric humidity), and γ is the psychometric “constant.” s and γ are

$$ {\displaystyle \begin{array}{c}s=\frac{de_s}{dT}=\frac{L_v}{R_v}\frac{e_s}{T^2},\\ {}\gamma =\frac{c_pp}{\epsilon {L}_v},\end{array}} $$

(71)

where L_v is latent heat, R_v is the gas constant for water vapor, e_s is saturation vapor pressure, T is air temperature, p is surface air pressure, and ϵ is the ratio of the molecular weight of water vapor to dry air (0.622). Soil heat flux is

$$ G=\frac{\lambda_T\left({T}_{sfc}-{T}_{ns}\right)}{\delta z}=\frac{\lambda_T\delta {T}_{ns}}{\delta z}, $$

(72)

where λ_T is soil thermal conductivity, T_sfc and T_ns are the surface skin and near-surface soil temperatures, respectively (δT_ns is the near-surface soil temperature gradient), and δz is the nominal thickness of the near-surface soil layer. Soil moisture (matric) potential (ψ, following Clapp and Hornberger 1978 and Cosby et al. 1984) and soil thermal conductivity (λ_T, following Al Nakshabandi and Kohnke 1965) are, respectively

$$ {\displaystyle \begin{array}{c}\psi ={\psi}_{sat}{\left(\frac{\Theta_{ns}}{\Theta_{sat}}\right)}^{-\beta },\\ {}{\lambda}_T=a\exp \left[-{\log}_{10}\left( c\psi \right)+d\right]=a\exp \left[-b\ln \left( c\psi \right)+d\right],\end{array}} $$

(73)

where ψ_sat is soil moisture potential at saturation, Θ_ns and Θ_sat are the near-surface and saturation (porosity) soil moisture values, respectively, and β is a coefficient, and a = 420, b = log(e), c = 100, and d = 2.7; ψ_sat, Θ_sat, and β are functions of soil type. Alternate functions for soil thermal conductivity may be used, e.g., Johansen (1975) as discussed in Peters-Lidard et al. (1998).

The changes in ψ, λ_T, and G with changing soil moisture are

$$ {\displaystyle \begin{array}{c}\frac{\partial \psi }{\mathrm{\partial \Theta }}=-\frac{\beta \psi}{\Theta_{ns}},\\ {}\frac{\partial {\lambda}_T}{\mathrm{\partial \Theta }}=\frac{b{\beta \lambda}_T}{\Theta_{ns}},\\ {}\frac{\partial G}{\mathrm{\partial \Theta }}=\frac{b\beta G}{\Theta_{ns}}.\end{array}} $$

(74)

The change in potential evaporative fraction with changing soil moisture is then

$$ \frac{\partial \ln e\;{f}_p}{\mathrm{\partial \Theta }}=\frac{1}{\Theta_{ns}}{\left[\frac{s\left({R}_n-G\right)}{\rho {c}_p{g}_a\delta e}+1\right]}^{-1}\frac{b\beta G}{R_n-G}. $$

(75)

Potential Evaporation Case, Strong Land-Atmosphere Coupling . Conditions that lead to a large change in ef_p with changing Θ_ns (i.e., strong land-atmosphere coupling) include strong surface-layer turbulence (g_a ≫ 0), very dry air (δe ≫ 0) and dry soil (Θ_ns small), and a large soil heat flux to available energy ratio (G/(R_n − G)) which yield

$$ \frac{\partial \ln e\;{f}_p}{\mathrm{\partial \Theta }}\to \frac{b\beta}{\Theta_{ns}}\frac{G}{\left({R}_n-G\right)}. $$

(76)

Potential Evaporation Case, Weak Land-Atmosphere Coupling . Conversely, conditions that lead to a small change in ef_p with changing Θ_ns (i.e., weak land-atmosphere coupling) include weak surface-layer turbulence (g_a → 0), very humid air (δe → 0) and moist soil (Θ_ns large), and a small soil heat flux to available energy ratio (G/(R_n − G)) which yield

$$ \frac{\partial \ln e\;{f}_p}{\mathrm{\partial \Theta }}\to 0. $$

(77)

5.1.2 NSLAI: Transpiration

Transpiration by vegetation (LE_t), using the “Penman-Monteith” approach (Monteith 1965) and the evaporative fraction for transpiration (ef_t) are

$$ {\displaystyle \begin{array}{c}{LE}_t=\frac{s\left({R}_n-G\right)+\rho {c}_p{g}_a\delta e}{s+\gamma \left(1+\frac{g_a}{g_c}\right)},\\ {}{ef}_t=\frac{s+\frac{\rho {c}_p{g}_a\delta \mathrm{e}}{R_n-G}}{s+\gamma \left(1+\frac{g_a}{g_c}\right)},\end{array}} $$

(78)

where g_c is canopy conductance. (Note that as g_c → ∞, LE_t → LE_p and ef_t → ef_p.) Following Jarvis (1976, and others), canopy conductance can be written as

$$ {g}_c={g}_{s_{max}}{LAIg}_{s\downarrow }{g}_T{g}_{\delta \mathrm{e}}{g}_{\Theta}, $$

(79)

where ${g}_{s_{max}}$ is maximum stomatal conductance, LAI is leaf area index (vegetation density), and g_s↓, g_T, g_δe, and g_Θ are transpiration factors accounting for the effects of incoming solar radiation, air temperature, atmospheric humidity deficit and soil moisture availability, respectively, all functions of vegetation type and environmental conditions. (Note that g_c = 1/r_c, as described in Eq. (45).) Soil moisture availability is defined as

$$ {\displaystyle \begin{array}{l}{g}_{\Theta}=\frac{\Theta_{rz}-{\Theta}_{wilt}}{\Theta_{r\mathrm{e}f}-{\Theta}_{wilt}},\\ {}\ =\frac{\delta {\Theta}_{rz}}{\Theta_{r\mathrm{e}f}-{\Theta}_{wilt}},\end{array}} $$

(80)

where Θ_rz is root zone soil moisture, Θ_wilt is soil moisture wilting point below which transpiration ceases, and Θ_ref is the soil moisture reference value above which transpiration is not soil moisture limited (δΘ_rz is root zone volumetric soil moisture availability). The change in g_c with changing soil moisture is

$$ \frac{\partial {g}_c}{\mathrm{\partial \Theta }}=\frac{g_c}{\delta {\Theta}_{rz}}. $$

(81)

Using Eqs. (78) and (81), the change in transpiration fraction with changing soil moisture is then

$$ \frac{\partial \ln e\;{f}_t}{\mathrm{\partial \Theta }}=\frac{1}{\delta {\Theta}_{rz}}\left\{{\left[\left(\frac{s+\gamma }{\gamma}\right)\frac{g_c}{g_a}+1\right]}^{-1}+{\left[\frac{s\left({R}_n-G\right)}{\rho {c}_p{g}_a\delta e}+1\right]}^{-1}\frac{\delta {\Theta}_{rz}}{\Theta_{ns}}\frac{b\beta G}{\left({R}_n-G\right)}\right\}. $$

(82)

Strictly speaking, Eq. (82) applies to the change in evaporative fraction with the change in root zone soil moisture, while the second term on the right hand side of Eq. (82) is with respect to near-surface soil moisture. But here we assume that Θ_rz ≈ Θ_ns so that Eq. (82) is still generally valid.

The relationship in Eq. (82) is described in Jacobs et al. (2008) (although without the second term on the right hand side) which follows Jarvis and McNaughton (1986) who define a “decoupling” parameter (Ω) as

$$ \Omega ={\left[\left(\frac{\gamma }{s+\gamma}\right)\frac{g_a}{g_c}+1\right]}^{-1}, $$

(83)

where Ω → 0 (Ω → 1) indicates strong (weak) land-atmosphere coupling. Instead, a “coupling” parameter, ω (= 1 − Ω) is defined as

$$ \omega ={\left[\left(\frac{s+\gamma }{\gamma}\right)\frac{g_c}{g_a}+1\right]}^{-1}, $$

(84)

where 0 ≤ ω ≤ 1, and ω → 1 (ω → 0) indicates strong (weak) land-atmosphere coupling. Further, the second term on the right hand side of Eq. (82) is an additional coupling parameter defined as

$$ {\omega}_G={\left[\frac{s\left({R}_n-G\right)}{\rho {c}_p{g}_a\delta e}+1\right]}^{-1}\frac{\delta {\Theta}_{rz}}{\Theta_{ns}}\frac{b\beta G}{\left({R}_n-G\right)}, $$

(85)

where 0 ≤ ω_G <≈ O(1), and ω_G ≫ 0 (ω_G → 0) indicates strong (weak) land-atmosphere coupling. ω_G is typically much smaller than ω and is included in the coupling parameter to account for “communication” between the soil and surface through the soil heat flux (G) and also depends on atmospheric turbulence (g_a), humidity (δe), and the available energy (R_n − G).

Using Eqs. (84) and (85), Eq. (82) may then be expressed simply as

$$ \frac{\partial \ln e\;{f}_t}{\mathrm{\partial \Theta }}=\frac{\omega +{\omega}_G}{\delta {\Theta}_{rz}}. $$

(86)

Vegetated Surface, Strong Land-Atmosphere Coupling. For very strong surface-layer turbulence (g_a ≫ 0), and very strong stomatal control (g_c → 0) (due to vegetation with strong stomatal control $\left(\mathrm{small}\ {g}_{s_{max}}\right)$, low vegetation density (small LAI), nonoptimal solar insolation (g_s↓ → 0), nonoptimal air temperature (g_T → 0), very dry air (δe ≫ 0 and g_δe → 0), dry soil (small δΘ_rz, g_Θ → 0, and small Θ_ns)), i.e., ω → 1, and for a large soil heat flux to available energy ratio (G/(R_n − G)), then

$$ \frac{\partial \ln e\;{f}_t}{\mathrm{\partial \Theta }}\to \frac{1}{\delta {\Theta}_{rz}}+\frac{b\beta G}{\Theta_{ns}\left({R}_n-G\right)}. $$

(87)

This is the case of strong land-atmosphere coupling, so for a given change in soil moisture, there is a large change in transpiration, e.g., an evergreen forest in dry conditions.

Vegetated Surface, Weak Land-Atmosphere Coupling. On the other hand, for very weak surface-layer turbulence (g_a → 0), and very weak stomatal control (g_c ≫ 0) (due to vegetation with weak stomatal control $\left(\mathrm{large}\ {g}_{s_{max}}\right)$, high vegetation density (large LAI), optimal solar insolation (g_s↓ → 1), optimal air temperature (g_T → 1), very humid air (δe → 0 and g_δe → 1), moist soil (large δΘ_rz, g_Θ → 1, and large Θ_ns)), i.e., ω → 0, and for a small soil heat flux to available energy ratio (G/(R_n − G)), then

$$ \frac{\partial \ln e\;{f}_t}{\mathrm{\partial \Theta }}\to 0. $$

(88)

This is the case of weak land-atmosphere coupling, so for a given change in soil moisture, there is little change in transpiration, e.g., a short crop canopy or grassland in wet conditions.

5.1.3 NSLAI: Bare Soil Evaporation

Bare soil (or direct) evaporation (LE_d) (Mahrt and Pan 1984) and the evaporative fraction for bare soil (ef_d) are

$$ {\displaystyle \begin{array}{c}{LE}_d={\rho}_w{L}_v\left[\left(\frac{\Theta_{ns}-{\Theta}_{dry}}{\delta z}\right){D}_{\Theta}+{K}_{\Theta}\right],\\ {}{ef}_d=\frac{\rho_w{L}_v}{R_n-G}\left[\frac{\delta {\Theta}_{ns}}{\delta z}{D}_{\Theta}+{K}_{\Theta}\right],\end{array}} $$

(89)

where ρ_w is water density, L_v is latent heat, Θ_dry is the soil moisture air-dry value which is the lower limit on surface soil moisture where evaporation can remain at the potential rate via soil moisture supplied from the soil (δΘ_ns is the near-surface soil moisture availability), and D_Θ and K_Θ are soil water diffusivity and soil hydraulic conductivity, respectively, both functions of soil moisture and soil type. Following Clapp and Hornberger (1978) and Cosby et al. (1984), D_Θ and K_Θ are defined as

$$ {\displaystyle \begin{array}{c}{D}_{\Theta}=\frac{bK_{\Theta_{sat}}{\psi}_{sat}}{\Theta_{sat}}{\left(\frac{\Theta_{ns}}{\Theta_{sat}}\right)}^{\beta +2},\\ {}{K}_{\Theta}={K}_{\Theta_{sat}}{\left(\frac{\Theta_{ns}}{\Theta_{sat}}\right)}^{2\beta +3},\end{array}} $$

(90)

where ${K}_{\Theta_{sat}}$ is saturated soil hydraulic conductivity, a function of soil type. Alternate functions for soil water diffusivity and soil hydraulic conductivity may be used, e.g., van Genuchten (1980).

When the value of soil moisture at the surface (Θ_sfc) is sufficiently wet such that Θ_sfc > Θ_dry, then evaporation proceeds at the potential rate (E_dir = E_pot: atmospheric demand control stage), so ef_d = ef_p. This corresponds to near-surface soil moisture (Θ_ns) where

$$ {\Theta}_{ns}\ge {\Theta}_{dry}+\frac{\delta z}{D_{\Theta}}\left[\frac{ef_p\left({R}_n-G\right)}{\rho_w{L}_v}-{K}_{\Theta}\right]. $$

(91)

But as the soil dries out, Θ_sfc = Θ_dry and evaporation proceeds only at the rate that the soil can diffuse water upward from below, so that evaporation is less than the potential rate (E_dir < E_p: soil moisture flux control stage), so ef_d < ef_p.

The changes in D_Θ and K_Θ with changing soil moisture are

$$ {\displaystyle \begin{array}{c}\frac{\partial {D}_{\Theta}}{\mathrm{\partial \Theta }}=\left(\beta +2\right)\frac{D_{\Theta}}{\Theta_{ns}},\\ {}\frac{\partial {K}_{\Theta}}{\mathrm{\partial \Theta }}=\left(2\beta +3\right)\frac{K_{\Theta}}{\Theta_{ns}}.\end{array}} $$

(92)

For the atmospheric demand control stage (ef_d = ef_p), the change in bare soil evaporative fraction with changing soil moisture is given by Eq. (75). But for the soil moisture flux control stage (ef_d < ef_p), the change in bare soil evaporative fraction with changing soil moisture is then

$$ \frac{\partial \ln e\;{f}_d}{\mathrm{\partial \Theta }}=\frac{1}{\Theta_{ns}}\left\{\frac{\left[{\Theta}_{ns}+\left(\beta +2\right)\delta {\Theta}_{ns}\right]{s}_{\Theta}+\left(2\beta +3\right)}{1+\delta {\Theta}_{ns}{s}_{\Theta}}+\frac{b\beta G}{R_n-G}\right\}, $$

(93)

where s_Θ = D_Θ/(δzK_Θ).

Bare Soil Surface, Strong Land-Atmosphere Coupling. Conditions that lead to a large change in ef_d with changing Θ_ns (i.e., strong land-atmosphere coupling) include dry soil (small Θ_ns) and a small value of s_Θ, and a large soil heat flux to available energy ratio (G/(R_n − G)) where

$$ \frac{\partial \ln e\;{f}_d}{\mathrm{\partial \Theta }}\to \frac{\left(2\beta +3\right)}{\Theta_{ns}}+\frac{b\beta}{\Theta_{ns}}\frac{G}{\left({R}_n-G\right)} $$

(94)

Bare Soil Surface, Weak Land-Atmosphere Coupling. Conversely, conditions that lead to a small change in ef_d with changing Θ_ns (i.e., weak land-atmosphere coupling) include moist soil (large Θ_ns) and a large value of s_Θ, and a small soil heat flux to available energy ratio (G/(R_n − G)) where

$$ \frac{\partial \ln e\;{f}_d}{\mathrm{\partial \Theta }}\to 0. $$

(95)

5.1.4 NSLAI: Canopy Evaporation

Evaporation of canopy-intercepted water (LE_c) and the evaporative fraction for canopy evaporation (ef_c) are

$$ {\displaystyle \begin{array}{c}{LE}_c={\left(\frac{C_w}{S_w}\right)}^n{E}_p,\\ {}{ef}_c={\left(\frac{C_w}{S_w}\right)}^n{ef}_p,\\ {}={\left(\frac{C_w}{S_w}\right)}^n\left(\frac{s+\frac{\rho {c}_p{g}_a\delta \mathrm{e}}{R_n-G}}{s+\gamma}\right),\end{array}} $$

(96)

where Eq. (70) has been used, and C_w (S_w) is the canopy water content (storage capacity), and n = 0.5 (following Pan and Mahrt 1987, who cite earlier studies). Using Eq. (75), the change in canopy water evaporative fraction with changing soil moisture is then

$$ \frac{\partial \ln e\;{f}_c}{\mathrm{\partial \Theta }}={\left(\frac{C_w}{S_w}\right)}^n{\left[\frac{s\left({R}_n-G\right)}{\rho {c}_p{g}_a\delta e}+1\right]}^{-1}\frac{b\beta G}{\Theta_{ns}\left({R}_n-G\right)}. $$

(97)

Canopy Evaporation Case, Strong Land-Atmosphere Coupling. Conditions that lead to a large change in ef_c with changing Θ_ns (i.e., strong land-atmosphere coupling) include a wet canopy (C_w → S_w), strong surface-layer turbulence (g_a ≫ 0), very dry air (δe ≫ 0) and dry soil (Θ_ns small), and a large soil heat flux to available energy ratio (G/(R_n − G)) which yield

$$ \frac{\partial \ln e\;{f}_c}{\mathrm{\partial \Theta }}\to \frac{b\beta G}{\Theta_{ns}\left({R}_n-G\right)}, $$

(98)

which is the same as Eq. (76) for the potential evaporation case.

Canopy Evaporation Case, Weak Land-Atmosphere Coupling. Conversely, conditions that lead to a small change in ef_c with changing Θ_ns (i.e., weak land-atmosphere coupling) include a dry canopy (C_w → 0), weak surface-layer turbulence (g_a → 0), very humid air (δe → 0) and moist soil (Θ_ns large), and a small soil heat flux to available energy ratio (G/(R_n − G)) which yield

$$ \frac{\partial \ln e\;{f}_c}{\mathrm{\partial \Theta }}\to 0. $$

(99)

5.1.5 NSLAI: Total Evapotranspiration

The total evapotranspiration (LE) and evapotranspirative fraction (ef) may be determined using terms from Sects. 5.1.2, 5.1.3, and 5.1.4, weighted by the green vegetation fraction (σ_f), so

$$ {\displaystyle \begin{array}{c} LE=\left(1-{\sigma}_f\right){E}_d+{\sigma}_f\left[1-{\left(\frac{C_w}{S_w}\right)}^n\right]{E}_t+{\sigma}_f{E}_c,\\ {} ef=\left(1-{\sigma}_f\right){ef}_d+{\sigma}_f\left[1-{\left(\frac{C_w}{S_w}\right)}^n\right]{ef}_t+{\sigma}_f{ef}_c,\end{array}} $$

(100)

where 0 ≤ σ_f ≤ 1. The corresponding change in evapotranspirative fraction with changing soil moisture is then

$$ \frac{\partial \ln e\;f}{\mathrm{\partial \Theta }}=\left(1-{\sigma}_f\right)\frac{\partial \ln e\;{f}_d}{\mathrm{\partial \Theta }}+{\sigma}_f\left[1-{\left(\frac{C_w}{S_w}\right)}^n\right]\frac{\partial \ln e\;{f}_t}{\mathrm{\partial \Theta }}+{\sigma}_f\frac{\partial \ln e\;{f}_c}{\mathrm{\partial \Theta }}. $$

(101)

5.2 Land-ABL Interaction

The atmospheric leg of land-atmospheric interaction determines the coupling between the surface fluxes and ABL development. Ek and Mahrt (1994) and Ek and Holtslag (2004) examined the daytime evolution of ABL-top relative humidity which is expected to control ABL cloud development. They showed that the relative humidity tendency at the ABL top involves a number of competing mechanisms, with relative humidity directly increasing due to surface evaporation and due to ABL growth (ABL-top temperature decreases), and relative humidity directly decreasing due to surface sensible heat flux and due to entrainment of warm and dry air into the ABL from above. The indirect role of surface evaporation is to reduce surface heating, thereby competing with ABL growth that is reduced due to reduced surface heating, although this diminishes ABL-top warm-and dry-air entrainment. In a similar type of study, De Bruin (1983) examined the effect of different land-surface and ABL processes on the Priestley-Taylor parameter (used in relating surface available energy to surface evaporation).

To further understand the role of soil moisture and other factors in ABL cloud development, we follow Ek and Holtslag (2004) and examine a useful equation for relative humidity tendency at the ABL top which assumes a well-mixed ABL, uses the Clauis-Clapeyron relationship, equation of state, and definition of potential temperature, as well as expressions for ABL growth (∂h/∂t) and dry air entrainment flux $\left(\overline{{w^{\prime }{q}^{\prime}}_h}\right)$ from Tennekes (1973) and Betts (1973), respectively, i.e.,

$$ {\displaystyle \begin{array}{c}\frac{\partial h}{\partial t}=\frac{{\overline{w^{\prime }{\theta}^{\prime}}}_s\left(1+{C}_{\theta}\right)}{h{\gamma}_{\theta }},\\ {}{\overline{w^{\prime }{q}^{\prime}}}_h=-\Delta q\frac{\partial h}{\partial t}.\end{array}} $$

(102)

where h is boundary-layer depth and t is time, $\overline{w^{\prime }{\theta}_s^{\prime }}$ is the surface sensible heat flux, C_θ is the (negative of the) ratio of ABL-top to surface sensible heat flux, γ_θ is the potential temperature lapse rate above the ABL, and Δq is the change in specific humidity across the ABL top (which is normally negative).

The RH tendency at the ABL-top can then be given as

$$ \frac{\partial RH}{\partial t}=\left(\frac{R_n-G}{\rho {L}_v{hq}_s}\right)\left[{e}_f+ ne\left(1-{e}_f\right)\right], $$

(103)

where R_n − G is available energy at the surface (R_n is net radiation and G is soil heat flux), ρ is air density, L_v is latent heat, h is ABL depth, and q_s is saturation specific humidity just below the ABL top. In Eq. (103), e_f is the surface evaporative fraction (of surface energy available for evaporation) defined as

$$ {e}_f=\frac{LE}{R_n-G}=\frac{LE}{H+ LE}, $$

(104)

where LE and H are the surface latent and sensible heat fluxes, respectively. Furthermore, ne(1 − e_f) reflects the direct effects of nonevaporative processes on relative humidity tendency, where ne is given by

$$ {\displaystyle \begin{array}{c} ne={L}_v/{c}_p\left(1+{C}_{\theta}\right)\left[\frac{\Delta q}{h{\gamma}_{\theta }}+ RH\left(\frac{c_2}{\gamma_{\theta }}-{c}_1\right)\right],\\ {}{c}_1=\frac{L_v}{R_v}\frac{q_s}{T^2}{\left(\frac{p}{p_s}\right)}^{R_d/{c}_p},\\ {}{c}_2=\left(\frac{L_v}{R_v}\frac{q_s}{T^2}-\frac{c_p}{R_d}\frac{q_s}{T}\right)\frac{g}{c_p}.\end{array}} $$

(105)

where c_p is specific heat, and c₁ and c₂ are functions of surface pressure, temperature and pressure at the ABL top, and constants. ne consists of three terms (each multiplied by L_v/c_p(1 + C_θ)): ABL-top dry-air entrainment (Δq/hγ_θ, a negative contribution to ABL-top relative humidity tendency), boundary-layer growth (RHc₂/γ_θ, a positive contribution), and boundary layer heating through surface warming and ABL-top warm-air entrainment (RHc₁, a negative contribution).

From Eq. (103) we see that the relative humidity tendency is proportional to available energy and inversely proportional to ABL depth and temperature (via saturation specific humidity), while the sign of the relative humidity tendency is determined by the sign of e_f + ne(1 − e_f). Examining Eq. (103), it is apparent that the direct role of e_f is to increase the ABL-top relative humidity, while the indirect role of surface evaporation (via reduced surface heating and diminished ABL growth and entrainment) is found in the expression ne(1 − e_f). Figure 15 shows how e_f + ne(1 − e_f) depends on e_f versus ne, where e_f + ne(1 − e_f) is the relative humidity tendency, ∂RH/∂t, normalized by the available energy term, (R_n − G)/(ρλ_v hq_s).

Fig. 15

ABL-top relative humidity tendency equation, e_f + ne(1 − e_f) (normalized by the available energy term), as a function of evaporative fraction (e_f) versus nonevaporative processes (ne)

When the above-ABL atmospheric stability is rather strong (larger γ_θ), or if the stability is rather weak and the above-ABL air is rather dry (larger Δq), then ne < 1 so that ∂RH/∂t increases as e_f increases, confirming intuition. (For the range 0 < ne < 1, ∂RH/∂t > 0 and increases with increasing e_f, while for ne < 0, ∂RH/∂t > 0 only when e_f exceeds some threshold value which increases for increasingly negative values of ne). This is the surface-moistening regime where soil moisture acts to increase ABL-top relative humidity and thus increases the probability of ABL cloud development given a sufficient initial ABL relative humidity.

On the other hand, with weaker above-ABL stability (smaller γ_θ), boundary-layer growth is less restricted over drier soils than over moister soils compared to the case with stronger stability. So with above-ABL air not too dry, then ne > 1 so that ∂RH/∂t increases as e_f decreases, which is somewhat counter-intuitive. This is the ABL-growth regime where soil moisture acts to limit the increase of ABL-top relative humidity and thus decreases the probability of ABL cloud development. Note that the largest values of ∂RH/∂t are achieved for ne > 1 suggesting that the greatest potential for ABL cloud development is not over moist soils, but rather over dry soils with weak stability and above-ABL air not too dry given a sufficient initial ABL relative humidity.

From Eqs. (103), (104), and (105), note that with drier air above the ABL (increasingly negative Δq), the value of ne decreases, and that as the soil moisture increases, generally e_f increases (that increase depending on the precise relationship between changing soil moisture and surface evaporation, i.e., as discussed in the Sect. 5.1; also see Wetzel and Chang 1987). But a change in stability above the ABL (γ_θ) affects both dry-air entrainment and boundary layer growth, two opposing processes in the ABL-top relative humidity tendency equation. So, only if the above-ABL specific humidity drop is greater (less negative) than some threshold Δq >  − RHhc₂ (at the ABL top), will ne increase with decreasing stability, which corresponds to ne >  − L_v/c_p(1 + C_θ)RHc₁. Note that this threshold value of Δq decreases (becomes more negative) for increasing RH, h, and c₂ (decreasing T). Finally, as Δq → 0, ne > 0 for γ_θ < c₂/c₁ < ≈ g/c_p ≈ 1 °C/100 m (dry adiabatic lapse rate).

6 Summary

This review of land-surface modeling and land-atmosphere interaction provides a basis to examine these processes in future observational and modeling studies, and further conceptual and theoretical developments. Land processes and the complex interaction of land and ABL processes must be better understood in order to be properly modeled. A number of efforts are addressing this need for process-level improvement in models, e.g., the international Land Model Benchmarking and Local Land-Atmosphere Coupling (LoCo) projects led by the Global Land/Atmosphere System Study (GLASS) panel in the Global Energy and Water Exchanges (GEWEX) project, where GEWEX is a core project of the World Climate Research Program (WCRP). See www.gewex.org.