Different Formulations of the Kansa Method: Domain Discretization

Abstract

In contrast to the traditional meshed-based methods such as finite difference, finite element, and boundary element methods, the RBF collocation methods are mathematically very simple to implement and are truly free of troublesome mesh generation for high-dimensional problems involving irregular or moving boundary. This chapter introduces the basic procedure of the Kansa method, the very first domain-type RBF collocation method. Following this, several improved formulations of the Kansa method are described, such as the Hermite collocation method, the modified Kansa method, the method of particular solutions, the method of approximate particular solutions, and the localized RBF methods. Numerical demonstrations show the convergence rate and stability of these domain-type RBF collocation methods for several benchmark examples.

In the last two decades, much effort has been devoted to developing a variety of meshless schemes for numerical discretization of partial differential equations. The driving force behind the scene is that mesh-based methods such as the standard FEM and BEM often require excessive computational effort to mesh or remesh the computational domain for high-dimensional, moving boundary, or complex-shaped boundary problems. Many of the meshless techniques available today are based on moving least squares (MLS). However, in some cases, shadow elements are still required for the numerical integration. Therefore, these methods are not entirely meshless. In contrast, the RBF collocation methods are exceedingly simple for numerical implementation and are truly meshless and integration-free because of their independency of dimensionality and complexity of problem geometry. Nardini and Brebbia in 1982 have actually applied the RBF concept to develop the popular dual reciprocity BEM without a notion of “RBF.” Only after Kansa’s pioneer work in 1990 [1, 2], the research on the RBF method for PDEs has become very active. In general, RBF collocation methods can be classified into domain- and boundary-type categories. This chapter focuses primarily on the domain-type RBF collocation methods.

The Kansa method [1, 2] is the very first domain-type RBF collocation scheme with easy-to-use merit, but the method lacks symmetric interpolation matrix due to the boundary collocation of mixed boundary conditions. The Hermite collocation method (HCM) [3] alleviates the unsymmetrical drawback. Similar to the Kansa method, however, the HCM suffers relatively lower accuracy in boundary-adjacent region. Namely, the numerical accuracy in the vicinity of boundary deteriorates by one to two orders compared with those in the central region. By using the Green second identity, Chen presented the symmetric domain-type modified Kansa method (MKM) [4] to significantly improve the numerical accuracy in the region near the boundary.

Inspired by the boundary collocation RBF techniques, the method of particular solutions (MPS) [5, 6] and the method of approximate particular solutions (MAPS) [5, 7] are developed to use the particular solution RBFs for the solution of PDEs.

The ill-conditioning and fully-populated interpolation matrix is the main challenge for the application of the traditional Kansa method and its variants mentioned above to large-scale problems. In addition, it remains an opening issue to determine the optimal shape parameter using the MQ-RBF in a global interpolation. To remedy these two perplexing problems, a number of the localized RBF methods [8–18] have been proposed in recent years and have attracted great attention in the science and engineering communities.

Let $\Upomega$ be a bounded and connected domain, and $\partial \Upomega = \Upgamma_{1} \cup \Upgamma_{2} ,$ $\, \Upgamma_{1} \cap \Upgamma_{2} = \emptyset$. Without loss of generality, we make a straightforward illustration of these methods through the following elliptical partial differential equation:

$$ \begin{aligned} \Re \left\{ {u\left( {\mathbf{x}} \right)} \right\} &= f\left( {\mathbf{x}} \right), \, {\mathbf{x}} \in \Omega \subset R^{n} , \hfill \\ B_{1} u\left( {\mathbf{x}} \right) \, &= R\left({\mathbf{x}} \right), \, {\mathbf{x}} \in \Gamma_{1} , \hfill \\ B_{2} u\left( {\mathbf{x}} \right) \, &= N\left( {\mathbf{x}} \right), \, {\mathbf{x}} \in \Gamma_{2} , \hfill \\ \end{aligned} $$

(3.1)

where $\Re$ is governing differential operator, $B_{1} ,B_{2}$ boundary differential operators, and $f\left( \mathbf {x} \right),R\left( \mathbf {x} \right),N\left(\mathbf {x} \right)$ are given functions.

3.1 The Kansa Method

First, we introduce the well-known Kansa method [1, 2]. The method employs both the RBFs and the polynomial basis to approximate the PDE solutions. However, Wertz et al. [19] recently found that it is unnecessary to augment polynomial term with the RBF approximate representation in solving PDEs. Thus, this book only introduces the Kansa method without augmented polynomial basis functions.

Let $\{ \mathbf{x}_{j} \}_{j = 1}^{{N_{i} }}$ be the interior points in the domain $\Upomega$, $\{ {\mathbf{x}}_{j} \}_{{j = N_{i} + 1}}^{{N_{i} + N_{1} }} \in \Upgamma_{1}$, and $\{ {\mathbf{x}}_{j} \}_{{j = N_{i} + N_{1} + 1}}^{N} \in \Upgamma_{2}$, where $N = N_{i} + N_{1} + N_{2}$. The Kansa method assumes the solution $u({\mathbf{x}})$ in Eq. (3.1) can be approximated by a linear combination of the RBFs at discrete nodes

$$ u({\mathbf{x}}) \simeq \tilde{u}({\mathbf{x}}) = \sum\limits_{j = 1}^{N} {\alpha_{j} \phi \left( {||{\mathbf{x}} - {\mathbf{x}}_{j} ||_{2} } \right)} , $$

(3.2)

where $\{ \alpha_{j} \}$ are unknown coefficients, $N$ the total number of the collocation knots, and $\phi ({\mathbf{x}})$ denotes the RBFs, such as MQ, IMQ, TPS, and Gaussian, etc. Substituting Eq. (3.2) into Eq. (3.1), the linear equations can be expressed in the following matrix form:

$$ {\mathbf{A\alpha = b}}, $$

(3.3)

where ${\varvec{\alpha}} = \left( {\alpha_{1} ,\alpha_{2} , \ldots ,\alpha_{N} } \right)^{T}$ is the unknown vector to be determined, and

$$ {\mathbf{b}} = \left( {f\left( {{\mathbf{x}}_{1} } \right), \cdots ,f\left( {{\mathbf{x}}_{{N_{i} }} } \right),R\left( {{\mathbf{x}}_{{N_{i} + 1}} } \right), \cdots ,R\left( {{\mathbf{x}}_{{N_{i} + N_{1} }} } \right),N\left( {{\mathbf{x}}_{{N_{i} + N_{1} + 1}} } \right), \cdots ,N\left( {{\mathbf{x}}_{N} } \right)} \right)^{T} . $$

The RBF interpolation matrix can be of the form

$$ {\mathbf{A}} = \left[ {\begin{array}{*{20}c} {\Re \{ \Upphi \} } \\ {B_{1} \left\{ \Upphi \right\}} \\ {B_{2} \left\{ \Upphi \right\}} \\ \end{array} } \right], $$

(3.4)

where $\Upphi = \left( {\Upphi_{ij} } \right) = \left( {\phi \left( {||{\mathbf{x}}_{i} - {\mathbf{x}}_{j} ||_{2} } \right)} \right)$. The Kansa method has been successfully applied to various physical and engineering problems, such as fractional diffusion problems [20], radiative transport problems [21], combustion problems [22], electromagnetic problems [23], electrostatic problems [24], heat conduction analysis [25], moving boundary problems [26], plate and shell analysis [27–32], fluid flow problems [33], Stefan problems [34, 35], microelectromechanical system analysis [36], groundwater contaminant transport [37], convection–diffusion problems [38–40]. However, the Kansa method produces unsymmetric interpolation matrix, and the rigorous mathematical proof of its solvability is still not available [41]. In addition, the method suffers relatively lower accuracy in boundary-adjacent region.

3.2 The Hermite Collocation Method

To make a symmetric RBF interpolation matrix, Fasshauer [3] applies the operator $\Re^{*}$ and $B_{1}^{ * } ,B_{2}^{ * }$ on both sides of the governing equation and the boundary conditions in Eq. (3.1), respectively, where $\Re^{*}$ and $B_{1}^{ * } ,B_{2}^{ * }$ are the self-adjoint operators of $\Re$ and $B_{1}^{{}} ,B_{2}^{{}}$. We call this modified version of the Kansa method as the Hermite collocation method (HCM). The HCM interpolation representation for Eq. (3.1) is given by

$$ \tilde{u}\left( {\mathbf{x}} \right) = \sum\limits_{j = 1}^{{N_{i} }} {\alpha_{j} \Re^{*} \phi \left( {||{\mathbf{x}} - {\mathbf{x}}_{j} ||_{2} } \right) + \sum\limits_{{j = N_{i} + 1}}^{{N_{i} + N_{1} }} {\alpha_{j} B_{1}^{ * } \phi \left( {||{\mathbf{x}} - {\mathbf{x}}_{j} ||_{2} } \right)} } + \sum\limits_{{j = N_{i} + N_{1} + 1}}^{N} {\alpha_{j} B_{2}^{ * } \phi \left( {||{\mathbf{x}} - {\mathbf{x}}_{j} ||_{2} } \right)} . $$

(3.5)

Its interpolation matrix is expressed as

$${\mathbf{A}} = \left[ {\begin{array}{*{20}c} {\Re \Re^{*} \left\{ \Phi \right\}} & {\Re B_{1}^{ * } \left\{ \Phi \right\}} & {\Re B_{2}^{ * } \left\{ \Phi\right\}} \\ {B_{1} \Re^{*} \left\{ \Phi \right\}} & {B_{1} B_{1}^{ * } \Phi } & {B_{1} B_{2}^{ * } \left\{ \Phi \right\}} \\ {B_{2} \Re^{*} \left\{ \Phi \right\}} & {B_{2} B_{1}^{ * } \left\{ \Phi \right\}} & {B_{2} B_{2}^{ * } \left\{ \Phi \right\}} \\ \end{array} } \right]. $$

(3.6)

It is worth noting that the matrix ${\mathbf{A}}$ is symmetric. Hence the numerical discretization equations are always solvable. The HCM is applied to 2D elastostatic [42], time-dependent [43–46], and nonlinear plate problems [47].

3.3 The Modified Kansa Method

In order to reduce the loss of accuracy near the boundary-adjacent region, Fedoseye et al. [4] propose the PDE collocation on the boundary (PDECB), which requires an additional set of nodes inside or outside of the physical domain yet adjacent to the boundary. It is not a trivial task to optimally place these fictitious boundary nodes for the best numerical accuracy and stability. Larsson [48] investigated and compared the numerical accuracy of the Kansa method, the HCM, and the PDECB in the context of the RBF shape parameter and the distribution of nodes.

Zhang et al. [49] also proposed a Hermite-type method to improve the numerical accuracy of 2D elasticity problems, which collocates both governing equations and boundary conditions on the same boundary nodes. However, the method is unsymmetric for mixed boundary problems and lacks the theoretical support.

Based on the Green second identity, Chen [50] developed a symmetric Hermite formulation, called the modified Kansa method (MKM). As mentioned in Sect. 2.3, the Green second identity leads to the following solution of a PDE problem

$$ \tilde{u}\left( {\mathbf{x}} \right) = \int_{\Upomega } {f\left( {\mathbf{s}} \right)u^{*} \left( {{\mathbf{x}},{\mathbf{s}}} \right)d\Upomega \left( {\mathbf{s}} \right)} + \int_{\Upgamma } {\left\{ {u\frac{{\partial u^{*} \left( {{\mathbf{x}},{\mathbf{s}}} \right)}}{{\partial n\left( {\mathbf{s}} \right)}} - \frac{\partial u}{{\partial n\left( {\mathbf{s}} \right)}}u^{*} \left( {{\mathbf{x}},{\mathbf{s}}} \right)} \right\}d\Upgamma \left( {\mathbf{s}} \right)} , $$

(3.7)

where $u^{ * }$ represents the fundamental solutions of differential operator $\Re$. If a numerical integral scheme is employed to discretize Eq. (3.7), we have

$$ \tilde{u}\left( {\mathbf{x}} \right) = \sum\limits_{j = 1}^{N} {w\left( {{\mathbf{x}},{\mathbf{x}}_{j} } \right)} f\left( {{\mathbf{x}}_{j} } \right)u^{*} + \sum\limits_{{j = N_{i} + 1}}^{N} {Q\left( {{\mathbf{x}},{\mathbf{x}}_{j} } \right)} \left[ {u\frac{{\partial u^{*} }}{\partial n} - \frac{\partial u}{\partial n}u^{*} } \right], $$

(3.8)

where $w\left( {{\mathbf{x}},{\mathbf{x}}_{j} } \right)$ and $Q\left( {{\mathbf{x}},{\mathbf{x}}_{j} } \right)$ denote the weighting functions dependent on the integral schemes. Perceiving the RBF as an approximate Green function, we can restate the representation (3.8) to construct the following interpolation formula:

$$ \begin{aligned} \tilde{u}\left( {\mathbf{x}} \right) &= \sum\limits_{j = 1}^{N} {\alpha_{j} \Re^{*} \phi \left( {||{\mathbf{x}} - {\mathbf{x}}_{j} ||_{2} } \right) + \sum\limits_{{j = N_{i} + 1}}^{{N_{i} + N_{1} }} {\alpha_{{j + N_{1} + N_{2} }} B_{1}^{ * } \phi \left( {||{\mathbf{x}} - {\mathbf{x}}_{j} ||_{2} } \right)} } , \hfill \\ \, &+ \sum\limits_{{j = N_{i} + N_{1} + 1}}^{N} {\alpha_{{j + N_{1} + N_{2} }} B_{2}^{ * } \phi \left( {||{\mathbf{x}} - {\mathbf{x}}_{j} ||_{2} } \right)} \hfill \\ \end{aligned} $$

(3.9)

where $N_{1} ,N_{2}$ and $N$ are defined as in Sect. 3.1. Note that the boundary nodes here are used twice to satisfy both the governing equation and boundary conditions. On the other hand, the MKM interpolation matrix inherits the symmetrical property of the HCM. It is noted that the MKM differs from the PDECB in that it no longer requires auxiliary boundary nodes and is derived naturally from the Green second identity. Consequently, theoretical and operational ambiguities in the PDECB are eliminated. At the end of this chapter, some numerical experiments will be presented to compare the MKM with the Kansa method and the HCM.

3.4 The Method of Particular Solutions

This section introduces the method of particular solutions (MPS). The PDE splitting approach [51] considers the solution $u$ of Eq. (3.1) a sum of homogeneous solution $u_{h}$ and particular solutions $u_{p}$

$$ u = u_{h} + u_{p}. $$

(3.10)

Note that the particular solution $u_{p}$ satisfies

$$ \Re \left\{ {u_{p} } \right\} = f\left( {\mathbf{x}} \right), \, {\mathbf{x}} \in \Upomega , $$

(3.11)

but does not necessarily satisfy boundary conditions. In contrast, the homogeneous solution has to satisfy not only the corresponding homogeneous equation

$$ \Re \left\{ {u_{h} } \right\} = 0, \, {\mathbf{x}} \in \Upomega , $$

(3.12)

but also the updated boundary conditions

$$ u_{h} \left( {\mathbf{x}} \right) = R\left( {\mathbf{x}} \right) - u_{p} \left( {\mathbf{x}} \right), \, {\mathbf{x}} \in \Upgamma_{1} , $$

(3.13)

$$ \frac{{\partial u_{h} \left( {\mathbf{x}} \right)}}{\partial n} = N\left( {\mathbf{x}} \right) - \frac{{\partial u_{p} \left( {\mathbf{x}} \right)}}{\partial n}, \, {\mathbf{x}} \in \Upgamma_{2} . $$

(3.14)

From Eqs. (3.10–3.14), it can be found that the nonhomogeneous problem is reduced to a homogeneous problem after the particular solution $u_{p}$ is separately obtained from Eq. (3.11). One can use the RBFs or some other basis functions [52] to evaluate the particular solution. In this study, we only consider the RBF methods.

Let $\{ {\mathbf{x}}_{j} \}_{j = 1}^{{N_{k} }} \in \Upomega$. We first approximate $f\left( {\mathbf{x}} \right)$ by a finite expansion series

$$ f\left( {\mathbf{x}} \right) \approx \hat{f}\left( {\mathbf{x}} \right) = \sum\limits_{j = 1}^{{N_{k} }} {\alpha_{j} \phi \left( {r_{j} } \right)} , $$

(3.15)

where $\{ \alpha_{j} \}$ are the unknown coefficients to be determined, and $r_{j} = \left\| {{\mathbf{x}} - {\mathbf{x}}_{j} } \right\|$ denotes the Euclidean distance between each pair of points ${\mathbf{x}}$ and ${\mathbf{x}}_{j}$. Then,

$$ f\left( {{\mathbf{x}}_{i} } \right) = \hat{f}\left( {{\mathbf{x}}_{i} } \right) = \sum\limits_{j = 1}^{{N_{k} }} {\alpha_{j} \phi \left( {r_{ij} } \right)} , \, 1 \le i \le N_{k} . $$

(3.16)

Assuming $\{ \alpha_{j} \}$ can uniquely be solved, the approximate particular solution $\hat{u}_{p}$ of Eq. (3.11) is given by

$$ \hat{u}_{p} = \sum\limits_{j = 1}^{{N_{k} }} {\alpha_{j} \Upphi \left( {r_{j} } \right)} , $$

(3.17)

where

$$ \phi \left( {r_{j} } \right) = \Re \left\{ {\Upphi \left( {r_{j} } \right)} \right\}. $$

(3.18)

The above evaluation procedure for the particular solution is called reverse differentiation process, which is introduced in Chap. 2, since the basis functions $\Upphi \left( r \right)$ in Eq. (3.17) are derived from Eq. (3.18) indirectly [5, 53, 54]. Some particular solutions $\Upphi \left( r \right)$ are presented in Sect. 2.2.4.

Another technique is called the direct differentiation approach and utilizes a traditional RBF $\Upphi \left( r \right)$ in Eq. (3.17) as the basis function. Then $\phi \left( r \right)$ in Eq. (3.15) can be easily derived from Eq. (3.18) by a differentiation process. This scheme is easy to implement, however, $\phi \left( r \right)$ may not be positive definite or conditionally positive definite RBFs to guarantee the invertibility of the resultant matrix in Eq. (3.16).

By implementing one of the above two approaches, evaluating particular solution $u_{p}$ is reduced to a function interpolation problem. Giving $N_{k}$ nonhomogeneous function values $\left\{ {f\left( {{\mathbf{x}}_{j} } \right)} \right\}$ at all the collocation knots $\left\{ {{\mathbf{x}}_{j} } \right\}_{j = 1}^{{N_{k} }}$, the unknown coefficients $\{ \alpha_{j} \}$ can be determined by using formula (3.16) and then the particular solution $u_{p}$ is obtained via the expression (3.17). After the particular solution is obtained, the homogeneous solution $u_{h}$ can be approximated by

$$ u_{h} \approx \hat{u}_{h} = \sum\limits_{i = 1}^{{N_{1} + N_{2} }} {\beta_{i} \phi_{h} \left( {r_{i} } \right)} $$

(3.19)

where $\{ \beta_{i} \}$ are the unknown coefficients, $N_{1} ,N_{2}$ are, respectively, the number of the collocation knots on $\Upgamma_{1}$ and $\Upgamma_{2}$, $\phi_{h} \left( {r_{j} } \right)$ represents the fundamental solution, RBF general solution, or harmonic function of the homogeneous governing equation in Eq. (3.12). For more details of these functions satisfying homogeneous equation, please see Sect. 2.2.1–2.2.3. Then, substituting Eq. (3.19) into boundary condition in Eqs. (3.13) and (3.14), the unknown coefficients $\{ \beta_{i} \}$ can be determined and the approximate homogeneous solution $\hat{u}_{h}$ can be calculated via Eq. (3.19). Finally, the solution of the original PDE can be obtained by using Eq. (3.10). The above solution procedure is commonly called the two-stage MPS.

More recently, Chen et al. [5, 6] presented one-stage MPS to combine the particular and homogeneous solutions together in a one-step process for solving PDEs. This one-stage MPS interpolation formula is given by

$$ \tilde{u}\left( {\mathbf{x}} \right) = \sum\limits_{j = 1}^{{N_{k} }} {\alpha_{j} \Upphi \left( {r_{j} } \right)} + \sum\limits_{i = 1}^{{N_{1} + N_{2} }} {\beta_{i} \phi_{h} \left( {r_{i} } \right)} $$

(3.20)

It should be mentioned that the MPS solution procedure is equivalent to the boundary-type RBF collocation methods in conjunction with dual reciprocity method (DRM). However, the MPS conducts the whole domain discretization to evaluate the particular solutions and is considered a special kind of domain-type RBF collocation method.

3.5 The Method of Approximate Particular Solutions

Recently, Chen et al. [5, 7] proposed the method of approximate particular solutions (MAPS) to improve the MPS by omitting the homogeneous solution part. The MAPS approximate solution $\hat{u}$ of Eq. (3.1) is represented by

$$ \hat{u}\left( {\mathbf{x}} \right) = \sum\limits_{j = 1}^{{N_{k} }} {\alpha_{j} \Phi \left( {r_{j} } \right)}. $$

(3.21)

It is worth noting that the MAPS representation (3.21) appears similar to Eq. (3.2) in the Kansa method. The major distinction between the MAPS and the Kansa method is that the MAPS uses the corresponding derived particular solution RBF by reverse differentiation process. Thus, the MAPS may have more sound mathematical foundation. Some numerical experiments demonstrate that the MAPS outperforms the Kansa method in both stability and accuracy, particularly in the evaluation of partial derivatives.

However, if the governing differential operator $\Re$ is complicated, it is difficult to find the integral-derived particular solutions $\Upphi \left( r \right)$ of Eq. (3.18). To implement the MAPS, we rewrite Eq. (3.1) as

$$ \Re^{\prime}\left\{ u \right\} = f\left( {\mathbf{x}} \right) + \left( {\Re^{\prime} - \Re } \right)\left\{ u \right\},{\mathbf{x}} \in \Upomega , $$

(3.22)

where $\Re^{\prime}$ is a simpler differential operator, and the corresponding formula

$$ \Re^{\prime}\Upphi \left( r \right) = \phi \left( r \right), $$

(3.23)

has the known particular solution $\Upphi \left( r \right)$ for the RBF $\phi \left( r \right)$. This approach allows the MAPS to solve a broad types of linear and nonlinear PDEs [55].

3.6 Localized RBF Methods

In the previous sections, the RBF numerical solution of a PDE of interest is interpolated by all the collocation points in the whole physical domain and boundary. Such methods are called global approximation. As a result, the resultant matrices are fully populated and thus ill-conditioned. This leads to unstable computation. In addition, the dense matrix equation is also computationally very expensive to solve. These RBF collocation methods are not applicable for large-scale problems.

In recent decades, several techniques have been developed to overcome the above-mentioned difficulties. The singular value decomposition (SVD) [56] performs well to regularize the ill-conditioning of the moderate-size RBF dense interpolation matrix [57–59]. Alternatively, one could also utilize the multi-grid approach [60], the greedy algorithm [61, 62], the extended precision arithmetic [63]. If a large number of interpolation points are required, the fast matrix computational algorithms have been introduced in the RBF collocation methods to significantly reduce computing costs and ill-conditioning, such as preconditioning methods [64, 65], Fast Multipole Methods (FMM) [66, 67], H-matrix [68], Domain Decomposition Method (DDM) [69–74], pre-corrected Fast Fourier Transform (pFFT) [75], and Adaptive Cross Approximation (ACA) [76].

Different from the above-mentioned methodologies and inspired by the idea of CS-RBFs, a number of localized RBF methods [8–18] have been proposed to alleviate the ill-conditioning of the resultant matrix, costly dense matrix of the RBF interpolation, and the uncertainty of the selection of the optimal shape parameter.

Consider the elliptical PDE (3.1) again and let $\left\{ {{\mathbf{x}}_{s} } \right\}_{s = 1}^{N} \in \Upomega$, the solution $u\left( {\mathbf{x}} \right)$ can be approximated by a localized formulation as follows:

$$ \tilde{u}\left( {{\mathbf{x}}_{s} } \right) = \sum\limits_{j = 1}^{n} {\alpha_{j}^{s} \phi \left( {||{\mathbf{x}}_{s} - {\mathbf{x}}_{j}^{s} ||_{2} } \right)} , $$

(3.24)

where $n$ is the number of nearest neighboring points $\left\{ {{\mathbf{x}}_{j}^{s} } \right\}_{j = 1}^{n}$ surrounding collocation point x _s , including the collocation point itself. $\left\{ {\alpha_{j}^{s} } \right\}$ are the unknown coefficients to be determined, $\phi \left( {\mathbf{x}} \right)$ is an RBF. If all the collocation points are distinct, it can be proved that the RBF interpolation matrix $\Upphi = \left( {\phi \left( {||{\mathbf{x}}_{i}^{s} - {\mathbf{x}}_{j}^{s} ||_{2} } \right)} \right)$ is nonsingular if $\phi \left( {\mathbf{x}} \right)$ is a positive definite RBF. Hence, the unknown coefficients in Eq. (3.24) have the following matrix form:

$$ {\varvec{\alpha}}^{s} = \Upphi^{ - 1} {\mathbf{u}}^{s} , $$

(3.25)

where ${\varvec{\alpha}}^{s} = \left( {\alpha_{1}^{s} , \ldots ,\alpha_{n}^{s} } \right)^{T}$, ${\mathbf{u}}^{s} = \left( {u\left( {{\mathbf{x}}_{1}^{s} } \right), \cdots ,u\left( {{\mathbf{x}}_{n}^{s} } \right)} \right)^{T}$. Then the approximate solution $\tilde{u}\left( {{\mathbf{x}}_{s} } \right)$ can be rewritten in terms of the given nodal values $u\left( {{\mathbf{x}}_{j}^{s} } \right)$ at its n-nearest neighboring points

$$ {\tilde{\mathbf{u}}}^{s} = \Upphi^{s} {\varvec{\alpha}}^{s} = \Upphi^{s} \Upphi^{ - 1} {\mathbf{u}}^{s} = \Uppsi^{s} {\mathbf{u}}^{s} , $$

(3.26)

where $\Upphi^{s} = \left( {\phi \left( {||{\mathbf{x}}_{s} - {\mathbf{x}}_{j}^{s} ||_{2} } \right)} \right)$ and $\Uppsi^{s} = \Upphi^{s} \Upphi^{ - 1} = \left\{ {\psi_{j}^{s} } \right\}$.

It stresses to point out that the number of selected nearest neighboring points for a specified collocation point is far smaller than the total number of collocation points, namely, $n \ll N$. If we rewrite Eq. (3.26) in terms of the approximate solution $\tilde{u}\left( {{\mathbf{x}}_{j} } \right)$ at all of the collocation points, it has

$$ {\tilde{\mathbf{u}}}^{s} = \Uppsi {\mathbf{u}}, $$

(3.27)

where $\Uppsi$ is a $N \times N$ sparse matrix only having $N \times n$ nonzero elements. Substituting Eq. (3.27) into Eq. (3.1) yields

$$ \left[ {\begin{array}{*{20}c} {\Re \Uppsi } \\ {B_{1} \Uppsi } \\ {B_{2} \Uppsi } \\ \end{array} } \right]{\tilde{\mathbf{u}}} = \left[ {\mathbf{b}} \right]. $$

(3.28)

Then, solving the above linear sparse system of equations, we get the approximate solutions $\tilde{u}$ at all of the collocation points. Comparing with the aforementioned global RBF collocation schemes, a wide variety of efficient sparse matrix solvers can be utilized to solve the localized RBF formulation of very large scale in a far more efficient manner.

Concerning the localized RBF methods, an important issue is an efficient algorithm to search the nearest neighboring source points surrounding a given collocation point from a large number of collocation points in a high-dimensional space. Lee et al. [15] defined an influence domain for each collocation point as the cut-off function, and then the nearest n neighbors of a given collocation point are located inside this influence domain. Chen and Yao [16, 17] employed the kd-tree algorithm [77, 78] for the method of approximate particular solutions (MAPS) to solve large-scale problems, for example, calcium dynamics in ventricular myocytes [79]. In computer science, there exist several other search algorithms to deal with this issue such as the quad-tree algorithm, the locality sensitive hashing algorithm [80], and the R-tree algorithm [81].

For reasons of limitations of space, we will only mention a few more RBF domain methods for numerical PDEs, such as the radial basis function network method [82, 83], global and local integrated radial basis function collocation method [84, 85], the MQ quasi-interpolation method [86], the local MQ-DQ method [87–89], the RBF-FD method [90–93], the RBF pseudo-spectral method [94], and the radial point interpolation method [95, 96], the Hermite-type radial point interpolation method [97], and the subdomain RBF collocation method [98].

3.7 Numerical Experiments

In this section, we first investigate the accuracy, stability, and convergence rate of the Kansa method, the Hermite collocation method (HCM), and the modified Kansa method (MKM) for some benchmark examples. In the following, ${\text{Aerr}}$ represents the $L_{2}$ absolute error, ${\text{Lerr}}$ represents the $L_{2}$ relative error, which are defined as follows:

$$ {\text{Aerr}} = \sqrt {\frac{1}{NT}\sum\limits_{i = 1}^{NT} {\left( {u\left( {{\mathbf{x}}_{i} } \right) - \tilde{u}\left( {{\mathbf{x}}_{i} } \right)} \right)^{2} } } , $$

(3.29)

$$ {\text{Lerr}} = \sqrt {\frac{1}{NT}\sum\limits_{i = 1}^{NT} {\left( {\frac{{u\left( {{\mathbf{x}}_{i} } \right) - \tilde{u}\left( {{\mathbf{x}}_{i} } \right)}}{{u\left( {{\mathbf{x}}_{i} } \right)}}} \right)^{2} } } , $$

(3.30)

where $NT$ is the total number of test points in the domain and on the boundary. In the following tests, the MQ-RBF $\phi \left( r \right) = \sqrt {r^{2} + c^{2} }$ is chosen as the basis function.

First, we compare the convergence rate and stability of the three schemes in the unit square domain. Figure 3.1 shows the mixed-type boundary conditions covered by uniform and random collocation points, respectively. In this case, the MQ shape parameter $c = {{16} \mathord{\left/ {\vphantom {{16} {\sqrt N }}} \right. \kern-0pt} {\sqrt N }}$ is selected and the test point is $51 \times 51$ uniform mesh grid, namely, $NT = 2,601$.

Fig. 3.1

Mixed-type boundary problem in square domain with (a) uniform and (b) random collocation points

Example 3.1:

Consider the 2D Poisson equation in the unit square domain shown in Fig. 3.1

$$ \Updelta u = \left( {3 + 4x^{2} } \right)e^{{x^{2} + y}} ,{\mathbf{x}} = \left( {x,y} \right) \in \Upomega , $$

(3.31)

whose boundary conditions are assigned in terms of the analytical solution $u = \text{e}^{{x^{2} + y}}$. $\Upgamma_{1}$ and $\Upgamma_{2}$ shown in Fig. 3.1 denote Dirichlet and Neumann boundary conditions, respectively.

Figure 3.2 depicts the accuracy variation of these three methods with respect to the number of uniform and random collocation points. In all three methods, the numerical accuracy improved with the increasing number of collocation points N. We observe that the HCM numerical result is as accurate as the Kansa method. The MKM performs much better than both the Kansa method and the HCM using the same number of collocation points. Figure 3.3 shows the condition number ${\text{Cond}}$ of the interpolation matrix ${\mathbf{A}} = \left[ {{\mathbf{A}}_{ij} } \right]$ of the three methods verses the number of collocation points N. We can see that all the condition numbers of these three methods increase rapidly when N becomes large.

Fig. 3.2

Convergence rates with (a) uniform and (b) random collocation points in Example 3.1

Fig. 3.3

Condition numbers with (a) uniform and (b) random collocation points in Example 3.1

Example 3.2:

Consider the following 2D modified Helmholtz equation in multi-connected domain shown in Fig.  3.4

Fig. 3.4

The profile of the multi-connected domain

$$ \left( {\Updelta - 2} \right)u = \left( {2 - 4x} \right)e^{{ - \left( {x + y} \right)}} , \, {\mathbf{x}} = \left( {x,y} \right) \in \Upomega . $$

(3.32)

The mixed-type boundary conditions can be easily derived from the analytical solution $u = x^{2} \text{e}^{{ - \left( {x + y} \right)}}$, where $\Upgamma_{1}$ and $\Upgamma_{2}$ shown in Fig. 3.4 denote Dirichlet and Neumann boundary conditions, respectively. In the numerical implementation, we choose MQ shape parameter $c = {{12} \mathord{\left/ {\vphantom {{12} {\sqrt N }}} \right. \kern-0pt} {\sqrt N }}$ and $NT = 1,510$.

Figure 3.5 displays the convergence rates and condition number curves by these three schemes. Both the Kansa method and the HCM produce similar results. Although having the largest condition number, the MKM performs the most accurate solutions among these three schemes. The numerical accuracy of the MKM is almost one order of magnitude better than the other two schemes. Figure 3.6 shows the profile of the analytical solution and relative errors by these three RBF schemes. Figure 3.6b–d illustrates that the errors are smaller on the boundary and the maximum error appears in the boundary-adjacent region. Compared with the other two methods, it can be observed from Fig. 3.6 that the MKM obtains better accuracy at close-to-boundary nodes by almost one order of magnitude.

Fig. 3.5

(a) Accuracy and (b) condition numbers versus collocation points $N$ in Example 3.2

Fig. 3.6

(a) The profile of analytical solution. (b–d) The relative numerical errors of Kansa, HCM, and MKM, respectively

Example 3.3:

Plate bending of the simply-supported unit square plate

The governing equation of a simply-supported thin plate under uniform loading is

$$ \nabla^{4} w = \frac{{q_{0} }}{D}, $$

(3.33)

with boundary conditions

$$ w = 0, $$

(3.34)

$$ M_{n} = - D\left\{ {\nu \nabla^{2} w + \left( {1 - \nu } \right)\left( {\cos^{2} \theta \frac{{\partial^{2} w}}{{\partial x^{2} }} + \sin^{2} \theta \frac{{\partial^{2} w}}{{\partial y^{2} }} + \sin 2\theta \frac{{\partial^{2} w}}{\partial x\partial y}} \right)} \right\} = 0, $$

(3.35)

where $w$ represents the deflection of the middle surface of the plate, $\nabla^{4}$ denotes the biharmonic operator, and $D = {{Eh^{3} } \mathord{\left/ {\vphantom {{Eh^{3} } {\left[ {12\left( {1 - \nu^{2} } \right)} \right]}}} \right. \kern-0pt} {\left[ {12\left( {1 - \nu^{2} } \right)} \right]}}$ is the flexural rigidity of the plate, $n = \left[ {\cos \theta ,\sin \theta } \right]$ the unit outward normal vector. The parameter values are $E = 2.1 \times 10^{11}$, $h = 0.01$, $\nu = 0.3$, $q_{0} = 10^{6}$. We choose MQ-RBF with shape parameter $c = {{40} \mathord{\left/ {\vphantom {{40} {N_{i} }}} \right. \kern-0pt} {N_{i} }}$. This case study will also investigate convergence rate and stability.

Numerical accuracy variation of these three methods with respect to the number of unknown coefficients is shown in Fig. 3.7a. The numerical accuracy improves with the increasing number of points. We observe from Fig. 3.7a that the HCM achieves similar accuracy as the Kansa method, but eliminates the error oscillation with the increasing number of points. It is noted that the MKM obtains the most accurate results among these three methods. On the other hand, the condition numbers of interpolation matrixes increase rapidly with the increasing number of points. This ill-conditioning problem may affect the numerical stability of these RBF collocation methods. It is necessary to introduce the additional techniques to mitigate the effect of ill-conditioning as mentioned in Sect. 3.5.

Fig. 3.7

(a) Numerical accuracy variations and (b) condition numbers versus the number of unknown coefficients in Example 3.3

Example 3.4:

This example compares the method of approximate particular solutions (MAPS) with the Kansa method of a 2D convection–diffusion problem

$$ \Updelta u + \left( {x^{2} + y^{2} } \right)u + y\,\,\cos \left( y \right)\frac{\partial u}{\partial x} + \sin \,h\left( x \right)\frac{\partial u}{\partial x} = f\left( {x,y} \right), \, \left( {x,y} \right) \in \Upomega , $$

(3.36)

$$ u = R\left( {x,y} \right), \, \left( {x,y} \right) \in \Upgamma , $$

(3.37)

where the physical domain $\Upomega$ is a star-shaped region as shown in Fig. 3.8 and its boundary is defined by the following parametric equation:

Fig. 3.8

Profiles of computational domain of Example 3.4 (Reprinted from Ref. [99], Copyright 2012, with permission from Elsevier)

$$ \Upgamma = \left\{ {\left( {x,y} \right)\left| {x = \rho \,\cos \theta ,y = \rho \,\sin \theta ,0 \le \theta < 2\pi } \right.} \right\}, $$

(3.38)

in which $\rho = 1 + \left( {\cos \left( {4\theta } \right)} \right)^{2}$. The given functions $f\left( {x,y} \right),R\left( {x,y} \right)$ are easily derived from the following analytical solution

$$ u\left( {x,y} \right) = \sin \left( {\pi x} \right)\cosh \left( y \right) - \cos \left( {\pi x} \right)\sinh \left( y \right). $$

(3.39)

Tsai et al. [99] employed a golden search method to find the good shape parameter $c$ in the MQ RBF. Table 3.1 shows the comparison of the absolute errors ${\text{Aerr}}$ by the MAPS and the Kansa method. The MAPS achieves the similar accuracy as the Kansa method using the same placement of the collocation points.

Table 3.1 Comparison of ${\text{Aerr}}$ by the MAPS and the Kansa method for Example 3.4

Example 3.5:

Let us consider the localized RBF formulations in the solution of the following Poisson problem:

$$ \begin{array}{*{20}c} {\Updelta u = f\left( {x,y} \right), \, \left( {x,y} \right) \in \Upomega } \\ {u = R\left( {x,y} \right), \, \left( {x,y} \right) \in \partial \Upomega } \\ \end{array} , $$

(3.40)

where the physical domain $\Upomega$ is a rectangular $\left[ {0,1} \right] \times \left[ {0,H} \right]$. The given functions $f\left( {x,y} \right),R\left( {x,y} \right)$ are given based on the following analytical solution:

$$ u\left( {x,y} \right) = \frac{{1.25 + \cos \left( {5.4y + 2.7} \right)}}{{6\left( {1 + \left( {3x + 0.5} \right)^{2} } \right)}} $$

(3.41)

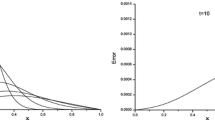
In the numerical implementation, all the interior and boundary points are distributed uniformly. The number of internal nodes is $N = S_{n}^{2} \left( {H - 1} \right) + \left( {S_{n} - 1} \right)H$, and the number of boundary nodes is $N_{i} = 2\left( {S_{n} - 1} \right)\left( {H + 1} \right)$. n is the number of nearest neighbor points, and $S_{n}$ denotes the number of partition in [0,1]. Table 3.2 lists numerical results obtained by the Localized Kansa method (LKM) and the Localized MAPS (LMAPS) using various number of nearest neighbor points and $H = 20,S_{n} = 25$. We observe that the LKM and the LMAPS have similar accuracy with the optimal shape parameter in Table 3.2. As $n$ increases, the accuracy of the localized RBF formulations improves while the computational efficiency decreases. Therefore, $n = 9$ is fixed to apply the localized formulations to the large-scale problems with millions of points. Table 3.3 shows numerical errors of the LKM and the LMAPS with various values $H$ for $n = 9,S_{n} = 30$. It should be mentioned that $30 \times 30$ uniform nodes are distributed inside $\left[ {0,1} \right] \times \left[ {i - 1,i} \right],i = 1, \cdots ,H$. Since the same collocation nodes in each square $\left[ {0,1} \right] \times \left[ {i - 1,i} \right]$ are used, the optimal shape parameter $c$ is stable and independent on $H$. From Table 3.3, it can be found that the localized methods can solve the problem with 900,000 interpolation points and obtain good accuracy. In Fig. 3.9 we present the errors ${\text{Aerr}}$ with respect to the shape parameter $c$ by the global MAPS (GMAPS) and the LMAPS with $n = 9,S_{n} = 10,H = 1$. In Fig. 3.9 the shape parameter $c$ in the LMAPS is more stable than the GMAPS. Hence the LMAPS alleviates the difficulty of choosing the shape parameter $c$ in the traditional RBF approaches. In this example it also reveals that the localized RBF formulation can provide highly accurate results for large-scale problems.

Table 3.2 Numerical results obtained by Localized Kansa and Localized MAPS with various number of nearest neighbor points using $S_{n} = 25,H = 20$ for Example 3.5

Table 3.3 Numerical results obtained by Localized Kansa and Localized MAPS with various $H$ values using $n = 9,S_{n} = 30$ for Example 3.5

Fig. 3.9

The errors ${\text{Aerr}}$ with respect to the shape parameter $c$ by MAPS and Localized MAPS with $n = 9,S_{n} = 10,H = 1$ for Example 3.5 (Reprinted from Ref. [17], Copyright 2012, with permission from Elsevier)