Keywords

1 Introduction

Electrical resistance tomography (ERT) is a visualization and measurement technique, investigated extensively during the past decades, which has been widely used in the industrial process imaging [1, 2]. It has the advantages of portability, safety, low-cost, non-invasiveness and rapid response, which makes it a promising imaging technique.

However, the ill-posedness of the inverse problem is the principal difficulty in image reconstruction for ERT [3]. And regularization methods are good ways to address this problem, among which the Tikhonov regularization and the TV regularization have been generally accepted as important algorithms. As Tikhonov regularization is a kind of \( l_{2} \) regularization, it makes the image edge over-smoothed. Although the TV regularization penalizes the transition amplitude, which makes it suitable for sharp transitions and better than Tikhonov regularization, it often suffers the staircase effect and the loss of fine details. Some improvements of TV regularization have been made, including using Primal Dual Method for solving the nondifferentiability of regularization function [4, 5], adaptive mesh refinement based on TV in the process of inverse problem [6] and the adaptive TV regularization that adaptively modifies the regularization factor according to the uncontinuity of the image boundaries [7]. However they do not consider the function of TV itself, which characterize the measurement of smoothness and leads to staircase effect.

In this paper, an novel TV function replaces the conventional TV regularization penalty term \( \int\limits_{\Upomega } {\left| {\nabla g} \right|d\Upomega } \) by \( \int\limits_{\Upomega } {\left| {\nabla g} \right|^{p} d\Upomega } \), in which \( p \) is selected as 1.5. By means of relaxing the smoothness constraints, this novel algorithm can preserve the edges of reconstruction images, which are more informative about the sizes and shapes of the inclusions than the smoothness approach (such as Tikhonov). And it also can overcome the shortage of TV regularization suffering from the staircase effect. Besides its reconstruction images are less sensitive to noise.

2 Theoretical Background

In the problem of ERT, let \( \Upomega \) be the support of the object, and \( \partial \Upomega \) its surface (boundary). We assume \( \Upomega \) contains material with electrical conductivity \( \sigma \left( x \right) \) satisfying \( \sigma \left( x \right) > 0 \). The electrical potential \( u\left( x \right) \) inside \( \Upomega \) satisfies

$$ - \nabla \cdot \left( {\sigma \nabla u} \right) = 0\;{\text{in}}\;\Upomega $$
(67.1)
$$ \sigma \frac{\partial u}{\partial n} = j\;{\text{on}}\;\partial \Upomega $$
(67.2)

where \( j \) is the applied current density \( \partial \Upomega \) on such that the following conservation of charge relation holds:

$$ \int_{\partial \Upomega } {jds = 0} $$
(67.3)

The inverse problem is to estimate the conductivity \( \sigma \) from experiments.

In the problem of ERT, the relationship between the measured edge voltage (\( u \)) and the conductivity distribution (\( \sigma \)) of measured object is non-linear:

$$ u\, = \,F\left( \sigma \right) $$
(67.4)

Based on the perturbation theory, functional (67.4) is

$$ \Updelta u = \frac{dF}{d\sigma }\left( {\Updelta \sigma } \right)\, + \,o\left( {\left( {\Updelta \sigma } \right)^{2} } \right) $$
(67.5)

If \( \Updelta \sigma \) is small enough, then \( o\left( {\left( {\Updelta \sigma } \right)^{2} } \right) \) can be ignored. With the aid of physical modeling and FEM discretization, functional (67.4) becomes

$$ \Updelta u\, = \,J\Updelta \sigma $$
(67.6)

where, \( J \) is the Jacobian matrix.

To simplify the reconstruction equation, Eq. (67.4) is normalized as

$$ b\, = \,Sg $$
(67.7)

where, \( S \) is the Jacobian matrix, \( b \) the measured voltage, \( g \) the conductivity of the object measured [3].

2.1 Tikhonov Regularization

Regularization methods have been developed for the solution of ill-posed inverse problems. Tikhonov regularization is one of the most popular regularization tools for solving ill-posed problems and has been applied to electrical tomography by Dobson and Santosa [8]. The general form of the Tikhonov regularization for conductivity distribution is given by:

$$ \hbox{min} \left\{ {\left\| {Sg - b} \right\|_{2}^{2} \, + \,\lambda^{2} \left\| g \right\|_{2}^{2} } \right\} $$
(67.8)

Here, the regularization factor \( \lambda \) is a positive that controls the weighting between the corresponding residual norm and the solution norm of the criterion function. Tikhonov regularization obtains stability in the reconstruction process, but it always imposes excessive smoothness to the edge of the reconstruction images.

2.2 Total Variation Regularization

The TV function was firstly employed by Rudin, Osher and Fatami for regularizing the restoration of noisy images [9]. TV regularization allows a much broader class of functions to be the solution of the inverse problem, including functions with discontinuities [10]. The total variation function, formulated as an unconstrained problem, is expressed as:

$$ \min \left\{ {\left\| {Sg - b} \right\|_{2}^{2} + uTV\left( g \right)} \right\} = \min \left\{ {\left\| {Sg - b} \right\|_{2}^{2} + u\int\limits_{\Omega } {\left| {\nabla g} \right|d\Omega } } \right\} $$
(67.9)

Here, \( \Upomega \) is the interested region. \( u \) is chosen to be a small positive constant as the regularization factor. The regularization factor \( u \) determines the balance between the solution norm and the corresponding residual norm. Suppose that the conductivity is described by piecewise constant elements, the discretized version of \( TV\left( g \right) \) can be expressed as:

$$ TV\left( g \right) = \sum\limits_{i} {\left\| {L{}_{i}g} \right\|} $$
(67.10)

where, \( L \) is a sparse matrix [6].

Usually, a smooth approximation is used to solve the nondifferentiability of \( \left| {\nabla g} \right| \) in the TV regularization function. Then function (67.5) becomes

$$ J\left( g \right) = \frac{1}{2}\left\| {Sg - b} \right\|^{2} + uTV_{\beta } \left( g \right) = \frac{1}{2}\left\| {Sg - b} \right\|^{2} + u\sum\limits_{i} {\sqrt {\left\| {L_{i} g} \right\|^{2} + \beta } } $$
(67.11)

where \( \beta > 0 \) is a predetermined small constant.

Although TV regularization can overcome the over-smoothed shortages from Tikhonov regularization and preserve discontinuities in reconstruction images, it often suffers the staircase effect and the loss of fine details.

3 The Improved Total Variation Regularization

An improved TV regularization is introduced to overcome the foregoing shortages. This improved TV function replaces the conventional TV regularization penalty term \( \int\limits_{\Upomega } {\left| {\nabla g} \right|d\Upomega } \) by \( \int\limits_{\Upomega } {\left| {\nabla g} \right|^{p} d\Upomega } \), in which \( p \) is selected as 1.5. By means of relaxing the smoothness constraints, the algorithm describes rapid variations in the object, as well as reducing the suffering of the staircase effect.

This improved TV function, formulated as an unconstrained problem, is expressed as:

$$ \min \left\{ {\left\| {Sg - b} \right\|_{2}^{2} + u\int\limits_{\Omega } {\left| {\nabla g} \right|^{{\left( {\frac{3}{2}} \right)}} d\Omega } } \right\} $$
(67.12)

Similarly to TV regularization, the object function is

$$ J\left( g \right) = \frac{1}{2}\left\| {Sg - b} \right\|^{2} + u\int\limits_{\Upomega } {\left| {\nabla g} \right|^{{\left( \frac{3}{2} \right)}} d\Upomega = \frac{1}{2}\left\| {Sg - b} \right\|^{2} + u\sum\limits_{i} {\sqrt {\left\| {L_{i} g} \right\|^{2} + \beta }^{{^{{\left( \frac{3}{2} \right)}} }} } } $$
(67.13)

The gradient and Hessian of \( J \) can be calculated as follows:

$$ J^{\prime} \left( g \right) = S^{T} \left( {Sg - b} \right) + uL_{\beta } \left( g \right)g $$
(67.14)
$$ H\left( g \right) = S^{T} S + uL_{\beta } \left( g \right) $$
(67.15)

where, \( S^{T} \) is the transpose of \( S \) and

$$ L_{\beta } \left( g \right) = \frac{3}{2}L^{T} \left( {diag\left( {\root{\frac{1}{2}} \of {{\left\| {L_{i} g} \right\|^{2} + \beta }}} \right)} \right)^{ - 1} L $$
(67.16)

In this paper, the Newton-Raphson iteration method is also used to solve the object function, as same as TV regularization.

4 Results and Discussion

4.1 Simulation Results

Simulations were carried out to evaluate the performance of this improved TV regularization, TV regularization and Tikhonov regularization. The forward problem is solved using a finite element method. The measured voltages were simulated using the complete electrode model and adjacent current patterns. A mesh of adaptive first-order triangular elements is used for the forward calculations. The reconstruction images present conductivity distribution for inverse problem using another mesh with 812 square elements. In the reconstruction images, the conductivity of background and the body in the object are set as 0.01 and 0.03 s/m. The regularization factor of the improved TV and TV are set as 1e-3, and the L-Curve is used to decide the regularization factor of Tikhonov regularization.

The simulation results of those three algorithms are shown in Fig. 67.1, in the first column of which are the five test distributions. And the noise level was 0.5 %, which is corresponding to the typical noise level in practical systems. It can be seen from Fig. 67.1 that the improved TV regularization method can give better quality of reconstruction than the TV regularization method and Tikhonov regularization.

Fig. 67.1
figure 1

Results from the reconstruction with three methods with noise level of 0.5 %

Full size image

The relative image errors (\( \varepsilon_{image} \)) and the correlation coefficient (\( \varepsilon_{corr} \)) of the reconstruction images compared to the true conductivity distribution are compared, which are shown in Table 67.1.

Table 67.1 Comparison of relative image errors and correlation coefficient for the reconstruction displayed in Fig. 67.1
Full size table
$$ \varepsilon_{image} = \frac{{\left\| {\sigma - \sigma^{ * } } \right\|_{2} }}{{\left\| {\sigma^{ * } } \right\|_{2} }} $$
(67.17)
$$ \varepsilon_{corr} = \frac{{\sum\limits_{i = 1}^{N} {\left( {\sigma_{i} - \bar{\sigma }} \right)\left( {\sigma_{i}^{ * } - \bar{\sigma }^{ * } } \right)} }}{{\sqrt {\sum\limits_{i = 1}^{N} {\left( {\sigma_{i} - \bar{\sigma }} \right)^{2} \sum\limits_{i = 1}^{N} {\left( {\sigma_{i}^{ * } - \bar{\sigma }^{ * } } \right)^{2} } } } }} $$
(67.18)

Where \( \sigma \) is the calculated conductivity, \( \sigma^{*} \) is the actual one, \( \bar{\sigma } \) is the average of the calculated one, \( \bar{\sigma }^{*} \) is the average of the actual one. The simulation results also demonstrate that the improved TV regulation method performs better.

4.2 Experimental Results

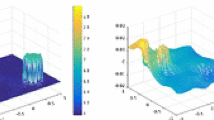
In practical measurements, the measured voltages would be different from the numerical ones in simulation due to the existence of the systematic and random errors together. An ERT system with 16 electrodes was used. Experiments have been conducted for plastic rods positioned in saline water. The true conductivity distribution and reconstructed images are shown in Fig. 67.2.

Fig. 67.2
figure 2

Reconstruction images of plastic rods by using three methods

Full size image

5 Conclusion

In this paper, an improved TV regularization algorithm is presented for ERT image reconstruction. Both simulation and experimental results have shown that the proposed method not only can overcome the corresponding shortages of Tikhonov regularization and TV regularization, but also its reconstruction images are less sensitive to noise than them. Based on this work, this improved TV regularization can perform better in the image reconstruction, it’s feasible to make a adaptive TV regularization, which can adjust the regularization function according to the smoothness of the edge automatically.