Dynamic Surface Control of Hypersonic Aircraft with Parameter Estimation

Abstract

This paper investigates the adaptive controller for the longitudinal dynamics of a generic hypersonic aircraft. The control-oriented model is adopted for design. The subsystem is transformed into the linearly parameterized form. Based on the parameter projection estimation, the dynamic inverse control is proposed via back-stepping. The dynamic surface method is employed to provide the derivative information of the virtual control. The proposed methodology addresses the issue of controller design with respect to parametric model uncertainty. Simulation results show that the proposed approach achieves good tracking performance in the presence of uncertain parameters.

1 Introduction

Hypersonic flight vehicles (HFVs) are intended to present a cost-efficient way to access space by reducing the flight time. The success of NASA’s X-43A experimental airplane in flight testing has affirmed the feasibility of this technology. The U.S. military launched an experimental hypersonic aircraft on its swan song test flight on May 1, 2013, acclerating the craft to more than five times the speed of sound in the longest-ever mission for a vechile of its kind.

The related hypersonic flight control has gained more and more attention. Based on linearizing the model at the trim state of the dynamics, the pivotal early works [1, 2] employed classic and multivariable linear control. The adaptive control [3] is investigated by linearizing the model at the trim state. Based on the input–output linearization using Lie derivative notation, the sliding mode control [4] is applied on Winged-Cone configuration [5]. The genetic algorithm [6] is employed for robust adaptive controller design.

In [7], the altitude subsystem is transformed into the strict-feedback form using the back-stepping scheme [8], the neural networks and Kriging system-based methods are investigated on discrete hypersonic flight control with nominal feedback [9–11]. The sequential loop closure controller design [12] is based on the equations decomposition into functional subsystems with the model from the assumed-modes version [13]. Based on locally valid linear-in-the-parameters nonlinear model the unknown parameters are adapted by Lyapunov-based updating law. However, during the controller design, the back-stepping design needs repeated differentiations of the virtual control and it introduces more unknown items [14].

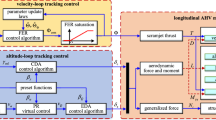
In this paper, the control-oriented model (COM) recently developed in [15] including the coupling effect of the engine to the airframe dynamics is studied. The subsystem is written into the linearly parameterized form. Instead of nominal feedback or fuzzy/nerual approximation [16], the dynamic inverse control is proposed via back-stepping based on the parameter projection estimation. To avoid the “explosion of complexity” during the back-stepping design [12], the dynamic surface method is employed.

This paper is organized as follows. Section 2 briefly presents the COM of the generic HFV longitudinal dynamics. In Sect. 3, the dynamic inverse control is designed for the subsystems. The simulation is included in Sect. 4. Section 5 presents several comments and final remarks.

2 Hypersonic Vehicle Modeling

The control-oriented model of the longitudinal dynamics of a generic hypersonic aircraft from [15] is considered in this study. This model is comprised of five state variables $X_h=\left[ V,h,\alpha ,\gamma ,q\right] ^{T}$ and two control inputs $U_h = \left[ \delta _e,\Phi \right] ^{T}$.

$$\begin{aligned} \dot{V}&= \dfrac{T\cos \alpha -D}{m}-g\sin \gamma \end{aligned}$$

(1)

$$\begin{aligned} \dot{h}&= V\sin \gamma \end{aligned}$$

(2)

$$\begin{aligned} \dot{\gamma }= \dfrac{L+T\sin \alpha }{mV}-\dfrac{g\cos \gamma }{V} \end{aligned}$$

(3)

$$\begin{aligned} \dot{\alpha }&= q-\dot{\gamma } \end{aligned}$$

(4)

$$\begin{aligned}\dot{q}= \dfrac{{{M}_{yy}}}{{{I}_{yy}}} \end{aligned}$$

(5)

where

$$\begin{aligned} T \approx&\, \bar{q}S\left( C_{T\Phi }^{{\alpha ^3}}{\alpha ^3} + C_{T\Phi }^{{\alpha ^2}}{\alpha ^2} + C_{T\Phi }^\alpha \alpha + C_{T\Phi }^0\right) \Phi + \bar{q}S\left( C_T^{{\alpha ^3}}{\alpha ^3} + C_T^{{\alpha ^2}}{\alpha ^2} + C_T^\alpha \alpha + C_T^0\right) \nonumber \\ D \approx&\, \bar{q} S(C_D^{{\alpha ^2}}{\alpha ^2} + C_D^\alpha \alpha + C_D^0)\nonumber \\ L =\,&{L_0} + {L_\alpha }\alpha \approx \bar{q} SC_L^0 + \bar{q} SC_L^\alpha \alpha \nonumber \\ M_{yy}=\,&{M_T} + {M_0}(\alpha ) + {M_{{\delta _e}}}{\delta _e}\approx {z_T}T + \bar{q}S\bar{c}(C_M^{{\alpha ^2}}{\alpha ^2} + C_M^\alpha \alpha + C_M^0)+ \bar{q}S\bar{c}C_M^{{\delta _e}}{\delta _e}\nonumber \\ \bar{q}=\,&\dfrac{1}{2}\rho V^2, \rho ={{\rho }_{0}}\exp \left[ -\dfrac{h-{{h}_{0}}}{{{h}_{s}}} \right] \nonumber \end{aligned}$$

It is assumed that all of the coefficients of the model are subjected to uncertainty. The vector of all uncertain parameters, denoted by $p \in {R^{L_p}}$, includes the vehicle inertial parameters and the coefficients that appear in the force and moment approximations. The nominal value of $p$ is denoted by $p_0$. For simplicity, the maximum uniform variation within $30\,\%$ of the nominal value has been considered, yielding the parameter set $\Omega _p=\{p \in {R^{L_p}}\mid p_i^L \le p_i \le p_i^U, i=1,\ldots ,L_p\}$ and $p_i^L=\text{ min }\left\{ 0.7 p_i^0, 1.3 p_i^0\right\}$, $p_i^U=\text{ max }\left\{ 0.7 p_i^0, 1.3 p_i^0\right\}$.

3 Control Design

The control problem considered in this work takes into account only cruise trajectories and does not consider the ascent or the reentry of the vehicle. In the study [7, 9, 11], by functional decomposition, the velocity is independent with other subsystems. The goal pursued in this study is to design a dynamic controller $\Phi$ and $\delta _e$ to steer system velocity and altitude from a given set of initial values to desired trim conditions with the tracking reference $V_r$ and $h_r$. Furthermore, the altitude command is transformed into the flight path angle (FPA) tracking. Define the altitude tracking error ${\tilde{h}} = {h}-{h_{r}}$. The demand of FPA is generated as

$$\begin{aligned} {\gamma _d} = \arcsin \left( {\dfrac{{ - {k_h}{{\tilde{h}}} + {{\dot{h}}_{r}}}}{V}} \right) \end{aligned}$$

(6)

where $k_h>0$ is the design parameter.

3.1 Dynamic Inversion Control of Velocity Subsystem

Define the velocity error

$$\begin{aligned} \tilde{V} = V - {V_r} \end{aligned}$$

(7)

From (7), the velocity dynamics are derived as

$$\begin{aligned} \dot{\tilde{V} }= \dfrac{{{T_\Phi }\cos \alpha }}{m}\Phi + \dfrac{{{T_0}\cos \alpha - D}}{m} - g\sin \gamma - {\dot{V}_r} \end{aligned}$$

(8)

Define ${g}_{v} = \dfrac{{{{T}_\Phi }\cos \alpha }}{m}, {f}_{v} = \dfrac{{{T}_{0}\cos \alpha - D}}{m}$. Then Eq. (8) becomes

$$\begin{aligned} \dot{\tilde{V}} = {g_v}\Phi + {f_v} - g\sin \gamma - {\dot{V}_r} \end{aligned}$$

(9)

where ${f}_{v}=\omega _{fv}^T {\theta _{fv}}, g_v=\omega _{gv}^T {\theta _{gv}}$ with

$$\begin{array}{*{20}l} {\omega _{fv}} =\, \bar{q}S \left[ \begin{array}{*{20}l} {\alpha ^3}\cos \alpha ,{\alpha ^2}\cos \alpha ,\alpha \cos \alpha ,\cos \alpha ,\\ - {\alpha ^2}, - \alpha , - 1 \end{array}\right] ^T\\ {\theta _{fv}} =\, \dfrac{1}{m} \left[ \begin{array}{*{20}l} C_T^{{\alpha ^3}}, C_T^{{\alpha ^2}}, C_T^\alpha , C_T^0, C_D^{{\alpha ^2}}, C_D^\alpha ,\\ C_D^0\end{array}\right] ^T\\ \omega _{gv}=\, \bar{q}S \left[\begin{array}{*{20}l} {\alpha ^3}\cos \alpha ,{\alpha ^2}\cos \alpha ,\alpha \cos \alpha ,\cos \alpha \end{array}\right] ^T\\ {\theta _{gv}}=\, \dfrac{1}{m}\left[\begin{array}{*{20}l} C_{T\Phi }^{{\alpha ^3}},C_{T\Phi }^{{\alpha ^2}},C_{T\Phi }^\alpha ,C_{T\Phi }^0\end{array}\right] ^T \end{array}$$

The throttle setting is designed as

$$\begin{aligned} {\hat{g}_v}{\Phi }= - {k_v}\tilde{V} - {\hat{f}_v} + g\sin \gamma + {\dot{V}_r} \end{aligned}$$

(10)

where $k_v>0$ is a design parameter, $\hat{f}_v=\omega _{fv}^T {\hat{\theta }_{fv}}$ and $\hat{g}_v=\omega _{gv}^T {\hat{\theta }_{gv}}$.

Then Eq. (8) can be expressed as

$$\begin{aligned} \dot{\tilde{V}}&= {\tilde{g}_v}\Phi + {\tilde{f}_v} - {k_v}\tilde{V} \end{aligned}$$

(11)

where ${\tilde{f}_v}=\omega _{fv}^T\left( {{\theta }_{fv}}-{\hat{\theta }_{fv}}\right) =\omega _{fv}^T\tilde{\theta }_{fv}, {\tilde{g}_v}=\omega _{gv}^T\left( {{\theta }_{gv}}-{\hat{\theta }_{gv}}\right) =\omega _{gv}^T \tilde{\theta }_{gv}$.

The control Lyapunov function candidate for the velocity error dynamics is selected as

$$\begin{aligned} {W_V} = \dfrac{1}{2}\left( {{{\tilde{V}}^2} + \tilde{\theta }_{{fv}}^T\Gamma _{{fv}}^{ - 1}{{\tilde{\theta }}_{{f_v}}} + \tilde{\theta }_{{gv}}^T\Gamma _{{gv}}^{ - 1}{{\tilde{\theta }}_{{gv}}}} \right) \end{aligned}$$

(12)

The derivative of $W_V$ is

$$\begin{aligned} {{\dot{W}}_V}&= \tilde{V} \dot{\tilde{V} }- \tilde{\theta }_{{f_v}}^T\Gamma _{{f_v}}^{ - 1}{{\dot{\hat{\theta }} }_{{fv}}} - \tilde{\theta }_{{gv}}^T\Gamma _{{gv}}^{ - 1}{{\dot{\hat{\theta }}}_{{gv}}} \nonumber \\&= - {k_v}{{\tilde{V}}^2} + \tilde{V}\omega _{{fv}}^T\tilde{\theta }_{{fv}}^{} + \tilde{V}\omega _{{gv}}^T\tilde{\theta }_{{gv}}{\Phi }- \tilde{\theta }_{{fv}}^T\Gamma _{{fv}}^{ - 1}{{\dot{\hat{\theta }}}_{{fv}}} - \tilde{\theta }_{{gv}}^T\Gamma _{{g_V}}^{ - 1}{{\dot{\hat{\theta }} }_{{g_V}}} \nonumber \\&= - {k_v}{{\tilde{V}}^2} - \tilde{\theta }_{{fv}}^T\left( {\Gamma _{{fv}}^{ - 1}{{\dot{ \hat{\theta }} }_{{fv}}} - \tilde{V}\omega _{{fv}}} \right) -\tilde{\theta }_{gv}^T\left( \Gamma _{gv}^{ - 1}{\dot{\hat{\theta }}}_{gv} - \tilde{V}\omega _{{gv}}{\Phi }\right) \end{aligned}$$

(13)

The adaptive law is designed as

$$\begin{aligned} {{\dot{\hat{\theta }}}_{{fv}}}&= {\text{ Proj }}\left( {\Gamma _{{fv}}\tilde{V}\omega _{{fv}}} \right) \end{aligned}$$

(14)

$$\begin{aligned} {{\dot{\hat{\theta }}}_{{gv}}}&= {\text{ Proj }}\left( {\Gamma _{{gv}}\tilde{V}\omega _{{gv}}{\Phi }} \right) \end{aligned}$$

(15)

Then

$$\begin{aligned} {{\dot{W}}_V} = - {k_v}{{\tilde{V}}^2} \end{aligned}$$

(16)

It is easy to know that the velocity is asymptotically stable.

3.2 Dynamic Surface Control of Attitude Subsystem

Define ${x_1} = \gamma , {x_2} = {\theta _p},{x_3} = q, {\theta _p}=\alpha +\gamma , u=\delta _e$. The following subsystem can be obtained

$$\begin{aligned} {{\dot{x}}_1}&= {g_1}{x_2} + {f_1} - \dfrac{g}{V}\cos {x_1} \nonumber \\ {{\dot{x}}_2}&= {x_3} \\ {{\dot{x}}_3}&= {g_3}u + {f_3}\nonumber \end{aligned}$$

(17)

where

$$\begin{aligned} {f_1} =\,&\dfrac{{{L_0} - {L_\alpha }\gamma + T\sin \alpha }}{{mV}} = \omega _{f1}^T{\theta _{f1}}\nonumber \\ {g_1} =\,&\dfrac{{{L_\alpha }}}{{mV}} = \omega _{g1}^T{\theta _{g1}}\nonumber \\ {f_3} =\,&\dfrac{{{M_T} + {M_0}\left( \alpha \right) }}{{{I_{yy}}}} = \omega _{f3}^T{\theta _{f3}}\nonumber \\ {g_3} =\,&\dfrac{{{M_{{\delta _e}}}}}{{{I_{yy}}}} = \omega _{g3}^T{\theta _{g3}}\nonumber \end{aligned}$$

with

$$\begin{aligned} {\omega _{f1}} =\,&\dfrac{{\bar{q}S}}{V}\left[ \begin{array}{l} 1, - \gamma ,{\alpha ^3}\Phi \sin \alpha ,{\alpha ^2}\Phi \sin \alpha ,\alpha \Phi \sin \alpha ,\\ \Phi \sin \alpha ,{\alpha ^3}\sin \alpha ,{\alpha ^2}\sin \alpha ,\alpha \sin \alpha ,\sin \alpha \end{array}\right] ^T\nonumber \\ {\theta _{f1}} =\,&\dfrac{1}{m}\left[ \begin{array}{l}C_L^0,C_L^\alpha ,C_{T\Phi }^{{\alpha ^3}},C_{T\Phi }^{{\alpha ^2}},C_{T\Phi }^\alpha ,C_{T\Phi }^0,\\ C_T^{{\alpha ^3}},C_T^{{\alpha ^2}},C_T^\alpha ,C_T^0\end{array} \right] ^T\nonumber \\ {\omega _{g1}} =\,&\dfrac{{\bar{q}S}}{V}, {\theta _{g1}} = \dfrac{1}{m}C_L^\alpha \nonumber \\ {\omega _{f3}} =\,&\bar{q}S\left[ {{\alpha ^3}\Phi ,{\alpha ^2}\Phi ,\alpha \Phi ,\Phi ,{\alpha ^3},{\alpha ^2},\alpha ,1,{\alpha ^2},\alpha ,1} \right] ^T\nonumber \\ {\theta _{f3}} =\,&\dfrac{1}{{{I_{yy}}}}\left[ \begin{array}{l} {z_T}\left( {C_{T\Phi }^{{\alpha ^3}},C_{T\Phi }^{{\alpha ^2}},C_{T\Phi }^\alpha ,C_{T\Phi }^0} \right) , \\ {z_T}\left( C_T^{{\alpha ^3}},C_T^{{\alpha ^2}},C_T^\alpha ,C_T^0 \right) ,\\ \bar{c}\left( {C_M^{{\alpha ^2}},C_M^\alpha ,C_M^0} \right) \\ \end{array} \right] ^T\nonumber \\ {\omega _{{{g}}3}} =\,&\bar{q} S,{\theta _{g3}} = \dfrac{1}{{{I_{yy}}}}\bar{c}C_M^{{\delta _e}}\nonumber \end{aligned}$$

Step 1. Define $\tilde{x}_1=x_1-x_{1d}$. The dynamics of the flight path angle tracking error $\tilde{x}_1$ are written as

$$\begin{aligned} {\dot{\tilde{x}}_1} = {\dot{x}_1} - {\dot{x}_{1d}} = {g_1}{x_2} + {f_1} - \dfrac{g}{V}\cos \gamma - {\dot{x}_{1d}} \end{aligned}$$

(18)

Take $\theta _p$ as virtual control and design ${x_{2c}}$ as

$$\begin{aligned} {\hat{g}_1}{x_{2c}} = - {k_1}{\tilde{x}_1} - {\hat{f}_1} + \dfrac{g}{V}\cos {x_1} + {\dot{x}_{1d}} \end{aligned}$$

(19)

where $k_1>0$ is the design parameter, ${\hat{f}_1} = \omega _{f1}^T{\hat{\theta }_{f1}}, {\hat{g}_1} = \omega _{g1}^T{\hat{\theta }_{g1}}$. Introduce a new state variable ${x_{2d}}$, which can be obtained by the following first-order filter

$$\begin{aligned} {\varepsilon _2}{\dot{x}_{2d}} +{x_{2d}} = {x_{2c}},{x_{2d}}\left( 0 \right) = {x_{2c}}\left( 0 \right) \end{aligned}$$

(20)

Define ${y_2} = {x_{2d}} - {x_{2c}}, {\tilde{x}_2} = {x_2} - {x_{2d}}$.

$$\begin{aligned} {{\dot{\tilde{x}}}_1}&= {g_1}{x_2} + {f_1} - \dfrac{g}{V}\cos \gamma - {{\dot{x}}_{1d}} \nonumber \\&= {{g}_1}\left( {{x_2} - {x_{2c}}} \right) + {{{g}}_1}{x_{2c}} - {{{{\hat{g}}}}_1}{x_{2c}} + {{{{\hat{g}}}}_1}{x_{2c}}+{f_1} - \dfrac{g}{V}\cos \gamma - {{\dot{x}}_{1d}} \nonumber \\&= {{{g}}_1}\left( {{x_2} - {x_{2c}}} \right) + {{{{\tilde{g}}}}_1}{x_{2c}} + {{\tilde{f}}_1} - {k_1}{{\tilde{x}}_1} \nonumber \\&= {{{g}}_1}{{\tilde{x}}_2} + {{{g}}_1}{y_2} + {{{{\tilde{g}}}}_1}{x_{2c}} + {{\tilde{f}}_1} - {k_1}{{\tilde{x}}_1} \end{aligned}$$

(21)

The adaption laws of the estimated parameters are

$$\begin{aligned} {{\dot{\hat{\theta }}}_{f1}}&= \text{ Proj }\left( {\Gamma _{f1}}{\omega _{f1}}{{\tilde{x}}_1}\right) \end{aligned}$$

(22)

$$\begin{aligned} {{\dot{\hat{\theta }}}_{g1}}&= \text{ Proj }\left( {\Gamma _{g1}}{\omega _{g1}}{{\tilde{x}}_1}x_{2c}\right) \end{aligned}$$

(23)

Step 2. The dynamics of the pitch angle tracking error $\tilde{x}_2$ are written as

$$\begin{aligned} {\dot{\tilde{x}}_2} = {\dot{x}_2} - {\dot{x}_{2d}} = {x_3} - {\dot{x}_{2d}} \end{aligned}$$

(24)

Take $q$ as virtual control and design ${x_{3c}}$ as

$$\begin{aligned} {x_{3c}} = - {k_2}{\tilde{x}_2} + {\dot{x}_{2d}} \end{aligned}$$

(25)

where $k_2>0$ is the design parameter.

Introduce a new state variable ${x_{3d}}$, which can be obtained by the following first-order filter

$$\begin{aligned} {\varepsilon _3}{\dot{x}_{3d}} +{x_{3d}} = {x_{3c}},{x_{3d}}\left( 0 \right) = {x_{3c}}\left( 0 \right) \end{aligned}$$

(26)

Define ${y_3} = {x_{3d}} - {x_{3c}}, {\tilde{x}_3} = {x_3} - {x_{3d}}$.

$$\begin{aligned} {{\dot{\tilde{x}}}_2}&= {x_3} - {{\dot{x}}_{2d}} \nonumber \\&= {x_3} - {x_{3d}} + {x_{3d}} - {x_{3c}} + {x_{3c}} - {{\dot{x}}_{2d}} \nonumber \\&= {{\tilde{x}}_3} + {y_3} - {k_2}{{\tilde{x}}_2} \end{aligned}$$

(27)

Step 3. The dynamics of the pitch rate tracking error $\tilde{x}_3$ are written as

$$\begin{aligned} {\dot{\tilde{x}}_3} = {\dot{x}_3} - {\dot{x}_{3d}} = {g_3}u + {f_3} - {\dot{x}_{3d}} \end{aligned}$$

(28)

Design the elevator deflection ${\delta _e}$ as

$$\begin{aligned} {\hat{g}_3}u = - {k_3}{\tilde{x}_3} - {\hat{f}_3} + {\dot{x}_{3d}} \end{aligned}$$

(29)

where $k_3>0$ is the design parameter, ${\hat{f}_3} = \omega _{f3}^T{\hat{\theta }_{f3}}, {\hat{g}_3} = \omega _{g3}^T{\hat{\theta }_{g3}}$.

The error dynamics are derived as

$$\begin{aligned} {\dot{{\tilde{x}}}_3}&= {g_3}u + {f_3} - {{\dot{x}}_{3d}} \nonumber \\&= \left( {{{\tilde{g}}_3} + {{\hat{g}}_3}} \right) u + {f_3} - {{\dot{x}}_{3d}} \nonumber \\&= {{\tilde{g}}_3}u - {k_3}{{\tilde{x}}_3} + {{\tilde{f}}_3} \end{aligned}$$

(30)

The adaption laws of the estimated parameters are

$$\begin{aligned} {{\dot{\hat{\theta }}}_{f3}}&= \text{ Proj }\left( {\Gamma _{f3}}{\omega _{f3}}{{\tilde{x}}_3}\right) \end{aligned}$$

(31)

$$\begin{aligned} {{\dot{\hat{\theta }}}_{g3}}&= \text{ Proj }\left( {\Gamma _{g3}}{\omega _{g3}}{{\tilde{x}}_3}u\right) \end{aligned}$$

(32)

Assumption 1

The FPA reference signal and its derivatives are smooth bounded functions.

Assumption 2

There exists constant $\bar{g}_1>|g_1|>0$.

Select Lypunov function

$$\begin{aligned} W = \sum \limits _{i = 1}^3 {{W_i}} \end{aligned}$$

(33)

with

$$\begin{aligned} {W_1} =\,&\dfrac{1}{2}\left( {{{\tilde{x}}_1}^2 + \tilde{\theta }_{f1}^T\Gamma _{f1}^{ - 1}{{\tilde{\theta }}_{f1}} + \tilde{\theta }_{g1}^T\Gamma _{g1}^{ - 1}{{\tilde{\theta }}_{g1}} + y_2^2} \right) \nonumber \\ {W_2} =\,&\dfrac{1}{2}\left( {\tilde{x}_2^2 + y_3^2} \right) \nonumber \\ {W_3} =\,&\dfrac{1}{2}\left( {\tilde{x}_3^2 + \tilde{\theta }_{f3}^T\Gamma _{f3}^{ - 1}{{\tilde{\theta }}_{f3}} + \tilde{\theta }_{g3}^T\Gamma _{g3}^{ - 1}{{\tilde{\theta }}_{g3}}} \right) \nonumber \end{aligned}$$

Theorem 1.

Consider system (17) with virtual control (19), (25), actual control (29) with adaption laws (22), (23), (31) and (32) under Assumptions 1–2. Then all the signals of (33) are uniformly ultimately bounded.

Remark for each $W_i$, one can follow the analysis procedure in velocity subsystem. The proof could be done by following the procedure in [14] and thus it is omitted here. The work was part of the design and analysis of the DSC based actuator saturation control [17].

4 Simulations

The rigid body of the hypersonic flight vehicle is considered in the simulation study. The parameters for COM can be found in [15]. The reference commands are generated by the filter

$$\begin{aligned} \dfrac{{{h_r}}}{{{h_c}}} = \dfrac{{{0.16}}}{{( s^2 + 0.76s + 0.16)}} \end{aligned}$$

(34)

$$\begin{aligned} \dfrac{{{V_r}}}{{{V_c}}} = \dfrac{{{0.16}}}{{( s^2 + 0.76s + 0.16)}} \end{aligned}$$

(35)

The control gains for the dynamic surface controller are selected as $\left[ 6,0.3,2,5,8\right]$ separately for $[k_v, k_h, k_1,k_2,k_3]$, and the first-order filter parameter for dynamic surface design is $\varepsilon _i=0.02,i=2,3$. Parameters for projection algorithm are selected as $\Gamma _{fi}=0.1I, \Gamma _{gi}=0.1I, i=1,3,v$.

Fig. 1

Altitude tracking

Fig. 2

Velocity tracking

The initial values of the states are set as $v_0=7,850\,\text{ ft/s }$, $h_0=86,000\,\text{ ft, } \alpha _0=3.5^\circ, \gamma _0=0, q_0=0$. The velocity tracks the step command with 200fst/s while the altitude follows the square command with period 100 s and magnitude 1,000 ft.

The satisfied tracking performance is depicted in Figs. 1 and 2.

Fig. 3

Elevator deflection

Fig. 4

Throttle setting

Fig. 5

Estimation of $C_L^\alpha /m$

The altitude follows the square signal while the velocity is responding to the step command. From the control input referred to

first period is larger than others. This is due to the fact that velocity is stepped from 7,850 to 8,050 ft/s in about 20 s and it is kept stable in the next periods with small variation which is caused from the square tracking of the altitude. The elevator deflection is changing fast at the beginning. The reason could be found in the parameter estimation in Fig. 5 where the estimation responds in a large domain and then later it is stable. The simulation shows the robustness of the algorithm regarding to the parameter uncertainty (Fig. 3).

5 Conclusions and Future Work

The dynamics of HFV are transformed into the linearly parameterized form. To avoid the “explosion of complexity,” the dynamic surface control is investigated on HFV. The closed-loop system achieves uniformly ultimately bounded stability. The effectiveness is verified by simulation study with parametric model uncertainty. For future work, we will focus on the design in the presence of flexible states.