Keywords

1 Introduction

Considering the product’s size and the complexity of the assembly line, two-sided assembly lines are widely used in assembly of large-sized products such as automobiles, buses, or trucks. It is very important for manufacturers to design an efficient two-sided assembly line. Two-sided assembly line balancing problem (TALBP) can be divided into two versions: TALBP-I consists of assigning tasks to work stations, such that the number of open position of the two-sided assembly line is minimized for a given production rate, and TALBP-II is to minimum cycle time for a given number of open position in the assembly line. In actual manufacturing enterprises, the optimization goals often refer to the second category in order to reduce the production cycle time.

TALBP are received widely attention in the past few years for the importance of two-sided assembly lines. Bartholdi [1] first proposed two-sided assembly line balancing problem, and a first-fit rule–based heuristic algorithm is given for TALBP-I. Kim et al. [2] and Lee et al. [3] used genetic algorithm for solving TALBP-I and join the group distribution strategy to optimize the correlation indicators between tasks. Simaria and Vilarinho [4] used ant colony optimization algorithm, named 2-ANTBAL, for solving TALBP-I. Baykasoglu and Dereli [5] first introduced the concept of regional constraints in TALBP-I and then proposed an ant colony algorithm to solve the problem. Wu and Hu proposed a branch-and-bound algorithm for TALBP-I [6].

Compare to TALBP-I, TALBP-II is less studied [7]. Ozcan [8] presented a Petri net-based heuristic to solve simple assembly line balancing problem type-II. To solve TALBP-II, Kim et al. [9] presented a mathematical model and a genetic algorithm, which adopted the strategy of localized evolution and steady-state reproduction to promote population diversity and search efficiency. In this paper, a new ant colony algorithm is proposed to solve the two-sided assembly line balance problem as the common problems of manufacturing enterprises, respectively, using the ant colony comprehensive search rules and task assignment rules to select and assign tasks. Considering the special features of TALBP-II, an ant colony the overall search process is introduced in this paper.

This paper is organized as follows: The TALBP-II is discussed in Sect. 2, and mathematical model is presented. In Sect. 3, the modified ant colony algorithm for TALBP-II is explained in detail. An example problem of a loader final assembly line is solved using the proposed method in Sect. 4. Finally, some conclusions are presented in Sect. 5.

2 Problems Statement and Formulation

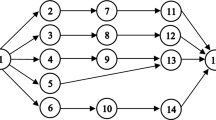
As shown in Fig. 1, in two-sided assembly line, both sides of the station can operate different tasks in parallel. Stations 1 and 2 can be described as a pair of stations (mated-station), the station 1 can be called an accompanied station of the station 2 (a companion), and the remaining work stations have the similar relationship. Tasks can be operated simultaneously when they do not have priority constraints.

Fig. 1
figure 1

Two-sided assembly line

Full size image

The mathematical model of two-sided assembly line balancing problem can be described as below. First, list the relevant variables: I—task set, I = {1, 2, …, N}; I D —to split the task set by the task operating position, D = L(left), R(right), or E(both sides), I E refers to the tasks can be assigned to both sides of the position, and so on; I j ′ I j ′—sets of tasks assigned to station j and j′; T j ′ R j —the total operating time and total delay time of station j; T j ′, R j ′—total operating time and total delay time of station j′; P(i)—set of all predecessors of task i; S—set of all the task i whose P(i) is empty, all this tasks can be used for distribution into the station because their pre-order tasks are already located; S′—set of tasks meet the cycle time constraints from S, the tasks can be assigned to the station directly; W—set of unassigned tasks; n—the number of opened position; N S —opened work stations; x ipk—the value is 1, if task i is assigned to position p, and the operating position is k, k ∈ {L, R}; 0, otherwise.

Constraints:

$$ {\text{If}}\;x_{\text{ipk}} = 1,\;{\text{then}}\;x_{\text{hgk}} = 0,\;h \in P(i),\;g,\;p = 1,\; 2,\; 3, \ldots ,\;n,\;{\text{and}}\;g > p $$
(1)
$$ \sum\limits_{i \in I} {\sum\limits_{p = 1}^{n} {x_{\text{ipk}} } = 1} ,\;k \in \left\{ {L,\;R} \right\} $$
(2)
$$ T_{j} = \sum\limits_{i \in I} {x_{\text{ipk}} } \cdot t_{i} ,\;{\text{and}}\;k = L, j = 2\;p - 1 $$
(3)
$$ T_{j}^{\prime } = \sum\limits_{i \in I} {x_{\text{ipk}} } \cdot t_{i} ,\;{\text{and}}\;k = R,\;j^{\prime } = 2\;p $$
(4)
$$ {\text{In}}\;{\text{any}}\;{\text{position}}\;p,\;T_{j} + \, R_{j} \le C,\;{\text{and}}\;T_{j}^{\prime } + \, R_{j} \prime \le C $$
(5)

Objective:

$$ {\text{Minimize}}\; C $$
(6)
$$ \hbox{max} \;{\text{LE}} = \left( {\sum\limits_{i \in I} {t_{i} } } \right)/\left( {N_{S} C} \right) $$
(7)
$$ \hbox{min} \;{\text{SI}} = \sqrt {\frac{{\sum\limits_{i = 1}^{{N_{S} }} {\left( {T_{\hbox{max} } - T_{i} } \right)^{2} } }}{{N_{S} }}} $$
(8)

Lower limit formulation of cycle time:

$$ C_{ \hbox{min} } = { \hbox{max} }\{ \left| {T_{\text{SUM}} / 2n} \right|,\left| {T_{\text{SUML}} /n} \right|,\left| {T_{\text{SUMR}} /n} \right|,t_{ \hbox{max} } \} $$
(9)

Constraint (1) is the assignment constraint which ensures that each task is assigned to exactly one station and all precedence relations between tasks are satisfied. Constraint (2) ensures the task must be assigned to a position p, and the allocated operating position only can be left or right. Constraints (3) and (4), respectively, refers to total operating time of station j and j’. Constraint (5) refers to the operating time of any mated-stations in any position p must satisfy the cycle time constraints. Objective function (6) as the main objective function this paper focused on TALBP-II, that is to minimize the cycle time when the number of positions opened in the assembly lines is determined. Functions (7) and (8) are secondary evaluation objective, to maximum line efficiency LE and minimum smoothness index SI can balance the stations’ load. When LE = 1 and SI = 0, every position has the same load. Formulation (9) is lower limit formulation of cycle time for TALBP-II; T SUM is the sum of task time in the set I; T SUML, T SUMR, and T SUME were the sum operating time of all tasks in I L , I R , and I E , respectively; t max is the task which has the longest operating time.

3 The Ant Colony Algorithm for TALBP-II

3.1 Ant Colony Comprehensive Search Rules

Selected tasks from the set S which have the earliest start time. These tasks constitute FT (the tasks in FT have the same earliest start time); if FT has only one task, select this task by task assignment rules. If FT has more than one tasks, then use the hybrid search mechanism to select the task, this mechanism borrow ideas called improved pheromone rule from the literature [10]:

$$ i = \left\{ {\begin{array}{*{20}c} {I_{1} :p_{{{\text{ij}}}} \, = \,\frac{{\left( {\sum\limits_{{k = 1}}^{j} {\tau _{{{\text{ih}}}} } } \right)^{\alpha } (\eta _{i} )^{\beta } }}{{\sum\limits_{{s \in {\text{FT}}}} {\left( {\sum\limits_{{h = 1}}^{j} {\tau _{{{\text{sh}}}} } } \right)^{\alpha } (\eta _{s} )^{\beta } } }}{\text{ }}} & {0 \le \,r\, \le r_{1} } \\ {I_{2} :\:\:{\text{random selection of}}\:i \in {\text{FT}}} & {r_{1} < \,r\, \le 1{\text{ }}} \\ \end{array} } \right. $$
(10)

r—random number between (0, 1); r 1—the user-defined parameter to meet 0 ≤ r 1 ≤ 1; FT—in the current sequence position j, the tasks that ant can be selected with the earliest start time; α, β—parameters determine the relative importance of pheromone intensity and heuristic information; η i —the heuristic information of task i, using pw i that is the position weight of task i as heuristic information:

$$ \eta_{i} = {\text{pw}}_{i} = t_{i} + \sum\limits_{{j \in F_{i} }} {t_{j} } ,\quad i = 1, \ldots ,N $$
(11)

F i —set of successor tasks of task i. Position weight heuristic rules account the sum of successor task operating time and the largest number of successor tasks simultaneity, tasks with largest successor task numbers and longer sum operating time of successor tasks has the greater probability of being select. In formulation (10), the random variable r determines using the rules below to select a task form FT: If the random number r satisfies 0 ≤ r ≤ r 1, then randomly select a task from the FT with the probability p ij; if the random number r satisfies r 1 < r ≤ 1, then randomly choose a task from the candidate FT.

3.2 Heuristic Task Distribution Rules

Rule 1: If the task’s operating position constraint is L(or R), it is placed on the left (or right) station; Rule 2: If this task’s operating position constraint is E, then put it into the side which it can began earlier; if it placed on both sides with the same start time, then selected one side randomly.

3.3 Construct the Feasible Solution in Ant Colony Algorithm

As shown in Fig. 2, the open position is the determined value n, and the optimization goal is to minimize the cycle time. In order to ensure that all tasks can be completely distributed, in the first n − 1 positions, the constraints of the optimal cycle time are used; in the final position of n, eliminating the cycle time constraint to assign all tasks into this location to meet the total number of the open position is exactly n, and feasible solutions are generated. Find out the latest completion time from all positions in this feasible solution as the cycle time searched by this ant.

Fig. 2
figure 2

Assignment of tasks to construct an ant solution

Full size image

3.4 Pheromone Updating Rule

Local pheromone update: The role is to reduce the attractive effect from earlier ants to the later one, thereby this method strengthens the random search capabilities of ants. When the ant assigned task i to the arranged location j, the pheromone in edge ij updated as formulation (12):

$$ \tau_{\text{ij}} \leftarrow \left( {1 - \rho_{1} } \right)\tau_{\text{ij}} + \rho_{1} \tau_{0} $$
(12)
ρ 1 :

local pheromone evaporation coefficient, 0 < ρ 1 < 1;

τ 0 :

initialized pheromone value, \( \tau_{0} = 1/(N \cdot K^{*} ),\;K^{*} = \left\lceil {\left( {\sum\limits_{i \in I} {t_{i} } } \right)/C_{\hbox{min} } } \right\rceil \).

Global pheromone update rule: As the establishment of an optimal solution set for each generation of ants’ search results in this paper, every optimal solution in the collection releases pheromone to the path. The global pheromone update formula is as follows:

$$ \tau_{\text{ij}} \leftarrow \left( {1 - \rho_{2} } \right)\tau_{\text{ij}} + \rho_{2} \Updelta \tau_{\text{ij}} $$
(13)

where

$$ \Updelta \tau_{\text{ij}}^{\text{gb}} = \left\{ {\begin{array}{*{20}c} {1/N_{S} ,} \hfill & {{\text{if}}{\kern 1pt} (i ,\; \, j )\in {\text{global-best-tour}}} \hfill \\ {0,} \hfill & {\text{otherwise}} \hfill \\ \end{array} } \right. $$
(14)
ρ 2 :

is global pheromone evaporation coefficient, 0 ≤ ρ 2 ≤ 1

The whole search plan of ant colony algorithm: The algorithm starts search the optimal solution at the theoretical minimum cycle time, C min. The first generation of ants search from the smallest cycle time C t (C t  = C min) at the start search. If it do not find the solution of C t , the standard value C t increased by 1 in the next generation of ant colony search, C t  = C t  + 1; if a generation of ant colony obtained the current search criteria C t , then the next generation of search will narrow the search criteria, that is, C t  = C t − 1; the entire ant colony uses this plan to search for the theoretical optimal solution until find out the optimal solution or the maximum search iteration is reached.

4 Computational Study

Precedence diagram of a loader assembly line [11] is given in Fig. 3. The proposed ant colony algorithm was coded in MATLAB 7.8 and run on a Notebook PC equipped with Intel Core i5-2410 M 2.30 GHz and 4 GB memory. In the proposed ACO, several parameters, such as number of ants n ant, maximize iteration number NCmax, α, β, ρ and e, affect the performance of the algorithm. Excessive experimental tests were conducted and found out the following value of parameters are more appropriate: n ant = N, NCmax = 400, α = 1, β = 2, ρ 1 = 0.1, ρ 2 = 0.1, r 1 = 0.8. By changing the number n (number of opened positions in the assembly line), the computational study shows the four kinds of optimization solutions as shown in Table 1. Figure 4 is the Gantt chart output by MATLAB as the second optimization solution in Table 1.

Fig. 3
figure 3

Precedence diagram of a loader assembly line

Full size image
Table 1 Four types of assignments for the test problem generated by ACO
Full size table
Fig. 4
figure 4

Gantt chart of assignment of tasks for the example problem

Full size image

In Table 1, four kinds of optimization results are all with a good balance rate. Assignment schedules of scheme 2 for the test problem generated by ACO refer to Table 2. To increase the practicality of the algorithm and the intuitive of the results, the Gantt chart display module was added to this program, refer to Fig. 3. The progress bar’s length is in accordance with the tasks’ operation time, and the number on top of the progress bar is the start time and end time of tasks; the horizontal axis is for the timeline for the task start and end time, the vertical axis is for the station, which on the left station of every position is odd, the right station in the same position is even. The time delayed by the pre-order tasks in the mated-station is clear in Fig. 1, so the Gantt chart display module has obvious practical significance.

Table 2 Assignment schedules of scheme 2
Full size table

5 Conclusions

In this paper, an ant colony algorithm was introduced to solve two-sided assembly line balance problem type-II. An ant colony search rules, heuristic task distribution rules were used for generate a feasible solution. The whole search plan of ant colony algorithm controls the optimal solution search process. Computational experiment demonstrated the validity of the proposed algorithm. In the future studies, we hope to apply the method to extensions of the TALBP-II, such as multiple-object TALBP-II.