Axial Capillary Forces (Dynamics)

Abstract

Up to now, we have only considered liquid bridges at equilibrium. Therefore, the forces applied by these menisci on solids they connect are only due to surface tension effects. If the meniscus is stretched or compressed with an important velocity or an important acceleration, viscous or inertial effects have to be added to capillary forces. Viscous effects will be governed by the viscosity of the liquid while inertial effects will be governed by density. Normally at small scales, density can be neglected, but attention must be paid in case of high accelerations, such those used in inertial micromanipulation [9]. From a mechanical point of view, these three terms form the well known Kelvin-Voigt model. After a brief state of the art, this chapter explains how to estimate the coefficients of this Kelvin-Voight model and compares the related results with numerical simulation and experiments.

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Introduction

This chapter focuses on the behaviour of the vertical dynamic force generated by an axisymmetric liquid bridge. The next section describes the problem and the main assumptions on the meniscus. Section 7.3 gives the mathematical background of the Kelvin-Voigt Model. The analytic development of the coefficients $k$, $b$ and $m$ are given in Sects. 7.4, 7.5 and 7.6 respectively. Analytic relations are validated on a simple case in Sects. 7.7 and 7.8. An experimental setup (Sect. 7.9) has been performed to validate the model. Results are given in Sect. 7.10. A conclusion (Sect. 7.11) ends the chapter.

2 Problem Description and Methodology

In this chapter, we will describe the liquid bridge as a mechanical join between two solids. The liquid bridge is assumed to be pinned by two circular and parallel interfaces providing an axial symmetry of the geometry around the $z$ axis. The dimensions are submillimetric, 750 ${{\upmu }\mathrm{m}}$ of radius and gap around 200 ${{\upmu }\mathrm{m}}$. The plate presents sharp edge to ensure the liquid to be pinned. This present the advantage to have a free contact angle. Indeed, the liquid will recede if the contact angle is below the receding angle $\theta _r$ and will advance if the contact angle is higher than the advancing angle $\theta _a$ (Fig. 7.1). Since the geometry present an edge, the advance of the liquid is done along the nearly vertical edge. The same argument can be done on this second edge. Thus, the liquid will spread out of the plate if the contact angle is higher than $\theta _m$. In a certain way, the pinning increases the advancing contact angle.

For small displacements, the dynamic study of these degrees of freedom may be decoupled into 6 frequential responses. The latter can be described in several ways, depending on how the system is excited (the input) on one hand and on how the effect of the excitation is passed on (the output) on the other hand. Typical input/output are the position of an interface, its velocity, its acceleration and its force. The choice of position, velocity, acceleration of force is usually driven by the convenience of the way of experimental measurements. It is not necessary to characterise the transfer function for every pair of input/output: they can be retrieved through mathematical relationships (the velocity is the derivative of the position, the force is the product of the mass and the acceleration...).

We will consider the input as a displacement of the top interface and the output as the force exerted on the bottom interface. The liquid bridge is replaced by a Kelvin-Voigt model: a system made up of a spring, a damper dashpot and an equivalent mass connected in parallel (Fig. 7.3). According to liquid properties, it is expected to have a stiffness depending on the surface tension $\gamma$, a damping coefficient of the viscosity $\mu$ and an equivalent mass of the density $\rho$.

Fig. 7.1

Pinning contact angle. When a liquid is pinned, the contact angle can be higher than the advancing contact angle. This figure was published in [11]. Copyright $\copyright$ 2013 Elsevier Masson SAS. All rights reserved

The methodology adopted to validate the results consists of two steps (see Fig. 7.2): (i) a comparison between the analytical approximations of the mechanical parameters derived from the Navier-Stokes problem and numerical simulations, and (ii) a comparison between experimental and numerical data. That is, the numerical simulations act like a buffer between analytical expressions and experiments. The first comparison supports the simplifications made with the Navier-Stokes equation to obtain the analytic expressions of $k$, $b$ and $m$. For the second comparison, we directly used experimental data in numerical simulations: due to experimental errors, the symmetry around the plane containing the neck ($z = 0$) was not exactly verified. The numerical simulations were performed with COMSOL MULTIPHYSICS 3.5a.

Fig. 7.2

Link between analytic, numeric and experimental results

This problem has already been partially addressed: the literature review on vertical dynamics highlights the works of van Veen et al. [12], Cheneler et al. [1] and Pitois et al. [9].

In [12] van Veen has developed an analytical study of the motion of the flip chip soldered components. The model is based on the computation of the free surface energy for axisymmetric geometries delimited by two parallel and circular interfaces. The free interface is developed as a fourth order polynomial and its derivative is the origin of the motion equation. A second order equation governs the time evolution of the height of the bump. Cheneler et al. [1] propose a quite close analysis of liquid bridge with a totally different goal: they developed a micro-rheometer intended to determine the viscosity of liquids. However the device is not defined in the paper, the underlying idea is that the liquid added between two solids generates a dashpot in series with a calibrated spring/mass system. By measuring the phase shift between the position of the solids and the force exerted, the friction can be deduced. The method used is based on an estimation of the stiffness and the friction. This stiffness is deduced from an analytical approximation of the free interface, that is in this case a revolution of a part of a sphere (a piece of tore). However, the stiffness was calculated with a corrective multiplicative term of the capillary force, instead of the calculus of the derivative. The friction force is estimated from shear stresses inside the liquid. This friction and the stiffness have been linearized and added in the Newton equation governing the motion of the component wetted by the meniscus. Its validation is done thanks an numerical analysis. However, the numerical analysis does not solve the Navier-Stokes equation inside the meniscus. Finally, the authors do not support their study with any experimental data. In [9], Pitois et al. have studied the evolution of the force between two spheres moving aside at a given constant velocity. The analytical model involves also estimation of stiffness and friction. The stiffness is computed from the derivative of the capillary force, itself calculated with geometrical approximation of the different order of magnitude. The friction force is based on similar assumption but a corrective term is added. Contrarily to Cheneler, the liquid bridge is not pinned and the contact surface varies in time. The study is based on an analytical approach of the problem together with an experimental setup. As the main result, they highlighted different behaviours of the capillary forces (negative and positive, according the separating distance $z$), the influence of the velocity illustrating the effect of viscosity. Nevertheless, the authors do not expose some important aspects, such as the way to control the volume (volumes are small and the viscosity high, making the use of pipette very difficult), the variation of the contact angles during the separation and, as a corollary, the motion of the triple line, making the interpretation of their results difficult.

3 Mathematical Background of the Kelvin-Voigt Model

The mechanical model of the axial degree of freedom is presented in Fig. 7.3: a Kelvin-Voigt system made up of a spring (of stiffness $k$), a damper dashpot (of damping coefficient $b$) and an equivalent inertial force (of mass $m$) connected in parallel. Such a system can be described by its frequential response and is entirely defined when the coefficient $k$, $b$ and $m$ are known.

Fig. 7.3

The Kelvin-Voigt model. Forces $f_k(t)$ and $f_b(t)$ represent the force of the spring and of the dashpot, respectively, while $f(t)$ represents the total force exerted by liquid bridge on the system. Origin is assumed at the free length position. The direction of forces are represented for a stretched spring $x(t) > 0$, upwards velocity $\dot{x}(t) > 0$ and upwards acceleration $\ddot{x}(t) > 0$. This figure was published in [11]. Copyright $\copyright$ 2013 Elsevier Masson SAS. All rights reserved

Typical input/output pairs are the position of an interface, its velocity, its acceleration and its force. The system can be completely described by the frequential response of a single input/output pair. Here, we will characterise the vertical translation considering as input the displacement of the top interface $x(t)$, and as output the force exerted on the bottom interface $F(t)$.

The gravitational effects can conversely be ignored because of the small dimension of the bridge. Furthermore, the gravitational force is completely static, without any effect on a dynamic study. The expression of the forces is:

$$\begin{aligned} \bar{f}_{k}(t) = -f_k(t) \bar{1}_{x}&= -k x(t) \bar{1}_{x} \end{aligned}$$

(7.1)

$$\begin{aligned} \bar{f}_{b}(t) = -f_b(t) \bar{1}_{x}&= -b \dot{x}(t) \bar{1}_{x} \end{aligned}$$

(7.2)

$$\begin{aligned} \bar{f}_{m}(t)= -f_m(t) \bar{1}_{x}&= -m \ddot{x}(t) \bar{1}_{x} \end{aligned}$$

(7.3)

The force exerted by the meniscus on the lower interface is thus:

$$\begin{aligned} \bar{F}(t) = F(t) \bar{1}_{x}= -\bar{f}_{k}(t) - \bar{f}_{b}(t) - \bar{f}_{m}(t) \end{aligned}$$

(7.4)

In the next section, we will present a semi-analytical development to approximate the coefficients of the Kelvin-Voigt model describing the liquid bridge. The aim is to decouple the liquid properties, namely the surface tension $\gamma$, the viscosity $\mu$ and the density $\rho$, into the stiffness $k$ (Sect. 7.4), the damping $b$ (Sect. 7.5) and the inertial mass $m$ (Sect. 7.6), respectively.

Briefly, the spring force considers the fluid at rest, the damping force considers only the viscous force driving the fluid, and the inertial force considers the force due to fluid acceleration. The Navier-Stokes equation is simplified consequently. The force applied by the fluid on the bottom interface is then computed, and the corresponding coefficients are derived. Gravitational effects are ignored, while inertial ones are contemplated where required.

4 Stiffness

4.1 Introduction

The force generated by a spring is independent of the speed at which its extremity moves. Therefore, to calculate the stiffness, it is appropriate to consider the liquid at rest. The pressure outside the liquid bridge $p_{\mathrm{out }}$ is assumed to be zero.

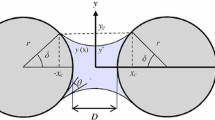
The geometry and the parameters are presented in Fig. 7.4. In addition to the axial symmetry, the geometry presents a symmetry with respect to the $r$ axis, which further reduces the parameters in the study. The input parameters are the radius of the plate $R$, the gap (or meniscus height) $h$, and the edge angle $\theta$. By fixing these three parameters, the meniscus volume is automatically determined.

Fig. 7.4

Geometry and parameters for the analytic model of $k$. This figure was published in [11]. Copyright $\copyright$ 2013 Elsevier Masson SAS. All rights reserved

The meniscus stiffness $k$ can be deduced from the derivative of the spring force $f_k$ as follows:

$$\begin{aligned} k = -\frac{\mathrm{d }f_k}{\mathrm{d }h} = \frac{\mathrm{d }F}{\mathrm{d }h} \end{aligned}$$

(7.5)

where $h$ is the height of meniscus, $f_k = -kz$ and $F$ is the total force exerted by the meniscus on the bottom pad.

Since the liquid is at rest, the inner pressure is only due to the curvature of the free interface:

$$\begin{aligned} p_{\mathrm{in }} = 2H\gamma \end{aligned}$$

(7.6)

As seen in Chap. 2, the force exerted by the liquid is thus the sum of the Laplace and the surface tension forces:

$$\begin{aligned} F = 2 \pi \gamma R \sin \theta - 2 H \gamma \pi R^2 \end{aligned}$$

(7.7)

A positive force $F$ means that the meniscus pull the substrate upwards while a negative force $F$ means that the meniscus push the meniscus downwards. The stiffness $k$ is given by:

$$\begin{aligned} k = \frac{\mathrm{d }F}{\mathrm{d }h} = 2 \pi \gamma R \cos \theta \frac{\mathrm{d }\theta }{\mathrm{d }h} - \pi \gamma R^2 \frac{\mathrm{d }(2H)}{\mathrm{d }h} \end{aligned}$$

(7.8)

The derivatives are done assuming the volume is constant. With the same convention,¹ the local curvature of an analytical axisymmetric shape $r(z)$ has already been given in (2.24):

$$\begin{aligned} 2H(z) = -\frac{r^{\prime \prime }(z)}{[1+r^{\prime 2}(z)]^{\frac{3}{2}}} + \frac{1}{r(z)\sqrt{1 + r^{\prime 2}(z)}} \end{aligned}$$

(7.9)

Unfortunately, there is no analytical solution $r(z)$ and digital solving was requested.

4.2 Numeric Approach

The first method is the numerical integration of (7.9). The derivative of the curvature and the edge angle is computed by the finite difference method, leading to the results shown in Fig. 7.6.

Fig. 7.5

Algorithm of numeric approach under Matlab, using bvp4c and fzero

Figure 7.5 shows the algorithm of the numerical approach. A first solution is computed with the boundary value problem bvp4c with the initial parameters (the radius $R$, the contact angle $\theta$ and the gap $h$). By giving an additional boundary value, the curvature $2H$ is handled as an unknown parameter to be determined by the solver. The volume $V$ is derived from an integration of the shape (solution of bvp4c). The problem is solved again with new gap ($h + \varDelta h$) and an arbitrary starting value of the contact angle (the input value $\theta$ was used). For each contact angle, an output volume is computed. The correct contact angle is the one that keeps the volume constant. The search of this contact angle is done with fzero, with the contact angle as input and the volume difference to be zeroed. After reaching the solution, the derivatives of the curvature and the contact angles can be computed by finite difference.

Fig. 7.6

Map of reduced stiffness $\hat{k} = k/\gamma$. This figure was published in [11]. Copyright $\copyright$ 2013 Elsevier Masson SAS. All rights reserved

The complexity of the algorithm is $N^2$, since the fzero (of complexity $N$) loops on bvp4c of complexity N. The computing time is below the second in most of cases.

4.3 Negative Stiffness

The reader will note that the stiffness coefficient is not always positive on Fig. 7.6. As illustrated in Fig. 7.7, when the gap increases, the meniscus curvature decreases, reducing the inner pressure. The second term of the derivative of the force (7.8) is always positive. On the contrary, the sign of the contribution of the surface tension force, expressed in the first term of (7.8), depend on the edge angle. The edge angle always decreases as the gap increases but the cosine is positive for angle below $90{^{\circ }}$. The contribution of the surface tension force is then negative when $\theta < 90{^{\circ }}$ and can be bigger than the Laplace force for high gap.

Figure 7.8a represents a part of the map of the reduced force $\hat{F} = F / r \gamma$ according to the edge angle $\theta$ and the reduced height $\hat{h}$. The bold line is the evolution of the $\theta$ when the gap increases at constant volume. The evolution of the force along this curve is represented in Fig. 7.8b (plain line). As the gap increases, the force reaches a maximum and begins to decrease. The derivative (i.e., the stiffness) is therefore negative (dashed line).

Consequently, for certain configurations the meniscus can be considered as an anti-spring. Anti-springs are unstable because the force tends to deviate from the equilibrium state. However, if the anti-spring is mechanically constrained—as in the case of a meniscus—it is not unstable: the gap is fixed externally, whatever the force.

Fig. 7.7

Evolution of edge angle and inner pressure as the gap increases at constant volume. This figure was published in [11]. Copyright $\copyright$ 2013 Elsevier Masson SAS. All rights reserved

Fig. 7.8

Illustration of origin of negative stiffness. a Map of the reduced force $\hat{F} = F / r \gamma$ according to the edge angle $\theta$ and the reduced height $\hat{h} = h/r$. The dashed line is a constant volume line. b Evolution of the reduced force and reduced stiffness along the constant volume line, in the direction of increasing gap. This figure was published in [11]. Copyright $\copyright$ 2013 Elsevier Masson SAS. All rights reserved

Fig. 7.9

Bode plots of the Kelvin-Voigt model within the stiffness is negative (plain lines) or positive (dashed lines), for two configurations: $\hat{m} < 1$ (left) and $\hat{m} > 1$ (right). The vertical line is the resonant frequency and the dashed lines are the cut-off frequencies delimiting the three states. a Gain of transfer function with $k = {-1}\,\mathrm{N/\mathrm{m}}$, $b = {5 10^{-1}}\,\mathrm{N\mathrm s/\mathrm{m}}$ and $m = {10^{-3}}\,{\mathrm{kg}}$ b Gain of transfer function with $k = {-1}\,\mathrm{N/\mathrm{m}}$, $b = {5 10^{-3}}\,\mathrm{N\mathrm s/\mathrm{m}}$ and $m = {10^{-3}}\,{\mathrm{kg}}$. c Phase of transfer function with $k = {-1}\,\mathrm{N/\mathrm{m}}$, $b = {5 \, 10^{-1}}\,\mathrm{N\, \mathrm s/\mathrm{m}}$ and $m = {10^{-3}}\,{\mathrm{kg}}$. d Phase of transfer function with $k = {-1}\,\mathrm{N/\mathrm{m}}$, $b = {5 \, 10^{-3}}\,\mathrm{N\, \mathrm s/\mathrm{m}}$ and $m = {10^{-3}}\,{\mathrm{kg}}$

The effect of the negative stiffness on Bode plots is depicted in Fig. 7.9 for a low inertial and high inertial system (plain lines). In addition, the dashed lines recall the plots of Fig. 6.2 (positive stiffness).

For a low inertial system, the gains (Fig. 7.9a) are identical. The phase (Fig. 7.9c) starts at $180{^{\circ }}$, reaches $90{^{\circ }}$ during the $b$-state and finishes at $180{^{\circ }}$ in the $m$-state.

For a high inertial system, $k$-state and $m$-state interact because the $b$-state vanishes. Since the phase of the $k$ and $m$-states are $180{^{\circ }}$, their effects are additive and the gain (Fig. 7.9b) does not show any minimum at the resonant frequency. The phase (Fig. 7.9d) is constant at $180{^{\circ }}$ except near the resonant frequency.

4.4 Geometrical Assumptions

Compared to the digital integration presented in Sect. 7.4.2, a second method is to assume the meniscus geometry, i.e. parabolic or circular shapes, which provides analytic relations. Yet, they do not have a constant curvature on the whole interface since they are not solution of (7.9). The curvature and its derivative are taken at the neck of the meniscus ($z = 0$). These relations are summarised in Table 7.1.

Table 7.1 Analytical expressions from the parabolic model and the circular model

Fig. 7.10

a Relative error on the reduced stiffness computed from parabolic model $(\hat{k}_{pm} - \hat{k})/\hat{k}$. b Relative error on the reduced stiffness computed from circular model $(\hat{k}_{cm} - \hat{k})/\hat{k}$. Relative error of analytical models according to the edge angle $\theta$ and the reduced height $\hat{h} = h/r$, in logarithmic scale. This figure was published in [11]. Copyright $\copyright$ 2013 Elsevier Masson SAS. All rights reserved

The relative errors on the parabolic and circular model are shown on Fig. 7.10a and b (computed with (7.8) and equations from Table 7.1), and prove that the circular approximation is more accurate. Special care must be used in the evaluation of the relative error near the region where the stiffness is zero: by definition, any small difference of value produces an error tending to infinity. The error tends to zero when the shape approaches a cylinder. The circular model gives an error below 30 % for form factor $\hat{h}<0.1$.

5 Damping Coefficient

Physically, the damping coefficient is related to any friction effect. In our case, it highlights the effect of the viscosity of the fluid, as given in (7.40). We will assume the surface tension having an negligible impact of the viscous forces: as explained in Sect. 7.3 the spring force is defined by the position of the system, the damping force by its velocity and the inertial effect by its acceleration. For a periodic excitation $h = H\cos (\omega t)$, the maximal displacement is $H$, the maximal velocity is $H \omega$ and the maximal acceleration is $H \omega ^2$. There is necessarily a pulse $\omega > \omega _{c^-}$ (see Chap. 6) for which the pressure inside the meniscus is driven only by viscous effects, vanishing the static effect of the surface tension. In addition, if $\omega < \omega _{c^+}$ the acceleration term can also be neglected, so that the Navier-Stokes equation contains only pressure and viscous terms. The 2D axisymmetric continuity and momentum equations read (full description of these equations are given in Appendix A):

$$\begin{aligned} \frac{1}{r}\frac{\partial (r u_r)}{\partial r} + \frac{\partial u_z}{\partial z}&= 0 \end{aligned}$$

(7.10)

$$\begin{aligned} - \frac{\partial p}{\partial r} + \mu \,\biggl ( \frac{\partial ^2 u_r}{\partial r^2} + \frac{\partial ^2 u_r}{\partial z^2} + \frac{1}{r} \frac{\partial u_r}{\partial r} - \frac{u_r}{r^2} \biggr )&=0\end{aligned}$$

(7.11)

$$\begin{aligned} - \frac{\partial p}{\partial z} + \mu \,\biggl (\frac{\partial ^2 u_z}{\partial r^2} + \frac{\partial ^2 u_z}{\partial z^2} + \frac{1}{r} \frac{\partial u_z}{\partial r} \biggr )&=0 \end{aligned}$$

(7.12)

The considered geometry is a cylinder whose parameters are depicted in Fig. 7.11. The contact angle fixed to $90{^{\circ }}$. Although a velocity field appears in the meniscus, the amplitude is small and we will consider the deformation of the meniscus small enough to be ignored: the geometry is constant.

Fig. 7.11

Geometry and parameters for the analytic model of $b$ and $m$

The force applied by the liquid on the bottom plate is defined by the sum of all the constrains on the plate:

$$\begin{aligned} F\bar{1}_{z}&= \biggl [\,\int \limits _{\varGamma }^{} (-p \mathrm{I }+ {\tau }) \cdot \mathrm{d }\bar{\mathrm{S }}\,\biggr ] \cdot \bar{1}_{z}\end{aligned}$$

(7.13)

$$\begin{aligned}&= \biggl [\,\int \limits _{\varGamma }^{}\Bigl (-p + 2\mu \frac{\partial u_z}{\partial z} \Bigr ) \;\mathrm{d }\mathrm{S }\,\biggr ]\,\bar{1}_{z} \end{aligned}$$

(7.14)

In the complete review of Engmann et al. [5], the authors propose some assumptions on the velocity profile of a film of liquid squeezed by two parallel plates at constant velocity. The vertical velocity field (i.e. the $z$ component) is assumed to be independent on $r$:

$$\begin{aligned} \bar{u}= u_r(t, r, z) \bar{1}_{r}+ u_z(t, z) \bar{1}_{z} \end{aligned}$$

(7.15)

Applying the continuity Eq. (7.10) (in the following, the $^{\prime }$ will refer to the derivative with respect to $z$):

$$\begin{aligned} u_r= -\frac{r}{2} u_z^{\prime }(t, z) \end{aligned}$$

(7.16)

Using (7.11) and (7.12):

$$\begin{aligned} -\frac{\partial p}{\partial r} - \mu \frac{r}{2} u_z^{\prime \prime \prime }(t, z)&= 0 \end{aligned}$$

(7.17)

$$\begin{aligned} -\frac{\partial p}{\partial z} + \mu u_z^{\prime \prime }(t, z)&= 0 \end{aligned}$$

(7.18)

The last equation gives:

$$\begin{aligned} \frac{\partial ^2 p}{\partial r \partial z} = 0 \end{aligned}$$

(7.19)

so that (7.11) becomes finally:

$$\begin{aligned} u_z^{\prime \prime \prime \prime }(t, z)&= 0 \nonumber \\ \Rightarrow \quad u_z(t, z)&= a(t) z^3 + b(t) z^2 + c(t) z + d(t) \end{aligned}$$

(7.20)

We need 4 boundary conditions to determine $a$, $b$, $c$ and $d$. They are provided by the velocity on upper and lower plates:

$$\begin{aligned} u_z(t, -\frac{h}{2})&= 0 \end{aligned}$$

(7.21)

$$\begin{aligned} u_z(t, \frac{h}{2})&= \dot{h}(t) \end{aligned}$$

(7.22)

$$\begin{aligned} u_r(t, r, -\frac{h}{2})&= 0 \quad \Rightarrow \quad u_z^{\prime }(t, -\frac{h}{2}) = 0 \end{aligned}$$

(7.23)

$$\begin{aligned} u_r(t, r, \frac{h}{2})&= 0 \Rightarrow u_z^{\prime }(t, \frac{h}{2}) = 0 \end{aligned}$$

(7.24)

where $\dot{h}(t)$ is the top plate velocity. The full velocity profile is finally given by:

$$\begin{aligned} \bar{u}(t, r, z) = \dot{h}(t) r \biggl (3 \frac{z^2}{h^3} - \frac{3}{4h}\biggr ) \bar{1}_{r}+ \dot{h}(t) \biggl (-2 \frac{z^3}{h^3} + \frac{3}{2} \frac{z}{h} + \frac{1}{2}\biggr ) \bar{1}_{z} \end{aligned}$$

(7.25)

To compute the force, pressure and velocity derivatives are required. The derivatives with respect to $r$ and $z$ are:

$$\begin{aligned} \frac{\partial \bar{u}}{\partial r}&= \dot{h}(t) \biggl (3 \frac{z^2}{h^3} - \frac{3}{4h}\biggr ) \bar{1}_{r}\end{aligned}$$

(7.26)

$$\begin{aligned} \frac{\partial \bar{u}}{\partial z}&= 6 \dot{h}(t) \frac{rz}{h^3} \bar{1}_{r}+ \dot{h}(t) \biggl (-6 \frac{z^2}{h^3} + \frac{3}{2h}\biggr ) \bar{1}_{z}\end{aligned}$$

(7.27)

The pressure is obtained by integrating (7.17):

$$\begin{aligned} p(r, t, z) = 3 \mu \dot{h}(t) \frac{r^2}{h^3} + f(t, z) \end{aligned}$$

With (7.18), $f^{\prime }(t, z)$ is known. Consequently:

$$\begin{aligned} p(r, t, z) = 3 \mu \dot{h}(t) \frac{r^2}{h^3} - 6 \mu \dot{h}(t) \frac{z^2}{h^3} + C(t) \end{aligned}$$

(7.28)

The last constant $C(t)$ (constant with respect to $r$ and $z$) is found thanks to the stress equilibrium at the free interface:

$$\begin{aligned} -p + ({\tau }\cdot \bar{1}_{r}) \cdot \bar{1}_{r}= -p_0 = 0 \end{aligned}$$

(7.29)

This expression is generally not satisfied. Indeed we assumed a particular vertical velocity profile that does not necessarily match with the condition at the interface [5]. However, several hypotheses can be found on the flow to define the constant $C$:

• 1. The total stress at the boundary is averaged and is equal to the outer pressure, giving $C_1$.

• 2. The total pressure at the boundary is averaged and is equal to the outer pressure, giving $C_2$.

• 3. The pressure is balanced at a particular point, that is the bottom triple line $(R, -\frac{h}{2})$ in this case, giving $C_3$.

The first condition leads to:

$$\begin{aligned}&\int \limits _{\varGamma }^{}-p \;\mathrm{d }\mathrm{S }+ \int \limits _{\varGamma }^{} ({\tau }\cdot \bar{1}_{r}) \cdot \bar{1}_{r}\;\mathrm{d }\mathrm{S }= 0 \end{aligned}$$

(7.30)

$$\begin{aligned} \Leftrightarrow&\quad C_1(t) = \mu \dot{h}(t) \Bigl (-3\frac{R^2}{h^3} - \frac{1}{2h} \Bigr ) \end{aligned}$$

(7.31)

With the second assumption, the constant $C_2(t)$ is:

$$\begin{aligned} C_2(t) = \mu \dot{h}(t) \Bigl (-3\frac{R^2}{h^3} + \frac{1}{2h} \Bigr ) \end{aligned}$$

(7.32)

For the third case, the viscous term is null at the triple line (at the top and the bottom plates as well). The balance of the pressure at the triple line is:

$$\begin{aligned}&p(t, R, \pm \frac{h}{2}) = 0 \nonumber \\ \Leftrightarrow&\quad C_3(t) = \mu \dot{h}(t) \Bigl (-3\frac{R^2}{h^3} + \frac{3}{2h} \Bigr ) \end{aligned}$$

(7.33)

If the ratio $R/h >> 1$, then $C_1(t) \approx C_2(t) \approx C_3(t)$ and the three assumptions give identical pressure field. Indeed, the height is small with respect to the radius, and the variation of the pressure due to the interface condition becomes negligible compared to the pressure induced by the friction forces inside the volume. According the boundary condition, at the bottom interface, the pressure is:

$$\begin{aligned} p_1(t, r, -\frac{h}{2})&= -3 \frac{\mu \dot{h}(t)}{h^3} (R^2 - r^2) - 2 \frac{\mu \dot{h}(t)}{h}\end{aligned}$$

(7.34)

$$\begin{aligned} p_2(t, r, -\frac{h}{2})&= -3 \frac{\mu \dot{h}(t)}{h^3} (R^2 - r^2) - \frac{\mu \dot{h}(t)}{h}\end{aligned}$$

(7.35)

$$\begin{aligned} p_3(t, r, -\frac{h}{2})&= -3 \frac{\mu \dot{h}(t)}{h^3} (R^2 - r^2) \end{aligned}$$

(7.36)

The viscous stresses are null on the interface, the force is the integration of the pressure on the bottom pad:

$$\begin{aligned} F_n(t) = \frac{3\pi }{2} \frac{\mu \dot{h}(t) R^4}{h^3} + B_n\pi \frac{\mu \dot{h}(t) R^2}{h} \end{aligned}$$

(7.37)

where $n$ is the case number corresponding to the n$^th$ boundary condition and the constant $B_n$ is defined by:

$$\begin{aligned} B_n = {\left\{ \begin{array}{ll} 2 &{} \text{ for } \text{ the } \text{ zero } \text{ averaged } \text{ stress, } \text{ case } \text{(1) }\\ 1 &{} \text{ for } \text{ the } \text{ zero } \text{ averaged } \text{ pressure, } \text{ case } \text{(2) } \\ 0 &{} \text{ for } \text{ the } \text{ zero } \text{ pointwise } \text{ pressure, } \text{ case } \text{(3) } \end{array}\right. } \end{aligned}$$

(7.38)

The force applied by the liquid is a viscous force. In the Kelvin-Voigt developed applied to this configuration, the force due to the damper is $f_b(t) = b \dot{h}(t)$. The damping coefficient is consequently:

$$\begin{aligned} b_n = \frac{3\pi }{2} \frac{\mu R^4}{h^3} + B_n \pi \frac{\mu R^2}{h} \end{aligned}$$

(7.39)

Here again, when $R / h >> 1$, the last term of (7.39) can be ignored and $b_1 \approx b_2 \approx b_3\approx b$ whatever the boundary conditions:

$$\begin{aligned} b\approx \frac{3\pi }{2}\frac{\mu R^4}{h^3} \end{aligned}$$

(7.40)

6 Inertial Effect

For the last coefficient of the Kelvin-Voigt model, $m$, we will assume the fluid to be governed by its density only. Following the argument developed in the previous section, there is a sufficiently high frequency ($\omega > \omega _{c^+}$) beyond which only inertial term (containing $\omega ^2$) will drive the pressure inside the meniscus. The 2D axisymmetric Navier-Stokes equation will contain only the inertial term and the pressure term. However, the convective term contains $(\bar{u}\cdot \bar{\nabla }) \bar{u}\propto H^2\omega ^2 / h$ while the acceleration term contains $\dot{\bar{u}} \propto H \omega ^2$. For a very small amplitude $H$, the convective term vanishes.

The geometry is identical to the one used to describe the damping coefficient (Fig. 7.11). The 2D axisymmetric continuity and momentum equations read:

$$\begin{aligned} \frac{1}{r}\frac{\partial (r u_r)}{\partial r} + \frac{\partial u_z}{\partial z} = 0 \end{aligned}$$

(7.10)

$$\begin{aligned} \rho \frac{\partial u_r}{\partial t}&= - \frac{\partial p}{\partial r}\end{aligned}$$

(7.41)

$$\begin{aligned} \rho \frac{\partial u_z}{\partial t}&= - \frac{\partial p}{\partial z} \end{aligned}$$

(7.42)

When inertia is important, a laminar flow is characterised by a boundary layer on the wall.² The thickness of the layer tends to zero when the velocity increases, so we will neglect the boundary layer. The reader will note that the thinner the layer is, the stronger the viscous forces are. Fortunately, those viscous forces are tangent to the surface and are not considered in calculus of the force normal to the surface.

Similarly to Sect. 7.5, the vertical velocity field $u_z$ is still assumed to be independent on $r$ (7.15), the mass conservation Eq. (7.10) leads to:

$$\begin{aligned} \bar{u}= -\frac{r}{2} u_z^{\prime }(t, z) \bar{1}_{r}+ u_z(t, z) \bar{1}_{z}\end{aligned}$$

(7.43)

Using (7.41) and (7.42):

$$\begin{aligned} \frac{\partial p}{\partial r} - \rho \frac{r}{2} \dot{u}_z^{\prime }(t, z)&= 0 \end{aligned}$$

(7.44)

$$\begin{aligned} \frac{\partial p}{\partial z} + \rho \dot{u}_z(t, z)&= 0 \end{aligned}$$

(7.45)

The last equation gives:

$$\begin{aligned} \frac{\partial ^2 p}{\partial r \partial z} = 0 \end{aligned}$$

(7.46)

so that (7.41) becomes finally:

$$\begin{aligned}&\dot{u}_z^{\prime \prime }(t, z) = 0 \nonumber \\ \Rightarrow \quad&\dot{u}_z(t, z) = a(t) z + b(t) \end{aligned}$$

(7.47)

We need two boundary conditions, given by the velocity on upper and lower plates. The acceleration of the top plate is fixed by $\ddot{h}(t)$:

$$\begin{aligned} \dot{u}_z\left( t, -\frac{h}{2}\right)&= 0 \end{aligned}$$

(7.48)

$$\begin{aligned} \dot{u}_z\left( t, \frac{h}{2}\right)&= \ddot{h}(t) \end{aligned}$$

(7.49)

The acceleration profile $\dot{\bar{u}}$ then writes:

$$\begin{aligned} \dot{\bar{u}}(t, r, z) = - \frac{r}{2h}\ddot{h}(t) \bar{1}_{r}+ \frac{z}{h}\ddot{h}(t) \bar{1}_{z} \end{aligned}$$

(7.50)

The radial acceleration is constant on cylinder of radius $r$ (surface normal to $\bar{1}_{r}$) and the axial acceleration is constant on plane normal to $\bar{1}_{z}$. The pressure is obtained by integrating (7.44):

$$\begin{aligned} p(t, r, z) = \rho \ddot{h}(t) \frac{r^2}{4h} + f(t, z) \end{aligned}$$

(7.51)

With (7.45), the $f^{\prime }(t, z)$ is known. Consequently:

$$\begin{aligned} p(t, r, z) = \rho \ddot{h}(t) \biggl ( \frac{r^2}{4h} - \frac{z^2}{2h} \biggr ) + C(t) \end{aligned}$$

(7.52)

The last constant $C(t)$ (constant with respect to $r$ and $z$) is found thanks to the stress equilibrium at the free interface:

$$\begin{aligned} -p = -p_{\mathrm{out }} = 0 \end{aligned}$$

(7.53)

As for the damping coefficient, this condition is generally not satisfied (we assumed a particular vertical velocity profile that does not necessarily match with the condition at the interface [5]). The hypotheses to define the constant $C$ are:

• 1. The total pressure at the boundary is averaged and is equal to the outer pressure, giving a constant $C_1$.

• 2. The pressure is balanced at a particular point, that is the bottom triple line $(R, -\frac{h}{2})$ in this case, giving a constant $C_2$.

Constant $C_1$ is:

$$\begin{aligned}&\int \limits _{\varGamma }^{}-p \;\mathrm{d }\mathrm{S }= 0 \nonumber \\ \Leftrightarrow&\quad C_1(t) = -\rho \ddot{h}(t) \biggl ( \frac{R^2}{4h} - \frac{h}{24} \biggr ) \end{aligned}$$

(7.54)

And $C_2$ is:

$$\begin{aligned}&p\left( t, R, -\frac{h}{2}\right) = 0 \nonumber \\ \Leftrightarrow&\quad C_2(t) = -\rho \ddot{h}(t) \biggl ( \frac{R^2}{4h} - \frac{h}{4} \biggr ) \end{aligned}$$

(7.55)

The force at the bottom is computed by considering only the pressure in (7.14). With constants $C_1(t)$ and $C_2(t)$, this reads:

$$\begin{aligned} F_1(t)&= \pi R^2 h \rho \ddot{h}(t) \biggl ( \frac{R^2}{8h^2} - \frac{1}{6} \biggr )\\ F_2(t)&= \pi R^2 h \rho \ddot{h}(t) \biggl ( \frac{R^2}{8h^2} + \frac{1}{8} \biggr ) \end{aligned}$$

If the equivalent mass is subject to the acceleration $\ddot{h}$, from 7.3 and 7.4 we have:

$$\begin{aligned} m_1&= \pi R^2 h \rho \biggl ( \frac{R^2}{8h^2} - \frac{1}{6} \biggr ) \end{aligned}$$

(7.56)

$$\begin{aligned} m_2&= \pi R^2 h \rho \biggl ( \frac{R^2}{8h^2} + \frac{1}{8} \biggr ) \end{aligned}$$

(7.57)

When $R/h>>1$ the stress balance assumptions give converging results towards an equivalent mass $m$ equal to:

$$\begin{aligned} m\approx m_1\approx m_2\approx \frac{\rho \pi R^4}{8h} \end{aligned}$$

(7.58)

7 Case Study and Numeric Validation of the Simplified Kelvin-Voigt Model

The analytical approximations established in Sects. 7.4–7.6 result from the approximated computation of the Navier-Stokes equations. These equations have been reduced considering only the relevant terms in $k$, $b$ or $m$-state, assuming some simplifications:

• The $k$-state characterises the stiffness of the meniscus. The liquid is at rest (velocity is zero), the pressure in the fluid is due to the free interface.

• The $b$-state characterises the friction of the meniscus. The velocity profile assumes the $z$ component to be independent of $r$. The pressure in the fluid is due to the viscous term.

• The $m$-state characterises the inertia of the meniscus. The velocity profile assumes the $z$ component to be independent of $r$. The pressure in the fluid is due to the accelerating term (just the second time-derivative term).

Practically, $k$, $b$ and $m$ can be found with Fig. 7.6, Eqs. (7.40) and (7.58), and henceforth the asymptotic gains defined in (6.8)–(6.18). At a specific pulse $\omega$, the working state is defined by the largest gain $G_k$, $G_b$ or $G_m$.

To go further these analytical approximations—and also to validate them digitally —, the computation of Navier-Stokes equations should be solved completely by numeric computation method like the finite elements method. We have applied this methodology to the case study of a cylindrical liquid bridge whose physical properties $\rho$, $\mu$ and $\gamma$ have been chosen to set the liquid bridge successively in $k$, $b$ and $m$-states.

Fig. 7.12

Evaluation of pressure during $k$-state at $t = {0}\,\mathrm{s}$ and $t = {0.25}\,\mathrm{s}$ (after half a period), at low viscosity ($\mu = {1}\,\mathrm{m\mathrm {Pa}\, \mathrm s}$) and low frequency $f = {1}\,\mathrm{Hz}$. Other parameters are $h = {0.15}\,\mathrm{m\mathrm{m}}$, $R = {0.75}\,\mathrm{m\mathrm{m}}$, $\theta = {90}{^{\circ }}$ and $\gamma = {20}\,\mathrm{m\mathrm N/\mathrm{m}}$. Note The mesh represented is coarser than the mesh used during the numerical computation .a Initial pressure ($t = {0}\,\mathrm{s}$). b Pressure at maximal velocity ($t = {0.25}\,\mathrm{s}$)

Fig. 7.13

Evaluation of velocity and pressure fields during $b$-state at $t = 12.5\,\mathrm{m\mathrm s}$ when the velocity of the top pad reaches a maximum (occurring at a phase shift of $\pi /4$), at high viscosity ($\mu = 1\,\mathrm{{Pa}\, \mathrm s}$) and medium frequency $f = {100}\,\mathrm{Hz}$. Other parameters are $h=0.15\,\mathrm{m\mathrm{m}}$, $R=0.75\,\mathrm{m\mathrm{m}}$, $\theta =90{^{\circ }}$ and $\gamma =20\,\mathrm{m\mathrm N/\mathrm{m}}$. Note The mesh represented is not the one used for computation. a Radial velocity. b Analytical radial velocity. c Vertical velocity. d Analytical vertical velocity. e Pressure field. f Analytical pressure field.

Fig. 7.14

Evaluation of velocity and pressure fields during $m$-state. Evaluation of velocity and pressure fields during $m$-state at $t = {0.15}\,\mathrm{m\mathrm s}$ when the acceleration of the top pad reaches a maximum (occurring at a phase shift of $\pi$), at low viscosity ($\mu = {1}\,\mathrm{m\mathrm {Pa}\, \mathrm s}$) and high frequency $f = {10}\,\mathrm{K\mathrm Hz}$. Other parameters are $h = {0.15}\,\mathrm{m\mathrm{m}}$, $R = {0.75}\,\mathrm{m\mathrm{m}}$, $\theta = {90}{^{\circ }}$ and $\gamma = {20}\,\mathrm{m\mathrm N/\mathrm{m}}$. Note The mesh represented is not the one used for computation. a Radial velocity. b Analytical radial velocity. c Vertical velocity. d Analytical vertical velocity. e Pressure field. f Analytical pressure field.

The comparison between the approximated method and the finite elements solving is provided in the following figures, each of them illustrating one of the three states: $k-$state in Fig. 7.12, $b-$state in Fig. 7.13 and $m-$state in Fig. 7.14.

• $k-$ state: Fig. 7.12 shows the pressure field in the liquid bridge at initial time $t=0\,\mathrm s$ (Fig. 7.12a) and at maximal velocity $t=0.25\,\mathrm s$ (Fig. 7.12b). Particularly, at $r=0$ and $z=0$ the pressure can be digitally measured³ at respectively $p_{t=0\,\mathrm s}=27.40\,\mathrm {Pa}$ and $p_{t=0.25\,\mathrm s}=54.23\,\mathrm {Pa}$ . The pressure difference $26.83\,\mathrm {Pa}=54.23\,\mathrm {Pa}-27.40\,\mathrm {Pa}$ during this time range can be related to the Laplace pressure variation in the meniscus due to the displacement of the top plate. Referring to Table 7.1 to compute the curvature $2H$ and the contact angle derivative $\frac{\mathrm{{d}}\theta }{\mathrm{{d}} h}$ (for both circular or parabolic models ) with $\theta =90^{\circ }$, $\varDelta h = {1}\,{{\upmu }\mathrm{m}}$, $\gamma ={20}\,\mathrm{m\mathrm N/\mathrm{m}}$), the pressure variation inside the meniscus is given by :

  $$\begin{aligned} p({0.25}\,\mathrm{s}) - p({0}\,\mathrm{s})&= {1}\,{{\upmu }\mathrm{m}} \gamma \biggl (\frac{3}{4 R h} - \frac{6 R}{h^3} \biggr ) \\&= {26.53}\,\mathrm{{Pa}} \end{aligned}$$

  which is a rather good estimate of the digital result provided here above. Similarly, the contact angle variation $\varDelta \theta$ has also been estimated digitally at $5.86^{\circ }$ (from the normal of the interface at the lower corner). According to Table 7.1, the contact angle variation is equal to:

  $$\begin{aligned} \varDelta \theta&= - 3 \frac{R}{h^2} {1}{{\upmu }\mathrm{m}} \\&= {5.73}{^{\circ }} \end{aligned}$$

• $b-$ state: Fig. 7.13 provides a comparison between digital and analytical results for the radial velocity field (Figs. 7.13a and b), for the vertical velocity field (Figs. 7.13c and d) and for the pressure field (Figs. 7.13e and f). These comparisons show good agreement for the radial velocity and pressure fields, indicating a good estimate by the analytical models. Concerning the vertical velocity field, it can be seen that the analytical approximation is quite fair on the major part of the domain. At the interface however, the estimation is poor. We could expect this result because when we have developed the damping coefficient, the interface stress equation was not verified. However this disagreement has low impact on the pressure field responsible of the force exerted by the liquid bridge.

• $m-$ state: Fig. 7.14 provides a comparison between digital and analytical results for the radial velocity field (Figs. 7.14a&b), the vertical velocity field (Figs. 7.14c&d) and the pressure field (Figs. 7.14e&f). The radial velocity respects the no-slip condition (appearing clearly at the bottom interface but less at the top interface because of the interpolation technique for colour rendering) and increases to a value independent of $z$. This illustrates the viscous boundary layers. As for the $b$-state, the approximations are poor near the interface because the analytical assumptions do not balance perfectly the stresses at the free interface balance. Finally, the free interface present some oscillation at high frequencies, but the effect of Laplace pressure is weak with respect to inertial effect.

8 Gain Curves

The previous section showed that the approximations are relevant when a particular state occurs. To validate the approximations with respect to frequency, we compared graphically the gain curves computed with (6.8–6.18) and the analytical coefficient with the gain curves obtained from numerical simulations (see Figs. 7.15 and 7.16).

$$\begin{aligned} \log G_k(\omega )&= \log k \end{aligned}$$

(7.59)

$$\begin{aligned} \log G_b(\omega )&= \log \omega + \log b \end{aligned}$$

(7.60)

$$\begin{aligned} \log G_m(\omega )&= 2\log \omega + \log m \end{aligned}$$

(7.61)

The set of parameters used in these comparisons is summarised in Table 7.2.

Fig. 7.15

Comparison of gain curves between numerical simulations and analytical approximations (part 1)

Fig. 7.16

Comparison of gain curves between numerical simulations and analytical approximations (part 2)

The numerical experimental space (made up of all the combinations of the parameters) cover a wide range of Reynold numbers and capillary numbers:

$$\begin{aligned} \mathrm{Re }&= \frac{\rho f h^2}{\mu } \quad {4 \, 10^{-5}}{} \rightarrow 400 \end{aligned}$$

(7.62)

$$\begin{aligned} \mathrm{Ca }&= \frac{\mu f h}{\gamma } {\, 10^{-5}}{} \rightarrow 100 \end{aligned}$$

(7.63)

These values are shown in Fig. 7.17 for each experiment (because Reynolds and capillary numbers do not depend on the contact angle, only $\theta = {90}{^{\circ }}$ have been represented). The states vary according to the frequency. The $m$-state appears when the Reynolds number increases, when the frequency is bigger than $f_{c^+}$ or $f_m$. When the capillary number increases, the $b$-state appears.

Table 7.2 Parameters of the digital simulations. This figure was published in [11]. Copyright $\copyright$ 2013 Elsevier Masson SAS. All rights reserved

Fig. 7.17

Plot of Reynold and Capillary numbers defined in (7.62) and (7.63) for results showed in Figs. 7.15 and 7.16 when frequency increases (only for $\theta = 90{^{\circ }}$, see Table 7.2 for parameters). For a low inertial system, the states change at frequencies $f_{c^-}$, $f_{c^+}$, for a high inertial system, the states change at $f_m$

In addition, we plot the cutting frequencies $f_{c^-}$ (downward triangle) between states $k$ and $b$, $f_{c^+}$ (upward triangle) between states $b$ and $m$, and the resonating frequency (hexagram):

$$\begin{aligned} f_{c^-}&= \frac{\sqrt{b^2 + 4 k m}-b}{4 \pi m} \end{aligned}$$

(7.64)

$$\begin{aligned} f_{c^+}&= \frac{\sqrt{b^2 + 4 k m}+b}{4 \pi m} \end{aligned}$$

(7.65)

$$\begin{aligned} f_r&= \frac{\sqrt{k m - b^2}}{2 \pi m} \approx \frac{1}{2 \pi }\sqrt{\frac{k}{m}} \end{aligned}$$

(7.66)

At these resonance frequencies, the approximations are the less correct because two different oscillating states contribute equivalently to the gain. The assumption made for the different states are not compatible. For example at $f_{c^+}$, the coefficient $b$ supposes the velocity profile to be driven only by viscous effect and the coefficient $m$ assume only inertial effect.

An interesting results may be highlighted between states $b$ and $m$. If we neglect the stiffness $k$ in (7.65), $f_{c^+}$ becomes:

$$\begin{aligned} f_{c^+} = \frac{b}{2 \pi m} \end{aligned}$$

(7.67)

Using the approximations (7.40) and (7.58), this reads:

$$\begin{aligned} f_{c^+} = \frac{1}{2 \pi } \frac{3\pi \mu R^4}{2 h^3} \frac{8h}{\rho \pi R^4} = \frac{6\mu }{\pi \rho h^2} \end{aligned}$$

(7.68)

The Reynolds number (7.62) at $f_{c^+}$ is:

$$\begin{aligned} \mathrm{Re }(f_{c^+}) = \frac{6}{\pi } \end{aligned}$$

(7.69)

This means that the $b$-state exists only for Reynolds number $\mathrm{Re }\,{<}\,\frac{6}{\pi }$, if the system has a low inertia. This results has a physical origin: the Reynolds number is a ratio between inertial effects and viscous effects while the frequency $f_{c^+}$ delimits a viscous state from an inertial state. They are somehow referring to the same phenomena.

9 Experimental Setup

This section presents the experimental setup designed to measure the transfer function of liquid bridges (Sect. 7.9.1), the experimental protocole (Sect. 7.9.2) and a brief description on the applied image processing (Sect. 7.9.3).

9.1 Experimental Bench

The particularity of the bench is the submillimetric size of the system. Size is below mm and force is below mN. The liquid bridges are confined between two circular solids constituting two parallel planes. As indicated in Fig. 7.18a, the bench is made of an actuator driven by an harmonic signal (to move the top of the liquid bridge), an imaging system to characterise the liquid meniscus, a force sensor on bottom of the liquid bridge and two circular pads able to confine the liquid bridge by pinning the triple lines.

Fig. 7.18

a Principle of the experimental test bed; b Force sensor FT-S270. This figure was published in [11]. Copyright $\copyright$ 2013 Elsevier Masson SAS. All rights reserved

The displacement was imposed thanks to a piezo-electric actuator [8, 9]. A commercial Femto-Tools force sensor was used (Fig. 7.18b). The principle of this sensor is a change of capacitance. This technique has two advantages: the sensor is very dynamic due to the absence of mechanical part and the stiffness is high (the value is not given by the constructor). The tip and the capacitor is mounted on a circuit board that integrates chips converting the change of capacitance into an output voltage. Each sensor is provided with its own unique characteristic (the sensitivity may vary from 9 to 1.1 $\mathrm m\mathrm{V}/ {\upmu }\mathrm N$). A major inconvenience is the reduced range of measurable force. These sensors are quite cheap (190 €) but the tips are extremely fragile. The maximum load of this sensor is $2 \, \mathrm m\mathrm N$, with a resolution equal to $0.4\, {\upmu }\mathrm N$ at $30\,\ \mathrm Hz$ and $2\,{\upmu }\mathrm N$ at $1\,\mathrm K\mathrm Hz$. Its stiffness is large enough to neglect the sensor deformation with respect to the gap amplitude imposed on the liquid bridge. The resonance frequency is about $6400 \, \mathrm Hz$, which is much more larger than with the first design. It will however limit our bandwidth.

Fig. 7.19

Measurement principle

This sensor was embedded in a design, whose principle is shown in Fig. 7.19: (1) the non contact displacement sensor LK-G10 points towards the top surface of a mechanical connector, linking the actuator imposing the harmonic displacement (2) to the top pad glued on the bottom of the connector. This harmonic displacement is measured by the signal $u$ of the displacement sensor. The displacement of the top pad is therefore known with a constant offset $u+$constant. The bottom pad (3) is fixed to the tip of the force sensor (4). Since the force sensor is assumed to be stiff enough, the position of the bottom pad is assumed to be a reference. Note well that the gap between both pads is actually not known with a precision better than $25\,\ {\upmu }\mathrm{m}$ the error was $\pm 8$ pixels, and 900 pixels represent 1.5mm. Figure 7.20 shows pictures of the manufactured test bench.

Fig. 7.20

Pictures of the test bed: (1) is the displacement sensor LK-G10, (2) is the piezo actuator imposing the harmonic displacement to the top pad, (3) is the bottom pad, (4) is the FT-S270 sensor and (5) is a lateral camera with optical axis perpendicular to the liquid bridge symmetry axis (vertical on these pictures). This figure was published in [11]. Copyright $\copyright$ 2013 Elsevier Masson SAS. All rights reserved

9.2 Experimental Protocol

Thanks to the data acquisition system, measurements were almost fully automated. For each experiment, the following steps were adopted:

• 1. The circular plates were cleaned with acetone and ethanol;

• 2. A small amount of liquid (around 1 ${\upmu }\mathrm L$) was dropped on the lower plate;

• 3. The upper plate was lowered until the contact with the liquid bridge;

• 4. The lower plate was accurately positioned and aligned thanks to the two cameras;

• 5. The gap was fixed. If the volume needed to be adjusted, the process restarted from step 2;

• 6. Two pictures were taken in order to compute the volume;

• 7. Dynamic parameters (frequency range, delays, amplitude of actuator) were defined;

• 8. A systematic acquisition program in Labview ⁴ was used:

  • a. An output was generated to the piezoelectric driver;

  • b. According to the oil viscosity and the frequency, a delay was inserted to avoid any effect of transient response;

  • c. Data were acquired and recorded in a text file;

• 9. Two pictures were taken to control the state of the meniscus.

The protocol was restarted from step 8 to successively acquire multiple experiments on the same system, from step 7 to get the effect of the amplitude of the actuator, from step 5 to change the gap and from step 1 to change the liquid.

9.3 Image Processing Towards Geometrical Parameters Acquisition

The pictures of the liquid bridges have been taken before and after each experimental sequence, with two cameras with intersecting optical axes, as shown in Fig. 7.21. In these images, the air-liquid interface here contains all necessary information to completely describe the geometry of the liquid bridge: their analysis provided the contact angle, the gap and the meniscus curvature.

10 Results

10.1 Experiments List

Experiments have been led with different liquids whose properties are summarized in Table 7.3.

Fig. 7.21

Example of control pictures taken before and after each experiments. All rights reserved. a Sketch of the pinned liquid bridge. b Picture taken with the camera 1. c Picture taken with camera 2. This figure was published in [11]. Copyright $\copyright$ 2013 Elsevier Masson SAS.

Table 7.3 Main physical properties of liquid used.The value are given for a temperature of ${25}\,{^{\circ }C}$.

An experiments list is also provided in Table 7.4, summarizing the geometrical data.

Table 7.4 Experimental results from both cameras

10.2 Gain and Phase Shift Curves

On each graph shown in Figs. 7.22 and 7.23, the experimental curve and numerical simulations have been superimposed. Four simulations were realised with each geometrical information, as well as a simulation with the average value of the parameters measured. The results are conclusive: indeed, all experimental data points are in between the numerical curves.

However, the variation of the geometric parameters gathered from image analysis produces an important dispersion of the stiffness. The dispersion may be explained for several reasons. First, the positioning error (mainly the tilt in both horizontal directions) gives slightly different profile of the liquid bridge for both cameras. Second, there is a small hysteresis inherent to the piezo actuator. Therefore, the gap and the edge angles may change accordingly. Finally, there is a small amount of liquid that is lost during the experiments, due to flooding outside the pad (in case the pinning was not perfect) or to evaporation.

These geometric errors are less visible on the $b$-state. Indeed, the equivalent damping depends on the volume that is relatively less sensitive to a variation of the free interface. We may see on experiments $11$ and $12$ that for high frequency, the curve goes under the linear asymptote. This is due to the sensor saturation. Consequently, the inertial state could not be observed experimentally because the level of force was too high.

Fig. 7.22

Gain and phase curves for experiments 1–7. The circle represents experimental data, the square the individual parameters and the triangle the mean value of the geometric parameters. Experimental parameters are given in Table 7.4. This figure was published in [11]. Copyright $\copyright$ 2013 Elsevier Masson SAS. All rights reserved

Fig. 7.23

Gain and phase curves for experiments 8–12. The circle represents experimental data, the square the individual parameters and the triangle the mean value of the geometric parameters. Experimental parameters are given in Table 7.4

The spring and anti-spring cases can be observed with the phase curves:

• Experiments 2, 4, 5, 7, 9 are spring cases because the phase starts at ${0}{^{\circ }}$.

• Experiments 1, 3, 8 are anti-springs because the phase starts at ${180}{^{\circ }}$.

• Experiments 10, 11, 12 are purely viscous because the phase starts around ${90}{^{\circ }}$. The $k$-state is observable at frequency lower than 0.1 Hz. Nevertheless, we can guess that experiments 10 is a spring case (the phase is below ${90}{^{\circ }}$) and experiments 12 is an anti-spring case (phase is higher than ${90}{^{\circ }}$).

11 Conclusions

In this chapter we characterised the behaviour of an axisymmetric liquid bridge under small vertical oscillations. The meniscus was modelled using a Kelvin-Voigt model, consisting of a spring, a damper and a mass in parallel. We proposed an abacus for the stiffness, and analytical expressions for the stiffness, the damping and the inertial coefficients.

The validation was provided through numerical simulations and experimental data. The numerical simulations acted as a buffer for results validation: they were first compared with analytical approximations (with a mirror symmetry with respect to the plane containing the neck of the meniscus), and then with experiments.

We showed that it is possible to characterise the meniscus by geometrical and physical parameters of liquids, and without downscaling the system to microscopic dimension. The proposed analytical laws were based on simplifications of the 2D axisymmetric Navier-Stokes equation. They can be used to quickly estimate the order of magnitude of the different parameters $k$, $b$, $m$. The first one involves the knowledge of the free liquid surface while the latter are based on the liquid volume. Consequently, the parameter $k$ is more difficult to evaluate: although it is a good approximation, the experimental values of the edge angle and of the free surface curvature may be rather difficult to estimate.

The results showed excellent agreement between analytical and numerical models, validating the assumptions on the state of the fluid (static flow for spring state, viscous flow for the damping state and inertial flow for the inertial state).

The results showed good agreement between experimental data and numerical simulation, although measurements were difficult to achieve. The present experimental bench did not allow us to inspect the inertial state experimentally since the needed input frequencies are very high and forces generated are too large for the sensor hereby adopted.

The interest of this model lies in the fact that important information can be derived from these coefficients: the step response, the impulse response or any frequential response. For small displacement the differential Eq. (7.4) associated to the system can be easily solved and often gives an analytical solution. For specific input $F(t)$ a numeric integration can be quickly computed. The reader will remind that the coefficients change according to the gap of the meniscus. For large displacement of an interface, the coefficients vary. However, the variation of the coefficients can be included in the numeric integration.

Appendix on Finite Element Method

In this appendix, we explain how we implement the free surface problem with COMSOL MULTIPHYSICS 3.5a. The software proposes built-in models for a large set of applications with predefined equations including Navier-Stokes and moving mesh. Moreover, the software allows to customise these equations to implement complex constraints, like surface tension in our case. Equations (Navier-Stokes and moving mesh) were formulated using the vectorised weak formulation [6].

Note that a general appendix on vectorial operators in provided in Appendix B at the end of this book.

1.1 Model

The geometry used for numeric simulations is depicted in Fig. 7.24. The following boundary conditions apply: the no-slip condition is imposed on the bottom boundary; a sinusoidal normal inflow moving with the mesh on the top boundary; the symmetry condition on the axis of symmetry boundary; the normal stress and the moving mesh on the free boundary. This is summarised in Table 7.5. The motion of the top boundary is downward and oscillate sinusoidally: $z_t(t) = h + A (\cos (2\pi f t) - 1)$. The amplitude $A$ has been set to ${0.5}\,{{\upmu }\mathrm{m}}$, small enough to stay in linear state.

Fig. 7.24

Domain for the numerical model

Table 7.5 Boundary conditions for the numerical model. Appl.

Table 7.6 Simulation parameters used for the comparison of finite element model with analytical expressions and experimental data

The force generated by the liquid bridge on the substrate is divided into the surface tension force and the viscous force [3]:

$$\begin{aligned} \bar{F} = \left[ 2 \pi R \gamma \sin \theta + \int \int \limits _{\varGamma } \left( - p + 2 \mu \frac{\partial v}{\partial z} \right) \mathrm{d }\mathrm{S }\right] \bar{1}_{z} \end{aligned}$$

(7.70)

In the following, we will refer by pressure force the second term, and by the viscous force the third one.

1.2 Mathematical Background

The weak formulation of the partial differential equations system is required to implement the free surface condition as a boundary condition in a fluid flow problem. Basically, the pressure is given by the curvature $2H$ (Table 7.6):

$$\begin{aligned} \varDelta p = 2H = \bar{\nabla }\cdot \bar{1}_{n}\end{aligned}$$

(7.71)

Unfortunately, Comsol is not able to compute the derivative of $\bar{1}_{n}$. In this section, we will present the mathematical development of the conventional $\bar{u}$-$p$ formulation and the stress-divergence form combined. The reader will refer to [4, 6] for further reading. This conventional $\bar{u}$-$p$ formulation exists in different forms, which is a scalar and a vector form. In literature, these forms are very common but the implementation of surface tension effect is rather rare. The implementation of surface tension in scalar form of our $\bar{u}$-$p$ formulation has already been discussed in [13]. The vector form is drawn up here. The vector notation will be used to remain independent of any coordinate system.

The main idea is that if an equation is verified, we can multiply this equation by a test-function and integrate it over the whole domain. Then, we reduce the order of derivative by applying successive integral theorems. The test-function are managed by Comsol. The reader will find further information in [6]. The starting point is the Navier-Stokes and continuity equations:

$$\begin{aligned} \rho \,\biggl ( \frac{\partial \bar{u}}{\partial t} + \bigl ( \bar{u}\cdot \bar{\nabla }\bigr ) \bar{u}\biggr )&= \rho \bar{g}- \bar{\nabla }p + \bar{\nabla }\cdot {\tau }\end{aligned}$$

(7.72)

$$\begin{aligned} \bar{\nabla }\cdot \bar{u}&= 0 \end{aligned}$$

(7.73)

These equations are multiplied at both sides by test functions and integrated on the domain $\varOmega$. The test functions are $\bar{v}$ and $q$:

$$\begin{aligned} \int \int \limits _{\varOmega }{\!\!\!\!}\int \biggl [\,\rho \,\biggl ( \frac{\partial \bar{u}}{\partial t} + \bigl ( \bar{u}\cdot \bar{\nabla }\bigr ) \bar{u}\biggr ) \cdot \bar{v}\,\biggr ] \;\mathrm{d }\mathrm{V }&= \int \int \limits _{\varOmega }{\!\!\!\!}\int \biggl [\,- \bar{\nabla }p \cdot \bar{v}+ \bar{v}\cdot \bigl (\bar{\nabla }{\tau }\bigr ) + \rho \bar{v}\cdot \bar{g}\,\biggr ] \;\mathrm{d }\mathrm{V }\end{aligned}$$

(7.74)

$$\begin{aligned} \int \int \limits _{\varOmega }{\!\!\!\!}\int q\bar{\nabla }\cdot \bar{u}\;\mathrm{d }\mathrm{V }&= 0 \end{aligned}$$

(7.75)

We will start with the Navier-Stokes equation. The purpose is to reduce the order of the derivatives in the integral. Using some divergence identities:

$$\begin{aligned} \bar{v}\cdot \bar{\nabla }p&= \bar{\nabla }\cdot ( p \bar{v}) - p \bar{\nabla }\cdot \bar{v}\end{aligned}$$

(7.76)

$$\begin{aligned} \bar{v}\cdot \bigl ( \bar{\nabla }\cdot {\tau }\bigr )&= \bar{\nabla }\cdot ({\tau }\cdot \bar{v}) - {\tau }: \bar{\nabla }\bar{v}\end{aligned}$$

(7.77)

Reordering by isolating divergence terms, the integral now reads:

$$\begin{aligned} \int \int \limits _{\varOmega }{\!\!\!\!}\int \biggl [\,\rho \,\biggl ( \frac{\partial \bar{u}}{\partial t} + \bigl ( \bar{u}\cdot \bar{\nabla }\bigr ) \bar{u}- \bar{g}\biggr ) \cdot \bar{v}- p \bar{\nabla }\cdot \bar{v}+ {\tau }: \bar{\nabla }\bar{v}\,\biggr ] \;\mathrm{d }\mathrm{V }\end{aligned}$$

(7.78)

$$\begin{aligned} = \int \int \limits _{\varOmega }{\!\!\!\!}\int \biggl [\,- \bar{\nabla }\cdot ( p \bar{v}) + \bar{\nabla }\cdot ({\tau }\cdot \bar{v}) \,\biggr ] \;\mathrm{d }\mathrm{V }\end{aligned}$$

(7.79)

Gauss’ theorem is applied to the right-hand side term to give, with the commutative matrix product:

$$\begin{aligned} \int \int \limits _{\varOmega }{\!\!\!\!}\int \bigl [\,- \bar{\nabla }\cdot ( p \bar{v}) + \bar{\nabla }\cdot ({\tau }\cdot \bar{v}) \,\bigr ] \;\mathrm{d }\mathrm{V }&= \int \limits _{\partial }{\!\!\!\!}\int \limits _{\varOmega } \bigl [\,-( p \bar{v}) + ({\tau }\cdot \bar{v}) \,\bigr ] \cdot \mathrm{d }\bar{\mathrm{S }}\nonumber \\&= \int \limits _{\partial }{\!\!\!\!}\int \limits _{\varOmega } \bigl [\,-( p \bar{1}_{n}) + ({\tau }\cdot \bar{1}_{n}) \,\bigr ] \cdot \bar{v}\;\mathrm{d }\mathrm{S }\nonumber \\&= \int \limits _{\partial }{\!\!\!\!}\int \limits _{\varOmega } \bigl [\,( -p \mathrm{I }+ {\tau }) \cdot \bar{1}_{n}\,\bigr ] \cdot \bar{v}\;\mathrm{d }\mathrm{S }\end{aligned}$$

(7.80)

Hence, the weak form of the Navier-Stokes equation is finally:

$$\begin{aligned}&\int \int \limits _{\varOmega }{\!\!\!\!}\int \biggl [\,\rho \,\biggl ( \frac{\partial \bar{u}}{\partial t} + \bigl ( \bar{u}\cdot \bar{\nabla }\bigr ) \bar{u}- \bar{g}\biggr ) \cdot \bar{v}- p \bar{\nabla }\cdot \bar{v}+ {\tau }: \bar{\nabla }\bar{v}\,\biggr ] \;\mathrm{d }\mathrm{V }\nonumber \\&\quad = \int \limits _{\partial }{\!\!\!\!}\int \limits _{\varOmega } \bigl [\,( -p \mathrm{I }+ {\tau }) \cdot \bar{1}_{n}\,\bigr ] \cdot \bar{v}\;\mathrm{d }\mathrm{S } \end{aligned}$$

The latter term should be divided into as much integrals as boundaries. In the next section, we explicit this latter term according the boundary conditions. The continuity Eq. 7.75 remains as it is.

1.3 Implementing Boundary Conditions

On the boundaries, the Dirichlet conditions applied on a variable must be also applied on the test function associated ($\bar{u}$ with $\bar{v}$ and $p$ with $q$). The boundaries are expressed in the integral ${\fancyscript{I}}$ computed on the boundary concerned (7.81). This integral can be rewritten in a decomposition of normal and tangent components:

$$\begin{aligned} {\fancyscript{I}}&= \int \limits _{\partial }{\!\!\!\!}\int \limits _{\varOmega } \bigl [\,-p + ({\tau }\cdot \bar{1}_{n}) \cdot \bar{1}_{n}\,\bigr ] (\bar{v}\cdot \bar{1}_{n}) \;\mathrm{d }\mathrm{S }+ \int \limits _{\partial }{\!\!\!\!}\int \limits _{\varOmega } \bigl [\,({\tau }\cdot \bar{1}_{n}) \cdot \bar{1}_{t}\,\bigr ] (\bar{v}\cdot \bar{1}_{t}) \;\mathrm{d }\mathrm{S }\end{aligned}$$

(7.81)

$$\begin{aligned}&= {\fancyscript{I}}_n+{\fancyscript{I}}_t \end{aligned}$$

(7.82)

• Inlet/outlet velocity This configuration include the no slip case, according to the value of $\bar{v}^{*}$. When both components are fixed, ${\fancyscript{I}}$ is removed and we have:

  $$\begin{aligned} {\fancyscript{I}} = 0 \Rightarrow \left\{ \begin{array}{cc} \bar{u}&{}= \bar{v}_{\varOmega } + \bar{u}^{*} \\ \bar{v}&{}= \bar{v}_{\varOmega } + \bar{u}^{*} \end{array}\right. \end{aligned}$$

  (7.83)

  The reason is that by defining $\bar{u}$, stresses are automatically define. If we give also a value to the stress, the problem is over-constrained. To clearly understand, let’s suppose that the stresses required to produce a particular velocity profile $\bar{v}_{\varOmega } + \bar{u}^{*}$ at the boundary is $\bar{f}^{*}$. We could use:

  $$\begin{aligned} \fancyscript{I}&= \int \limits _{\partial }{\!\!\!\!}\int \limits _{\varOmega } \bar{f}^{*} \cdot \bar{v}\;\mathrm{d }\mathrm{S }\end{aligned}$$

  (7.84)
  $$\begin{aligned} \bar{v}&= \bar{v}_{\varOmega } + \bar{u}^{*} \end{aligned}$$

  (7.85)

  giving the solution $\bar{u}= \bar{v}_{\varOmega } + \bar{u}^{*}$. A similar formulation is used when using Lagrange multipliers, see [2].

• Viscous slipping We have mixed conditions, on the normal velocity on one hand, and on the tangent component of the normal stress $({\tau }\cdot \bar{1}_{n}) \cdot \bar{1}_{t}$. The same argument as previous boundary condition stands for the normal component of the normal stress. We have thus:

  $$\begin{aligned} {\fancyscript{I}}_t&= \int \limits _{\partial }{\!\!\!\!}\int \limits _{\varOmega } - \mu \frac{\bar{u}- \bar{v}_{\varOmega }}{\beta }\cdot \bar{1}_{t}(\bar{v}\cdot \bar{1}_{t}) \;\mathrm{d }\mathrm{S }\end{aligned}$$

  (7.86)
  $$\begin{aligned} {\fancyscript{I}}_n&= 0 \Rightarrow \left\{ \begin{array}{cc} \bar{u}\cdot \bar{1}_{n}&{}= \bar{v}_{\varOmega }\cdot \bar{1}_{n}\\ \bar{v}\cdot \bar{1}_{n}&{}= \bar{v}_{\varOmega }\cdot \bar{1}_{n}\end{array}\right. \end{aligned}$$

  (7.87)

  This configuration include the total slipping case, by considering $\beta \rightarrow \infty$ (and $\fancyscript{I}_t = 0$).

• Inlet/outlet pressure The viscous stress is zero and the pressure is constrained. The equations are:

  $$\begin{aligned} {\fancyscript{I}}_n&= \int \limits _{\partial }{\!\!\!\!}\int \limits _{\varOmega }-p \bar{v}\cdot \bar{1}_{n}\;\mathrm{d }\mathrm{S }\end{aligned}$$

  (7.88)
  $$\begin{aligned} {\fancyscript{I}}_t&= 0 \end{aligned}$$

  (7.89)
  $$\begin{aligned} p&= p^* \end{aligned}$$

  (7.90)
  $$\begin{aligned} q&= p^* \end{aligned}$$

  (7.91)

• Surface force The integrals read:

  $$\begin{aligned} \fancyscript{I}_n&= \int \limits _{\partial }{\!\!\!\!}\int \limits _{\varOmega } f_n^* \bar{v}\cdot \bar{1}_{n}\;\mathrm{d }\mathrm{S }\end{aligned}$$

  (7.92)
  $$\begin{aligned} \fancyscript{I}_t&= \int \limits _{\partial }{\!\!\!\!}\int \limits _{\varOmega } f_t^* \bar{v}\cdot \bar{1}_{t}\;\mathrm{d }\mathrm{S }\end{aligned}$$

  (7.93)

• Surface tension interface This is a particular case that needs some development because of the curvature, as mentioned previously. Actually, this boundary is the reason that requires the setting of the weak equations. Without loss of generality, we will consider that outer pressure is zero. Since the surface tension is constant, the tangential stresses are zero and therefore, we may write:

  $$\begin{aligned} \fancyscript{I} = \int \limits _{\partial }{\!\!\!\!}\int \limits _{\varOmega } 2H\gamma \bar{1}_{n}\cdot \bar{v}\;\mathrm{d }\mathrm{S }\end{aligned}$$

  (7.94)

  We will use the surface divergence theorem saying that:

  $$\begin{aligned} \int \int \limits _{\varGamma } \bar{\nabla }_{s}\cdot \bar{u} \;\mathrm{d }\mathrm{S }= \int \limits _{\partial \varGamma }^{} \bar{u} \cdot \bar{1}_{m}\;\mathrm{d }\mathrm{l }+ \int \int \limits _{\varGamma } 2H \bar{u} \cdot \bar{1}_{n}\;\mathrm{d }\mathrm{S }\end{aligned}$$

  (7.95)

  The surface integral is

  $$\begin{aligned} \fancyscript{I} = \int \limits _{\partial }{\!\!\!\!}\int \limits _{\varOmega } \gamma \bar{\nabla }_{s}\cdot \bar{v}\;\mathrm{d }\mathrm{S }- \int \limits _{\partial ^2\varOmega }^{} \gamma \bar{v}\cdot \bar{1}_{m}\;\mathrm{d }\mathrm{l } \end{aligned}$$

  (7.96)

  where $\bar{\nabla }_{s}$ is the surface divergence operator and $\bar{1}_{m}$ is the binormal vector, such as $\bar{1}_{t}\times \bar{1}_{n}= \bar{1}_{m}$, in Fig. 7.25. This vector $\bar{1}_{m}$ gives the slope of the surface on the triple line. Therefore it contains the contact angle information. The surface divergent operator may be computed after removing the derivative along the normal direction [13, 14]. Hence

  $$\begin{aligned} \bar{\nabla }_{s}\cdot \bar{u} = \bigl (\mathsf{I } - \bar{1}_{n} \otimes \bar{1}_{n}\bigr ) : \bigl (\bar{\nabla }\bar{u}\bigr ) \end{aligned}$$

  (7.97)

Fig. 7.25

Tangent, normal and binormal vectors. They are orthonormed and $\bar{1}_{t}\times \bar{1}_{n}= \bar{1}_{m}$