Keywords

1 Introduction

Disperse multiphase flows frequently occurs in different chemical, mechanical and thermal processes, for example, gas-particle or gas-droplet flows, coal combustion, pneumatic conveying, and erosion phenomena [1]. In these flows a gaseous continuous phase is seeded with droplets or particle (disperse phase) and in which it is necessary to evaluate the relative motion between them, in order, to evaluate the performance of the system or device. Further, the particle–particle interactions play an important role in determining flow pattern [2].

Several industrial processes, such as mineral processing, petroleum refining, food processing, environmental cleaning and chemical processes, requires particles separation from liquids or gas streams. Thus, different technologies, including fabric filters, scrubber, electrostatic precipitations, air classifiers, cyclone and hydrocyclone separations has been used for liquid–solid, liquid–liquid and gas–solid separations, and air pollution control [3–16].

Drying is one of the oldest and most popular process used in the agricultural products, and food, mineral, polymer, chemical, textile and pharmaceutical products industries.

There are different types of dryers (band, flash, conveyor, drum, fluid-bed, vacuum, rotary, spray and cyclone dryers). They are of diverse sizes, shapes and varieties. Because of particular characteristics of the material to be dried, each group of material is dried in a specific dryer (or class of dryers), in ways batch as continuous operation [17]. The movement of gaseous fluids through of a particle bed is inherent to drying unit operations. In the convective drying, the heated drying air and material (cold and moist) being dried are in an intimate contact continuously. Thus, heat is supplied to material, being responsible to increase the temperature and evaporate moisture of it.

The moisture evaporated at the surface of material (or into the material but that moves to surface) is carried out by fluid (drying air) flowing around of material. Obviously, in a porous particles bed inside the dryer, heat transfer occurs between particles, and between particles and dryer walls. Thus, temperature of the material is changed also because of these thermal effects.

Despite of the importance to study the different types of dryers, herein, special attention is given to more recent one, the cyclonic dryer.

2 Cyclone

2.1 Basic Concepts

Cyclone is simple mechanical equipment with no moving parts, that operates by the action of centrifugal, gravitational and drag forces. A typical schematic diagram of a most commonly used, tangential inlet and reverse flow cyclone is illustrated in Fig. 1.

Fig. 1
figure 1

Schematic diagram of a cyclone geometry and representative nomenclature

Full size image

On the basis of the Fig. 1, the principle of operation is described following. The cyclone works by inducing a strongly swirling turbulent flow which is used to separate phases with different densities (a two-phase system). This two-phase mixture (fluid-particle) entering under pressure in the top of the cylindrical body of the cyclone by one tangential inlet (rectangular or circular) generates a complex three-dimensional swirling motion (spinning motion) within the cyclone, which forces particles (denser phase) toward the outer wall (because of their inertia forces) where they collide, lose momentum, and spiral in the downward direction. Following, the particles are collected in the outlet located at the base of the conical section of the cyclone (underflow). From this separation, gas phase moves upward in the central core and leaves the cyclone through the gas outlet tube at the top, so-called vortex finder (overflow). The vortex finder protrudes within the cyclone body for two reasons: to shield the inner vortex from the high inlet velocity, and to stabilize it [18].

Depending upon of the particle diameter, fine particles (smaller particles) are carried out by gas stream, and leave through the top.

The forces acting on a particle are either fluid dynamic or external-field forces. They include gravity, drag and centrifugal forces, the force resulting from the local velocity gradient of the fluid (the Saffman force), the force resulting from the pressure gradient (Faxen force) and force created by rotation of the particle (Magnus force). Sometimes, magnetic and electrostatic forces, and forces due to high acceleration rate in the fluid or particle (Basset force) may appear too. The Saffman, Magnus and Faxen forces are considered lift forces.

If a particle rotates transverse pressure differences appear on the surface of the particle that has resulted in additional forces (Magnus force or slip-rotation lift). The direction of this force is perpendicular to the plane of the relative velocity and the axis of rotation [19, 20].

According to Blei and Sommerfield [19], the Saffman force (or slip-shear lift) is create by shear gradients in the flow that lead to pressure gradients across the particle surface; it acts in a direction perpendicular to the velocity gradient. When the velocity of the particle is less than that of the gas phase, the Saffman force vector will point towards the axis of the cyclone, whereas it will point to the surface of the wall if the particle velocity is greater than that of the gas phase. This force can be negligible for fine particle and very small particle Reynolds number and/or low shear rates [21, 22].

The Faxen forces appear in nonuniform shear field, especially near the wall. This force is significant in particles of large diameter and high pressure gradients, for example, in shock waves. This force act in a direction perpendicular the plane defined by the relative velocity vector and the shear vector [21].

When the flow (or the particle) is accelerated at a high rate, there is a temporal delay in boundary layer development (transient effect). The Basset forces represent this transient and enhanced viscous drag effect [21]. Besides, the flow within the cyclone leads to a very large number of particle–particle and particle–wall collisions. Thus, interaction forces among the particles and interaction forces between the particles and wall surface of the cyclone occurs too.

According to Brennen et al. [2] and Kleinstreuer [21], interaction particle–particle affect individual particle trajectories and fluid flow between neighboring particles that may result in nonuniform spatial distribution of the particles. The particle–wall interaction may occur by direct impacting, interception, bouncing, rolling, and resuspension. These two-way coupling phenomena may cause particle deformation, particle aggregation or particle fission (break), and to affect particle residence time and collection efficiency of the cyclone. In turbulent flow, particle agglomeration occur, especially for small particle in the size range about 1–10 μm, where Brownian motion and gravitational setting can be negligible compared to turbulence-induced motion, and in higher inlet particle concentration [23, 24]. Additional comments about particles interactions can be found in Oweis et al. [25].

The competitions among the forces cited are responsible by the complex gas–solid flow pattern within the cyclone and the separation efficiency of this device. In general, it is accepted that all the forces can be treated separated, thus, the principle of superposition can be applied to calculate the magnitude of the overall force acting on the particle [19].

From this comprehensive explanation, swirl and turbulence are the two competing mechanisms that affect the separation process. According to Derksen et al. [26] the swirl induces a centrifugal force on the particulate phase which is the driving force behind the separation; turbulence disperses the particulate phase and enhances the probability that particles get caught in the exit stream (gas phase). This complex two-phase system is useful as it promote an intimate contact between the particles and the fluid (gas) and the particles and wall of the cyclone which facilitate, for example, the heat and mass transfer coupling phenomena between them.

Cyclone presents many advantages such as: few maintenance problems, low operating and capital cost, temperature and pressure limitation occurs only by the materials of constructions, it can be designed to handle a wider range of operation conditions, relatively low operating pressure drop, dry collection and disposal, low particle residence time, and requires relative small physical space. The following disadvantages can be cited: inefficiency for collecting smaller particles (<5–10 μm in diameter), when operating with large gas flow rates require multiple-unit or other designs, not suitable for collecting sticky materials that would tend to cling in the interior wall, or other particle types that might tend to agglomerate and clog the exit duct, and require secondary collector to meet emissions control regulations [11, 27–30].

Mainly because of their simple structure, high separation efficiency, low cost and ease of operation, cyclone has been the oldest and most widely used equipment to separate dispersed particles from their carrying gases [8, 18, 23, 24, 26, 29, 31–41] and more recently as modern drying technology (dryer) [2, 5, 10, 11, 15–17, 24, 38, 41–44].

However, due to the extremely complex 3D swirling flows within the cyclone, to understand the separation process is crucial and it is still not completely explained. An understanding of this mechanism is essential to help in the design of the new cyclone more efficiently to operate, mainly with high inlet particle concentrations.

2.2 Selection and Design of Cyclone

Cyclone design consists of selecting an ideal configuration to be used based in particle size, separation efficiency, pressure drop, energy requirement, and cost. There is different configuration of cyclone available in the literature that offers different performance for this device (Fig. 2).

Fig. 2
figure 2

Different cyclone configurations. a Tangential inlet arrangements. b Body arrangements

Full size image

The optimization of cyclone dimensions and configuration is, however, mainly determined by experiment, because the analyses of multiphase flow (particle and gas) are very complex. Besides, numerical calculation has been conducted too, however, by assuming severs hypothesis.

2.3 Collection Efficiency (Separation Performance)

Collection efficiency is one of the most important parameters used in evaluating the performance of a cyclone. Separation efficiency is affected by different parameters such as inlet particle concentration, inlet mixture velocity, cyclone geometry, wall roughness of the cyclone, particle diameter, particle density, particle–particle and particle–wall interactions, and other effects.

There is two ways for specify the ability of a cyclone to separate solid particle from gas stream: cut size and the particle separation efficiency. Thus, many theories have been used to predict the cyclone efficiency, consequently, various theoretical equations to calculate collection efficiency has been reported in the literature [18, 32, 35, 45, 46]. In these theories, the authors each have considered different hypothesis such as: gravitational forces negligible compared to centrifugal forces, gas density negligible compared to particle density, spherical particles, of small size and low relative velocity, relative velocity is purely radial, and radial acceleration and radial velocity of gas negligible.

The particle cut size is defined like the size of the smallest particle that is theoretically separated from the gas stream, and thus, it will be collected. On the other hand, particle collection efficiency is defined as the fraction of the inlet flow rate of solids separated in the cyclone, i.e., ratio of particles collected to particles injected. Since a cyclone usually collects particles with different sizes and shapes, it is common to calculate different efficiencies, each defined for a particular and narrow interval of particle sizes [18, 47].

Imagining indefinitely small intervals, we get a fractional or grade-efficiency of the cyclone \( \eta \left( {\overline{dp} } \right) \) for a particle of size \( \overline{dp} \). Thus if f(\( \overline{dp} \)) is the particle size distribution at the cyclone inlet, we can calculate the overall collection efficiency as follows [18, 47].

$$\eta = \int_{0}^{\infty } {f(\overline{dp})} \eta (\overline{dp})d\,\overline{dp}$$
(1)

The overall collection efficiency can be defined still as the mass of particles removed divided by the mass entering the cyclone per unit time. It can be calculated by integrating the grade-efficiency over the particle size distribution as follows [28]:

$$ \eta = \int_{0}^{1} {\eta_{i} \, df} $$
(2)

where f is the mass fraction of solids less than that size in the feed stream and \( \eta_{i} \) is the grade-efficiency.

Several modeling approaches to determine grade-efficiency \( \eta_{i} \) has been reviewed by Licht [48], Leith and Licht [10], Hashemi [27], Kanaoka et al. [47] and Cortés and Gil [18].

Tan [37] reports a model to predict the fractional efficiency of a cyclone with tangential inlet. For this author, the total efficiency of this cyclone to separate particles with a diameter dp from a gas stream can be calculates as:

$$ \eta = 1\, - \,\exp \left[ { - \pi \left( {\frac{{\rho_{p} d_{p}^{2} V}}{18\mu }} \right)\frac{{(r_{2} \, + \,r_{1} )}}{{r_{2} }}\frac{L}{HW}} \right] $$
(3)

where \( r_{2} \) and \( r_{1} \) are the radiuses of the outer and inner tubes, respectively. The parameters H and W are the height and width of the rectangular inlet, respectively. The effective separation length L correspond to distance from the center of the inlet (\( {H \mathord{\left/ {\vphantom {H 2}} \right. \kern-0pt} 2} \)) to the end of the solid inner tube (the length of the annular chamber), and V is the average gas velocity at the cyclone inlet. ρ p and d p are density and diameter of the particles, respectively, and μ represents the gas viscosity.

When many particles cyclones are in series, the total separation efficiency can be expressed as follows [47]:

$$ \eta \, = \,1\, - \,(1\, - \,\eta_{1} )(1\, - \,\eta_{2} )\, \ldots\, (1\, - \,\eta_{n} ) $$
(4)

where η 1, η 2, …, η n, are the separation cyclone efficiencies of the each cyclone, and n is the number of cyclones.

Figure 3 illustrates a typical curve (no scale) of cyclone separation efficiency as a function of particle diameter.

Fig. 3
figure 3

Typical curve of collection efficiency

Full size image

2.4 Pressure Drop

One of the most important parameters and major criteria used to evaluate the cyclone separation efficiency (cyclone performance) is the pressure drop inside the cyclone. An accurate prediction of cyclone pressure drop is very important because it relates to operating costs [32]. This parameter depends on the gas flow rate, gas temperature, solids loading, cyclone geometry, and particle properties. The total pressure drop over a cyclone consists of a sum of local losses and frictional losses. The following contributions can be cited: losses at the inlet (gas expansion loss), contraction losses at the entrance of the outlet tube (vortex finder) because of the abrupt flow area of the outlet tube, frictional loss in the double vortex within the separation space due to swirling (friction between the gas flow and the cyclone wall), and dissipation loss of the gas in the outlet. Among them, the expansion losses are of minor importance and the losses in the vortex finder present the largest results and represents about 80 % of the total pressure drop [18, 31, 32]. According to Hashemi [27], for a given feed flow rate, the pressure drop in spiral cyclones is lower than the pressure drop in tangential cyclones.

In general, the pressure drop over a cyclone is calculated by the difference of static pressure between the inlet pipe and outlet pipe at a given condition. For instance, the static pressure distribution at the inlet cross-section is uniform (no swirling motion), however, in the outlet pipe, this parameter is very different from its cross-sectional average due to the strong swirling flow. Thus, the dynamic pressure stored in the swirling motion may be significant [31].

In the tentative to help researcher and engineer, several empirical, theoretical and semi-theoretical formulaes to calculate the pressure drop in a cyclone has been reported in the literature [17, 18, 27, 28, 31, 32, 49].

Most of these correlations focus on solid-free flow (clean gas). However, pressure drop decrease as the solid concentration increases [27, 28], but different behavior are detailed by Yang et al. [40]. According to the author, researches with solid loading are rather limited.

The calculations of pressure drop in a cyclone are required so that system power consumption can be estimated and also, in order, to select an adequate exhaust air fan.

According to Jumah and Mujumdar [28], cyclones are commercially in sizes to process 50–50,000 m3/h. When pressure drop range 0.5–1.0 kPa cyclone is considered of low-efficiency and for high-efficiency a range 2.0–2.5 kPa is expected. Gimbun et al. [32] reports that higher inlet velocities give higher collection efficiencies for a given cyclone, but this also increase the pressure drop across the cyclone. Thus, combination of higher collection efficiency and low pressure drop is the goal, for a cyclone.

Besides, inlet velocities higher than 30 m/s cause turbulence which, in turn, leads to by passing and re-entrainment of separated particles and hence a decrease in efficiency [17]. Generally, the cyclone pressure drop is proportional to the velocity head as follows:

$$ \Updelta P = \alpha \frac{{\rho_{g} V^{2} }}{2} $$
(5)

where ρ g is gas density, and α and V are the pressure drop coefficient and the inlet velocity of the cyclone, respectively.

Dimensionless pressure drop coefficient α is also called the Euler number, being dependent of the solid loading and properties, and cyclone geometry [18, 24, 26, 27, 31, 32, 36, 40, 49].

3 Cyclone Dryer: Heat and Mass Transfer and Multiphase Flow Theory

3.1 Background

Fundamentally, drying consists in a simultaneous heat and mass transfer phenomenon coupled with dimensions variations of the particle being dried. An appropriated dryer selection is related to drying cost, heat supply, energy saving, type and product quality, and an others important parameters [17, 42, 50, 51]. Strumillo and Kudra [51] reported different forms to classify dryers. One of them is based on hydrodynamic regime (active and no-active regime). Based on this classification, cyclone can be classified as dispersion dryer with active hydrodynamic regime (flowing stream).

For material with high sensitivity to heat both higher drying rate and lower residence time are the most essential drying parameters, in order, to reduce drying cost and to obtain the required final moisture content and high product quality of the dried material. In this sense, cyclone as dryer appears like an appropriated modern drying technology for provides drying of these disperse materials. Unfortunately, drying of moist particulate materials in cyclone has been little studied in the past and there are few reports available in the open access literature. Table 1 summarizes some different theoretical and experimental researches reported in the literature about cyclone as dryer.

Table 1 Different works that have used cyclone as dryer
Full size table

From a review of literature, we verify that different parameters affect performance of the cyclone dryer and particle residence time, for example, cyclone geometry [52–55]. The cyclone dryer provides solid residence times from few seconds up to several minutes, thus facilitating drying operation and moisture removal. This device has been usually employed as a stand-alone-dryer and combined with other drying system, for example, pneumatic dryer. In the combined mode, the cyclone operates as cyclone separated [43, 56–61].

Early works confirmed that gas velocity, particle density, particles diameter, increase particle residence time, whereas it decreased for an increased solid–gas loading [53–55, 59]. On the other hand, Silva and Nebra [62] has considered particle shrinkage effect together heat and mass transfer and fluid flow within the cyclone dryer. According to these authors to consider shrinkage effect on the mathematical modeling provides poor results.

Besides, from analysis of the theoretical and experimental results published by the authors cited before, we verify that greatest variation in temperature and velocity takes place into the cyclone, specially, near the cyclone wall where high particles concentration is found and thus, heat transfer and friction effects are occurring more strongly.

Because of a lack of understanding of the highly complex flow patterns within the cyclone dryer and few data related in the literature, it has been designed using data correlation based on experience from existing installation and pilot plant tests.

Mathematical modeling and numerical prediction of the drying process by using cyclone dryer is a difficult task. Numerical analysis of drying process requires rigorous multiple and coupled nonlinear conservation and constitutive equation solutions. This is not a trivial mathematical problem to solve easily.

In present day, computational fluid dynamics (CFD) have now created to possibility of new related and accurate studies for these flows, including coupled heat and mass transfer, three-dimensional effects, swirl and rotation, given great improvements in modeling and in understanding of physical phenomena [53, 54, 57, 58, 63].

Now that we have discussed about drying of moist particulate material in cyclone dryer, the next step is to address discussion about modeling and simulation applied to drying process by using this drying equipment on an overall basis (macroscopic scale).

3.2 Mathematical Modeling for Multiphase Flow

For the study of multiphase systems, a distinction is usually made between systems of separated streams and dispersed flows. This distinction is a result of the required computational approach. We can distinguish the following computational strategies: Eulerian–Lagrangian approach and Eulerian–Eulerian approach. The first one is applied to very dilute flows where small discrete particles are considered in the control volume formulating the governing microscopic model equations. The second one is useful for dense flows where a relatively large number of particles are considered determining a continuous phase in the control volume formulating the governing microscopic model equations [64, 65].

According to Renade [64] in the Eulerian–Lagrangian approach the explicit motion of the interface is not modeled, which means small-scale fluid motions surrounding the particles are not considered. In this case, the continuous phase is treated as a continuum by solving the momentum equations, while the dispersed phase is solved by tracking each individual particle (solid, bubble, or droplet) using Newtonian equations of motion. In the Eulerian–Lagrangian approach, particle-level process such as reaction, heat and mass transfer, water evaporation and drying can be simulated with adequate detail. Moreover, this approach has some disadvantages, such as: Turbulent flow is necessary to use a large number of particle trajectories to obtain meaningful average which requires greater computational effort, thus limiting the volume fraction of the dispersed phase in the multiphase flow [64].

In the particular case of gas-particle flow in a cyclone dryer, which it is generally dominated by a dispersed flow, we can use the Eulerian–Lagrangian approach. In this approach, the trajectories of particles are obtained by solving an equation of motion for each particle, while the behavior of the continuous phase is modeled using the conservation equations of motion conventional. The behavior of the continuous phase is affected by motion of particles due to the viscous drag and other effects related to velocity difference between the particles and fluid. The viscous effect of the fluid tends to slow the movement of the particles.

The governing equations generally employed in the Eulerian–Lagrangian approach following are presented.

3.2.1 Continuous Phase

The liquid or gas phase is solved with the standard mass and momentum transport equations written as follows:

3.2.1.1 Conservation of Mass
$$ \frac{\partial \rho }{{\partial {\kern 1pt} t}}\, + \,\nabla \cdot (\rho {\kern 1pt} \vec{V}) = 0 $$
(6)

where ρ is the fluid density, \( \vec{V} \) is the velocity vector and t is the time.

3.2.1.2 Conservation of Momentum
$$ \frac{{\partial \left( {\rho {\kern 1pt} \vec{V}} \right)}}{{\partial {\kern 1pt} t}}\, + \,\nabla \cdot (\rho \,{\kern 1pt} \vec{V} \otimes {\kern 1pt} \vec{V}) = - \nabla P\, + \,\nabla \cdot \tau \, + \,S_{M} $$
(7)

where P is the pressure, S M is the momentum source and τ is the shear stress defined as:

$$ \tau = \mu \left[ {\nabla \vec{V}\, + \,\left( {\nabla \vec{V}} \right)^{T} \, - \,\frac{2}{3}\delta {\kern 1pt} \nabla \cdot \vec{V}} \right] $$
(8)

where μ is the dynamic viscosity, δ is Kronecker Delta function.

In the Eq. (7), the dyadic operator (or tensor product) of two vectors \( \vec{V} \) and \( \vec{V}^{\prime} \) is given by:

$$ \vec{V} \otimes {\kern 1pt} \vec{V}^{\prime} = \left[{\begin{array}{*{20}c} {V_{x} V_{x}^{\prime}} & {V_{x}V_{y}^{\prime} } & {V_{x} V_{z}^{\prime} } \\ {V_{y}V_{x}^{\prime} } & {V_{y} V_{y}^{\prime} } & {V_{y} V_{z}^{\prime} } \\{V_{z} V_{x}^{\prime} } & {V_{z} V_{y}^{\prime} } & {V_{z} V_{z}^{\prime} } \\\end{array} } \right] $$
(9)

and the term \( \nabla \cdot (\rho \,{\kern 1pt} \vec{V} \otimes {\kern 1pt} \vec{V}) \) can be obtained by:

$$ \nabla \cdot (\rho \,{\kern 1pt} \vec{V} \otimes {\kern 1pt} \vec{V}) = \left[ {\begin{array}{*{20}c} {\frac{\partial }{\partial x}\left( {\rho \vec{V}_{x} \vec{V}_{x} } \right)\, + \,\frac{\partial }{\partial y}\left( {\rho \vec{V}_{y} \vec{V}_{x} } \right)\, + \,\frac{\partial }{\partial z}\left( {\rho \vec{V}_{z} \vec{V}_{x} } \right)} \\ {\frac{\partial }{\partial x}\left( {\rho \vec{V}_{x} \vec{V}_{y} } \right)\, + \,\frac{\partial }{\partial y}\left( {\rho \vec{V}_{y} \vec{V}_{y} } \right)\, + \,\frac{\partial }{\partial z}\left( {\rho \vec{V}_{z} \vec{V}_{y} } \right)} \\ {\frac{\partial }{\partial x}\left( {\rho \vec{V}_{x} \vec{V}_{z} } \right)\, + \,\frac{\partial }{\partial y}\left( {\rho \vec{V}_{y} \vec{V}_{z} } \right)\, + \,\frac{\partial }{\partial z}\left( {\rho \vec{V}_{z} \vec{V}_{z} } \right)} \\ \end{array} } \right] $$
(10)

For an incompressible flow (i.e. low Mach number) the dilatation term on the right-hand side of Eq. (8) is neglected so that

$$ \frac{{\partial \left( {\rho {\kern 1pt} \vec{V}} \right)}}{{\partial {\kern 1pt} t}}\, + \,\nabla \cdot (\rho \,\vec{V} \otimes {\kern 1pt} \vec{V}) = - \nabla P\, + \,\nabla \cdot \left\{ {\mu \left[ {\nabla \vec{V}\, + \,\left( {\nabla \vec{V}} \right)^{T} } \right]} \right\}\, + \,S_{M} $$
(11)

In principle, Eqs. (6, 7 and 11) can be applied to describe the laminar and turbulent flows without additional information. However, according Bogdanović et al. [66], “turbulent flows at realistic Reynolds numbers span a large range of turbulent length and time scales, and would generally involve length scales much smaller than the smallest finite volume mesh, which can be practically used in a numerical analysis”. In this sense, several turbulence models have been developed to account these effects without recourse to a prohibitively fine mesh and direct numerical simulation.

3.2.1.3 Turbulent Models

Inserting the instantaneous variables into a mean value and a fluctuating value (\( \vec{V}\, = \,\vec{\varvec{U}}\, + \,\vec{u}\;\;\;{\text{and}}\;\;\;P\, = \,\varvec{P}\, + \,p \)) we obtain the time averaged continuity equation and Reynolds Averaged Navier–Stokes (RANS) equations as follows:

$$ \frac{\partial \rho }{{\partial {\kern 1pt} t}}\, + \,\nabla \cdot (\rho {\kern 1pt} \vec{\varvec{U}}) = 0 $$
(12)
$$ \frac{{\partial \left( {\rho {\kern 1pt} \vec{\varvec{U}}} \right)}}{{\partial {\kern 1pt} t}}\, + \,\nabla \cdot (\rho \,\vec{\varvec{U}} \otimes {\kern 1pt} \vec{\varvec{U}})\, = \, - \nabla \varvec{P}\,\varvec{ + }\,\nabla \cdot \left\{ {\mu \left[ {\nabla \vec{\varvec{U}}\, + \,\left( {\nabla \vec{\varvec{U}}} \right)^{T} \, - \,\rho \overline{{\vec{u}\vec{u}}} } \right]} \right\}\, + \,S_{M} $$
(13)

where the term \( \overline{{\vec{u}\vec{u}}} \) that appears on the right-hand side of Eq. (13) is called the Reynolds stress tensor. In this case, we need a model for \( \overline{{\vec{u}\vec{u}}} \) to close the Eq. (13).

However, the averaging procedure introduces additional unknown terms (called turbulent or Reynolds stresses) containing products of the fluctuating quantities. These terms act like additional stresses in the fluid and are difficult to be determined directly. According to Davidson [67] different levels of approximation to achieve this model can be cited:

  1. a.

    Algebraic models. These simplest turbulence models also referred to as zero equation models use a turbulent viscosity (eddy viscosity) approach to calculate the Reynolds stress.

  2. b.

    One-equation models. A transport equation is solved for the turbulent kinetic energy and the unknown turbulent length scale must be given. Generally an algebraic expression is used to obtain this turbulent length scale.

  3. c.

    Two-equation models. These models provide independent transport equations for both the turbulence length scale, or some equivalent parameter, and the turbulent kinetic energy. Here two transport equations are derived which describe transport of two scalars. Then, the Reynolds stress tensor is solved using an assumption which relates the Reynolds stress tensor to an eddy viscosity and the velocity gradients.

  4. d.

    Reynolds stress models. In these models, one transport equation must be added for determining the length scale of the turbulence.

The models of turbulence associated with the RANS equations like Standard k-ε model, Zero Equation model, RSM model—(Reynolds Stress Model), RNG k-ε model (Re-normalized Group Model), NKE k-ε model (New k-ε Model due to Shih), GIR k-ε model (Model due to Girimaji), SZL k-ε model (Shi, Zhu, Lumley Model), Standard k-ω model and SST model (Shear Stress Transport Model) have been widely used in engineering and scientific research works. The choice of which turbulence model we must use is not a trivial matter. This chapter will first focus on the some turbulence models.

In the two-equation turbulence models the turbulence velocity scale is computed from the turbulent kinetic energy, which is provided from the solution of the transport equation. The turbulent length scale is estimated from two properties of the turbulence field, usually the turbulent kinetic energy and its dissipation rate. The dissipation rate of the turbulent kinetic energy is provided from the solution of the transport equation.

Two-equation model introduces two new variables into the system of equations. Thus, the continuity equation assumes the forms:

$$ \frac{\partial \rho }{{\partial {\kern 1pt} t}}\, + \,\nabla \cdot (\rho {\kern 1pt} \vec{\varvec{U}}) = 0 $$
(14)
$$ \frac{{\partial \left( {\rho {\kern 1pt} \vec{\varvec{U}}} \right)}}{{\partial {\kern 1pt} t}}\, + \,\nabla \cdot (\rho \,\vec{\varvec{U}} \otimes {\kern 1pt} \vec{\varvec{U}})\, = \, - \nabla \varvec{P}\,\varvec{ + }\,\nabla \cdot \left\{ {\mu_{ef} \left[ {\nabla \vec{\varvec{U}}\, + \,\left( {\nabla \vec{\varvec{U}}} \right)^{T} } \right]} \right\}\, + \,S_{M} $$
(15)

where μ ef is the effective viscosity (dynamic viscosity plus turbulent viscosity), P is the modified pressure as defined by:

$$ \varvec{P} = P\, + \,\frac{2}{3}\rho k\, + \,\frac{2}{3}\mu_{t} \nabla \cdot \vec{\varvec{U}} $$
(16)

From the two-equation turbulence model we can cite the following models:

3.2.1.3.1 k-ε Model

The k-ε model is based on the eddy viscosity concept, so that:

$$ \mu_{ef} = \mu \, + \,\mu_{t} $$
(17)

where μ t is the turbulence viscosity. The k-ε model assumes that the turbulence viscosity is linked to the turbulence kinetic energy and dissipation based on the relationship:

$$ \mu_{t} = c_{\mu } \rho \frac{{k^{2} }}{\varepsilon } $$
(18)

where c μ is a constant.

The values of k and ε come directly from the differential transport equations for the turbulence kinetic energy and turbulence dissipation rate as follows:

$$ \frac{{\partial \left( {\rho {\kern 1pt} k} \right)}}{{\partial {\kern 1pt} t}}\, + \,\nabla \cdot (\rho \,\vec{\varvec{U}}k) = \nabla \cdot \left[ {\left( {\mu \, + \,\frac{{\mu_{t} }}{{\sigma_{k} }}} \right)\nabla k} \right]\, + \,p_{k} \, - \,\rho \varepsilon $$
(19)
$$ \frac{{\partial \left( {\rho {\kern 1pt} \varepsilon } \right)}}{{\partial {\kern 1pt} t}}\, + \,\nabla \cdot (\rho \,\vec{\varvec{U}}\varepsilon ) = \nabla \cdot \left[ {\left( {\mu \, + \,\frac{{\mu_{t} }}{{\sigma_{\varepsilon } }}} \right)\nabla \varepsilon } \right]\, + \,\frac{\varepsilon }{k}\left( {C_{\varepsilon 1} p_{k} \, - \,C_{\varepsilon 2} \rho \varepsilon } \right) $$
(20)

where C ε1 , C ε2 , σ ε , and σ k are constants (1.44, 1.92, 1.3 and 2.0, respectively), \( p_{k} \) is the turbulence production due to viscous and buoyancy forces, defined by:

$$ p_{k} = \mu_{t} \nabla \vec{\varvec{U}} \cdot \left( {\nabla \vec{\varvec{U}}\, + \,\nabla \vec{\varvec{U}}^{T} } \right)\, - \,\frac{2}{3}\nabla \cdot \vec{\varvec{U}}\left( {3\mu_{t} \nabla \cdot \vec{\varvec{U}}\,\varvec{ + }\,\rho k} \right)\, + \,p_{kb} $$
(21)

The first term that appears on the left-hand side represents the rate of change of turbulent kinetic energy and the second the convective transport. On the right-hand side, we have diffusive transport, rate of production and rate of destruction, respectively.

For incompressible flow, \( \nabla \cdot \vec{\varvec{U}} \) is small and the second term on the right-hand side of Eq. (21) does not contribute significantly to the production. If the full buoyancy model is being used, the buoyancy production term \( p_{kb} \) is modeled as:

$$ p_{kb} = - \frac{{\mu_{t} }}{{\rho \sigma_{\rho } }}\vec{g} \cdot \nabla \rho $$
(22)

If the Boussinesq buoyancy model is being used we can write:

$$ p_{kb} = - \frac{{\mu_{t} }}{{\rho \sigma_{\rho } }}\rho \beta \vec{g} \cdot \nabla T $$
(23)

where β is the coefficient of thermal expansion.

3.2.1.3.2 RNG k-ε Model

In this turbulent model, the transport equations for turbulence generation and dissipation are the same as those for the standard k-ε model, but the model constants are different. Then, we can write:

$$ \frac{{\partial \left( {\rho {\kern 1pt} k} \right)}}{{\partial {\kern 1pt} t}}\, + \,\nabla \cdot (\rho \,\vec{\varvec{U}}k) = \nabla \cdot \left[ {\left( {\mu \, + \,\frac{{\mu_{t} }}{{\sigma_{k}^{*} }}} \right)\nabla k} \right]\, + \,p_{k} \, - \,\rho \varepsilon $$
(24)
$$ \frac{{\partial \left( {\rho {\kern 1pt} \varepsilon } \right)}}{{\partial {\kern 1pt} t}}\, + \,\nabla \cdot (\rho \,\vec{\varvec{U}}\varepsilon ) = \nabla \cdot \left[ {\left( {\mu \, + \,\frac{{\mu_{t} }}{{\sigma_{\varepsilon }^{*} }}} \right)\nabla \varepsilon } \right]\, + \,\frac{\varepsilon }{k}\left( {C_{\varepsilon 1}^{*} p_{k} \, - \,C_{\varepsilon 2}^{*} \rho \varepsilon } \right) $$
(25)

where:

$$ C_{\varepsilon 1}^{ * } = 1.42 - \frac{{\eta \left( {1\, - \,\frac{\eta }{4.38}} \right)}}{{\left( {1\, + \,\beta^{\prime} \eta^{3} } \right)}} $$
(26)

being \( \sigma_{k}^{*} \), \( \sigma_{\varepsilon }^{*} \), \( \beta^{\prime} \) and \( C_{\varepsilon 2}^{*} \) are constants (0.7179, 0.7179, 0.012 and 1.68, respectively), and

$$ \eta = \sqrt {\frac{{p_{k} }}{{\rho \varepsilon C_{\mu }^{\prime} }}} $$
(27)
3.2.1.3.3 Reynolds Stress Models

The Boussinesq assumption is not used in the Reynolds stress models. In this case, a partial differential equation for the stress tensor is derived from the Navier–Stokes equation. These models do not use the eddy viscosity hypothesis, but solve an equation for the transport of Reynolds stresses in the fluid.

The Reynolds averaged momentum equations for the mean velocity are given by Eq. (13) rewrite as follows:

$$ \frac{{\partial \left( {\rho {\kern 1pt} \vec{\varvec{U}}} \right)}}{{\partial {\kern 1pt} t}}\, + \,\nabla \cdot (\rho \,\vec{\varvec{U}} \otimes {\kern 1pt} \vec{\varvec{U}}) = - \nabla \varvec{P}\, + \,\nabla \cdot \left\{ {\mu \left[ {\nabla \vec{\varvec{U}}\, + \,\left( {\nabla \vec{\varvec{U}}} \right)^{T} \, - \,\rho \overline{{\vec{u}\vec{u}}} } \right]} \right\}\, + \,S_{M} $$
(28)

where P is a modified pressure define by

$$ \varvec{P} = P\, + \,\nabla \cdot \vec{\varvec{U}}\left( {\frac{2}{3}\mu \, - \,\xi } \right) $$
(29)

where ξ is the bulk viscosity.

In the differential stress model, \( \overline{{\vec{u}\vec{u}}} \) is made to satisfy a transport equation. A separate transport equation must be solved for each of the six Reynolds stress components of \( \rho \overline{{\vec{u}\vec{u}}} \). The differential Reynolds stress transport equation is:

$$ \frac{{\partial \left( {\rho {\kern 1pt} \overline{uu} } \right)}}{{\partial {\kern 1pt} t}}\, + \,\nabla \cdot (\vec{\varvec{U}}\rho \,\overline{{u_{i} u_{j} }} {\kern 1pt} )\, - \,\nabla \cdot \left[ {\left( {\mu \, + \,\frac{2}{3}\rho C\frac{{k^{2} }}{\varepsilon }} \right)\nabla \overline{{u_{i} u_{j} }} } \right] = p_{R} \, - \,\frac{2}{3}\delta \rho \varepsilon \, + \,G\, + \,\phi $$
(30)

where \( p_{R} \) is shear turbulence production and \( G \) is the buoyancy turbulence production, \( \phi \) is the pressure-strain correlation, and C is a constant.

The production term \( p_{R} \) is given by

$$ p_{R} = - \rho \,\left[ {\overline{{\vec{u}\vec{u}}} \left( {\nabla \vec{\varvec{U}}} \right)^{T}\,+\,\overline{{\vec{u}\vec{u}}} \left( {\nabla \vec{\varvec{U}}} \right)} \right] $$
(31)

As the turbulence dissipation appears in the individual stress equations, an equation for ε is still required. This one now has the form:

$$ \frac{{\partial \left( {\rho {\kern 1pt} \varepsilon } \right)}}{{\partial {\kern 1pt} t}}\, + \,\nabla \cdot (\rho \,\vec{\varvec{U}}\varepsilon ) = \nabla \cdot \left[ {\left( {\mu \, + \,\frac{{\mu_{t} }}{{\sigma_{\varepsilon } }}} \right)\nabla \varepsilon } \right]\, + \,\frac{\varepsilon }{k}\left( {C_{\varepsilon 1} p_{R} \, - \,C_{\varepsilon 2} \rho \varepsilon } \right) $$
(32)

where C ε1 , C ε2 , σ ε , and σ k are constants (1.44, 1.92, 1.3 and 2.0, respectively).

The pressure-strain correlations can be expressed in the general form:

$$ \phi = \phi_{1} \,+\, \phi_{2} $$
(33)

where:

$$ \phi_{1} = - \rho \varepsilon \left[ {C_{s1} \vec{a}\, + \,C_{s2} \left( {\vec{a}\vec{a}\, - \,\frac{1}{3}\vec{a} \cdot \vec{a}\delta } \right)} \right] $$
(34)
$$ \begin{aligned} \phi_{2} = -& C_{r1} p_{R} \vec{a}\, + \,C_{r2} \rho k\vec{S}\, - \,C_{r3} \rho k\vec{S}\sqrt {\vec{a} \cdot \vec{a}} \\ + & C_{r4} \rho k\left( {\vec{a}\vec{S}^{T} \, + \,\vec{S}\vec{a}^{T} \, - \,\frac{2}{3}\vec{a} \cdot \vec{S}\delta } \right)\, + \,C_{r5} \rho k\left( {\vec{a}\vec{W}^{T} \, + \,\vec{W}\vec{a}^{T} } \right) \\ \end{aligned} $$
(35)

with the anisotropy tensor \( \vec{a} \) given by:

$$ \vec{a} = \frac{{\overline{{\vec{u} \otimes \vec{u}}} }}{k}\, - \,\frac{2}{3}\delta $$
(36)

In the Eq. (35), the strain rate \( \vec{S} \) is given as follows:

$$ \vec{S} = \frac{1}{2}\left[ {\nabla \vec{\varvec{U}}\,\varvec{ + }\,\left( {\nabla \vec{\varvec{U}}} \right)^{T} } \right] $$
(37)

and the vorticity \( \vec{W} \) is given by:

$$ \vec{W} = \frac{1}{2}\left[ {\nabla \vec{\varvec{U}}\,\varvec{ - }\,\left( {\nabla \vec{\varvec{U}}} \right)^{T} } \right] $$
(38)

There are three varieties of the standard Reynolds stress models available. These are known as LRR-IP, LRR-QI (Launder, Reece and Rodi) and SSG (Speziale, Sarkar and Gatski). Each model has different model constants and are shown in the Table 2.

Table 2 Different constants for the Reynolds stress models
Full size table
3.2.1.4 Total Energy Equation
$$ \frac{{\partial \left( {\rho {\kern 1pt} h_{tot} } \right)}}{{\partial {\kern 1pt} t}}\, - \,\frac{\partial p}{\partial t}\, + \,\nabla \cdot (\rho \,\vec{\varvec{U}}h_{tot} ) = \nabla \cdot \left( {\lambda \nabla T} \right)\, + \,\nabla \cdot \left( {\vec{\varvec{U}} \cdot \tau } \right)\, + \,\vec{\varvec{U}} \cdot S_{M} \, + \,S_{E} $$
(39)

where T is the temperature, h tot is the total enthalpy, related to the static enthalpy by:

$$ h_{tot} = h\, + \,\frac{1}{2}\vec{\varvec{U}} $$
(40)

The term \( \nabla \cdot \left( {\vec{\varvec{U}} \cdot \tau } \right) \) represents the work due to viscous stresses and is called the viscous work term. The term \( \vec{\varvec{U}} \cdot S_{M} \) represents the work due to external momentum sources and is currently neglected.

3.2.1.5 Multicomponent Equation

The transport equations for the mass fractions of components A in a multicomponent flow is given by:

$$ \frac{{\partial \left( {\rho {\kern 1pt} Y_{A} } \right)}}{{\partial {\kern 1pt} t}}\, + \,\nabla \cdot (\rho \,\vec{\varvec{U}}Y_{A} ) = \nabla \cdot \left[ {\rho D_{A} \left( {\nabla Y_{A} } \right)} \right]\, + \,S_{A} $$
(41)

where Y A is the mass fraction of component A, i.e. \( Y_{A} = {{\rho_{A} } \mathord{\left/ {\vphantom {{\rho_{A} } \rho }} \right. \kern-0pt} \rho } \), ρ A is the density of component A, ρ is the density, D A is kinematic diffusivity and S A is the source term for component A which includes the effects of chemical reactions.

3.2.2 Disperse Phase

To evaluate the particulate phase, we can adopt the particle transport Lagrangean model, in which the particle phase is modeled by tracking a small number of particles (solid particles, drops or bubbles) through the continuum fluid.

3.2.2.1 Momentum Transfer

When considering a particle traveling in a fluid medium we can say that the forces acting over them affect the particle acceleration. This fact is attributed to the difference in velocity between the particle and fluid and the displacement of fluid by the particle. The equation of motion describing this behavior is given by:

$$ m_{p} \frac{{d\vec{U}_{p} }}{dt} = \vec{F}_{D} \, + \,\vec{F}_{B} \, + \,\vec{F}_{R} \, + \,\vec{F}_{VM} \, + \,\vec{F}_{P} \, + \,\vec{F}_{BA} $$
(42)

Herein \( m_{p} \) and \( \vec{U}_{P} \) represent the mass and velocity vector of particle, respectively. The right-hand side represents the total force acting on the disperse phase particle. The drag force, \( \vec{F}_{D} \), due to surface shear and pressure distribution can be written as follows:

$$ \vec{F}_{D} = \frac{1}{2}C_{D} \rho_{F} A_{F} \left| {\vec{U}_{F} \, - \,\vec{U}_{P} } \right|\left( {\vec{U}_{F} \, - \,\vec{U}_{P} } \right) $$
(43)

where A F is the effective particle cross section (frontal particle surface area), \( \vec{U}_{F} \) and \( \vec{U}_{P} \) represent the velocity vector of the fluid (continuous phase) and particle (particulate phase), respectively. The drag coefficient, C D , which is introduced to account for experimental results on the viscous drag of a solid sphere, depends on the flow regime (particle Reynolds number) and the properties of the continuous phase. In the literature it has been reported a large number of empirical correlations to estimate the drag coefficient [64, 65, 68–70].

The buoyancy force due to gravity (body force), \( \vec{F}_{B} \), correspond the weight of the displaced fluid given by:

$$ \vec{F}_{B} = \left( {m_{P} \, - \,m_{F} } \right)\vec{g} $$
(44)

where m P and m F represent mass of the particle and fluid, respectively, and \( \vec{g} \) is the gravity vector. If gravity effect is dominant, this term determines the motion of bubbles in liquids and leads solid particle sedimentation when immersed in liquids or gases.

The rotation force, \( \vec{F}_{R} \), in the Eq. (42), can be determined by:

$$ \vec{F}_{R} = m_{P} \left( { - 2\overrightarrow {\Upomega } \, \times \,\vec{U}_{P} \, - \,\overrightarrow {\Upomega } \, \times \,\overrightarrow {\Upomega } \, \times \,\overrightarrow {{r_{P} }} } \right) $$
(45)

with m p is the particle mass, Ω is the angular velocity and r p is the radius of particle.

The virtual mass force or added mass force, \( \vec{F}_{VM} \), in the Eq. (42), is observed when a particle in motion accelerates the surrounding fluid [64, 65], which can be written as follows:

$$ \vec{F}_{VM} = \frac{{C_{VM} }}{2}m_{F} \left( {\frac{{d\vec{U}_{F} }}{dt} - \frac{{d\vec{U}_{P} }}{dt}} \right) $$
(46)

where C VM is the virtual mass coefficient, generally equal to 1.

The pressure gradient force, \( \vec{F}_{P} \), in the Eq. (42), can be calculated by:

$$ \vec{F}_{P} = \frac{{m_{F} }}{{\rho_{F} }}\nabla p $$
(47)

where ρ F represent fluid density.

According to Ansys CFX Guide [44] this force is only important if large fluid pressure gradients exist and if the particle density is smaller than or similar to the fluid density.

Finally, \( \vec{F}_{BA} \) is the Basset force or history term, which is the force associated with past movements of the particle. This force becomes important when the particle is accelerated or decelerated in the fluid. The Basset force can be derived from the motion of a single accelerating sphere in the Stokes regime [65, 71] as follows:

$$ \vec{F}_{BA} = \frac{3}{2}d_{p}^{2} \sqrt {\pi \rho_{F} \mu_{F} } \int_{0}^{t} {\frac{1}{{\sqrt {t - \tau_{*} } }}} \frac{{\partial \left( {\left| {\vec{U}_{F} - \vec{U}_{P} } \right|} \right)}}{{\partial \tau_{*} }}d\tau_{*} $$
(48)

where \( \left( {t - \tau_{*} } \right) \) represents the time elapsed since past accelerated from 0 to \( \tau_{*} \).

3.2.2.2 Heat Transfer

The rate of change of temperature for the particle is obtained from:

$$ \sum {\left( {m_{C} C_{P} } \right)} \frac{dT}{dt} = Q_{C} + Q_{M} + Q_{R} $$
(49)

where m C is the mass of the constituent in the particle, C P is the specific heat of the particle, Q C is the convective heat transfer given by:

$$ Q_{C} = \pi d_{p} k_{F} {\text{Nu}}\left( {T_{F} - T} \right) $$
(50)

where d p is the particle diameter, k F is the thermal conductivity of the fluid, T F and T are the temperatures of the fluid and of the particle, respectively, and Nu is the Nusselt number defined by

$$ {\text{Nu}} = 2\, + \,0.6\text{Re}^{0.5} \left( {\mu \frac{{C_{P}^{*} }}{{k_{F} }}} \right)^{{{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 3}}\right.\kern-0pt} \!\lower0.7ex\hbox{$3$}}}} $$
(51)

where \( C_{P}^{*} \) is the specific heat of the fluid.

In the Eq. (44), Q M represents the heat transfer associated with mass transfer defined by:

$$ Q_{M} = \sum {\frac{{dm_{C} }}{dt}} \,L_{V} $$
(52)

where L V is the latent heat of vaporization.

The parameter, Q R represents the radiative heat transfer defined by:

$$ Q_{R} = \frac{1}{4}\varepsilon_{p} \pi d_{p}^{2} \left( {I_{f} \, - \,\sigma_{SB} n_{R} T_{p}^{4} } \right) $$
(53)

where \( I_{f} \) is the irradiation flux on the particle surface at the location of the particle, \( n_{R} \) is the refractive index of the fluid, and \( \sigma_{SB} \) is the Stefan-Boltzmann constant.

3.2.2.3 Liquid Evaporation Model

The liquid evaporation model is applied to particles with heat transfer and one component of mass transfer, and in which the continuous gas phase is at a higher temperature than the particles. The model uses two mass transfer correlations depending on whether the droplet is above or below the boiling point.

When the particle is above the boiling point, we can use

$$ \frac{{dm_{C} }}{dt} = - \frac{{Q_{C} }}{{L_{V} }} $$
(54)

Otherwise,

$$ \frac{{dm_{C} }}{dt}\, = \,\pi d_{p} \rho_{F} D_{F} {\text{Sh}}\frac{{M_{V} }}{{M_{M} }}\log \left( {\frac{{1\, - \,X_{eq} }}{{1\, - \,X_{G} }}} \right) $$
(55)

where ρ F D F is the dynamic diffusivity of the mass fraction in the continuum, M V e M M are the molecular weights of the vapor and the mixture in the continuous phase, X G is the molar fraction in the gas phase, and X eq is the equilibrium mole fraction at the droplet surface defined as:

$$ X_{eq} = \frac{{P_{vap} }}{{P_{C} }} $$
(56)

where P C is the pressure of the continuous phase and P vap is the vapor pressure determinate through the Antoine equation as follows:

$$ P_{vap} = P_{ref} \exp \left( {A - \frac{B}{T \,+\, C}} \right) $$
(57)

where P ref is the reference pressure and A, B and C are user-supplied coefficients.

3.3 Application: Drying of Sugar-Cane Bagasse Using Cyclone

3.3.1 Physical Problem Description

The drying process of sugar-cane bagasse is very important in sugar and alcohol industries. This biomass is used as an alternative source of energy that is used in the steps of the sugar and alcohol production processes, and it constitutes in more an income source, because the excess energy produced in the plants is sold [45, 72, 73]. These authors have studied the drying of the sugar-cane bagasse in a cyclone.

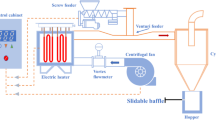
Herein, the cyclone was used to dry moist sugar-cane bagasse. The drying equipment is similar to that used by Corrêa [72] without the device of particle feeder (Venturi feeder) as illustrated in the Fig. 4. Then, particle and gas enter in the cyclone as a fluid/particle mixture.

Fig. 4
figure 4

Illustration of a cyclone dryer

Full size image

3.3.2 Boundary Conditions and Physical Properties

A numerical solution for conservation equations was developed using ANSYS CFX commercial code which the following boundary conditions were applied to the cyclone dryer illustrated in Fig. 4.

  1. a.

    Inlet: Velocity profile of the gas phase in y direction was defined by a polynomial equation of degree 5 (five), by fitting to the experimental data available in Corrêa [72], Eq. (58), whereas the velocity components in the x and z directions were assumed null. For the gas phase (air), we use the following drying conditions: air temperature 489 K and air relative humidity 3.41 %.

$$ u_{in} = u_{\hbox{max} } \left[ {1 - \left( \frac{z}{a} \right)^{8} } \right] $$
(58)
  1. b.

    Wall: No slip conditions at the cyclone wall/fluid interface, i.e., velocity components equal to zero, and adiabatic boundary condition, i.e. heat flux null.

  2. c.

    Outlet: Prescribed static pressure on the outlets cyclone dryer (underflow and overflow) equal to 101.3 kPa.

The thermo-physical properties of the gas (air) and particle (sugar-cane bagasse) used in all simulations are shown in Table 3.

Table 3 Thermo-physical properties of the fluid and particle
Full size table

3.3.3 Results Analysis

All simulations were developed using the numerical grid illustrated in Fig. 5. This mesh was generated using Ansys ICEM-CFD with 325,200 elements, which was optimal for good predictions and reasonable computational time in all simulations.

Fig. 5
figure 5

Numerical grid used in the simulations

Full size image

In order to reach a better understanding of the gas phase flow, the Fig. 6 shows the streamlines inside the cyclone. They originate in two points (x = 0.315; y = 0.364; z = 0.615) and (x = 0.333; y = 0.664; z = 0.685). These locations are close to the first half, starting at the base of the feeding duct. From the analysis of this figure we can observe the ascending behavior pattern of the gas phase in the cyclone, and the descending one near the cylindrical-conical walls, according to literature, for either cyclones or hydrocyclones [45, 74–78].

Fig. 6
figure 6

Streamlines inside the cyclone starting from two points at the cyclone inlet

Full size image

Figure 7 illustrates the pressure distribution at the surface of the cyclonic dryer. This pressure field represents the forces that the fluid exerts on the walls of the cyclone, caused by the fluid flow that enters tangentially, per unit area. Note that in general the pressure distribution remains almost uniform at the wall of the cylinder, except in the region immediately after the entry duct. In this region, it is observed an area that is severely impacted by the direct contact of solid and gas particles, thus causing a wear on the walls of the cyclone. So, this region is crucial in the design of such equipment, especially when the solid particle is very abrasive [79–81].

Fig. 7
figure 7

Gas pressure field at the cyclone walls

Full size image

Figure 8 illustrates the mapping of pressure on the XZ and YZ plans through the axis of the cyclone. There is a similar behavior in the pressure field, where the regions of high pressure are close to the cylindrical wall. The region of lower pressure occurs into gas exit tube. Thus, provides a drop in pressure of 332 Pa. It should be noted, moreover, that there is another area of low pressure near the axis of symmetry. This is caused by the reversal flow of the gas in the proximities of the cylindrical and conical regions.

Fig. 8
figure 8

Gas pressure field: a XZ and YZ plans; b XZ plan; c YZ plan through the axis cyclone

Full size image

Figure 9 show the mapping of gas temperature on the XZ and YZ plans passing through the axis of the cyclone. It can be seen that the temperature fields are similar, with higher temperatures near the cylindrical walls of the cyclone. This fact can be explained by the phenomenon of heat transfer between particles and hot air (drying agent). The particles in contact with the hot air start to lose mass by water evaporation thus, affecting its moisture content and temperature. This fact is confirmed by tracking of the particles inside the cyclone, as can be seen in Fig. 10. In this figure one can observe that most of the particles are in the conical part of the cyclone, thereby reducing the temperature of the drying air in this location (Fig. 9).

Fig. 9
figure 9

Gas temperature field: a XZ and YZ plans; b XZ plan; c YZ plan through the axis cyclone

Full size image
Fig. 10
figure 10

Particles tracking inside the cyclone

Full size image

Regarding the material transport and to show the effect of the particle diameter on the drying process, in the Figs. 11 to 13 are shown the behavior of temperature, moisture content, and shrinkage of two particles with initial diameters 0.42 and 0.84 mm. It can be clearly seen that initial diameter of the particles has an important role on the sugar-cane bagasse drying.

Fig. 11
figure 11

Temperature of the sugar-cane bagasse particles as a function of time

Full size image

Figure 11 show that the temperature of the particles has reached a constant value after 0.3 s, which may provide evidence to compensation between the heat transfer and mass transfer. This behavior is characteristic of a constant period of drying (constant drying rate). However, after this period, the particle with 0.42 mm diameter undergoes a sudden increase in temperature. From this moment the particle does not contain any more water (equilibrium condition), as can be seen in Fig. 12, and thus, its temperature increase quickly. This fact might indicate that the particles are internally heated by thermal conduction (dry particle). Then, is no longer, the observed shrinkage of the particles with 0.42 mm diameter (to see Fig. 13).

Fig. 12
figure 12

Moisture content of the sugar-cane bagasse particles as a function of time

Full size image
Fig. 13
figure 13

Shrinkage of the sugar-cane bagasse particles during drying process

Full size image

From the analysis of the Fig. 12 we can see that the particle with lower diameter dry first. This behavior is related to area/volume relationships of the particle. When the area/volume ratio is higher, the higher drying rate and shrinkage velocity is observed and, thus, the higher moisture removal and higher heating of the particle in verified. So, smaller particle is dried and heated more quickly.

Figure 14 shows the sugar-cane bagasse particle travelling distance during the drying process. It can see that the particles with 0.84 mm diameter have traveled distance 2.17 times larger than the particles with 0.42 mm. This behavior is linked to effect of the forces acting over the particles, mainly drag and gravitational forces [81]. The competition of these forces dominates the residence time of the particle into the cyclone.

Fig. 14
figure 14

Particle traveling distance during the drying of sugar-cane bagasse

Full size image

4 Concluding Remarks

This chapter focuses advanced topics related to heat and mass transfer and turbulent gas-particle flow (dispersed flow) in cyclone dryer. This type of physical problem is motivated by its importance in many industrial processes such as mineral processing, food processing, environmental cleaning and chemical processes.

Fundamentals information about principle of operation, design, selection and classification, pressure drop and overall separation efficiency of a cyclone are given.

A mathematical modeling based on the Eulerian–Lagrangian approach is introduced to explain the complex flow of the gas phase, particle trajectory, particle residence time and heat and mass transfer between the moist particle and gas phase inside the cyclone operating as a dryer.

The three-dimensional model considers steady-state and turbulent flow for gas phase and transient state for heat and mass transfer in the particulate phase. The effect of different forces acting on the particles (that affect particle trajectory and cyclone residence time) such as drag, gravitational, centrifugal, Saffman, Magnus, Faxen and Basset forces, collisions interparticles, collisions between particle and cyclone wall, and moisture content, temperature, and shrinkage phenomena (dimensions variations) of the particle are also analyzed.

Application to predict drying process of sugar and alcohol industry residues is performed and numerical studies were conducted for different inlet particle size.

Predicted results of the moisture content and particle residence time qualitatively agree well with the experimental results of sugar-cane bagasse drying.

The numerical calculations have visualized different flow pattern and behavior of the solids concentration distribution within the device. The solids concentration is lower in the inner region of the cyclone and increases greatly in the outer region. Large particles generally have higher concentration near the wall region and small particles have higher concentration in inner vortex region.

The effects of operating conditions and geometric parameters of the cyclone in the drying were also studied.

Different results such as drying and heating kinetics and trajectory of the particles, velocity, temperature, and pressure distributions of the gas phase during drying process illustrate the effectiveness versatility and performance of the rigorous mathematical model and numerical treatment performed.

From the good results obtained we can cite that the model showed herein can be used with great confidence to predict drying process and dispersed turbulent flow in several complex practical applications.