Keywords

1 Introduction

The technique of Precise Point Positioning (PPP) is based on GPS carrier phase and code (pseudo-range) observations of a single receiver, employing corrections for, among others, satellite orbits, clocks and ionospheric delays obtained from a worldwide network of GPS stations, for example the permanent GPS network of the International GNSS Service (IGS; Dow et al. (2009)). PPP was introduced in Zumberge et al. (1997) and the attainable instantaneous precision for a single-frequency user who employs global corrections is typically at the level of a few dm (van Bree and Tiberius 2012; Huisman et al. 2012).

The key to fast and cm-level PPP lies in resolving the ambiguities that are present in the phase data to integer values. Unfortunately, with the standard PPP technique this is not possible, because the ambiguities cannot be separated from the satellite hardware biases in the phase and code data. In this contribution we will present an approach that allows the single-receiver user to perform integer ambiguity resolution within short time spans and consequently enable high-precision positioning. This PPP-RTK (Wuebbena et al. 2005) approach is like standard PPP based on applying corrections for satellite clocks and ionospheric delays, but, crucial to enable ambiguity resolution, are corrections for the satellite phase biases, provided that they are defined in an appropriate way.

Integer ambiguity resolution enabled PPP has been described earlier, see e.g. Laurichesse and Mercier (2007), Collins et al. (2008), Ge et al. (2008), Geng et al. (2011), Loyer et al. (2012). However, these approaches are all based on the ionosphere-free combination of dual-frequency GPS observations, requiring long convergence times (i.e. tens of minutes) for ambiguity resolution. Advantage of our PPP-RTK approach is that it is not only suitable for dual-frequency users (Teunissen et al. 2010), but also for those employing low-cost single-frequency receivers. Without alteration, our method is even applicable to multi-frequency (e.g. triple-frequency) receivers. Although multiple-frequency users can do without ionospheric corrections, they are essential to speed up integer ambiguity resolution for single-frequency users.

In this paper our PPP-RTK concept is demonstrated based on corrections determined from a regional CORS network with inter-station distances of less than 100 km. The advantage of such a relatively dense regional network is that the ionospheric corrections can be determined much more precise than by using a global network and this should benefit single-frequency applications. In this context we mention that the PPP-RTK concept in Li et al. (2011) as well as Trimble’s commercial RTX service (Chen et al. 2011) also make use of a regional augmentation network; however they only present results for dual-frequency users. An important advantage of regionally augmented PPP-RTK over existing Network-RTK concepts (e.g. Vollath et al. (2000)) is that with PPP-RTK the correction information sent to users can be represented using a “state-space” approach (Wuebbena et al. 2005). This means that the different error components are represented individually and not lumped together which is the case with Network-RTK approaches. Hence, using a state-space representation the update rate of the information sent to the user is only high for highly variable parameters, such as satellite clocks and ionospheric delays, but can be lower for slower varying parameters (satellite phase biases). In case of Network-RTK the update rate of the correction information should be high, since all error terms are lumped together. Another advantage of the PPP-RTK concept is that there is a smooth transition to standard PPP if PPP-RTK ambiguity resolution is not possible, because the ambiguity-float PPP-RTK solution exactly corresponds to the standard PPP solution (this is not the case for Network-RTK).

In this paper it is assumed that a regional network provides corrections for satellite clocks, phase biases and ionospheric delays, but not for satellite orbits. These are computed by employing the IGS orbit information. By determining the satellite clocks based on a regional network, they are fully consistent with the satellite phase biases and ionospheric corrections, since these are determined from the same network. In addition to the corrections themselves, the PPP-RTK user needs to account for their uncertainty and in this contribution we present an easy-to-evaluate closed-form expression for the variance matrix of the network corrections.

The paper is organized as follows: The next section reviews the GPS phase and code observation equations, while the CORS network corrections that enable both regional PPP and PPP-RTK are discussed after that. Finally, results are presented of the performance of both techniques based on single-frequency GPS data.

2 GPS Phase and Code Observation Equations

Let us start by assuming a receiver r tracking dual-frequency GPS phase and code data. Since the focus of this paper is on the satellite-dependent effects, our starting point is formed by the between-satellite single differences (SD) of the phase and code observation equations from which all receiver-specific unknowns are removed, in units of distance:

$$\displaystyle\begin{array}{rcl} \begin{array}{lcl} E(\phi _{r,j}^{\mathit{ps}}) & =&\rho _{r}^{\mathit{ps}} - (d{t}^{\mathit{ps}} +\delta _{,j}^{\mathit{ps}}) -\mu _{j}\imath_{r}^{\mathit{ps}} {+\psi }^{\mathit{ps}}\tau _{r} +\lambda _{j}M_{r,j}^{\mathit{ps}} \\ E(p_{r,j}^{\mathit{ps}})& =&\rho _{r}^{\mathit{ps}} - (d{t}^{\mathit{ps}} + d_{,j}^{\mathit{ps}}) +\mu _{j}\imath_{r}^{\mathit{ps}} {+\psi }^{\mathit{ps}}\tau _{r}\\ \end{array} \quad & &{}\end{array}$$
(1)

These between-satellite single differences are formed between satellite s and a chosen pivot satellite p. It is assumed that the positions of these satellites are known. Furthermore, the symbols in Eq. (1) have the following meaning: E(⋅ ) denotes the mathematical expectation, \(\phi _{r,j}^{\mathit{ps}}\) and \(p_{r,j}^{\mathit{ps}}\) the SD observables for phase and code, respectively on frequency j = 1, 2, \(\rho _{r}^{\mathit{ps}}\) denotes the SD receiver-satellite range, \(d{t}^{\mathit{ps}}\) the SD satellite clock error, \(\delta _{,j}^{\mathit{ps}}\) and \(d_{,j}^{\mathit{ps}}\) the SD satellite phase and code hardware biases, \(\imath_{r}^{\mathit{ps}}\) the SD ionospheric delay with \(\mu _{j} =\lambda _{ j}^{2}/\lambda _{1}^{2}\) its frequency-dependent coefficient, τ r the zenith tropospheric delay (ZTD), with ψ ps the SD mapping function, λ j the wavelength, and \(M_{r,j}^{\mathit{ps}}\) the SD phase ambiguity that consists of the initial phases of satellite plus an integer SD ambiguity, in units of cycle. All clock errors and hardware biases are given in units of distance. Both phase and code data are assumed to be a priori corrected for effects such as hydrostatic troposphere, phase center offsets, phase wind-up, solid earth tides, ocean loading, etc. More details on these corrections can be found in Kouba and Heroux (2001).

3 CORS-Based Single-Frequency PPP-RTK

In this section the corrections are discussed that need to be estimated from a CORS network in order for a user to carry out single-frequency PPP, as well as PPP-RTK. For PPP-RTK it is shown that by using satellite phase bias corrections with an appropriate definition the ambiguities for the user become integer.

3.1 Regional CORS Network Corrections

Regional CORS GPS network processing is based on the observation equations (1), keeping the positions fixed of both receivers (since these are precisely known), as well as of the satellites (from IGS orbit information). Unknown network parameters are then, in terms of between-satellite single differences: satellite clocks, satellite phase biases, ZTDs, ionospheric delays and phase ambiguities. Since the network model is not of full rank, it is only possible to estimate combinations of the individual parameters as given in Eq. (1). These combinations depend on the choice of S-basis, i.e., the minimum set of parameters that needs to be constrained to eliminate the rank deficiency (Lannes and Teunissen 2011). A particular choice was made in Teunissen et al. (2010); for this paper another S-basis is chosen, resulting in the following network observation equations, for j = 1, 2 frequencies and \(r = 1,\ldots,n\) CORS stations:

$$\displaystyle\begin{array}{rcl} \begin{array}{lcl} E(\phi _{r,j}^{\mathit{ps}} -\rho _{r}^{\mathit{ps}}) & =& -\widetilde{ d{t}}^{\mathit{ps}} -\tilde{\delta }_{,j}^{\mathit{ps}} -\mu _{j}\tilde{\imath}_{r}^{\mathit{ps}} {+\psi }^{\mathit{ps}}\tilde{\tau }_{r} +\lambda _{j}\tilde{M}_{r,j}^{\mathit{ps}} \\ E(p_{r,j}^{\mathit{ps}} -\rho _{r}^{\mathit{ps}}) & =& -\widetilde{ d{t}}^{\mathit{ps}} +\mu _{j}\tilde{\imath}_{r}^{\mathit{ps}} {+\psi }^{\mathit{ps}}\tilde{\tau }_{r} \\ E(\imath_{r}^{\mathit{ps}} - \imath_{1}^{\mathit{ps}})& =&\tilde{\imath}_{r}^{\mathit{ps}} -\tilde{ \imath}_{1}^{\mathit{ps}},\ \ \ \mbox{ for}\ \ r = 2,\ldots,n\\ \end{array} & &{}\end{array}$$
(2)

As can be seen, in addition to the phase and code observation equations, constraints on the relative between-receiver ionospheric delays are incorporated in order to ‘tune’ the presence of the ionosphere in the model. The estimable parameter functions are denoted using the tilde on top of the symbol, where \(\widetilde{d{t}}^{\mathit{ps}}\) denotes the SD satellite clock parameter, \(\tilde{\delta }_{,j}^{\mathit{ps}}\) the estimable SD satellite phase bias parameter, \(\tilde{\imath}_{r}^{\mathit{ps}}\) the estimable SD ionospheric delay parameter, \(\tilde{\tau }_{r}\) the estimable ZTD parameter, and finally, \(\tilde{M}_{r,j}^{\mathit{ps}}\) denotes the estimable SD ambiguity parameter. Most striking difference with existing approaches such as described by Laurichesse and Mercier (2007), Collins et al. (2008), Ge et al. (2008), Loyer et al. (2012) is that in the latter approaches the network processing is based on elimination of the ionospheric delays by using the ionosphere-free combination, whilst in Eq. (2) the ionospheric delays are explicitly solved as they are needed for the interpolation to provide to the user.

In addition to the functional relations as described in Eq. (2), for the network processing a stochastic model is used, capturing the noise of the observations:

$$\displaystyle\begin{array}{rcl} D(\left [\begin{array}{cc} { \phi }^{\mathit{ps}} \\ {p}^{\mathit{ps}} \\ imat{h}^{\mathit{ps}}\\ \end{array} \right ])\ =\ (q_{p}^{2} + q_{ s}^{2})\left [\begin{array}{cc} \left (\begin{array}{cc} C_{\phi } \\ &C_{p}\\ \end{array} \right ) \otimes I_{n} \\ &c_{\imath}^{2}D_{n}^{T}D_{n}\\ \end{array}\right ]& &{}\end{array}$$
(3)

Here \(D(\cdot )\) denotes the mathematical dispersion, and \({\phi }^{\mathit{ps}}\) and \({p}^{\mathit{ps}}\) collect all dual-frequency phase and code observations, respectively of all receivers corresponding to one between-satellite single difference in one vector. In addition, \(imat{h}^{\mathit{ps}}\) contains the between-receiver difference of the SD ionospheric pseudo-observations. Furthermore, ⊗ denotes the matrix Kronecker product, I n the identity matrix of dimension n, e n the n-vector with ones, and \(D_{n}^{T} = [-e_{n-1}\ I_{n-1}]\), the between-receiver difference matrix. Both 2 × 2 cofactor matrices C ϕ and C p model the undifferenced precision of the dual-frequency phase and code observations in zenith, where \(c_{\imath}^{2}\) denotes the undifferenced variance factor of the ionospheric pseudo observations in zenith as well. Through the factors q p and q s it is possible to model the elevation-dependency of the noise of the observations. It is finally remarked that the above stochastic model applies to just one between-satellite single difference. When between-satellite single differences are processed simultaneously the correlation between them is taken into account.

We will now discuss the estimable network parameters in more detail. Due to space limitation we will present these parameter functions without proof; this will be given elsewhere. In this paper we consider the regional CORS network to have inter-station distances below 100 km for which absolute ZTDs (per receiver) are poorly estimable, since all receivers in the network experience more or less an identical elevation to the same satellite. To solve this, we do not estimate the ZTD of the pivot receiver (r = 1) in the network, and parameterize all other ZTDs relative to that of the pivot receiver:

$$\displaystyle\begin{array}{rcl} \tilde{\tau }_{r} =\tau _{r} -\tau _{1},\ \ \ r = 2,\ldots,n& &{}\end{array}$$
(4)

The estimable satellite clock parameters can be shown to be a function of the ‘true’ satellite clocks, plus the code biases on L1 and L2, and the ZTD of the network’s pivot receiver:

$$\displaystyle\begin{array}{rcl} \begin{array}{lcl} \widetilde{d{t}}^{\mathit{ps}} & =&d{t}^{\mathit{ps}} + d_{,1}^{\mathit{ps}} + \frac{\mu _{1}} {\mu _{2}-\mu _{1}}{ \mathit{DCB}}^{\mathit{ps}} {-\psi }^{\mathit{ps}}\tau _{1}\\ \end{array} & &{}\end{array}$$
(5)

Here \({\mathit{DCB}}^{\mathit{ps}} = d_{,1}^{\mathit{ps}} - d_{,2}^{\mathit{ps}}\) denotes the Differential Code Bias, see Schaer (1999). Although the estimable satellite clock is biased by the tropospheric delay of the pivot station in the network, this is not an issue for PPP-RTK users as we will show in the next subsection. The estimable satellite phase bias can be given by the following parameter function:

$$\displaystyle\begin{array}{rcl} \begin{array}{lcl} \tilde{\delta }_{,j}^{\mathit{ps}} & =& -\lambda _{j}\left [M_{1,j}^{\mathit{ps}} -\frac{1} {\lambda _{j}}(\delta _{,j}^{\mathit{ps}} - d_{,1}^{\mathit{ps}} - (\frac{\mu _{j}} {\mu _{1}} + 1) \frac{\mu _{1}} {\mu _{2}-\mu _{1}}{ \mathit{DCB}}^{\mathit{ps}})\right ]\\ \end{array} & &{}\end{array}$$
(6)

This between-satellite phase bias parameter is a combination of the true between-satellite phase bias, biased by a combination of the satellite code biases on L1 and L2, plus the (non-integer) ambiguity of the network’s pivot receiver. The estimable SD ionospheric delay for each of the network stations can be interpreted as the ‘true’ ionospheric delay, biased by a scaled SD differential code bias:

$$\displaystyle\begin{array}{rcl} \begin{array}{lcl} \tilde{\imath}_{r}^{\mathit{ps}} & =&\imath_{r}^{\mathit{ps}} + \frac{1} {\mu _{2}-\mu _{1}}{ \mathit{DCB}}^{\mathit{ps}},\ \ \ r = 1,\ldots,n\\ \end{array} & &{}\end{array}$$
(7)

The estimable phase ambiguity is—like the estimable ZTD parameter—the SD phase ambiguity of each receiver relative to the SD phase ambiguity of the pivot receiver in the network:

$$\displaystyle\begin{array}{rcl} \begin{array}{lcl} \tilde{M}_{r,j}^{\mathit{ps}} & =&M_{r,j}^{\mathit{ps}} - M_{1,j}^{\mathit{ps}}\\ \end{array} & &{}\end{array}$$
(8)

Consequently, the estimable ambiguity parameter is a double-differenced ambiguity and thus integer, since the initial satellite phase biases that were present in the SD ambiguity terms get eliminated.

To enable PPP and/or PPP-RTK at the location of the user, the CORS network should broadcast at least the satellite clock parameters to the user. Furthermore, for users employing single-frequency receivers, the network should provide corrections for the ionosphere. For ‘standard (global) PPP’ these are often extracted from external Global Ionospheric Maps, but in presence of a dense regional CORS network a more sophisticated ionospheric product can be generated, in which the ionospheric delay is obtained from the network ionospheric delays by means of Ordinary Kriging interpolation, e.g., Wackernagel (2003). Then we can write for the network ionospheric correction, denoted as \(\tilde{\imath}_{u}^{\mathit{ps}}\):

$$\displaystyle\begin{array}{rcl} \begin{array}{lcl} \tilde{\imath}_{u}^{\mathit{ps}} & =&h_{u}^{T}{\left [\tilde{\imath}_{1}^{\mathit{ps}},\ \ldots,\ \tilde{\imath}_{n}^{\mathit{ps}}\right ]}^{T} = \imath_{u}^{\mathit{ps}} + \frac{1} {\mu _{2}-\mu _{1}}{ \mathit{DCB}}^{\mathit{ps}}\\ \end{array} & &{}\end{array}$$
(9)

with \({(\cdot )}^{T}\) denoting a transposed vector. Furthermore, n-vector h u denotes the Ordinary Kriging interpolation coefficient vector evaluated at the approximate user location for which holds that the entries sum up to 1 (\(h_{u}^{T}e_{n} = 1\)), and where \(\imath_{u}^{\mathit{ps}}\) denotes the ‘true’ SD interpolated ionospheric delay at the approximate user location. Finally, to enable integer ambiguity resolution for the PPP user, the CORS network should provide corrections for the satellite phase bias parameters on the frequency corresponding to that of the single-frequency user. As a last remark, we emphasize that the network parameters should be transmitted to the users with the best possible precision, so after the network ambiguities are fixed to integers.

3.2 Regional Network-Based PPP and PPP-RTK

Before presenting the observation equations for PPP-RTK, a user can perform—similar to standard or ‘global PPP’—‘regional PPP’ by correcting his phase and code observations by the ionosphere-free satellite clocks and interpolated ionospheric delay from the regional CORS network. The single-frequency (L1; j = 1) user thus applies the following corrections:

$$\displaystyle\begin{array}{rcl} \varDelta \tilde{\phi }_{u,1}^{\mathit{ps}} =\widetilde{ d{t}}^{\mathit{ps}} +\mu _{ 1}\tilde{\imath}_{u}^{\mathit{ps}};\ \ \ \ \varDelta \tilde{p}_{ u,1}^{\mathit{ps}} =\widetilde{ d{t}}^{\mathit{ps}} -\mu _{ 1}\tilde{\imath}_{u}^{\mathit{ps}}& &{}\end{array}$$
(10)

With these corrections, the (linearized) single-frequency regional PPP observation equations read as follows:

$$\displaystyle\begin{array}{rcl} \begin{array}{lcl} E(\phi _{u,1}^{\mathit{ps}} +\varDelta \tilde{\phi }_{ u,1}^{\mathit{ps}}) & =& -{ (\mathbf{u}_{u}^{\mathit{ps}})}^{T}x_{u} {+\psi }^{\mathit{ps}}\tilde{\tau }_{u} +\lambda _{1}\tilde{M}_{u,1}^{\mathit{ps}} \\ E(p_{u,1}^{\mathit{ps}} +\varDelta \tilde{ p}_{u,1}^{\mathit{ps}})& =& -{ (\mathbf{u}_{u}^{\mathit{ps}})}^{T}x_{u} {+\psi }^{\mathit{ps}}\tilde{\tau }_{u}\\ \end{array} & &{}\end{array}$$
(11)

where \(\phi _{u,1}^{\mathit{ps}}\) and \(p_{u,1}^{\mathit{ps}}\) denote the observed-minus-computed SD phase and code observables and \(\mathbf{u}_{u}^{\mathit{ps}}\) the SD receiver-satellite line-of-sight vector. Satellite positions are held fixed; the user should compute them in the same way as the network. The following estimable parameters appear in these PPP observation equations: the user position x u , the ZTD, which is defined relative to the network’s pivot station, i.e., \(\tilde{\tau }_{u} =\tau _{u} -\tau _{1}\), and an L1 phase ambiguity that is defined as follows:

$$\displaystyle\begin{array}{rcl} \begin{array}{lcl} \tilde{M}_{u,1}^{\mathit{ps}} & =&M_{u,1}^{\mathit{ps}} -\frac{1} {\lambda _{1}} (\delta _{,1}^{\mathit{ps}} - d_{,1}^{\mathit{ps}} - \frac{2\mu _{1}} {\mu _{2}-\mu _{1}}{ \mathit{DCB}}^{\mathit{ps}})\end{array} & &{}\end{array}$$
(12)

Thus, the estimable PPP ambiguity parameter is a combination of the original ambiguity term, lumped with phase and code satellite hardware biases. It can be shown that this ambiguity corresponds to the ‘narrow-lane uncalibrated phase delay’ parameter as used in Ge et al. (2008). Clearly, this parameter is not an integer.

Integer ambiguities become estimable when the PPP user applies the network’s satellite bias corrections to his phase data. The observation equations then remain exactly the same as in Eq. (11), as well as the corrected code observations, however the correction to be applied to the phase observations is different:

$$\displaystyle\begin{array}{rcl} \varDelta \tilde{\phi }_{u,1}^{\mathit{ps}} =\widetilde{ d{t}}^{\mathit{ps}} +\tilde{\delta }_{,1}^{\mathit{ps}} +\mu _{ 1}\tilde{\imath}_{u}^{\mathit{ps}};\ \ \ \ \varDelta \tilde{p}_{ u,1}^{\mathit{ps}} =\widetilde{ d{t}}^{\mathit{ps}} -\mu _{ 1}\tilde{\imath}_{u}^{\mathit{ps}}\quad & &{}\end{array}$$
(13)

Since the satellite phase bias parameter contains the combined term \((\delta _{,1}^{\mathit{ps}} - d_{,1}^{\mathit{ps}} - \frac{2\mu _{1}} {\mu _{2}-\mu _{1}}{ \mathit{DCB}}^{\mathit{ps}})\), see Eq. (6), this is exactly what is needed to remove the same term from Eq. (12), and the estimable ambiguity parameter becomes:

$$\displaystyle{ \begin{array}{lcl} \tilde{M}_{u,1}^{\mathit{ps}} + \frac{1} {\lambda _{1}} \tilde{\delta }_{,1}^{\mathit{ps}} & =&M_{u,1}^{\mathit{ps}} - M_{1,1}^{\mathit{ps}}\ =\ \mbox{ integer}\end{array} }$$
(14)

Thus, the estimable PPP-RTK ambiguity parameter is the difference between the SD ambiguity of the PPP user and the SD ambiguity of the network’s pivot station. This resulting parameter is consequently a double-differenced ambiguity and thus integer.

3.3 Regional PPP-RTK Correction Variance Matrix

The network corrections are stochastic and their variance matrix should be taken into account by the PPP-RTK user in order to have the best possible results for both his ambiguity resolution and positioning. In order to limit the amount of information sent to the user, we will present an easy-to-use closed-form expression for the network correction variance matrix such that a user can compute this matrix himself. For a between-satellite single-differenced pair of phase and code data, the variance matrix of the ambiguity-fixed network corrections that a single-frequency user needs to apply, can be shown to read as follows for a certain observation epoch:

$$\displaystyle\begin{array}{rcl} \begin{array}{l} D(\left [\begin{array}{c} \varDelta \check{\tilde{\phi }}_{u,1}^{\mathit{ps}} \\ \varDelta \check{\tilde{p}}_{u,1}^{\mathit{ps}}\\ \end{array} \right ]) \triangleq \\ \underbrace{\mathop{(q_{p}^{2} + q_{s}^{2})\left [ \frac{1} {n}\left (\begin{array}{cc} c_{\phi }^{2}& \\ &c_{p}^{2}\\ \end{array} \right ) + c_{\check{\imath}\vert \rho }^{2}\left ([h_{u}^{T}h_{u}] - \frac{1} {n}\right )\left (\begin{array}{r} - 1\\ 1\\ \end{array} \right ){\left (\begin{array}{r} - 1\\ 1\\ \end{array} \right )}^{T}\right ]}}\limits _{Q_{ 1}} \\ \\ \ +\ \underbrace{\mathop{c_{\tau }^{2}{{(\psi }^{\mathit{ps}})}^{2}{\left (\frac{c_{\check{\imath}\check{\rho }}} {c_{\check{\rho }}} \right )}^{2}\left ([h_{ u}^{T}h_{ u}] - \frac{1} {n}\right )\left (\begin{array}{r} - 1\\ 1\\ \end{array} \right ){\left (\begin{array}{r} - 1\\ 1\\ \end{array} \right )}^{T}}}\limits _{Q_{ 2}}\\ \end{array} & &{}\end{array}$$
(15)

where q p and q s are the factors to model satellite-elevation dependency, see Eq. (3), and c ϕ and c p the undifferenced standard deviations of the single-frequency phase and code data used in the network processing. These standard deviations plus the function to model the elevation dependency should be known by the user, as well as the number of CORS network stations n, plus their locations (in order to compute the interpolation vector h u ). It should be mentioned that the variance matrix as presented here is not the complete one of the actual PPP-RTK corrections, but the equivalent S-basis invariant form of it (this is why the equivalent sign has been used in Eq. (15)). While the PPP-RTK corrections themselves do depend on the choice of the network’s pivot receiver (in this case receiver 1), it can be shown that only the S-invariant form of it is needed to properly weigh the corrections for position determination. Now we will take a closer look at the different components of this closed-form variance matrix.

In the first part of the variance matrix, i.e., Q 1 in Eq. (15), the variance factor \(c_{\check{\imath}\vert \rho }^{2}\) reflects the precision with which the (ambiguity-fixed) ionospheric delays can be estimated in the CORS network. Assuming the precision of phase to be much better than of code, i.e., \(c_{\phi }^{2}/c_{p}^{2} \approx 0\), and for dual-frequency GPS CORS networks \(c_{\phi }^{2}/c_{\imath}^{2} \approx 0\), such that the square root of the variance factor can be approximated as:

$$\displaystyle{\begin{array}{l} c_{\check{\imath}\vert \rho }\approx c_{\phi } \frac{1} {\sqrt{\mu _{1 }^{2 }+\mu _{2 }^{2}}} \approx 0.5c_{\phi },\ \ \mbox{ since}\ \ \mu _{1} = 1,\ \mu _{2} = {(77/60)}^{2} \\ \end{array} }$$

Thus, the precision of the ambiguity-fixed network ionospheric delays is very high: about half the standard deviation of the undifferenced phase observations. The scalar \([h_{u}^{T}h_{u}]\) appears due to the interpolation of these network ionospheric delays, and it can be proved that \(\frac{1} {n} \leq [h_{u}^{T}h_{ u}] \leq 1\). This means that the factor \([h_{u}^{T}h_{u}] - \frac{1} {n}\) in Eq. (15) varies between 0 and \(1 - \frac{1} {n}\).

The part Q 2 of Eq. (15) is due to the ZTD estimation in the network. The scalar c τ 2 represents the variance factor with which the ZTD can be estimated in a standard single point positioning model, based on all satellites in view. It is possible to evaluate this standard deviation using a closed-form expression as well, by assuming that the elevation-dependency of the observation noise can be modeled as \(q_{i} = 1{/\sin \epsilon }^{i}\), with ε i the elevation of satellite i = 1, …, m. In addition, if we approximate the tropospheric mapping function by the same, i.e., \({\psi }^{i} \approx 1{/\sin \epsilon }^{i}\), the user can apply the following approximation:

$$\displaystyle{ \begin{array}{l} c_{\tau }\ \approx \ \sqrt{ \frac{1} {m} \frac{\sum _{i=1}^{m}\sin {}^{2}{\epsilon }^{i}} {\sum _{i=1}^{m}{(\sin {\epsilon }^{i}-\overline{\sin \epsilon })}^{2}}} \ \ \mbox{ with}\ \ \overline{\sin \epsilon } = \frac{1} {m}\sum _{i=1}^{m}\sin {\epsilon }^{i} \end{array} }$$
(16)

This factor does not vary much during a day; using a cut-off elevation of 10∘ and a number of GPS satellites varying between 6 and 9, c τ typically varies between 0.8 and 2.4 with an average of 1.2. Furthermore, in part Q 2, \(\frac{c_{\check{\imath}\check{\rho }}} {c_{\check{\rho }}}\) denotes the ratio of the covariance and the standard deviation with which the ionospheric delays and ranges can be estimated using the geometry-free single-baseline model, having the DD ambiguities fixed, see Odijk and Teunissen (2008). Using the same assumptions as done for \(c_{\check{\imath}\vert \rho }\), it is possible to approximate this ratio as:

$$\displaystyle{\begin{array}{l} \frac{c_{\check{\imath}\check{\rho }}} {c_{\check{\rho }}} \approx c_{\phi } \frac{\mu _{1}+\mu _{2}} {(\mu _{2}-\mu _{1})\sqrt{\mu _{1 }^{2 }+\mu _{2 }^{2}}} \approx 2.1c_{\phi }\\ \end{array} }$$

so about twice the undifferenced phase standard deviation.

Thus, since both factors \(c_{\check{\imath}\vert \rho }\) and \(\frac{c_{\check{\imath}\check{\rho }}} {c_{\check{\rho }}}\) are governed by the phase precision, while the factors \([h_{u}^{T}h_{u}] - \frac{1} {n}\) and c τ are always smaller or close to 1, it follows that the network correction for the PPP-RTK user’s phase data has phase precision (as it should be), while the PPP-RTK user’s code correction is driven by the network’s code noise (since c p 2 in Eq. (15) is dominating over the phase-based terms).

4 Experimental Results of Regional PPP and PPP-RTK

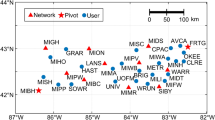
In order to test the performance of our PPP-RTK concept, we determined corrections from a regional CORS network and applied these to single-frequency user data. The CORS network is depicted in Fig. 1 and consists of (n = 4) four stations at distances of about 60 km in Western Australia around Perth, all equipped with identical Trimble NetR5 receivers. The location at Curtin University Bentley campus (CUT0) was assigned as a (static) rover station. At this station, GPS data were collected using two receivers: a high-grade dual-frequency Trimble NetR9 receiver, plus a low-grade single-frequency u-blox AEK-4T receiver. For all CORS network stations dual-frequency phase and code observations have been collected above a cut-off elevation of 10∘ during the full day of 23 October 2010 with a sampling interval of 30 s.

4.1 Example of PPP-RTK Correction Variance Matrix

From the dual-frequency CORS network data precise estimates for satellite clock parameters, satellite phase bias parameters and interpolated ionospheric delays (for location CUT0) were obtained after network ambiguity resolution. In addition to the computation of these correction values, the closed-form expression as given in Eq. (15) has been employed to compute the variance matrix of the network corrections. As an example, for a particular between-satellite single difference (SD) at a particular epoch of the day, we present this variance matrix numerically. For this, the network processing has been done based on the following observable standard deviations (undifferenced and in zenith): c ϕ  = 2.5 mm, c p  = 25 cm and \(c_{\imath}\) = 10 cm. In addition, the observations are weighted according to: \(q_{i} = 1{/\sin \epsilon }^{i}\). The Kriging interpolation vector evaluated at CUT0 equals: \(h_{u}^{T} = (-0.02,0.24,0.66,0.12)\), based on station ordering: TORK–ROTT–MIDL–MDAH. At the particular epoch 8 satellites were tracked, resulting in c τ  ≈ 1. 1. From these satellites we selected two satellites, one with \({\epsilon }^{p} = 56.{7}^{\circ }\) and the other with \({\epsilon }^{s} = 27.{1}^{\circ }\). For this pair \({\psi }^{\mathit{ps}} \approx -1.0\) and the two matrices in Eq. (15) are computed as:

$$\displaystyle\begin{array}{rcl} \begin{array}{l} Q_{1} \approx \left [\begin{array}{rr} \mathtt{1.25E-5}&\mathtt{-2.72E-6}\\ \mathtt{-2.72E - 6 } & \mathtt{0.098}\\ \end{array} \right ],\\ \\ \\ \\ Q_{2} \approx \left [\begin{array}{rr} \mathtt{8.80E-6}&\mathtt{-8.80E-6}\\ \mathtt{-8.80E - 6 } & \mathtt{8.80E - 6}\\ \end{array} \right ]\end{array} & & {}\\ \end{array}$$

This results in the following variance matrix the PPP-RTK user needs to apply to account for the uncertainty of the network corrections at this epoch:

$$\displaystyle{ D(\left [\begin{array}{c} \varDelta \check{\tilde{\phi }}_{u,1}^{\mathit{ps}} \\ \varDelta \check{\tilde{p}}_{u,1}^{\mathit{ps}}\\ \end{array} \right ]) \approx \left [\begin{array}{rr} \mathtt{2.13E-5}&\mathtt{-1.15E-5}\\ \mathtt{-1.15E - 5 } & \mathtt{0.098} \end{array} \right ]\ \ {\mbox{ m}}^{2} }$$
(17)

Thus, the phase correction is very precise, having a standard deviation of just 5 mm, while the standard deviation of the code correction is about 31 cm.

Fig. 1
figure 1

CORS network (yellow triangles) used for generating the PPP (-RTK) products for user location CUT0 ((\(-3{2}^{\circ },11{6}^{\circ }\)); red triangle)

Full size image
Fig. 2
figure 2

PPP and PPP-RTK positioning results based on CORS-network corrected single-frequency GPS phase and code data. The left two graphs (top: North-East position scatter; bottom: Up position time series) correspond to PPP based on the high-grade receiver, while the two graphs second from left depict the PPP counterparts obtained using the data of the low-grade receiver. The two columns on the right side are those corresponding to PPP-RTK

Full size image

4.2 Performance of PPP-RTK at the User

In a next step the network corrections are applied to correct the user’s single-frequency phase and code data and perform single-receiver ambiguity resolution and positioning. Due to the weakness of the single-epoch, single-frequency observation model (11), instantaneous or epoch-by-epoch ambiguity resolution was not feasible. However, successful ambiguity resolution was obtained by accumulating epochs in a Kalman filter incorporating the constancy of the ambiguities. In this way the average time to successfully resolve the integers is 2.5 min for the Trimble receiver and 4 min for the u-blox receiver. These short time spans could be achieved since—in contrast to current practice—the network corrections have been weighted in the processing, by applying the variance matrix of Eq. (15) for each epoch. On the other hand, the measurements were obtained in October 2010, during solar minimum and under relatively mild ionospheric conditions. However, to give an idea of the time to fix the ambiguities during more disturbed ionospheric conditions, we artificially increased the standard deviation of the ionospheric corrections by a factor 10. The resulting average time to fix the integers using these more uncertain network corrections increased to 6.5 min for the Trimble receiver and to 9.5 min for the u-blox receiver. So the mean time to fix is expected to be a factor 2–3 longer under a more disturbed ionosphere.

After ambiguity resolution, the rover position could be solved kinematically with a horizontal precision at sub-cm level, and a vertical precision of about 2 cm, for both types of receivers; see Fig. 2 (right two columns). The position errors are obtained by comparing the estimates with the known coordinates of station CUT0. To compare, the two left columns of Fig. 2 show the positioning results which would have been obtained without integer ambiguity resolution, i.e. ‘regional single-frequency PPP’, thus including interpolated ionospheric corrections, but without the phase data corrected for the satellite phase biases. In order to enable a fair comparison with PPP-RTK, the PPP results shown are based on a same number of epochs as was needed for PPP-RTK ambiguity resolution. It is stressed that apart from the satellite phase bias corrections, the assumptions underlying the PPP and PPP-RTK solutions are exactly the same (i.e. stochastic model of phase and code, initial receiver positions from standard single point positioning, number of satellites, etc.). The comparison clearly shows the impact of integer ambiguity resolution: the horizontal precision is improved from a level of a few dm (PPP) to sub-cm (PPP-RTK), while the vertical component improves from 3–4 dm (PPP) to about 2 cm (PPP-RTK). The difference in precision between PPP high-grade and PPP low-grade is mainly due to the lower quality of the code data for the u-blox receiver as compared to the Trimble receiver.

The accuracy of the PPP-RTK positioning results is in agreement of what can be expected if the integer ambiguities are resolved and all other biases have been properly taking into account: the phase data, having mm-precision (even for the low-cost receiver), start to act as if they are very precise code data, resulting in cm-precision or better. The horizontal sub-cm precision and vertical precision of a few cm is similar to the results described in e.g. Geng et al. (2011).

5 Conclusions

In this contribution the focus has been on integer ambiguity resolution enabled single-receiver Precise Point Positioning applications. While the observation model of this ‘PPP-RTK’ method is intrinsically the same as for ‘standard PPP’, the difference lies in the corrections applied to the user’s phase data. Standard PPP is based on corrections for at least satellite clocks (in addition to the orbits), however the essential correction that enables integer ambiguity resolution is the satellite phase bias parameter, which can be shown to be a combination of the (true) satellite phase bias, together with the (non-integer) ambiguity of the network’s pivot station and dual-frequency satellite code biases. The PPP-RTK approach demonstrated in this paper is not only suitable for dual-frequency but also for single-frequency applications. In this paper we presented a closed-form expression which enables the single-frequency PPP-RTK user to computes the variance matrix of the network corrections by himself. Experimental results show that single-frequency PPP ambiguity resolution is feasible in less than 10 min, even using low-grade receivers. The kinematic position accuracy with the integer ambiguities fixed is at sub-cm level horizontally, and at the level of a few cm in the vertical direction.