Keywords

1 Introduction

In the past years, many control strategies, such as proportional control, optimal control, sliding mode control and H2/H∞ were proposed to improve the two-axle vehicle’s lateral stability. Furukawa [1] summarized those control strategies and pointed out their effectiveness and limits. However, few works expand those control algorithms to multi-axle vehicle, especially for four-axle vehicles. Huh [2] proposed a proportional backward control for three-axle vehicle. Lane change simulation under 18 DOF nonlinear vehicle model demonstrated the advantage of the proposed control law. An [3] proposed an optimal control for three-axle vehicle, where the sideslip angle and yaw rate were controlled to improve the maneuverability by independent control of the steering angles of the six wheels. A numerical simulation and a scaled-down vehicle experiment showed its good effective. Qu [4] proposed a SMC for three-axle vehicle. The SMC tried to make the steering characteristics of uncertain vehicle mode follow the characteristics of the reference mode, even exiting outer disturbance and uncertain parameters. Kerem [5] extended 4WS idea to an n-axle vehicle and attempted to determine the best steering strategy. It is found that few controllers are designed for four-axle vehicle, and many of them do not consider parameter perturbations and external disturbances. Moreover, many of them aim at reducing turning radius at low velocity, and do not work at high velocity. However, for familiar DFAS four-axle vehicle, which demands both maneuverability and stability, all-wheel steering is an effective method to improve the stability.

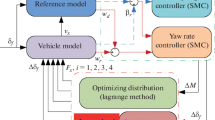
In the paper, a sliding mode controller to control the steering angle of the third axle and forth axle is proposed for four-axle vehicle to improve handling and stability.

2 Vehicle Model

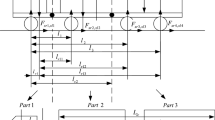
Two degrees of freedom (2DOF) vehicle model is considered in this paper, shown in Fig. 1. L i(i = 1,2,3,4) represents the distances between the ith axle and the center of gravity. It is important to keep in mind that an axle located behind the vehicle center of gravity is located by a negatively signed distance [6]. In here, L 3 and L 4 are negative.

Fig. 1
figure 1

2DOF vehicle model

Full size image

Considering the tire cornering stiffness perturbations and crosswind disturbance, a linearized equation of motion of all-wheel steer vehicle becomes

$$ \left\{ \begin{array}{l} mu\left( {\dot{\beta } + r} \right) = - \beta \sum {K_{\alpha i} } - \frac{{\sum {L_{i} K_{\alpha i} } }}{u}r + \sum {K_{\alpha i} \delta_{i} + F_{d} } \hfill \\ I_{z} \dot{r} = - \beta \sum {L_{i} K_{\alpha i} } - \frac{{\sum {L_{i}^{2} K_{\alpha i} } }}{u}r + \sum {L_{i} K_{\alpha i} \delta_{i} + L_{d} F_{d} } \end{array} \right. $$
(1)

where m is vehicle mass, I z is yaw inertia, u is the forward velocity, δ i is steering angle of ith axle, β is the sideslip angle at CG, r is the yaw rate, K αi = K α0i + ΔK αi, K α0i is defined as the nominal value of ith axle cornering stiffness, ΔK αi is defined as the perturbation value of ith axle, F d is assumed to be the external disturbance force impacting on the vehicle, and L d is the distance from the CG to the point where F d acts on vehicle.

For traditional DFAS vehicle, we can set δ 2 = kδ 1. Then the vehicle model can be written as

$$ {\dot{\mathbf{X}}} = \left( {{\mathbf{A}}_{{\mathbf{0}}} + {\mathbf{\Updelta A}}} \right){\mathbf{X}} + \left( {{\mathbf{B}}_{{{\mathbf{u0}}}} + {\mathbf{\Updelta B}}_{{\mathbf{u}}} } \right){\mathbf{U}} + \left( {{\mathbf{B}}_{{{\mathbf{w0}}}} + {\mathbf{\Updelta B}}_{{\mathbf{w}}} } \right)\delta_{1} + {\mathbf{B}}_{{\mathbf{d}}} F_{d} $$
(2)

where

$$ \begin{aligned}{\mathbf{A}}_{{\mathbf{0}}} &= \left[ {\begin{array}{*{20}c} {\frac{{ - \sum {K_{{\alpha_{0} i}} } }}{mu}} & {\frac{{ - \sum {L_{i} K_{{\alpha_{0} i}} } }}{{mu^{2} }} - 1} \\ {\frac{{ - \sum {L_{i} K_{{\alpha_{0} i}} } }}{{I_{z} }}} & {\frac{{ - \sum {L_{i}^{2} K_{{\alpha_{0} i}} } }}{{I_{z} u}}} \\ \end{array} } \right],{\mathbf{X}} = \left[ {\begin{array}{*{20}c} \beta \\ r \\ \end{array} } \right],{\mathbf{U}} = \left[ {\begin{array}{*{20}c} {\delta_{3} } \\ {\delta_{4} } \\ \end{array} } \right],{\mathbf{\Updelta A}} = \left[ {\begin{array}{*{20}c} {\frac{{ - \sum {\Updelta K_{\alpha i} } }}{mu}} & {\frac{{ - \sum {L_{i} \Updelta K_{\alpha i} } }}{{mu^{2} }}} \\ {\frac{{ - \sum {L_{i} \Updelta K_{\alpha i} } }}{{I_{z} }}} & {\frac{{ - \sum {L_{i}^{2} \Updelta K_{\alpha i} } }}{{I_{z} u}}} \\ \end{array} } \right],{\mathbf{B}}_{{\mathbf{d}}} = \left[ {\begin{array}{*{20}c} \frac{1}{mu} \\ {\frac{{L_{d} }}{{I_{z} }}} \\ \end{array} } \right] \\ {\mathbf{B}}_{{{\mathbf{w0}}}} &= \left[ {\begin{array}{*{20}c} {\frac{{K_{{\alpha_{0} 1}} + kK_{{\alpha_{0} 2}} }}{mu}} \\ {\frac{{L_{1} K_{{\alpha_{0} 1}} + kL_{2} K_{{\alpha_{0} 2}} }}{{I_{z} }}} \\ \end{array} } \right],{\mathbf{\Updelta B}}_{{\mathbf{w}}} = \left[ {\begin{array}{*{20}c} {\frac{{\Updelta K_{\alpha 1} + k\Updelta K_{\alpha 2} }}{mu}} \\ {\frac{{L_{1} \Updelta K_{\alpha 1} + kL_{2} \Updelta K_{\alpha 2} }}{{I_{z} }}} \\ \end{array} } \right],{\mathbf{B}}_{{{\mathbf{u0}}}} = \left[ {\begin{array}{*{20}c} {\frac{{K_{{\alpha_{0} 3}} }}{mu}} & {\frac{{K_{{\alpha_{0} 4}} }}{mu}} \\ {\frac{{L_{3} K_{{\alpha_{0} 3}} }}{{I_{z} }}} & {\frac{{L_{4} K_{{\alpha_{0} 4}} }}{{I_{z} }}} \\ \end{array} } \right],{\mathbf{\Updelta B}}_{{\mathbf{u}}} = \left[ {\begin{array}{*{20}c} {\frac{{\Updelta K_{\alpha 3} }}{mu}} & {\frac{{\Updelta K_{\alpha 4} }}{mu}} \\ {\frac{{L_{3} \Updelta K_{\alpha 3} }}{{I_{z} }}} & {\frac{{L_{4} \Updelta K_{\alpha 4} }}{{I_{z} }}} \\ \end{array} } \right] \end{aligned}$$

Due to B u0 is full rank and reciprocal matrix, the vehicle model satisfies matching condition. It means that there are matrices M x, M u, M w and M d which made Equation (3) tenable.

$$ {\mathbf{\Updelta A = B}}_{{{\mathbf{u0}}}} {\mathbf{M}}_{{\mathbf{x}}} {\mathbf{,}}\quad {\mathbf{\Updelta B}}_{{\mathbf{u}}} {\mathbf{ = B}}_{{{\mathbf{u0}}}} {\mathbf{M}}_{{\mathbf{u}}} ,\quad {\mathbf{\Updelta B}}_{{\mathbf{w}}} {\mathbf{ = B}}_{{{\mathbf{u0}}}} {\mathbf{M}}_{{\mathbf{w}}} {\mathbf{,}}\quad {\mathbf{B}}_{{\mathbf{d}}} {\mathbf{ = B}}_{{{\mathbf{u0}}}} {\mathbf{M}}_{{\mathbf{d}}} $$
(3)

The physical meaning of a matching condition is that the system uncertainty and control action are on a same channel. So by taking appropriate control effect, it is possible to offset directly or weaken influence of uncertainty.

Then, the vehicle model can be written as

$$ {\dot{\mathbf{X}}} = {\mathbf{A}}_{{\mathbf{0}}} {\mathbf{X + B}}_{{{\mathbf{u0}}}} \left[ {{\mathbf{U + d(x,t)}}} \right] + {\mathbf{B}}_{{{\mathbf{w0}}}} \delta_{1} $$
(4)

where d(x,t) = M x X + M u U + M w δ1 + M d Fd is the total uncertainty of the system.

3 The Reference Model

The ideal steering state for AWS is [7]: its steering sensitivity (steady-state gain of yaw rate) is always consistent with the traditional DFAS vehicle. In other words, it is to keep the driver feel no great change compared with that of old vehicle, while its sideslip angle at CG is always zero value as far as possible (in order to keep no sideslip during cornering). According to above requirement, the reference model can be established as follows

$$ {\dot{\mathbf{X}}}_{{\mathbf{d}}}\, = {\mathbf{A}}_{{\mathbf{d}}} {\mathbf{X}}_{{\mathbf{d}}}\,+\,{\mathbf{B}}_{{\mathbf{d}}} \delta_{1} $$
(5)

where

$$ {\mathbf{A}}_{{\mathbf{d}}} = \left[ {\begin{array}{*{20}c} { - 1/\tau_{\beta } } & 0 \\ 0 & { - 1/\tau_{r} } \\ \end{array} } \right],{\mathbf{B}}_{{\mathbf{d}}} = \left[ {\begin{array}{*{20}c} {k_{\beta d} /\tau_{\beta } } \\ {k_{rd} /\tau_{r} } \\ \end{array} } \right],{\mathbf{X}}_{{\mathbf{d}}} = \left[ {\begin{array}{*{20}c} {\beta_{d} } \\ {r_{d} } \\ \end{array} } \right] $$

where β d , r d represent sideslip angle and yaw rate of the reference model respectively, scale factor k rd is taken as the steady-state gain of yaw rate of DFAS vehicle with same structural parameters, k βd  = 0, τ β , τ r are lag time constants of the first-order inertia link to sideslip angle and yaw rate respectively. Here τ β  = τ r  = 0.2s.

4 Sliding Mode Controller Design

We define the state tracking error between the actual state and the reference model e as

$$ {\mathbf{e}} = {\mathbf{X}} - {\mathbf{X}}_{{\mathbf{d}}} = \left[ {\begin{array}{*{20}c} {e_{1} } \\ {e_{2} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {\beta - \beta {}_{d}} \\ {r - r_{d} } \\ \end{array} } \right] $$
(6)

Then, the derivative of tracking error e is

$$ \begin{aligned} \dot{\mathbf{e}} =\,& \dot{\mathbf{X}} \,-\, \dot{\mathbf{X}}_{{\mathbf{d}}} \\ {\mathbf{ =\, }} & {\mathbf{A}}_{{\mathbf{0}}} {\mathbf{X \,+\, B}}_{{{\mathbf{u0}}}} \left[ {{\mathbf{U} + \mathbf{d}(\mathbf{x},\mathbf{t})}} \right]{\,+\,\mathbf{B}}_{{{\mathbf{w0}}}} \delta_{1} -{\mathbf{A}}_{{\mathbf{d}}} {\mathbf{X}}_{{\mathbf{d}}} -{\mathbf{B}}_{{\mathbf{d}}} \delta_{1} \\ = \, & {\mathbf{A}}_{{\mathbf{0}}} {\mathbf{e}} \,+\,\left( {{\mathbf{A}}_{{\mathbf{0}}} -{\mathbf{A}}_{{\mathbf{d}}} } \right){\mathbf{X}}_{{\mathbf{d}}} \, +\, {\mathbf{B}}_{{{\mathbf{u0}}}} \left[ {{\mathbf{U} \,+\, \mathbf{d}(\mathbf{x},\mathbf{t})}} \right] \, +\, \left( {{\mathbf{B}}_{{{\mathbf{w0}}}} -{\mathbf{B}}_{{\mathbf{d}}} } \right)\delta_{1} \\ \end{aligned} $$
(7)

Here, we need to construct a switching function as follows

$$ {\mathbf{S}} = \left[ {\begin{array}{*{20}c} {s_{1} } \\ {s_{2} } \\ \end{array} } \right] = {\mathbf{Ce}} = \left[ {\begin{array}{*{20}c} 1 & {c_{1} } \\ 1 & {c_{2} } \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {e_{1} } \\ {e_{2} } \\ \end{array} } \right] $$
(8)

where c 1 and c 2 are positive undetermined parameters.

The derivative of switching function is

$$ {\dot{\mathbf{S}}}={\mathbf{C}}{\dot{\mathbf{e}}}={\mathbf{C}}\left[ {{\mathbf{A}}_{{\mathbf{0}}} {\mathbf{e \,+\, }}\left( {{\mathbf{A}}_{{\mathbf{0}}} - {\mathbf{A}}_{{\mathbf{d}}} } \right){\mathbf{X}}_{{\mathbf{d}}} } \right]{\mathbf{ + C}}\left[ {{\mathbf{B}}_{{{\mathbf{u0}}}} \left[ {{\mathbf{U + d(x,t)}}} \right]{\mathbf{ \,+\, }}\left( {{\mathbf{B}}_{{{\mathbf{w0}}}} {\mathbf{ - B}}_{{\mathbf{d}}} } \right)\delta_{1} } \right] $$
(9)

Let \( {\dot{\user2{S}}} \) = 0 and d(x,t) = 0, we can get the equivalent control.

$$ {\mathbf{U}}_{{{\mathbf{eq}}}} {\mathbf{ \,=\, }} - \left( {{\mathbf{CB}}_{{{\mathbf{u0}}}} } \right)^{{ - {\mathbf{1}}}} {\mathbf{C}}\left[ {{\mathbf{A}}_{{\mathbf{0}}} {\mathbf{e \,+\, }}\left( {{\mathbf{A}}_{{\mathbf{0}}} - {\mathbf{A}}_{{\mathbf{d}}} } \right){\mathbf{X}}_{{\mathbf{d}}} {\mathbf{ \,+\, }}\left( {{\mathbf{B}}_{{{\mathbf{w0}}}} - {\mathbf{B}}_{{\mathbf{d}}} } \right)\delta_{1} } \right] $$
(10)

The equivalent control just works for nominal vehicle model, but it cannot restrain parameter perturbations and external disturbances. In order to has robust ability, a robust control with a constant reaching law is given

$$ {\mathbf{U}}_{{{\mathbf{rob}}}} {\mathbf{ \,=\, }} - \left( {{\mathbf{CB}}_{{{\mathbf{u0}}}} } \right)^{{ - {\mathbf{1}}}} {\mathbf{Gsgn(S) = }} - \left( {{\mathbf{CB}}_{{{\mathbf{u0}}}} } \right)^{{ - {\mathbf{1}}}} \left[ {\begin{array}{*{20}c} {g_{1} } & 0 \\ 0 & {g_{2} } \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {\text{sgn} (s_{1} )} \\ {\text{sgn} (s_{2} )} \\ \end{array} } \right] $$
(11)

where g 1 and g 2 are undetermined parameters.

So, the controller is

$$ {\mathbf{U = U}}_{{{\mathbf{eq}}}} {\mathbf{ \,+\, U}}_{{{\mathbf{rob}}}} $$
(12)

Substituting Eq. (12) into (10) we obtain

$$ {\dot{\mathbf{S}}}= - {\mathbf{Gsgn(S) + CB}}_{{{\mathbf{u0}}}} {\mathbf{d(x,t)}} $$
(13)

In addition, in order to decouple the sliding, assuming

$$ {\mathbf{CB}}_{{{\mathbf{u0}}}} = \left[ {\begin{array}{*{20}c} 1 & {c_{1} } \\ 1 & {c_{2} } \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {\frac{{K_{{\alpha_{0} 3}} }}{mu}} & {\frac{{K_{{\alpha_{0} 4}} }}{mu}} \\ {\frac{{L_{3} K_{{\alpha_{0} 3}} }}{{I_{z} }}} & {\frac{{L_{4} K_{{\alpha_{0} 4}} }}{{I_{z} }}} \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {\rho_{1} } & 0 \\ 0 & { - \rho_{2} } \\ \end{array} } \right] $$
(14)

where

$$ c_{1} = \frac{{ - I_{z} }}{{muL_{4} }} > 0,\quad c_{2} = \frac{{ - I_{z} }}{{muL_{3} }} > 0,\quad \rho_{1} = \frac{{K_{3} }}{mu}\left( {1 - \frac{{L_{3} }}{{L_{4} }}} \right) > 0,\quad \rho_{2} = \frac{{K_{4} }}{mu}\left( {\frac{{L_{4} }}{{L_{3} }} - 1} \right) > 0 $$
(15)

Constructing a Lyapunov function V T = S T S/2, then the time derivative of V T can be obtained

$$ \begin{aligned} {\dot{V}}_{T}&= {\mathbf{S}}^{{\mathbf{T}}} {\dot{\mathbf{S}}} = {\mathbf{S}}^{{\mathbf{T}}} \left[ {{\mathbf{ - Gsgn(S) + CB}}_{{{\mathbf{u0}}}} {\mathbf{d(x,t)}}} \right] \\ &= - \left[ {\begin{array}{*{20}c} {s_{1} } & {s_{2} } \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {g_{1} } & 0 \\ 0 & {g_{2} } \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {\text{sgn} (s_{1} )} \\ {\text{sgn} (s_{2} )} \\ \end{array} } \right] + \left[ {\begin{array}{*{20}c} {s_{1} } & {s_{2} } \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {\rho_{1} } & 0 \\ 0 & { - \rho_{2} } \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {d_{1} (x,t)} \\ {d_{2} (x,t)} \\ \end{array} } \right] \\ &= - g_{1} \left| {s_{1} } \right| - g_{2} \left| {s_{2} } \right| + \rho_{1} s_{1} d_{1} (x,t) - \rho_{2} s_{2} d_{2} (x,t) \\ &\le - \left| {s_{1} } \right|\left( {g_{1} - \rho_{1} \left| {d_{1} (x,t)} \right|} \right) - \left| {s_{2} } \right|\left( {g_{2} - \rho_{2} \left| {d_{2} (x,t)} \right|} \right) \\ \end{aligned} $$
(16)

Equation (16) indicates that the control system can be guaranteed to be asymptotically stable (because the derivative of Lyapunov function V T is no more than 0) if we choose two parameters g 1 and g 2 satisfying Eq. (17).

$$ \left\{ \begin{gathered} \left| {d_{1} (x,t)} \right| \le g_{1} /\rho_{1} \hfill \\ \left| {d_{2} (x,t)} \right| \le g_{2} /\rho_{2} \hfill \\ \end{gathered} \right. $$
(17)

In addition, in order to reduce the chattering, the sgn(∙) function is substituted by a saturation function.

$$ sat(s_{i} ) = \left\{ {\begin{array}{*{20}c} 1 & {s_{i} > 1} \\ {s_{i} } & {\left| {s_{i} } \right| \le 1} \\ { - 1} & {s_{i} < - 1} \\ \end{array} ,\quad i = 1,2} \right. $$
(18)

5 The Modified Controller

Unlike the two-axle vehicle, the sliding model controller designed for all-wheel steering of four-axle vehicle cannot be applied directly because of the adverse-phase steering angle inputs to the third and fourth axle. The simple step steer simulation under linear 2DOF mode illustrates this problem. Vehicle starts step steer at 0.1 s with a constant velocity 65 km/h and steering angle of the first axle input 3º. The parameters of four-axle vehicle are shown in Table 1. The results are shown in Figs. 2, 3 and 4.

Table 1 Vehicle and control parameters
Full size table
Fig. 2
figure 2

The sideslip angle. a Eq. (12), b Eq. (19)

Full size image
Fig. 3
figure 3

The yaw rate. a Eq. (12), b Eq. (19)

Full size image
Fig. 4
figure 4

The steer angles of 3rd and 4th axle. a Eq. (12), b Eq. (19)

Full size image

It can be seen from the Figs. 2a and 3a that the controller got from Eq. (12) can make the sideslip zero and keep the yaw rate tracking the yaw rate of DFAS vehicle. However, Fig. 3a illustrates that it brings about the adverse-phase steering inputs to the third and fourth axle which will result in serious tire wear. Moreover, large adverse-phase steering angle will reduce stability and bring driver bad handling feeling. So a modified controller is proposed as follows

$$ {\mathbf{U}}^{{\mathbf{'}}} = \frac{1}{2}\left[ {\begin{array}{*{20}c} k & k \\ 1 & 1 \\ \end{array} } \right]{\mathbf{U}} $$
(19)

For the modified controller, the same step steer simulation is carried out. And results are also shown in Figs. 2, 3 and 4. It is shown in Fig. 2b that although the sideslip angle is not zero, it is a very small. Correspondingly, in Fig. 3b, the yaw rate does not track the DFAS vehicle, but it is not so far than the reference. Those prove the modified controller almost does not deteriorate the performance. The adverse-phase steering turns into a same-phase steering shown in Fig. 3b with small value.

6 Co-simulation and Results

In order to investigate the effect of the modified controller, double lane change test and crosswind disturbance test are carried out [8]. The modified controller is built in Matlab/Simulink. And a high precision vehicle model is developed in TruckSim where we choose the “Military: Armored combat vehicle, 8 × 8(ii–ii)” and adopt the default driver model. The real velocity, the steering angle of first axle, the sideslip angle and the yaw rate computed from the vehicle model are considered as the feedback inputs for the controller. Then the steering angles of 3rd axle and 4th axle are outputted by the controller. Though this co-simulation, two types of tests of driver-controller-vehicle close-loop system can be easily accomplished.

6.1 Double Lane Change Test

“Double Lane Change @ 65 km/h” procedure containing a preview driver mode and a given double lane change road is adopted for double lane change test. Here, two road surface conditions were prepared: dry road (tire-road friction coefficient μ = 0.85) and wet road (μ = 0.3). Vehicle velocity is 65 km/h. The results are shown in Figs. 5, 6, 7, 8, and 9.

Fig. 5
figure 5

Vehicle trajectory. a μ = 0.85, b μ = 0.3

Full size image
Fig. 6
figure 6

The sideslip angle. a μ = 0.85, b μ = 0.3

Full size image
Fig. 7
figure 7

The yaw rate. a μ = 0.85, b μ = 0.3

Full size image
Fig. 8
figure 8

The steer angles of 3rd axle and 4th axle. a μ = 0.85, b μ = 0.3

Full size image
Fig. 9
figure 9

The steering wheel angle. a μ = 0.85, b μ = 0.3

Full size image

It can be seen from Fig. 5, whether on dry road or wet road, AWS vehicle has smaller lateral offset than DFAS vehicle. However, compared to the reference trajectory, the real trajectory on wet road has larger lateral offset than that on dry road. This illustrates that although the driver tries to cover this test, the reduced lateral force of tire makes it difficult to accomplish. Comparing the sideslip angle (Fig. 6) and the yaw rate (Fig. 7), driver inclines the AWS vehicle because of its smaller sideslip angle and nearly unchanged yaw rate whether on dry road or wet road. Figure 8 shows the steering angle of 3rd axle and 4th axle which come from the modified controller outputs. The max steering angle is 1.5º on dry road, and 4º on wet road. This is an acceptable value at the high velocity 65 km/h. In Fig. 9 the steering wheel angle indicates the AWS vehicle reduces the driver’s work. In summary, the double lane change test under two road surface conditions shows that the modified controller has good robustness in the tire cornering stiffness perturbation, and improves handling and stability.

6.2 Crosswind Disturbance Test

Like double lane change test, we adopt default crosswind test procedure which has “No Offset w/1 s. Preview” driver path follower, the default vehicle velocity 80 km/h and the default wind velocity 100 km/h. Driver tries to keep a straight line to pass through a left crosswind disturbance firstly then a right crosswind disturbance. The simulation results are shown in Figs. 10, 11, 12 and 13.

Fig. 10
figure 10

Vehicle trajectory

Full size image
Fig. 11
figure 11

The sideslip angle

Full size image
Fig. 12
figure 12

Steer angle of 3rd axle and 4th axle

Full size image
Fig. 13
figure 13

The steering wheel angle

Full size image

Figure 10 shows that the vehicle trajectory of AWS vehicle with modified sliding mode controller has the smaller lateral offset than the DFAS vehicle. In Fig. 11, the max sideslip angle of DFAS vehicle is 1.7º, but just 0.5º of AWS vehicle. The smaller lateral offset and sideslip angle show the modified controller has better performance in rejection of crosswind disturbance. The max steering angle of 3rd axle and 4th axle is 1.2º shown in Fig. 12, which imply its few energy input. At last, the smaller steering wheel angle of AWS vehicle shows the reducing of driver’s work.

7 Conclusion

A sliding mode controller to control the steering angles of the third axle and forth axle is proposed for a four-axle vehicle to improve handling and stability. In order to avoid the adverse-phase steering angle input for the third and fourth axle, a modified controller is given which is a compromise between the control performance and the tire wear. Then the effectiveness of the modified controller is verified though double lane test and crosswind disturbance test. The simulation results show that the modified SMC has robustness to vehicle parameter perturbations and insensitivity to crosswind disturbance. Moreover, it could enhance the handling performance and stability of all-wheel steering four-axle vehicle compared with traditional DFAS vehicle.