Reconstruction-Based a Posteriori Error Estimators for the Transport Equation

Abstract

We present a unified approach to build error estimators based on H(div)-reconstructed fluxes on the primal mesh, inspired by the hypercircle method. Here, the transport equation is considered and discretized by discontinuous Galerkin, nonconforming and conforming finite elements. We describe the local computation of fluxes on patches, obtain upper error bounds and show some numerical tests.

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Introduction

In order to achieve mesh adaptivity, one needs reliable and efficient, easily computable a posteriori error estimators. A recent approach for their definition is based on the reconstruction of locally conservative fluxes in the Raviart-Thomas finite element space, yielding an a posteriori error estimator which consists only of the L ²-norm of a piecewise H(div)-vector.

Our aim is to propose a unified framework for several finite element approximations (conforming, nonconforming and discontinuous Galerkin). In this paper, we focus on the transport equation but the method can be extended to other operators.

The idea of using H(div)-reconstruction was initially proposed in [4] and has since been developed in several papers. As regards the diffusion-convection-reaction problem, the works [3] for the dG method and [5] for the mixed finite element method yield a unified approach, in which the fluxes are constructed on a dual mesh formed by dual volumes around each vertex of the primal mesh.

The main advantage of our approach is to use, contrarily to the previous references, only the primal mesh for the flux reconstruction, which presents certain facilities from a computational point of view. For this purpose, the construction of the H(div)-vector is inspired by the hypercircle method [1] and is achieved on patches, which may overlap and which depend on the type of the employed finite elements. The definition of the patches is related to the support of the basis functions.

In this paper, we explain the main ideas of the method and show first numerical results. In particular, we describe the construction of the a posteriori estimator for three discretizations on triangular meshes: discontinuous Galerkin, nonconforming and continuous elements. The two latter methods necessitate stabilization. For the sake of brievety, we discuss here only SUPG stabilization in the conforming case.

2 Unified Framework: The Main Ideas

We consider the model problem in a polygonal domain Ω of ${\mathbb{R}}^{2}$:

$$\begin{array}{rcl} \boldsymbol \beta \cdot \nabla u& =& f\text{ in }\Omega \\ u& =& g\text{ on }\partial {\Omega }^{-}\end{array}$$

(1)

where $\boldsymbol \beta \in {\mathbb{R}}^{2}$, $f \in {L}^{2}(\Omega )$, $g \in {L}^{2}(\partial {\Omega }^{-})$ are given data and where the inflow boundary is defined by $\partial {\Omega }^{-} = \left \{x \in \partial \Omega ;\boldsymbol \beta \cdot \vec{ n}(x) < 0\right \}$. We also put $\partial {\Omega }^{+} = \partial \Omega \setminus \partial {\Omega }^{-}$.

The weak formulation of (1) consists in finding u ∈ V ^g such that

$$a(u,v) = \int \limits _{\Omega }fv\,dx,\quad \forall v \in {V }^{0}$$

where

$$\begin{array}{rcl} & a(u,v) = \int \limits _{\Omega }\boldsymbol \beta \cdot \nabla u\,v\,dx, & \\ & V = \left \{v \in {L}^{2}(\Omega );\boldsymbol \beta \cdot \nabla v \in {L}^{2}(\Omega )\right \},\quad {V }^{g} = \left \{v \in V ;\,v_{\vert \partial {\Omega }^{-}} = g\right \}.& \\ \end{array}$$

Let $(\mathcal{K}_{h})_{h>0}$ be a regular family of triangulations of Ω consisting of triangles and let $\mathcal{S}_{h}^{int}$ the set of internal edges. We denote by $\vec{n}$ the outward unit normal to $\partial \Omega$. On any $S \in \mathcal{S}_{h}^{int}$ such that $\left \{S\right \} = \partial K_{1} \cap \partial K_{2}$, we define a unit normal $\vec{n}_{S}$ and for a function ψ with $\psi _{\vert K_{i}} \in \mathcal{C}(K_{i})$ we set: ${\psi }^{in}(\vec{x}) =\lim _{\epsilon \rightarrow 0}\psi \left (\vec{x} - \epsilon \vec{n}_{S}\right )$, ${\psi }^{ex}(\vec{x}) =\lim _{\epsilon \rightarrow 0}\psi \left (\vec{x} + \epsilon \vec{n}_{S}\right )$ and the jump $\left [\psi \right ] = {\psi }^{in} - {\psi }^{ex}$. For $x \in \mathbb{R}$, let ${x}^{-} =\min \{0,x\}$ and ${x}^{+} = x - {x}^{-}$. It is useful to recall the Raviart-Thomas space $RT_{k} = P_{k}^{2} +\vec{ x}P_{k}$, $k \in \mathbb{N}$.

We solve Eq. (1) by any of the following finite element methods: discontinuous Galerkin, nonconforming or conforming, leading to a discrete weak formulation

$$u_{h} \in V _{h},\quad \quad a_{h}(u_{h},v_{h}) = l_{h}(v_{h})\quad \forall v_{h} \in V _{h}$$

where the finite dimensional space V _h and the bilinear and linear forms $a_{h}(\cdot ,\cdot )$, l _h ( ⋅) will be specified later; the boundary conditions are treated by Nitsche’s method.

The goal of the method is to define an approximation $\boldsymbol \sigma$ of $\boldsymbol \beta u$ satisfying

$$\begin{array}{rcl} \boldsymbol \sigma & \in & H(\mathrm{div},\Omega ),\end{array}$$

(3)

$$\begin{array}{rcl} \mathrm{div}\boldsymbol \sigma & =& f_{h}\quad \text{ in}\,\,\,\Omega ,\end{array}$$

(4)

$$\begin{array}{rcl} \boldsymbol \sigma \cdot \vec{ n}& =& \boldsymbol \beta \cdot \vec{ n}g_{h}\quad \text{ on}\,\,\,\partial {\Omega }^{-},\end{array}$$

(5)

$$\begin{array}{rcl} \boldsymbol \sigma \cdot \vec{ n}& =& \boldsymbol \beta \cdot \vec{ n}u_{h}\quad \text{ on}\,\,\,\partial {\Omega }^{+},\end{array}$$

(6)

where f _h and g _h are appropriate projections of the data f and g.

Actually, we do not compute $\boldsymbol \sigma$ but $\boldsymbol \tau =\boldsymbol \sigma -\boldsymbol \beta \tilde{u}_{h}$ with {u} _h either equal to u _h itself or to a correction, depending on the employed method. The local and global a posteriori error estimators are then given by $\eta _{K}^{2} =\Vert \boldsymbol \tau \Vert _{0,K}^{2}$ and ${\eta }^{2} = \sum \limits _{K\in \mathcal{K}_{h}}\eta _{K}^{2} =\Vert \boldsymbol \tau \Vert _{0,\Omega }^{2}$.

The global vector $\boldsymbol \tau$ is obtained as the sum of local contributions $\boldsymbol \tau _{\omega }$ on (overlapping or non-overlapping) patches, a patch ω being defined as the support of a finite element basis function. On each ω, we built a piecewise H(div)-vector $\boldsymbol \tau _{\omega }$ satisfying $\left (\boldsymbol \tau _{\omega }\right )_{\vert K} \in RT_{k}$ for any $K \subset \omega$. Its computation is achieved by imposing the values of $\int \limits _{K}\boldsymbol \tau _{\omega } \cdot \mathbf{r}\,dx$ for any $\mathbf{r} \in P_{k-1}^{2}$ if k > 0 and of $\int \limits _{S}\boldsymbol \tau _{\omega } \cdot \mathbf{n}\varphi \,ds$ on any edge $S \subset \partial \omega$, for any basis function $\varphi$ such that $S \subset \mathrm{ supp}\,\varphi$. In addition, we impose certain values of $\int \limits _{K}\mathrm{div}\boldsymbol \tau _{\omega }\varphi \,dx$ for $K \subset \omega$ and of $\int \limits _{S}\left [\boldsymbol \tau _{\omega } \cdot \mathbf{n_{s}}\right ]\varphi \,ds$ on any edge S internal to the patch.

Note that there are more equations than degrees of freedom to be determined. For each finite element method, the corresponding values are computed such that the above linear system is compatible and moreover, the relations (3)–(6) hold.

As regards the error analysis, we focus here on upper bounds with respect to the following weak norm on V + V _h :

$$\vert \vert \vert u\vert \vert \vert =\sup _{v\in W}\frac{-\int \limits _{\Omega }u\boldsymbol \beta \cdot \nabla vdx + \int \limits _{\partial {\Omega }^{+}}\boldsymbol \beta \cdot \mathbf{n}uv\,ds} {\Vert \nabla v\Vert _{0,\Omega }}$$

(7)

where the Hilbert space W is defined by $W = \left \{v \in {H}^{1}(\Omega );v_{\vert \partial {\Omega }^{-}} = 0\right \} \subset {V }^{0}$.

For the discontinuous Galerkin and the nonconforming methods, we obtain by integration by parts, for any v ∈ W and $v_{h} \in V _{h}$, that:

$$\begin{array}{rcl} & -\int \limits _{\Omega }(u - u_{h})\boldsymbol \beta \cdot \nabla vdx + \int \limits _{\partial {\Omega }^{+}}\boldsymbol \beta \cdot \mathbf{n}(u - u_{h})v\,ds & \\ & = a(u,v) - a_{h}(u_{h},v) & \\ & = -\int \limits _{\mathcal{K}_{h}}\boldsymbol \tau \cdot \nabla (v - v_{h})\,dx + \int \limits _{\Omega }(f - f_{h})(v - v_{h})\,dx.&\end{array}$$

(8)

As regards the conforming method, it is well-known that it necessitates an additional stabilization term, which we denote by $s_{h}(\cdot ,\cdot )$. The norm of the error is then modified correspondingly. In the case of the SUPG method, we can show:

$$\begin{array}{rcl} & -\int \limits _{\Omega }(u - u_{h})\boldsymbol \beta \cdot \nabla vdx + \int \limits _{\partial {\Omega }^{+}}\boldsymbol \beta \cdot \mathbf{n}(u - u_{h})v\,ds + s_{h}(u - u_{h},v)& \\ & = a(u,v) - a_{h}(u_{h},v) + s_{h}(u,v) &\end{array}$$

(9)

which will be further discussed in Sect. 3.3.

Finally, for any of the three methods one deduces the upper error bound:

$$\vert \vert \vert u - u_{h}\vert \vert \vert \leq \,\,\, \eta + ch\Vert f - f_{h}\Vert _{0,\Omega }.$$

(10)

3 Computation of Local Vectors on Patches

In what follows, we describe how to compute the vectors on a patch for the discontinuous Galerkin, the nonconforming and the conforming methods. For simplicity of presentation, we consider here k = 1 although it is possible to extend the methods to higher polynomial degrees. Nevertheless, the extension in the dG case being trivial, we allow for arbitrary k in this case.

3.1 Discontinuous Galerkin Method

The discrete formulation is obtained by taking V _h the space of (fully discontinuous) piecewise polynomials of degree k on any cell and

$$\begin{array}{rcl} a_{h}(u_{h},v_{h})& =& \int \limits _{\mathcal{K}_{h}}\boldsymbol \beta \cdot \nabla u_{h}v_{h}\,dx + \int \limits _{\mathcal{S}_{h}^{int}}F(v_{h},\mathbf{n}_{S},-\boldsymbol \beta )[u_{h}]\,ds + \int \limits _{\partial {\Omega }^{-}}\vert \boldsymbol \beta \cdot \mathbf{n}\vert u_{h}v_{h}ds, \\ l_{h}(v_{h})& =& \int \limits _{\mathcal{K}_{h}}fv_{h}\,dx + \int \limits _{\partial {\Omega }^{-}}\vert \boldsymbol \beta \cdot \mathbf{n}\vert gv_{h}\,ds, \\ \end{array}$$

where the upwind numerical flux on an internal edge S is given by:

$$F(v_{h},\mathbf{n}_{S},\boldsymbol \beta ) = {(\boldsymbol \beta \cdot \mathbf{n}_{S})}^{+}v_{ h}^{in} + {(\boldsymbol \beta \cdot \mathbf{n}_{ S})}^{-}v_{ h}^{ex}.$$

For any cell K, we take ω _K  = K and we define $\boldsymbol \tau _{\omega _{K}} \in RT_{k}$ by imposing

$$\begin{array}{rcl} \int \limits _{K}\boldsymbol \tau _{\omega _{K}} \cdot \mathbf{r}\,dx& =& 0,\quad \forall \mathbf{r} \in P_{k-1}^{2}\quad \text{ if }k > 0\end{array}$$

(11)

$$\begin{array}{rcl} \int \limits _{S}\boldsymbol \tau _{\omega _{K}} \cdot \vec{ n}\varphi \,ds& =& -\int \limits _{S}{(\boldsymbol \beta \cdot \vec{ n})}^{-}[u_{ h}]\varphi \,ds,\quad \forall S \subset \partial K,\quad \forall \varphi \in P_{k}.\end{array}$$

(12)

On a boundary edge S, we put [u _h ] = 0 if $S \subset \partial {\Omega }^{+}$ and $[u_{h}] = u_{h} - g_{h}$ if $S \subset \partial {\Omega }^{-}$, with g _h the piecewise P _k L ²-orthogonal projection of g. The conditions (11) and (12) correspond to the degrees of freedom of RT _k and thus completely determine $\boldsymbol \tau _{\omega _{K}}$.

By taking as test-function in the weak formulation $\varphi \chi _{K}$ with $\varphi \in P_{k}$ and χ _K the characteristics function of the cell K, it follows thanks to the previous relations that

$$\mathrm{div}\boldsymbol \tau _{\omega _{K}} = f_{h} -\boldsymbol \beta \cdot \nabla u_{h}\quad \mathrm{ and}\quad \left [\boldsymbol \tau _{\omega _{K}}\right ] \cdot \vec{ n}_{S} = -\boldsymbol \beta \left [u_{h}\right ] \cdot \vec{ n}_{S},$$

for all $K \in \mathcal{K}_{h}$ and $S \subset \partial K$, with f _h the L ²-orthogonal projection of f on piecewise P _k elements. We finally put $\boldsymbol \tau = \sum \limits _{K\in \mathcal{K}_{h}}\boldsymbol \tau _{\omega _{K}}$ and $\boldsymbol \sigma =\boldsymbol \tau +\boldsymbol \beta u_{h}$.

Note that (8) is obtained by writing $a_{h}(\cdot ,\cdot )$ in the following equivalent form:

$$a_{h}(u_{h},v_{h}) = -\int \limits _{\mathcal{K}_{h}}u_{h}\boldsymbol \beta \cdot \nabla v_{h}\,dx+\int \limits _{\mathcal{S}_{h}^{int}}F(u_{h},\mathbf{n}_{S},\boldsymbol \beta )[v_{h}]\,ds+\int \limits _{\partial {\Omega }^{+}}\boldsymbol \beta \cdot \mathbf{n}u_{h}v_{h}ds.$$

3.2 Nonconforming Method

We now consider V _h the space of piecewise linear functions, continuous at the midpoints of the internal edges and we take the same forms as in the dG case.

To any edge S, we associate a patch ω _S consisting of the support of the basis function $\varphi _{S}$ associated to S. In the case of an internal edge $\{S\} = \partial K_{1} \cap \partial K_{2}$, we have $\omega _{S} = K_{1} \cup K_{2}$ and we build $\boldsymbol \tau _{\omega _{S}}$ with $(\boldsymbol \tau _{\omega _{S}})_{\vert K_{i}} \in RT_{1}$ for $1 \leq i \leq 2$ by defining the corresponding 16 degrees of freedom as follows. We impose for i = 1, 2:

$$\begin{array}{rcl} \boldsymbol \tau _{\omega _{S}} \cdot \mathbf{n}& =& 0\quad \text{ on}\,\,\partial \omega _{S}\end{array}$$

(13)

$$\begin{array}{rcl} \int \limits _{K_{i}}\boldsymbol \tau _{\omega _{S}}\,dx& =& \vec{0},\end{array}$$

(14)

$$\begin{array}{rcl} \int \limits _{K_{i}}\mathrm{div}\boldsymbol \tau _{\omega _{S}}\varphi _{S}\,dx& =& \int \limits _{K_{i}}(f -\boldsymbol \beta \cdot \nabla u_{h})\varphi _{S}\,dx + \int \limits _{\partial K_{i}\setminus S}{(\boldsymbol \beta \cdot \mathbf{n})}^{-}[u_{ h}]\varphi _{S}\,ds\end{array}$$

(15)

$$\begin{array}{rcl} \int \limits _{K_{i}}\mathrm{div}\boldsymbol \tau _{\omega _{S}}\varphi _{2}^{(i)}\,dx& =& -\int \limits _{S}{(\boldsymbol \beta \cdot \mathbf{n})}^{-}[u_{ h}]\varphi _{2}^{(i)}\,ds.\end{array}$$

(16)

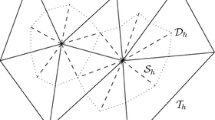
Here above, $\varphi _{2}^{(i)}$ and $\varphi _{3}^{(i)}$ denote the two other basis functions on K _i , see Fig. 1a.

Remark 1.

Note that thanks to the relation $\varphi _{S} + \varphi _{2}^{(i)} + \varphi _{3}^{(i)} = 1$ on K _i for $1 \leq i \leq 2$, one can impose either $\int \limits _{K_{i}}\mathrm{div}(\boldsymbol \tau _{\omega _{S}})\varphi _{2}^{(i)}\,dx$ or $\int \limits _{K_{i}}\mathrm{div}(\boldsymbol \tau _{\omega _{S}})\varphi _{3}^{(i)}\,dx$ in (16).

By taking as test-function in the discrete formulation $\varphi _{S}$ and by using that $(\varphi _{S})\vert _{S}\,=\,1$, it follows from (13), (15) and (16) that

$$\begin{array}{rcl} \int \limits _{S}[\boldsymbol \tau _{\omega _{S}} \cdot \mathbf{n}_{S}]ds& =& -\int \limits _{S}\boldsymbol \beta \cdot \mathbf{n}_{S}[u_{h}]ds \\ \int \limits _{S}[\boldsymbol \tau _{\omega _{S}} \cdot \mathbf{n}_{S}]\varphi _{2}^{(i)}\,ds& =& -\int \limits _{S}\boldsymbol \beta \cdot \mathbf{n}_{S}[u_{h}]\varphi _{2}^{(i)}\,ds\quad i = 1,\end{array}$$

(2.)

Since ${\varphi _{2}^{(1)}}_{\vert S} = {\varphi _{2}^{(2)}}_{\vert S}$ and $\left \{1,{\varphi _{2}^{(1)}}_{\vert S}\right \}$ is a basis of P ₁ on S, we deduce from the two previous equalities that $[\boldsymbol \tau _{\omega _{S}} \cdot \mathbf{n}_{S}] = -\boldsymbol \beta \cdot \mathbf{n}_{S}[u_{h}]$ on S. Since $\boldsymbol \tau = \sum \limits _{S\in \mathcal{S}_{h}}\boldsymbol \tau _{\omega _{S}}$ satisfies $[\boldsymbol \tau \cdot \mathbf{n}_{S}] = [\boldsymbol \tau _{\omega _{S}} \cdot \mathbf{n}_{S}]$ on any S, it follows that $\boldsymbol \sigma =\boldsymbol \tau +\boldsymbol \beta u_{h}$ belongs to $H(\mathrm{div},\Omega )$.

Fig. 1

Patch and basis functions for the nonconforming and conforming methods. (a) Nonconforming. (b) Conforming

3.3 Conforming Method

V _h is now the space of piecewise linear and continuous functions. For any node N we define the patch $\omega _{N} = \bigcup _{1\leq i\leq i_{N}}K_{i}$ where $\{K_{i}\}_{1\leq i\leq i_{N}}$ is the set of cells containing N as node. We consider the discrete formulation with SUPG stabilization (cf. [2]), which yields:

$$\begin{array}{rcl} a_{h}(u_{h},v_{h})& =& \int \limits _{\Omega }\boldsymbol \beta \cdot \nabla u_{h}v_{h}\,dx + \int \limits _{\partial {\Omega }^{-}}\vert \boldsymbol \beta \cdot \mathbf{n}\vert u_{h}v_{h}\,ds + s_{h}(u_{h},v_{h}), \\ s_{h}(u_{h},v_{h})& =& \sum \limits _{K\in \mathcal{K}_{h}}\varDelta _{K} \int \limits _{K}\boldsymbol \beta \cdot \nabla u_{h}\boldsymbol \beta \cdot \nabla v_{h}\,dx, \\ l_{h}(v_{h})& =& \int \limits _{\Omega }fv_{h}\,dx + \sum \limits _{K\in \mathcal{K}_{h}}\varDelta _{K} \int \limits _{K}f\boldsymbol \beta \cdot \nabla v_{h} + \int \limits _{\partial {\Omega }^{-}}\vert \boldsymbol \beta \cdot \mathbf{n}\vert gv_{h}\,ds \\ \end{array}$$

and δ _K a stabilization parameter. In the case of an internal node N, we define the local vector $\boldsymbol \tau _{\omega _{N}}$ such that $(\boldsymbol \tau _{\omega _{N}})_{\vert K_{i}} \in RT_{0}$ for $1 \leq i \leq i_{N}$ and the corresponding 3 i _N degrees of freedom are given by:

$$\begin{array}{rcl} \boldsymbol \tau _{\omega _{N}} \cdot \mathbf{n}& =& 0\quad \text{ on}\,\,\partial \omega _{N},\end{array}$$

(17)

$$\begin{array}{rcl} \int \limits _{K_{i}}\mathrm{div}\boldsymbol \tau _{\omega _{N}}\varphi _{N}\,dx& =& \frac{1} {3}\int \limits _{K_{i}}(f -\boldsymbol \beta \cdot \nabla u_{h})\varphi _{N}\,dx\quad 1 \leq i \leq i_{N},\end{array}$$

(18)

$$\begin{array}{rcl} \int \limits _{S_{i}}[\boldsymbol \tau _{\omega _{i}} \cdot \mathbf{n}_{S_{i}}]\varphi _{N}\,ds& =& \frac{1} {2}\int \limits _{S_{i}}\boldsymbol \beta \cdot \mathbf{n}_{S_{i}}[\varDelta _{K}(\boldsymbol \beta \cdot \nabla u_{h} - f_{h})]\varphi _{N}\,ds\quad 1 \leq i \leq i_{N}\end{array}$$

(19)

where S _i denotes an interior edge of the patch which has N as a node. Note that the above linear system (17)–(19) is compatible but does not have a unique solution. Indeed, let us denote by $\mathcal{A}_{N}$ the linear operator of the previous system. Then one can see that $\mathrm{Ker}\mathcal{A}_{N}$ is of dimension 1 and contains the vectors of $H(\mathrm{div},\omega _{N})$ which are divergence free, piecewise RT ₀ and of zero normal trace on $\partial \omega _{N}$. One can also show that the kernel of $\mathcal{A}_{N}$ is characterized by:

$$\boldsymbol \theta \in \mathrm{ Ker}\mathcal{A}_{N}\,\,\Longleftrightarrow\,\, \int \limits _{\Omega }\boldsymbol \theta \cdot \nabla vdx = 0,\quad \forall v \in {H}^{1}(\Omega ).$$

Let us next consider the orthogonal decomposition $\boldsymbol \tau _{\omega _{N}} =\boldsymbol \tau _{\omega _{N}}^{\perp } +\boldsymbol \tau _{\omega _{N}}^{Ker}$. According to (8), it now follows that only $\boldsymbol \tau _{\omega _{N}}^{\perp }$ contributes to the error estimator η. Therefore, in order to determine it, we add to the system (17)–(19) the condition $\boldsymbol \tau _{\omega _{N}} \perp \mathrm{ Ker}\mathcal{A}$.

We set $\boldsymbol \tau = \sum \limits _{N\in \mathcal{N}_{h}}\boldsymbol \tau _{\omega _{N}}$. The numerical scheme leads to a flux $\boldsymbol \sigma =\boldsymbol \tau +\boldsymbol \beta \tilde{u}_{h}$, where {u} _h represents a correction of u _h defined on each cell by $\tilde{u}_{h} = u_{h} - \varDelta _{K}(\boldsymbol \beta \cdot \nabla u_{h} - f_{h})$, with f _h the piecewise constant L ²-orthogonal projection of f.

As regards the a posteriori error analysis, we obtain by imposing appropriate values of $\boldsymbol \tau \cdot \mathbf{n}$ on the boundary $\partial \Omega$ that

$$\begin{array}{rcl} a(u,v) - a_{h}(u_{h},v) + s_{h}(u,v)& =& -\int \limits _{\mathcal{K}_{h}}\boldsymbol \tau \cdot \nabla (v - v_{h})\,dx + \int \limits _{\Omega }(f - f_{h})(v - v_{h})\,dx \\ & & +\sum \limits _{K\in \mathcal{K}_{h}}\varDelta _{K} \int \limits _{K}(f - f_{h})\boldsymbol \beta \cdot \nabla (v - v_{h})\,dx, \\ \end{array}$$

which implies the desired estimate (10).

4 Numerical Results

We show next our first numerical results, obtained with our C$++$ library Concha. We consider $\Omega ={ \left ]-1,1\right [}^{2}$ with data such that $u(\vec{x}) =\mathrm{ {e}}^{-\frac{\Vert \vec{x}-\vec{x}_{0}\Vert } {\varDelta } }$ is an exact solution, where $\vec{x}_{0} = (0.5,0.5)$ and δ = 0. 03. We employ the dG method with k = 0 and then k = 1. We represent in Figs. 2 and 3 the error and the estimator with respect to the number of cells, for uniform and adaptive mesh refinements. We have used the L ²(Ω)-norm of the error since the weaker norm $\Vert \vert \cdot \vert \Vert$ is not easily computable. Besides the obvious gain, one can also see that both the error and the estimator converge with the same convergence rate $O({N}^{-\frac{k+1} {2} })$. For k = 1, we show in Fig. 4 a sequence of adapted meshes. As expected, the refinement takes place near $\vec{x}_{0}$.

Fig. 2

L ²-error versus estimator for dG approximation (k = 0) in log-log scale (Uniform mesh (left), Adaptive mesh (right))

Fig. 3

L ²-error versus estimator for dG approximation (k = 1) in log-log scale (Uniform mesh (left), Adaptive mesh (right))

Fig. 4

Sequence of adapted meshes for dG approximation (k = 1)