Corrected Stabilized Non-conforming Nodal Integration in Meshfree Methods

Abstract

A novel approach is presented to correct the error from numerical integration in Galerkin methods for meeting linear exactness. This approach is based on a Ritz projection of the integration error that allows a modified Galerkin discretization of the original weak form to be established in terms of assumed strains. The solution obtained by this method is the correction of the original Galerkin discretization obtained by the inaccurate numerical integration scheme. The proposed method is applied to elastic problems solved by the reproducing kernel particle method (RKPM) with first-order correction of numerical integration. In particular, stabilized non-conforming nodal integration (SNNI) is corrected using modified ansatz functions that fulfill the linear integration constraint and therefore conforming sub-domains are not needed for linear exactness. Illustrative numerical examples are also presented.

1 Introduction

As the name implies, meshfree methods are based on a discretization of the continuous problem without using a mesh, as opposed to the finite element method and related mesh-based methods. Meshfree methods therefore have several obvious advantages, especially when the mesh is the source of problems, e.g. in the large deformation analysis of structures or in the simulation of discontinuities such as cracks.

A crucial issue in Galerkin meshfree methods is domain integration, typically carried out by Gauß or nodal quadrature. In the former case, integration is performed using a regular cell structure or background mesh. Here, significant integration errors arise when the background mesh is not aligned with shape function supports, see [10]. Nodal integration, on the other hand, yields low convergence rates since the integrands are poorly integrated, and it also suffers from rank instability due to the shape function derivatives nearly vanishing at the particles. To cope with these problems Beissel and Belytschko [4] suggested a stabilization method for nodal integration that relies on a least squares residual term which is added to the total potential energy functional. Bonet and Kulasegaram [5] added terms to the derivatives of the shape functions to obtain an improved method. Chen et al. [8, 9, 13] proposed stabilized conforming nodal integration (SCNI), based on gradient smoothing which passes the linear patch test. However, its non-conforming counterpart termed stabilized non-conforming nodal integration (SNNI), see [7], is often used in practice because of its simplicity, particularly for fragment-impact type problems where the construction of conforming strain smoothing sub-domains is tedious, see [11]. The use of non-conforming strain smoothing with divergence operation in SNNI fails to pass the linear patch test, and integration error becomes an issue. Figure 1 illustrates the failure of SNNI. In this figure, the convergence curves for SCNI and SNNI are compared for the tube inflation problem, as presented in Sect. 5.2, and the low convergence rate in the case of SNNI is apparent.

Fig. 1

Failure of SNNI for the tube problem discussed in Sect. 5.2

Whenever a Galerkin discretization is used to find an approximate solution of the model problem at hand, its discretization error (the difference between the true solution and its Galerkin approximation) has to be controlled to obtain reliable numerical results. More precisely, error control means that the error is estimated by a reliable a posteriori error estimator. This is in general the best that can be done, since the error itself is in the infinite-dimensional trial and test space and therefore not easy to grasp. For further details on discretization error control the reader may consult Stein and Rüter [14] and Babuška et al. [3]. In addition to the discretization error, for numerical integration schemes such as SNNI the integration error (the difference between the true Galerkin solution and its quadrature approximation) has to be taken into account. However, since the integration error is in the same finite-dimensional trial and test space as both the true Galerkin solution and its quadrature approximation, there is, in principle, a chance to compute it exactly. Therefore, the integration error can be corrected rather than just estimated, which is demonstrated in this paper for the case of SNNI.

Babuška et al. [1] propose an energy norm a priori error estimate for the combined discretization and integration error (the difference between the true solution and its Galerkin quadrature approximation), provided that the integration error was corrected by a simple correction of the stiffness matrix to fulfill the so-called zero row-sum condition. This estimate was later extended by Babuška et al. [2] from linear basis functions to higher-order basis functions.

In this paper, we devise a scheme to correct the integration error induced from using SNNI. This correction approach is based on a modification of the test functions to fulfill the linear integration constraint as required to pass the linear patch test. With the corrected test functions, it becomes possible, under certain assumptions, to compute the true Galerkin solution using a modified bilinear form with SNNI.

The paper is organized as follows: in Sect. 2, the model problem of linear elasticity in its strong and weak forms is presented, as well as the associated Galerkin discretization. In Sect. 3, the correction approach to correct the error from numerical integration is introduced using the true Galerkin solution as the Ritz projection of the integration error. The correction is then applied to meshfree methods in Sect. 4, specifically to RKPM with SNNI employed. Numerical examples are presented in Sect. 5, where the correction approach is applied to problems in linear elasticity. The paper concludes with Sect. 6 which summarizes the major findings achieved from theoretical and numerical points of view.

2 The Model Problem of Linear Elasticity

This section gives a brief account of the model problem of linear elasticity in its strong and weak forms as well as its Galerkin discretization in an abstract setting.

2.1 Strong Form of the Model Problem

Let an isotropic, linear elastic body be given by the open, bounded, polygonal or polyhedral domain $\Omega \subset {\mathbb{R}}^{d}$ with dimension d. Its boundary $\Gamma = \partial \Omega$ consists of two disjoint parts such that $\Gamma =\bar{ {\Gamma }}_{D} \cup \bar{ {\Gamma }}_{N}$ with ${\Gamma }_{D}$ and ${\Gamma }_{N}$ being the portions of Γ where Dirichlet and Neumann boundary conditions are imposed, respectively.

The strong form of the elliptic, self-adjoint model problem of linear elasticity is to find the displacement field $u$ such that the field equations

$$\begin{array}{rcl} -\mathrm{div}\ \sigma (u) = f\quad \text{ in }\Omega & &\end{array}$$

(1a)

$$\begin{array}{rcl} \sigma - \mathbb{C} : \epsilon (u) = \mathbf{0}\quad \text{ in }\Omega & &\end{array}$$

(1b)

$$\begin{array}{rcl} \epsilon -{\nabla }^{\text{ sym}}u = \mathbf{0}\quad \text{ in }\Omega & &\end{array}$$

(1c)

subjected to the boundary conditions

$$\begin{array}{rcl} u = \bar{u}\quad \text{ on }{\Gamma }_{D}& &\end{array}$$

(1d)

$$\begin{array}{rcl} \sigma (u) \cdot n = \bar{t}\quad \text{ on }{\Gamma }_{N}& &\end{array}$$

(1e)

are fulfilled. Here, the given body forces $f$ and the prescribed boundary tractions $\bar{t}$ are assumed to be in ${L}_{2}(\Omega )$ and ${L}_{2}({\Gamma }_{N})$, respectively. Furthermore, $\sigma$ is the stress tensor, and $\epsilon$ is the strain tensor, which are related via the elasticity tensor $\mathbb{C}$ that depends on Young’s modulus E and Poisson’s ratio ν.

2.2 Weak Form of the Model Problem

In the weak form associated with (1a) we seek $u \in \mathcal{V} =\{ v \in { H}^{1}(\Omega )\,;\,{v}_{{\vert }_{{\Gamma }_{ D}}} = \bar{u}\}$ such that

$$a(u,v) = F(v)\quad \forall v \in {\mathcal{V}}_{0}$$

(2)

with ${\mathcal{V}}_{0} =\{ v \in { H}^{1}(\Omega )\,;\,{v}_{{\vert }_{{\Gamma }_{ D}}} = \mathbf{0}\}$. Moreover, $a : \mathcal{V}\times {\mathcal{V}}_{0} \rightarrow \mathbb{R}$ and $F : {\mathcal{V}}_{0} \rightarrow \mathbb{R}$ are bilinear and linear forms defined as

$$a(u,v) =\int\limits_{\Omega }\sigma (u) : \epsilon (v)\,\text{ d}V$$

(3)

and

$$F(v) =\int\limits_{\Omega }f \cdot v\,\text{ d}V +\int\limits_{{\Gamma }_{N}}\bar{t}\cdot v\,\text{ d}A,$$

(4)

respectively. Since a is coercive, and both a and F are bounded, $u \in \mathcal{V}$ exists and is the unique solution to (2) owing to the Lax-Milgram theorem.

2.3 Galerkin Discretization

In order to solve the weak form (2) using a Galerkin method, e.g. either a mesh-based method such as the finite element method (FEM) or a meshfree method such as RKPM, the Galerkin discretization of (2) is introduced. For this, the variational problem (2) is projected onto a finite-dimensional subspace ${\mathcal{V}}_{h}$ of $\mathcal{V}$ and we solve

$$a({u}_{h},{v}_{h}) = F({v}_{h})\quad \forall {v}_{h} \in {\mathcal{V}}_{0,h} \subset {\mathcal{V}}_{0}$$

(5)

for an approximate solution ${u}_{h} \in {\mathcal{V}}_{h}$. Since ${\mathcal{V}}_{h} \subset \mathcal{V}$, the approximate solution ${u}_{h}$ exists in ${\mathcal{V}}_{h}$ and is unique. Another conclusion that can be drawn from ${\mathcal{V}}_{0,h} \subset {\mathcal{V}}_{0}$ is that ${v}_{h} \in {\mathcal{V}}_{0}$ and thus we may subtract (5) from (2) to see that

$$a(u-{u}_{h},{v}_{h}) = 0\quad \forall {v}_{h} \in {\mathcal{V}}_{0,h},$$

(6)

which is the well-known Galerkin orthogonality condition, meaning that the discretization error $u-{u}_{h}$ is orthogonal to the test space ${\mathcal{V}}_{0,h}$.

3 Correction of the Numerical Integration Error

In this section, numerical integration in Galerkin methods is discussed, and a method to provide the correction (with specific form for the first-order correction shown in Sect. 4) of the associated integration error is derived to recover the true Galerkin solution that possesses the important Galerkin orthogonality relation.

3.1 Numerical Integration in Galerkin Methods

Whenever a Galerkin method is employed, numerical integration may become an issue. This is especially true for meshfree methods, owing to the overlapping supports of shape functions and the rational functions that need to be integrated. This is also true for mesh-based Galerkin methods, such as the extended finite element method (XFEM), where the derivatives of the enrichment functions have singularities at the crack tip. In these cases, we can only approximate a and F. We denote these approximations by a _h and F _h , respectively. Substituting a _h and F _h into (5), we now search for a solution ${u}_{hh}$ as an approximation of ${u}_{h}$ in the same space ${\mathcal{V}}_{h}$ such that

$${a}_{h}({u}_{hh},{v}_{h}) = {F}_{h}({v}_{h})\quad \forall {v}_{h} \in {\mathcal{V}}_{0,h}.$$

(7)

If the coercivity of ${a}_{h}$, and boundedness of ${a}_{h}$ and ${F}_{h}$ are not lost by the numerical integration, ${u}_{hh}$ is the unique solution to (7) in ${\mathcal{V}}_{h}$. However, the Galerkin orthogonality (6) is violated in this case, i.e. $a(u-{u}_{hh},{v}_{h})\neq 0$ for all ${v}_{h} \in {\mathcal{V}}_{0,h}$, since (7) is not a Galerkin discretization of (2). The Galerkin discretization (5) of the weak form (2) was obtained by replacing the trial and test spaces $\mathcal{V}$ and ${\mathcal{V}}_{0}$ with ${\mathcal{V}}_{h}$ and ${\mathcal{V}}_{0,h}$, respectively, while keeping the same model in the sense of a and F. Conversely, (7) is obtained from the Galerkin discretization (5) by replacing a and F with ${a}_{h}$ and F _h , respectively, while keeping the same spaces ${\mathcal{V}}_{h}$ and ${\mathcal{V}}_{0,h}$.

3.2 Correction of the Integration Error

In order to recover the true Galerkin solution ${u}_{h}$, the general idea in SCNI, see [8], is to modify the bilinear form ${a}_{h}$ in such a way that ${u}_{h}$ becomes the solution of (7) rather than its approximation ${u}_{hh}$. A similar idea is employed herein.

Let us first add and subtract ${u}_{h}$ in ${a}_{h}$ to see that (7) can be recast into

$${a}_{h}({u}_{h},{v}_{h}) - {a}_{h}({u}_{h} -{u}_{hh},{v}_{h}) = {F}_{h}({v}_{h})\quad \forall {v}_{h} \in {\mathcal{V}}_{0,h}.$$

(8)

The above variational problem can be interpreted as follows: in order to recover ${u}_{h}$ from (7), we propose to correct ${a}_{h}({u}_{h},{v}_{h})$ by the integration error represented as ${a}_{h}({u}_{h} -{u}_{hh},{v}_{h})$. However, to obtain the exact Galerkin solution from (8), it is necessary that the first argument in the second term of the left-hand side also depends on ${u}_{h}$ only. To this end, let us introduce the bilinear form $\mathop{a}\limits^{{{}_{\Delta }}}_{h} : {\mathcal{V}}_{h} \times {\mathcal{V}}_{0,h} \rightarrow \mathbb{R}$ defined as

$$\mathop{a}\limits^{{{}_{\Delta }}}_{h}({u}_{h},{v}_{h}) = -{a}_{h}({u}_{h} -{u}_{hh},{v}_{h})\quad \forall {v}_{h} \in {\mathcal{V}}_{0,h},$$

(9)

i.e. we introduce ${u}_{h}$ as the Ritz projection of ${u}_{h} -{u}_{hh}$. The bilinear form $\mathop{a}\limits^{{{}_{\Delta }}}_{h}$ can be designed such that the first argument is the same as in a _h , whereas the integration error is embedded in the second argument and thus $\mathop{a}\limits^{{{}_{\Delta }}}_{h}$ takes the general form

Here, the bar in the integral sign represents numerical integration, and $\epsilon ^{{}_{\Delta }}$ is an assumed strain tensor that takes the effect of the integration error into account as we shall see later in Sect. 4.3. With the definition (9), the weak form (8) turns into

$${a}_{h}({u}_{h},{v}_{h}) +\mathop{ a}\limits^{{{}_{\Delta }}}_{h}({u}_{h},{v}_{h}) = {F}_{h}({v}_{h})\quad \forall {v}_{h} \in {\mathcal{V}}_{0,h},$$

(11)

or, more concisely, into

$$\hat{{a}}_{h}({u}_{h},{v}_{h}) = {F}_{h}({v}_{h})\quad \forall {v}_{h} \in {\mathcal{V}}_{0,h},$$

(12)

which we can now solve for ${u}_{h} \in {\mathcal{V}}_{h}$ directly. In the above, the bilinear form $\hat{{a}}_{h} : {\mathcal{V}}_{h} \times {\mathcal{V}}_{0,h} \rightarrow \mathbb{R}$ is defined as $\hat{{a}}_{h}(\cdot,\cdot ) = {a}_{h}(\cdot,\cdot ) +\mathop{ a}\limits^{{{}_{\Delta }}}_{h}(\cdot,\cdot )$, which, thanks to (3) and (10), can be expressed as

in terms of the assumed strain tensor $\hat{\epsilon } = \epsilon +\mathop{ \epsilon }\limits^{{}_{\Delta }}$. At first sight, the correction seems to be computationally expensive, since it appears to involve solving two global systems. However, (12) is the only problem we need to solve, since it replaces the original problem (7). Furthermore, the stiffness matrix associated with the bilinear form $\hat{{a}}_{h}$ requires approximately the same computational costs as a _h as will be shown later in Sect. 4.3.

Note that since $\hat{{a}}_{h}$ differs from ${a}_{h}$ by the second argument only, (12) can be interpreted as a Petrov-Galerkin correction of (7). Therefore, the associated stiffness matrix is unsymmetric and thus requires a different class of iterative solvers. Nevertheless, if ${a}_{h}$ is coercive and bounded, so is $\hat{{a}}_{h}$ provided that (9) holds. Consequently, the solution ${u}_{h}$ to the problem (12) exists and is unique. Moreover, since ${u}_{h}$ also satisfies (5), the Galerkin orthogonality (6) is recovered. As mentioned above, in other correction methods such as SCNI the stiffness matrix is symmetric, since in SCNI assumed strains are used for both arguments in the bilinear form $\hat{{a}}_{h}$, see [13].

If the integration method is accurate and ${u}_{hh} ={ u}_{h}$, i.e. the integration error vanishes, the method is consistent in the sense that nothing has to be corrected and it turns out that $\hat{{a}}_{h} = {a}_{h} = a$ and thus the associated stiffness matrix becomes symmetric.

It should finally be noted that the recovered Galerkin solution ${u}_{h}$ and the recovered Galerkin orthogonality (6) allow the estimation of the discretization error with the various error estimation techniques developed over the years. If the integration error could not be corrected, estimation of the discretization error would be much more cumbersome, since the Galerkin orthogonality is an important requirement used in most a posteriori discretization error estimates.

4 Meshfree Methods

All that remains to show is how the assumed strain tensor $\hat{\epsilon }$ can be constructed for a specific Galerkin method. In this paper, we consider the reproducing kernel particle method as representative of meshfree Galerkin methods. Emphasis is placed on its numerical integration using stabilized non-conforming nodal integration.

4.1 The Reproducing Kernel Particle Method (RKPM)

In RKPM, the approximate solution ${u}_{h}$ can be expressed in terms of the following form

$${ u}_{h} =\sum\limits_{{n}_{P}}{\Psi }_{I}(x){u}_{I},$$

(14)

where ${n}_{P}$ is the number of particles ${x}_{I}$, i.e. ${n}_{P} = \mathrm{card}\ \{{x}_{I}\,;\,{x}_{I} \in \bar{ \Omega }\}$, ${u}_{I}$ are the coefficients, and ${\Psi }_{I}$ are the meshfree shape functions. In the case of the reproducing kernel particle method, ${\Psi }_{I}$ takes the form

$${\Psi }_{I}(x) = \Phi (x-{x}_{I}){H}^{T}(\mathbf{0}){M}^{-1}(x)H(x-{x}_{ I})$$

(15)

with the kernel function $\Phi$, the vector of monomial basis functions $H$, and the moment matrix

$$M(x) =\sum\limits_{{n}_{P}}\Phi (x-{x}_{I})H(x-{x}_{I}){H}^{T}(x-{x}_{ I}).$$

(16)

In this paper, linear basis functions are employed facilitating linear completeness which is one of the requirements to achieve linear exactness in the Galerkin approximation.

Since, in general, meshfree Galerkin approximations are not kinematically admissible, the essential boundary conditions need to be imposed carefully, e.g. by the Lagrange multiplier method, the penalty method or Nitsche’s method. Here, we review the latter as introduced in [12] to impose the Dirichlet boundary conditions (1d) in a weak sense. In this case, the bilinear form $a$ and the linear form F, as defined in (3) and (4), are extended to

$$\begin{array}{rcl} a(u,v)& =& \int\limits_{\Omega }\sigma (u) : \epsilon (v)\,\text{ d}V -\int\limits_{{\Gamma }_{D}}v \cdot \sigma (u) \cdot n\,\text{ d}A \\ & -& \int\limits_{{\Gamma }_{D}}u\cdot \sigma (v) \cdot n\,\text{ d}A +\int\limits_{{\Gamma }_{D}}\beta u\cdot v\,\text{ d}A \end{array}$$

(17)

and

$$F(v) =\int\limits_{\Omega }f\cdot v\,\text{ d}V +\int\limits_{{\Gamma }_{N}}\bar{t}\cdot v\,\text{ d}A-\int\limits_{{\Gamma }_{D}}\bar{u}\cdot \sigma (v)\cdot n\,\text{ d}A+\int\limits_{{\Gamma }_{D}}\beta \bar{u}\cdot v\,\text{ d}A,$$

(18)

respectively, with parameter $\beta \in {\mathbb{R}}^{+}$ to ensure coercivity of a. As a consequence of the weak fulfillment of the Dirichlet boundary conditions, the trial and test space now takes the simple form $\mathcal{V} ={ H}^{1}(\Omega )$. With the RKPM approximation (14) at hand, we may now define the finite-dimensional subspace ${\mathcal{V}}_{h} \subset \mathcal{V}$ as ${\mathcal{V}}_{h} =\{{ v}_{h} \in { H}^{1}(\Omega )\,;\,{v}_{h}\text{ as in }(<InternalRef RefID="Equ16">14</InternalRef>)\}$.

4.2 Stabilized Conforming and Non-conforming Nodal Integration

A crucial point in numerical integration is the fulfillment of the associated linear integration constraint obtained by satisfying (7) with linear solution, see [7] for details,

which is necessary to achieve linear exactness in the Galerkin approximation and therefore to pass the linear patch test. Linear exactness can also be interpreted as the linear portion of the integration error vanishing. We remark that for high-order exactness, high-order integration constraints need to be met. For further details on the construction of generalized integration constraints we refer the reader to Chen et al. [6].

To keep the meshfree nature of RKPM, in this paper nodal integration is considered rather than Gauß integration to evaluate the integrals in (17) and (18). In nodal integration, the integrals are evaluated at the particles and weighted with a representative integration domain. It is well known, however, that nodal integration yields rank instability and low convergence rates.

A remedy for both problems is obtained using smoothed gradients for nodal integration introduced by Chen et al. [8], rather than standard gradients. The smoothed gradient operator $\tilde{\nabla }$ is defined as

$$\tilde{\nabla }{(\cdot )}_{{\vert }_{{x}_{ L}}} = \frac{1} {\vert {\Omega }_{L}\vert }\int\limits_{{\Omega }_{L}}\nabla {(\cdot )}_{{\vert }_{x}}\,\text{ d}V = \frac{1} {\vert {\Omega }_{L}\vert }\int\limits_{\partial {\Omega }_{L}}{(\cdot )}_{{\vert }_{x}}n\,\text{ d}A,$$

(20)

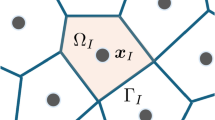
where ${\Omega }_{L}$ is the representative domain of node L, which is also referred to as smoothing domain. Here, the gradient is first smoothed over the domain ${\Omega }_{L}$, and the divergence theorem is then applied to convert the domain integral to a surface integral.

In the case that the representative domains ${\Omega }_{L}$ are conforming, i.e. they are disjoint and $\bar{\Omega } =\bigcup\limits_{{n}_{P}}\bar{{\Omega }}_{L}$, e.g. using Voronoi cells, it is easily verified using definition (20) and nodal integration with weight $\vert {\Omega }_{L}\vert$ that

holds and thus the linear integration constraint (19) is fulfilled for the smoothed gradient operator $\tilde{\nabla }$. Owing to the conforming nature of the integration domains ${\Omega }_{L}$ as depicted in Fig. 2, this method is termed stabilized conforming nodal integration. This integration method, however, has the drawback that the conforming domains are sometimes difficult to construct, e.g. in a semi-Lagrangian formulation for fragment-impact problems, see [11]. To cope with this problem, stabilized non-conforming nodal integration has been introduced in [7, 11]. As the name implies, the domains ${\Omega }_{L}$ are not conforming as shown in Fig. 3, which is a simplicity taken in order to overcome the difficulty of constructing conforming domains. For this method, the last equality in (21) no longer holds since the domains are not conforming, and as a consequence the linear integration constraint (19) is not fulfilled which may result in considerable integration error and deterioration of convergence rate.

Fig. 2

Smoothing domains ${\Omega }_{L}$ in SCNI using Voronoi cells

Fig. 3

Smoothing domains ${\Omega }_{L}$ in SNNI

4.3 The Assumed Strain Tensor $\epsilon$

As we have seen, the linear integration constraint (19) is fulfilled by SCNI. We therefore examine the first-order correction of SNNI to pass the linear patch test. To satisfy the linear integration constraint (19) for SNNI, we introduce the modified ansatz function (for the gradients)

$$\nabla {\hat{\Psi }}_{I} = \nabla {\Psi }_{I} +\underbrace{{ \sum\limits_{d}{\xi }_{dI}\nabla {\hat{\Psi }}_{dI}} }_{=\nabla \Psi ^{{{}_{\Delta }}}_{I}}$$

(22)

in terms of gradients of the standard ansatz function $\nabla {\Psi }_{I}$ and a first-order correction term $\nabla \Psi ^{{{}_{\Delta }}}_{I}$ to account for the integration error which depends on the unknown coefficients ${\xi }_{dI}$ and the gradient of the correction ansatz functions $\nabla {\hat{\Psi }}_{dI}$. It should be clear that since the test space ${\mathcal{V}}_{h}$ is constructed in terms of the modified ansatz functions ${\hat{\Psi }}_{I}$, the choice for the first-order correction ansatz functions ${\hat{\Psi }}_{dI}$ is restricted.

As an example, we express $\nabla {\hat{\Psi }}_{dI}$ in terms of the shape function supports

$${ \Theta }_{I}(x) = \left \{\begin{array}{@{}l@{\quad }l@{}} 1\quad &\text{ if }x \in \ \mathrm{supp}{\Psi }_{I}(x) \\ 0\quad &\text{ if }x\notin \ \mathrm{supp}{\Psi }_{I}(x) \end{array} \right..$$

(23)

In order to determine $\nabla \Psi ^{{{}_{\Delta }}}_{I}$ and thus to be able to compute $\epsilon ^{{}_{\Delta }}$ and consequently the assumed strain tensor $\hat{\epsilon }$, we substitute (22) into the linear integration constraint (19) to see that

holds with additional terms arising from the modified gradient in (22) and the shape function supports (23). In the above, ${\Psi }_{I,x}$ and ${\Psi }_{I,y}$ are the derivatives of ${\Psi }_{I}$ with respect to x and y, respectively. The unknown coefficients ${\xi }_{1I}$ and ${\xi }_{2I}$ can then be determined as

Note that the computation of the coefficients ξ_1I and ξ_2I is inexpensive, since it can be done locally. This is in contrast to previous integration corrections presented in [5, 13], where a global system needs to be solved. Furthermore, the proposed algorithm to compute ${\xi }_{1I}$ and ${\xi }_{2I}$ can be easily implemented into an existing RKPM code.

We are now in a position to define the assumed strain tensor $\hat{\epsilon }$ used in the bilinear form $\mathop{a}\limits^{{{}_{\Delta }}}_{h}$ in (13). With (22) the tensor takes the form

$$\hat{\epsilon }({v}_{h}) =\sum\limits_{{n}_{P}}{\nabla }^{\text{ sym}}[{\hat{\Psi }}_{I}(x){v}_{I}].$$

(26)

Note that for imposing Dirichlet boundary conditions in a weak sense using Nitsche’s method, we further need to compute assumed stresses $\hat{\sigma }({v}_{h})$ in (17) and (18), which can be done by the constitutive relation $\hat{\sigma }({v}_{h}) = \mathbb{C} : \hat{\epsilon }({v}_{h})$.

With the assumed strain tensor $\hat{\epsilon }$ at hand, the bilinear form $\hat{{a}}_{h}$ as defined in (13) can be computed. Thus, the modified variational problem (12) can be solved for the Galerkin solution ${u}_{h}$ to pass the linear patch test. From the construction of $\hat{\epsilon }$ in (26) it is clear that when the linear integration constraint (19) is met, a problem with linear solution can be recovered. For the recovery of high-order solutions and for use with different integration methods, such as Gauß integration or direct nodal integration (DNI), we refer to the unified framework for domain integration as recently presented by Chen et al. [6].

5 Numerical Examples

In this section, we present numerical results obtained by the first-order correction of integration presented in the preceding sections. In particular, we focus on SNNI and its first-order correction and compare the results with uncorrected SNNI and SCNI.

5.1 Beam Problem

In our first example, the system is a plane-stress cantilever beam subjected to a parabolic in-plane shear traction with the total load P = 2, 000 kN on the free end, as depicted in Fig. 4. The beam is modeled using anti-symmetric boundary conditions on bottom of the beam. The length of the beam is L = 10 m, its height is H = 2 m and it is made of an isotropic, linear elastic material with the properties: Young’s modulus $E = 30 \cdot 1{0}^{6}$ kN/m² and Poisson’s ratio ν = 0. 3.

Fig. 4

System and loading for the cantilever beam problem

The sub-domains of the strain smoothing used for SCNI and SNNI are plotted in Fig. 5. As can be observed, the smoothing zones are much easier to construct for SNNI, since SCNI requires Voronoi cells.

Fig. 5

Smoothing schemes for SCNI (top) and SNNI (bottom)

The deflection error along the centroid of the beam is shown in Fig. 6. First-order correction of SNNI shows similar performance as SCNI with tip displacement accuracies shown in Table 1.

Fig. 6

Deflection error along the centroid of the beam

Table 1 Tip displacement accuracy (numerical solution normalized by the analytical solution)

Next, convergence of the methods is considered with the uniform node refinements of the half beam as shown in Fig. 7 using 51, 165, 585, and 2,193 nodes. The model parameters for this example are L = 5 m and H = 2 m.

Fig. 7

Discretizations of the modeled half beam for convergence

The associated convergence is plotted in Fig. 8. As can be seen, corrected SNNI shows a large improvement in error as well as convergence rate. It should be noted, however, that the true Galerkin solution cannot be fully recovered in this case, since the proposed correction restores linear solutions only and thus there is still integration error left.

Fig. 8

Convergence for the beam problem

Finally, we increase Poisson’s ratio to ν = 0. 49999999 to let the material be nearly incompressible. Furthermore, we let L = 10 m, H = 2 m, and use a plane-strain structure. Even in this case corrected SNNI yields very good results with nearly vanishing deflection error as can be observed from Fig. 9. The reason is that nodal integration acts, by construction, as an under integration method and thus locking does not become an issue, whereas Gauß integration with 5 ×5 integration points yields locking.

Fig. 9

Deflection error along the centroid of a nearly incompressible beam

5.2 Tube Problem

In the next example, the structure is an isotropic tube in a plane-strain state with outer radius R = 1 m and thickness T = 0. 5 m subjected to internal pressure $p = 10 \cdot 1{0}^{6}$ kN/m², as shown in Fig. 10. Due to symmetry conditions, only one quarter of the domain is modeled with anti-symmetric boundary conditions. The material data is the same as in the previous problem for the compressible case.

Fig. 10

A plane-strain tube subjected to an internal pressure

The modeled domain is discretized by 32, 105, 377, and 1,425 nodes with irregular node distributions, as depicted in Fig. 11.

Fig. 11

Discretizations of the modeled quarter tube for convergence

The convergence curves in this example, as plotted in Fig. 12, show similar behavior as in the previous example, i.e. without first-order correction SNNI has a low convergence rate, whereas with the correction the convergence rate is restored and is similar to the result from SCNI.

Fig. 12

Convergence for the tube problem

6 Conclusions

A method was derived to correct the integration error in Galerkin methods and therefore recover the true Galerkin approximation of the continuous model problem at hand. The cornerstone of the proposed correction method is to modify the bilinear form of the original method using the same numerical integration scheme. This modified bilinear form can be viewed as accounting for the integration error by using test functions that fulfill the associated requirements for exactness. In particular, the method was applied to recover linear exactness under the framework of reproducing kernel approximations with stabilized non-conforming nodal integration, which is known to fail the linear integration constraint. Further, the proposed assumed strain to meet integration constraint only requires solving a small linear system locally. Numerical examples showed that the correction method performs well even for nearly incompressible elastic problems, and thus offers a viable alternative to constructing conforming cells previously used in SCNI.