Representing Terrain with Mathematical Operators

Abstract

This work describes a mathematical representation of terrain data consisting of a novel operation, the “drill”. It facilitates the representation of legal terrains, capturing the richness of the physics of the terrain’s generation by digging channels in the surface. Given our current reliance on digital map data, hand-held devices, and GPS navigation systems, the accuracy and compactness of terrain data representations are becoming increasingly important. Representing a terrain as a series of operations that can procedurally regenerate the terrains allows for compact representation that retains more information than height fields, TINs, and other popular representations. Our model relies on the hydrography information extracted from the terrain, and so drainage information is retained during encoding. To determine the shape of the drill along each channel in the channel network, a cross section of the channel is extracted, and a quadratic polynomial is fit to it. We extract the drill representation from a mountainous dataset, using a series of parameters (including size and area of influence of the drill, as well as the density of the hydrography data), and present the accuracy calculated using a series of metrics. We demonstrate that the drill operator provides a viable and accurate terrain representation that captures both the terrain shape and the richness of its generation.

1 Introduction

This paper presents a novel representation of terrain data consisting of a series of mathematical operations that produce hydrographically sound legal terrains. These include terrains that have discontinuities on the surface (such as cliff faces and caves), few if any local minima (pits), and whose digital formation mimics physical phenomena associated with geological terrain formation (such as erosion, digging, and faulting/folding).

Local minima are known to exist in certain terrains, such as those consisting of Karst topography or natural basins (e.g. endorheic basins). However, most local minima present in terrain data are a result of the sampling procedure used to collect it, which may miss channels that are too small for the spacing of the grid and may pass between sample points (sometimes called “posts”). In addition, most data collection techniques cannot differentiate between tree cover, lake surfaces, and land, resulting in elevation inaccuracies and pits where there should be none. Collection procedures often fail to adhere to the Nyquist Sampling Theorem. One of the principal features of this new representation is that it facilitates the restriction of local minima, especially along the terrain’s channel network, by drawing a connection between the representation and the physics of the terrain’s formation.

Given our current reliance on digital map data, hand-held devices, and GPS navigation systems, the accuracy and compactness of terrain data representations are becoming increasingly important. Traditional representations do not maintain hydrographical information, critical when using algorithms to site dams or map flood plains, beyond what is present in the spatial data (elevations and grid locations). If more accurate data were to be universally available in a digital format traditional representations, which can limit the effectiveness of these algorithms, would be less necessary. For these reasons, it is imperative that a representation that retains important hydrographical properties while maintaining the characteristics of legal terrain be developed.

Fig. 1

Four depictions of a $400 \times 400$ mountainous dataset visualized as a height field of pixels. Color indicates elevation, where white is the highest elevation, followed by brown, then green, and finally blue indicates the lowest elevation. Below each data set is the threshold value used to extract the channel network depicted on the surface of each terrain. Notice the difference in the densities of the channel pixels as the threshold increases

We present the drill operator, a mathematical operation that carves out terrain by “drilling” into it along the channel segments of its extracted channel network, changing its shape to fit the terrain’s profile at each position along the channel’s length. This representation allows for procedural generation of a terrain surface by mimicking the physical process of digging out the surface. We will demonstrate how this operator succeeds in the representation of legal terrains. We also provide the results of a series of accuracy tests on a real terrain dataset, providing evidence of the utility of the drill operator.

1.1 Existing Terrain Representations

The most common current representations of terrain are height fields (matrices of point elevations), and triangulated irregular networks (piecewise linear triangulated splines, known as TINs), both of which fail to capture the richness of the physics of the terrain surface. Height fields are two dimensional grids of elevation values, isometric to greyscale image data. Each grid space, or “pixel”, is single-valued (contains a single elevation). A TIN is a similar representation, but the surface is represented by triangles with single-valued vertices. An example of a height field can be seen in Fig. 1, the mountainous dataset that will be used for testing and comparison for the remainder of the paper.

Both representations benefit from the assumption that terrain is at least $C^{0}$ continuous. However, this assumption is not always true. Discontinuities are apparent in real terrain (e.g. the Grand Canyon), but the information necessary to represent them is lost as the terrain is stored as a height field or TIN, as multiple vertices at a single grid space would be required.

Also, the accuracy of both height fields and TINs is subject to the resolution of the data points. Coarser resolutions have a profound and negative effect on the accuracy of the representation (Gao 1997). This limitation can be somewhat mitigated by allowing for variable resolution. This is possible for both representations (such as in Abdelguerfi et al. 1998; De Floriani and Puppo 1995; Bartholdi and Goldsman 2004; Velho et al. 1999), but even this solution is limited as each representation is inherently grid-based, and as such is limited in its precision.

A second option for representing terrain surfaces is the use of Fourier transforms, or other surface-shape modeling functions, such as B-Splines (Farin 2002, Faux and Pratt 1979). While these methods are more powerful when modeling terrain, as they allow local control over the shape of the terrain and provide a degree of local coherence (in that the elevation of a pixel corresponds in some way to the elevation of its neighbor), they still model a surface that is overly smooth ($C^{1}$, i.e. continuous and differentiable everywhere), and represent no physical process of terrain generation.

In addition to surface representations, there are popular volumetric terrain representations. Terrain can be stored as a voxel grid, allowing for multiple soil types. While this representation can, with a fine enough resolution, produce legal terrains, it is often not feasible to store terrains in this manner due to its substantial memory footprint. A layered height field ( Benes and Forsbach 2001) combines several advantages of each of height fields and voxel grids. In this structure, the terrain is divided into a two dimensional grid, like a height field, but each grid space contains an array of heights. Modeling surface sculpting presents a challenge similar to terrain modeling, and so the two share some data representations, such as the “slab” data structure (Agarwala 1999), used for surface sculpting of volumetric models by converting the surface into a series of height fields layered over volumetric information.

Mathematical operators have been used to represent terrain surfaces in the past. This work most closely resembles the work presented by Franklin et al. (2006), where the scoop operator is introduced. Variations on the scoop operator perform similarly to our drill operator. Given a trajectory, the scoop operator digs out a portion of the terrain, and a terrain dataset can be represented with a series of scoops. The scoop shapes are determined by low order polynomials, each with its own advantages and disadvantages.

Terrains can be generated from scratch in most cases by either fractal generation or erosion simulation. Fractal terrain generation does not result in legal terrains, as it relies on controlled randomization of the elevations of height fields. Height field pixels store no neighborhood information, and fractal generation schemes introduce more randomness than is generally seen in terrain due to a lack of user control and correlation to terrain features. Erosion simulations generate realistic looking terrains, but also rely on the underlying height field structure, and are not feasibly stored as a procedural generation. We seek a representation of terrain that produces legal terrains while being closely tied with physical processes that produced the terrain, such as digging, or erosion.

Various compression schemes are used to store terrain data. The most common are variations on the JPEG algorithm which are, in general, very successful. However, terrain surfaces have also been modeled using overdetermined linear systems (ODETLAP) as a training model to find a well-compressed lossy representation (Inanc 2008). These lossy compressions are comparable (and, in some cases, even exceed) JPEG compressions, though without regard to hydrographic data and physical processes we wish to retain with our representation.

2 Representing Terrain as a Series of Drill Operations

We represent terrain data as a series of mathematical “drill” operations applied to an initial high plateau. The series of operations are extracted from a given terrain, $T$, where each elevation in the $n \times n$ grid is referred to as a pixel $\mathbf {p}$. A list of operations can be stored in lieu of the height field. The process for determining the series of drill operations is as follows:

• 1. Extract the channel network of $T$, using any common method.

• 2. For each pixel in the channel network $\mathbf p _{i}$, collect cross sections of the channel centered at $\mathbf p _{i}$.

• 3. Find the union of all cross sections to determine the “thinnest” channel cross-section.

• 4. Use least-squares fitting to fit a quadratic function to the union.

The coefficients of the fitted quadratic function and the position of the pixel completely describe a single drill operation. Like surface shape-modeling functions, the drill operator maintains the local coherence of terrain through its connection to the process of digging, by mimicking the physical process of digging in a controlled and efficient way. The drill operator introduces local continuities, but does not prevent discontinuities, such as on the edge of a channel, where one might expect to see them.

2.1 Channel Network Extraction

To extract the hydrographic channel network from the terrain, we use a hybrid of the method first presented by O’Callaghan and Mark (1984) and the method presented by Metz et al. (2011). For each pixel of the terrain, prioritized based on elevation (lowest elevation with highest priority), the direction of the neighbor (of eight possible neighbors) with the highest priority is set as the flow direction. Once the flow directions have been determined, the pixels are sorted by priority, and flow accumulation is calculated, where each pixel contributes its flow value to that of its flow neighbor, cumulatively. The channel network consists of those pixels whose flow values exceed a user-defined threshold, $\tau$. Slight variations in geometry or threshold value can have a profound impact on the shape and size of the channel network. In fact, determining the ideal threshold from which to extract the channel network is a closely related area of research, and as such $\tau$ is one of three user-defined parameters to our system. It is important to note that this is a black box process, and any channel network extraction tool can be used. It is also important to note that a pixel’s entire flow is applied to a single neighbor, and so channels can not split. An example of an extracted channel network is seen in Fig. 1.

2.2 Determining Drill Shape

Next, the shape of the drill is determined for each pixel $\mathbf p _{i}$ in the channel network. To accomplish this, we fit a quadratic curve to the channel profile at $\mathbf p _{i}$, which then represents the shape of the widest drill that can fit in the channel. The overall channel profile is represented by the union of all collected cross sections at $\mathbf p _{i}$.

Fig. 2

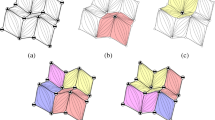
A visualization of the process of determining the union of the cross sections of the terrain’s channels. The left image depicts the process of gathering the cross sections. Each red plane is a cutting plane, and the cross section of the terrain determined by each one is collected. The right image depicts finding the union of all cross sections. The colored thin lines represent the set of all cross sections at pixel $\mathbf {p}$, each one a collection of elevations of length $w$. The thick black line represents the final union

At each pixel $\mathbf p _{i}$, a set of 120 cross sections of the terrain is collected, each three degrees apart. This provides a profile of a channel at 120 distinct, uniformly spaced angles. A sample of this procedure is shown in Fig. 2. The cross sections span a distance $w$ (a user-defined parameter) from the center of $\mathbf p _{i}$, the second user-defined parameter to our system. The larger the value for $w$ is, the larger the area of influence on the terrain surface that is considered when determining the drill shape. For each pixel in the channel network, uniformly spaced sample elevation points are collected in each direction along the crossing plane representing the cross section. Most of these sample points do not fall directly in the center of a pixel, and so we use bilinear interpolation to estimate the elevation of any sample point that does not exactly match a pixel center.

Once the set of cross sections is collected, we calculate its union. To do this, we take the maximum elevation value at each sampled distance from $\mathbf p _{i}$, as depicted in Fig. 2. This new channel profile represents the widest channel that a drill can be fit to in order to conservatively carve the channel. A thinner drill will not carve a wide enough channel, and a wider drill will carve too much terrain away and make the channel too large. We then fit a quadratic equation to the union by treating the fitting as a constrained linear least-squares problem over the $w$ elevations of the union. We constrain only the center point of the union, the elevation of $\mathbf p _{i}$. The coefficients of this fitted quadratic equation represent the shape of the drill at $\mathbf p _{i}$.

The terrain is completely represented by the list of pixels in the channel network and their associated drill’s quadratic coefficients.

Fig. 3

The left image depicts the regenerated terrain with the lowest RMSE value, and the right image depicts the regenerated terrain with the lowest AHD error. The parameters responsible for the terrain are listed below the images

2.3 Terrain Regeneration

To regenerate the terrain from the drill representation, we begin with a flat plateaued terrain of elevation $m$, where $m$ is the maximum elevation of $T$. A new terrain is procedurally generated by iteratively applying operations to this initial plateau, $T_{0}$. The $i$th drill, which corresponds with a pixel $\mathbf p _{i}$ in the channel network of $T$, is represented by a $\left(2k + 1\right) \times \left(2k + 1\right)$ matrix $D_{i}$, where $k$ is referred to as the drill’s “influence”. Essentially, this is how large of an area of the terrain each drill operation affects, and is the third and final user-defined parameter to the system. The width and length of $D_{i}$ must be odd because it must have a center pixel.

In order to drill the terrain $T_{i-1}$, $D_{i}$ is centered over pixel $\mathbf p _{i}$. The procedural generation is defined in Eq. 1:

$$\begin{aligned} T_{i} = \min \left( T_{i-1}, D_{i} \right) \end{aligned}$$

(1)

where the $\min \left(\right)$ function operates over the $2k + 1 \times 2k + 1$ area of $D_{i}$ and outputs a new matrix of minimum values between the pixels of $D_{i}$ and corresponding pixels of $T_{i-1}$. The resulting terrain has been drilled, and the process is repeated for the next operation. The results of this procedural generation can be seen in Fig. 3.

3 Accuracy and Efficiency Testing

Accuracy tests were performed to determine how closely the drill representation modeled the $400 \times 400$ mountainous dataset seen in Fig. 1. All tests were performed in Ubuntu 11.04 with a quad-core AMD Phenom II X4 945 Processor, with 8GB of RAM. The code was written in MATLAB.

The three parameters of the system, as described above, are the threshold used to extract the original terrain’s channel network, $\tau$, the size of the cross section, $w$, and the influence of a drill (size of the representative matrix), $k$. Each of 3 thresholds, 3 cross-section sizes, and 6 influence values were used to build regenerated terrains in this factorial experiment. For each set of parameter values, the total error between the generated terrain and the initial terrain was calculated. Two metrics were used: the standard root mean squares error (RMSE) metric, and the averaged Hausdorff distance (AHD) metric as described by Stuetzle et al. (2011).

RMSE measures the root of the average squared difference in heights across the terrain, as shown in Eq. 2:

$$\begin{aligned} RMSE \left( T_{0}, T_{1}\right) = \sqrt{ \dfrac{\displaystyle \sum \nolimits _{x < X} \displaystyle \sum \nolimits _{y < Y} { \left( T_{0}\left(x,y\right) - T_{1}\left(x,y\right) \right)^2 } }{ X * Y } } \end{aligned}$$

(2)

where each dataset, $T_{0}$ and $T_{1}$, is $X \times Y$ pixels, and $T\left(x,y\right)$ is the elevation value at location $x,y$.

For any two sets of pixels (in this case, the sets of all pixels in the channel network of each terrain), AHD finds the average of the shortest distance between their pixels, as shown in Eq. 3:

$$\begin{aligned} AHD = \max \left\{ \overline{\inf _\mathbf{p _{j} \in N^{T_{1}}_{\tau }, \mathbf p _{i} \in N^{T_{0}}_{\tau }} d\left(\mathbf p _{i}, \mathbf p _{j}\right)}, \overline{\inf _\mathbf{p _{i} \in N^{T_{0}}_{\tau }, \mathbf p _{j} \in N^{T_{1}}_{\tau }} d\left( \mathbf p _{i}, \mathbf p _{j} \right)} \right\} \end{aligned}$$

(3)

where $\mathbf p _{i} \in N^{T_{0}}_{\tau }$ is the $i$th pixel of the set of channel network pixels of $T_{0}$ extracted using threshold $\tau$, $N^{T_{0}}_{\tau }$. The overline means “mean value of”. It is important to note that AHD is limited to the channel networks of the terrain, whereas RMSE is applied globally. Limiting RMSE to only $N_{\tau }$ would not give an accurate picture of how close the terrains’ hydrography networks are, since the network pixels are found by looking at the global flow pattern. Even if the elevations of the pixels in $N_{\tau }$ are comparable, it does not indicate that the overall terrain shape is similar. In addition, slight variations in the location of the pixels in $N_{\tau }$ would render RMSE unusable. We look at the results for both metrics and analyze them in context of their maximum error and what they mean from a physical standpoint.

Fig. 4

The results of our accuracy testing. The left column depicts the error measured using the RMSE metric, and the right column depicts error measured used the AHD metric. Each row shows a different value for the cross section window size (parameter $w$). Each metric’s data is normalized. Red indicates high error, whereas blue indicates low error, local to each dataset

3.1 Results and Discussion

The results for our accuracy tests are provided in Fig. 4. The left column of Fig. 4 presents the data for the RMSE metric, and the data for the AHD is on the right. The error divisor for RMSE was the total elevation range of the original terrain, whereas the error divisor of AHD was the distance between pixel 0,0 and pixel $n$,$n$, the corners of the terrain. Since elevation is ignored for this divisor, it is possible for AHD error be greater than 1.0.

$\tau$ values of 25 created considerably denser channel networks than $\tau$ values above 100, and so they are both more accurate and take considerably longer to calculate. The two channel networks can be seen in Fig. 1. For reference, the maximum flow value for a pixel in our dataset is 102,245, and a threshold of 25 resulted in a channel network with ${\approx }19,000$ pixels, whereas a threshold of 100 resulted in a network of ${\approx }12,000$ pixels. Calculating the drill representation of a terrain with a flow threshold of 25 took approximately eight minutes, and times decreased linearly with the increase in threshold value. The time for regenerating the terrain from the drill representation was quicker by a factor of ten, approximately. It is important to note that time optimization was not a focus for this paper, and there exist many techniques that will be utilized in the future to reduce the time the algorithm takes.

There are several observations to be made regarding our accuracy data. The first is that, with “good” parameters (meaning none that create outliers in the error data), the accuracy is actually quite high with regard to both RMSE and AHD metrics, between 0.015 and 0.025. As with any algorithm, there is a trade-off between time and accuracy. The lower the threshold, the more pixels in the hydrography network, and so the slower the process, but the more accurate the results become. This is true in every case, and it makes intuitive sense.

$\tau$ is the most influential parameter with regard to both metrics. This makes sense, since the drill shape calculation is constrained to pass through the center of $N^{i}_{\tau }$. Since AHD measures how close the channel networks are to one another, the more pixels there are in the channels, the more likely it is that the channel networks overlap. By nature of the AHD, this will result in very low error. If the channel network is not dense enough, then the drill may not reach much of the terrain at all, and so the RMSE is also very much influenced by the value of $\tau$. More interesting is that the minimum RMSE occurred for when $w = 10$ and $k = 20$. It makes sense that a drill will need some influence over the area around the channel in order to reduce the RMSE, because without it there would be large areas of the terrain untouched by any drill, adding considerably to the overall error (that AHD would ignore).

From a purely visual standpoint, many of the terrains pass the eyeball test. A side-by-side comparison of the terrains that represent the lowest error for each of the metrics is found in Fig. 3. Notice is that the channels do seem to be somewhat wider in the RMSE winner, whereas they are more pointed, but areas of the terrain are missed by drills completely, in the AHD winner. Interestingly, the left image in Fig.  3 is one of the terrains we deem to be the most “visually pleasing”. These often have higher $k$ and $w$ values, which may be a result of drills that flatten artifacts out of the terrain. This result demonstrates why, when choosing parameters for the drill operator, it is often smart to take both error metrics into account.

4 Conclusion

We have presented the drill operator, the first in a series of mathematical operators applied to terrain datasets. It creates a robust, effective, and accurate representation of terrain data. It adheres strictly to two of the three criteria laid out in Sect. 1 for legal terrain generation. First, it allows for the existence of discontinuities, which can exist at the edge of, and on the border between, two drills. Second, its conception and execution is based on an actual physical process that can affect terrain shape, and that information is inherent in the representation. However, while locally the drill prevents minima due to the monotonically increasing nature of the drill shape, it has no such restriction on a global scale in its present state. This is discussed further in Sect. 4.1.

The drill has been shown to represent terrain to a sufficient degree of accuracy, and its resultant terrains are visibly pleasing and comparable to the original terrain. Hydrography information is well maintained, and as such our representation holds more information about the terrain, especially regarding its formation and hydrography, than traditional spatial representations. This representation will extend naturally to compression schemes, and work well in algorithms regarding path planning, flood plain mapping, and dam siting, as they all require hydrographically accurate terrain. In addition, the representation has a naturally deep and interesting mathematical component that will be explored and exploited in the future.

4.1 Future Work

A single drill is represented by a pixel and a polynomial, a total of 4 values that must be stored. These can be represented as integers. To represent a $400 \times 400$ terrain well enough, approximately 13,000 drills are required, bringing the total number of values stored for a single terrain to 52,000, or roughly one third of the total number of values stored in a height field. This yields an RMSE of less than 4 %, and is visually pleasing. While this does not represent a compression scheme in its current form, with further emphasis on optimization (both spatial and temporal) this representation will be a viable candidate for compression. In addition, it more accurately maintains hydrography and formation information, an advantage over other more frequently used schemes.

There are several ways in which the algorithm can be optimized. The first is by storing channel segments as opposed to individual pixels, such as with Freeman chain codes (Freeman 1974) or line generalization (Ramer 1972). If a channel network can be stored as a series of segments, with begin points, end points, and channel trajectories, along with a function of drill shape (allowing it to change along the length of the channel), then the overall storage of a terrain can be greatly reduced. Storing the channels as trajectories also allows for a post-processing step that forces the trajectories to be monotonic and decreasing, thus forcing a lack of local minima and allowing the drill operator to adhere to the second criterion for a “legal terrain” described in Sect. 1.

With regards to temporal optimization, the drill creation algorithm bottlenecks at the quadratic function fitting. A better method of function fitting (or an easier-to-fit shape) may significantly improve the performance of the algorithm. Drills can be any shape, including simple cones, and have a width along the bottom. If the restriction that the drill shape functions be monotonic and increasing is lifted, a drill can be ball-shaped, which could model caves. These new parameters would allow for more customizability while maintaining a small memory footprint.

Two more operators will be added to the set of operators: the erosion operator, and the mudslide operator. The erosion operator picks up sediment from a high elevation and deposits it at a lower elevation, and the mudslide operator adds sediment to the terrain along a trajectory. Deeper mathematics of these three operators will be explored, including how to define the composition of two operations, and whether that creates a group over the composition operation.

Finally, we will investigate ways to post-process terrain to deal with small areas untouched by drill operations. A simple interpolation of the untouched areas may be a solution, or more sophisticated algorithms may be more useful. Also, the system, as it currently stands, has three user-defined parameters ($\tau$, $w$, and $k$). We will investigate ways to automatically determine the ideal value for each of these parameters before operation extraction, thus not relying on user knowledge to create the best representation. Ideally, every operator will store its own value for $k$.