Atomic Force Acoustic Microscopy

Abstract

This chapter shortly reviews the scientific background of Atomic Force Acoustic Microscopy (AFAM), the basic theoretical models, the experimental techniques to obtain quantitative values of local elastic constants, and non-linear AFAM. Analytical and finite element models describing transverse flexural vibrations of AFM cantilevers with and without tip-surface contact are recapitulated. The models are suitable for micro fabricated silicon cantilevers of approximately rectangular cross section which are typically used in AFAM. Experimental methods to obtain single-point as well as array measurements and full spectroscopy images are discussed in combination with the respective reference methods for calibration. In a non-linear AFAM experiment, the vibration amplitudes of the sample surface and the cantilever are measured quantitatively with an interferometer at different excitation amplitudes, and the full tip-sample interaction force curve is reconstructed using a frequency dependent transfer function.

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

5.1 Introduction

In the beginning of the 1990s, atomic force microscopy (AFM) [1] became increasingly well known, commercial instruments were available and relatively easy to handle, and images demonstrating nanometer scale and even “atomic resolution” were published. On the other hand, the emerging progress in nanotechnology provided a need to examine materials non-destructively at nanometer scale. A common non-destructive inspection method is ultrasonic microscopy [2], which is used to reveal flaws and inhomogeneities inside components and materials and to measure elastic properties with high precision. However, as implied by Abbe’s principle, a conventional acoustic microscopy can hardly reach nanometer local resolution. Therefore, a variety of combinations of AFM with acoustic microscopy were developed with the aim to make atomic or nanometer local resolution available to ultrasonic probing. Examples for such inventions are atomic force acoustic microscopy (AFAM) [3], Ultrasonic Force Microscopy (UFM) [4], ultrasonic atomic force microscopy (UAFM) [5], scanning acoustic force microscopy (SAFM) [6], and scanning microdeformation microscopy (SMM) [7]. The main difference to conventional microscopy is that—instead of using a focusing lens or transducer—the ultrasonic waves are detected or excited locally with the tip of a scanning force microscope. In this case, the local resolution is determined by the tip-sample contact radius of a few nanometers, and not by the acoustic wavelength, which can be orders of magnitude larger. One general limitation of such near-field microscopes is that the high local resolution is only attained in the near field, i.e., in close proximity to the tip. This means that AFAM and related techniques provide mainly information on the sample surface or sample regions in close proximity to the surface—in contrast to conventional ultrasonic techniques using propagating waves. Ongoing research on subsurface contrast using mixing and heterodyning techniques is currently extending these limits (Chap. 10).

Different strategies are possible to detect ultrasonic vibration with an AFM. In techniques like UFM (Chap. 9) and SAFM the AFM sensor is treated as an oscillator having a resonant frequency that is considerably lower than the ultrasonic frequency. The nonlinearity of the tip-sample interaction forces is exploited to down-convert the high-frequency ultrasonic signal into a frequency range, which is detectable by the AFM cantilever. In techniques like AFAM, UAFM (Chap. 6), or SMM (Chap. 8) ultrasonic sample surface vibration is directly detected by exciting vibration modes of the cantilever beams with frequencies equal to the excitation frequencies. A variety of other dynamic operation modes of the AFM are known, in which the cantilever is vibrated while the sample surface is scanned, and the amplitude, phase, or resonant frequency is recorded. In AFAM and related modes, the sensor tip of the AFM is constantly in contact with the sample surface while the cantilever vibrates (Fig. 5.1). The flexural and torsional resonance frequencies of commercial cantilevers with lengths of a few hundreds micron are predominantly higher than 20 kHz, and hence in the ultrasonic frequency range. The tip-sample forces in the contact area influence the mechanical boundary conditions of the cantilever, and therefore its frequencies increase considerably compared to the frequencies in air. The shift of the resonance frequencies is evaluated to measure lateral and normal sample surface stiffness and elasticity, and the width of the resonance peaks is used to measure viscoelasticity [8] and internal friction [9] (Chap. 14) in the sample. If the amplitude of vibration is increased above a critical threshold, the resonance curves develop plateaus or asymmetries, which are typical for nonlinear oscillators (Sect. 5.5).

Fig. 5.1

AFM cantilever vibrating in contact with a sample surface. The vibration of the cantilever is excited by an out-of-plane sample surface vibration. The mechanical forces of the tip-sample contact area influence the resonance frequencies of the system. The repulsive tip-sample contact is visualized on the right hand side

In the AFAM-mode, an ultrasonic wave is excited inside the sample by a conventional transducer (a piezoelectric element) attached to one side of the sample. The ensuing out-of-plane or in-plane sample surface vibration transfers to the tip of the AFM and excites a forced flexural (Fig. 5.1), lateral bending, or torsional vibration of the cantilever, respectively. Wave phenomena in the sample such as reflection and interference are not exploited in AFAM, in contrast, multiple reflections in the sample should be avoided because interference patterns at the sample surface can lead to sample surface areas with low vibration amplitudes. A sample surface amplitude as homogeneous as possible in the scanned area is favorable. AFAM is a contact-resonance technique, which probes the local elastic properties of the sample. In the last years, the term contact-resonance AFM (CR-AFM) [10, 11] has been introduced as a generic term comprehending all methods, in which the contact-resonance frequencies of the cantilevers are measured as a function of position and evaluated to obtain elastic and inelastic sample surface properties. Some authors understand CR-AFM as an extension of force modulation microscopy [12] to higher frequencies [13, 14]. Contact resonances can not only be used to measure mechanical properties of the sample surface, but they are also proved to be useful for signal enhancement in other contact techniques such as piezo-mode AFM [15, 16].

5.2 Analytical and Finite-Element Models for AFAM

AFM cantilevers are small flexible beams, which are suspended at one end and free at the other end that carries the sensor tip (Fig. 5.2). As a response to dynamic excitation, AFM cantilevers exhibit different sets of vibration modes, such as transverse and lateral flexural and torsional modes. All types of modes show an infinite set of resonance frequencies, which depend on the shape, the geometrical dimensions, the material of the cantilever, and on its mechanical boundary conditions. A variety of microfabricated cantilevers are available. Cantilevers with triangular shape ($V$-shape) were used for contact-resonance spectroscopy [17], and their vibration modes were studied with analytical and finite-element models [18, 19]. In the following, only cantilevers with approximately rectangular shape will be treated, because their vibration can be described with relatively simple analytical models. Lateral contact-modes of rectangular cantilevers with bending vibration in width direction [20] and torsional modes can be used to measure in-plane elastic tip-sample forces and friction [21, 22]. If torsional contact-resonances are evaluated quantitatively in addition to flexural modes, a second elastic constant of the sample, the Poisson’s ratio, can be obtained [10]. However, this chapter will restrict to transverse flexural modes, i.e., flexural modes with deflections in thickness direction of the cantilever.

Fig. 5.2

Scanning electron micrographs showing a a side-view of an AFM cantilever made of single crystal silicon, b a view from the bottom side where the tip is mounted, and c the mechanical model of an AFM cantilever with constant cross-section (clamped-free beam)

5.2.1 Analytical Model of the Cantilever Vibrating in Air

The Euler–Bernoulli equation describes transverse flexural vibration of a straight beam with constant cross-section [23]:

$$\begin{aligned} EI\frac{\partial ^{4}y}{\partial x^{4}}+\eta \rho A\frac{\partial y}{\partial t} +\rho A\frac{\partial ^{2}y}{\partial t^{2}}=0. \end{aligned}$$

(5.1)

Here, x is the coordinate in length direction of the beam (Fig. 5.2c), E is the Young’s modulus of the cantilever, $\rho$ is its mass density, A is the area of its cross-section, I is the area moment of inertia, and $\eta$ is a damping constant expressing the internal friction in the cantilever and dissipation caused by air. In case of a rectangular cross-section of the cantilever with width w and thickness b, the area moment of inertia is $I=wb^{3}/12$. A harmonic solution in time with angular frequency $\omega = 2\pi f$ is searched for the local deflection y(x, t) at position x:

$$\begin{aligned} y(x,t)=y(x)\cdot y(t) = (a_{1} \mathrm{e}^{\alpha x}+a_{2} \mathrm{e}^{-\alpha x}+a_{3} \mathrm{e}^{\mathrm{i} \alpha x}+a_{4} \mathrm{e}^{-\mathrm{i} \alpha x})\mathrm{e}^{\mathrm{i}\omega t}, \end{aligned}$$

(5.2)

where $a_{1}$, $a_{2}$, $a_{3}$, and $a_{4}$ are constants and i is the imaginary unit. By substituting the general solution Eq. 5.2 into the equation of motion Eq. 5.1, one obtains the dispersion relation for a flexural wave with complex wave number $\alpha$:

$$\begin{aligned} EI\alpha ^{4}+\mathrm{i}\rho A\eta \omega -\rho A\omega ^{2}=0 \Rightarrow \quad \alpha _{\pm }=\pm \root 4 \of {\frac{\rho A}{EI}(\omega ^{2}\mp \mathrm{i}\eta \omega )}. \end{aligned}$$

(5.3)

If the second term in the partial differential Eq. 5.1, which contains the damping is omitted, the wave number $k = 2\pi /\lambda$ is real, and the dispersion equation simplifies to:

$$\begin{aligned} EIk^{4}-\rho A\omega ^{2}=0 \Rightarrow \quad k=\root 4 \of {\frac{\rho A}{EI}\omega ^{2}} \quad \Rightarrow \quad f=\frac{\left( {kL} \right)^{2}}{2\pi }\frac{1}{L^{2}}\sqrt{\frac{EI}{\rho A}}. \end{aligned}$$

(5.4)

The boundary conditions of the beam of finite length L depend on its suspension and on the tip-sample forces. Without surface contact a cantilever can be considered as a clamped-free beam Fig. 5.2c, the small mass of the sensor tip is neglected. In this case, the mechanical boundary condition at the clamped end $(x=0)$ and at the free end $(x=L)$ are as follows:

$$\begin{aligned} x=0:\left\{ {\begin{array}{l} y(x)=0 \\ [2mm] \frac{\partial y(x)}{\partial x}=0 \\ \end{array}} \right. \quad x = L:\left\{ {\begin{array}{l} \frac{\partial ^{2}y(x)}{\partial x^{2}}=0 \\ [2mm] \frac{\partial ^{3}y(x)}{\partial x^{3}}=0 \\ \end{array}} \right. . \end{aligned}$$

(5.5)

By substituting the general solution 5.2 into the boundary conditions, a characteristic equation is found, which defines the discrete wave numbers $k_{n}, n = \{1, 2, 3, \cdots \}$ of the resonant modes of the system:

$$\begin{aligned} \cos k_{n} L\cosh k_{n} L+1=0. \end{aligned}$$

(5.6)

The first seven roots of Eq. 5.6 are listed in Table 5.1.

Table 5.1 The first seven normalized wave numbers $k_{n}L$ of the clamped-free beam and the corresponding resonance frequency ratio $f_{n}$/$f_{1}$

The resonance frequencies of the clamped-free beam are obtained by using the normalized wave numbers in Table 5.1 and the dispersion Eq. 5.4. For a beam with rectangular cross-section $(A=wb)$ the result is:

$$\begin{aligned} f_{n} = \frac{{\left( {k_{n} L} \right)^{2} }}{{2\pi }}\frac{b}{{L^{2} }}\sqrt{\frac{E}{{12\rho }}} = \frac{{\left( {k_{n} L} \right)^{2} }}{{c_\mathrm{C}^{2} }}. \end{aligned}$$

(5.7)

The geometrical and material data of the cantilever can be combined in a constant $c_\mathrm{C}$ defined as:

$$\begin{aligned} c_\mathrm{C}=L\sqrt{2\pi \sqrt{\frac{12\rho }{b^{2}E}}}. \end{aligned}$$

(5.8)

The resonance frequencies $f_{n}$ are proportional to the square of the wave numbers, which means that the phase velocity of the flexural modes is not constant, i.e., the modes are dispersive and not equidistant. However, equation 5.7 shows that the frequency ratio of the flexural modes is independent of the material and geometry data of the cantilever. The ratio of the higher resonance frequencies to the first flexural frequency is shown in the third row of Table 5.1.

The resonance frequencies of the clamped-free cantilever play an important role in quantitative AFAM. The geometrical data of the commercial cantilevers made of single crystal silicon are subject to unavoidable deviations caused by the batch fabrication process. These geometrical variations cause wide frequency and spring-stiffness ranges for the same type of cantilever (up to 100 % variation is possible depending on the beam type). It is time consuming to measure the geometrical dimensions of individual beams by optical or electron microscopy. Furthermore, the errors in the obtained geometry data are so high that the resonance frequencies calculated with these data are not precise enough. It is relatively easy to measure the first few flexural resonance frequencies of a cantilever in air either using forced vibration excited at the cantilever holder or just by observing the noise spectrum. In spite of the air damping the Q-values of the lower modes are generally much higher than 50 [24], therefore the free resonance frequencies can be measured with high precision, and they can be used to calculate the cantilever constant $c_\mathrm{C}$. Some authors suggest to retrieve the geometrical cantilever dimensions from the frequencies of their higher modes and use these data for calibration of the spring constants [25–27].

A comparison of the experimental frequency ratio to the theoretical one shows how well commercial rectangular cantilevers fit the model [24, 28]. The Euler–Bernoulli beam equation does not take into account shear deformation and rotary inertia, which is only a good assumption if thickness b and width w are much smaller than the length L. Thin, long, and soft cantilevers like the ones used for contact and lateral force mode obey much better this requirement than the thicker, shorter, and stiffer cantilevers with static spring constants of 20 N/m and more that are used for intermittent contact and non-contact techniques. Furthermore, the geometry of real cantilevers differs from the model, for example the cross-section is not exactly constant and of trapezoidal form, and the suspension is not infinitely stiff and symmetrical [29] but made of silicon like the cantilever (see Fig. 5.2). For example, the higher resonance frequencies of silicon cantilevers of the approximate dimensions (225 $\upmu$m $\times$ 30 $\upmu$m $\times$ 7 $\upmu$m [30]) are slightly lower than the frequencies predicted by the flexural beam model [28]. The same tendency and order of magnitude of frequency deviation from the Euler model is obtained theoretically when the flexural vibration frequencies of AFM cantilevers are calculated with the more precise Timoshenko beam model [31]. The difference between the Euler–Bernoulli model and the Timoshenko model was examined theoretically for the free resonance frequencies and the contact-resonance frequencies including damping [32].

5.2.2 Contact-Resonance Models

In linear AFAM, the vibration amplitude of the tip is assumed to be small, and the tip-sample forces such as elastic forces, adhesion forces and viscoelastic forces are represented by linear springs and dashpots. The complete mechanical model for linear contact resonance vibration is shown in Fig. 5.3.

Fig. 5.3

Mechanical model of an AFM cantilever with constant cross-section vibrating in contact with a sample surface (clamped spring-coupled beam)

The length of the cantilever from the clamped end to the free end is L. The sensor tip is located at position $L_{1}$, and $L_{2}=L-L_{1}$ is the distance between the sensor tip position and the free end. Forces normal to the surface are represented by the normal contact stiffness$k^{*}$ and the contact damping$\gamma$, and forces lateral to the surface are represented by the lateral contact stiffness$k_\mathrm{Lat}^{*}$ and a lateral contact damping$\gamma _{\text{ Lat}}$. For technical reasons the cantilever is tilted with respect to the surface by an angle $\alpha _{0}$ (11–15$^{\circ }$). The characteristic equation of the model defined in Fig. 5.3 can be found by defining two solutions for the two parts of the cantilever. The boundary conditions at the clamped end (zero displacement and slope) and the free end (zero bending moment and shear force) are the same as in Eq. 5.5. At the tip position $x = L_{1}$, additional boundary conditions arise, which contain the shear force and the bending moment caused by the tip-sample forces, and which ensure the continuity of displacement and slope at $x = L_{1}$ where the two partial solutions meet.

The characteristic equation of the complete system including tip position, lateral forces and damping can be found in the literature [28]. Four simpler versions of models for quantitative AFAM without contact damping are shown in Fig. 5.4. The models and their characteristic equations are special cases of the complete solution in [28]. The characteristic equations of these models are as follows:

• (a) Simple model (24):

  $$\begin{aligned} \frac{1}{3}\frac{k_{C}}{k^{*}}\left({k_{n} L} \right)^{3}\left( {1{+}\cos k_{n} L\cosh k_{n} L} \right)+\left({\sin k_{n} L\cosh k_{n} L-\sinh k_{n} L\cos k_{n} L} \right){=}0 \end{aligned}$$

  (5.9)

• (b) Tip-position model [8, 24, 33]:

  $$\begin{aligned}&\frac{2}{3}\frac{k_C }{k^{*}}\left( {k_n L_1 } \right)^{3}\left( {1+\cos k_n L\cosh k_n L} \right) \nonumber \\&\quad +\left( {\sin k_n L_1 \cosh k_n L_1 -\sinh k_n L_1 \cos k_n L_1 } \right)\cdot \left( {1+\cos k_n L_2 \cosh k_n L_2 } \right)\nonumber \\&\quad -\left( {\sin k_n L_2 \cosh k_n L_2 {-}\sinh k_n L_2 \cos k_n L_2 } \right)\cdot \left( {1{-}\cos k_n L_1 \cosh k_n L_1 } \right)=\!0 \end{aligned}$$

  (5.10)

• (c) Lateral force model without tip position [13, 34]

  $$\begin{aligned}&\frac{1}{3}\frac{k_C }{k^{*}}\left( {k_n L} \right)^{4}A+\left( {k_n L} \right)^{3}\frac{h^{2}}{L^{2}}\left( {\sin ^{2}\alpha _0 +\frac{k_\mathrm{Lat}^*}{k^{*}}\cos ^{2}\alpha _0 } \right)D\nonumber \\&\quad +2\left( {k_n L} \right)^{2}\frac{h}{L}\sin \alpha _0 \cos \alpha _0 \left( {\frac{k_\mathrm{Lat}^*}{k^{*}}-1} \right)\sin (k_n L)\sinh (k_n L)\nonumber \\&\quad +k_n L\left( {\cos ^{2}\alpha _0 +\frac{k_\mathrm{Lat}^*}{k^{*}}\sin ^{2}\alpha _0 } \right)B+3\frac{k_\mathrm{Lat}^*}{k_C }\frac{h^{2}}{L^{2}}C=0 \end{aligned}$$

  (5.11)

• (d) Lateral force and tip-position model [10]:

  $$\begin{aligned}&\frac{2}{3}\frac{k_C }{k^{*}}\left( {k_n L_1 } \right)^{4}A+\left( {k_n L_1 } \right)^{3}\frac{h^{2}}{L_1^2 }\left( {\sin ^{2}\alpha _0 +\frac{k_\mathrm{Lat}^*}{k^{*}}\cos ^{2}\alpha _0 } \right) \cdot \left[ {D_{1} A_2 -D_2 C_1 } \right]\nonumber \\&+2\left( {k_n L_1 } \right)^{2}\frac{h}{L_1 }\sin \alpha _0 \cos \alpha _0 \left( {\frac{k_\mathrm{Lat}^*}{k^{*}}-1} \right)\nonumber \\&\cdot \left[ {\sin (k_n L_1 )\sinh (k_n L_1 ) A_2 +\sin (k_n L_2 )\sinh (k_n L_2 ) C_1 } \right] \nonumber \\&+k_n L_1 \left( {\cos ^{2}\alpha _0 +\frac{k_\mathrm{Lat}^*}{k^{*}}\sin ^{2}\alpha _0 } \right) \left[ {B_1 A_2 -B_2 C_1 } \right]\nonumber \\&+3\frac{k_\mathrm{Lat}^*}{k_C }\frac{h^{2}}{L_1^2 }C_1 A_2 =0, \end{aligned}$$

  (5.12)

  where

  $$\begin{aligned} A&=1+\cos (k_n L)\cosh (k_n L) \nonumber \\ B&=\sin (k_n L)\cosh (k_n L) -\sinh (k_n L)\cos (k_n L)\nonumber \\ C&=1-\cos (k_n L)\cosh (k_n L)\nonumber \\ D&=\sin (k_n L)\cosh (k_n L) +\sinh (k_n L)\cos (k_n L). \end{aligned}$$

  (5.13)

  The subscripts 1, 2 are used in cases where the argument is ${k_{n}}{L_{1}}$, or ${k_{n}}{L_{2}}$, respectively. For example:

  $$\begin{aligned} A_{1}=1+\cos (k_n L_1 )\cosh (k_n L_1 ) \quad \text{ and}\, A_{2} =1+\cos (k_n L_2 )\cosh (k_n L_2 ). \end{aligned}$$

  (5.14)

The same holds for B, C, and D. The static flexural spring constant $k_{C}$ of the cantilever is used to normalize the contact stiffness $k^{*}$. A variety of methods are known to determine the static spring constant $k_{C}$ [35, 36].

Fig. 5.4

Mechanical models without damping for contact-resonance vibration. a simple model b tip-position model c lateral force model d tip-position and lateral force model

The contact-resonance frequencies are obtained numerically by finding the roots $k_{n}L$ of the characteristic equations, and by using the dispersion relation 5.7 to calculate the resonance frequencies $f_{n}$. In a contact-resonance experiment, the inverse problem arises: contact-resonance frequencies $f_{n}$ are measured, and the aim is to calculate the contact stiffness. As already discussed above, it is favorable to use the resonance frequencies of the clamped-free beam and the known wave numbers in Table 5.1 to calculate the cantilever parameter $c_{C}$. In cases where the frequency ratio of the modes deviates from the Euler model, each contact-resonance frequency should be used in combination with the free resonance frequency of the same mode number:

$$\begin{aligned}&(k_n L)_\mathrm{Cont} =c_\mathrm{C} \sqrt{f_{n,\mathrm{Cont}} }=(k_n L)_\mathrm{Free} \sqrt{\frac{f_{n,\mathrm{Cont}} }{f_{n,\mathrm{Free}} }}\nonumber \\&\text{ for} \text{ example:} (k_1 L)_\mathrm{Cont}=1.8751 \sqrt{\frac{f_{n,\mathrm{Cont}} }{f_{n, \mathrm{Free}} }} \end{aligned}$$

(5.15)

Equation 5.9 describing the model in Fig. 5.4a can then be solved for the normalized contact stiffness $k^{*}$/$k_{C}$:

• (a) Simple model:

  $$\begin{aligned}&\frac{k*}{k_C }=\frac{\left( {k_n L} \right)^{3}\left( {1+\cos k_n L\cosh k_n L} \right)}{3(-\sin k_n L\cosh k_n L+\sinh k_n L\cos k_n L)}\nonumber \\&=\frac{\left( {c_\mathrm{C}\sqrt{f_{n,\mathrm{Cont}} }} \right)^{3}\left[ {1+\cos \left( {c_\mathrm{C} \sqrt{f_{n,\mathrm{Cont}} }} \right)\cosh \left( {c_\mathrm{C} \sqrt{f_{n,\mathrm{Cont}} }} \right)} \right]}{3\left[ {-\sin \left( {c_\mathrm{C} \sqrt{f_{n,\mathrm{Cont}} }} \right)\cosh \left( {c_\mathrm{C} \sqrt{f_{n,\mathrm{Cont}} }} \right)+\sinh \left( {c_\mathrm{C} \sqrt{f_{n,\mathrm{Cont}} }} \right)\cos \left( {c_\mathrm{C} \sqrt{f_{n,\mathrm{Cont}} }} \right)} \right]}. \end{aligned}$$

  (5.16)

  Tip position as a parameter to fit the analytical model to the real cantilever has been discussed in different publications [37, 38]. The tip position${L_{1}}/L$ has either to be estimated from optical micrographs or it can be determined by fitting the tip position using at least two different contact-resonance frequencies. The wave numbers of the two parts of the cantilever are:

  $$\begin{aligned} (k_{n} L_{1} )_\mathrm{Cont}=\frac{L_{1} }{L}(k_n L)_\mathrm{Free} \sqrt{\frac{f_{n,\mathrm{Cont}}}{f_{n,\mathrm{Free}} }} \quad (k_n L_2 )_\mathrm{Cont} =\frac{L_2 }{L}(k_n L)_\mathrm{Free} \sqrt{\frac{f_{n,\mathrm{Cont}} }{f_{n,\mathrm{Free}} }}. \end{aligned}$$

  (5.17)

  The contact stiffness for the tip-position model is obtained by solving the characteristic Eq. 5.10 for ${k^{*}}/{k_C}$.

• (b) Tip-position model:

  $$\begin{aligned} \frac{k^{*}}{k_C}=\frac{2\left( {k_n L_1 } \right)^{3}A}{3(-B_1A_2 +B_2 C_1 )} \end{aligned}$$

  (5.18)

  With increasing complexity of the models, more parameters are needed for the evaluation. The height of the sensor tip h (typical values 10–17 $\upmu$m) is usually specified by the cantilever manufacturers, and the cantilever tilt angle $\alpha _{0}$ is a technical parameter of the AFM instrument. Models (c) and (d) contain two unknown tip-sample spring constants, the normal contact stiffness $k^{*}$, and the lateral contact stiffness $k^{*}_{\text{ Lat}}$. The ratio $k^{*}_{\text{ Lat}}/k^{*}$ ranges between 2/3 and 18/19 for most materials with an average value of 0.85 (13). If one assumes the ratio $k^{*}_{\text{ Lat}}/k^{*}$to be known, Eqs. 5.11 and 5.12 can be solved for $k^{*}/k_{C}:$

• (c) Lateral force model without tip position $(k_\mathrm{Lat}^*\ne 0)$:

  $$\begin{aligned} \left( {\frac{k^*}{k_C }} \right)_{1;2} =-\frac{\varsigma L^{2}}{6c_P h^{2}C}\pm \sqrt{\left( {\frac{\varsigma L^{2}}{6c_P h^{2}C}} \right)^{2}-\frac{\left( {k_n L} \right)^{4}L^{2}A}{9c_P L^{2}C}}, \end{aligned}$$

  (5.19)

  where $c_P = k^{*}_{\text{ Lat}}/k^{*}$ is the known lateral to normal contact stiffness ratio and

  $$\begin{aligned} \varsigma&=\left( {k_n L} \right)^{3}\frac{h^{2}}{L^{2}}\left( {\sin ^{2}\alpha _0 +c_P \cos ^{2}\alpha _0 } \right)D\nonumber \\&\quad +2\left( {k_n L} \right)^{2}\frac{h}{L}\sin \alpha _0 \cos \alpha _0 \left( {c_P -1} \right)\sin (k_n L)\sinh (k_n L)\nonumber \\&\quad +k_n L\left( {\cos ^{2}\alpha _0 +c_P \sin ^{2}\alpha _0 } \right) B \end{aligned}$$

  (5.20)

• (d) Lateral force and tip-position model $(k_\mathrm{Lat}^*\ne 0)$

  $$\begin{aligned} \left( {\frac{k^{*}}{k_C }} \right)_{1;2} =-\frac{{\upsilon }{L_1^2}}{6c_P h^2 C_1 A_2 }\pm \sqrt{\left( {\frac{{\upsilon }L_1^2}{6c_P h^2 C_1A_2 }} \right)^{2}-\frac{2\left({k_n L_1 } \right)^{4}h^2 A}{9c_P h^{2}C_1 A_2 }}, \end{aligned}$$

  (5.21)

  where $c_{P}$ is again the lateral to normal contact stiffness ratio and

  $$\begin{aligned} \upsilon&=\left( {k_n L_1 } \right)^{3}\frac{h^{2}}{L_1^2 }\left( {\sin ^{2}\alpha _0 + c_P \cos ^{2}\alpha _0 } \right)\left[ {D_1 A_2 -D_2 C_1 } \right]\nonumber \\&\quad +2\left( {k_n L_1 } \right)^{2}\frac{h}{L_1 }\sin \alpha _0 \cos \alpha _0 \left( {c_P -1} \right)\nonumber \\&\quad \cdot \left[ {\sin (k_n L_1 )\sinh (k_n L_1 )A_2 +\sin (k_n L_2 )\sinh (k_n L_2 ) C_1 } \right]\nonumber \\&\quad +k_n L_1 \left( {\cos ^{2}\alpha _0 +c_P \sin ^{2}\alpha _0 } \right) \left[ {B_1 A_2 -B_2 C_1 } \right] \end{aligned}$$

  (5.22)

The advantage of analytical models is that they can be directly solved for the contact stiffness and that they can be quickly evaluated with varying parameters. Analytical models become increasingly complicated if more details in the shape of the cantilever like the triangular end (dagger shaped cantilever) [39], the suspension [29] or shear stiffness and rotary inertia are considered [32].

5.2.3 Finite-Element Models (FEM)

Several publications can be found in the literature presenting numerical models and finite-element (FE) calculations of AFM cantilevers and their vibrations [14, 26] [17, 27] (Chap. 4). In order to improve quantitative evaluation of AFAM by FEM, important details in the geometric shape, the elastic anisotropy of single crystal silicon cantilevers, and the elasticity of the suspension of AFM cantilevers should be considered in the model. An FE model was created, which considers the geometrical shape of the cantilevers with a trapezoidal cross-section and a triangular free end, the cubic symmetry of silicon single crystal, and the elastic coupling of the cantilevers to the holder [40]. Figures 5.2a and 5.2b show scanning electron micrographs (SEM) of a commercial single crystal silicon cantilever. For the geometrical model, a Cartesian coordinate system with the $x^{\prime }$-, $y^{\prime }$-, and $z^{\prime }$-axes in the cantilever length, thickness, and width directions, respectively, was used (Fig. 5.5). These axes coincide with the crystallographic axes [110], [001], and [$1\bar{{1}}0$] of the cubic single crystal material, respectively. Figure 5.5b shows the FE model of the cantilever after meshing. It comprises 3D tetrahedral elements with linear dimensions of about 1.5 $\upmu$m in average for both the beam and the tip. In the regions where higher strain was to be expected, the density of the grid elements was increased. The tip-sample contact forces were modeled as three springs in a coordinate system {X, Y, Z} aligned to the sample surface (Figs. 5.5b). The coordinate system {X, Y, Z} was chosen to coincide with the cantilever system {$x^{\prime }$, $y^{\prime }$, $z^{\prime }$} for $\theta = 0^{\circ }$. The spring constants $k^{*}$ and $k^{*}_{\text{ Lat}}$ are the tip-sample contact stiffness values in out-of-plane ($Y$-axis) and in-plane direction ($X$- and $Z$-axes), respectively. The FE model was fitted to the experiments in a two-step iterative procedure. In a first step, the measured free resonance frequencies of the lowest bending, torsional, and lateral bending modes of an individual cantilever were used to fit the geometrical cantilever dimensions. Subsequently, tip length and cantilever inclination $\alpha _{0}$ were fitted to match the measured CR frequencies of the first and the third bending mode. The FE model also allows a precise calculation of the spring constant $k_{C}$ of the cantilever. With the obtained FE cantilever model, the remaining free bending as well as the torsional resonances were predicted and compared to the experimental spectra. For the first three bending modes and for the first free torsional mode errors less than 1 % were achieved [40], which means that the model presented in Fig. 5.5 is able to simulate the free resonance frequencies of the cantilevers more precisely than the usual analytical models.

Fig. 5.5

Schematic sketch of the cantilever a with its coordinate system {x $^{\prime }$,y $^{\prime }$,z $^{\prime }$} inclined by an angle $\theta$ relative to the sample surface coordinate system {X,Y,Z}. The tip-sample forces are modeled by three springs with spring constants $k^{*}$ and ${k^{*}}_\mathrm{Lat}$ for vertical and lateral contact stiffness, respectively; b FE model of the cantilever after meshing [40]

In order to investigate the influences of the different geometrical parameters on the resonance frequencies, several cantilevers of similar shape with only small differences in their geometrical dimensions were examined. It was shown that the modeling of the shape and elasticity of the sensor tip and of its contact to the sample surface are the most critical points rather than the differences in the analytical and the more realistic FE model of the cantilever geometry.

AFAM measurements on fused silica and nickel were numerically modeled to obtain values of out-of-plane, $k^{*}$, and in-plane, ${k^{*}}_\mathrm{Lat}$, stiffness [40]. The normal spring constant for a cantilever inclined relative to the sample surface was determined by FEM, and used to calculate the static force from the static cantilever deflection. The obtained normal contact stiffness values were within the range covered by the theoretical values for nickel and for fused silica calculated with the Hertzian contact model and a tip radius of 80 nm. The values obtained for the in-plane surface stiffness ${k^{*}}_\mathrm{Lat}$ were too low as compared to those calculated from contact mechanics theories. This was probably due to tip-sample interactions involving contamination layers that were not included in the model.

5.3 Experimental Methods for Quantitative AFAM

The AFAM technique employs the contact-resonance frequencies of an AFM cantilever for quantitative measurement of elastic properties of sample surfaces. In the last years, several methods have been developed to measure the contact-resonance frequencies and to determine the sample surface properties. An important aspect of quantitative AFAM is the strategy to determine the geometrical and material parameters of the tip and the cantilever [41], which have to be known in order to calculate the sample surface properties.

5.3.1 Experimental Setup

A schematic sketch of a typical AFAM setup is shown in Fig. 5.6. In the configurations discussed here, the investigated sample is placed on top of an ultrasonic transducer. The amplitude of the cantilever vibrations is measured with the laser beam deflection detector of the AFM. The frequency and the amplitude of the longitudinal wave that propagates in the sample are controlled by a waveform generator. Contact-resonance spectra are measured by recording the amplitude of the cantilever vibration as a function of the excitation frequency.

Fig. 5.6

Schematic representation of the AFAM experimental set-up

As indicated in Fig. 5.6, one can utilize different approaches to acquire a contact-resonance spectrum. One can use a lock-in amplifier to analyze the photodiode signal at the excitation frequency. In this case, the transducer is excited with a single frequency. To create the contact-resonance spectrum, the frequency is changed stepwise, and the amplitude component of the lock-in output signal is digitized, sent to a computer and plotted as a function of the excitation frequency. A lock-in amplifier can be easily combined with AFM instruments, and it can be used for the real-time acquisition of qualitative AFAM images, where the amplitude of the cantilever vibrations at a fixed frequency is evaluated as a function of position and used as an imaging quality. However, even in combination with a down-converter [37], lock-in amplifiers are relatively slow when used in the spectroscopy mode. A short sweep time is essential for the acquisition of a statistically significant amount of data. For a fast spectral analysis, an analog frequency modulation detector [42] and a digital-signal-processor based resonance tracking system were developed [43]. Furthermore, one can excite the transducer with a pulse and extract the spectrum by fast fourier transformation (FFT) of the cantilever vibration signal. It is favorable to tailor the frequency content of the pulse in such a way that its spectrum comprehends an appropriate interval around the center frequency of the contact resonance, like in the band excitation method [44].

5.3.2 Single Point Measurements

In the early work in AFAM single point measurements were performed, i.e., the contact-resonance spectra were acquired at a single position on the sample surface at several static loads [33, 39, 45, 46]. The CR frequencies of at least two contact modes are needed to allow for the tip-position determination required for models Fig. 5.4c and d. Figure 5.7 presents the CR frequencies measured on fused silica and single crystal silicon samples for the first and the second contact modes. A commercially available AFM beam ($L =225\,\upmu$m, $b=8\,\upmu$m, $w=38\,\upmu$m) was used, with free resonance frequencies of 175 kHz and 1,081 kHz for the first and the second mode, respectively. The spring constant of the cantilever was about 45 N/m. The static load applied to the tip increased from 90 nN to 1350 nN in 20 steps.

Fig. 5.7

a Contact-resonance frequencies $f_{1,Cont}$ and $f_{2,Cont}$ measured on the single crystal silicon (Si) and fused silica reference samples. b Normalized contact stiffness k$^{*}/k_\mathrm{C}$ calculated from the resonance frequencies presented in a

As can be seen in Fig. 5.7a, the contact-resonance frequencies recorded for the fused silica sample are significantly lower than those measured on the single crystal silicon sample because the elastic constants of fused silica are lower than those of silicon. Accordingly, the values of the normalized contact stiffness$k^{*}$/$k_{C}$ calculated for fused silica are lower than those calculated for silicon for each value of the applied static load (Fig. 5.7b). In addition, the dependence of the resonance frequency values on the applied static load contains information about the tip-sample geometry. A systematic record of stiffness–load curves during a series of measurements also holds information on the changes in the tip shape and dimension.

Usually, the single point measurements are done in a precisely defined sequence. First, the contact-resonance frequencies are measured on a reference sample for at least two contact modes at several values of the static load. Then, the resonance frequencies are measured on the unknown sample at exactly the same values of the static loads like those used on the reference sample. The recurrence of the reference measurement closes the sequence, which is usually repeated several times. The repetition with recurrence to the reference sample is necessary to account for the influence of the tip wear on the accuracy of the AFAM measurement.

The single point measurements must be repeated at several random locations on the sample surface to create a statistically significant data base. The tip-sample contact occurs at an area of few tens of nanometers squared. Small local differences in the surface morphology and the unpredictable progress of the tip wear [47] influence the measurement of the CR frequency values (Chap. 13). In typical AFAM measurements with a stiff cantilever ($k_{C}=30\,\text{--}\,40$ N/m), the contact-resonance frequencies can be measured with an accuracy of about 0.2 and 1 % for the first and the second mode, respectively [48]. These relatively small values of the measurement error may lead to about 5–10 % of uncertainty in the calculated values of the tip-sample contact stiffness $k^{*}$.

5.3.3 Grid Measurements

An alternative to the single point measurements are grid measurements, where an array of measurement points is distributed over a certain area [49]. Figures 5.8a and b present the grid images obtained on Au and MgF$_{2}$ samples for the first and the second mode, respectively.

Fig. 5.8

Grid measurements of the contact-resonance frequencies performed on surfaces of Au and MgF$_{2}$ samples for the (a) first and (b) second mode. Histograms of the occurrence of a contact-resonance frequency value for the (c) first and (d) second contact mode (49). The data used to create the images and histograms were provided by G. Stan, NIST, Gaithersburg, Maryland, USA

The images consist of 10 $\times$ 10 points measured on an area of 3 $\times$ 3 $\upmu$m. The free resonance frequencies of the cantilever used in this experiment were 114 and 725 kHz for the first and the second mode, respectively. The contact-resonance frequency data were evaluated statistically to obtain a histogram of occurrence of a given frequency value. Examples of such histograms calculated form the grid images presented in Fig. 5.8a and b are presented in Fig. 5.8c and d for the first and the second mode, respectively. As can be easily seen, the distribution of the contact-resonance frequency values measured for the first mode on Au and for the first and second modes on MgF$_{2}$ can be described by a Gaussian curve. The values of the second contact-resonance frequency measured for the gold sample show a bimodal distribution. In this case, the split in the values of the CR can be associated with a sudden change in the tip shape, which also explains the sudden change in the contrast of the corresponding grid image (Fig. 5.8b). The CR frequency value with the highest occurrence count is determined from the histograms and used to calculate the tip-sample contact stiffness $k^{*}$.

Grid measurements deliver low resolution images, which inform immediately on the uniformity of the samples in their elastic properties. Furthermore, the grid measurement yields values of the contact resonance-frequencies that are representative for the tested area. However, the tip scans the sample surface while relatively high static loads are applied. Continuous scanning of the sample promotes tip wear, which changes the contact-resonance frequencies. Therefore, the tip should be worn intentionally to a certain amount prior the grid measurement such that the progress in wear is less pronounced than in the case of a new, sharp tip [50]. As all the measurements are performed at the same static load, no additional information on the tip geometry is available. Such information can be either obtained by performing additional single point measurements on a reference sample or by for example SEM studies of the tip geometry [33, 51].

5.3.4 Contact-Resonance Frequency Images

Single-point or grid measurements work well on flat, homogenous samples. However, in case of multiphase materials, such as polycrystalline samples or composites containing phases with different elastic properties, difficulties arise in the interpretation of the frequency statistics.

Therefore, the number of points in the frequency image must be increased to generate a more detailed map. In most of the reported studies the CR images consist of 128 $\times$ 128 points or more [34, 53–58]. In most of the cases, the images are acquired for the first and the second contact mode. The contact-resonance frequencies of the two modes are used later for calculation of the contact stiffness image. Figure 5.9 shows topography (a) and contact-resonance frequency images (b, c) of a blanket film of organosilicate glass (SiOC) containing trenches filled with deposited copper lines [52]. The SiOC film was approximately 280 nm thick. The topography image shows the blanket film and the copper “fingers.” The contact-resonance frequency images clearly reveal the areas corresponding to the glass and copper “fingers.”

Fig. 5.9

a Topography and contact-resonance frequency images obtained for b the first and c the second mode for an organosilicate glass containing copper filled trenches [52]. The images were provided by D.C. Hurley, NIST, Boulder, Colorado, USA

5.4 Contact Mechanics and Calibration Methods

The previous sections dealt with the experimental procedures to measure contact-resonance frequencies. The contact-resonance frequencies and one of the models describing the cantilever dynamics that are explained in detail in Sect. 5.2 are utilized to calculate the normalized contact stiffness $k^{*}$/$k_{C}$. In order to obtain elastic constants of the sample surface from the local contact stiffness, contact mechanics models, such as for example Hertz or Maugis models [59] are needed. The Hertzian model describes the contact between two nonconforming elastic bodies of general anisotropy [60]. In the simplest case, the bodies are mechanically isotropic, the sample is considered as flat and the sensor tip is represented by a hemisphere with radius R (see Fig. 5.1). If a normal force $F_{n}$ acts, a circular contact area forms with radius $a_{C}$:

$$\begin{aligned} a_{C} =\root 3 \of {3F_{n} R/4E^{*}}. \end{aligned}$$

(5.23)

It is important for the validity of the model that the contact area is small compared to the tip radius, i.e. $a_{C} \ll R$. If the adhesion forces are so small that they can be neglected, the normal force $F_{n}$ is given by the static deflection of the cantilever multiplied with the spring constant of the cantilever $F_{n} =dk_{C}$, where d is the cantilever deflection. The normal contact stiffness$k^{*}$ is in this case:

$$\begin{aligned} k^{*}=2a_{C}E^{*}=\root 3 \of {6E^{*2}RF_{n} }. \end{aligned}$$

(5.24)

$E^{*}$ is the reduced Young’s modulus that combines the elastic properties of the tip (t) and the sample (s) in the following equations:

$$\begin{aligned} \frac{1}{E^{*}}=\frac{1-\nu _t^2 }{E_t }+\frac{1-\nu _s^2 }{E_s }, \end{aligned}$$

(5.25)

where $E_{s}$, $E_{t}$, $\nu$ $_{s}$, $\nu$ $_{t}$, are the Young’s moduli and the Poisson’s ratios of the surface and the tip, respectively. AFM sensor tips made of single crystalline silicon are not elastically isotropic, and this holds for other tip and sample materials as well. In special cases of symmetry Eqs. 5.24 and 5.25 remain valid if the isotropic reduced elastic modulus$E$/(1-$\nu$ $^{2})$ is replaced by an indentation modulus that is calculated numerically from single crystal elastic constants [61, 62]:

$$\begin{aligned} \frac{1}{E^{*}}=\frac{1}{M_\mathrm{t} }+\frac{1}{M_\mathrm{s} }, \end{aligned}$$

(5.26)

where $M_{s}$ and $M_{t}$ are the indentation modulus of the sample and the tip, respectively. The required symmetry holds for silicon sensor tips, which are oriented in (001) crystallographic direction.

5.4.1 Single Reference Method

The expression for the contact stiffness presented in Eq. 5.24 contains two unknown parameters, namely, the tip radius R and the reduced Young’s modulus $E^{*}$ of the sample. One method to obtain these data involves using a reference sample with known elastic properties [45]. The contact stiffness $k^{*}$ is determined at several static loads for the reference sample. These values of $k^{*}$ will be referred to as “reference contact stiffness” $k^{*}_\mathrm{ref}$. They are compared to the values of the contact stiffness obtained for the sample with unknown elastic properties $k^{*}_{s}$ at the same static load $F_{n}$ as used for the reference measurements. Using Eqs. 5.24–5.26, an expression for the indentation modulus of the sample $M_{s}$ can be derived that is independent of the tip radius and the static load:

$$\begin{aligned} \frac{k_s^{*} }{k_\mathrm{ref}^{*} }=\root 3 \of {\frac{6RF_n E_s^{*2} }{6RF_n E_\mathrm{ref}^{*2} }}=\root 3 \of {\frac{E_s^{*2} }{E_\mathrm{ref}^{*2} }}, \end{aligned}$$

(5.27)

$$\begin{aligned} E_{s}^{*}=E_\mathrm{ref}^{*} \left({\frac{k_s^{*} }{k_\mathrm{ref}^{*} }} \right)^{3/2}, \end{aligned}$$

(5.28)

$$\begin{aligned} M_{s}=\left({\frac{1}{E_{s}^{*} }-\frac{1}{M_t }} \right)^{-1}. \end{aligned}$$

(5.29)

As already mentioned in Sect. 5.3.2, the contact stiffness variation as a function of static load contains information on the tip geometry. An increase of the contact stiffness $k^{*}$ with the static load $F_{n}$, follows from Eq. 5.24 if the tip apex has hemispherical geometry. As the tips wear and break, different tip shapes arise (see Fig. 5.10). If the values of $k^{*}$ remain constant, a flat punch geometry can be assumed, and the radius of the contact area $a_{C}$ can be assumed to be constant. Different tip shapes can be considered by introducing a tip geometry factor $n$, changing between 1 and 3/2 for a flat punch and a sphere, respectively. Equation 5.28 is replaced by

$$\begin{aligned} E_{s}^{*}=E_\mathrm{ref}^{*} \left({\frac{k_{s}^{*} }{k_\mathrm{ref}^{*} }} \right)^{n}. \end{aligned}$$

(5.30)

SEM images of various AFM tips used in AFAM experiments confirmed that the contact stiffness—load dependence is strongly influenced by the tip geometry and that consideration of the geometry factor $n$ may improve the accuracy of the AFAM measurement [33]. Figure 5.10 shows examples of the normalized contact stiffness values obtained for a fused silica sample with two cantilevers with very similar spring constants $k_{C}$ but sensor tips of different geometries [51].

Fig. 5.10

a Normalized contact stiffness $k^{*}$/$k_{C}$ as a function of cantilever deflection d. The data sets were obtained with tips with geometries of b flat punch and c hemisphere confirmed by corresponding scanning electron micrographs [51]

The single reference sample calibration does not only allow for efficient elimination of the dependence of the contact stiffness on the tip geometry but also eliminates the static spring constant of the cantilever. However, a detailed analysis of AFAM experimental data showed that the values obtained for the indentation modulus $M_{s}$ were either too large if the reference sample was much stiffer than the unknown sample or too low if the reference sample was more compliant than the tested sample [48, 63]. Furthermore, the elastic constants of the sensor tips were not always known, especially in cases where the tip was coated for example with a diamond layer or diamond like carbon layer to improve its wear resistance.

5.4.2 Dual Reference Method

If two different reference samples are available, each of the samples can be used for calibration, and the results can be averaged, or the contact stiffness data can be used to eliminate not only the tip geometry parameter, but also the tip indentation modulus $M_{t}$. The two reference samples are chosen such that their elastic constants bracket the elastic properties of the unknown samples. By comparing the values of the contact stiffness $k^{*}_{1}$ and $k^{*}_{2}$ measured for two reference samples at the same static load and using Eqs.5.24 and 5.26, the expression for the indentation modulus $M_{t}$ takes the following form [48]:

$$\begin{aligned} M_{t}=\frac{M_{1} M_{2} \left({1-\left({\frac{k_1^{*} }{k_{2}^{*} }} \right)^{n}} \right)}{\left({\left({\frac{k_{1}^{*} }{k_{2}^{*} }} \right)^{n}M_{2}-M_{1} } \right)}, \end{aligned}$$

(5.31)

where $M_{1}$ and $M_{2}$ are the indentation moduli of the two different reference samples. With this method, the elastic properties of diamond coated tips [62] were determined, using silicon and strontium titanate single crystal samples as a reference. Hurley et al. [39] used two reference samples of borosilicate glass ($M_{g}$ = 85 GPa) and silicon single crystal ($M_{Si}$ = 139 GPa) that bracketed the expected values of the indentation modulus for a tested niobium sample ($M_\mathrm{Nb}$ = 116–133 GPa). The indentation modulus of niobium was calculated by using each reference material individually and subsequent averaging of the results. As can be seen from the data presented in Table 5.2, the values of the indentation modulus $M_\mathrm{Nb}$ obtained for niobium films depended strongly on the choice of the reference material. Employing the glass reference sample yielded values of $M_\mathrm{Nb}$ that were much lower than those expected from the literature values. On the other hand, using silicon as a reference sample, the values of $M_\mathrm{Nb}$ were close to the upper limit expected for the indentation modulus of niobium. Averaging yielded results that were in good agreement with the literatures data as well as the indentation modulus $M_\mathrm{Nb}$ obtained by nanoindentation measurements performed on the same niobium film.

Table 5.2 AFAM results for the indentation modulus of a niobium film

Several authors observed an increasing difference between the expected indentation modulus and the value obtained by AFAM with increasing difference in the elastic properties of the unknown and the reference samples [48, 63]. This problem is especially pronounced for sharp tips. Stan et al. [49] used the dual reference method and Eq. 5.31 to determine the indentation modulus of a silicon tip. A variety of samples such as Au (111), CaF$_{2}$ (100), Si (100), and MgF$_{2}$ (001) were used and yielded results in the range from 60 to 180 GPa, depending on the choice of the reference sample, the tip position parameter, the influence of the lateral stiffness, and the tip geometry. The authors explained these large variations in the values of $M_{t}$ by discrepancy in the actual shape of the AFM tip and the assumptions of the existing models for the contact mechanics. Despite these variations, the reason of which will have to be examined in future, it was also shown in this study that the dual reference method allows to measure the indentation modulus with an accuracy of about 3 %.

5.4.3 AFAM Image Calibration

During the last ten years, the development of methods for fast acquisition of contact-resonance spectra [42, 43] opened the possibility to take contact-resonance frequency images with an increasing number of points. Once such contact-resonance frequency images are obtained for at least two modes, the calibration techniques discussed in the previous sections can be applied to create a contact stiffness image. Figure 5.11 shows (a) the normalized contact stiffness and (b) the indentation modulus obtained for the SiOC glass thin-film sample with the copper filled trenches presented in Fig. 5.9.

Fig. 5.11

a Normalized contact stiffness and b indentation modulus images obtained for SiOC thin film sample with copper filled trenches [52]. The images were provided by D.C. Hurley, NIST, Boulder, Colorado, USA

The contact stiffness image was calculated pixel-by-pixel from the contact resonance images of the two modes. To obtain a calibrated image of the indentation modulus, one can use the single or dual reference method [55, 62]. However, a calibration before or after taking an image with 16,000 points and more is problematic, as the tip shape might change because of wear. The elastic constant image in Fig. 5.11b was obtained using a part of the contact stiffness image with known elastic constants for calibration [64]. For this “self calibration,” additional single point measurements were performed directly on the SiOC film using a borosilicate glass as a reference material. Then, the value of the reduced Young’s modulus of 44 GPa obtained for the SiOC film was used as a reference $E^{*}_{ref}$ for the rest of the image. In order to obtain a value for the reference contact stiffness $k^{*}_{ref}$/$k_{C}$, an average value was calculated directly from the contact stiffness image in the SiOC region. A similar self-calibrating approach was used in Refs. [53, 57].

5.5 Nonlinear AFAM

In most of the quantitative contact-resonance spectroscopy measurements the tip-sample contact is modeled as a system of linear springs and dashpots. However, the various physical forces acting between the tip and the surface depend nonlinearly on the distance. Linear approximations are restricted to tip-sample displacements covering small parts of the interaction force curve, i.e., to small vibration amplitudes of the tip-sample distance. If operated beyond these limits the nonlinearity of the system becomes noticeable. In the regime of small nonlinearity, when the tip remains in contact with the sample surface during its vibration cycle, the contact resonance curves become asymmetric. They develop a steep edge at frequencies below the contact resonances, and the maximum shifts to lower frequencies in case of softening nonlinearity [65]. Hardening nonlinearity causes a reversed behavior. Nonlinear effects are further noticeable by higher or subharmonics in the spectrum of the cantilever vibration [66–68]. An experimental procedure based on perturbation analysis and higher order spectra measurements was proposed [67, 68] to identify the interaction force in a third-order polynomial approximation around the static set-point. Single mode excitation [67] and modal interactions in the presence of two-to-one auto-parametric resonance between two modes [68] was considered.

The downwards shift of the contact- resonance frequency as well as the generation of higher and subharmonics in the cantilever vibration with increasing excitation amplitude were numerically simulated for a pure Hertzian contact [69, 70] and for a Hertzian contact with adhesion forces added [71]. Experimental investigations of contact-resonance frequency variations and higher harmonics generation caused by the nonlinear part of a Hertzian contact were carried out by a scanning microdeformation microscope [72]. Different vibration amplitudes and static loads were considered.

An analytical model of the nonlinear dynamics of cantilever tip-sample interactions for various acoustic AFM modes treats the cantilever and the substrate as independent linear systems coupled by a nonlinear force acting between the sensor tip and a small sample volume [73] (Chap. 3). Equations for the maximum nonlinearity regime, i.e. around the minimum of the force curve, were obtained by perturbation theory using a second order polynomial expansion of the force curve. Equations for the hard contact (linear) regime were also derived.

Fig. 5.12

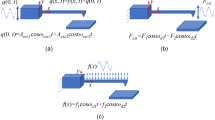
a Set-up of a commercial AFM combined with a heterodyne interferometer to measure absolute vibration amplitudes of the cantilever and the sample surface; b Examples for calibrated spectra Y(f) of the cantilever vibration obtained by FFT [74]

5.5.1 Evaluation of the Full Force Curve

The nonlinear AFAM methods mentioned above have access only to a small part of the tip-sample interaction force curve around the static set-point. A more general approach allows the reconstruction of the full curve as a function of the tip-sample distance [74, 75]. A frequency dependent transfer function ($T\omega )$ was derived for the flexural contact modes of an AFM cantilever modeled as a beam with constant cross-section. The cantilever contact-vibration amplitudes were measured quantitatively at increasing amplitudes of excitation. The time signals were Fourier transformed to obtain the spectra of the cantilever vibration. By multiplying the measured cantilever vibration spectra with the transfer function and subsequent Fourier back-transformation, the nonlinear contact and adhesion forces were calculated as a function of time. Additionally, the sample surface vibration was measured in close proximity to the cantilever tip. With these data the tip-sample interaction forces as a function of the tip-sample distance were reconstructed.

A schematic sketch of the experimental setup is shown in Fig. 5.12. Like in linear AFAM the cantilever was forced to flexural vibrations by vertical sample surface vibrations excited with an ultrasonic transducer below the sample. The static set-point of the cantilever was controlled by the beam-deflection detector and the feedback loop of the AFM. A heterodyne Mach–Zehnder interferometer (bandwidth: $\sim$100 kHz–80 MHz) was used for calibrated detection of ultrasonic vibrations. By a dichroic beam splitter added to the AFM the green beam of the interferometer was directed to the cantilever. Two mirrors were used to position the focal spot on the surface of the cantilever. The mirrors and the focusing lens were mounted on a motor-driven translation stage. In this way, the focal spot could be exactly positioned and the entire cantilever could be scanned during experiments to examine the shapes of the modes.

Fig. 5.13

Measured cantilever vibration in contact with a PZT sample, excitation at the 2nd flexural contact eigen-mode of 175 kHz; the mode shapes of the vibration of the 1st to the 6th harmonic were detectable

Figure 5.13 shows scans of the surface of the cantilever during nonlinear contact vibration. A single crystal silicon cantilever (Nanosensors, NanoWorld, Neuchâtel, Switzerland, length $\sim$485 $\upmu$m, static spring constant $\sim$0.2 N/m) and a polished PZT ceramic sample were used for these experiments. For reconstruction of the force curve, the focal spot of the interferometer was directed to a fixed position on the cantilever as close to the tip position as possible. The calibrated time signal of the interferometer y(t) was stored by a fast digitizer card and subsequently filtered and Fourier transformed. Thus, the spectral representation of the cantilever deflection Y(f) was obtained. Examples for spectra at different amplitudes of excitation are shown in Fig. 5.12b. The spectra contain the amplitude of the excitation frequency, and it can be clearly seen that the amplitudes of the harmonics increase with increasing amplitude of excitation. In order to improve the signal-to-noise ratio multiple spectra were acquired and averaged continuously. By repositioning the focal spot of the interferometer, the amplitudes and phases of the sample surface vibration were measured in the vicinity of the sensor tip. Fourier transformation revealed a spectrum containing only the excitation frequency proving that there was no signal distortion by the transducer.

The frequency dependent transfer function ($T\omega )$ follows from the theory of flexural vibrations of a rectangular beam of constant cross-section [74, 76]. The deflection y(x, t) of the beam is a function of the spatial coordinate x in longitudinal direction and of the time t described by the Euler–Bernoulli equation 5.1. Due to the linearity of this differential equation the principle of superposition is valid, and the general solution may be written as the sum of a part constant in time (the static deflection of the beam) and an infinite number of harmonic oscillations of circular frequency $\omega$ [77, 78]:

$$\begin{aligned} y(x,t)&=\sum _{{ v}=0}^{3} {B_\nu x^{\nu }+} \sum _\omega {\left[{Y(x,\omega )\mathrm{e}^{i\omega t}+\left({Y(x,\omega )\mathrm{e}^{i\omega t}} \right)^{*}} \right]}, \nonumber \\ y(t)&=y(L_{1} ,t), L_{1}=\text{ tip} \text{ position};\end{aligned}$$

(5.32)

$$\begin{aligned} Y(x,\omega )&=\sum _{\nu =0}^3 {\left[{A_\nu (\omega )\mathrm{e}^{i^{\nu }\alpha (\omega ) x}} \right]} , \alpha (\omega )=\root 4 \of {\frac{\rho A}{EI}\omega ^{2}\left({1-i\frac{\eta }{\omega }} \right)}, Y(\omega )=Y(L_1 ,\omega ).\nonumber \\ \end{aligned}$$

(5.33)

The constants $B_{ v}$ and $A_{ v}(\omega )$, ${ v}$ = {0, 1, 2, 3}, are determined by the mechanical boundary conditions of the beam.

Once the tip is in contact to the vibrating sample surface the cantilever is forced to vibrations via the tip-sample interaction forces F. The forces depend on the tip-sample distance and on the relative tip-sample velocity, which in turn are time-dependent because of the vibration. As a consequence the force acting onto the tip and indirectly onto the cantilever becomes a function of time, F(t), which may be expressed in terms of a Fourier series f($\omega )$. Note, $F$ is not directly, but indirectly time-dependent due to its distance and velocity dependency. The described relations yield the frequency dependent transfer function T($\omega )$. A detailed derivation is given in [74]. Multiplication of the cantilever vibration spectraY($\omega )$ with the transfer function T($\omega )$ yields the Fourier components f($\omega )$ of the force F(t), which then follows by Fourier back-transformation. This procedure is schematically depicted in Fig. 5.14. Figure 5.14a shows a small time interval of filtered tip vibration signals y $_\mathrm{dyn}$(t), Figs. 5.14b and c show amplitude $\Vert T\Vert$ and phase $\theta$(T) of the transfer function T($\omega )$, and Fig. 5.14d shows a small time interval of the force F(t). The four signals in Figs. 5.14a and d were obtained with the same static deflection of the cantilever, but with different amplitudes of excitation applied to the transducer.

Fig. 5.14

a Tip vibration $y_\mathrm{dyn}$(t); b amplitude and c phase of the transfer function T($\omega )$; d reconstructed force F(t). The four different signals in figures (a) and (d) correspond to four different amplitudes of excitation (0.5, 2, 5, and 10 Vpp), which were applied to the ultrasonic transducer

Fig. 5.15

a Surface vibration amplitude a(t); b dynamic part of the tip-sample distance $z_\mathrm{dyn}(t)=y_\mathrm{dyn}(t)-a(t)$, and c time-dependent force as a function of tip-sample distance. The four different signals in the figures correspond to four different amplitudes of excitation 0.5, 2, 5, and 10 Vpp, which were applied to the ultrasonic transducer. The points with zero tip-sample velocity correspond to the maxima and minima of $z_\mathrm{dyn}(t)$ and are marked with arrows in c [75]

Dynamic interaction forces as function of the tip-sample distance can be obtained by correlating the difference of the measured cantilever vibration and sample surface vibration, i.e., the dynamic part of the tip-sample distance $z_\mathrm{dyn}(t)=y_\mathrm{dyn}(t)$ – a(t), (see Figs. 5.14a and 5.15a) and the force F(t) (Fig. 5.14d). As shown in Fig. 5.15c for several different excitation amplitudes, dynamic force–distance hysteresis loops were obtained. The extrema in distance of the loops are reversal points in the relative sample surface–sensor tip movement, i.e., points with a relative sample surface–sensor tip velocity of zero. Those points cannot contain damping forces, i.e., can be used to reconstruct the quasistatic force curve from dynamic force–distance hysteresis loops. This means that each force hysteresis loop will yield at least two points of the quasistatic force curve. The map of all extrema of 20 force loops is shown in Fig. 5.16a. The force loops were obtained from a measurement series with 20 different amplitudes of excitation ranging from 0.5 to 10 V [75].

Fig. 5.16

Reconstructed force curve, a quasistatic forces obtained from the turning points of the hysteresis loops some of which are shown in Figs. 5.15c and 5.15b corrected force curve obtained by shifting each pair of turning points in horizontal direction as indicated by the arrows in a [74, 75]

Due to the lower cutoff frequency of 100 kHz of the heterodyne interferometer, it was not possible to measure the absolute static cantilever and sample surface positions. The static cantilever deflection was kept constant during the measurements by the feedback loop of the AFM. Only ac-signals were applied to the ultrasonic transducer. However, the nonlinearity of the interaction forces can cause an increase of the mean tip-sample distance with increasing ultrasonic excitation amplitudes. The feedback loop of the AFM compensates for this additional static tip deflection as it does for thermal drifts. The distance between the cantilever and the rest position of the sample surface is unknown. Therefore, the force curve reconstructed as described above (Fig. 5.16a) has to be corrected with respect to an unknown static shift. In a simple tentative approach, it was assumed that the contact stiffness was approximately constant in the repulsive region entailing a force curve being approximately linear at high loads in the repulsive region. The slope of the linear force curve was defined by the pair of turning points deduced from the elliptic hysteresis loop with the lowest amplitude of excitation stemming from a vibration, which covers only an approximately linear range of the interaction force curve. Each pair of data points from the other hysteresis loops was shifted parallel to the horizontal axis, so that the left points of the pairs formed a straight line corresponding to the contact stiffness in the repulsive region. The arrows in Fig. 5.16a show an example of how one pair of points was shifted. The quasistatic force curve corrected in this way is plotted in Fig. 5.16b. The center of the linear hysteresis loop generated by the low amplitude excitation was chosen as zero-point of the horizontal axis displaying the corrected tip-sample distance $z^{*}$. As the vibration is sinusoidal and consequently symmetric to the origin, this zero-point corresponds to the initially chosen static set-point position.

A direct and quantitative measurement of the cantilever vibrations was achieved by combining an AFM with a heterodyne Mach–Zehnder interferometer. No a priori assumptions about the shape of the force curve and the kind of forces were required. The force curve shown in Fig. 5.16c was obtained with a soft cantilever with a spring constant of approximately 0.15 N/m. In quasistatic measurements the cantilever jumps into contact when the tip-sample force gradient becomes larger than the spring constant of the cantilever. The dynamic approach presented here allows one to reconstruct intervals of the force curve which are not accessible in quasistatic measurements.

5.6 Conclusions

In this chapter frequently used mechanical models and experimental methods were reviewed, which have been used in quantitative AFAM. In many different applications AFAM or CR-AFM has proven to be a very useful tool for measurement of elastic constants with high local resolution. Since the invention of AFAM, there has been strong progress in its theoretical as well as in its experimental aspects. For example, the analytical and finite-element models for the theoretical description of the cantilever vibrations have been improved, the influence of the different parameters on the quantitative results, and various aspects of sensitivity have been examined. While the first quantitative AFAM results were obtained with single point measurements, the acquisition of contact-resonance frequency images is now state of the art due to the development of methods for fast acquisition of contact-resonance spectra. However, despite the advantages of CR imaging, AFAM amplitude imaging can be the technique of choice in cases where the contact-resonance frequency variations in the scanned area are small. In addition to linear AFAM, nonlinear AFAM techniques were treated. With an approach based on a transfer function of the cantilever beam, the full non-linear tip-sample force curve can be reconstructed from measurements with soft cantilevers with spring constants of approximately 0.2 N/m. In contrast to linear contact-resonance spectroscopy, which exploits the shift of the resonant frequencies, the reconstruction of the nonlinear forces is based on amplitude measurements, which are more difficult in AFM than frequency measurements.