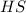Abstract
An algorithm for splitting permutation representations of a finite group over fields of characteristic zero into irreducible components is described. The algorithm is based on the fact that the components of the invariant inner product in invariant subspaces are operators of projection into these subspaces. An important part of the algorithm is the solution of systems of quadratic equations. A preliminary implementation of the algorithm splits representations up to dimensions of hundreds of thousands. Examples of computations are given in the appendix.
Access provided by CONRICYT-eBooks. Download conference paper PDF
Similar content being viewed by others
1 Introduction
One of the central problems of group theory and its applications in physics is the decomposition of linear representations of groups into irreducible components. In general, the problem of splitting a module over an associative algebra into irreducible submodules is quite nontrivial. An overview of the algorithmic aspects of this problem can be found in Chap. 7 of [1]. For vector spaces over finite fields, the most efficient is the Las Vegas algorithmFootnote 1 called MeatAxe [2]. This algorithm played an important role in solving the problem of classifying finite simple groups. However, the approach used in the MeatAxe is ineffective in characteristic zero, whereas quantum-mechanical problems are formulated just in Hilbert spaces over zero characteristic fields. Our algorithm deals with representations over such fields, and its implementation copes with dimensions up to hundreds of thousands, which is not less than the dimensions achievable for the MeatAxe. The algorithm requires knowledge of the centralizer ring of the considered group representation. In the general case, the calculation of the centralizer ring is a problem of linear algebra, namely, solving matrix equations of the form  . For permutation representations, there is an efficient way to compute the centralizer ring, which reduces to constructing the set of orbitals. In addition, permutation representations are fundamental in the sense that any linear representation of a finite group is a subrepresentation of some permutation representation, and we use this fact in some quantum mechanical considerations [3, 4]. Thus, we consider only permutation representations here.
. For permutation representations, there is an efficient way to compute the centralizer ring, which reduces to constructing the set of orbitals. In addition, permutation representations are fundamental in the sense that any linear representation of a finite group is a subrepresentation of some permutation representation, and we use this fact in some quantum mechanical considerations [3, 4]. Thus, we consider only permutation representations here.
2 Mathematical Preliminaries
Let  (or
(or  ) be a transitive permutation group on a set
) be a transitive permutation group on a set  . We will denote the action of
. We will denote the action of  on
on  by
by  . A representation of
. A representation of  in an
in an  -dimensional vector space over a field
-dimensional vector space over a field  by the matrices
by the matrices  with the entries
with the entries  , where
, where  is the Kronecker delta, is called a permutation representation. We assume that the permutation representation space is a Hilbert space
is the Kronecker delta, is called a permutation representation. We assume that the permutation representation space is a Hilbert space  . We will assume that the base field
. We will assume that the base field  is a constructive splitting field of the group
is a constructive splitting field of the group  . In particular, such a field can be a subfield of the
. In particular, such a field can be a subfield of the  th cyclotomic field, where
th cyclotomic field, where  is a suitable divisor of the exponent of
is a suitable divisor of the exponent of  . Such a constructive field
. Such a constructive field  , being an abelian extension of the field
, being an abelian extension of the field  , is a dense subfield of
, is a dense subfield of  or
or  .
.
An orbit of  on the Cartesian square
on the Cartesian square  is called an orbital [5]. The number of orbitals, called the rank of
is called an orbital [5]. The number of orbitals, called the rank of  , will be denoted by
, will be denoted by  . An orbital
. An orbital  is called self-paired, if
is called self-paired, if  , i.e.,
, i.e.,  . Among the orbitals of a transitive group, there is one diagonal orbital,
. Among the orbitals of a transitive group, there is one diagonal orbital,  , which will always be fixed as the first element in the list of orbitals:
, which will always be fixed as the first element in the list of orbitals:  . For transitive action of
. For transitive action of  , there is a natural one-to-one correspondence between the orbitals of
, there is a natural one-to-one correspondence between the orbitals of  and the orbits of a point stabilizer
and the orbits of a point stabilizer  :
:
The  -orbits are called suborbits and their cardinalities will be called the suborbit lengths. Note that
-orbits are called suborbits and their cardinalities will be called the suborbit lengths. Note that  .
.
The invariance condition for a bilinear form  in the Hilbert space
in the Hilbert space  can be written as the system of equations
can be written as the system of equations  It is easy to verify that in terms of the entries these equations have the form
It is easy to verify that in terms of the entries these equations have the form  Thus, the basis of all invariant bilinear forms is in one-to-one correspondence with the set of orbitals: with each orbital
Thus, the basis of all invariant bilinear forms is in one-to-one correspondence with the set of orbitals: with each orbital  is associated a basis matrix
is associated a basis matrix  of the size
of the size  with the entries
with the entries
It is clear that the matrix of a self-paired orbital is symmetric. For the diagonal orbital, we have  . The matrices
. The matrices
form a basis of the centralizer ring (or centralizer algebra) of the representation  . The multiplication table for this basis has the form
. The multiplication table for this basis has the form
where  are non-negative integers. The commutativity of the centralizer ring indicates that the permutation representation
are non-negative integers. The commutativity of the centralizer ring indicates that the permutation representation  is multiplicity-free.
is multiplicity-free.
3 Algorithm
Let  be a transformation (we can assume that
be a transformation (we can assume that  is a unitary matrix) that splits the permutation representation
is a unitary matrix) that splits the permutation representation  into
into  irreducible components:
irreducible components:
where  is a
is a  -dimensional irreducible subrepresentation,
-dimensional irreducible subrepresentation,  denotes the direct sum of matrices, i.e.,
denotes the direct sum of matrices, i.e.,  .
.
The identity matrix  is the standard inner product in any orthonormal basis. In the splitting basis, we have the following decomposition of the standard inner product
is the standard inner product in any orthonormal basis. In the splitting basis, we have the following decomposition of the standard inner product

The inverse image of this decomposition in the original permutation basis has the form

where  is defined by the relation
is defined by the relation

The set  contains complete information about irreducible decomposition of the representation
contains complete information about irreducible decomposition of the representation  . In particular, the transformation matrix can be obtained from the linear system
. In particular, the transformation matrix can be obtained from the linear system 
The main idea of the algorithm is based on the fact that  ’s form a complete set of orthogonal projectors, i.e., in addition to the completeness (3), we have the idempotency
’s form a complete set of orthogonal projectors, i.e., in addition to the completeness (3), we have the idempotency
and the mutual orthogonality

It follows from (4) that
We see that all  ’s can be obtained as solutions of the equation
’s can be obtained as solutions of the equation

for the generic invariant form
Using the multiplication table (2), we can write the left-hand side of (8) as a set of  polynomials (we will call them idempotency polynomials)
polynomials (we will call them idempotency polynomials)
and Eq. (8) can be written symbolically as
Each polynomial in (9) has the structure  , where
, where  is a homogeneous quadratic polynomial in the indeterminates
is a homogeneous quadratic polynomial in the indeterminates  .
.
In the basis (1), the projector  can be represented as
can be represented as
where the vector \({~B_m=\left[ b_{m,1},\ldots ,b_{m,\mathrm {R}}\right] ~}\) is a solution of Eq. (10).
Since only  has nonzero diagonal elements, we have
has nonzero diagonal elements, we have
Combining this with (7) we can fix the coefficient  :
:
Thus, the only relevant values of  in (10) are
in (10) are  for some
for some  ’s from the interval
’s from the interval  . Any relevant natural number
. Any relevant natural number  is either an irreducible dimension or a sum of such dimensions. Using the orthogonality condition (6) for the irreducible projectors, we can exclude the consideration of dimensions that are sums of irreducible ones. The generic orthogonality condition can be written as
is either an irreducible dimension or a sum of such dimensions. Using the orthogonality condition (6) for the irreducible projectors, we can exclude the consideration of dimensions that are sums of irreducible ones. The generic orthogonality condition can be written as
where  Equation (11) is a system of linear equations for the indeterminates
Equation (11) is a system of linear equations for the indeterminates  with the parameters
with the parameters  . Again, using the multiplication table (2), we can write the left-hand side of (11) as a system of
. Again, using the multiplication table (2), we can write the left-hand side of (11) as a system of  bilinear forms, which we denote by
bilinear forms, which we denote by
and call orthogonality polynomials.
The core part of the algorithm is a loop on dimensions that starts with  and ends when the sum of irreducible dimensions becomes equal to
and ends when the sum of irreducible dimensions becomes equal to  .
.
The current  is processed as follows.
is processed as follows.
-
We solveFootnote 2 the system of equations

-
If the system is incompatible, then go to the next
 .
. -
If
 describes a zero-dimensional ideal, then we have
describes a zero-dimensional ideal, then we have  (including
(including  ) different
) different  -dimensional irreducible subrepresentations.
-dimensional irreducible subrepresentations. -
If the polynomial ideal has dimension
 , then we encounter an irreducible component with a multiplicity
, then we encounter an irreducible component with a multiplicity 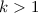 . The corresponding component of the centralizer algebra has the form
. The corresponding component of the centralizer algebra has the form  , where
, where  is an arbitrary
is an arbitrary  matrix, and
matrix, and  denotes the Kronecker product. The idempotency condition
denotes the Kronecker product. The idempotency condition  implies
implies 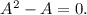 The complete family of solutions of this equationFootnote 3 is a manifold of dimension
The complete family of solutions of this equationFootnote 3 is a manifold of dimension  In this case, we select, by a somewhat arbitrary procedure,
In this case, we select, by a somewhat arbitrary procedure,  convenient mutually orthogonal representatives in the family of equivalent subrepresentations.
convenient mutually orthogonal representatives in the family of equivalent subrepresentations. -
In any case, if at the moment we have a solution
 , we append
, we append  to the list of irreducible projectors, and exclude from the further consideration the corresponding invariant subspace by adding the linear orthogonality polynomials
to the list of irreducible projectors, and exclude from the further consideration the corresponding invariant subspace by adding the linear orthogonality polynomials  to the polynomial system: $$\begin{aligned} {E\!\left( x_1,x_2,\ldots ,x_\mathrm {R}\right) \leftarrow {}E\!\left( x_1,x_2,\ldots ,x_\mathrm {R}\right) \cup \left\{ \mathcal {B}_{m}X\right\} .} \end{aligned}$$
to the polynomial system: $$\begin{aligned} {E\!\left( x_1,x_2,\ldots ,x_\mathrm {R}\right) \leftarrow {}E\!\left( x_1,x_2,\ldots ,x_\mathrm {R}\right) \cup \left\{ \mathcal {B}_{m}X\right\} .} \end{aligned}$$ -
After processing all
 ’s of dimension
’s of dimension  , go to the next
, go to the next  .
.
4 Implementation
Our approach involves some widely used methods of polynomial computer algebra. Therefore, it is reasonable, at least for the preliminary experience, to take advantage of computer algebra systems with developed tools for working with polynomials.
The complete algorithm is implemented by two procedures, the pseudocodes of which are given below.
-
1.
The procedure PreparePolynomialData is a program written in C. The input data for this program is a set of permutations of
 that generates the group
that generates the group  The program computes the basis of the centralizer ring and its multiplication table, constructs the idempotency and orthogonality polynomials, and generates the code of the procedure SplitRepresentation that processes the polynomial data. The main parameter that determines the run time for PreparePolynomialData is the dimension of the representation. The example in Sect. A.3 shows that the PC implementation copes with a dimension of about one hundred thousand in a time of about one hour.
The program computes the basis of the centralizer ring and its multiplication table, constructs the idempotency and orthogonality polynomials, and generates the code of the procedure SplitRepresentation that processes the polynomial data. The main parameter that determines the run time for PreparePolynomialData is the dimension of the representation. The example in Sect. A.3 shows that the PC implementation copes with a dimension of about one hundred thousand in a time of about one hour. -
2.
The procedure SplitRepresentation implements the above described loop on dimensions that splits the representation of the group into irreducible components. It is generated by the C program PreparePolynomialData. Currently, the code is generated in the Maple 2017.3 language, and the polynomial equations are processed by the Maple implementation of the Gröbner bases algorithms. The run time for SplitRepresentation depends mainly on the rank of the representation. Problems of rank
 take about
take about  hours on a PC.
hours on a PC.



Comments on the procedure SplitRepresentation:
-
The procedure NextRelevantDimension can be implemented in different ways, depending on the available information about the group and the representation:
-
The simplest implementation is “
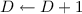 ”.
”. -
The implementation “repeat
 ” is about
” is about  faster than the simplest one. In fact, the size of the group is always known.
faster than the simplest one. In fact, the size of the group is always known. -
Knowledge of the character decomposition provides the most efficient loop on dimensions. Sometimes this information is available. Actually, computing the character decomposition is much easier than computing the decomposition of the representation.
-
-
The procedures SolveAlgebraicSystem and NumberOfFreeParameters involve the polynomial algebra functions available in the computer algebra system used. At present, we use the Maple implementation of Gröbner basis techniques.
-
The PickBestSolution procedure is applied in the case of nontrivial multiplicity of the irreducible component. It selects a particular solution in the parametric set of solutions. Currently, the choice of solutions with zero values of parameters is used. Such an oversimplified approach sometimes leads to “ugly roots” that go beyond the “natural” splitting field. This can be illustrated by the example of a
 -dimensional representation of the Held group whose decomposition into irreducible components is given in Sect. A.2. The decomposition contains a
-dimensional representation of the Held group whose decomposition into irreducible components is given in Sect. A.2. The decomposition contains a  -dimensional irreducible component of multiplicity two. Representatives of this component obtained by the simple version of PickBestSolution contain irrationality
-dimensional irreducible component of multiplicity two. Representatives of this component obtained by the simple version of PickBestSolution contain irrationality  and
and  expressions), which belongs to the quadratic field
expressions), which belongs to the quadratic field  , while the representation in question splits over the “much smaller” field
, while the representation in question splits over the “much smaller” field  . Therefore, the PickBestSolution procedure requires improvement using strategies that lead to minimal extensions of the field
. Therefore, the PickBestSolution procedure requires improvement using strategies that lead to minimal extensions of the field  .
.
4.1 Comparison with the Magma Implementation of the MeatAxe
The Magma database contains a  -dimensional permutation representation of the exceptional group of Lie type
-dimensional permutation representation of the exceptional group of Lie type  . The decomposition into irreducible components of this representation over the field
. The decomposition into irreducible components of this representation over the field  is given in [6] as an illustration of the possibilities of the MeatAxe.
is given in [6] as an illustration of the possibilities of the MeatAxe.
The application of our algorithm to this problem shows that in the characteristic zero, the considered representation is split over the field  . The calculation produces the following data:
. The calculation produces the following data:
Rank:  . Suborbit lengths:
. Suborbit lengths: 

Time C:  s. Time Maple:
s. Time Maple:  s.
s.
Magma failed to split the  -dimensional representation over the field
-dimensional representation over the field  due to memory exhaustion after long computation, but we can simulate to some extent the case of characteristic zero, using a field of a characteristic that does not divide
due to memory exhaustion after long computation, but we can simulate to some extent the case of characteristic zero, using a field of a characteristic that does not divide  . The smallest such field is
. The smallest such field is  .
.
Below is the session of the corresponding Magma V2.21-1 computation on a computer with two Intel Xeon E5410 2.33 GHz CPUs (time is given in seconds).

5 Conclusion
The algorithm described here is based on the use of methods of polynomial algebra, which are considered algorithmically difficult. However, our approach leads to a small number (in typical cases) of low-degree polynomials. Recall that the idempotency system (9) is a set of  square polynomials. Calculations of Gröbner bases in Maple on PC are limited in practice to
square polynomials. Calculations of Gröbner bases in Maple on PC are limited in practice to  . Among the
. Among the  permutation representations available in the Atlas [7],
permutation representations available in the Atlas [7],  (i.e.,
(i.e.,  ) have ranks
) have ranks  . As can be seen in Appendix A, even a straightforward implementation of the approach can cope with rather large tasks. The data presented in the appendix shows that the most restrictive parameter for the Maple part of the implementation is the rank of representations, i.e., the number of polynomial indeterminates. A possible way to improve performance is to try to develop specialized algorithms that take into account the very special type of polynomial equations that arise in the problem instead of the universal Gröbner basis methods.
. As can be seen in Appendix A, even a straightforward implementation of the approach can cope with rather large tasks. The data presented in the appendix shows that the most restrictive parameter for the Maple part of the implementation is the rank of representations, i.e., the number of polynomial indeterminates. A possible way to improve performance is to try to develop specialized algorithms that take into account the very special type of polynomial equations that arise in the problem instead of the universal Gröbner basis methods.
Notes
- 1.
A Las Vegas algorithm is a randomized algorithm, each iteration of which either produces the correct result, or reports a failure. An algorithm of this type always gives the correct answer, but the run time is indeterminate.
- 2.
The solution is always algorithmically realizable, since the problem involves only polynomial equations with abelian Galois groups.
- 3.
It is well known that any solution of the matrix equation
 can be represented as
can be represented as  where
where  is an arbitrary invertible
is an arbitrary invertible  .
.
References
Holt, D.F., Eick, B., O’Brien, E.A.: Handbook of Computational Group Theory. Chapman & Hall/CRC, Boca Raton (2005)
Parker, R.: The computer calculation of modular characters (the Meat-Axe). In: Atkinson, M.D. (ed.) Computational Group Theory, pp. 267–274. Academic Press, London (1984)
Kornyak, V.V.: Quantum models based on finite groups. J. Phys.: Conf. Ser. 965, 012023 (2018). http://stacks.iop.org/1742-6596/965/i=1/a=012023
Kornyak, V.V.: Modeling quantum behavior in the framework of permutation groups. EPJ Web Conf. 173, 01007 (2018). https://doi.org/10.1051/epjconf/201817301007
Cameron, P.J.: Permutation Groups. Cambridge University Press, Cambridge (1999)
Bosma, W., Cannon, J., Playoust, C., Steel, A.: Solving Problems with Magma. University of Sydney. http://magma.maths.usyd.edu.au/magma/pdf/examples.pdf
Wilson, R., et al.: Atlas of finite group representations. http://brauer.maths.qmul.ac.uk/Atlas/v3
Acknowledgments
I am grateful to Yu.A. Blinkov, V.P. Gerdt and R.A. Wilson for fruitful discussions and valuable advice.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
A Examples of Computations
A Examples of Computations
-
Generators of representations are taken from the section “Sporadic groups” of the Atlas [7].
-
For a group

-
 denotes the Schur multiplier, the
denotes the Schur multiplier, the  nd homology group
nd homology group  ,
, -
 denotes the outer automorphism group of
denotes the outer automorphism group of  ,
, -
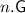 denotes a covering group of
denotes a covering group of  , a central extension of
, a central extension of  by
by 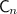 .
.
-
-
The results presented below assume the following ordering for the centralizer ring basis matrices

The matrices within the first sublist are ordered by the rule:
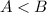 if
if 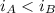 , where
, where  . The same rule is applied to the first elements of the pairs of asymmetric matrices.
. The same rule is applied to the first elements of the pairs of asymmetric matrices. -
Representations are denoted by their dimensions in bold (possibly with some signs added to distinguish different representations of the same dimension). Permutation representations are underlined. Multiple subrepresentations are underbraced in the decompositions.
-
We omit the irreducible projectors related to the trivial subrepresentation: these projectors have the standard form
 .
. -
All timing data refer to a PC with 3.30 GHz Intel Core i3 2120 CPU.
1.1 A.1 Higman–Sims Group 
Main properties:



\(\varvec{11200}\)-dimensional Representation of \(\varvec{2.HS}\)
Rank:  . Suborbit lengths:
. Suborbit lengths: 



Time C:  s. Time Maple:
s. Time Maple:  h
h  min
min  s.
s.
1.2 A.2 Held Group 
Main properties:



\(\varvec{29155}\)-dimensional Representation of \({\varvec{He}}\)
Rank:  . Suborbit lengths:
. Suborbit lengths:  .
.


Time C:  s. Time Maple:
s. Time Maple:  s.
s.
1.3 A.3 Suzuki Group 
Main properties:



\(\varvec{65520}\)-dimensional Representation of \(\varvec{2.Suz}\)
Rank:  . Suborbit lengths:
. Suborbit lengths:  .
.
Time C:  min
min  s. Time Maple:
s. Time Maple:  s.
s.
\(\varvec{98280}\)-dimensional Representation of \(\varvec{3.Suz}\)
Rank:  . Suborbit lengths:
. Suborbit lengths:  .
.

 is the basic primitive
is the basic primitive  rd root of unity.
rd root of unity.
Time C:  min
min  s. Time Maple:
s. Time Maple:  min
min  s.
s.
Rights and permissions
Copyright information
© 2018 Springer Nature Switzerland AG
About this paper
Cite this paper
Kornyak, V.V. (2018). Splitting Permutation Representations of Finite Groups by Polynomial Algebra Methods. In: Gerdt, V., Koepf, W., Seiler, W., Vorozhtsov, E. (eds) Computer Algebra in Scientific Computing. CASC 2018. Lecture Notes in Computer Science(), vol 11077. Springer, Cham. https://doi.org/10.1007/978-3-319-99639-4_21
Download citation
DOI: https://doi.org/10.1007/978-3-319-99639-4_21
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-99638-7
Online ISBN: 978-3-319-99639-4
eBook Packages: Computer ScienceComputer Science (R0)





 .
. describes a zero-dimensional ideal, then we have
describes a zero-dimensional ideal, then we have  (including
(including  ) different
) different  -dimensional irreducible subrepresentations.
-dimensional irreducible subrepresentations. , then we encounter an irreducible component with a multiplicity
, then we encounter an irreducible component with a multiplicity 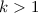 . The corresponding component of the centralizer algebra has the form
. The corresponding component of the centralizer algebra has the form  , where
, where  is an arbitrary
is an arbitrary  matrix, and
matrix, and  denotes the Kronecker product. The idempotency condition
denotes the Kronecker product. The idempotency condition  implies
implies 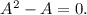 The complete family of solutions of this equation
The complete family of solutions of this equation In this case, we select, by a somewhat arbitrary procedure,
In this case, we select, by a somewhat arbitrary procedure,  convenient mutually orthogonal representatives in the family of equivalent subrepresentations.
convenient mutually orthogonal representatives in the family of equivalent subrepresentations. , we append
, we append  to the list of irreducible projectors, and exclude from the further consideration the corresponding invariant subspace by adding the linear orthogonality polynomials
to the list of irreducible projectors, and exclude from the further consideration the corresponding invariant subspace by adding the linear orthogonality polynomials  to the polynomial system:
to the polynomial system:  ’s of dimension
’s of dimension  , go to the next
, go to the next  .
. that generates the group
that generates the group  The program computes the basis of the centralizer ring and its multiplication table, constructs the idempotency and orthogonality polynomials, and generates the code of the procedure SplitRepresentation that processes the polynomial data. The main parameter that determines the run time for PreparePolynomialData is the dimension of the representation. The example in Sect.
The program computes the basis of the centralizer ring and its multiplication table, constructs the idempotency and orthogonality polynomials, and generates the code of the procedure SplitRepresentation that processes the polynomial data. The main parameter that determines the run time for PreparePolynomialData is the dimension of the representation. The example in Sect.  take about
take about  hours on a PC.
hours on a PC. ”.
”. ” is about
” is about  faster than the simplest one. In fact, the size of the group is always known.
faster than the simplest one. In fact, the size of the group is always known. -dimensional representation of the Held group whose decomposition into irreducible components is given in Sect.
-dimensional representation of the Held group whose decomposition into irreducible components is given in Sect.  -dimensional irreducible component of multiplicity two. Representatives of this component obtained by the simple version of PickBestSolution contain irrationality
-dimensional irreducible component of multiplicity two. Representatives of this component obtained by the simple version of PickBestSolution contain irrationality  and
and  expressions), which belongs to the quadratic field
expressions), which belongs to the quadratic field  , while the representation in question splits over the “much smaller” field
, while the representation in question splits over the “much smaller” field  . Therefore, the PickBestSolution procedure requires improvement using strategies that lead to minimal extensions of the field
. Therefore, the PickBestSolution procedure requires improvement using strategies that lead to minimal extensions of the field  .
. can be represented as
can be represented as  where
where  is an arbitrary invertible
is an arbitrary invertible  .
.
 denotes the Schur multiplier, the
denotes the Schur multiplier, the  nd homology group
nd homology group  ,
, denotes the outer automorphism group of
denotes the outer automorphism group of  ,
,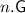 denotes a covering group of
denotes a covering group of  , a central extension of
, a central extension of  by
by 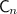 .
.
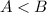 if
if 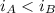 , where
, where  . The same rule is applied to the first elements of the pairs of asymmetric matrices.
. The same rule is applied to the first elements of the pairs of asymmetric matrices. .
.