Keywords

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Introduction

Synthesizing an approximate circuit from an arbitrary circuit, presumably accurate, is one of the key challenges in approximate computing. While recently many methodologies have proposed targeting approximate arithmetic building blocks (e.g., approximate adders, multipliers, and dividers) [2,3,4,5, 9], it is harder to generate approximate circuits for arbitrary circuits. Synthesis techniques in the literature operate either on gate-level [8, 11, 12, 16, 18, 19], RTL, and behavioral hardware descriptions [15], or high-level software descriptions [7].

This chapter describes our method for approximate logic synthesis using Boolean matrix factorization [17]. Non-negative matrix factorization (NNMF) factors an input matrix into two smaller matrices, such that in all three matrices all elements are non-negative [6]. The original input matrix is then approximated by matrix multiplication of the two factorized matrices. Furthermore, the non-negativity is an inherent constraint in many physical domains, such as data clustering and computer vision [21]. Recently, with advances in the applied mathematics, NNMF has been extended to Boolean matrices, where operations are performed using Boolean mathematics (GF(2)), such that multiplications are performed using logical AND, and additions are performed using logical OR (for Boolean semi-ring implementations) and logical XOR (for Boolean field implementations) [13, 14]. In our approach we first build the truth table of a given multi-input, multi-output logic circuit and then approximate its truth table using BMF. The approximate truth table is then synthesized into an approximate circuit.

In order to scale our proposed BMF-based methodology to larger circuits, we introduce a decomposition methodology, effectively breaking down a large circuit to smaller subcircuits with reduced number of inputs and outputs. Furthermore, to efficiently explore the design space, we propose an algorithm to identify an optimal sequence of approximations for different subcircuits. In addition, to better account for binary representations, rather than using the standard L 2 norm, we introduce modified quality-of-results (QoR) functions. Our proposed methodology offers a wide range of smooth trade-offs between accuracy and design metrics. In order to demonstrate the trade-offs offered by our approach, we implement and test our methodology on a wide range of error tolerant applications. Our results highlight the benefits achieved by our methodology while introducing insignificant errors in the output.

The organization of this chapter is as follows. We discuss the details of our proposed method in Sect. 7.2. In this section, we discuss our idea for using BMF for approximate logic synthesis, as well as our methodology for approximating larger circuits. We report the results of our method’s performance and the trade-offs offered in Sect. 7.3. Finally, Sect. 7.4 summarizes our conclusions as well as possible directions for future expansion.

2 BMF-Based Approximation for Arbitrary Circuits

BMF is a factorization technique where a k × m matrix M is factored into two Boolean: a k × f matrix B and an f × m matrix C, such that M ≈BC, where matrix operations are carried in Galois field of two elements, GF(2). In such domain, multiplications can be performed using logical AND, while additions are performed using logical OR (for Boolean semi-ring implementations) and logical XOR (for Boolean field implementations) [13, 14]. BMF algorithms, essentially, compress the data representation in an approximate fashion and depending on the degree of factorization [21]. In the mathematical statistical community, the factorization degree, f, determines the number of “features” that are computed [13]. The factorization degree, f, represents a trade-off between quality of factorization and storage amount.

Figure 7.1 provides an example of a 3-input, 4-output arbitrary logic circuit. First, we construct the truth table of the original circuit. We also synthesize the circuit. Here we use 65 nm libraries and Synopsys DC as the logic synthesis tool, which gives an original circuit area of 22.3 μm2. The truth table is provided as input to the BMF factorization algorithm, along with the desired factorization degree. Here we choose a factorization degree f = 2. We then factor the matrix using ASSO the BMF algorithm [13, 14] into two matrices 16 × 2 and 2 × 4. Thus, the approximate truth table has a Hamming distance of 6 from the original truth table, i.e., QoR changes only by 9.3%. The next step is to synthesize the two truth tables. The 16 × 2 truth table of the compressor circuit is used to create a 16 × 2 sum-of-product circuit with 4 inputs and 2 outputs using the established logic synthesis techniques [20]. The 2 × 4 table for the decompressor is then used to synthesize a second circuit that ORes the outputs of the SOP circuit to produce the four outputs as illustrated in Fig. 7.2. The two circuits are then given to the logic synthesis tool to produce one final circuit from both of them. In this particular example, the synthesis tool generates an approximate circuit with area of 16.2 μm2. That is, we can reduce the area by 27.3%, while compromising the QoR by only 9.3%.

Fig. 7.1
figure 1

An example of BMF-based approximations

Full size image
Fig. 7.2
figure 2

The OR-based decompressor circuit for the example of Fig. 7.1

Full size image

As demonstrated in the figure, our methodology provides a synthesis method that enables controlled trade-offs between accuracy and design costs based on the degree of approximation. Figure 7.3 illustrates our example with different factorization degrees, therefore resulting in different trade-offs. In this example and for f = 3, f = 2, and f = 1, our methodology results in approximate circuits with Hamming distance of 3, 6, and 13, respectively, and circuit areas of 19.1, 16.2, and 9.4 μm2, respectively. Figure 7.3 illustrates our example with factorization degrees f = 3, f = 2, and f = 1, which lead to approximate circuits of Hamming distance of 3, 6, and 13 respectively, with circuit areas of 19.1, 16.2, and 9.4 μm2.

Fig. 7.3
figure 3

Impact of factorization on accuracy and area

Full size image

There are two main challenges:

  1. 1.

    In typical NNMF application the index or location of the error does not bear any significance since NNMF algorithms utilize the L 2 norm as a metric for the quality of factorization. In the case of Boolean matrices, L 2 norm translates to Hamming distance. Since the binary outputs of many circuits have corresponding numerical association (e.g., 8-bit number), we need a metric for QoR with knowledge of output representation. Such QoR metrics are crucial in approximate hardware design.

  2. 2.

    As our technique introduces approximations by operating on circuit truth table, the scalability can be limited as the size of the truth table increases exponentially as a function of the number of inputs. Therefore, we need methodologies to enable the scaling of our method to larger circuits.

2.1 Circuit Factorization for Arbitrary QoR Metrics

In BMF algorithms, the objective is to minimize ||M −BC||2, which translates to Hamming distance in Boolean systems. In approximate circuit design, however, such metric does not provide a good representation of QoR in many cases. As an example, if the columns of an m-column matrix represent an m bit signal, minimizing the Hamming distance as the cost function can lead to significant errors in numerical value. For instance, a bit flip in the least significant bit will lead to a numerical error of 1, whereas a bit flip in the nth bit leads to an error of 2n−1.

To account for the bit significance, we augment existing BMF algorithms with custom QoRs enabling weighted cost functions. Specifically, we propose to define the cost function as ||(M −BC)w||2, where w is a constant weight vector, instead of ||M −BC||2 as the standard Hamming distance cost function. Here, if the numerical difference is the objective QoR, then w will be defined to introduce bit significances based on powers-of-two (e.g., 8, 4, 2, 1), therefore, giving different numerical weights for different bit positions. In our experiments, we modify the ASSO [14] algorithm as to penalize mismatches on higher bit indices more than lower significant bits. We will provide experimental results showcasing the benefits of such weighting schemes in contrast to uniform weights (Hamming distance) in Chap. 7.3.1.

2.2 Scaling Up for Large Circuits

As our methodology operates on the truth table of the input circuit, the size of the input matrix, i.e., the number of rows, grows exponentially as the number of primary inputs increases. Furthermore, BMF is a NP-hard problem, and the existing methodologies are based on heuristics [6, 13, 14]. Therefore, the applicability of our method can be limited as the complexity of the circuit increases. Therefore, we propose a circuit decomposition technique to scale the BMF algorithm for larger circuits. The overall idea of our method is to first decompose a large circuit into a number of subcircuits, such that each subcircuit has a maximum of k inputs and m outputs as illustrated in Fig. 7.4a and then each of the subcircuits is approximated as shown in Fig. 7.4b. The values for k and m are determined based on the afforded runtime of the factorization algorithm. While this approach closely resembles FPGA mapping algorithms, it is different from such algorithms as (1) such breakdowns are performed purely to reduce the computational complexity, (2) the resulting approximate circuit can be synthesized using any target FPGA or ASIC technology, and (3) in contrast to FPGA mapping, the number of outputs can be larger than one. Therefore, instead of using classical k-cut algorithms, e.g., [1], we propose to use k × m-cut algorithms (e.g., KL algorithm [10]) to break down a large circuit into subcircuits with a maximum of k inputs and maximum of m outputs.

Fig. 7.4
figure 4

Illustrated methodology for decomposing circuits

Full size image

Dividing a large circuit into smaller subcircuits of size k × m requires a change to the way we compute the QoR. More specifically, we can no longer evaluate the accuracy of a subcircuit in isolation, as errors in one component can propagate through the circuit leading to larger errors in the final outputs. Therefore, in our work instead of evaluating the QoR of a subcircuit individually, we evaluate the QoR of the entire approximate circuit, denoted by \(Cir(s_i\rightarrow T_{s_i,f_i})\), where an accurate subcircuit, s i, is substituted by its approximate version, \(T_{s_i,f_i}\), with a factorization degree of f i.

Since a large input circuit will have multiple subcircuits, the order and the degree to which the approximations are introduced to the circuit has to be carefully analyzed. We devise Algorithm 1 to gradually approximate the circuit. In our algorithm, first, the circuit is broken down into smaller subcircuits (Line 1). In the next stage (lines 3–9) and for each subcircuit, the set of potential approximate versions under various approximation degrees are profiled. Next, and starting from the accurate design, approximations are gradually added to the input design by exploring the neighbors of the current design (lines 14–22). Here, neighbors of a given subcircuit are defined as subcircuits for which the degrees of approximation only differ in one subcircuit. Here in lines 15–18, for each neighbor, first the degradations in overall QoR metrics are assessed. The subcircuit with the least degradation in QoR is then chosen to replace the current circuit for next iteration in lines 19–21. The process is repeated iteratively until the QoR gets lower than a predefined threshold.

Algorithm 1: BLASYS: Boolean level approximate circuit synthesis

3 Experimental Results

In this section we demonstrate, experimentally, the benefits achievable from using our BMF-based logic approximation (BLASYS) methodology. For our experiments we explore a broad range of applications ranging from arithmetic circuits (adder and multiplier) to more complicated datapaths. We report our results for circuits amenable for approximations, including a multiply-accumulate circuit (MAC), a butterfly network (BUT), a sum of absolute differences (SAD) circuit, and finite impulse response (FIR) circuit [16, 18]. In Table 7.1, we summarize the hardware characteristics of the evaluated accurate circuits, including the number of inputs and outputs, design area, power consumption, and critical path delay. To evaluate the design metrics, we used Synopsys design compiler with an industrial 65 nm technology library in typical processing corner.

Table 7.1 The list of benchmarks evaluated using the proposed NNMF methodology
Full size table

For all our experiments, we first decompose each circuit to a maximum of 10 × 10 (i.e., k = 10 and m = 10) subcircuits and then perform factorization. We use the ASSO algorithm for BMF [13, 14]. In addition, to evaluate the accuracy of the approximate applications, we utilize Monte Carlo simulations with one million randomly generated input test cases. In our results, the average relative error is defined as

$$\displaystyle \begin{aligned} \mbox{Average Relative Error}=\frac{1}{N}\sum_{i=1}^{N} \frac{|R_{i}-R^{\prime}_{i}|}{R_{i}}, \end{aligned} $$
(7.1)

and average absolute error as

$$\displaystyle \begin{aligned} \mbox{Average Absolute Error}=\frac{1}{N}\sum_{i=1}^{N} |R_{i}-R^{\prime}_{i}|, \end{aligned} $$
(7.2)

where N denotes the size of the test case, and R and R′ denote accurate and approximate results, respectively.

In the next subsection we report our results highlighting the impact of arbitrary QoR functions in contrast to standard, uniformly weighted L 2 metric used in Boolean matrix factorization. Then, and in the second subsection, we summarize the benefits achieved when BLASYS utilized within our applications. Here, we also compare our work against state of the art.

3.1 Impact of QoR Metric

As previously described, we utilize a BMF algorithm, ASSO in this work, with a custom weighted cost function. Specifically, as the matrix columns represent the outputs of the circuit, in many cases a bit disparity on higher significance bits should generate higher penalties compared to errors on lower indices.

Figure 7.5 shows the accuracy versus design complexity trade-offs offered for the approximate Mult8 design when comparing an off-the-shelf factorization algorithm using standard L 2 QoR with uniform bit weighting against the proposed weighted QoR. The trends in average relative error, normalized average absolute error, and the normalized Hamming distance are provided. In this plot, the solid lines denote the weighted QoR (WQoR) results, and the results for the original uniform QoR (UQoR) are shown with dashed lines.

Fig. 7.5
figure 5

Comparison of the trade-offs offered using the proposed weighted QoR vs. the original factorization algorithm

Full size image

As shown in the figure, for same circuit complexity, the proposed weighted QoR offers consistent improvements in all three accuracy metrics when compared against the uniform QoR. Therefore, for binary representations, significant benefits can be achieved by modifying the BMF algorithm to utilize a weighted QoR. In the next subsection, trade-offs offered by BLASYS are evaluated for all of our application circuits and using our heuristic design space exploration. We report the benefits in design area, power consumption, and critical path delay offered by our methodology.

3.2 Circuit Results

As described in Sect. 7.2, in order to tackle larger circuits, our technique first decomposes a circuit into smaller subcircuits with lower number of input and output ports. For all subcircuits, the possible approximate subcircuits, using different factorization degrees, are then profiled. Next, the heuristic proposed in Algorithm 1 iteratively approximates the subcircuits while assessing the impact on the QoR of the whole circuit through simulation. For design area and power, these metrics for the whole circuit are defined as the sum of design metrics of the k × m-cut subcircuits. In our experiments we chose design area as our design metric, as the summation of the subcircuits design area values better represents the total area, while the power consumption shows more variations. In addition, note that for our design space exploration, our design area model only represents the portion of the subcircuits blocks being approximated, while register files and controls paths act as an area bias and they do not affect the relative gradients.

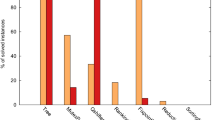
Figure 7.6 shows the trade-offs offered by our method, BLASYS, for our six benchmarks. In this figure we plot the normalized design metric as a function of average relative error, shown in black and using the bottom x axis, and average normalized absolute error, shown in red and using the top x axis. In the case of average absolute error, as the range can differ significantly based on output bit-width, we normalize the values to the highest possible output to better illustrate its significance. Note that the average absolute error is in log scale to better demonstrate the trend.

Fig. 7.6
figure 6

The trade-offs offered for each application. (a) Adder32, (b) Mult8, (c) BUT, (d) MAC, (e) SAD, and (f) FIR

Full size image

As evident from the figure, using our methodology, in all applications a wide range of fine-grains trade-offs are available. Intuitively, at each iteration, the proposed design space exploration heuristic tries to find the optimum design point, effectively the design with minimum design area, for a given degree of approximation. The degree of approximation is then incremented by one in each iteration. This insight explains the smooth trade-offs for larger circuits, whereas the characteristics of smaller circuits can change significantly in one iteration. Furthermore, in some cases, we observed an increase in the area utilization as more approximations are introduced. This phenomenon is explained by an overall increase in the total number of literals in the intermediate signals. In other words, while BLASYS compresses the outputs into f signals, these f signals can have higher complexity compared to their accurate counterparts. Our design space exploration methodology, however, can navigate through these temporary increases to find a minimal design point offering significant savings in design metrics. Based on the circuit, benefits of approximately 25–60% can be achieved for average relative errors of 20%.

Utilizing the design space exploration methodology, the results of our six evaluated applications, and for two accuracy thresholds of 5% and 25% are summarized in Table 7.2. For both error thresholds, our methodology delivers significant benefits in all design metrics, as demonstrated in the table. In our experiments and for a tight threshold of 5%, benefits of approximately 8–47% can be achieved in the case of design area, while the same benefits for a threshold of 25% range from 26 to 65%.

Table 7.2 The hardware characteristics of the approximate test cases for two accuracy thresholds, namely 5% and 25%
Full size table

4 Conclusion

In this chapter we described a new direction for approximate logic synthesis using Boolean matrix factorization. Our proposed methodology leads to a systematic approach to trade-off accuracy with circuit complexity. To scale our approach to handle large circuits, we propose a circuit decomposition method that breaks down a large circuit into smaller circuits that are amenable for BMF. Our algorithm leads to a smooth trade-off between the complexity of entire large circuits with accuracy. We also described how to incorporate different QoR metrics into the circuit factorization. Our experimental results show robust trade-off between accuracy and circuit area. Our technique is developed into BLASYS, which is a fork of the popular logic synthesis tool YOSYS, and it is available to download at http://github.com/scale-lab/BLASYS. Our approach opens many doors for investigation in logic synthesis, including improved techniques for BMF and improved k × m circuit decomposition.